Abstract
Data Analytics plays an important role in the decision making process. Insights from such pattern analysis offer vast benefits, including increased revenue, cost cutting, and improved competitive advantage. However, the hidden patterns of the frequent itemsets become more time consuming to be mined when the amount of data increases over the time. Moreover, significant memory consumption is needed in mining the hidden patterns of the frequent itemsets due to a heavy computation by the algorithm. Therefore, an efficient algorithm is required to mine the hidden patterns of the frequent itemsets within a shorter run time and with less memory consumption while the volume of data increases over the time period. This paper reviews and presents a comparison of different algorithms for Frequent Pattern Mining (FPM) so that a more efficient FPM algorithm can be developed.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
According to a global CIOs survey conducted by Gartner, data analytics has been ranked as the top technologies priority (King 2016). This is because data analytics enables the stakeholders of a company to make informed decision for their business when actionable information can be extracted from the large volume of data available in the entire organization (Chee et al. 2016). When the company stakeholders are able to make fact-based decision using the capability of data analytics, the company will have a greater likelihood of increased revenue, cost-cutting, and improved competitive advantage. To date, data analytics has been widely adopted to support the operations in many businesses or industries like healthcare (McGlothlin and Khan 2013), electricity supply (Qiu et al. 2013), manufacturing (Jesus and Bernardino 2014), railway safety management (Lira et al. 2014), financial service (Chang 2014), tourism (Rebón et al. 2015), education (Haupt et al. 2015), monitoring of quality for web services (Hasan et al. 2014), monitoring for quality-of-experience in high-density wireless network (Qaiyum et al. 2016) and even not-for-profit organizations (Oakley et al. 2015).
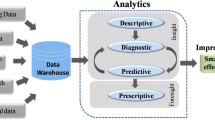
Figure 1 depicts the entire implementation process of a typical data analytics practice (Gullo 2015). First, the data is selected from its original source into the target data sets for pre-processing and transformation. Then, it is mined into significant patterns that can be interpreted or evaluated into useful knowledge. Among the various phases, data mining plays an important role in discovering significant patterns that may exist frequently in the transformed data. This is because identifying the hidden patterns of a data set enables users to make the appropriate decision and action especially in a critical situation. In the midst of diverse techniques of data mining, Frequent Pattern Mining (FPM) is one of the most important techniques because of its ability to locate the repeating relationships between different items in a data set and represent them in the form of association rules.

Reproduced with permission from (Gullo 2015)
Process of knowledge discovery in databases (KDD).
FPM issues has been extensively studied by many researchers because of its abundant applications to a range of data mining tasks like classification, clustering, and outlier analysis (Aggarwal 2014). To improve the method for classifying or clustering a set of data, and detecting the outliers or anomalies set of data, FPM plays an important role in performing many tasks for data mining. Apart from this, FPM has various applications in different domains like spatiotemporal data analysis, biological data analysis, and software bug detection (Aggarwal 2014). It is the fundamental step to identify the hidden patterns that exist frequently in a data set for generating association rules to be used in data analysis.
Many algorithms have been proposed by different researchers to enhance the technique in FPM. However, improvements are still required to be done towards the performance of the existing FPM algorithms because most of the current algorithms are not suitable for mining a huge data set with an increasingly large number of data. The two major challenges faced by most of the FPM algorithms are: lengthy run time and huge consumption of memory space in executing the algorithm to mine all the hidden frequent patterns (Jamsheela 2015). Therefore, the aim of this research is to construct an algorithm that is able to mine all the significant frequent patterns within a data set in an efficient manner while the amount of data can increase continuously from time to time. The objective of this paper is to review the advantages and disadvantages of some significant and recent FPM algorithms so that a more efficient FPM algorithm can be developed.
2 Literature review
Analyzing all the data that is collected in the data store or warehouse is definitely a necessity for every enterprise because a more proper decision can be made considering all data sets. In order to provide users with information that is more useful for data analysis and decision making, it is important to mine and identify all the significant hidden patterns that exist frequently in a data set. Therefore, this paper analyzes a number of FPM algorithms to provide an overview of the FPM state-of-the-art. The previous works done on FPM algorithms are presented in Sects. 2.1 to 2.10, while Sect. 2.11 presents a table which provides a comparison of the fundamental and significant FPM algorithms that have been proposed by other researchers.
2.1 Apriori algorithm
Apriori (Agrawal and Srikant 1994) is an algorithm that mines frequent itemsets for generating Boolean association rules. It uses an iterative level-wise search technique to discover (k + 1)-itemsets from k-itemsets. A sample of transactional data that consists of product items being purchased at different transactions is shown in Table 1. First, the database is scanned to identify all the frequent 1-itemsets by counting each of them and capturing those that satisfy the minimum support threshold. The identification of each frequent itemset requires of scanning the entire database until no more frequent k-itemsets is possible to be identified. According to Fig. 2, the minimum support threshold used is 2. Therefore, only the records that fulfill a minimum support count of 2 will be included into the next cycle of algorithm processing.

Reproduced with permission from (Han et al. 2012)
Generation of candidate itemsets and frequent itemsets.
In many cases, the Apriori algorithm reduces the size of candidate itemsets significantly and provides a good performance gain. However, it is still suffering from two critical limitations (Han et al. 2012). First, a large number of candidate itemsets may still need to be generated if the total count of a frequent k-itemsets increases. Then, the entire database is required to be scanned repeatedly and a huge set of candidate items are required to be verified using the technique of pattern matching.
2.2 FP-Growth algorithm
Frequent Pattern Growth (FP-Growth) (Han et al. 2000) is an algorithm that mines frequent itemsets without a costly candidate generation process. It implements a divide-and-conquer technique to compress the frequent items into a Frequent Pattern Tree (FP-Tree) that retains the association information of the frequent items. The FP-Tree is further divided into a set of Conditional FP-Trees for each frequent item so that they can be mined separately. An example of the FP-Tree that represents the frequent items is shown in Fig. 3.

Reproduced with permission from (Han et al. 2012)
Frequent pattern tree (FP-Tree).
The FP-Growth algorithm solves the problem of identifying long frequent patterns by searching through smaller Conditional FP-Trees repeatedly. An example of the Conditional FP-Tree associated with node I3 is shown in Fig. 4, and the details of all the Conditional FP-Trees found in Fig. 3 are shown in Table 2. The Conditional Pattern Base is a “sub-database” which consists of every prefix path in the FP-Tree that co-occurs with every frequent length-1 item. It is used to construct the Conditional FP-Tree and generate all the frequent patterns related to every frequent length-1 item. In this way, the cost of searching for the frequent patterns is substantially reduced. However, constructing the FP-Tree is time consuming if the data set is very large (Meenakshi 2015).

Reproduced with permission from (Han et al. 2012)
Conditional FP-Tree associated with Node I3.
2.3 EClaT algorithm
Equivalence Class Transformation (EClaT) (Zaki 2000) is an algorithm that mines frequent itemsets efficiently using the vertical data format as shown in Table 3. In this method of data representation, all the transactions that contain a particular itemset are grouped into the same record. First, the EClaT algorithm transforms data from the horizontal format into the vertical format by scanning the database once. The frequent (k + 1)-itemsets are generated by intersecting the transactions of the frequent k-itemsets. This process repeats until all the frequent itemsets are intersected with one another and no frequent itemsets can be found as shown in Tables 4 and 5.
For the EClaT algorithm, the database is not required to be scanned multiple times in order to identify the (k + 1)-itemsets. The database is only scanned once to transform data from the horizontal format into the vertical format. After scanning the database once, the (k + 1)-itemsets are discovered by just intersecting the k-itemsets with one another. Apart from this, the database is also not required to be scanned multiple times in order to identify the support count of every frequent itemset because the support count of every itemset is simply the total count of transactions that contain the particular itemset. However, the transactions involved in an itemset can be quite a lot, making it to take extensive memory space and processing time for intersecting the itemsets.
2.4 TreeProjection algorithm
TreeProjection (Agarwal et al. 2001) is an algorithm that mines frequent itemsets through a few different searching techniques for constructing a lexicographic tree, such as breadth-first, depth-first, or a mixture of the two. In this algorithm, the support of each frequent itemset in every transaction is counted and projected onto the lexicographic tree as a node. This greatly improves the performance of calculating the total transactions that contain a particular frequent itemset. An example of the lexicographic tree that represents the frequent items is shown in Fig. 5.

Reproduced with permission from (Agarwal et al. 2001)
Lexicographic Tree.
In the hierarchical structure of a lexicographic tree, only the subset of transactions that can probably hold the frequent itemsets will be searched by the algorithm. The search is performed by traversing the lexicographic tree with a top-down approach. Apart from the lexicographic tree, a matrix structure is used to provide a more efficient method for calculating the frequent itemsets that have very low level of support count. In this way, cache implementations can be made available efficiently for the execution of the algorithm. However, the main problem faced by this algorithm is that different representations of the lexicographic tree present different limitations in terms of efficiency at memory consumption (Aggarwal et al. 2014).
2.5 COFI algorithm
Co-Occurrence Frequent Itemset (COFI) (El-Hajj and Zaiane 2003) is an algorithm that mines frequent itemsets using a pruning method that reduces the use of memory space significantly. Its intelligent pruning method constructs relatively small trees from the FP-Tree on the fly, and it is based on a special property that is derived from the top-down approach mining technique of the algorithm. Some examples of the COFI-Trees are shown in Fig. 6.

Reproduced with permission from (El-Hajj and Zaiane 2003)
COFI-Trees.
Comparing to the FP-Growth algorithm, the COFI algorithm is better mainly in terms of memory consumption and occasionally in terms of execution runtime. This is because of the following two implementations: (1) A non-recursive method is used during the process of mining to traverse through the COFI-Trees in order to generate the entire set of frequent patterns. (2) The pruning method implemented in the algorithm has removed all the non-frequent patterns, so only frequent patterns are left in the COFI-Trees. However, if the threshold value of the minimum support is low, the performance of the algorithm degrades in a sparse database (Gupta and Garg 2011).
2.6 TM algorithm
Transaction Mapping (TM) (Song and Rajasekaran 2006) is an algorithm that mines frequent itemsets using the vertical data representation like the EClaT algorithm. In this algorithm, the transaction IDs of every itemset are transformed and mapped into a list of transaction intervals at another location. Then, intersection will be performed between the transaction intervals in a depth-first search order throughout the lexicographic tree to count the itemsets. An example of the transaction mapping technique is shown in Fig. 7.

Reproduced with permission from (Song and Rajasekaran 2006)
Example of transaction mapping.
When the value of minimum support is high, the transaction mapping technique is able to compress the transaction IDs into the continuous transaction intervals significantly. As the itemsets are compressed into a list of transaction intervals, the intersection time is greatly saved. The TM algorithm is proven to be able to gain better performance over the FP-Growth and dEClaT algorithms on data sets that contain short frequent patterns. Even though it is so, the TM algorithm is still slower in terms of processing speed compared to the FP-Growth* algorithm.
2.7 P-Mine algorithm
P-Mine (Baralis et al. 2013) is an algorithm that mines frequent itemsets using a parallel disk-based approach on a multi-core processor. It decreases the time required to produce a dense version of the data set on disk using the VLDBMine data structure. A Hybrid-Tree (HY-Tree) is used in the VLDBMine data structure to store the entire data set and other information required to support the data retrieval process. To enhance the efficiency for disk access, a pre-fetching technique has been implemented to load multiple projections of the data set into different processor cores for mining the frequent itemsets. Finally, the results are gathered from each processor core and merged in order to construct the entire frequent itemsets. The architecture of the P-Mine algorithm is shown in Fig. 8.

Reproduced with permission from (Baralis et al. 2013)
Architecture of the P-Mine Algorithm.
As the data set is represented in the VLDBMine data structure, the performance and scalability of frequent itemset mining are further improved. This is because the HY-Tree of the VLDBMine data structure enables the data to be selectively accessed in order to effectively support the data-intensive loading process with a minimized cost. Apart from this, when the process of frequent itemset mining is executed across different processor cores in parallel at the same time, the performance is optimized locally on every node. However, the algorithm can only be optimized to the maximum level when multiple cores are available in the processor.
2.8 LP-Growth algorithm
Linear Prefix Growth (LP-Growth) (Pyun et al. 2014) is an algorithm that mines frequent itemsets using arrays in a linear structure. It minimizes the information required in the data mining process by constructing a Linear Prefix Tree (LP-Tree) that is composed of arrays instead of pointers. With this implementation, the efficiency in memory usage is increased since the information of connection between different nodes is reduced significantly. A structure of the Linear Prefix Nodes (LPNs) in the LP-Tree is shown in Fig. 9. One LP-Tree is composed of multiple LPNs in a linear structure. Every set of frequent items is stored into different nodes that are composed of multiple arrays. In order to link all the arrays together, every array consists of a header in its first location to indicate its parent array. If the LPN is the first node to be inserted in the LP-Tree, the header of that LPN indicates the root of the LP-Tree.

Reproduced with permission from (Pyun et al. 2014)
Structure of linear prefix nodes (LPNs).
The LP-Growth algorithm is able to generate the LP-Tree in a faster manner compared to the FP-Growth algorithm. This is because a series of array operations are used in the LP-Growth algorithm to create multiple nodes at the same time, while the FP-Growth algorithm creates the nodes one at a time. As the nodes are saved in the form of arrays, any parent or child nodes are accessible without using any pointers while searching through the LP-Tree. In addition, it is also possible to traverse through the LP-Tree in a faster manner because the corresponding memory locations can be directly accessed when all the nodes are stored using the array structure. Apart from this, when pointers are not utilized to link up all the nodes, the memory usage for every node becomes comparatively less as well. However, the LP-Growth algorithm has a limitation in the insertion process of nodes because the items from a transaction may be saved in various LPNs (Jamsheela and Raju 2015). Therefore, to insert a transaction into the LP-Tree successfully, the memory needs to be freed continuously.
2.9 Can-Mining algorithm
Can-Mining (Hoseini et al. 2015) is an algorithm that mines frequent itemsets from a Canonical-Order Tree (Can-Tree) in an incremental manner. Similar to the FP-Growth algorithm, a header table that contains information of all the database items is used in the algorithm. The header table consists of the frequency of each item and its pointers to the first and last nodes that contain the item in the Can-Tree. In order to extract frequent patterns from the Can-Tree, a list of frequent items is required for the algorithm to perform the mining operation. The Can-Mining algorithm is able to reduce the time of mining in nested Can-Trees because only frequent items are appended into the trees in a predefined order. When the minimum support has a high threshold value, the Can-Mining algorithm is able to outperform the FP-Growth algorithm. However, if the threshold value of the minimum support is much lower, the FP-Growth algorithm is more efficient. The architecture of the Can-Mining algorithm is shown in Fig. 10.

Reproduced with permission from (Hoseini et al. 2015)
Architecture of the Can-mining algorithm.
2.10 EXTRACT algorithm
EXTRACT (Feddaoui et al. 2016) is an algorithm that mines frequent itemsets using the mathematical concept of Galois lattice. The architecture of the EXTRACT algorithm is shown in Fig. 11. It is partitioned into four functions for calculating the support count, combining the itemsets, eliminating the itemsets that are repeated, and extracting association rules from the frequent itemsets.

Reproduced with permission from (Feddaoui et al. 2016)
Architecture of the EXTRACT algorithm.
First, EXTRACT calculates the support count of each frequent 1-itemset that satisfied the minimum support. All frequent 1-itemset that did not satisfy the minimum support will be removed from the calculation. Then, it will combine the itemsets to discover all the possible combinations of frequent itemsets. After identifying them, the combinations of frequent itemsets that are redundant will be eliminated. Once all the unique frequent itemsets are mined, the association rules that satisfied the minimum confidence will be generated. All association rules that did not satisfy the minimum confidence will be removed from the rule discovery process. EXTRACT outperforms the Apriori algorithm for mining more than 300 objects and 10 attributes with an execution time that does not exceed 1200 ms. However, since the frequent itemsets that have been mined are not stored in any disk or database, the algorithm is required to be executed again in order to mine the new set of frequent itemsets if there is a change in the data set.
2.11 Classification and comparison of Frequent Pattern Mining algorithms
In general, the algorithms for Frequent Pattern Mining (FPM) can be classified into three main categories (Aggarwal et al. 2014), namely Join-Based, Tree-Based, and Pattern Growth as shown in Fig. 12. First, the Join-Based algorithms apply a bottom-up approach to identify frequent items in a data set and expand them into larger itemsets as long as those itemsets appear more than a minimum threshold value defined by the user in the database. Then, the Tree-Based algorithms use set-enumeration concepts to solve the problem of frequent itemset generation by constructing a lexicographic tree that enables the items to be mined through a variety of ways like the breadth-first or depth-first order. Finally, the Pattern Growth algorithms implement a divide-and-conquer method to partition and project databases depending on the presently identified frequent patterns and expand them into longer ones in the projected databases. The advantages and disadvantages of various significant FPM algorithms are summarized in Table 6.
Amongst the existing Pattern Growth algorithms, most of them are evolved from the FP-Growth algorithm. This is because FP-Growth generates all the frequent patterns using only two scans for the data set, representing the entire data set with a compressed tree structure, and decreases the execution time by removing the need to generate the candidate itemsets (Mittal et al. 2015). Although the existing FPM algorithms are able to mine the frequent patterns in a data set by identifying the association between different data items, a lengthy processing time and a large consumption of memory space are still the two major problems faced by FPM especially when the amount of data increases in a data set. Therefore, a more robust FPM algorithm needs to be developed for identifying the significant frequent patterns of an increasing data set that performs in a more efficient manner.
3 Result and discussion
Many experimental testings have been done by different researchers for the performance of Frequent Pattern Mining (FPM) algorithms from the aspects of execution run time and memory consumption in mining the frequent itemsets from a data set. The execution run time of some algorithms for horizontal layout data are presented in Fig. 13 and Table 7. According to the experimental results, the average execution run time for mining the frequent itemsets with an average transaction size of 15 in the horizontal layout data is 30.87 s. This shows that the time required to mine the frequent itemsets will surely rise sharply when the data increases to a larger amount.

Reproduced with permission from (Meenakshi 2015)
Runtime of different horizontal layout algorithms.
The execution run time of some algorithms for vertical layout data are presented in Fig. 14 and Table 8. For an average transaction size of 28 in the vertical layout data, an average execution run time of 34.01 s is required to mine the frequent itemsets. Similarly, this indicates that the time required to mine the frequent itemsets will also rise sharply when the data increases to a larger amount even though the data is stored in the vertical layout format.

Reproduced with permission from (Meenakshi 2015)
Runtime of different vertical layout algorithms.
The memory usage of some algorithms is presented in Fig. 15 and Table 9. According to the experimental results, an average of 37.63 megabytes (MB) of memory is required to mine the frequent itemsets with an average transaction size of 15. Likewise, this shows that the memory consumption for mining the frequent itemsets will definitely rise a lot as well when the data increases to a larger amount.

Reproduced with permission from (Meenakshi 2015)
Memory usage of existing FPM algorithms.
4 Future work
After conducting a study to compare the different algorithms for Frequent Pattern Mining (FPM), the next step of our research is to construct a more efficient FPM algorithm. The algorithm will be designed to mine the data from a data warehouse in order to identify the patterns that exist frequently and being hidden from the normal view of users. All the frequent patterns that have been mined from the data warehouse will be stored in a Frequent Pattern Database (FP-DB) using the technology of Not-Only Structure Query Language (NoSQL) (Gupta et al. 2017). The FP-DB will be updated continuously so that the hidden patterns of data can be mined within a shorter run time using less memory consumption even when the amount of data increases over the time.
5 Conclusion
The objective of this study is to review the strengths and weaknesses of the important and recent algorithms in Frequent Pattern Mining (FPM) so that a more efficient FPM algorithm can be developed. In summary, two major problems in FPM have been identified in this research. First, the hidden patterns that exist frequently in a data set become more time consuming to be mined when the amount of data increases. It causes large memory consumption as a result of heavy computation by the mining algorithm. In order to solve these problems, the next stage of the research aims to: (1) formulate an FPM algorithm that efficiently mines the hidden patterns within a shorter run time; (2) formulate the FPM algorithm to consume less memory in mining the hidden patterns; (3) evaluate the proposed FPM algorithm with some existing algorithms in order to ensure that it is able to mine an increased data set within a shorter run time with less memory consumption. By implementing the proposed FPM algorithm, users will be able to reduce the time of decision making, improve the performance and operation, and increase the profit of their organizations.
References
Agarwal RC, Aggarwal CC, Prasad VVV (2001) A tree projection algorithm for generation of frequent item sets. J Parallel Distrib Comput 61(3):350–371
Aggarwal CC (2014) An introduction to Frequent Pattern Mining. In: Aggarwal CC, Han J (eds) Frequent Pattern Mining. Springer, Basel, pp 1–14
Aggarwal CC, Bhuiyan MA, Hasan MA (2014) Frequent Pattern Mining algorithms: a survey. In: Aggarwal CC, Han J (eds) Frequent Pattern Mining. Springer, Basel, pp 19–64
Agrawal R, Srikant R (1994) Fast algorithms for mining association rules. In: Paper presented at the proceedings of the 20th international conference on very large data bases, Santiago
Baralis E, Cerquitelli T, Chiusano S, Grand A (2013) P-Mine: parallel itemset mining on large datasets. In: Paper presented at the 2013 IEEE 29th international conference on data engineering workshops (ICDEW), Brisbane
Chang V (2014) The business intelligence as a service in the cloud. Future Gener Comput Syst 37:512–534
Chee C-H, Yeoh W, Tan H-K, Ee M-S (2016) Supporting business intelligence usage: an integrated framework with automatic weighting. J Comput Inf Syst 56(4):301–312
El-Hajj M, Zaiane OR (2003) COFI-Tree mining—a new approach to pattern growth with reduced candidacy generation. In: Paper presented at the workshop on frequent itemset mining implementations (FIMI’03) in conjunction with IEEE-ICDM, Melbourne
Feddaoui I, Felhi F, Akaichi J (2016) EXTRACT: new extraction algorithm of association rules from frequent itemsets. In: Paper presented at the 2016 IEEE/ACM international conference on advances in social networks analysis and mining (ASONAM), San Francisco
Gullo F (2015) From patterns in data to knowledge discovery: what data mining can do. Phys Proc 62:18–22
Gupta B, Garg D (2011) FP-tree based algorithms analysis FPGrowth, COFI-Tree and CT-PRO. Int J Comput Sci Eng 3(7):2691–2699
Gupta A, Tyagi S, Panwar N, Sachdeva S (2017) NoSQL databases: critical analysis and comparison. In: Paper presented at the 2017 international conference on computing and communication technologies for smart nation (IC3TSN), Gurgaon
Han J, Pei J (2000) Mining frequent patterns by pattern-growth: methodology and implications. ACM SIGKDD Explor Newsl: Special issue on “Scalable Data Mining Algorithms”, 2(2): 14–20
Han J, Pei J, Yin Y (2000) Mining frequent patterns without candidate generation. ACM SIGMOD Rec 29(2):1–12
Han J, Kamber M, Pei J (2012) Data mining concepts and techniques. Elsevier, Atlanta
Hasan MH, Jaafar J, Hassan MF (2014) Monitoring web services’ quality of service: a literature review. Artif Intell Rev 42(4):835–850
Haupt R, Scholtz B, Calitz A (2015) Using business intelligence to support strategic sustainability information management. In: Paper presented at the 2015 annual research conference on South African institute of computer scientists and information technologists, Stellenbosch
Hoseini MS, Shahraki MN, Neysiani BS (2015) A new algorithm for mining frequent patterns in CanTree. In: Paper presented at the international conference on knowledge-based engineering and innovation, Tehran
Jamsheela O, Raju G (2015) Frequent itemset mining algorithms: a literature survey. In: Paper presented at the 2015 IEEE international advance computing conference (IACC), Banglore
Jesus E, Bernardino J (2014) Open source business intelligence in manufacturing. In: Paper presented at the 18th international database engineering and applications symposium, Porto
King T (2016) Gartner: BI and analytics top priority for CIOs in 2016. Retrieved from https://solutionsreview.com/business-intelligence/gartner-bi-analytics-top-priority-for-cios-in-2016/ Accessed 5 May 2017
Lira WP, Alves R, Costa JMR, Pessin G, Galvão L, Cardoso AC, de Souza CRB (2014) A visual-analytics system for railway safety management. IEEE Comput Graphics Appl 34(5):52–57
McGlothlin JP, Khan L (2013) Managing evolving code sets and integration of multiple data sources in health care analytics. In: Paper presented at the 2013 international workshop on data management and analytics for healthcare, San Francisco
Meenakshi A (2015) Survey of Frequent Pattern Mining algorithms in horizontal and vertical data layouts. Int J Adv Comput Sci Technol 4(4):48–58
Mittal A, Nagar A, Gupta K, Nahar R (2015) Comparative study of various Frequent Pattern Mining algorithms. Int J Adv Res Comput Commun Eng 4(4):550–553
Oakley RL, Iyer L, Salam AF (2015) Examining the role of business intelligence in non-profit organizations to support strategic social goals. In: Paper presented at the 48th Hawaii international conference on system sciences, Kauai
Pyun G, Yun U, Ryu KH (2014) Efficient Frequent Pattern Mining based on linear prefix tree. Knowl-Based Syst 55:125–139
Qaiyum S, Aziz IA, Jaafar J (2016) Analysis of big data and quality-of-experience in high-density wireless network. In: Paper presented at the 2016 3rd international conference on computer and information sciences (ICCOINS), Kuala Lumpur
Qiu Q, Fleeman JA, Ball DR, Rackliffe G, Hou J, Cheim L (2013) Managing critical transmission infrastructure with advanced analytics and smart sensors. In: Paper presented at the 2013 IEEE power and energy society general meeting, Vancouver
Rebón F, Ocariz G, Gerrikagoitia JK, Alzua-Sorzabal A (2015) Discovering insights within a Blue Ocean based on business intelligence. In: Paper presented at the 3rd international conference on strategic innovative marketing, Madrid
Song M, Rajasekaran S (2006) A transaction mapping algorithm for frequent itemsets mining. IEEE Trans Knowl Data Eng 18(4):472–481
Zaki MJ (2000) Scalable algorithms for association mining. IEEE Trans Knowl Data Eng 12(3):372–390
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Chee, CH., Jaafar, J., Aziz, I.A. et al. Algorithms for frequent itemset mining: a literature review. Artif Intell Rev 52, 2603–2621 (2019). https://doi.org/10.1007/s10462-018-9629-z
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10462-018-9629-z