Abstract
Support vector machines (SVMs) are a supervised classifier successfully applied in a plethora of real-life applications. However, they suffer from the important shortcomings of their high time and memory training complexities, which depend on the training set size. This issue is especially challenging nowadays, since the amount of data generated every second becomes tremendously large in many domains. This review provides an extensive survey on existing methods for selecting SVM training data from large datasets. We divide the state-of-the-art techniques into several categories. They help understand the underlying ideas behind these algorithms, which may be useful in designing new methods to deal with this important problem. The review is complemented with the discussion on the future research pathways which can make SVMs easier to exploit in practice.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Support vector machine (SVM) (Cortes and Vapnik 1995) is a supervised classifier which has been proved highly effective in solving a wide range of pattern recognition and computer vision problems (Arana-Daniel and Bayro-Corrochano 2006; Cyganek 2008; Arana-Daniel et al. 2009; Bayro-Corrochano and Arana-Daniel 2010; Cyganek et al. 2015; Li et al. 2016; Rodan et al. 2016). Nowadays, in the era of big data, the machine learning community faces new challenges concerned with applying SVMs in real-life scenarios, which result from data variety, volume, velocity, and veracity. The amount of data (of varying quality) which is being generated every day grows tremendously in the majority of scientific and engineering domains, including, among others, medical imaging, text categorization, computational biology, genomics and banking. Although it may appear quite beneficial at the first glance—more data could mean more possibilities of extracting and revealing useful underlying knowledge—training SVMs from extremely large and difficult datasets became a pivotal issue due to the high time and memory complexity of the SVM training (Liu et al. 2016; Qiu et al. 2016).
SVM training consists in determining a hyperplane to separate the training data belonging to two classes. Its position is defined with a (usually small) subset of vectors from the training set (\(\varvec{T}\)), called support vectors (SVs). Knowing which vectors are selected as SVs increases the interpretability of the SVM decisions. Though the hyperplane separates the data linearly, SVMs are applicable to non-linear problems, thanks to mapping the data into higher-dimensional spaces, in which they are linearly separable—this mapping is achieved using kernel functions. A crucial drawback of SVMs lies in their high \(O(t^3)\) time and \(O(t^2)\) memory training complexities, where \(t\) is the cardinality of \(\varvec{T}\). This problem has attracted significant attention from the researchers—developed techniques are aimed either at improving the training phase, or at extracting reduced (significantly smaller) SVM training sets from which SVs are likely to be determined. This review summarizes the achievements in this field. To the best of our knowledge, this is the first review of methods devoted to selecting the SVM training sets reported in the literature so far.
1.1 Broader context
To better contextualize this review in the literature, we highlight the main problems related to SVMs which are actively being tackled and should be inevitably resolved—they reach far beyond dealing with large datasets. These problems concern selecting the SVM hyperparameters (Sect. 1.1.1) and learning SVMs from data of questionable quality (Sect. 1.1.2). Both issues, along with selecting SVM training data from large datasets, significantly affect the applicability of the SVM classifier in practice. Addressing them successfully will help exploit this classifier in emerging big data scenarios.
1.1.1 Model selection for SVMs
Model selection for SVMs—being a problem of determining the SVM hyperparameters, including a kernel function and its parameters—is a pivotal, yet computationally expensive task (Gold and Sollich 2003; Ding et al. 2015). Automatic model selection is a crucial issue, since improperly tuned parameters can affect the SVM performance. Although there exist techniques tailored to tune pre-defined kernels (Tang et al. 2009), the research effort is put into designing algorithms which determine the desired kernels.
Friedrichs and Igel (2005) proposed the covariance matrix adaptation evolution strategy to determine a kernel from a parameterized kernel space. Their experimental study showed that this strategy easily outperforms a standard grid-search approach for selecting these hyperparameters (which is obviously not scalable for large numbers of parameters). Lessmann et al. (2006) incorporated the model selection criterion into the fitness function of their genetic technique. In the hybrid genetic algorithm (GA), the evolutionary optimization was combined with the gradient descent method (Zhou and Xu 2009). GAs were recently used for the smooth twin parametric-margin SVMs (Wang et al. 2013b). In the latest algorithm by Chou et al. (2014), the SVM parameters were optimized using a fast messy Ali and Smith-Miles (2006) explored the possibility of applying rule-based classifiers to generate SVM models. Other interesting approaches include tabu searches (Lebrun et al. 2008), compression-based techniques (Luxburg et al. 2004), and genetic-programming-based systems (Sullivan and Luke 2007). Zhang and Song (2015) noticed that various kernels may perform equally well for a certain dataset, and proposed a multi-label kernel recommendation method built on the data characteristics. An interesting model adaptation, which combines the swarm intelligence with a grid search, was proposed by Kapp et al. (2012).
To speed up the process of model selection for SVMs, a number of parallel algorithms have been proposed (Devos et al. 2014). However, their underpinning approaches are often very simple (Shi and Liu 2012; Ripepi et al. 2015). A promising research direction includes algorithms to construct new kernels tailored for a problem at hand (Lessmann et al. 2006). Such approaches include neuro-fuzzy systems which construct kernels from scratch (Simiński 2014). This algorithm was used in the preliminary research on parameter-less SVMs (Nalepa et al. 2015b). It is worth mentioning that determining the desired SVM model should be coupled with techniques for training SVMs from large datasets (especially for reducing the cardinality of SVM training sets), because the best-performing kernel may be dependent on the outcome of a training set selection algorithm. This research direction has not been exploited so far, and we believe it will significantly change in the nearest future.
1.1.2 Learning from weakly-labeled, noisy, and poor-quality data
Retrieving correctly labeled datasets is an expensive and challenging task, because it may involve repeating experiments or performing time-consuming annotation procedures (e.g., in the field of medical imaging). Therefore, learning from weakly-labeled data became an important issue. All weak-label problems are divided into several groups, based on the label characteristics. They include problems with (i) partially-known labels (most of the training set vectors are unlabeled and only some of them are labeled), (ii) implicitly-known labels (training vectors are grouped into bags for which the labels are knownFootnote 1—the labels of the training set vectors are implicit and they are based on their bag membership), and (iii) unknown labels (Li et al. 2013). Other potential issues concerned with the data quality relate to the label and/or feature noise, which can adversely impact the classifier performance. It is especially visible in practical medical applications, in which a majority of diagnostic tests are not 100% accurate, and cannot be considered a gold standard (Frenay and Verleysen 2014) (e.g., there may be discrepancies between the segmentation of the same medical image analyzed by two independent radiology experts). The consequences of the label noise on the behavior of a classifier can be very severe. First, its performance may be significantly deteriorated, the learning requirements can be easily affected (e.g., an appropriate cardinality of the training set can notably increase to compensate mislabeled or noisy data points), the final model can be much more complex than it should be, and the other algorithms (e.g., for feature selection) may be polluted as well. Frenay and Verleysen (2014) indicate that the label noise affects the observed frequencies of medical test results, hence leads to incorrect conclusions on population characteristics.
There exist three main groups of approaches for dealing with noisy sets (manual analysis should not be considered, because it is unacceptably time-consuming and infeasible for real-life data). First, there are classifiers that are said to be robust against the noise (however, the underlying nature and model of such noise is not considered in these techniques at all) (Duan and Wu 2017). Alternatively, it is possible to build a noise model (typically, it is retrieved in parallel with the learned classifier, and they are finally coupled for the higher-quality classification). Such embedded data cleansing was used for SVMs (Xu et al. 2006), also for adversarial label noise (Xiao et al. 2015). The last group encompasses algorithms which filter noisy and/or mislabeled vectors from the input set. Although it appears quite tempting (and natural), since it resembles removing outliers and anomalies from the data, it is not trivial. These filtering algorithms include various graph- and ensemble-based methods, and those which detect mislabeled vectors by analyzing their impact on the learning procedure. There are works indicating that evolutionary techniques can effectively detect and remove (or just identify) the noise (Ghoggali and Melgani 2009; Han and Chang 2013). A generic solution for learning SVMs from weak labels was introduced by Li et al. (2013)—labels are subject to the optimization. This is effective, if vectors belonging to the opposite classes form well-separated clusters in the kernel space, but this assumption may not hold in many scenarios (Cour et al. 2009; Tapaswi et al. 2015).
Handling poor quality data attracts more and more research attention nowadays (Zhu et al. 2014). It concerns not only dealing with noisy and weakly-labeled sets, but also with detecting ambiguous or duplicated data (with overlapping feature values), and outliers (Tsyurmasto et al. 2014; Kourou et al. 2015). As mentioned by Frenay and Verleysen (2014), most of the algorithms make assumptions concerning the data, and are characterized by difficult-to-tune parameters. These approaches should be validated using a larger number of real-life scenarios to find the real noise characteristics. Evolving labels can significantly improve the SVM performance for weakly-labeled sets, as shown by Kawulok and Nalepa (2015). An interesting research direction involves algorithms which evolve both labels and reduced training sets. Such methods could address the problems of training SVMs from large datasets and coping with low-quality data comprehensively.
1.2 Motivation and goals
The problem of training SVMs from large datasets is becoming increasingly important since the amount of data grows extremely rapidly (note that the term large dataset is very ambiguous in the literature—sizes of such datasets range from hundreds to millions of training vectors). There exist generic training set selection techniques [also referred to as instance selection algorithms in the literature (Olvera-López et al. 2010)], and those designed for other classifiers [k-nearest neighbors (Angiulli 2005), neural networks (Reeves and Taylor 1998), and many other (Hernandez-Leal et al. 2013; Wenyuan et al. 2013)], but—due to the specific characteristics of the SVM training process and operation—the majority of SVM training set selection algorithms are crafted for this classifier. In this review, we summarize the state-of-the-art algorithms for selecting SVM training data from large datasets.
The purpose of this review is twofold:
-
We present an extensive review of the state-of-the-art methods for selecting SVM training sets. Not only do we report these methods, but we also discuss their potential weaknesses, strengths, and ideas behind them. This will allow for better understanding (i) how to cope with massive real-life sets, and (ii) how to select an appropriate method for a problem at hand.
-
We believe that this review will notably help in developing new approaches for selecting SVM training sets. The presented taxonomy should be useful in identifying the potential pitfalls of emerging training set selection algorithms, and in determining which techniques could be successfully combined into hybrid algorithms to further boost all available knowledge concerning the \(\varvec{T}\) vectors (e.g., those methods which utilize complementary sources of information in search of valuable training vectors). The literature in this field is very diverse—we hope that this review will clearly highlight the areas which should (or should not) be further explored.
1.3 Structure of the review
Section 2 serves as a short theoretical introduction to SVMs. Section 3 begins with the proposed taxonomy to classify the methods of selecting SVM training data from large datasets. We discuss in detail techniques which help reduce the size of the SVM training sets, and highlight their most important characteristics. Section 4 concludes the review and serves as an outlook to the future work.
2 Theoretical background
Consider a set \(\varvec{T}\) of \(t\) training feature vectors \(\varvec{x}_i\in \mathbb {R}^\mathrm{\mathcal {D}}\), \(i=1,\dots ,t\), and the corresponding class labels \(y_i\in \{+1, -1\}\) (for the binary classification). Vectors with the class label \(+1\) are the positive ones (class \(\mathcal {C}_{+}\)), whereas the others belong to the negative class \(\mathcal {C}_{-}\).
2.1 Linear SVMs
Linear SVMs separate data in the \(\mathcal {D}\)-dimensional input space with the use of the decision hyperplane defined as
where \(\varvec{w}\) is the hyperplane normal vector, \(\varvec{w}\in \mathbb {R}^\mathrm{\mathcal {D}}\), and \(b/\left| \left| \varvec{w}\right| \right| \) is the perpendicular distance between the hyperplane and the origin (\(\left| \left| \cdot \right| \right| \) is the 2-norm), \(b\in \mathbb {R}\). This hyperplane is positioned such that the distance between the closest vectors of the opposite classes to the hyperplane is maximal.
For two linearly separable classes (as already mentioned, with the class labels \(y_i\in \{+1, -1\}\)), the training data must satisfy the following conditions:
which can be re-written as:
The equalities from Eq. (4) hold for the vectors positioned on two parallel hyperplanes, with the distance to the origin given as \(\left| 1-b\right| /\left| \left| \varvec{w}\right| \right| \) and \(\left| -1-b\right| /\left| \left| \varvec{w}\right| \right| \), respectively. There are no vectors between these two planes, and the distance between the separating hyperplane and each of these planes is \(1/\left| \left| \varvec{w}\right| \right| \). Hence, the maximal theoretical margin possible to generate by the decision hyperplane is
Since we intend to maximize the separating margin, the value of \(\left| \left| \varvec{w}\right| \right| =\sqrt{\varvec{w}^T\varvec{w}}\) should be minimized:
To simplify the calculations, it can be given as the quadratic term:
The optimization is performed with respect to the constraints in Eq. (4)—it becomes a quadratic programming (QP) problem. This formulation of the problem is called the primal form. The resulting hyperplane is exploited to classify the incoming data based on the decision function
where \(\varvec{a}\) is a feature vector to be classified.
If we re-write Eqs. (4) and (7) to get the Lagrangian in its primal form, we have
where \(\alpha _i\) are the Lagrange multipliers. This transformation allows for representing the constraints given in Eq. (4) as the constraints on the Lagrange multipliers. In this formulation, the data in both training and test sets will appear in the form of the dot product between the vectors (Burges 1998).
Since retrieving the SVM hyperplane is a convex optimization problem, determining the hyperplane is equivalent to finding a solution to the Karush–Kuhn–Tucker (KKT) conditions (Fletcher 2013). The KKT conditions for Eq. (9) are:
such that
Incorporating the equation for \(\varvec{w}\) from Eq. (10) into Eq. (9)
and knowing that
we have
where \(\mathcal {L}_D\) denotes the dual form of the Lagrangian. The dual problem may be solved by maximizing \(\mathcal {L}_D\) with respect to \(\alpha \), subject to the constraints given in Eqs. (11)–(13) (this is the Wolfe dual of the problem) (Burges 1998; Fletcher 2013). Only a small subset (containing \(s\) vectors) of the entire \(\varvec{T}\) (i.e., SVs) contributes to the position of the hyperplane. The Lagrange multipliers \(\alpha _i\) corresponding to the SVs are greater than zero. Finally, the decision function becomes:
In order to apply the above reasoning for non-separable cases, it is necessary to relax the constraints given in Eqs. (2) and (3), and to introduce an additional cost of this operation (Cortes and Vapnik 1995):
where \(\xi _i\) denotes a positive slack variable. The objective function should be modified to take into account the classification errors:
such that
where \(C\) is the parameter that controls the trade-off between the margin and the slack penalty (the larger the value of \(C\), the higher penalty to the errors). Considering this trade-off allows for introducing the soft-margin SVMs. As in the separable case, Eq. (21) can be easily transformed into its Wolfe’s dual form:
It is to be maximized, subject to
Finally, we have
As in the separable case, we can retrieve the Lagrangian in its primal form:
where \(\mu _i\) enforces the positivity of \(\xi _i\). The KKT conditions can be retrieved for the non-separable case following the reasoning presented for the separable one.
2.2 Non-linear SVMs
Many real-life recognition problems are not linearly solvable and require a non-linear decision function. The kernel trick was introduced to obtain a non-linear hyperplane in SVMs (Boser et al. 1992). It consists in defining a kernel function [which must satisfy the conditions presented by Mercer (1909)] that computes the inner product of two feature vectors in a derived non-linear feature space:
where \(\phi :\mathbb {R}^\mathrm{\mathcal {D}}\rightarrow \mathbb {F}\) is a mapping of a vector \(\varvec{a}\) from the input into a non-linear (possibly infinitely dimensional) feature space \(\mathbb {F}\), in which vectors are linearly separable, and \(\mathcal {K}:\mathbb {R}^\mathrm{\mathcal {D}}\times \mathbb {R}^\mathrm{\mathcal {D}}\rightarrow \mathbb {R}\). The kernel does not require calculating the \(\phi \) mapping explicitly (note that the kernel matrix which contains all of the kernel values computed between every pair of \(t\) vectors, is of a \(t\times t\) size). The non-linear decision function is
where \(\alpha _i\) is a Lagrange multiplier (Tayal et al. 2014). To determine the SVM response in a non-linear kernel space, it is not necessary to calculate the mapping \(\phi \) of any vector given the kernel function \(\mathcal {K}\).
An example of mapping a dataset from (a) a two-dimensional space into a (b) higher-dimensional one is rendered in Fig. 1. In the original input space, feature vectors belonging to two classes (visualized as red and blue dots) are not linearly separable. However, when these vectors are mapped into a three-dimensional space, then it is possible to determine a hyperplane (shown in yellow) which separates vectors, and it is used for classification.
Determining the SVM decision hyperplane is a constrained QP optimization problem—see Eqs. (21) and (22). This QP problem can be solved in \(O(t^3)\) time with \(O(t^2)\) memory, where \(t\) is the cardinality of \(\varvec{T}\), using a standard QP solver (Zeng et al. 2008b). It quickly becomes infeasible for massively large, real-life datasets. Although there exist techniques aimed at accelerating the SVM training which include—among others—decomposition-based (Joachims 1999), parallel (Li et al. 2011; Ferragut and Laska 2012) and approximation (Le et al. 2014) approaches, many of them introduce additional memory burden during the optimization (Alamdar et al. 2016). Hence, algorithms for reducing the size of SVM training sets are considered an immediate remedy to the problem of learning SVMs from large datasets. Also, the SVM classification time is linearly dependent on the number of SVs [see Eqs. (17) and (29)—only those vectors for which the Lagrange multipliers are greater than zero contribute to the decision]. Therefore, the number of SVs should be kept low to speed up the classification of incoming (unseen) vectors. The number of SVs indirectly depends on the cardinality of a training set—the smaller the number of vectors in \(\varvec{T}\), the less SVs are determined in the training process. A more extensive background information on SVMs, complemented with numerous examples and analogies which further illustrate the concepts behind SVMs are explained in an excellent tutorial by Burges (1998).
3 Selecting SVM training sets
All algorithms for dealing with training SVMs from large datasets can be divided into two main categories including techniques which (i) speed up the SVM training, and (ii) reduce the size of training sets by selecting candidate vectors (i.e., those vectors which are likely to be annotated as SVs). In the first case, existing techniques are applied to either reduce the complexity of the underlying optimization problem, or to handle the optimization process more efficiently. However, this approach still induces the problem of high memory complexity of the SVM training process which is challenging and has to be endured in big data problems (Guo and Boukir 2015; Wang and Xu 2004). The algorithms from the second category select vectors from \(\varvec{T}\) to form significantly smaller training sets—in this review, we focus on approaches for selecting SVM training sets from large datasets.
There are a number of various techniques to reduce the cardinality of a training set which may be classified into several categories, based on the underpinning optimization strategy. A high-level classification of the algorithms for selecting SVM training sets is given in Fig. 2.
This section gathers the algorithms which extract refined SVM training sets in order to reduce the computational and storage burden of the training. We divide these techniques into five main categories: (i) data geometry analysis algorithms (investigating the geometry of \(\varvec{T}\) in search of candidate vectors that should be included into the refined sets \(\varvec{T'}\)’s), (ii) neighborhood analysis methods (exploiting the statistical properties of \(\varvec{T}\) and investigating the local neighborhoods of \(\varvec{T}\) vectors), (iii) evolutionary techniques (evolving refined training sets), (iv) active learning, and (v) random sampling techniques.
3.1 Data geometry analysis methods
The following section discusses approaches which exploit the information about the training set structure to extract SV candidates (i.e., such vectors, which are likely to be selected as SVs in the training process). These vectors are then used to form refined training sets of significantly smaller sizes than the original dataset. All approaches can be divided into two groups—the first encompasses clustering-based techniques, whereas the second contains the remaining geometry-based algorithms.
3.1.1 Clustering-based methods
Clustering-based algorithms have been intensively studied for selecting refined training sets. Lyhyaoui et al. (1999) indicate their theoretical advantages: (i) clustering-based techniques can always eliminate the useless vectors from \(\varvec{T}\), (ii) they are applicable to multi-class problems, (iii) their cost objectives may be freely established for a given problem. However, these methods suffer from a difficult problem of determining a potentially large number of parameters (the clustering parameters, and the number of vectors annotated as important for each cluster are the most important parameters).
A flowchart visualizing a standard training set selection algorithm which utilizes clustering is given in Fig. 3. After setting the algorithm parameters, vectors from \(\varvec{T}\) are clustered using a given clustering techniqueFootnote 2. Then, the clusters to be further analyzed are selected (this step may be omitted for algorithms investigating all clusters, thus it is annotated with the dashed line in the flowchart), and the SV candidates are finally included in a refined set. This procedure is most often performed for each class in \(\varvec{T}\) independently.
Lyhyaoui et al. (1999) applied the frequency-sensitive competitive learning to cluster training set vectors (Scheunders and Backer 1999), with various numbers of centroids for each class. Once centroids are determined, they are further analyzed to extract the most important (critical) centroids. First, each of them is visited and the nearest opposite-class centroid is found. If two centroids (denoted as the centroids A and B) are the nearest to one another in both senses (thus when the centroid A is the closest centroid for B and vice versa), then they are put into the pool of critical centroids. Finally, the already selected critical centroids are utilized to classify the remaining ones using the 1-nearest neighbor algorithm, and the wrongly classified centroids are considered important and annotated as critical (they will most likely lay near the decision hyperplane). The authors developed four different sample selection mechanisms to extract the final vectors which are to be included in the refined training set. These approaches are based on: (i) analysis of the dispersion of the vectors, (ii) the vector’s neighborhood analysis (i.e., the nearest opposite-class vector of the one added to \(\varvec{T'}\) is added to \(\varvec{T'}\) as well), (iii) the combination of (i) and (ii), and (iv) analysis of the relations between vectors and centroids. The authors concluded that applying different selection algorithms does not drastically influence the classification score (however, the two-class training set used in the experiments was very small).
The k-means clustering has been utilized by Barros de Almeida et al. (2000) in their refined training set selection algorithm referred to as SVM-KM. In SVM-KM, k clusters (where k is a user-defined input parameter of the algorithm) are formed for the entire training set (not for vectors belonging to different classes independently). Then, the one-class clusters (i.e., those containing vectors belonging to a single class) are disregarded and only their centroids survive in a refined set, whereas all vectors from the heterogeneous clusters (containing vectors from different classes) are appended to \(\varvec{T'}\). It is worth noting that the data distribution may significantly affect the performance of SVM-KM (it is suitable for dense datasets and may misbehave for the sparse ones). Also, the value of k should be set with care, since it can easily jeopardize the algorithm behavior.
In the clustering-based SVMs (abbreviated as CB-SVMs), Yu et al. (2003) applied a hierarchical micro-clustering (Zhang et al. 1996), which scans a training set in search of valuable vectors. CB-SVM builds a micro-cluster tree (referred to as the clustering feature [CF] tree) by adding the incoming \(\varvec{T}\) vectors to clusters. It does not allow for backtracking, thus the data distribution may influence its capabilities, but the CF trees can still extract main data distribution patterns. A clustering feature (for a given cluster \(c_i\)) is given as the following triple:
where \(t_i\) denotes the number of vectors in this cluster, LS and SS are the linear and the square sums of \(t_i\) vectors in \(c_i\) given as
and
respectively. A CF tree is a height-balanced tree characterized by two parameters: the branching factor (\(b_\mathrm{CF}\)), and the threshold (\(t_\mathrm{CF}\)). Each non-leaf node encompasses at most \(b_\mathrm{CF}\) entries of the form \((\mathrm CF_j, child_j)\), where \(j=1,2,\dots ,b_\mathrm{CF}\), whereas the leaf nodes do not have children. Thus, each non-leaf node may be interpreted as a cluster composed of the subclusters represented by its children. The threshold \(t_\mathrm{CF}\) is the maximal cluster radius in any leaf node. The CF trees are built following procedures resembling those applied in the B\(+-\) trees. A noteworthy feature and the advantage of this clustering is a possibility of handling outliers and noisy vectors—those leaf entries which contain significantly smaller number of vectors than the other ones are considered as outliers.
In CB-SVM, the CF trees are constructed for both classes separately, and SVMs are trained using centroids of the root entries (there is at least one entry in the root, each entry being a cluster, therefore there is at least one centroid) of both trees. If there are too few vectors in this set, then the second level entries of the trees are included in a refined set. Then, the entries positioned near the hyperplane (so-called the low margin clusters) are de-clustered, and the child entries de-clustered from the parents are added to \(\varvec{T'}\) along with the non-de-clustered parents. Another SVM is finally trained using the centroids of \(\varvec{T'}\) entries—this process is continued until there are no entries to be de-clustered. Although the method appeared to be well-scalable for large datasets, the authors pointed out that it is currently limited to linear kernels since the hierarchical micro-clusters will not be isomorphic to high-dimensional feature spaces. Also, the algorithm parameters (\(b_\mathrm{CF}\) and \(t_\mathrm{CF}\)) should be selected with care for an analyzed dataset.
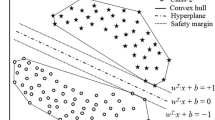
Koggalage and Halgamuge (2004) proposed a very interesting approach similar to SVM-KM—first, the k-means clustering is applied to find the initial clusters, then the crisp clusters are determined (i.e., those clusters containing one-class vectors), and finally vectors to be rejected from \(\varvec{T}\) are determined. The authors showed that some vectors from the crisp clusters may be annotated as SVs, thus they should not be automatically removed from refined sets. Therefore, for each crisp cluster, there is a safety region defined which contains its crucial vectors (positioned near the cluster border). The process of rejecting internal vectors from a crisp cluster is visualized in Fig. 4. The width of the safety region (in yellow) is determined based on the number of vectors in a cluster and the radius of the cluster, therefore it is variable for different clusters.
Wang and Xu (2004) proposed a heuristic SVM (HSVM), in which the vector similarity measure (\(s_\mathrm{HSVM}\)) is defined at first, and then vectors are grouped into \(k_\mathrm{HSVM}\) groups. The similarity function is given as
where \(\varvec{a}_i\ne \varvec{a}_j\), and \(f(x)=x\)—the larger the value of the similarity measure, the closer (geometrically) the corresponding vectors are. For each group, the average vector is found and used to remove other training vectors, if their \(s_\mathrm{HSVM}\) values (with respect to the average vector) are larger than the assumed threshold. As in other methods which exploit some pre-defined thresholds, this threshold must be selected very carefully (sensitivity to these threshold values is a disadvantage of such techniques).
In the algorithm proposed by Cervantes et al. (2008), the concept of the minimum enclosing ball (MEB) clustering has been introduced. The MEB of a given set \(S_\mathrm{MEB}\) is the smallest ball enclosing all balls and vectors in \(S_\mathrm{MEB}\). The ball is denoted as \(B(c_B,r_B)\), where \(c_B\) and \(r_B\) are the center and the radius of B. Since finding an optimal ball for a given set is very challenging, the authors proposed to use the \((1+\epsilon )\)—approximation of MEBs. After the MEB clustering, a refined set contains all the vectors from mixed-class clusters, along with centroids of one-class clusters. After the SVM training, an additional de-clustering is applied to recover other potentially valuable \(\varvec{T}\) vectors which lay near the decision hyperplane and to append them to \(\varvec{T'}\).
A similar approach (named SebSVM) was proposed by Zeng et al. (2008). Here, the convex hull vectors are selected to form refined training sets in the feature space. This is performed by solving the MEB problem in the feature space: at first, data are mapped into a higher-dimensional kernel space, and two MEBs are created (for both classes independently). Based on those MEBs, the convex hull vectors from \(\varvec{T}\) are extracted. Similar to Koggalage and Halgamuge (2004), the safety region is utilized in SebSVM to avoid removing useful vectors from \(\varvec{T'}\).
Wang and Shi (2008) proposed an algorithm for reducing the size of training sets by data structure analysis (abbreviated as SR-DSA). In their approach, the authors used the Ward-linkage clustering (Ward 1963), which enables obtaining ellipsoidal clusters. The Ward’s linkage for two clusters (\(c_1\) and \(c_2\)) is given as
where \(\varvec{\mu }_{1}\) and \(\varvec{\mu }_{2}\) are the average vectors. Initially, each vector is a separate cluster, and these clusters are subsequently merged. The value of the Ward’s linkage increases once the number of clusters is decreased during the clustering process. This may be visualized in the merge distance curve which is usually used to find the knee point (utilized to determine the desired number of clusters). After this procedure, a refined training set is elaborated—the interior vectors from each cluster are removed along with those vectors which are distant from other-class clusters based on the Mahalanobis metric. Each class is processed separately using SR-DSA. A visualization of this process is shown in Fig. 5. The main disadvantage of this method is the necessity of selecting its various parameters (the final number of clusters or the number of internal vectors removed from each cluster being the most important). These values should be investigated independently for each incoming training set.
Creating the refined set using SR-DSA: a the entire \(\varvec{T}\) (two colors indicate two classes), b vectors are grouped into clusters—the interior vectors and the exterior vectors are rejected (they are rendered in gray and black, respectively). This figure is inspired by Wang and Shi (2008). (Color figure online)
An interesting technique which combines the k-means clustering with edge detection within the entire training set has been proposed by Li et al. (2009). In this algorithm, the training set is interpreted as a color image (there are two distinct colors for binary classification denoting two classes). Relying on image processing techniques, a pixel’s neighborhood is scanned to detect strong changes of brightness and color which may correspond to edges. In the edge detection exploited by Li et al. (2009), vectors from \(\varvec{T}\) are analyzed—if at least one neighboring vector is of a different class than the investigated one (\(\varvec{a}\)), then \(\varvec{a}\) survives in \(\varvec{T'}\) (the neighboring vectors are rejected). This process is complemented with the k-means clustering which aims at finding the centroids from \(\varvec{T}\), which are also appended to the refined training set.
Chau et al. (2013) proposed the convex-concave hull analysis algorithm to select \(\varvec{T'}\) (referred to as CCHSVM). The authors pointed out that in the linearly non-separable case, convex hulls which encompass two classes in a training set will overlap thus it is necessary to “shrink” convex hulls (CHs) to avoid the overlapping. In the proposed algorithm, a CH generated for each class independently is not modified, however the concave hull is utilized to extract vectors which are closest to the exterior boundary of the CH (all vectors lie on the same side of the CH edge). Since the “closeness” to the CH may be varying across different \(\varvec{T}\) vectors, the authors search for k nearest points for the edge defined using two adjacent reference points on the CH. It is worth noting that various values of k may affect the shape of the final convex-concave hull (Lopez-Chau et al. 2012). Also, the set of CH points is a subset of the convex-concave hull which implies that the algorithm will perform well in the linearly separable cases. The authors pointed out that the method will perform well for uniformly distributed data. The distribution is usually not known beforehand, thus they perform the \(\varvec{T}\) pre-processing in which \(\varvec{T}\) is partitioned using the grid-based clustering. In the higher-dimensional cases, principal component analysis (PCA) is used to reduce the number of dimensions. Then, the convex-concave analysis is applied to data partitions, and the boundary convex-concave vectors are included in \(\varvec{T'}\). An example is presented in Fig. 6.
The analysis of convex hulls have been applied in numerous other algorithms for selecting refined training sets (also for e.g., artificial neural networks) (Wang et al. 2007). These approaches include interesting analyses of CHs exploited for the online classifier training (Khosravani et al. 2013; Wang et al. 2013a). In these techniques, SVMs are updated dynamically when new vectors arrive to the system (based on the skeleton samples—being the vertices of convex hulls—extracted either offline or online, when new vectors appear). The authors indicated that the algorithm may not be applicable in the case of noisy datasets, and they suggest to incorporate de-noising methods before the offline selection of the \(\varvec{T'}\) vectors (removing noisy vectors in the online update step still requires investigation).
In a recent redundant data reduction algorithm, Shen et al. (2016) proposed to remove unnecessary training set vectors via the analysis of cluster boundaries complemented with the investigation of other inter-cluster relations. For each cluster (k-means clustering is exploited to cluster the entire \(\varvec{T}\)), the distance density set is calculated (the distance density counts the number of vectors which fall into a circle centered in the cluster centroid and having the radius equal to the distance between the centroid and a given \(\varvec{T}\) vector). It is assumed that vectors situated near the centroid are “dense”, whereas those positioned far from the centroid are sparse. Finally, the Fisher’s discriminant analysis is utilized to find the boundary between the dense and the sparse parts of each cluster (Makris et al. 2011)—only the sparse vectors are included in \(\varvec{T'}\). A removal of the internal cluster vectors is shown in Fig. 7.
An additional technique introduced by Shen et al. (2016) concerns removing redundant clusters. The initial clusters retrieved using k-means clustering are further divided into one-class and heterogeneous clusters. The latter ones are then sub-clustered to distinguish one-class inner clusters. The authors point out that SVs will be derived from the heterogeneous clusters with a higher probability, and some \(\varvec{T}\) vectors can be safely deleted from one-class clusters. Redundant one-class clusters are removed using the max-min cluster distance algorithm, and the vectors belonging to these clusters are rejected from \(\varvec{T'}\).
Since clustering techniques may become quite time-consuming, there appeared approaches which utilize various parallel architectures (e.g., graphics processing units) in order to speed up the \(\varvec{T'}\) selection process (Yuan et al. 2015), and they were applied to real-life problems. Another important issue of these methods which needs to be addressed is a proper selection of their crucial parameters, which can easily affect refined training sets. Finally, in many cases it is still necessary to analyze the entire \(\varvec{T}\) to extract useful information.
3.1.2 Non-clustering methods
Apart from clustering-based methods, there are a number of approaches which exploit the geometrical information about a training set without grouping the data. Abe and Inoue (2001) estimate which \(\varvec{T}\) vectors are positioned near the SVM decision boundary using a classifier based on the Mahalanobis distance. This approach is especially suitable for polynomial kernel functions, since the decision boundaries are expressed by polynomials when the Mahalanobis distance (which is invariant for linear transformations of the input variables) is applied. First, the centers and the covariance matrices are found for all \(\varvec{T}\) vectors (for both classes independently). Then, for each vector, the relative difference of distances (\(r_\mathrm{MD}\)) is calculated. For a positive-class vector, it becomes
where \(\mathrm{MD}_{+}(\varvec{a})\) denotes the Mahalanobis distance between \(\varvec{a}\) and the average positive-class vector, \(\mathrm{MD}_{-}(\varvec{a})\) is the Mahalanobis distance between \(\varvec{a}\) and the average negative-class vector, and \(\eta _\mathrm{MD}\), where \(\eta _\mathrm{MD}>0\), is the parameter controlling the “nearness” to the decision boundary. If the value of \(r_\mathrm{MD}(\varvec{a})\) is negative, then \(\varvec{a}\) is misclassified and it is most likely positioned near the SVM decision hyperplane, thus should be included in a refined training set. All \(\varvec{T}\) vectors are finally sorted according to their \(r_\mathrm{MD}\) values, and \(t'_\mathrm{MD}\) ones with the lowest values are selected to form \(\varvec{T'}\) (\(t'_\mathrm{MD}/2\) are therefore retrieved for each class to avoid biasing \(\varvec{T'}\) with one-class vectors).
The lune-based \(\beta \)-skeleton algorithm for extracting useful \(\varvec{T}\) vectors was applied by Zhang and King (2002). The \(\beta \)-skeleton is a parameterized family of neighborhood graphs—let \(V_{\beta }\) denote the set of points in \(\mathbb {R}^\mathrm{\mathcal {D}}\), \(\delta _\beta (\varvec{a},\varvec{a}')\) be the distance between \(\varvec{a}\) and \(\varvec{a}'\), and \(B_\beta (\varvec{a},r_\beta )\) be the circle centered in \(\varvec{a}\) with the radius \(r_\beta \). The neighborhood \(\mathcal {N}_{(\varvec{a},\varvec{a}')}(\beta )\) is then defined for any \(\beta \), where \(1 \le \beta \le \infty \), as the intersection of two spheres:
where
and
The \(\beta \)-skeleton of \(V_{\beta }\) is a neighborhood graph with the following set of edges:
if and only if
It means that two points \(\varvec{a}\) and \(\varvec{a}'\) are connected with an edge if and only if there are no points in the set \(V_{\beta } \setminus \left\{ \varvec{a},\varvec{a}'\right\} \) which belong to the neighborhood \(\mathcal {N}_{(\varvec{a},\varvec{a}')}(\beta )\) [as defined in Eq. (36)]. Zhang and King (2002) claim that various proximity graphs (e.g., Gabriel graphs) provide geometrical information about a training set and may be effectively used to find the decision boundary. The \(\beta \)-skeleton algorithm can be therefore applied to locate potential SVs, and to reduce the size of the training set. It is worth mentioning that both Gabriel and relative neighborhood graphs may be described using the \(\beta \)-skeleton algorithm with an appropriate parameter setting (\(\beta =1\) and \(\beta =2\), respectively). Also, the authors highlighted the monotonicity feature of this parameterized family of graphs (with respect to the \(\beta \) parameter): \(V_{\beta _1}\subset V_{\beta _2}\), if \(\beta _1>\beta _2\). Although different classes of graphs may be obtained by updating the \(\beta \) parameter (e.g., for different \(\beta \), \(1\le \beta \le 2\), different nearest neighbor rules will be generated), it is unclear how to tune \(\beta \) for a new dataset (the authors exploited the trial-and-error techniques in their study). For more details on the \(\beta \)-skeleton algorithms, see the paper by Kowaluk and Majewska (2015).
Angiulli and Astorino (2010) proposed an interesting technique which utilizes the fast nearest neighbor condensation classification rule (FCNN) (Angiulli 2007). In their algorithm (abbreviated as FCNN-SVM), SVMs are coupled with the FCNN—unlike clustering-based methods, the vector selection criteria are guided by the decision boundary. The FCNN rules start with an initial refined training set composed of the centroids generated for each class independently. Then, for each vector \(\varvec{a}\) in \(\varvec{T'}\), a point belonging to the Voronoi cell (i.e., the Voronoi cell of \(\varvec{a}\) is a set of \(\varvec{T}\) vectors that are positioned closer to \(\varvec{a}\) compared with any other vector in the current \(\varvec{T'}\)) of \(\varvec{a}\), but annotated with an opposite-class label is included in a refined set. The algorithm continues until there are no more vectors from \(\varvec{T}\) to be appended to \(\varvec{T'}\). Although the algorithm is quite simple, it proved to be efficient and retrieves high-quality refined training sets.
3.2 Neighborhood analysis methods
A significant research effort has been put into proposing techniques which exploit statistical properties of the training set vectors (or their neighborhoods) in search of high-quality refined training sets. Shin and Cho (2002) proposed a k-nearest neighbors (k-NN) based pattern selection algorithm which aims at selecting correctly-labeled patterns near the SVM decision hyperplane. The authors introduced two notions: the proximity and correctness. Vectors that are close to the boundary will likely have mixed-class neighbors, and their proximity may be estimated using entropy of their k-nearest neighbors. The entropy calculated for a vector \(\varvec{a}\) for its k-nearest neighbors is
where
and \(k_i\) denotes the number of neighboring vectors belonging to the i-th class. Vectors with positive proximity (\(E>0\)) tend to lay near the hyperplane and are processed. Only the correctly labeled vectors from the set extracted in the previous step are included in \(\varvec{T'}\). The correctness is defined as the k-NN voting probability of the neighboring vectors. If this probability is larger than a threshold, then the corresponding vector survives in a refined set.
The k-NN analysis may become quite computationally intensive. The same authors improved this technique to speed up the computation (Shin and Cho 2003). The improved algorithm is based on a simple observation, that the neighbors of a vector which is positioned near the hyperplane are also situated in its vicinity. This observation has been used to reduce the search space—a significant number of \(\varvec{T}\) vectors can be pruned once some of vectors positioned near the hyperplane are found. The k value notably affects the performance of this technique, therefore it should be carefully tuned (Shin and Cho 2007).
Guo et al. (2010) exploited ensemble classifiers in their training set selection algorithm. Using a standard margin definition (Schapire et al. 1998) for the binary classification, the margin (\(\phi _M\)) of a positive-class vector \(\varvec{a}\) is given as
where \(v_{\mathcal {C}_{+}}\) denotes the number of votes (of the base classifiers) for the true class \(\mathcal {C}_{+}\), \(v_{\mathcal {C}_{-}}\) is the number of votes for the opposite class, and \(-1 \le \phi _M(\varvec{a})\le 1\). If \(\phi _M(\varvec{a})\) is positive, then it means that \(\varvec{a}\) has been correctly classified (it is annotated with an incorrect class otherwise). Also, a large value of \(\phi _M(\varvec{a})\) indicates that the majority of the base classifiers have classified this vector correctly, therefore it is most likely positioned in the center of the positive class distribution (and perhaps surrounded by the same-class vectors). On the other hand, if the value of \(\phi _M(\varvec{a})\) is large negative, then \(\varvec{a}\) is probably an outlier (or a noisy vector). Finally, if \(\phi _M(\varvec{a}) \approx 0\), then \(\varvec{a}\) is positioned near the decision boundary, since a similar number of base classifiers classified this vector to two opposite classes. Guo et al. modified the original margin concept and introduced a new one in which the information about the correct class of a sample \(\varvec{a}\) is omitted:
where \(C_1\) is the more voted class (not necessarily the correct one). Therefore, \(0 \le \phi _M'(\varvec{a}) \le 1\), and the smaller values of \(\phi _M'(\varvec{a})\) indicate that the vector is close to the hyperplane. Based on that, the authors build an ensemble classifier with all \(\varvec{T}\) vectors, calculate the margin of each vector, sort them according to the margin values and select vectors with the smallest \(\phi _M'(\varvec{a})\)’s as SV candidates to form a refined training set. The base classifiers were the classification and regression trees (Loh 2011) (bagging was used to create an ensemble). This approach is suitable also for imbalanced datasets.
A simple yet effective neighborhood analysis of each \(\varvec{T}\) vector was proposed by Wang et al. (2005). For each training vector, the largest sphere which contains only vectors of the same class is determined, and the number of vectors encompassed by this sphere is verified (\(N_{\varvec{a}}\) for each \(\varvec{a}\)). Then, all \(\varvec{T}\) vectors are sorted ascendingly according to the \(N_{\varvec{a}}\) values—\(t'/2\) vectors with the lowest \(N_{\varvec{a}}\)’s (for each class) are appended to a refined set, since vectors surrounded by the same-class vectors will most likely not be SVs and can be safely removed from \(\varvec{T'}\). The rejected \(\varvec{T}\) vectors are thus characterized by large \(N_{\varvec{a}}\) values. This approach slightly resembles the MEB-based techniques.
In a recent paper, Guo and Boukir (2015) extended their ensemble margin-based algorithm—they pointed out that classic bagging trees are not effective in the case of large training sets and the large dimensionality of the input data. They proposed to exploit more powerful ensemble methods including random forests and a very small ensemble referred to as the small votes instance selection (SVIS). In SVIS, the authors decreased the size of the classifier committee. Ensemble classifiers were utilized in other algorithms to tackle real-world problems, e.g., selecting refined training sets from biomedical data (Oh et al. 2011).
Li (2011) proposed a technique for selecting training sets for one-class SVMs, which can be adapted for two-class SVMs. In this algorithm, vectors belonging to a single class cluster are contained in a surface—this surface may consist of convex and concave shapes, and it is so “tight” that it passes through all extreme datapoints of the cluster. An example of a cluster is visualized in Fig. 8. Depending on the shape curvature, all neighboring vectors of the extreme vectors will be positioned on the same side of the tangent plane (rendered as the dotted line for the extreme points \(P_1\) and \(P_2\) in Fig. 8), or the majority of neighbors will be positioned on the same side of this plane. The authors proposed an approximation algorithm which analyzes the neighboring vectors of a given one (say \(\varvec{a}\)) in search of the normal vector of the tangent plane at \(\varvec{a}\). When all of the extreme vectors are found, they should survive in a refined set.
Li and Maguire (2011) proposed a method for selecting critical patterns from the input dataset which combines various techniques. First, the surface which passes through all extreme points and encompassing one-class vectors is created, and then the hyperplane is positioned at the tangent to this surface. The position of the vectors will depend on the curvature of the surface (if it is convex, then all vectors will appear on the same size of the plane). To deal with the overlapping patterns in the input space, the authors enhanced the algorithm with a remedy which removes the class overlap in the set. This strategy is based on the Bayes posterior probability of a vector \(\varvec{a}\) belonging to a class \(\mathcal {C}\), denoted as \(\mathcal {P}(\mathcal {C},\varvec{a})\). For two-class sets, both \(\mathcal {P}(\mathcal {C}_{+},\varvec{a})\) and \(\mathcal {P}(\mathcal {C}_{-},\varvec{a})\) are estimated. If the larger probability is obtained for the class which \(\varvec{a}\) does not belong to, then this vector is removed from the training set. Finally, any duplicated patterns from \(\varvec{T}\) are removed from the dataset during the pre-processing. The authors showed that their algorithm is competitive to four state-of-the-art techniques and is applicable to other classifiers.
In a recent paper, Cervantes et al. (2015) incorporated an induction tree to reduce the size of SVM training sets. The main idea behind the proposed technique is to train SVMs using significantly smaller refined training sets, and then to label vectors from \(\varvec{T}\) as those which are close or far from the decision hyperplane. A decision tree is utilized to identify vectors which have similar characteristics to those annotated as SVs. The initial selection of a small subset of \(\varvec{T}\) is accomplished with a very simple heuristics in which the level of dataset imbalance is investigated. The authors classify the incoming dataset (based on two pre-defined thresholds, \(\tau _{u}=0.1\) and \(\tau _{b}=0.25\), and the imbalance ratio \(\mathcal {I}\) of the dataset, given as \(\mathcal {I}=\frac{\min \left\{ t_{+},t_{-}\right\} }{t}\), where \(t_{+}\) and \(t_{-}\) denote the numbers of vectors from each class in \(\varvec{T}\)) to one out of the following classes: (i) balanced, (ii) slightly imbalanced (if \(\tau _{b}\le \mathcal {I}\le 0.5\)), (iii) moderately imbalanced (\(\tau _{u}\le \mathcal {I}<\tau _{b}\)), or (iv) highly imbalanced (\(\mathcal {I}<\tau _{u}\)). If a dataset is balanced, then the initial subset is retrieved using random sampling. Otherwise, if a dataset is slightly or moderately imbalanced, the inverse probability proportional to the dataset cardinality is applied (e.g., if \(80\%\) of vectors come from the negative class, hence \(\mathcal {I}=0.2\), then random sampling draws \(80\%\) of positive-class vectors). If a dataset is highly imbalanced, then all vectors from the less numerous class survive in \(\varvec{T'}\). Based on the decision hyperplane obtained using \(\varvec{T'}\), a decision tree is induced to model the distribution of SVs. This tree is used to retrieve those vectors which were not annotated as SVs, but follow a similar distribution—they are included in \(\varvec{T'}\).
He et al. (2011) introduced a neighborhood-based rough set model (FARNeM) to search for boundary vectors in \(\varvec{T}\). This model is used to divide the vectors into three regions: (i) the positive region, (ii) the noisy region, and (iii) the boundary region. Additionally, all input data features are partitioned into: (i) strongly relevant features, (ii) weakly relevant and indispensable features, (iii) weakly relevant and redundant features, and (iv) irrelevant ones. The authors find a feature space based on these feature groups, and then look for important \(\varvec{T}\) vectors which should be added to \(\varvec{T'}\). The aim of the feature selection algorithm is to retrieve the minimum number of attributes which characterize the input data as good as all attributes, thus it incrementally increases the subset of attributes until the dependence is not boosted. FARNeM proceeds with the analysis of training set vectors to distinguish between SV candidates (those vectors positioned in the boundary region are probable SVs), useless vectors and noisy ones based on the neighborhood rough set model. The authors use two important thresholds which affect the performance of FARNeM—they should be tuned with care since their improper selection can quite easily jeopardize the algorithm performance.
3.3 Evolutionary methods
Although evolutionary algorithms (EAs) have been shown very effective in solving a wide range of pattern recognition and optimization tasks (Pietruszkiewicz and Imada 2013; Li et al. 2007; Wrona and Pawełczyk 2013; Acampora et al. 2015; Nalepa et al. 2015a), they have not been extensively explored to select refined SVM training sets so far (Kawulok 2007). Nishida and Kurita (2008) proposed a hybrid algorithm (RANSAC–SVM) which couples random sampling, consensus approach (Fischler and Bolles 1981) and a simple evolutionary technique to retrieve \(\varvec{T'}\)’s. In their approach, several refined training sets of a small size are randomly drawn at first. Then—based on the classification scores of SVMs learned using the corresponding refined sets—the best \(\varvec{T'}\) is determined (by means of the best consensus). Additionally, the authors employed a simple GA with a multi-point crossover to further improve the refined sets (pairs of these refined sets are crossed over to form child solutions which inherit random training set vectors from both parents). The entire procedure (including random selection of SVM training sets and their evolution) is repeated multiple times, hence numerous potentially uncorrelated populations are processed.
In the genetic algorithm (GASVM) proposed by Kawulok and Nalepa (2012), a population of individuals (chromosomes), representing refined training sets of a given size, evolves in time. This evolution encompasses standard genetic operators—selection, crossover, and mutation. The fitness of each individual is the area under receiver operating characteristic curve (or the classification accuracy) retrieved for \(\varvec{T}\). Although this algorithm appeared very effective, and outperformed random sampling techniques, it was unclear how to select the size of individuals (which could not be changed later). This issue was tackled in the adaptive genetic algorithm (AGA) suggested by the same authors (Nalepa and Kawulok 2014a)—the size of individuals, along with the population size and the selection scheme, have been adapted on the fly to respond to the evolution progress as best as possible. This adaptation was steered by the parameters set a priori. Hence, improperly tuned parameter values could easily jeopardize the search (e.g., exploiting smaller refined sets and exploring larger ones could have been not balanced). The dynamically adaptive genetic algorithm (DAGA) (Kawulok and Nalepa 2014a) introduced the adaptation scheme which can be updated during the evolution, based on the characteristics of best individuals (i.e., the expected ratio of SVs within the refined sets). The expected ratio has to be determined beforehand, which is non-trivial.
Memetic algorithms (MA) combine EAs with refinement procedures to boost the solutions already found. They can exploit the knowledge attained during the evolution or extracted beforehand. Such techniques have been shown extremely effective in solving numerous challenging problems (Nalepa and Blocho 2016). Nalepa and Kawulok (2014b) proposed the first MA (termed MASVM) for selecting refined SVM training sets. The pool of important vectors (which were selected as SVs during the evolution) is maintained and used to educate the population, and to introduce super individuals—refined sets composed of SVs only. Hence, the knowledge gained dynamically is exploited in MASVM. This algorithm was utilized in the parameter-less SVMs proposed by Nalepa et al. (2015b). In the above-mentioned algorithms, initial populations were sampled randomly from \(\varvec{T}\).
In the adaptive MA (PCA\(^2\)MA), Nalepa and Kawulok (2016a, b) introduced a pre-processing step, in which the geometry of \(\varvec{T}\) is analyzed in search of potentially valuable vectors (before the evolution). This set of candidate vectors is used not only to create the initial population (it helps generate higher-quality refined sets which later undergo the evolution), but also to compensate children (if they contain less vectors than expected—in Fig. 9, the process of generating a child for a pair of chromosomes \((p_a,p_b)\), representing refined sets, is presented), and to create new chromosomes during the execution (to diversify the search). Also, the pool of SVs is used in PCA\(^2\)MA. Hence, PCA\(^2\)MA exploits the knowledge attained during the evolution, and extracted beforehand. Moreover, the parameter-less adaptation scheme was introduced, which does not require any parameters to be given a priori. The experimental study performed on various types of data revealed that EAs (especially PCA\(^2\)MA) outperform other state-of-the-art techniques, and refined sets obtained using these algorithms allow for training well-performing SVMs (with smaller numbers of SVs).
Creating a child in PCA\(^2\)MA. This figure was inspired by Nalepa and Kawulok (2016a)
Other works on EAs for this task have been reported recently. Fernandes et al. (2015) applied a multi-objective evolutionary technique in order to evolve balanced refined training sets extracted from imbalanced datasets. The objectives were to elaborate diverse and well-performing classifiers, and to combine them into the classifier ensemble. The experiments performed for several benchmark sets showed that the evolutionary approach is able to outperform other state-of-the-art techniques for dealing with large and imbalanced datasets.
Pighetti et al. (2015) enhanced a genetic evolution with the locality sensitive hashing (to find the nearest vector in \(\varvec{T}\) for any generated vector during the optimization) (Gorisse et al. 2010), and used it for tackling multi-class classification problems (one-versus-all strategy was exploited). Although the approach is promising, it is unclear when to stop the optimization for multi-class tasks (the authors terminated the evolution once 60 vectors from each category have been retrieved).
Verbiest et al. (2016) recently investigated the performance of different evolutionary techniques for selection of SVM training sets: (i) a standard genetic algorithm, (ii) the adaptive genetic algorithm, which dynamically updates the crossover threshold [only notably different parents can be crossed over (Eshelman 1991)], and (iii) the steady state genetic algorithm [two parents are selected to generate offspring (Cano et al. 2003)]. Interestingly, the fitness involved not only the classification accuracy of the SVM classifier, but also the reduction ratio, indicating how much the input \(\varvec{T}\) has been shrunk. These wrapper techniques were initially used for the k-NN classification, and the extensive experimental study clearly proved that they can be easily tailored for SVMs as well.
In their recent paper, Kawulok and Nalepa (2015) showed that evolving both training vectors and labels can be effectively used to handle learning SVMs from weakly-labeled training sets. In their memetic approach, the best individual in a population is an expert, and it is used in the tuition operation. The training set is relabeled if necessary, and the other individuals are refined (the vectors which changed the label during the tuition are replaced). Albeit the algorithm performed very well for mislabeled datasets, its performance deteriorated for correctly labeled \(\varvec{T}\)’s—this issue requires further investigation.
An interesting alternating genetic algorithm (abbreviated as ALGA) for optimizing the SVM model alongside SVM training sets has been proposed by Kawulok et al. (2017). The authors observed that different SVM models (i.e., kernel functions and their hyper-parameter values) may be optimal for different training sets. In ALGA, two independent populations (one representing refined training sets, and the other the SVM models) are alternately evolved to solve two optimization problems having a common fitness function (classification accuracy over the validation set obtained using an SVM trained with the best refined training set and kernel function). The alternating process continues as long as at least one of these two subsequent optimization phases manages to improve the average population fitness. The experiments performed for both artificially generated and benchmark datasets revealed that ALGA can effectively select an SVM training set without the necessity to tune the SVM hyper-parameters beforehand. Although the authors focused on the radial-basis function (RBF) kernel, this method can be easily tailored to any other kernel function. An interesting research direction would be to enhance ALGA with an additional step of selecting features for high-dimensional datasets.
3.4 Active learning methods
In active learning models, vectors are initially not labeled, and the goal of an active learner is to infer a predictor of labels from the input data. It is accomplished in an interactive manner, in which the learner may request a label of a particular vector (this operation is associated with an appropriate cost). Hence, active learning may be interpreted as the process of obtaining labels for unlabeled data, and it can be applied for the entirely unlabeled datasets, as well as for those sets which encompass vectors with missing labels.
An active learning technique for selecting refined sets was proposed by Schohn and Cohn (2000)—they utilized a computationally efficient heuristics to label vectors lying near the SVM decision hyperplane. The authors exploit the selective sampling approach (being a form of active learning), in which learners are presented with a large unlabeled dataset, and are given the opportunity of labeling these vectors themselves (labeling of each vector “costs” some artificial fee). The learners attempt to minimize the error on the data which will appear in the system in the future. In the heuristic algorithm suggested by Schohn and Cohn (2000), one active learning criterion is to search for vectors which are orthogonal to the space spanned by the current refined training set. Additionally, the information about the already known data dimensions is boosted by narrowing the existing margin—only those vectors which are close to the decision hyperplane are effectively retrieved.
SVMs enhanced with active learning algorithms have been successfully applied in many real-life applications (Tong and Koller 2002). Tong and Chang (2001) exploited such techniques in their system to conduct effective relevance feedbackFootnote 3 for image retrieval, and proposed the pool-based active learning approach. A pool contains unlabeled \(\varvec{T}\) vectors which are analyzed and appended to \(\varvec{T'}\) if necessary. The classifier is trained using a labeled set (if it is the first feedback round, then the user is asked to label a number of randomly drawn vectors; otherwise, the user labels some pool images which are the closest to the decision boundary).
3.5 Random sampling methods
In random sampling techniques for selecting refined SVM training sets, the \(\varvec{T}\) vectors are drawn randomly, and—based on additional heuristics—are appended to \(\varvec{T'}\)’s or not. The simplicity of such methods makes them straightforward to implement and becomes their biggest advantage in practical scenarios. Also, they appear sufficient in a number of real-life circumstances (when the size of the desired refined sets can be estimated), and they are not dependent on the cardinality of \(\varvec{T}\). However, they can easily misbehave for very large and noisy datasets, since removing mislabeled vectors from \(\varvec{T'}\)’s (affecting the SVM performance) is often quite time-consuming (Nalepa and Kawulok 2016a).
A simple approach to reduce \(t\) is to sample \(t'\) vectors from \(\varvec{T}\) randomly (Balcázar et al. 2001). In this sampling algorithm, a random subset of \(\varvec{T}\) is drawn according to the weights assigned to the training set vectorsFootnote 4 (the higher the weight, the larger the probability of including the corresponding vector in \(\varvec{T'}\)). Then, an SVM classifier is trained using this subset, and \(\varvec{T}\) is analyzed to verify which vectors were correctly classified using the resulting decision hyperplane. The weights of those vectors which were misclassified are doubled so that they are more likely to be selected and included in \(\varvec{T'}\) in the next sampling round. If the number of rounds is sufficiently large, then the important vectors (hopefully including SVs) will have higher weights than the other vectors, and a refined set will be composed of these SVs. The “optimal” size of \(\varvec{T'}\) is not known beforehand, thus the number of sampled vectors should be determined carefully (usually in a time-consuming trial-and-error fashion). This becomes a significant drawback of this algorithm especially in the case of massively large datasets. Also, random sampling approaches may ignore important (and useful) relations which occur within the dataset—if these training set features were exploited during the execution, the convergence time of such techniques could be greatly reduced (e.g., only the vectors lying near the boundary of one-class vector groups could be sampled because they would likely influence the position of the SVM hyperplane).
3.6 Summary of the SVM training set reduction methods
Table 3 summarizes the algorithms for reducing the size of the SVM training sets. They have been split into several categories, based on the optimization strategies. Additionally, we report the most important characteristics of the approaches discussed at length in the previous sections. These features include:
-
Type—indicates whether the method is one-pass or iterative. In the iterative approaches, the initial refined training set is gradually improved in order to include better vectors from \(\varvec{T}\). Such methods encompass algorithms which (i) keep enhancing the refined sets of a given (constant) size, and those which (ii) decrease or (iii) increase refined sets to boost their quality.
-
Source—being the underlying source of information concerning a training set. The knowledge extracted from this source is then used for generating refined sets during the optimization process. We distinguish five possible sources of information which can be utilized for this purpose—they are summarized in Table 1. Note that there exist methods which exploit several sources of information.
-
Randomized—shows whether the algorithm is randomized or deterministic.
-
Dependent on\(t\)—shows whether the algorithm is dependent on the cardinality of \(\varvec{T}\). If so, it may require analyzing the entire training set which is often not possible in massively large real-life datasets. Hence, the techniques which are independent from \(t\) should be preferred in practical applications.
-
Data—indicates which types of datasets were used to validate the corresponding algorithm (A—artificially generated, B—benchmark, R—real-life datasets).
-
Maximum\(t\)—indicates (roughly) the maximum size of the dataset for which the method was tested in the referenced paper. As mentioned in Sect. 1, the term large dataset is quite ambiguous in the literature (the cardinality of large sets may vary from hundreds to millions of \(\varvec{T}\) vectors).
3.7 Assessing SVM training set selection algorithms
Assessing the quality of emerging SVM training set selection algorithms is a difficult and multi-fold task. These techniques can be investigated both quantitatively and qualitatively (e.g., by visualizing the extracted refined sets together with SVs and verifying whether they form any specific geometrical patterns). In this section, we discuss the quantitative measures which are used to assess new and existing training set selection algorithms alongside the standard experimental setup and datasets (together with their characteristics) that are usually adopted in the experiments. Finally, we present several practical applications in which various algorithms for selecting refined SVM training sets have been utilized.
3.7.1 Quantitative measures
The following quantitative measures have been widely adopted in the literature to assess the performance of new training set selection techniques—for each measure we indicate whether its value is to be maximized (\(\uparrow \)) or minimized (\(\downarrow \)):
-
Classification performance of an SVM trained using a refined set (\(\uparrow \)) The performance of classifiers (including SVMs) is assessed based on ratios derived from the number of (a) correctly classified positive-class vectors—true positives (TP), (b) correctly classified negative-class vectors—true negatives (TN), (c) incorrectly classified negative-class vectors—false positives (FP), and (d) incorrectly classified positive-class vectors—false negatives (FN) obtained for a test set which was not used during the training (see Table 2). Utilizing the unseen dataset allows for verifying the generalization capabilities of a classifier.
The derived ratios include, among others, the true positive rate:
$$\begin{aligned} \mathrm{TPR}=\frac{\mathrm{TP}}{\mathrm{TP+FN}} \end{aligned}$$(45)and the false positive rate:
$$\begin{aligned} \mathrm{FPR}=\frac{\mathrm{FP}}{\mathrm{FP+TN}.} \end{aligned}$$(46)TPR and FPR are often presented in a form of receiver operating characteristic (ROC) curves (Fawcett 2006). Each point in this curve is the performance of an SVM for a given decision threshold (Yu et al. 2015). Calculating the area under this curve (AUC) reduces a ROC curve into a single scalar value representing the classifier performance (the higher the AUC values, the better, and \(0\le \mathrm{AUC} \le 1\)). The area under the ROC curve and the accuracy (ACC):
$$\begin{aligned} \mathrm{ACC}=\frac{\mathrm{TP}+\mathrm{TN}}{\mathrm{TP}+\mathrm{TN}+\mathrm{FP}+\mathrm{FN}} \end{aligned}$$(47)are the most widely used measures exploited to quantify the performance of training set selection algorithms (the classification performance of an SVM trained using a refined set should be maximized). Other common measures include precision, recall and the F-measure (Khosravani et al. 2013).
-
Size of the refined training set (\(\downarrow \)) The main objective of training set selection algorithms is to minimize the cardinality of the training set (ideally without decaying the SVM classification performance). Hence, the number of vectors in the refined sets elaborated using such approaches is almost always investigated. To make this measure easier to interpret for datasets of different sizes, it is very often presented as the reduction rate (\(\mathcal {R}\)):
$$\begin{aligned} \mathcal {R}=\frac{t}{t'}, \end{aligned}$$(48)where \(t'\) is the cardinality of the refined training set, and \(t\) is the size of the original dataset. This reduction rate should be maximized.
-
The number of support vectors (\(\downarrow \)) As already mentioned, the number of SVs influences (linearly) the SVM classification time. Therefore, it should be minimized to speed up the operation of a trained classifier.
-
The percentage of vectors in a refined training set selected as support vectors (\(\uparrow \) Determining the desired cardinality of refined sets is often a critical step in training set selection algorithms. Such refined sets should be small and should include important vectors which are likely to be selected as SVs during the SVM training. In several works, the percentage of vectors in refined training sets selected as SVs has been investigated (Nalepa and Kawulok 2016a; Verbiest et al. 2016). This percentage should be maximized to keep the number of “useless” vectors in a refined set as small as possible. However, this measure can easily become misleading—selecting all training set vectors as SVs can be a sign of overfitting and lack of generalization capabilities.
-
Training set selection, SVM training and classification times (\(\downarrow \)) In all state-of-the-art approaches, the execution time of a training set selection algorithm should be minimized. Also, the SVM training and classification times are to be minimized (these times are correlated with the size of a refined training set and the number of determined SVs).
-
Combined quality measure (\(\uparrow \)) Although the above-mentioned measures are usually investigated separately, this approach becomes infeasible in several practical scenarios, e.g., in real-time systems in which a trained SVM should work extremely fast even if it delivers slightly worse results (i.e., minimizing the number of SVs may be more important than maximizing the classification accuracy). In such cases, the problem of selecting SVM training sets can be considered as a two- (or multi-) objective optimization problem: the first objective is to maximize the classification accuracy of an SVM trained with a refined set, and the second is to minimize the number of SVs. Nalepa (2016) transformed these two objectives into a single quality function
$$\begin{aligned} Q(\mathrm{AUC},s)=q \cdot \frac{\mathrm{AUC}}{\mathrm{AUC}^\mathrm{B}} + (1 - q) \cdot \frac{s^\mathrm{B}}{s}, \end{aligned}$$(49)where \(\mathrm{AUC}^\mathrm{B}\) denotes the best (the largest) AUC obtained for the test set (note that AUC can be replaced by any other classification performance measure in this formula), \(s^\mathrm{B}\) is the best (the lowest) number of determined SVs across the investigated training set selection algorithms, and q denotes the importance of the first objective (\(0 < q \le 1\)). The largest Q value is retrieved for the best training set selection algorithm.
3.7.2 Standard experimental setup
In a standard experimental setup, each new training set selection algorithm is compared with (i) a number of existing selection techniques, and (ii) SVMs trained using the entire training set (it may be impossible for extremely large datasets). Randomized approaches (see Table 3) are often executed multiple times (usually at least \(30\times \)) and then the quantitative results are averaged. To deeply investigate the generalization abilities of the algorithms, the experiments are almost always performed following the k-fold cross-validation strategy (a dataset is divided into a training and a test set k times without any overlaps—a training set includes \((k-1)\) data chunks, whereas a test set only one chunk; then, the results obtained for each fold are averaged). The experiments are divided into two groups:
-
Sensitivity analysis The impact of the most important components of a new algorithm on its overall performance is verified in the sensitivity analysis. Usually, one (or more) components are enabled (the other components are disabled), and the experiments are repeated for each configuration.
-
Comparison with other training set selection algorithms and SVMs trained using the entire set The comparison with the state of the art is always crucial for new training set selection algorithms. Also, they are commonly compared qualitatively and quantitatively (using the measures discussed in the previous section) with SVMs trained using the entire set—without any training set selection applied (however, it may be impossible due to the cardinality of this set) and other techniques from the literature (very often from different categories).
Since the number of algorithms that are being compared is usually large and each of them can perform differently for different datasets, executing appropriate (non-parametric) statistical tests to investigate the statistical importance of the obtained results became a standard procedure in the machine learning field. A standard null hypothesis saying that applying the algorithm A leads to obtaining the results of the same quality as those elaborated by the algorithm B is often verified with the two-tailed Wilcoxon signed-rank tests (Woolson 2007) (Shin and Cho (2007) exploited the McNemar’s test for this purpose). In experiments encompassing multiple datasets, the Friedman test is executed to check which algorithm outperforms other techniques taking into account all investigated datasets (Friedman 1937).
3.7.3 Datasets and practical applications
The effectiveness of emerging training set selection algorithms is commonly tested using three kinds of datasets:
-
Artificially generated datasets Vectors in artificial datasets are usually generated to follow a known distribution (e.g., the Gaussian distribution). Therefore, the underlying data characteristics are known (which is not always achievable in the case of benchmark and real-life sets). Additionally, artificially generated sets are often straight-forward to visualize. Such datasets are used to understand the behavior of new training set selection algorithms (e.g., whether the vectors in the refined sets are positioned near the decision hyperplane or whether there are any vectors that could be removed from the refined sets as they are not selected as SVs). Several artificially generated datasets are available at http://sun.aei.polsl.pl/~jnalepa/SVM/ (see example datasets in Fig. 10—white and black pixels visualize vectors from the positive \(\varvec{T}_{+}\) and negative \(\varvec{T}_{-}\) classes; training set vectors are grouped into clusters in the \(\alpha \) versions of these 2D sets).
-
Benchmark datasets Such datasets (of different characteristics) are exploited to compare the performance of training set selection algorithms (benchmark sets were used in more than \(70\%\) of papers presented in this review). These datasets can be downloaded from the following repositories:
-
UC Irvine (UCI) machine learning repositoryhttps://archive.ics.uci.edu/ml/index.phpFootnote 5.
-
Knowledge Extraction based on Evolutionary Learning (KEEL) repository: http://www.keel.es/.
-
LibSVM repository: https://www.csie.ntu.edu.tw/~cjlin/libsvmtools/datasets/.
In Table 4, we gather the characteristics of ten most frequently used (in the analyzed papers) benchmark sets alongside the repository name (the same dataset can be often downloaded from more than one repository). For multi-class sets (e.g., Yeast), pairwise coupling is performed—the multi-class classification problem is decomposed into two-class problems and the majority voting principle is used (a number of binary SVMs vote for the final class label for an incoming vector). Although the sizes of these benchmark datasets are not very large, they are widely used in the literature to compare training set selection algorithms (also thanks to a well-defined experimental protocol which is often presented at a repository website—it makes the comparisons much easier).
-
-
Practical applications and real-life datasets Although the amount of generated data is steadily growing nowadays and the size of training sets became a real obstacle in exploiting SVMs in practice, only less than \(45\%\) of all investigated training set selection algorithms were tested using real-life datasets.Footnote 6 The most interesting practical scenarios in which training set selection algorithms have been tested and utilized include:
-
Hand-written digits classification In several works (Shin and Cho 2003, 2007; Nishida and Kurita 2008), the authors tackled the multi-class hand-written digits classification problem and exploited the MNIST dataset (http://yann.lecun.com/exdb/mnist/). They applied SVM training set selection algorithms to retrieve useful data from \(6\times 10^5\) training images (hand-written digits belonging to 10 classes, see Fig. 11). Important applications of the automated analysis of the digitalized hand-written text include bank check processing, postal address identification, analysis of historical documents or biometric authentication.
-
Skin detection and segmentation Detecting pixels representing human skin in color images (which is a preliminary step of the skin region segmentation process whose aim is to determine the boundaries of skin regions) is a difficult and important pattern recognition task. Its applications include content filtering, hand and face detection and tracking, human-computer interaction and many more (Kawulok et al. 2014). Kawulok and Nalepa (2012) generated the Skin dataset of skin and non-skin pixels (in the YC\(_{b}\)C\(_{r}\) color space; \(4\times 10^6\) pixels in total)—they exploited images from the ECU face and skin detection database elaborated by Phung et al. (2005) (see example images in Fig. 12—note that skin pixels expose different color and intensity characteristics), and used this set to test their several SVM training set selection algorithms (Nalepa and Kawulok 2014a, b, 2016a; Kawulok and Nalepa 2014a; Nalepa 2016).
-
Hand pose estimation Kawulok and Nalepa (2014b) applied SVMs to recognize hand poses based on the shape context descriptors (Belongie et al. 2002). In their approach, vectors of differences between two hand shapes are classified to determine whether they represent the same pose (hence, the class decision is indirect). The authors showed that training sets can become very large even for a relatively small number of gestures (i.e., for n gestures, \(\frac{n!}{2\cdot (n-2)!}\) feature vectors are obtained). To make SVMs applicable in this scenario, a genetic technique was utilized for selecting refined SVM training sets (Kawulok and Nalepa 2012).
-
Face detection Kawulok (2007) and Wang et al. (2013a) verified their SVM training set selection algorithms in the face detection problem—Wang et al. (2013a) exploited a dataset with almost 3500 images, whereas Kawulok (2007) used 1000 images from the famous Feret database presented by Phillips et al. (1998). Face detection is a pattern recognition task aimed at determining whether or not an input image contains a human face. Face detection algorithms are being exploited in surveillance systems, human–computer interaction and entertainment applications, human gait characterization, gender classification and many more (Paul and Haque 2013).
-
Detection of deceptive facial expressions Facial image analysis is an active topic—new research directions focus on facial dynamics recognition and understanding for deception detection, behavioral analysis and diagnosis of psychological disorders. Kawulok et al. (2016) used fast smile intensity detectors to elaborate textural facial features that are fed into the SVM classification pipeline to distinguish between posed and spontaneous expressions in video sequences from the UvA-NEMO database containing 1240 sequences, including 643 posed and 597 spontaneous smiles (Dibeklioğlu et al. 2012)—see examples in Fig. 13. Since these features are extracted for each frame (also those which are neutral, without any features exposing the smile characteristics), SVM training sets may become very large and often contain “useless” vectors. To deal with these issues, the authors utilized their memetic training set selection algorithm (Nalepa and Kawulok 2016a).
-
Image retrieval Tong and Chang (2001) showed that their SVM active learning training set selection algorithm can be successfully applied for image retrieval. It selects the most informative images to effectively query a user and quickly learn the decision hyperplane which should separate unlabeled \(\varvec{T}\) images to satisfy the user’s query. With the use of real-life datasets (encompassing up to 2000 images collected from the Internet), the authors proved their technique to be outperforming other state-of-the-art image retrieval approaches. Such image retrieval techniques are commonly applied in the textiles industry, nudity-detection filtering engines, picture and art archives, and even medical diagnosis (Trojacanec et al. 2009).
-
Biomedical applications Selecting appropriate training sets is an important problem in biomedical applications since the data quality and volume are big issues in this field. The following points summarize the most interesting biomedical applications in which SVM training set selection algorithms have been tested and utilized.
-
RNA classification SVMs have been successfully applied to detect non-coding RNAs (ncRNAs) in sequenced genomes (Uzilov et al. 2006). However, RNA datasets are very large which affects the SVM training. Cervantes et al. (2008) exploited their clustering-based training set selection algorithm for two RNA datasets (the first one included almost \(5\times 10^5\) vectors with 8 features, and the second—\(2\times 10^3\) vectors with 84 features) and showed that is it quite competitive with the state of the art for such large-scale data. Wang et al. (2013a) tested their training set selection algorithm on an interesting problem of deciding whether the incoming vector represents RNA of cod fish (the entire training set encompassed more than \(3\times 10^5\) vectors with 8 features).
-
Diseases classification (e.g., leukemia, diabetes, Parkinson’s disease, hepatitis) There are a bunch of approaches that have been tested on various disease classification tasks. In a standard medical image analysis scenario, the cardinality of a training set is not very large, but such datasets are highly imbalanced (usually, there are much more healthy examples compared with the pathological ones). Therefore, applying an appropriate approach for selecting desired training sets is inevitable. Oh et al. (2011) investigated their SVM training set selection using such imbalanced sets for various diseases (leukemia, diabetes, Parkinson’s disease, hepatitis, breast cancer and cardiac diseases). These datasets included up to 800 vectors (Diabetes dataset), and the number of features was up to almost 7200 in the Leukemia dataset.
-
-
Network intrusion detection Yu et al. (2003) focused on an important network intrusion detection problem. Its aim is to build a classifier which is able to distinguish between “bad” connections (intrusions and/or attacks) and normal connections. To test their approaches, the authors exploited a dataset containing a variety of intrusions simulated in a military network environment (42 features, \(4\times 10^6\) vectors). This dataset is available at http://kdd.ics.uci.edu/databases/kddcup99/kddcup99.html, and it was used as a benchmark at the Third International Knowledge Discovery and Data Mining Tools Competition, which was held in conjunction with The Fifth International Conference on Knowledge Discovery and Data Mining (KDD-99). Interestingly, the test data does not follow the same probability distribution as the training data (it includes 14 specific attack types that are not present in \(\varvec{T}\) in which 24 training attack types are given). Yu et al. (2003) showed that their clustering-based training set selection technique can easily outperform random sampling in this scenario.
-
Text classification Text classification, being the problem of determining to which topic a given text document belongs (it may be in one, multiple or no category because of the overlaps across these categories), is an important research topic which has been accelerated by the rapid growth of online information. Its applications include spam filtering, language identification, e-mail routing, readability assessment and more. Schohn and Cohn (2000) and Tong and Koller (2002) tackled this problem to verify the capabilities of their active-learning SVM approaches. They exploited the Reuters-21578 dataset (http://www.daviddlewis.com/resources/testcollections/reuters21578/) in the ModApte data split configuration (there are several pre-defined training-test splits provided by the authors of this dataset) with almost \(1.3\times 10^4\) articles (about \(10^4\) features each) and considered 10 most frequently occurring categories. Another commonly used text-classification dataset is Newsweeder (Lang 1995), also investigated in these papers.
-
Credit screening Lyhyaoui et al. (1999) tested their SVM training set selection using a dataset of 690 examples (15 features, 2 classes) reflecting customer creditworthiness. Although this dataset is known to be noisy (Quinlan 1999), the authors were able to surpass \(90\%\) of the classification accuracy with the use of their clustering-based technique.
-
Examples of a posed and b spontaneous smiles (selected frames). This figure is inspired by Kawulok et al. (2016)
4 Conclusions and outlook
The amount of data produced every day grows tremendously in most real-life domains, including medical imaging, genomics, text categorization, computational biology, and many others. Although it appears beneficial at the first glance (more data could mean more possibilities of extracting and revealing useful underlying knowledge), handling massively large datasets became a challenging issue and attracts attention of researchers from multiple fields, especially in the era of big data. This big data revolution affected many research fields, including statistics, machine learning, parallel computing, and computer systems in general (Haykin et al. 2016). Albeit SVMs have proved extremely effective in solving a variety of pattern recognition tasks, their main drawback lies in huge time and memory complexities, depending on the training set size cardinality. This is a severe shortcoming (it may be even impossible to train the classifier using a dataset encompassing a very large number of vectors), and it may prevent users from using SVMs in real-life scenarios which often require processing massively large datasets. Finally, the classification time grows linearly with the number of SVs, which indirectly depends on the training set size (as already mentioned, the number of SVs is notably smaller for reduced sets, hence the classification is much faster).
In this review, we analyzed the current advances in selecting the SVM training data from large datasets. We divided all the methods into several classes, comprising algorithms utilizing similar approaches (e.g., for extracting information about SV candidates) in their core, as well as exposing similar characteristics. We believe that this taxonomy can be effectively used for emerging techniques, and will help highlight and understand their potential strengths and weaknesses. We presented the main sources of information concerning training set vectors, which are commonly used to assess the importance of these vectors (only important vectors should be assembled into refined sets, because they are likely to be selected as SVs). As presented in Sect. 3.6, the number of algorithms for selection of refined sets is quite large, but their underpinning strategies for extracting such information can be classified into just five categories. Although some methods combine different information sources (see Table 1), they are in the minority, and this approach has not been intensively investigated in the literature so far.
Training SVMs from large datasets remains an open research problem. A plethora of methods for tackling the SVM training from such datasets are an excellent point of departure for further research. We believe that emerging metaheuristics (especially population-based ones), combined with refinement procedures should be intensively investigated towards parameter-less SVMs. Such engines would be extremely useful, since determining appropriate parameter values of an algorithm at hand is very time-consuming for massive sets, especially if the trial-and-error approach is exploited. It will be beneficial to construct hybrid algorithms, which couple methods for selecting refined training sets, and for enhancing the SVM training. It has not been explored in the literature—we believe that it could become an immediate answer to some of the big data problems, where the data veracity, velocity, volume, and variety play the pivotal role and should be treated comprehensively.
An important research direction encompasses creating algorithms, which utilize various information sources in search of important training set vectors. We believe that such techniques (ideally independent from the cardinality of \(\varvec{T}\)) will be the main stream of development soon, since they allow for extracting various bits of information about the dataset, and for combining them into the solid knowledge about the \(\varvec{T}\) vectors. On the other hand, incorporating those methods which benefit from the same source of information into hybrid approaches will most likely not result in boosting the quality of the refined sets. Due to the wide availability of a variety of parallel architectures, it will be beneficial to develop algorithms which analyze datasets in the complementary ways in parallel. Then, the results could be merged in the final decision engine, used for assessing the \(\varvec{T}\) vectors. Finally, algorithms which target learning SVMs from imbalanced and weakly-labeled datasets are becoming crucial due to the nature of the available data (Sáez et al. 2016).
Finally, the research summarized in this survey needs to be confronted with deep learning—a very powerful classification tool for a variety of pattern recognition tasks (LeCun et al. 2016). However, it has also been criticized for being difficult to tune and easy to fool, domain-agnostic, and hard to interpret (Nguyen et al. 2015). A very interesting research direction includes coupling deep convolutional neural networks (CNNs) with SVMs (alongside training set selection algorithms) in a comprehensive classification engine. Convolutional layers of CNNs are in fact feature extractors—features automatically elaborated in such layers could be classified using SVMs. This would allow for omitting a tedious process of preparing hand-engineered features (which is particularly important in the case of image and video data).
Notes
In most applications, a bag is labeled positive if it contains at least one positive-class vector—it is negative otherwise. Therefore, the implicit labels of all negative-class vectors belonging to a positive-class bag are in fact incorrect (Li et al. 2013).
It was shown that the choice of the clustering technique does not influence the next \(\varvec{T'}\) selection steps significantly (Lyhyaoui et al. 1999).
This process interactively extracts the desired content for a user based on the user feedback—the user decides whether the presented data are relevant or not.
All \(\varvec{T}\) vectors have the same weight at the beginning of the algorithm execution.
All repositories and datasets discussed in this section were accessed on July 7\(\mathrm{th}\), 2017.
Numerous benchmark datasets are derived for practical problems, however their cardinalities are often much smaller compared with real-life scenarios.
References
Abe S, Inoue T (2001) Fast training of support vector machines by extracting boundary data. In: Proceedings of the international conference on artificial neural networks. Springer, Berlin, pp 308–313. https://doi.org/10.1007/3-540-44668-0_44
Acampora G, Pedrycz W, Vitiello A (2015) A competent memetic algorithm for learning fuzzy cognitive maps. IEEE Trans Fuzzy Syst 23(6):2397–2411. https://doi.org/10.1109/TFUZZ.2015.2426311
Alamdar F, Ghane S, Amiri A (2016) On-line twin independent support vector machines. Neurocomputing 186:8–21. https://doi.org/10.1016/j.neucom.2015.12.062
Ali S, Smith-Miles KA (2006) A meta-learning approach to automatic kernel selection for support vector machines. Neurocomputing 70(13):173–186. https://doi.org/10.1016/j.neucom.2006.03.004
Angiulli F (2005) Fast condensed nearest neighbor rule. In: Proceedings of the 22nd international conference on machine learning, ACM, New York, NY, USA, ICML ’05, pp 25–32. https://doi.org/10.1145/1102351.1102355
Angiulli F (2007) Fast nearest neighbor condensation for large data sets classification. IEEE Trans Knowl Data Eng 19(11):1450–1464. https://doi.org/10.1109/TKDE.2007.190645
Angiulli F, Astorino A (2010) Scaling up support vector machines using nearest neighbor condensation. IEEE Trans Neural Netw 21(2):351–357. https://doi.org/10.1109/TNN.2009.2039227
Arana-Daniel N, Bayro-Corrochano E (2006) MIMO SVMs for 3D object classification. In: The 2006 IEEE international joint conference on neural network proceedings, pp 1628–1635. https://doi.org/10.1109/IJCNN.2006.246629
Arana-Daniel N, López-Franco C, Bayro-Corrochano E (2009) Improving recurrent CSVM performance for robot navigation on discrete labyrinths. In: Bayro-Corrochano E, Eklundh JO (eds) Proceedings on progress in pattern recognition, image analysis, computer vision, and applications: 14th Iberoamerican conference on pattern recognition, CIARP 2009. Springer, Berlin, pp 834–842. https://doi.org/10.1007/978-3-642-10268-4_98
Balcázar JL, Dai Y, Watanabe O (2001) A random sampling technique for training support vector machines. In: Proceedings of the international conference on algorithmic learning theory. Springer, Berlin, pp 119–134. https://doi.org/10.1007/3-540-45583-3_11
Barros de Almeida M, De Padua Braga A, Braga J (2000) SVM-KM: speeding SVMs learning with a priori cluster selection and \(k\)-means. In: Proceedings of the sixth Brazilian symposium on neural networks, pp 162–167. https://doi.org/10.1109/SBRN.2000.889732
Bayro-Corrochano EJ, Arana-Daniel N (2010) Clifford support vector machines for classification, regression, and recurrence. IEEE Trans Neural Netw 21(11):1731–1746. https://doi.org/10.1109/TNN.2010.2060352
Belongie S, Malik J, Puzicha J (2002) Shape matching and object recognition using shape contexts. IEEE Trans Pattern Anal Mach Intell 24(4):509–522. https://doi.org/10.1109/34.993558
Boser BE, Guyon IM, Vapnik VN (1992) A training algorithm for optimal margin classifiers. In: Proceedings of the fifth annual workshop on computational learning theory, ACM, COLT ’92, pp 144–152. https://doi.org/10.1145/130385.130401
Burges CJ (1998) A tutorial on support vector machines for pattern recognition. Data Min Knowl Discov 2(2):121–167. https://doi.org/10.1023/A:1009715923555
Cano JR, Herrera F, Lozano M (2003) Using evolutionary algorithms as instance selection for data reduction in KDD: an experimental study. IEEE Trans Evol Comput 7(6):561–575. https://doi.org/10.1109/TEVC.2003.819265
Cervantes J, Li X, Yu W, Li K (2008) Support vector machine classification for large data sets via minimum enclosing ball clustering. Neurocomputing 71(46):611–619. https://doi.org/10.1016/j.neucom.2007.07.028
Cervantes J, Lamont FG, López-Chau A, Mazahua LR, Ruíz JS (2015) Data selection based on decision tree for SVM classification on large data sets. Appl Soft Comput 37:787–798. https://doi.org/10.1016/j.asoc.2015.08.048
Chau AL, Li X, Yu W (2013) Convex and concave hulls for classification with support vector machine. Neurocomputing 122:198–209. https://doi.org/10.1016/j.neucom.2013.05.040
Chou JS, Cheng MY, Wu YW, Pham AD (2014) Optimizing parameters of support vector machine using fast messy genetic algorithm for dispute classification. Expert Syst Appl 41(8):3955–3964. https://doi.org/10.1016/j.eswa.2013.12.035
Cortes C, Vapnik V (1995) Support-vector networks. Mach Learn 20(3):273–297. https://doi.org/10.1007/BF00994018
Cour T, Sapp B, Jordan C, Taskar B (2009) Learning from ambiguously labeled images. In: Proceedings of the IEEE computer vision and pattern recognition conference, pp 919–926. https://doi.org/10.1109/CVPR.2009.5206667
Cyganek B (2008) Color image segmentation with support vector machines: applications to road signs detection. Int J Neural Syst 18(04):339–345. https://doi.org/10.1142/S0129065708001646
Cyganek B, Krawczyk B, Woźniak M (2015) Multidimensional data classification with chordal distance based kernel and support vector machines. Eng Appl Artif Intell 46:10–22. https://doi.org/10.1016/j.engappai.2015.08.001
Devos O, Downey G, Duponchel L (2014) Simultaneous data pre-processing and SVM classification model selection based on a parallel genetic algorithm applied to spectroscopic data of olive oils. Food Chem 148:124–130. https://doi.org/10.1016/j.foodchem.2013.10.020
Dibeklioğlu H, Salah AA, Gevers T (2012) Are you really smiling at me? Spontaneous versus posed enjoyment smiles. In: Proceedings of the 12th European conference on computer vision—volume part III, ECCV’12. Springer, Berlin, pp 525–538. https://doi.org/10.1007/978-3-642-33712-3_38
Ding Y, Cheng L, Pedrycz W, Hao K (2015) Global nonlinear kernel prediction for large data set with a particle swarm-optimized interval support vector regression. IEEE Trans Neural Netw Learn Syst 26(10):2521–2534. https://doi.org/10.1109/TNNLS.2015.2426182
Duan Y, Wu O (2017) Learning with auxiliary less-noisy labels. IEEE Trans Neural Netw Learn Syst 28(7):1716–1721. https://doi.org/10.1109/tnnls.2016.2546956
Eshelman LJ (1991) The CHC adaptive search algorithm: How to have safe search when engaging in nontraditional genetic recombination. Foundations of genetic algorithms, vol 1. Elsevier, Amsterdam, pp 265–283. https://doi.org/10.1016/B978-0-08-050684-5.50020-3
Fawcett T (2006) An introduction to ROC analysis. Pattern Recogn Lett 27(8):861–874. https://doi.org/10.1016/j.patrec.2005.10.010
Fernandes ERQ, de Carvalho ACPLF, Coelho ALV (2015) An evolutionary sampling approach for classification with imbalanced data. In: 2015 international joint conference on neural networks (IJCNN), pp 1–7. https://doi.org/10.1109/IJCNN.2015.7280760
Ferragut E, Laska J (2012) Randomized sampling for large data applications of SVM. In: Proceedings of IEEE international conference on machine learning and applications, vol 1, pp 350–355. https://doi.org/10.1109/ICMLA.2012.65
Fischler MA, Bolles RC (1981) Random sample consensus: a paradigm for model fitting with applications to image analysis and automated cartography. Commun ACM 24(6):381–395. https://doi.org/10.1145/358669.358692
Fletcher R (2013) Quadratic programming. In: Practical methods of optimization. Wiley, New York, pp 229–258. https://doi.org/10.1002/9781118723203.ch10
Frenay B, Verleysen M (2014) Classification in the presence of label noise: a survey. IEEE Trans Neural Netw Learn Syst 25(5):845–869. https://doi.org/10.1109/TNNLS.2013.2292894
Friedman M (1937) The use of ranks to avoid the assumption of normality implicit in the analysis of variance. J Am Stat Assoc 32(200):675–701. https://doi.org/10.2307/2279372
Friedrichs F, Igel C (2005) Evolutionary tuning of multiple SVM parameters. Neurocomputing 64:107–117. https://doi.org/10.1016/j.neucom.2004.11.022
Ghoggali N, Melgani F (2009) Automatic ground-truth validation with genetic algorithms for multispectral image classification. IEEE Trans Geosci Remote Sens 47(7):2172–2181. https://doi.org/10.1109/TGRS.2009.2013693
Gold C, Sollich P (2003) Model selection for support vector machine classification. Neurocomputing 55(12):221–249. https://doi.org/10.1016/S0925-2312(03)00375-8
Gorisse D, Cord M, Precioso F (2010) Scalable active learning strategy for object category retrieval. In: 2010 ieee international conference on image processing, pp 1013–1016. https://doi.org/10.1109/ICIP.2010.5653635
Guo L, Boukir S (2015) Fast data selection for SVM training using ensemble margin. Pattern Recogn Lett 51:112–119. https://doi.org/10.1016/j.patrec.2014.08.003
Guo L, Boukir S, Chehata N (2010) Support vectors selection for supervised learning using an ensemble approach. In: 2010 20th international conference on pattern recognition (ICPR), pp 37–40. https://doi.org/10.1109/ICPR.2010.18
Han X, Chang X (2013) An intelligent noise reduction method for chaotic signals based on genetic algorithms and lifting wavelet transforms. Inf Sci 218:103–118. https://doi.org/10.1016/j.ins.2012.06.033
Haykin S, Wright S, Bengio Y (2016) Big data: theoretical aspects. Proc IEEE 104(1):8–10. https://doi.org/10.1109/JPROC.2015.2507658
He Q, Xie Z, Hu Q, Wu C (2011) Neighborhood based sample and feature selection for SVM classification learning. Neurocomputing 74(10):1585–1594. https://doi.org/10.1016/j.neucom.2011.01.019
Hernandez-Leal P, Carrasco-Ochoa JA, Martí-nez-Trinidad J, Olvera-Lopez JA (2013) InstanceRank based on borders for instance selection. Pattern Recogn 46(1):365–375. https://doi.org/10.1016/j.patcog.2012.07.007
Joachims T (1999) Making large-scale SVM learning practical. In: Schölkopf B, Burges CJC, Smola AJ (eds) Advances in kernel methods. MIT Press, Cambridge, pp 169–184. http://dl.acm.org/citation.cfm?id=299094.299104
Kapp MN, Sabourin R, Maupin P (2012) A dynamic model selection strategy for support vector machine classifiers. Appl Soft Comput 12(8):2550–2565. https://doi.org/10.1016/j.asoc.2012.04.001
Kawulok M (2007) Genetic algorithms for classifiers’ training sets optimization applied to human face recognition. J Med Inform Technol 11:135–143. http://jmit.us.edu.pl/cms/jmitjrn/11/MIT_2007-13.pdf
Kawulok M, Nalepa J (2012) Support vector machines training data selection using a genetic algorithm. In: Gimel’farb G, Hancock E, Imiya A, Kuijper A, Kudo M, Omachi S, Windeatt T, Yamada K (eds) Structural, syntactic, and statistical pattern recognition. Lecture notes in computer science, vol 7626. Springer, Berlin, pp 557–565. https://doi.org/10.1007/978-3-642-34166-3_61
Kawulok M, Nalepa J (2014a) Dynamically adaptive genetic algorithm to select training data for SVMs. In: Bazzan ALC, Pichara K (eds) Advances in artificial intelligence - IBERAMIA 2014: 14th Ibero-American conference on AI, Santiago de Chile, Chile, November 24–27 2014, Proceedings. Springer, Cham, pp 242–254. https://doi.org/10.1007/978-3-319-12027-0_20
Kawulok M, Nalepa J (2014b) Hand pose estimation using support vector machines with evolutionary training. In: 2014 international conference on systems, signals and image processing (IWSSIP), pp 87–90. http://ieeexplore.ieee.org/document/6837637/. Accessed 31 Dec 2017
Kawulok M, Nalepa J (2015) Towards robust SVM training from weakly labeled large data sets. In: 2015 3rd IAPR Asian conference on pattern recognition (ACPR), pp 464–468. https://doi.org/10.1109/ACPR.2015.7486546
Kawulok M, Kawulok J, Nalepa J (2014) Spatial-based skin detection using discriminative skin-presence features. Pattern Recogn Lett 41:3–13. https://doi.org/10.1016/j.patrec.2013.08.028
Kawulok M, Nalepa J, Nurzynska K, Smolka B (2016) In search of truth: analysis of smile intensity dynamics to detect deception. In: Montes y Gómez M, Escalante HJ, Segura A, Murillo JdD (eds) Advances in artificial intelligence—IBERAMIA 2016: 15th Ibero-American conference on AI, proceedings. Springer International Publishing, Cham, pp 325–337. https://doi.org/10.1007/978-3-319-47955-2_27
Kawulok M, Nalepa J, Dudzik W (2017) An alternating genetic algorithm for selecting SVM model and training set. In: Carrasco-Ochoa JA, Martínez-Trinidad JF, Olvera-López JA (eds) Pattern recognition: 9th Mexican conference, MCPR 2017, proceedings. Springer International Publishing, Cham, pp 94–104. https://doi.org/10.1007/978-3-319-59226-8_10
Khosravani H, Ruano A, Ferreira P (2013) A simple algorithm for convex hull determination in high dimensions. In: 2013 IEEE 8th international symposium on intelligent signal processing (WISP), pp 109–114. https://doi.org/10.1109/wisp.2013.6657492
Koggalage R, Halgamuge S (2004) Reducing the number of training samples for fast support vector machine classification. Neural Inf Process Lett Rev 2(3):57–65. https://pdfs.semanticscholar.org/8530/7b7ac9c559537b6e43ef024888050512a10f.pdf
Kourou K, Exarchos TP, Exarchos KP, Karamouzis MV, Fotiadis DI (2015) Machine learning applications in cancer prognosis and prediction. Comput Struct Biotechnol 13:8–17. https://doi.org/10.1016/j.csbj.2014.11.005
Kowaluk M, Majewska G (2015) \(\beta \)-skeletons for a set of line segments in R\(^2\). In: Kosowski A, Walukiewicz I (eds) Fundamentals of computation theory: 20th international symposium, FCT 2015, proceedings. Springer International Publishing, Cham, pp 65–78. https://doi.org/10.1007/978-3-319-22177-9_6
Lang K (1995) Newsweeder: learning to filter netnews. In: Proceedings of the twelfth international conference on machine learning. Morgan Kaufmann, pp 331–339. https://doi.org/10.1.1.22.6286
Le QV, Sarlós T, Smola AJ (2014) Fastfood: approximate kernel expansions in loglinear time, pp 1–8. CoRR http://arxiv.org/abs/1408.3060
Lebrun G, Charrier C, Lezoray O, Cardot H (2008) Tabu search model selection for SVM. Int J Neural Syst 18(01):19–31. https://doi.org/10.1142/S0129065708001348
LeCun Y, Bengio Y, Hinton G (2016) Deep learning. Nature 521:436–555. https://doi.org/10.1038/nature14539
Lessmann S, Stahlbock R, Crone SF (2006) Genetic algorithms for support vector machine model selection. In: Proceedings of the IEEE international joint conference on neural networks, pp 3063–3069. https://doi.org/10.1109/IJCNN.2006.247266
Li Y (2011) Selecting training points for one-class support vector machines. Pattern Recogn Lett 32(11):1517–1522. https://doi.org/10.1016/j.patrec.2011.04.013
Li Y, Maguire L (2011) Selecting critical patterns based on local geometrical and statistical information. IEEE Trans Pattern Anal Mach Intell 33(6):1189–1201. https://doi.org/10.1109/TPAMI.2010.188
Li R, Bhanu B, Krawiec K (2007) Hybrid coevolutionary algorithms versus SVM algorithms. In: Proceedings of the 9th annual conference on genetic and evolutionary computation, ACM, New York, NY, USA, GECCO ’07, pp 456–463. https://doi.org/10.1145/1276958.1277057
Li YF, Tsang IW, Kwok JT, Zhou ZH (2013) Convex and scalable weakly labeled SVMs. J Mach Learn Res 14(1):2151–2188. www.jmlr.org/papers/volume14/li13a/li13a.pdf
Li J, Fong S, Zhuang Y, Khoury R (2016) Hierarchical classification in text mining for sentiment analysis of online news. Soft Comput 20(9):3411–3420. https://doi.org/10.1007/s00500-015-1812-4
Lin Y, Lv F, Zhu S, Yang M, Cour T, Yu K, Cao L, Huang T (2011) Large-scale image classification: fast feature extraction and SVM training. In: 2011 IEEE conference on computer vision and pattern recognition (CVPR), pp 1689–1696. https://doi.org/10.1109/CVPR.2011.5995477
Liu P, Choo KKR, Wang L, Huang F (2016) SVM or deep learning? A comparative study on remote sensing image classification. Soft Comput. https://doi.org/10.1007/s00500-016-2247-2
Li B, Wang Q, Hu J (2009) A fast SVM training method for very large datasets. In: International joint conference on neural networks, IJCNN 2009, pp 1784–1789. https://doi.org/10.1109/IJCNN.2009.5178618
Loh WY (2011) Classification and regression trees. Wiley interdisciplinary reviews: data mining and knowledge discovery 1(1):14–23. https://doi.org/10.1002/widm.8
Lopez-Chau A, Li X, Yu W (2012) Convex-concave hull for classification with SVM. In: Proceedings of international conference on data mining, pp 431–438. https://doi.org/10.1109/icdmw.2012.76
Luxburg UV, Bousquet O, Schölkopf B (2004) A compression approach to support vector model selection. J Mach Learn Res 5:293–323. http://dl.acm.org/citation.cfm?id=1005343
Lyhyaoui A, Martinez M, Mora I, Vaquez M, Sancho JL, Figueiras-Vidal A (1999) Sample selection via clustering to construct support vector-like classifiers. IEEE Trans Neural Netw 10(6):1474–1481. https://doi.org/10.1109/72.809092
Makris A, Kosmopoulos D, Perantonis S, Theodoridis S (2011) A hierarchical feature fusion framework for adaptive visual tracking. Image Vis Comput 29(9):594–606. https://doi.org/10.1016/j.imavis.2011.07.001
Mercer J (1909) Functions of positive and negative type, and their connection with the theory of integral equations. Philos Trans R Soc Lond 209:415–446. https://doi.org/10.1098/rsta.1909.0016
Nalepa J (2016) Genetic and memetic algorithms for selection of training sets for support vector machines. Ph.D. thesis, Silesian University of Technology
Nalepa J, Blocho M (2016) Adaptive memetic algorithm for minimizing distance in the vehicle routing problem with time windows. Soft Comput 20(6):2309–2327. https://doi.org/10.1007/s00500-015-1642-4
Nalepa J, Kawulok M (2014a) Adaptive genetic algorithm to select training data for support vector machines. In: Esparcia-Alcazar AI, Mora AM (eds) Applications of evolutionary computation. Lecture notes in computer science. Springer, Berlin, pp 514–525. https://doi.org/10.1007/978-3-662-45523-4_42
Nalepa J, Kawulok M (2014b) A memetic algorithm to select training data for support vector machines. In: Proceedings of the 2014 conference on genetic and evolutionary computation, ACM, GECCO ’14, pp 573–580. https://doi.org/10.1145/2576768.2598370
Nalepa J, Kawulok M (2016a) Adaptive memetic algorithm enhanced with data geometry analysis to select training data for SVMs. Neurocomputing 185:113–132. https://doi.org/10.1016/j.neucom.2015.12.046
Nalepa J, Kawulok M (2016b) The smaller, the better: selecting refined SVM training sets using adaptive memetic algorithm. In: Proceedings of the 2016 on genetic and evolutionary computation conference companion, ACM, New York, NY, USA, GECCO ’16 Companion, pp 165–166. https://doi.org/10.1145/2908961.2930950
Nalepa J, Cwiek M, Kawulok M (2015a) Adaptive memetic algorithm for the job shop scheduling problem. In: 2015 international joint conference on neural networks (IJCNN), pp 1–8. https://doi.org/10.1109/ijcnn.2015.7280409
Nalepa J, Siminski K, Kawulok M (2015b) Towards parameter-less support vector machines. In: 2015 3rd IAPR Asian conference on pattern recognition (ACPR), pp 211–215. https://doi.org/10.1109/ACPR.2015.7486496
Nguyen A, Yosinski J, Clune J (2015) Deep neural networks are easily fooled: high confidence predictions for unrecognizable images. In: Proceedings of the IEEE computer vision and pattern recognition conference, pp 427–436. https://doi.org/10.1109/cvpr.2015.7298640
Nishida K, Kurita T (2008) RANSAC–SVM for large-scale datasets. In: 19th International conference on pattern recognition, ICPR 2008, pp 1–4. https://doi.org/10.1109/icpr.2008.4761280
Oh S, Lee MS, Zhang BT (2011) Ensemble learning with active example selection for imbalanced biomedical data classification. IEEE/ACM Trans Comput Biol Bioinform 8(2):316–325. https://doi.org/10.1109/TCBB.2010.96
Olvera-López JA, Carrasco-Ochoa JA, Martínez-Trinidad JF, Kittler J (2010) A review of instance selection methods. Artif Intell Rev 34(2):133–143. https://doi.org/10.1007/s10462-010-9165-y
Paul M, Haque SME, Chakraborty S (2013) Human detection in surveillance videos and its applications: a review. EURASIP J Adv Signal Process 1:176. https://doi.org/10.1186/1687-6180-2013-176
Phillips P, Wechsler H, Huang J, Rauss PJ (1998) The FERET database and evaluation procedure for face-recognition algorithms. Image Vis Comput 16(5):295–306. https://doi.org/10.1016/S0262-8856(97)00070-X
Phung S, Bouzerdoum A, Chai D (2005) Skin segmentation using color pixel classification: analysis and comparison. IEEE Trans Pattern Anal Mach Intell 27(1):148–154. https://doi.org/10.1109/TPAMI.2005.17
Pietruszkiewicz W, Imada A (2013) Artificial intelligence evolved from random behaviour: departure from the state of the art. Springer Berlin, pp 19–41. https://doi.org/10.1007/978-3-642-29694-9_2
Pighetti R, Pallez D, Precioso F (2015) Improving SVM training sample selection using multi-objective evolutionary algorithm and LSH. In: Proceedings of the IEEE symposium on computational intelligence, pp 1383–1390. https://doi.org/10.1109/ssci.2015.197
Qiu J, Wu Q, Ding G, Xu Y, Feng S (2016) A survey of machine learning for big data processing. EURASIP J Adv Signal Process 1:1–16. https://doi.org/10.1186/s13634-016-0355-x
Quinlan J (1999) Simplifying decision trees. Int J Hum Comput Stud 51(2):497–510. https://doi.org/10.1006/ijhc.1987.0321
Reeves CR, Taylor SJ (1998) Selection of training data for neural networks by a genetic algorithm. In: Eiben AE, Bäck T, Schoenauer M, Schwefel HP (eds) Parallel problem solving from nature—PPSN V: 5th international conference, 1998 proceedings. Springer, Berlin, pp 633–642. https://doi.org/10.1007/bfb0056905
Ripepi G, Clematis A, DAgostino D (2015) A hybrid parallel implementation of model selection for support vector machines. In: Proceedings of the Euromicro international conference on parallel, distributed, and network-based processing, pp 145–149. https://doi.org/10.1109/PDP.2015.97
Rodan A, Sheta AF, Faris H (2016) Bidirectional reservoir networks trained using SVM + privileged information for manufacturing process modeling. Soft Comput. https://doi.org/10.1007/s00500-016-2232-9
Sáez JA, Krawczyk B, Woźniak M (2016) Analyzing the oversampling of different classes and types of examples in multi-class imbalanced datasets. Pattern Recogn 57:164–178. https://doi.org/10.1016/j.patcog.2016.03.012
Schapire RE, Freund Y, Bartlett P, Lee WS (1998) Boosting the margin: a new explanation for the effectiveness of voting methods. Ann Stat 26(5):1651–1686. https://doi.org/10.1214/aos/1024691352
Scheunders P, Backer SD (1999) High-dimensional clustering using frequency sensitive competitive learning. Pattern Recogn 32(2):193–202. https://doi.org/10.1016/S0031-3203(98)00136-8
Schohn G, Cohn D (2000) Less is more: active learning with support vector machines. In: Proceedings of the international conference on machine learning, ICML, pp 839–846. http://dl.acm.org/citation.cfm?id=657802. Accessed 31 Dec 2017
Shen XJ, Mu L, Li Z, Wu HX, Gou JP, Chen X (2016) Large-scale support vector machine classification with redundant data reduction. Neurocomputing 172:189–197. https://doi.org/10.1016/j.neucom.2014.10.102
Shi GY, Liu S (2012) Model selection of RBF kernel for C-SVM based on genetic algorithm and multithreading. In: Proceedings of the IEEE international conference on machine learning and cybernetics, vol 1, pp 382–386. https://doi.org/10.1109/ICMLC.2012.6358944
Shin H, Cho S (2002) Pattern selection for support vector classifiers. In: Yin H, Allinson N, Freeman R, Keane J, Hubbard S (eds) Intelligent Data engineering and automated learning IDEAL 2002. Lecture notes in computer science, vol 2412. Springer, Berlin. https://doi.org/10.1007/3-540-45675-9_70
Shin H, Cho S (2003) Fast pattern selection for support vector classifiers. In: Whang KY, Jeon J, Shim K, Srivastava J (eds) Advances in knowledge discovery and data mining. Lecture notes in computer science, vol 2637. Springer, Berlin, pp 376–387. https://doi.org/10.1007/3-540-36175-8_37
Shin H, Cho S (2007) Neighborhood property-based pattern selection for SVMs. Neural Comput 19(3):816–855. https://doi.org/10.1162/neco.2007.19.3.816
Simiński K (2014) Neuro-fuzzy system based kernel for classification with support vector machines. In: Gruca A, Czachorski T, Kozielski S (eds) Man–machine interactions, advances in intelligent systems and computing, vol 3. Springer, Berlin, pp 415–422. https://doi.org/10.1007/978-3-319-02309-0_45
Sullivan KM, Luke S (2007) Evolving kernels for support vector machine classification. In: Proceedings of GECCO, ACM, New York, NY, USA, pp 1702–1707. https://doi.org/10.1145/1276958.1277292
Tang Y, Guo W, Gao J (2009) Efficient model selection for support vector machine with Gaussian kernel function. In: Proceedings of the IEEE symposium on computational intelligence and data mining, pp 40–45. https://doi.org/10.1109/CIDM.2009.4938627
Tapaswi M, Bäuml M, Stiefelhagen R (2015) Improved weak labels using contextual cues for person identification in videos. In: Proceedings of the IEEE face and gesture recognition conference, vol 4, pp 1–8. https://doi.org/10.1109/fg.2015.7163083
Tayal A, Coleman TF, Li Y (2014) Primal explicit max margin feature selection for nonlinear support vector machines. Pattern Recogn 47(6):2153–2164. https://doi.org/10.1016/j.patcog.2014.01.003
Tong S, Chang E (2001) Support vector machine active learning for image retrieval. In: Proceedings of the ninth ACM international conference on multimedia, ACM, New York, NY, USA, MULTIMEDIA ’01, pp 107–118. https://doi.org/10.1145/500156.500159
Tong S, Koller D (2002) Support vector machine active learning with applications to text classification. J Mach Learn Res 2:45–66. https://doi.org/10.1162/153244302760185243
Trojacanec K, Dimitrovski I, Loskovska S (2009) Content based image retrieval in medical applications: an improvement of the two-level architecture. In: IEEE EUROCON 2009, pp 118–121. https://doi.org/10.1109/EURCON.2009.5167614
Tsyurmasto P, Zabarankin M, Uryasev S (2014) Value-at-risk support vector machine: stability to outliers. J Comb Optim 28(1):218–232. https://doi.org/10.1007/s10878-013-9678-9
Uzilov AV, Keegan JM, Mathews DH (2006) Detection of non-coding RNAs on the basis of predicted secondary structure formation free energy change. BMC Bioinform 7(1):173. https://doi.org/10.1186/1471-2105-7-173
Verbiest N, Derrac J, Cornelis C, Garcí-a S, Herrera F (2016) Evolutionary wrapper approaches for training set selection as preprocessing mechanism for support vector machines: experimental evaluation and support vector analysis. Appl Soft Comput 38:10–22. https://doi.org/10.1016/j.asoc.2015.09.006
Wang D, Shi L (2008) Selecting valuable training samples for SVMs via data structure analysis. Neurocomputing 71:2772–2781. https://doi.org/10.1016/j.neucom.2007.09.008
Wang W, Xu Z (2004) A heuristic training for support vector regression. Neurocomputing 61:259–275. https://doi.org/10.1016/j.neucom.2003.11.012
Wang J, Neskovic P, Cooper L (2005) Training data selection for support vector machines. In: Wang L, Chen K, Ong Y (eds) Advances in natural computation, lecture notes in computer science, vol 3610. Springer, Berlin, pp 554–564. https://doi.org/10.1007/11539087_71
Wang J, Neskovic P, Cooper LN (2007) Selecting data for fast support vector machines training. In: Chen K, Wang L (eds) Trends in neural computation, studies in computational intelligence, vol 35. Springer, Berlin, pp 61–84. https://doi.org/10.1007/978-3-540-36122-0_3
Wang D, Qiao H, Zhang B, Wang M (2013a) Online support vector machine based on convex hull vertices selection. IEEE Trans Neural Netw Learn Syst 24(4):593–609. https://doi.org/10.1109/TNNLS.2013.2238556
Wang Z, Shao YH, Wu TR (2013b) A GA-based model selection for smooth twin parametric-margin support vector machine. Pattern Recogn 46(8):2267–2277. https://doi.org/10.1016/j.patcog.2013.01.023
Ward J (1963) Hierarchical grouping to optimize an objective function. J Am Stat Assoc 58(301):236–244. https://doi.org/10.1080/01621459.1963.10500845
Wenyuan L, Jing M, Changwu W, Baowen W, Yongqiang L (2013) The training set selection methods of microRNA precursors prediction based on machine learning approaches. In: 2013 third international conference on intelligent system design and engineering applications (ISDEA), pp 1566–1569. https://doi.org/10.1109/ISDEA.2012.376
Woolson RF (2007) Wilcoxon signed-rank test. Wiley, New York, pp 4739–4740. https://doi.org/10.1002/9780471462422.eoct979
Wrona S, Pawełczyk M (2013) Controllability-oriented placement of actuators for active noise-vibration control of rectangular plates using a memetic algorithm. Arch Acoust 38(4):529–536. https://doi.org/10.2478/aoa-2013-0062
Xiao H, Biggio B, Nelson B, Xiao H, Eckert C, Roli F (2015) Support vector machines under adversarial label contamination. Neurocomputing 160:53–62. https://doi.org/10.1016/j.neucom.2014.08.081
Xu L, Crammer K, Schuurmans D (2006) Robust support vector machine training via convex outlier ablation. In: Proceedings of the AAAI conference on artificial intelligence, pp 536–542. http://dl.acm.org/citation.cfm?id=1597625. Accessed 31 Dec 2017
Yu H, Mu C, Sun C, Yang W, Yang X, Zuo X (2015) Support vector machine-based optimized decision threshold adjustment strategy for classifying imbalanced data. Knowl Based Syst 76:67–78. https://doi.org/10.1016/j.knosys.2014.12.007
Yuan X, Song M, Zhou F, Wang Y, Chen Z (2015) A novel fast training method for SVM and its application in fault diagnosis of service robot. Int J Online Eng 11(6):4–9. https://doi.org/10.3991/ijoe.v11i6.4846
Yu H, Yang J, Han J (2003) Classifying large data sets using SVMs with hierarchical clusters. In: Proceedings of the ninth ACM SIGKDD international conference on knowledge discovery and data mining, ACM, New York, NY, USA, KDD ’03, pp 306–315. https://doi.org/10.1145/956750.956786
Zeng ZQ, Xu HR, Xie YQ, Gao J (2008a) A geometric approach to train SVM on very large data sets. In: Proceedings of the international conference on intelligent systems and knowledge engineering, vol 1, pp 991–996. https://doi.org/10.1109/ISKE.2008.4731074
Zeng ZQ, Yu HB, Xu HR, Xie YQ, Gao J (2008b) Fast training support vector machines using parallel sequential minimal optimization. In: 2008 3rd international conference on intelligent system and knowledge engineering, vol 1, pp 997–1001. https://doi.org/10.1109/ISKE.2008.4731075
Zhang W, King I (2002) Locating support vectors via \(\beta \)-skeleton technique. In: Proceedings of the international conference on neural information processing, pp 1423–1427. https://doi.org/10.1109/ICONIP.2002.1202855
Zhang X, Song Q (2015) A multi-label learning based kernel automatic recommendation method for support vector machine. PLoS One. https://doi.org/10.1371/journal.pone.0120455
Zhang T, Ramakrishnan R, Livny M (1996) BIRCH: an efficient data clustering method for very large databases. In: Proceedings of the 1996 ACM SIGMOD international conference on management of data, ACM, New York, NY, USA, SIGMOD ’96, pp 103–114. https://doi.org/10.1145/233269.233324
Zhou X, Xu J (2009) A SVM model selection method based on hybrid genetic algorithm and empirical error minimization criterion. In: Wang H, Shen Y, Huang T, Zeng Z (eds) Proceedings of the international symposium on neural networks. Springer, Berlin, pp 245–253. https://doi.org/10.1007/978-3-642-01216-7_26
Zhu J, Mao J, Yuille AL (2014) Learning from weakly supervised data by the expectation loss SVM (e-SVM) algorithm. In: Advances in Neural Information Processing Systems, NIPS, pp 1125–1133. http://dl.acm.org/citation.cfm?id=2968952. Accessed 31 Dec 2017
Acknowledgements
JN and MK were supported by the National Science Centre, Poland, under Research Grant No. DEC-2017/25/B/ST6/00474, and JN was supported by the Silesian University of Technology under the Grant for young researchers (BKM-509/RAu2/2017). The authors are grateful to the anonymous Reviewers for their constructive and valuable comments that helped improve the paper.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Ethical approval
This article does not contain any studies with human participants or animals performed by any of the authors.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Nalepa, J., Kawulok, M. Selecting training sets for support vector machines: a review. Artif Intell Rev 52, 857–900 (2019). https://doi.org/10.1007/s10462-017-9611-1
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10462-017-9611-1