1 Introduction

Urban segregation is a complex phenomenon that reverberates across various socio-economic contexts—from everyday social interactions to education [1,2,3,4,5,6,7]. Segregation can hinder social mobility and lead to social exclusion, exacerbating existing urban inequalities [1, 3]. This phenomenon is not limited to the choice of residence; it extends to other domains of life such as workplaces, entertainment venues, and school selection for children [8]. As a result, urban segregation can become a self-reinforcing process that, if not mitigated, could be perpetuated and difficult to tackle [2, 7].

In the context of education, recent studies have shown that urban segregation is reflected and amplified in school admission, even in situations where parents have the freedom of choice [2, 7, 9,10,11]. Distance to school and commuting time are very important factors for choosing a school, however, similarity in socio-economic status (homophily) can be just as important [2, 7, 12]. Parents often opt for schools outside their residential neighbourhoods for their children. This tendency is more noticeable when their neighbourhood does not reflect their ethnicity or socio-economic status. Moreover—as we also confirm in our experiments—data reveals that if parents would choose local schools, then school segregation would be reduced compared with present levels [12, 13].

To address various issues stemming from unrestricted school choice, such as fairness, equality of opportunity, transparency, and guarding against manipulation, local governments worldwide have turned to centralized school admission mechanisms [14,15,16]. Such systems are implemented in the form of mechanisms like Deferred Acceptance and Random Serial Dictatorship [15, 17, 18]. Under these systems, school choice remains unrestricted and is expressed through preference lists over schools. In this case, a central authority is responsible for determining how these preferences translate into actual allocations. Deferred Acceptance allows both schools and students to submit preferences regarding each other, creating a two-sided matching process. Random Serial Dictatorship, however, considers only the preferences of students, determining their priority through a random lottery. As expected, factors like school accessibility, popularity, and composition significantly influence the lists and the final allocations.

Except for high-income households, most others do not tend to move house, thus their choice is limited by their location [9]. Intervening in public transportation networks can impact segregation and enable citizens from diverse societal groups to access a wider range of schools. This raises the central question of our work: Can interventions in public transportation networks effectively decrease school segregation?

In this paper, we resort to agent-based modelling (ABM) to explore the previous question. Prior studies focused on the complexity of residential and school segregation via ABMs [2, 19], and preference models based on both school composition and distance have been explored [2, 7, 20]. However, these works do not study the effect of strategically increasing accessibility to specific schools. Graph-based interventions have been employed before to improve more inclusive accessibility [21], but they have not been utilized for addressing school segregation or assessing the long-term effects of such interventions. Our goal is to close this research gap. Therefore, we summarize this paper’s contributions as follows:

  • We design and develop an agent-based model that leverages the structure of networks to study the phenomenon of school segregation. We release the code and datasets used to the public.Footnote 1

  • We assess the conditions under which, even in segregated environments, school segregation decreases over time, without intervening in the transportation network.

  • We assess whether graph-based transportation interventions can be used to reduce disparities in group composition within schools, under a centralized admission system.

  • We test transport network intervention strategies based on greedy optimization of classic graph centrality measures such as closeness and betweenness centrality.

  • We propose new, group-based network centrality measures and conduct interventions based on schools greedily improving their group-based centralities.

  • We conduct experiments in a synthetic and a real-world environment in the city of Amsterdam and show that targeted interventions can lead to a significant reduction in segregation over time.

The paper is structured as follows: we first provide an overview of previous research in the field and identify current gaps (Sect. 2). Then, we introduce the ABM framework proposed to address the problem and explain the methodology used for our experiments (Sect. 3). Lastly, we present and analyze the most significant findings from our study (Sects. 4 and 5).

2 Related work

In this paper, we merge insights from agent-based modelling, network science, and transportation network interventions to explore ways to mitigate school segregation. We provide an overview of each field and demonstrate their application in our study.

2.1 Agent-based models of school segregation

Agent-based modelling (ABM) is a widely used approach for studying social processes by simulating the behaviors of agents and their interactions within a specified environment [22, 23]. Numerous ABMs have been developed to understand how residential segregation emerges under varying homophily preferences by agents. These models often extend the classic Schelling model [24] and integrate more refined preferences and interactions. For instance, they incorporate housing restrictions based on diverse preference parameters and constraints [19, 25, 26], conduct empirical evaluations [27], and, more recently, explore methodologies such as Reinforcement Learning [28].

Recently, ABMs also started to be employed to study school segregation. Much of previous work on school segregation focused on empirical analysis [10, 14, 29,30,31,32,33], but recent works attempt to use ABMs to model school preferences and devise a theoretical understanding of the dynamics of school segregation and how it is impacted by existing residential segregation patterns [2, 7, 20, 34]. Most of these studies focus on the emergence of school segregation under different preference configurations, such as homophily, tolerance, and general preferences for in-group interactions.

Our research draws inspiration from the recently developed models by Sage and Flache [7] and Dignum et al. [2]. We complement this research by formalizing environments as complex networks (as opposed to grids), allowing for a more detailed and realistic representation of transportation possibilities and travel time. Additionally, we integrate insights from network analysis for testing interventions. Moreover, we conduct experiments in Amsterdam and present a modular framework that can be expanded to various environments, preference models, and admission mechanisms.

2.1.1 The role of networks

Spatial agent-based models are typically designed for grid-like environments, assuming structured connections between areas [2, 7]. However, social phenomena involving movement and transportation interventions can benefit from integrating network science methods [35, 36]. To achieve this, agents’ environments are modeled as heterogeneous networks, providing a more realistic representation of physical space and, in this case, transportation networks. Multiple models have been proposed where agents interact within a network-based environment, with applications in Game Theory, Economics, Ecology and Sociology (for comprehensive reviews see [37] and [38]). Analyzing spatial networks can offer a deeper understanding of the role of space and distance in agents’ interactions.

Inspired by previous works, we model a city’s environment as a network of connected census tracts, enabling a more realistic approach to modelling travel time and transport interventions. As a result, we offer, originally, the possibility of directly relating interventions on transportation networks and dynamics of school segregation.

2.2 Transport network interventions

Network augmentation via edge interventions, with the aim of reducing inequalities and enhancing fairness, has been extensively studied in both social [21, 39,40,41,42,43,44] and spatial network settings [21, 45,46,47,48]. The problem is typically formalized by creating new edges in the network under a budget constraint to satisfy specific metrics, such as information access, social capital, or travel time to amenities.

A subset of research on edge augmentation focuses on enhancing network centrality measures, representing a significant advancement in this field by incorporating insights from network science. Several studies have demonstrated the effectiveness of this approach in elevating the importance of nodes within a network [47,48,49,50]. However, the impact of targeted transportation network interventions on school choice and, consequently, segregation, has not been thoroughly explored. A recent study focused on redrawing attendance boundaries of United States schools to reduce segregation, which is a geographical intervention affecting distance to schools [51]. Our method is related to this approach in that it can also be seen as a top-down intervention to tackle segregation. However, our framework can also be applied to settings with no attendance boundaries, thus offering no limit on school choice.

While testing the effect of interventions on network centrality measures requires static network data alone, understanding the impact of interventions on school preferences requires understanding the interrelated process of school allocations, preference formation, and long-term citizens’ observation of schools’ demographic composition. In this study, we aim to take the first step towards a comprehensive understanding of the effects of such interventions. Our intervention method is inspired by the previously mentioned works, where we conduct greedy transportation interventions to mitigate segregation by enhancing global group-centrality-based metrics for segregated schools.

Fig. 1
figure 1

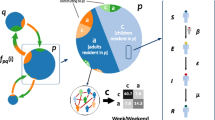
Proposed agent-based model to study the impact of transport network interventions on school segregation. We consider an environment where citizens, schools, and a transportation graph are distributed in a spatial network (Sect. 3.1). At each round, agents A generate preferences for schools F, using a preference model (Sect. 3.2). Agents are assigned to schools via an allocation method (Sect. 3.3), which is evaluated on segregation (Sect. 3.3.1). An intervention model creates edge-based interventions to the transportation network, aiming at reducing segregation (Sect. 3.4)

Full size image

3 Methods

We propose an agent-based modelling framework to simulate the school choice process over multiple time steps. In this section, we describe each component of the framework, including the agents, the network, and the environment, as well as the preference, allocation, and intervention models. Our model is summarized in Fig. 1.

3.1 Environment: citizens, transportation networks, and schools

We model a city as an undirected graph \({\mathbb {G}}=(V, E)\), where \(V = \{v_1,..., v_{n_v}\}\) are nodes, one for each census tract in the city, and \(E = \{e_{i, j}\}, i,j \in V, i \ne j\) are edges that represent transportation connections between nodes. For simplicity, edges are unweighted, but the model can be effortlessly extended to consider weighted edges (e.g., representing transportation times). We assume that the graph is connected; there exists at least one path between all nodes. We define the shortest path between i and j as \(t_{i,j}, \; i,j \in V\), and in practice shortest distances are calculated using Dijkstra’s algorithm. The travel time between two adjacent nodes is 1.

We define a set of N agents (citizens), \(A=\{a_1,..., a_{N}\}\) that operate within the city environment. An agent’s starting location is considered its residence node \(v_{a} \in V\). Each agent is a member of a group \(g \in G\), defined based on characteristics such as ethnicity, income, or other socio-economic status. Note that groups are defined beforehand and do not change throughout a simulation. Finally, each agent has a homophily attribute, \(h_i \in [0, 1]\), defining a preference for an optimal fraction of agents from the same group attending a school [2, 24]. We conduct experiments with different settings of homophily but, within a simulation, homophily is also considered constant. Note that agents are abstract entities that represent students in a city. In reality, it is mostly parents/households that decide on the preference lists.

We define schools \(f \in F\) as being amenities located in specific nodes \(v_{f} \in V\). Each school is associated with a capacity (maximum number of allowed students) \(s_f \in [0, N]\) and a group composition \(c_{g, f} \in [0, 1], \; g \in G\), which represents the fraction of assigned agents from each group. While the capacity is fixed over time, group composition depends on agents’ preferences and the resulting process of school allocation. Note that \(\sum \limits _{g} c_{g, f} = 1, \; \forall f \in F\).

The model we propose can be applied in both synthetic and real-world graph environments. Here, we define a real-world city environment based on Amsterdam’s neighbourhoods, utilizing real demographic and transportation data; and two generated environments (Grid and Stochastic Block Model). The first is based on a two-dimensional lattice graph, to enable analysis on a structured graph and for sanity checks. The second is based on the Stochastic Block Model (SBM) [52], allowing us to control the level of modularity and segregation in a hypothetical city. Figure 2 displays these graphs.

Fig. 2
figure 2

We study three environments, a Grid (i.e., a lattice graph) (a), a synthetic community-structured graph generated through the Stochastic Block Model (SBM) (b—a sample of the studied realizations), and a real-world graph representing neighbourhood adjacency and schools’ location in the city of Amsterdam (c). All nodes represent neighbourhoods and yellow nodes (also marked with *) indicate nodes with schools. In Amsterdam, school nodes are selected based on real data; in the synthetic environments, schools are placed so that they are close to their respective communities. By considering synthetic environments, we aim to test the generality of our approach in environments with a wide range of residential segregation, school offer, and transportation accessibility

Full size image

3.1.1 Grid environment

We create a grid environment in the form of an undirected lattice graph, as shown in Fig. 2a. The environment is divided into two distinct communities: one occupying the north-east nodes and another occupying the south-west nodes of the grid. Both communities are equal in terms of total population size (250 agents each). We introduce high-residential segregation into the environment, by setting the majority population of a group in its respective community to \(80\%\) and the minority to \(20\%\) respectively. There are two schools, each located at the centre of its respective community, at the node with the highest closeness centrality within each community. We set the capacity of each school to be |A| / |F| so that all agents will be assigned to a school. The initial group composition of each school is set to be equal to the group composition of the node it is located in.

While a lattice may not precisely mirror the spatial graph of a city, we employ it to investigate segregation dynamics and the effects of interventions within a clearly defined, structured environment. This approach aligns with conventional practices in prior ABM studies that have utilized lattices for similar purposes [2, 25, 28]. Furthermore, we utilize this environment as a comprehensive sanity check, validating that interventions can be effectively implemented using a straightforward and easily comprehensible setting.

3.1.2 SBM environment

The Stochastic Block Model (SBM) graph is a synthetic environment, specifically generated to form clusters of communities, where nodes are densely connected with other nodes in their community and scarcely connected with nodes outside of it [53].

We use the SBM to generate environments that resemble the degree distribution, edge distribution, total schools, and school capacity of the city of Amsterdam. This creates a flexible, synthetic environment in which we study the effect of different school preference parameters and network interventions on varying levels of connectivity between communities. An SBM graph \({\mathbb {G}}=(V, E)\) is generated by a set of nodes, communities, and a symmetric probability matrix \({\mathbb {P}}\), \({\mathbb {P}}_{ij} \in [0, 1]\), which controls the probabilities of edges between nodes of different communities. Throughout the paper, we use undirected SBMs with two communities; hence, \({\mathbb {P}}\) is a \(2\times 2\) matrix characterized by two probabilities: \(p_{in}\), controlling edges within each community, and \(p_{out}\), controlling edges between the two communities. We define a new parameter m that controls the modularity of the (undirected) connections of the SBM graph. The higher the modularity, the fewer inter-community edges exist in the graph. We thus update the edge probability definitions as follows:

$$\begin{aligned} \begin{aligned} p_{in} = p_{base} + m \\ p_{out} = p_{base} - m \end{aligned} \end{aligned}$$
(1)

where \(p_{base}\) is the base probability of an edge existing between two nodes. To resemble the degree distribution of Amsterdam in the SBM environment, we set \(p_{base} = 0.06\). To resemble other environments, we suggest setting \(p_{base}\) accordingly. We set \(m \in [0.0, 0.06)\), where \(m=0\) means no modularity and an equal probability of in and out edges, and \(m \approx 0.06\) means full modularity, with very few connections between the two communities. Figure 3 shows sample realizations of SBM environments with different levels of modularity.

Fig. 3
figure 3

SBM environments with different levels of modularity m. As modularity increases, the probability of intra-community edges increases and the probability of inter-community edges decreases. We aim at generating scenarios with a varying degree of neighborhood segregation and, as a result, varying potential to observe school segregation. \(p_{in}\) and \(p_{out}\) denote the probability of having an edge within or between a community, respectivelys

Full size image

We generated a population of \(N=1500\) agents and sampled both their residence node and their group membership from a total of 2 groups. Group samples here are chosen similarly to the grid environment, with an \(80\%\) majority and a \(20\%\) minority population in the nodes of each community. Finally, we placed a total of ten schools on the graph using the same criteria as in the grid environment. The total number of schools and the capacity of each school resemble those of Amsterdam, with a total of \(\approx 150\) students per school. The initial group composition of each school here is also set to be equal to the group composition of the node it is located in.

Fig. 4
figure 4

The impact of Homophily and Modularity on school segregation. Results are generated with 5 random realizations (with different seeds) of the SBM environment. We measure the Dissimilarity Index, DI (Eq. 7), noting that higher DI corresponds to higher segregation levels. a School segregation can be reduced if citizens’ do not have strong preferences for being in schools with individuals from the same group (i.e., if homophily is reduced). This effect is observed for different values of \(\alpha\), i.e., the importance of group composition on school preferences, as opposed to travel time. As changing individual preferences for group interactions is in reality challenging, we test how transportation network interventions can also contribute to reduce school segregation; in (b), we illustrate that even assuming high homophily \((h = 0.8)\), segregation decreases with lower modularity (low m). Thus, strategically enhancing connectivity between communities can reduce segregation, even in the presence of high homophily preferences

Full size image

3.1.3 Amsterdam environment

To model the real-world environment of Amsterdam, we create a graph where census tracts are converted to nodes, which are connected with their neighbouring tracts via an unweighted edge. This graph structure has recently been used to quantify segregation and community structure on graphs because it offers the possibility to define methods (based on random walks) of that are independent of cities’ scale and structure [36, 54]. In total, the graph consists of \(n_v=517\) nodes and \(n_e = 1611\) edges. In Fig. 2c, we show the graph used for the Amsterdam experiments.

In the Amsterdam environment, agents are generated to represent the real-world population, which is split into groups of western (W) and non-western (NW) ethnic background, representing \(65\%\) and \(35\%\) of the population respectively.Footnote 2 We generate 7000 agents because this is the number of households that apply for secondary schools in Amsterdam each year. Evidence has shown that ethnicity is a major driver of segregation in Amsterdam [4], especially between these two groups. Here, the homophily parameter is assumed to be equal to that of the node’s majority population percentage. Thus, if a node has a \(50\%-50\%\) population split between the two groups, we assume its resident-agents have a homophily of 0.5. This is done to increase variety of preferences among agents, aligning more closely with real-world scenarios, rather than making the assumption of uniform preference parameters.

We use the publicly available Amsterdam secondary school dataset provided by DUOFootnote 3 which contains 47 secondary schools and their locations. We combine this information with the School Guide datasetFootnote 4 collected by Municipality of Amsterdam that provides the capacities for each school based on the average number of students admitted in the previous years.

3.2 Preference model

At every round, each agent \(a_i \in A\) creates a preference list \(P_i = f_1 \succ ... \succ f_j\), \(\{f_1,..., f_j\} \subseteq F\) over schools. Each school appears once on the list. The preference list is based on a utility function \(U_{if}, f \in F\), and schools are sorted in descending order based on the total utility. Formally, the preference list P is defined as follows:

$$\begin{aligned} P_i = \{ U_{if}^\downarrow \}, \quad i \in A, f \in F \end{aligned}$$
(2)

Here \(\downarrow\) indicates the descending order. Accordingly, we consider a utility function \(U_i\),

$$\begin{aligned} U_i(\alpha ): F \rightarrow {\mathbb {R}}, \end{aligned}$$
(3)

which assigns a utility value to each school in F according to its composition and travel time to agent i; here \(\alpha\) is a set of parameters used as input to the weight agents’ relative preference between travel time and group composition.

We adopt the widely used Cobb-Douglas utility function, based on a function of school composition \(C: c_{g,f} \rightarrow {\mathbb {R}}\) and travel time from the agent’s residence to the school \(t_{i,f}\) [2, 7, 20].

$$\begin{aligned} U_{i,f} = c_{g, f}^{\; \alpha }\;t_{i,f}^{\;(1-\alpha )}, \end{aligned}$$
(4)

where g denotes the group that agent \(a_i\) belongs to and \(0 \le \alpha \le 1\) is a parameter that controls the importance of the group composition’s parameter over the travel time in the agents’ utility. When \(\alpha = 0\), agents only care about the travel time to a school, without considering its group composition. Travel time is normalized by the maximum value and is calculated as follows [2]:

$$\begin{aligned} t'_{i,f} = {\left\{ \begin{array}{ll} \frac{t_{max,i} \; - \; t_{i,f}}{t_{maxi} \; - \; t_{min, i}}, &{} \text {if } t_{i,f}\le t_{max,i} \\ 0, &{} \text {otherwise}. \end{array}\right. } \end{aligned}$$
(5)

For the school composition, we use a single-peaked utility function, that is maximized when the number of agents of the same group in a school \(x_{g,f}\) is equal to the homophily attribute \(h_i\) [2, 20]. Values above \(h_i\) incur a constant penalty M:

$$\begin{aligned} C(x_{g,f}, h_{i}, M) = {\left\{ \begin{array}{ll} \frac{x_{g,f}}{h_i}, &{} \text {if } x_{g,f} \le h_i \\ M + \frac{(1-x_{g, f}) (1-M)}{1-h_i}, &{}\text {if } x_{g,f} > h_i \end{array}\right. } \end{aligned}$$
(6)

M controls the level of dissatisfaction when the fraction of similar agents exceeds the optimal \(h_i\). In our experiments, we set no penalty on the homophily utility function (\(M=1\)), following Schelling’s segregation model. According to this model, once an agent is satisfied with the percentage of similar agents in a school, their utility does not diminish with the addition of further agents [24].

Interventions in the transportation network are performed to reduce the travel time \(t_{i,f}\) of agents to school, with the goal of increasing utility towards more segregated schools. We do test different conditions of both homophily (h), and group composition importance (\(\alpha\)), but network intervention strategies only affect the travel time \(t_{i,f}\).

3.3 Allocation method

Once the preference lists P are generated for all agents \(a_i \in A\) in each simulation round, they are then utilized as input for a school allocation mechanism denoted as R. The mechanism is defined as a function \(R: P \rightarrow F\) which takes as input a preference list \(p_i\) for agent \(a_i\) and capacity \(s_f\) for all \(f \in F\) and assigns a school \(f_i \in p_i\). Various allocation methods exist in both the academic literature and real-world admission systems [15, 17, 18]. To maintain consistency between the synthetic and real-world environments, we primarily focus on the Random Serial Dictatorship mechanism. This mechanism is widely used, including in Amsterdam’s school admission process.

Random Serial Dictatorship (RSD) is a popular mechanism for one-sided matching between schools and students [18]. In RSD, each student submits their preferences and is assigned a uniformly drawn lottery number. Subsequently, students are allocated to their top-preferred schools in increasing order of their lottery numbers, provided the school has available capacity. As a consequence, students with lower lottery numbers have a higher likelihood of being admitted to their top-preferred school. We utilize the RSD mechanism within the framework for allocations in each round. We assume that schools have the collective capacity to facilitate all students, i.e., \(\sum s_f \ge N\), and thus every student is ensured to be allocated to a school. Furthermore, the preference model outlined in Sect. 3.2 generates a ranking of all schools for every student. The allocation result is then aggregated for evaluation.

3.3.1 Evaluating the allocation

We are interested in studying the school segregation dynamics. Thus, in each simulation round, the allocation of agents to schools is evaluated on segregation. To quantify segregation, we use the Dissimilarity Index (DI), a measure that captures the differences in the proportions of agents from two distinct groups assigned to a school [55]. DI is a widely used measure for assessing segregation, as it takes into account the total number of agents from each group, making it suitable to use even when one group is a minority [56]. DI is defined for two groups (\(g_1\) and \(g_2\)) as follows:

$$\begin{aligned} DI=\frac{1}{2} \sum \limits _{f=1}^{|F|} |\frac{g_{1,f}}{G_1} - \frac{g_{2,f}}{G_2}|, \quad DI \in [0, 1] \end{aligned}$$
(7)

Here, \(g_{1,f}\) and \(g_{2,f}\) represent the number of agents in groups 1 and 2, respectively, in school f. \(G_1\) and \(G_2\) denote the total number of agents in groups 1 and 2 in the entire population. The Diversity Index (DI) value ranges from 0 (indicating minimal segregation) to 1 (indicating maximal segregation). While DI can be extended to account for more than two groups, we restrict our experiments to two groups, hence utilizing the fundamental equation.

3.4 Intervention model

In Eqs. 4–6 we showed that both travel time to a school and its composition are major components of an agent’s utility function. In reality, it is hard to intervene in the composition component of the utility function, as homophilic preferences tend to develop over the life course [19, 57]. Therefore, we investigate the effects of intervening in public transportation networks with the goal of decreasing travel time to popular, yet segregated schools. This intervention aims to facilitate easier access for members of minority groups, enabling them to include these schools in their preferences. Transport interventions consist of graph augmentations (edge additions), which lead to the creation of a new edge set \(E': {\mathbb {G}}\) in the spatial graph, under a budget \(B,: |E'| = B\).

$$\begin{aligned} E': {\mathbb {G}}, B \rightarrow \mathbb {G'} \end{aligned}$$
(8)

It follows that \(\mathbb {G'} = (V, E \cup E')\). Interventions can be seen as a proxy for the creation/expansion of public transportation lines in a real city, such as new bus routes, metro lanes, tram lines, or the planning of school bus routes. We constrain the total number of interventions to a budget B, to reflect a city’s resource limitations.

3.4.1 Greedy centrality optimization

Making a school more accessible is a non-trivial optimization problem, especially for large graphs [50]. We use a greedy algorithm to approximate the optimal set of interventions to apply to the graph with respect to accessibility. This translates to increasing a school node centrality \({\mathbb {C}}\) with respect to the other nodes. We evaluate strategies based on the classic graph measures of closeness (\({\mathbb {C}}_C\)) and betweenness (\({\mathbb {C}}_B\)) network centrality. We consider these two metrics as they can be understood as proxies for average proximity of citizens to specific points of interest in a city. While closeness centrality can directly translate the average distance between neighbourhoods and specific points of interest, betweenness centrality can convey how relevant is a specific location (e.g., a school) in being accessible to pairs of endpoints (e.g., two neighbourhoods with a different demographic composition).

At every intervention step, we find the school that has the lowest centrality measure with respect to any group and then add the intervention that leads to the maximum increase in this node’s centrality. The process is described in Algorithm 1.

Algorithm 1
figure a

Greedy Centrality Optimization

Full size image

3.4.2 Group-based centrality

Classic centrality measures fail to effectively capture group dynamics in a graph. In segregated environments like metropolitan cities, central areas can theoretically exhibit high overall closeness centrality, despite specific groups having low accessibility to them. Examples of this phenomenon include modern cities where low-income households concentrate in the outskirts, while high-income households are situated closer to the centre, and vice-versa. To account for this disparity in measurement, we introduce group-based extensions of the classic centrality measures \({\mathbb {C}}^g,\; g \in G\), that take into account the distribution of groups within nodes. Those are namely group-based closeness \({\mathbb {C}}^g_C\) and group-based betweenness \({\mathbb {C}}^g_B\) centrality. Let \(D_g, \; g \in G\) be the distribution of group g on all nodes V in the network such that \(\sum _g D_g = 1\).

3.4.3 Group-based closeness centrality

Group-based closeness \({\mathbb {C}}^g_C\) of a node \(v \in V\) is defined as the reciprocal of the sum of travel times from all other nodes u, weighted by the fraction of agents of group g in u, defined as p(g|u).

$$\begin{aligned} {\mathbb {C}}^g_C(v) = \sum \limits _u \frac{1}{t(u,v) \; p(g|u)} \end{aligned}$$
(9)

Where t(u, v) is the travel time between nodes u and v. This metric expands upon the conventional definition of overall closeness for a node by introducing |G| centrality measures. Each centrality measure represents the closeness of the node with respect to a specific group \(g \in G\).

3.4.4 Group-based betweenness centrality

Group-based betweenness \({\mathbb {C}}^g_B\) of a node \(v \in V\) is defined as the number of shortest paths \(\sigma\) from all nodes \(o \in V\) to all nodes \(d \in V, o \ne d\), that pass through v, weighted by the fraction of agents of group g in d. p(g|d).

$$\begin{aligned} {\mathbb {C}}^g_B(v) = \sum \limits _{o\ne v \ne d} \frac{\sigma _{t_{o,d} (v)}}{\sigma _{t_{o,d}}} p(g|d) \end{aligned}$$
(10)

Accordingly, this metric is also expanded with respect to groups and represents the total number of shortest paths that pass through v for agents of a specific group g.

School segregation depends not only on preferences, but also on the allocation method (section 3.3), which has a random element to it. Therefore, optimizing directly for the dissimilarity index is not possible. Instead, we look for the best set of edges \(E'\) to add to the graph, so as to accessibility to certain schools for certain groups, aiming to affect the agent’s preferences in such a way that segregation is reduced.

We test two classes of greedy interventions: (1) Centrality and (2) Group-based Centrality Optimization. We identify the schools that have the lowest network centrality measure (closeness or betweenness) with respect to any group and then add the intervention that leads to the maximum increase in that node’s corresponding (1) centrality or (2) group-based centrality.

3.5 Simulation details

Together with the paper, we release the code utilized for running simulations, which replicates the structure illustrated in Fig. 1. The framework is exclusively Python-based and relies on igraph as the primary library for computing centralities and manipulating networks.Footnote 5 Additionally, we provide the code for computing the proposed group-based centralities. The framework code is modular, meaning that each core component (environment, preference, allocation, evaluation, and intervention) resides in its own Python module and can be expanded simply by defining a new method within the module. Moreover, we offer the code for generating the synthetic and real-world environments used in our experiments. Finally, the code integrates a logging module that records detailed metrics and result figures for every simulation round. More details on the code can be found in the GitHub repository.Footnote 6 Table 1 shows the parameters used to run the experiments in this paper.

Table 1 Parameters used in running the experiments
Full size table

4 Results

In this section, we present the results of our study, providing a comprehensive analysis of the simulations and the most important parameters of our framework, as well as the impact of network interventions on school segregation.

4.1 Reducing segregation without transportation interventions is difficult

In Fig. 4a, we display varying levels of school segregation across different parameters of the utility equation (Eq. 4). Specifically, we examine the in-group preference parameter h (representing homophily or the optimal fraction of students from the same group) and \(\alpha\) (indicating the importance weight of group composition in the preference function). In panel (b), we depict a similar plot while maintaining \(h=0.8\). We illustrate the outcomes in environments characterized by extremely high segregation and high homophily, while altering the network structure to be more or less connected (via m). Panel (a) demonstrates that in environments with initially high segregation, households start opting for more diverse schools, but only if their homophily is significantly reduced (\(0.0 \le h \le 0.4\)). This requires a significant shift in citizens’ attitudes towards individuals from different groups when selecting schools.

Panel (b) showcases the impact of altering the graph structure while keeping homophily high and constant. It reveals that as the graph becomes more modular, segregation increases. This effect is more pronounced with a higher \(\alpha\), signifying that agents strongly consider the group composition of the school when creating their preference lists. When \(\alpha = 0\), agents only consider distance, resulting in a significant reduction in school segregation when modularity is reduced. Even with \(0.1 \le \alpha < 0.4\), a parameter range considered more realistic [9], segregation decreases with modularity. This suggests that, generally, enhancing connectivity between communities in highly segregated environments can effectively reduce school segregation. However, the figure also highlights the need for strategic interventions, as sometimes an increase in modularity can lead to a reduction in segregation (as depicted in the line for \(\alpha =0.5\)).

Next, we analyze the impact of inter-community interventions in segregation.

4.2 Inter-community transport interventions can reduce segregation

To investigate the effects of interventions on school segregation, we conducted experiments in both the synthetic environments and Amsterdam. Figure 5 illustrates the outcomes obtained by applying the greedy centrality improvement algorithm to the Grid (top) and SBM (bottom) environments. For SBM, we examined results for a realization with high modularity (\(m \approx 0.06\)).

In each environment, 30 simulation rounds were executed. In each round, agents generated preference lists for schools and were assigned a lottery number using the Random Serial Dictatorship (Sect. 3.3). To mitigate stochastic variance, five different lottery generations were conducted for each round, and the average values were plotted. Interventions occurred at intervals of 3 rounds, with an intervention budget of 5 for SBM and 1 for Grid (due to its smaller scale). By considering interventions over multiple rounds we aim at capturing the long-term effects of network interventions while considering that such policies occur over the same time scale at which agents are forming their preferences for schools and being allocated.

As depicted in Fig. 5 (left column), when \(\alpha = 0.0\), any intervention that reduces travel time leads to a decrease in segregation in both settings. This outcome is expected, given that, when \(\alpha = 0.0\), agents consider only the distance to a school. Therefore, an ideal, complete graph would yield the minimum achievable school segregation. However, as the figures depict, a sensible strategy needs to be devised for efficient reduction of segregation: under all values for \(\alpha\), random edge interventions are either ineffective, or perform worse than strategic ones based on centrality measures.

When \(\alpha > 0.0\), we observe that the best strategy to use is not straightforward. In the SBM environment, interventions focused on greedily enhancing the betweenness and group betweenness centrality of a segregated school demonstrated the most significant impact on segregation in the long term. Although both strategies converge to a similar segregation measure, group-based betweenness interventions had the most immediate impact. This finding aligns with the setup of the SBMs, where both generated communities have an equal number of schools near their residential nodes, thus ensuring that no community is disadvantaged in terms of travel time (we demonstrate in Sect. 4.3 a case where a community is clearly disadvantaged). Consequently, interventions that aim to reduce the distance between nodes in one community and schools in the other prove less effective, as these agents already have schools sufficiently close to select them instead.

Conversely, betweenness-based interventions do not directly bring remote schools closer to a community, but instead connect them to other nodes with higher betweenness, incorporating them into the path of many more nodes to that school, as opposed to just a few. This leads to a more effective reduction of segregation, and the proposed group-based betweenness centrality strategy outperforms the classic measure in terms of effectiveness and efficiency.

In both environments, a delay is observed between the first interventions and the reduction of segregation. This is due to each community being well-structured and in close proximity to their respective schools. Thus, adding a few new links is insufficient to disrupt this structure and compel agents to choose schools in the other community. Similarly, we see that, after a certain point, segregation reaches a plateau, and further interventions can event exacerbate it. This occurs because, once the graph becomes densely connected, new interventions are no longer beneficial. Overall, we conclude that distinct graph structures require varied intervention strategies. Further research is needed to study optimal strategies for interventions under diverse structures.

Fig. 5
figure 5

Analysis of SBM and grid environments. Results for \(\alpha > 0.4\) are omitted since the Dissimilarity Index (DI) stays stable at the maximum (DI = 1). We study the effect of regular interventions on the transportation network by introducing new transit connections according to different network centrality criteria: (1) random; (2) closeness centrality or (3) betweeness centrality. We observe that interventions based on betweeness centrality lead to more expedite and effective segregation reduction

Full size image

4.3 A reduction of segregation is possible in Amsterdam with transportation interventions

We perform the same analysis on Amsterdam. Figure 6 illustrates the impact of transport network interventions on school segregation within the context of Amsterdam over a span of 30 simulation rounds, considering different values of \(\alpha\) (here, we consider a wider range of \(\alpha\). The preference generation and school allocation procedures remained consistent with previous experiments but we notably incorporated real-world residential segregation levels and school capacities from Amsterdam into our simulations.

Firstly, when \(\alpha =0\) (top-left panel) and preference only depends on the distance of a school, baseline school segregation is low and interventions do not have a discernible impact. This also confirms empirical findings that if school choice only depended on distance it would result into more mixed schools (\(DI_{residential} = 0.40, DI_{school} = 0.25\)) [12, 13].

For \(0.2 \le \alpha \le 0.6\), the results overall indicate that school segregation in Amsterdam can be reduced over time using interventions based on closeness centrality. This is in contrast to the synthetic environments where betweenness worked best. Moreover, we observe that also in contrast to the synthetic environments, group-based centrality strategies are not generally more efficient than classic measures-based ones. In Sect. 4.4, we analyze this phenomenon and discuss the impact of our strategies on different graph structures.

We also observe that when \(\alpha > 0.6\), and too much emphasis is given to the ethnic composition of schools, transportation interventions do not exhibit a substantial impact on school segregation levels. Compared to the synthetic environments, the proposed strategies in Amsterdam are more resilient to high \(\alpha\) agents, and segregation is reduced even when agents care slightly more about homophily than travel time. This outcome extends previous theoretical findings, which observed that increased tolerance among parents reduces school segregation most prominently for \(0.2 \le \alpha \le 0.6\) [7]. Here we show that in a real-world example, transportation interventions are also limited when the importance of group composition is high on students’ preferences

Fig. 6
figure 6

In Amsterdam, targeted interventions in the network can decrease segregation over time, particularly for values of alpha in the range of \(0.2 \le \alpha \le 0.6\). Strategies based on closeness perform best over other centrality measures

Full size image

4.4 Different graph structures require different strategies

In our earlier findings, we observed that a strategy based on betweenness centrality works best for the SBM environment, while in the real-world Amsterdam environment, closeness improvement is the best strategy. Here, we investigate how the effectiveness of each strategy is influenced by the underlying graph structure.

Figure 7 illustrates the group-specific distributions of closeness, betweenness, and degree for both SBM and Amsterdam’s school nodes. It is evident that SBM communities, characterized by equal total population and easily accessible schools, have comparable centrality distributions. In contrast, Amsterdam’s schools reveal a notable disparity in accessibility between the two groups. Specifically, individuals of non-Western backgrounds face greater average distances to schools, exacerbating the existing population disadvantage. Hence, interventions based on group closeness are the most effective strategy in this scenario. By targeting nodes primarily populated by individuals from non-Western backgrounds, travel time to schools can be reduced in general, which leads to a reduction in segregation.

Fig. 7
figure 7

Plotting group-based centrality histograms reveals hidden disadvantages between groups and hints towards a good strategy for interventions. Here, we show a big disparity in closeness centrality between the two groups in the Amsterdam environment. Non-western areas are, on average, further away from schools than their Western counterparts. This makes group-based centrality a good strategy to follow, as it reduces this disparity

Full size image

5 Discussion

With this study, we investigate the impact of transportation interventions on school segregation within various environments. Our framework introduces a novel approach to analyze the potential of transportation networks to mitigate school segregation. Building upon prior research on urban segregation dynamics, we analyze the relationship between citizens’ preferences, school allocation policies, and interventions within complex networks. Our analysis extends recent works by incorporating synthetic data for generalizability and by examining a real-world case study. That said, there are several limitations to our study; here we outline the most important ones.

In our model of Amsterdam, each area is represented as a node and is linked to its immediate neighbours through edges. While this approach benefits from being easily generalizable to cities with different scales and typologies [36], it assumes uniformity in the size and surrounding environment of each area. In reality, areas vary in their accessibility to neighbouring regions, with some areas being less accessible overall. Additionally, we assume that all agents within an area start from the same node, which leads to inaccuracies when estimating the travel time, especially in larger areas.

In our experiments, we assumed a constant (unit) travel time between any two connected nodes. This simplification helps us create a framework that can be used in various cities. However, it doesn’t consider differences in real travel times, which can vary based on factors like location, geography, and how crowded an area is. Effectively, the greedy intervention strategies would not be altered, as they account for network travel time. But the specific nodes we target for intervention might change, since their original centralities would be altered. In other words, while our overall approach stays the same, considering actual travel times will likely lead us to focus on different areas, which could have a different impact on reducing segregation.

In the Amsterdam experiments, we examined the effects of different values of \(\alpha\), representing varying levels of significance regarding the group composition of schools. Furthermore, we assumed that the homophily parameter of each agent aligns with the majority group’s distribution in their residential node. These parameters were not calibrated using real-world preference data; alternatively, we analyzed the impact of the most important ones and based others on previous studies [2, 9].

Lastly, when introducing new interventions into the network, we do not impose distance restrictions. Theoretically, any node can be connected to any other node via a new edge. This intentional decision allows us to investigate the potential for reducing segregation through interventions, which necessitates the relaxation of certain constraints. Furthermore, we aim to consider the possibility of adding rapid transportation methods like trains and metros, which generally can facilitate connections over larger distances compared to, for example, buses.

We demonstrated the usefulness of introducing group-based centrality measures in network-based ABMs. They unveil hidden patterns of inequality that traditional metrics miss. However, we cannot definitively claim that interventions focused on greedily increasing group-based centralities are universally more efficient. We noted that this efficiency varies based on network structure and population distribution. Further research is needed to provide more conclusive assertions.

6 Conclusion

We introduced a novel agent-based simulation framework to investigate the influence of transportation network interventions on school segregation within the context of both free school choice and centralized school admission mechanisms. We first demonstrated that reducing segregation at the school level requires a significant shift in citizens’ preferences regarding out-group interactions. As such preferences can persist over time, we illustrate that, alternatively, interventions on transportation has the potential to diminish segregation, even without altering attitudes towards the out-group. Our experiments involved both synthetic and real-world settings, highlighting that targeted transportation interventions, by reducing travel barriers between specific schools and communities, can progressively mitigate school segregation. We also proposed novel group-based centrality metrics to provide finer-grained measurements of centrality concerning specific groups within agent-based networks. Furthermore, we showed that different graph structures necessitate different intervention strategies, and conducted an analysis of the graph conditions favoring one strategy over another.

The proposed framework has the potential to be extended to consider other mechanisms for centralized admission [58], and even beyond schools, enabling the study of segregation in various aspects of daily interactions. Future studies could delve into exploring diverse spatial networks and evaluating the impact of less myopic, more long-term intervention strategies. Additionally, while this paper does not delve into the impact of new modes of transportation on household preference functions beyond travel time, the proposed framework can be adapted to account for it.