Abstract
Egalitarian considerations play a central role in many areas of social choice theory. Applications of egalitarian principles range from ensuring everyone gets an equal share of a cake when deciding how to divide it, to guaranteeing balance with respect to gender or ethnicity in committee elections. Yet, the egalitarian approach has received little attention in judgment aggregation—a powerful framework for aggregating logically interconnected issues. We make the first steps towards filling that gap. We introduce axioms capturing two classical interpretations of egalitarianism in judgment aggregation and situate these within the context of existing axioms in the pertinent framework of belief merging. We then explore the relationship between these axioms and several notions of strategyproofness from social choice theory at large. Finally, a novel egalitarian judgment aggregation rule stems from our analysis; we present complexity results concerning both outcome determination and strategic manipulation for that rule.
Similar content being viewed by others
Explore related subjects
Find the latest articles, discoveries, and news in related topics.Avoid common mistakes on your manuscript.
1 Introduction
Judgment aggregation is an area of social choice theory concerned with turning the individual binary judgments of a group of agents over logically related issues into a collective judgment [22]. Being a flexible and widely applicable framework, judgment aggregation provides the foundations for collective decision making settings in various disciplines, like philosophy, economics, legal theory, and artificial intelligence [38]. The purpose of judgment aggregation methods (rules) is to find those collective judgments that better represent the group as a whole. Following the utilitarian approach in social choice, the will of the majority has traditionally been considered an “ideal” such collective judgment. In this paper we challenge this perspective, introducing a more egalitarian point of view.
In economic theory, utilitarian approaches are often contrasted with egalitarian ones [55]. In the context of judgment aggregation, an egalitarian rule must take into account whether the collective outcome achieves equally distributed satisfaction among agents and ensure that agents enjoy equal consideration. A rapidly growing application domain of egalitarian judgment aggregation (that also concerns multiagent systems with practical implications like in the construction of self-driving cars) is the aggregation of moral choices [15], where utilitarian approaches do not always offer appropriate solutions [3, 57]. One of the drawbacks of majoritarianism is that a strong enough majority can cancel out the views of a minority, which is questionable in several occasions.
For example, suppose that the president of a student union has secured some budget for the decoration of the union’s office and she asks her colleagues for their opinions on which paintings to buy (perhaps imposing some constraints on the combinations of paintings that can be simultaneously selected, due to clashes on style). If the members of the union largely consist of pop-art enthusiasts that the president tries to satisfy, then a few members with diverting taste will find themselves in an office that they detest; an arguably more viable strategy would be to ensure that—as much as possible—no-one is strongly dissatisfied. Consider a similar situation in which a kindergarten teacher needs to decide what toys to complement the existing playground with. In that case, the teacher’s goal is to select toys that equally (dis)satisfy all kids involved, so that no extra tension is created due to envy, which the teacher will have to resolve—if the kids disagree a lot, then the teacher may end up choosing toys that none of them really likes.Footnote 1
Besides our toy examples, egalitarian principles are also taken into consideration within social contexts of larger scale, like in laws that aim to prevent price-gouging: If an upper bound is enforced to the price of a commodity implying that no seller will have an interest to supply it, then consumers will not have access to the commodity and sellers will make no profit from it. Although this situation causes less happiness overall, it is considered fair because no person can become much happier than another one (in other words, the difference in happiness is minimised).
In order to formally capture scenarios like the above, this paper introduces two fundamental properties (also known as axioms) of egalitarianism to judgment aggregation, inspired by the theory of justice. The first captures the idea behind the so-called veil of ignorance of Rawls [60], while the second speaks about how happy agents are with the collective outcome relative to each other.
Our axioms closely mirror properties in other areas of social choice theory. In belief merging, egalitarian axioms and merging operators have been studied by Everaere et al. [28]. The nature of their axioms is in line with the interpretation of egalitarianism in this paper, although the two main properties they study are logically weaker than ours, as we further discuss in Sect. 3.1.Footnote 2 Also, in resource allocation, fairness has been interpreted both as maximising the share of the worst off agent [11] as well as eliminating envy between agents [31].
Unfortunately, egalitarian considerations often come at a cost. A central concern in many areas of social choice theory, from which judgement aggregation is not exempted, is that agents may have incentives to manipulate, i.e., to misrepresent their judgments aiming for a more preferred outcome [19]. Frequently, it is impossible to simultaneously be fair and avoid strategic manipulation. For both variants of fairness in resource allocation, rules satisfying them usually are susceptible to strategic manipulation [1, 9, 13, 54]. The same type of results have recently been obtained for multiwinner elections [49, 58]. It is not easy to be egalitarian while disincentivising agents from taking advantage of it.
Inspired by notions of manipulation stemming from voting theory, we explore how our egalitarian axioms affect the agents’ strategic behaviour within judgment aggregation. Our most important result in this vein is showing that the two properties of egalitarianism defined in this paper clearly differ in terms of their relationship to strategyproofness.
Our axioms give rise to two concrete egalitarian rules—one that has been previously studied, and one that is new to the literature. For the latter, we are interested in exploring how computationally complex its use is in the worst-case scenario. This kind of question, first addressed by Endriss et al. [27], is regularly asked in the literature of judgment aggregation [4, 24, 51]. As Endriss et al. [25] wrote recently, the problem of determining the collective outcome of a given judgment aggregation rule is “the most fundamental algorithmic challenge in this context”.
The remainder of this paper is organised as follows. Section 2 reviews the basic model of judgment aggregation, while Sect. 3 introduces our two original axioms of egalitarianism and the rules they induce. Section 4 analyses the relationship between egalitarianism and strategic manipulation in judgment aggregation, and Sect. 5 focuses on relevant computational aspects: although the general problems of outcome determination and of strategic manipulation are proven to be very difficult, we propose a way to confront them with the tools of Answer Set Programming [35]. Section 6 concludes, and Sect. 1 contains additional technical details that were missing from the previous version of the paper [7].
2 Basic model
Our framework relies on the standard formula-based model of judgment aggregation [52], but for simplicity we also use notation commonly employed in binary aggregation [37].
Let \({\mathbb {N}}\) denote the (countably infinite) set of all agents that can potentially participate in a judgment aggregation setting. In every specific such setting, a finite set of agents \(N \subset {\mathbb {N}}\) of size \(n\ge 2\) express judgments on a finite and nonempty set of issues (formulas in propositional logic) \(\Phi = \{\varphi _1, \dots , \varphi _m \}\), called the agenda.Footnote 3\({\mathcal {J}}(\Phi ) \subseteq \{0,1 \}^m\) denotes the set of all admissible opinions on \(\Phi \). Then, a judgment J is a vector in \({\mathcal {J}}(\Phi )\), with 1 (0) in position k meaning that the issue \(\varphi _k\) is accepted (rejected). \({\bar{J}}\) is the antipodal judgment of J: for all \(\varphi \in \Phi \), \(\varphi \) is accepted in \({\bar{J}}\) if and only if it is rejected in J. For example, for the agenda \(\Phi = \{p,q,p\wedge q \}\), the formuas p, q, and \(p \wedge q\) are the issues, and the set of all admissible opinions is \({\mathcal {J}}(\Phi ) = \{(1,1,1), (1,0,0), (0,1,0), (0,0,0)\} \); each of the four vectors in \({\mathcal {J}}(\Phi ) \) may be a judgment J. For simplicity, we will often abbreviate a judgment by only keeping its numerical values: e.g., (1, 1, 1) may be abbreviated to 111.
A profile \({\varvec{J}}= (J_1, \dots J_n) \in {\mathcal {J}}(\Phi )^n\) is a vector of individual judgments, one for each agent in a group N. We write \({\varvec{J}}' =_{-i} {\varvec{J}}\) when the profiles \({\varvec{J}}\) and \({\varvec{J}}'\) are the same, besides the judgment of agent i. We write \({\varvec{J}}_{-i}\) to denote the profile \({\varvec{J}}\) with agent i’s judgment removed, and \(({\varvec{J}}, J) \in {\mathcal {J}}(\Phi )^{n+1}\) to denote the profile \({\varvec{J}}\) with judgment J added—importantly, in our variable population framework, the profile \({\varvec{J}}_{-i}\) where agent i abstains is admissible. A judgment aggregation rule F is a function that maps every possible profile \({\varvec{J}}\in {\mathcal {J}}(\Phi )^n\), for every group N and agenda \(\Phi \), to a nonempty set \(F({\varvec{J}})\) of collective judgments in \({\mathcal {J}}(\Phi )\). Note that a judgment aggregation rule is defined over groups and agendas of variable size, and may return several, tied, collective judgments.
The agents that participate in a judgment aggregation scenario will naturally have preferences over the outcome produced by the aggregation rule. First, given an agent i’s truthful judgment \(J_i\), we need to determine when agent i would prefer a judgment J over a different judgment \(J'\). Preferences defined by the Hamming distance constitute one among several ways to define agents’ preferences in judgment aggregation—yet, they are the most prevalent ones in the literature [5, 6, 8, 64]. They correspond to commonly considered preferences based on the swap-distance in preference aggregation, and to preferences based on the size of the symmetric difference between an agent’s true approval set and the outcome in multiwinner approval voting [10]. In order to be able to compare our results with previous one of the literature, in this paper we also assume Hamming-distance preferences.
The Hamming distance between two judgments J and \(J'\) equals the number of issues on which these judgments disagree—concretely, it is defined as \(H(J,J')= \sum _{\varphi \in \Phi } |J(\varphi ) - J'(\varphi )|\), where \(J(\varphi )\) denotes the binary value in the position of \(\varphi \) in J. For example, \(H(100, 111)=2\). Then, the (weak, and analogously strict) preference of agent i over judgments is defined by the relation \(\succeq _i\) (where \(J \succeq _i J'\) means that i’s utility from J is not lower than that from \(J'\)):
But an aggregation rule often outputs more than one judgment, and thus we also need to determine agents’ preferences over sets of judgments.Footnote 4
We define two requirements guaranteeing that the preferences of the agents over sets of judgments are consistent with their preferences over single judgments. To that end, let \(\mathrel {\mathring{\succeq }}_i\) (with strict part \(\mathrel {\mathring{\succ }}_i\)) denote agent i’s preferences over sets \(X,Y \subseteq {\mathcal {J}}(\Phi )\). We require that \(\mathrel {\mathring{\succeq }}_i\) is related to \(\succeq _i\) as follows:
-
\(J \succeq _i J'\) if and only if \(\{J\} \mathrel {\mathring{\succeq }}_i \{J'\}\), for any \(J,J' \in {\mathcal {J}}(\Phi )\);
-
\(X \mathrel {\mathring{\succ }}_i Y\) implies that there exist some \(J \in X\) and \(J' \in Y\) such that \(J \succ _i J'\) and \(\{J,J'\} \not \subseteq X \cap Y\).
The above conditions hold for almost all well-known preference extensions. For example, they hold for the pessimistic preference (\(X \succ ^{\textit{pess}}Y\) if and only if there exists \(J'\in Y\) such that \(J \succ J'\) for all \(J \in X\)) and the optimistic preference (\(X \succ ^{\textit{opt}}Y\) if and only if there exists \(J\in X\) such that \(J \succ J'\) for all \(J' \in Y\)) of Duggan and Schwartz [20], as well as the preference extensions of Gärdenfors [32] and Kelly [43]. The results provided in this paper abstract away from specific preference extensions.
3 Egalitarian axioms and rules
This section focuses on two axioms of egalitarianism in judgment aggregation. We examine them in relation to each other and to existing properties from belief merging, as well as to the standard majority property defined below. Most of the well-known judgment aggregation rules return the majority opinion, when that opinion is logically consistent [23].Footnote 5
Let \(m({\varvec{J}})\) be the judgment that accepts exactly those issues accepted by a strict majority of agents in \({\varvec{J}}\). A rule F is majoritarian when for all profiles \({\varvec{J}}\), \(m({\varvec{J}}) \in {\mathcal {J}}(\Phi )\) implies that \(F({\varvec{J}})=\{J\}\).
Our first axiom with an egalitarian flavour is the maximin property, suggesting that we should aim at maximising the utility of those agents that will be worst off in the outcome. Assuming that everyone submits their truthful judgment during the aggregation process, this means that we should try to minimise the distance of the agents that are furthest away from the outcome. Formally:
- \(\blacktriangleright \):
-
A rule F satisfies the maximin property if for all profiles \({\varvec{J}}\in {\mathcal {J}}(\Phi )^n\) and judgments \(J\in F({\varvec{J}})\), there is no judgment \(J'\) such that the following holds:
$$\begin{aligned} \max _iH(J_i,J') < \max _i H(J_i,J) \end{aligned}$$
Example 1
Consider the agenda \(\Phi =\{p, q, p\wedge q\}\) such that \({\mathcal {J}}(\Phi ) = \{(1,1,1), (1,0,0), (0,1,0), (0,0,0)\} \), and take the profile \({\varvec{J}}\) consisting of one agent with judgment \(J= (1,0,0)\), and two agents with judgment \(J'= (0,1,0)\). Consider the well known median judgment aggregation rule[56]Footnote 6 defined as follows:

We have that \(\text {MedHam}({\varvec{J}}) = \{(0,1,0)\}\). Also, \(\text {MedHam}\) does not satisfy the maximin property because \(1 = \max _i H(J_i,000) < \max _i H(J_i,010) = 2\).
Although the maximin property is quite convincing, there are settings like those motivated in the Introduction where it does not offer sufficient egalitarian guarantees. We thus consider a different property next, which we call the equity property. This axiom requires that the gaps in the agents’ satisfaction be minimised. In other words, no two agents should find themselves in very different distances with respect to the collective outcome. Formally:
- \(\blacktriangleright \):
-
A rule F satisfies the equity property if for all profiles \({\varvec{J}}\in {\mathcal {J}}(\Phi )^n\) and judgments \(J\in F({\varvec{J}})\), there is no judgment \(J'\) such that the following holds:

No rule that satisfies either the maximin property or equity property can be majoritarian—this observation subsumes Example 1 about the median rule that also is majoritarian. As an illustration, in a profile of only two agents who disagree on some issues, any egalitarian rule will try to reach a compromise, and this compromise will not be affected if any agents holding one of the two initial judgments are added to the profile—in contrast, a majoritarian rule will simply conform to the crowd.
Proposition 1 shows that it is also impossible for the maximin property and the equity property to simultaneously hold. Therefore, we have established the logical independence of all three axioms discussed so far: maximin, equity, and majoritarianism.
Proposition 1
No judgment aggregation rule can satisfy both the maximin property and the equity property.
Proof
Take an agenda \(\Phi \) such that \({\mathcal {J}}(\Phi ) = \{J_1 = 1110, J_2 = 0111, J = 0000\}\), and consider the profile \({\varvec{J}}= (J_1,J_2)\). Then, the equity property would require that \(F({\textbf{J}}) = \{J\}\) as J gives utility 1 to both agents (thus minimising the difference between the best off and the worst off agent), while the maximin property would require that \(F({\textbf{J}}) \subseteq \{J_1,J_2\}\) (as both these judgments give the worst off agent utility 2). So, no rule F can satisfy the two properties at the same time. \(\square \)
From Proposition 1, we also know now that the two properties of egalitarianism generate two disjoint classes of aggregation rules. In particular, in this paper we focus on the maximal rule that meets each property: a rule F is the maximal one of a given class if, for every profile \({\varvec{J}}\), the outcomes obtained by any other rule in that class are always outcomes of F too. Although maximal rules produce many ties, they are useful because their outcomes only rely on a specific property, and as such are more easily explained and justified.Footnote 7
The maximal rule satisfying the maximin property is the rule MaxHam (see, e.g., Lang et al. [50]). For all profiles \({\varvec{J}}\in {\mathcal {J}}(\Phi )^n\), the following holds:

Analogously, we define a rule new to the judgment aggregation literature, which is the maximal one satisfying the equity property. For all profiles \({\varvec{J}}\in {\mathcal {J}}(\Phi )^n\), the following holds:

To better understand these rules, consider the agenda \(\Phi =\{p, q, p\wedge q\}\). Suppose that there are only two agents in a profile \({\varvec{J}}\), holding judgments \(J_1=(111)\) and \(J_2=(010)\). Then, we have that \(\text {MaxHam}({\varvec{J}})=\{(111),(010),(100)\}\), while \(\text {MaxEq}=\{(100)\}\). In this example, the difference in spirit between the two rules of our interest is evident. Although the MaxHam rule could fully satisfy exactly one of the agents without causing much harm to the other, it has the potential to create greater unbalance than the MaxEq rule, which in turn ensures that the two agents are equally happy with the outcome (under Hamming-distance preferences). In that sense, MaxEq is better suited for a group of agents that do not want any of them to feel particularly put upon, while MaxHam seems more desirable when a minimum level of happiness is asked for.
The MaxHam rule is also similar to the minimax approval voting rule [10]. The approval voting framework is a special case of judgment aggregation, where there are no logical constraints on the judgments and the agents can accept any subset of the given issues. Brams et al. [10] are also interested in manipulability questions (and work with Hamming-distance preferences), but the specific variant of the minimax rule that they consider differentiates their results from ours. In particular, their proposed rule weighs the judgments that appear in a profile with respect to their proximity to other judgments, while this is not the case for MaxHam. As finding the outcome of minimax is computationally hard, Caragiannis et al. [12] provide approximation algorithms that circumvent this problem. Caragiannis et al. also demonstrate the interplay between manipulability and lower bounds for the approximation algorithm—establishing strategyproofness results for approximations of minimax.
3.1 Relations with egalitarian belief merging
A framework closely related to ours is that of belief merging [45], which is concerned with how to aggregate several (possibly inconsistent) sets of beliefs into one consistent belief set. Egalitarian belief merging is studied by Everaere et al. [28], who examine interpretations of the Sen-Hammond equity condition [63] and the Pigou-Dalton transfer principle [17]—two properties that are logically incomparable.Footnote 8 We situate our egalitarian axioms within the context of these egalitarian axioms from belief merging;
we reformulate these axioms into our framework.
- \(\blacktriangleright \):
-
Fix an arbitrary profile \({\varvec{J}}\), agents i, j, and any two judgments \(J, J' \in {\mathcal {J}}(\Phi )\). An aggregation rule F satisfies the Sen-Hammond equity property if whenever
$$\begin{aligned} H(J_i, J)< H(J_i,J')< H(J_j,J') < H(J_j, J) \end{aligned}$$and \(H(J_{i'}, J) = H(J_{i'}, J')\) for all other agents \(i' \in N\setminus \{i,j\}\), then \(J \in F({\varvec{J}})\) implies \(J' \in F({\varvec{J}})\).
For maximin it is easy to see that Sen-Hammond is a weaker axiom. While maximin requires us to maximise the minimum utility in all cases, Sen-Hammond only requires this in case a particular condition is satisfied. As far as equity is concerned, the maximal rule satisfies Sen-Hammond, as we show in Proposition 2 below.
Proposition 2
MaxEq satisfies the Sen-Hammond equity property.
Proof
Let \({\varvec{J}}\) be a profile and let \(i^*, j^*\) be agents, and \(J, J'\) judgments such that \(H(J_{i^*},J)< H(J_{i^*},J')<H(J_{j^*},J') <H(J_{j^*},J)\). Further, let \(H(J_{i}, J) = H(J_{i}, J')\) for all other agents \(i \in N\setminus \{i^*,j^*\}\). Let \(F = \text {MaxEq}\)—the maximal rule satisfying equity. We want to show that F must satisfy the Sen-Hammond property. To this end, we show that \(J \in F({\varvec{J}})\) implies \(J' \in F({\varvec{J}})\).
First, we define \(d_e({\varvec{J}}, J)\) to be the maximal difference in utility for J given agents’ judgments in \({\varvec{J}}\). Formally, \(d_e({\varvec{J}}, J) = \max _{i,j\in N} |H(J_i,J)-H(J_j,J)|\).
We know that the maximal difference in utility for \(J'\) cannot be the difference in utilities between the agents \(i^*\) and \(j^*\): Indeed, by equity we know that if \(J \in F({\varvec{J}})\) then it cannot be the case that \(|H(J_{i^*}, J') - H(J_{j^*}, J')| < |H(J_{i^*}, J) - H(J_{j^*}, J)|\). We also know that if the maximal difference in utility for \(J'\) is the difference in utilities between agents in \(N\setminus \{i^*, j^*\}\), then we are done, since \(H(J_{i}, J) = H(J_{i}, J')\) for all agents \(i \in N\setminus \{i^*,j^*\}\).
So, suppose the maximal difference in utility for \(J'\) is the difference in utilities between \(i^*\) and some agent \(k \ne j^*\), i.e., \(d_e({\varvec{J}}, J') = |H(J_{i^*},J')-H(J_{k},J')|\). The case for \(j^*\) and some agent \(k \ne i^*\) is symmetric. Let \(x = H(J_k, J) = H(J_k, J')\).
-
If \(x > H(J_{i^*},J)\), then we know that \(|H(J_{i^*}, J) - x| > |H(J_{i^*}, J') - x|\) because \(H(J_{i^*},J) < H(J_{i^*},J')\) by assumption.
-
If \(x \le H(J_{i^*},J)\), then we know that \(|H(J_{j^*}, J) - x| > |H(J_{i^*}, J') - x|\) because \(H(J_{j^*},J) > H(J_{i^*},J')\).
In either case, it cannot be that \(J \in F({\varvec{J}})\) as it should hold that \(d_e({\varvec{J}}, J) > d_e({\varvec{J}}, J')\). \(\square \)
The second axiom originating in belief merging is defined as follows:
-
\(\blacktriangleright \) Given a profile \({\varvec{J}}=(J_1, \ldots , J_n)\) and agents i and j such that:
-
\(H(J_i, J)< H(J_i,J') \le H(J_j,J') <H(J_j, J)\),
-
\( H(J_i,J') - H(J_i,J) = H(J_j,J) - H(J_j,J')\), and
-
\(H(J_{i^*}, J) = H(J_{i^*}, J')\) for all other agents \(i^* \in N\setminus \{i,j\}\),
-
F satisfies the Pigou-Dalton transfer principle if \(J \in F({\varvec{J}})\) implies \(J' \in F({\varvec{J}})\).
We refer to these axioms simply as Sen-Hammond, and Pigou-Dalton. Note that Pigou-Dalton is also a weaker version of our equity property, as it stipulates that the difference between utility in agents should be lessened under certain conditions, while the equity property always aims to minimise this distance. Thus, Pigou-Dalton is concerned with reaching equity via the possible transfer of utility between agents, and only comes into play when there are two agents such that we can “transfer” utility from one to the other.
Just as we can find a rule that satisfies both the equity property and a weakening of the maximin property, viz. Sen-Hammond, we can do the same by weakening the equity property.
Proposition 3
MaxHam satisfies the Pigou-Dalton property.
Proof
Let \({\varvec{J}}\) be a profile, and let i, j be agents, and \(J, J'\) judgments such that \(H(J_i, J)< H(J_i,J') \le H(J_j,J') <H(J_j, J)\), \( H(J_i,J') - H(J_i,J) = H(J_j,J) - H(J_j,J')\), and \(H(J_{i^*}, J) = H(J_{i^*}, J')\) for all other agents \(i^* \in N\setminus \{i,j\}\). Let \(F = \text {MaxHam}\). We want to show that \(J \in F({\varvec{J}})\) implies \(J' \not \in F({\varvec{J}})\).
Suppose therefore that \(J \in F({\varvec{J}})\). Further, suppose for contradiction that \(J' \not \in F({\varvec{J}})\). Let \(d_e(J) = max_{i^*\in N} H(J_{\ell },J)\). Since \(J' \not \in F({\varvec{J}})\), it must be that \(d_e(J') > d_e(J)\). Since both \(H(J_i, J') < H(J_j, J)\) and \(H(J_j, J') < H(J_j,J)\), this must mean that there is some agent \(\ell \in N\setminus \{i,j\}\) such that \(H(J_{i^*}, J') > H(J_{i^*}, J)\). This, of course, contradicts our assumption that \(H(J_{i^*}, J) = H(J_{i^*}, J')\) for all agents \(i^* \in N\setminus \{i,j\}\). \(\square \)
We summarise the observations of this section in Fig. 1.
The dashed line denotes incompatibility between the relevant notions: there is no rule that satisfies both simultaneously. The line drawn with both dashes and dots denotes incomparability: there are rules that satisfy both the notions, only one of them, or neither. The loosely dotted lines denote implication for the maximal rules: MaxEq satisfies Sen-Hammond and MaxHam satisfies Pigou-Dalton. Finally, the property at the beginning of an arrow with a solid line implies the property at the end of it
4 Strategic manipulation
This section provides an account of strategic manipulation with respect to the egalitarian axioms defined in Sect. 3. We start off with presenting the most general notion of strategic manipulation in judgment aggregation, introduced by Dietrich and List [19].Footnote 9 We assume Hamming preferences throughout this section. Recall that we write \(F({\varvec{J}}') \mathrel {\mathring{\succ }}_i F({\varvec{J}})\) to capture that agent i prefers the outcome \(F({\varvec{J}}') \) to the outcome \(F({\varvec{J}})\), and \(\mathrel {\mathring{\succ }}_i\), denotes the relation of the preference extension induced by \(J_i\).
Definition 1
A rule F is susceptible to manipulation by agent i in profile \({\varvec{J}}\), if there exists a profile \({\varvec{J}}' =_{-i} {\varvec{J}}\) such that \(F({\varvec{J}}') \mathrel {\mathring{\succ }}_i F({\varvec{J}})\).
We say that F is strategyproof in case F is not manipulable by any agent \(i \in N\) in any profile \({\varvec{J}}\in {\mathcal {J}}(\Phi )^n\).
Proposition 4 shows an important fact: In judgment aggregation, egalitarianism is incompatible with strategyproofness.Footnote 10
Proposition 4
If an aggregation rule is strategyproof, it cannot satisfy the maximin property or the equity property.
Proof
We show the contrapositive. Let \(\Phi \) be an agenda such that \({\mathcal {J}}(\Phi ) = 0000,1000,1100,1111\), and consider the following two profiles \({\varvec{J}}\) (left) and \({\varvec{J}}'\) (right).

In profile \({\varvec{J}}\), both the maximin and the equity properties prescribe that 1000 should be returned as the single outcome, while in profile \({\varvec{J}}'\) they agree on 1100. Because \({\varvec{J}}' = ({\varvec{J}}_{-i}, J'_i)\), and \(1100 \succ _i 1000\), this is a successful manipulation. Thus, if F satisfies the maximin or the equity property, it fails strategyproofness. \(\square \)
Strategyproofness according to Definition 1 is a strong requirement, which many known rules fail [8].
We investigate two more nuanced notions of strategyproofness that are novel to judgment aggregation, yet have familiar counterparts in voting theory.
First, no-show manipulation happens when an agent can achieve a preferable outcome simply by not submitting any judgment, instead of reporting an untruthful one.
Definition 2
A rule F is susceptible to no-show manipulation by agent i in profile \({\varvec{J}}\) if \( F({\varvec{J}}_{-i}) \mathrel {\mathring{\succ }}_i F({\varvec{J}})\).
We say that F satisfies participation if it is not susceptible to no-show manipulation by any agent \(i \in N\) in any profile.Footnote 11
Second, antipodal strategyproofness poses another barrier against manipulation, by stipulating that an agent cannot change the outcome towards a better one for herself by reporting a totally untruthful judgment. This is a strictly weaker requirement than full strategyproofness, serving as a protection against excessive lying.
Definition 3
A rule F is susceptible to antipodal manipulation by agent i in profile \({\varvec{J}}\) if \(F({\varvec{J}}_{-i},\bar{J_i}) \mathrel {\mathring{\succ }}_i F({\varvec{J}})\).
We say that F satisfies antipodal strategyproofness if it is not susceptible to antipodal manipulation by any agent \(i \in N\) in any profile. Similarly to participation, antipodal strategyproofness is a weaker notion of strategyproofness.
In voting theory, Sanver and Zwicker [61] show that participation implies antipodal strategyproofness (or half-way monotonicity, as called in that framework) for rules that output a single winning alternative. Notably, this is not always the case in our model (see Example 2). This is not surprising, as obtaining such a result independently of the preference extension would be significantly stronger than the result by Sanver and Zwicker [61]. We are, however, able to reproduce this relationship between participation and strategyproofness in Theorem 1, for a specific type of preferences.
Example 2
Consider an agenda \(\Phi \) with \({\mathcal {J}}(\Phi )=\{00,01,11\}\).Footnote 12 We construct an anonymous rule F that is only sensitive to which judgments are submitted and not to their multiplicity:
For the pessimistic preference extension, no agent can be strictly better off by abstaining. However, compare the profiles (01, 00) and (01, 11): agent 2 with truthful judgment 00 can move from outcome \(\{01,11\}\) to outcome \(\{01\}\), which is strictly better for her.
On the other hand, consider the same agenda as above and the following rule, which also is anonymous and not sensitive to the number of different judgments that are submitted:
For the optimistic preference, no agent can be strictly better off by reporting the antipodal judgment of her truthful one. However, compare the profiles (01, 00) and (01): agent 2 with truthful judgment 00 can move from outcome \(\{01,11\}\) to outcome \(\{00,11\}\), which is strictly better for her.
Note that the rules demonstrated are quite unnatural for simplicity of the presentation. More natural and elaborate rules also exist.Footnote 13
While the two axioms are independent in the general case, participation implies antipodal strategyproofness (Theorem 1) if we stipulate that
-
\(X \mathrel {\mathring{\succ }}_i Y\) if and only if there exist some \(J \in X\) and \(J' \in Y\) such that \(J \succ _i J'\) and \(\{J,J'\} \not \subseteq X \cap Y\).
If a preference extension satisfies the above condition, we say that it is decisive: it determines a relation between many sets of judgments. This condition gives rise to a preference extension equivalent to the large preference extension of Kruger and Terzopoulou [48]. Note that a decisive preference is not necessarily acyclic—in fact, it may even be symmetric. The interpretation of such a preference extension is slightly different than the usual one; when we say that a rule is strategyproof for a decisive preference where both \(X \mathrel {\mathring{\succ }}Y\) and \(Y \mathrel {\mathring{\succ }}X\) hold, we mean that no agent i with \(X \mathrel {\mathring{\succ }}_i Y\) and no agent \(j\ne i\) with \(Y \mathrel {\mathring{\succ }}_j X\) will ever have an incentive to manipulate. For example, if \(X=\{J_1,J_4\}\) and \(Y=\{J_2,J_3\}\) with \(J_1\succ _i J_2\) and \(J_3\succ _i J_4\), the decisive preference extension considers ranking X above Y and vice versa both as reasonable options.
Using Lemma 1, we can now prove a result analogous to the one in voting theory, to give a complete picture of how these axioms relate to each other in judgment aggregation.
Lemma 1
For judgments \(J, J'\) and \(J''\): \(H(J, J') > H(J,J'')\), if and only if \(H({\bar{J}}, J') < H({\bar{J}},J'')\).
Proof
For judgments \(J, J' \in {\mathcal {J}}(\Phi )\), we have that \(H({\bar{J}}, J') = m - H(J, J')\). Suppose now that \(H(J, J') > H(J,J'')\). Then \(H({\bar{J}}, J') = m - H(J, J') < m - H(J,J'') = H({\bar{J}}, J'')\). The other direction is analogous. \(\square \)
Theorem 1
For decisive preferences over sets of judgments, participation implies antipodal strategyproofness.
Proof
Working on the contrapositive, suppose that F is susceptible to antipodal manipulation. We will prove that F is susceptible to no-show manipulation.
By assumption, we know that there exists \(i \in N\) such that \(F({\varvec{J}}_{-i},\bar{J_i}) \mathrel {\mathring{\succ }}_i F({\varvec{J}}_{-i}, J_i)\), for some profile \({\varvec{J}}\). This means that there exist \(J' \in F({\varvec{J}}_{-i},\bar{J_i})\) and \(J \in F({\varvec{J}}_{-i}, J_i)\) such that
Since agent i has decisive preferences, we also know that
Recall that \({\textbf{J}}_{-i}\) is the profile \({\textbf{J}}\) with agent i’s judgment removed. Our goal is to show that there always exists a no-show manipulation from either \(({\textbf{J}}_{-i}, \bar{J_i})\) or \({\textbf{J}}\), to \({\textbf{J}}_{-i}\). To this end, let \(J'' \in F({\varvec{J}}_{-i})\). We now examine two cases.
Case 1 Suppose that \(H({\bar{J}}_i, J'') < H({\bar{J}}_i, J')\). If \(J'' \not \in F({\varvec{J}}')\) or \(J'\not \in F({\varvec{J}}_{-i})\), then F is susceptible to no-show manipulation by agent i (with decisive preferences) in the profile \(({\varvec{J}}_{-i}, \bar{J_i})\). So we only need to examine the case where both \(J'' \in F({\varvec{J}}')\) and \(J' \in F({\varvec{J}}_{-i})\).
If \(J\not \in F({\textbf{J}}_{-i})\), there is a no-show manipulation from \({\textbf{J}}\) to \({\textbf{J}}_{-i}\) for agent i with decisive preferences, since \(J' \not \in F({\textbf{J}}_{-i})\) and \(H(J_i, J) > H(J_i, J')\) (from Eq. 1).
We only have left to consider when \(J'' \in F({\varvec{J}}')\), \(J' \in F({\varvec{J}}_{-i})\), and \(J \in F({\textbf{J}}_{-i})\). From Eq. 2 we know that either \(J \not \in F({\textbf{J}}_{-i},{\bar{J}}_i) \text { or } J' \not \in F({\textbf{J}}_{-i}, J_i)\).
-
Suppose \(J \not \in F({\textbf{J}}_{-i},{\bar{J}}_i)\). By Lemma 1 and Eq. 1, we know that \(H({\bar{J}}_i, J') > H({\bar{J}}_i, J)\). So there is a no-show manipulation from \(({\textbf{J}}_{-i},{\bar{J}}_i)\) to \({\textbf{J}}_{-i}\) by agent i with decisive preferences.
-
Suppose instead \(J' \not \in F({\textbf{J}}_{-i}, J_i)\). Then similarly, there must be a no-show manipulation from \({\textbf{J}}\) by agent i with decisive preferences, as \(H(J_i, J) > H(J_i, J')\).
Case 2 Suppose now that \(H({\bar{J}}_i, J'') \ge H({\bar{J}}_i, J')\).
From Lemma 1 we have that \(H(J_i, J'') \le H(J_i, J')\), which together with Eq. (2) tells us \(H(J_i, J'') < H(J_i, J)\). The proof proceeds similarly.
If \(J'' \not \in F({\varvec{J}})\) or \(J\not \in F({\varvec{J}}_{-i})\), then F is susceptible to no-show manipulation by agent i( with decisive preferences) in the profile \({\varvec{J}}\). So we only need to examine the case where both \(J'' \in F({\varvec{J}})\) and \(J \in F({\varvec{J}}_{-i})\).
If \(J' \not \in F({\textbf{J}}_{-i})\) there is a no-show manipulation from \(({\textbf{J}}_{-i},{\bar{J}}_i)\) to \({\textbf{J}}_{-i}\) for agent i with decisive preferences, since \(J \in F({\textbf{J}}_{-i})\) and \(H({\bar{J}}_i, J) < H({\bar{J}}_i, J')\) (from Eq. 1 and Lemma 1).
Thus, we only have left to consider when \(J' \in F({\textbf{J}}_{-i})\). From Eq. (2) we know that either \(J \not \in F({\textbf{J}}_{-i},{\bar{J}}_i) \text { or } J' \not \in F({\textbf{J}}_{-i}, J_i)\).
-
Suppose \(J \not \in F({\textbf{J}}_{-i},{\bar{J}}_i)\). By Lemma 1 and Eq. (1), we know that \(H({\bar{J}}_i, J') > H({\bar{J}}_i, J)\). So there is a no-show manipulation from \(({\textbf{J}}_{-i},{\bar{J}}_i)\) to \({\textbf{J}}_{-i}\) by agent i with decisive preferences.
-
Suppose instead \(J' \not \in F({\textbf{J}}_{-i}, J_i)\). Then similarly, there must be a no-show manipulation from \({\textbf{J}}\) by agent i with decisive preferences, as \(H(J_i, J) > H(J_i, J'')\).
Finally, we have shown that there always exists a no-show manipulation from either \({\varvec{J}}\) or \(({\textbf{J}}_{-i}, \bar{J_i})\), as desired. \(\square \)
We next prove that any rule satisfying the maximin property is immune to both no-show manipulation and antipodal manipulation (Theorem 2), while this is not true for the equity property (Proposition 5).Footnote 14 We emphasise that the theorem holds for all preference extensions. These results—holding for two independent notions of strategyproofness—are significant for two reasons. First, they bring to light the conditions under which we can have our cake and eat it too, simultaneously satisfying an egalitarian property and a degree of strategyproofness. In addition, they provide a further way to distinguish between the properties of maximin and equity: the former is better suited in contexts where we may worry about the agents’ strategic behaviour.
Theorem 2
The maximin property implies participation and antipodal strategyproofness.
Proof
The proofs for the two properties are similar, but only one of them utilises Lemma 1—we provide them separately for the sake of completeness.
Proof for participation Suppose for contradiction that F satisfies the maximin property but violates participation. Then there must exist agent \(i \in N\) and profile \({\varvec{J}}\) where \(J_i\) is agent i’s truthful judgment, such that \(F({\varvec{J}}_{-i}) \mathrel {\mathring{\succ }}_i F({\varvec{J}})\). This means there must exist judgments \(J \in F({\varvec{J}})\) and \(J' \in F({\varvec{J}}_{-i})\) such that \(J' \succ _i J\) and \(\{J, J'\} \not \subseteq F({\varvec{J}}) \cap F({\varvec{J}}_{-i})\). Because agent i strictly prefers \(J'\) to J, this means that \(H(J_i, J) > H(J_i, J')\). We consider two cases.
Case 1 Suppose that \(J' \not \in F({\varvec{J}})\). Let k be the distance between the worst off agent’s judgment in \({\varvec{J}}\) and any judgment in \(F({\varvec{J}})\). Then,
We know that \(H(J_i, J') < k\) because \(H(J_i, J) \le k\), and agent i strictly prefers \(J'\) to J. From Inequality (3), this means that if \(J'\) is not among the outcomes in \(F({\varvec{J}})\), there has to be some \(j \in N \setminus \{i\}\) such that \(H(J_j, J') > k\). But all judgments submitted to profile \({\varvec{J}}_{-i}\) by agents in \(N \setminus \{i\}\) are at most at distance k from J by Inequality (3), so any rule satisfying the maximin property will select J as an outcome of \(F({\varvec{J}}_{-i})\)—instead of \(J'\), which is a contradiction.
Case 2 Suppose that \(J' \in F({\varvec{J}})\), meaning that \(J \not \in F({\varvec{J}}_{-i})\). Analogously to the first case, let \(k'\) be the distance between the worst off agent’s judgment in \({\varvec{J}}_{-i}\) and any judgment in \(F({\varvec{J}}_{-i})\). Then,
Moreover, since \(J \not \in F({\varvec{J}}_{-i})\), it is the case that
In profile \({\varvec{J}}\), Inequalities (4) and (5) still hold. In addition, we have that \(H(J_i, J) > H(J_i, J')\) because agent i strictly prefers \(J'\) to J. So, for any rule satisfying the maximin property, judgment \(J'\) will be strictly better as an outcome of \(F({\varvec{J}})\) than J, which is a contradiction because \(J \in F({\varvec{J}})\).
Proof for antipodal strategyproofness. Suppose for contradiction that F satisfies the maximin property but violates antipodal strategyproofness. Then there must exist agent \(i \in N\) and profile \({\varvec{J}}\) where \(J_i\) is agent i’s truthful judgment, such that \(F({\varvec{J}}_{-i}, \bar{J_i}) \mathrel {\mathring{\succ }}_i F({\varvec{J}})\). This means there must exist judgments \(J \in F({\varvec{J}})\) and \(J' \in F({\varvec{J}}_{-i}, \bar{J_i})\) such that \(J' \succ _i J\) and \(\{J, J'\} \not \subseteq F({\varvec{J}}) \cap F({\varvec{J}}_{-i}, \bar{J_i})\). Because agent i strictly prefers \(J'\) to J, this means that \(H(J_i, J) > H(J_i, J')\). We consider two cases.
Case 1 Suppose that \(J' \not \in F({\varvec{J}})\). Let k be the distance between the worst off agent’s judgment in \({\varvec{J}}\) and any judgment in \(F({\varvec{J}})\). The following holds:
We know that \(H(J_i, J') < k\) because \(H(J_i, J) \le k\), and agent i strictly prefers \(J'\) to J. From Inequality (6), this means that if \(J'\) is not among the outcomes in \(F({\varvec{J}})\), there has to be some \(j \in N \setminus \{i\}\) such that \(H(J_j, J') > k\). But all judgments submitted to profile \({\varvec{J}}_{-i}\) by agents in \(N \setminus \{i\}\) are at most at distance k from J by Inequality (6). In addition, by Lemma 1 and the fact that agent i strictly prefers \(J'\) to J, we know that \(H(\bar{J_i},J) < H(\bar{J_i},J')\). So any rule satisfying the maximin property will select J as an outcome of \(F({\varvec{J}}_{-i}, \bar{J_i})\)—instead of \(J'\), which is a contradiction.
Case 2 Suppose that \(J' \in F({\varvec{J}})\), meaning that \(J \not \in F({\varvec{J}}_{-i}, \bar{J_i})\). Analogously to the first case, let \(k'\) be the distance between the worst off agent’s judgment in \(({\varvec{J}}_{-i},\bar{J_i})\) and any judgment in \(F({\varvec{J}}_{-i},\bar{J_i})\). Then, the following holds:
Moreover, since \(J \not \in F({\varvec{J}}_{-i}, \bar{J_i})\), the following is the case:
However, by Lemma 1 and the fact that agent i strictly prefers \(J'\) to J, we know—together with Inequality 7—that \(H(\bar{J_i},J) < H(\bar{J_i},J') \le k\). Hence, the following holds:
Now, In profile \({\varvec{J}}\), Inequalities (7) and (9) still hold. In addition, we have that \(H(J_i, J) > H(J_i, J')\) because agent i strictly prefers \(J'\) to J. So, for any rule satisfying the maximin property, judgment \(J'\) will be strictly better as an outcome of \(F({\varvec{J}})\) than J, which is a contradiction because \(J \in F({\varvec{J}})\). \(\square \)
Corollary 1
The rule MaxHam satisfies antipodal strategyproofness and participation.
Proposition 5
No rule that satisfies the equity property can satisfy participation or antipodal strategyproofness .
Proof
We first give a counterexample for antipodal strategyproofness.
Consider the following profiles \({\varvec{J}}= (J_i, J_j)\) and \({\varvec{J}}' = ({\varvec{J}}_{-i}, \bar{J_i})\). We give a visual representation of the profiles as well as the outcomes under an arbitrary rule F that satisfies the equity principle. We specify that \({\mathcal {J}}(\Phi ) = \{00110, 00000, 01110, 10000, 11111\}\).

Each edge from an individual judgment to a collective one is labelled with the Hamming distance between the two. It is clear that agent i will benefit from her antipodal manipulation, as her true judgment is much closer to the singleton outcome in \({\varvec{J}}'\) than the singleton outcome in \({\varvec{J}}\).
We now give a similar counterexample for participation. Consider the following profiles \({\varvec{J}}= (J_i, J_j, J_k)\) and \({\varvec{J}}' = (J_j, J_k)\)—meaning \({\varvec{J}}'\) is equivalent to \({\varvec{J}}\) with agent i removed. We give a visual representation of the profiles as well as the outcomes under an arbitrary rule F that satisfies the equity principle. We specify that \({\mathcal {J}}(\Phi ) = \{00110, 00000, 01110, 10000, 11111\}\) as above.

We can see from the figure that agent i benefits by not participating as her true judgment is closer to the singleton outcome in \({\varvec{J}}'\)—where she does not participate—than the singleton outcome in \({\varvec{J}}\)—where she does participate. \(\square \)
Corollary 2
The rule MaxEq does not satisfy participation or antipodal strategyproofness.
5 Computational aspects
We have discussed two aggregation rules that reflect desirable egalitarian principles—the MaxHam and MaxEq rules—and examined whether they give agents incentives to misrepresent their truthful judgments. In this section we consider how complex it is, computationally, to employ these rules, and the complexity of determining whether an agent can manipulate the outcome.
The MaxHam rule has been considered from a computational perspective before [39,40,41]: it was shown that a decision variant of the outcome determination problem for it is \(\Theta ^{\text { \textsf {p}}}_{2}\)-complete. Here, we extend this analysis to the MaxEq rule, and we compare the two rules with each other on their computational properties.
We primarily establish some computational complexity results; motivated by these, we then illustrate how some computational problems related to these rules can be solved using the paradigm of Answer Set Programming (ASP) [35].
5.1 Computational complexity
We investigate some computational complexity aspects of the judgment aggregation rules that we have considered. To ease readability, we only describe the main lines of our results in the main body of the paper—for full details, we refer to the Appendix (Sect. 1).
Consider the problem of outcome determination (for a rule F). This is most naturally modelled as a search problem, where the input consists of an agenda \(\Phi \) and a profile \({\varvec{J}}= (J_1,\dotsc ,J_n) \in {\mathcal {J}}(\Phi )^{n}\). The problem is to produce some judgment \(J^{*} \in F({\varvec{J}})\).
We will show that for the MaxEq rule, this problem can be solved in polynomial time with a logarithmic number of calls to an oracle for NP search problems (where the oracle also produces a witness for yes answers—also called an FNP witness oracle). Said differently, the outcome determination problem for the the MaxEq rule lies in the complexity class \( \textsf {FP}^{\textsf {NP}}\textsf {[log,wit]}\). We also show that the problem is complete for this class (using the standard type of reductions used for search problems: polynomial-time Levin reductions).
Theorem 3
The outcome determination problem for the MaxEq rule is \( \textsf {FP}^{\textsf {NP}}\textsf {[log,wit]}{}\)-complete under polynomial-time Levin reductions.
Proof
We only provide the basic idea of the proof here—for the whole proof see the Appendix. Membership in \( \textsf {FP}^{\textsf {NP}}\textsf {[log,wit]}\) can be shown by giving a polynomial-time algorithm that solves the problem by querying an FNP witness oracle a logarithmic number of times. The algorithm first finds the minimum value k of \(\max _{J',J'' \in {\varvec{J}}} |H(J,J') - H(J,J'')|\) by means of binary search—requiring a logarithmic number of oracle queries. Then, with one additional oracle query, the algorithm can produce some \(J^{*} \in {\mathcal {J}}(\Phi )\) with \(\max _{J',J'' \in {\varvec{J}}} |H(J^{*},J') - H(J^{*},J'')| = k\).
To show \( \textsf {FP}^{\textsf {NP}}\textsf {[log,wit]}{}\)-hardness, we reduce from the problem of finding a satisfying assignment of a (satisfiable) propositional formula \(\psi \) that sets a maximum number of variables to true [14, 44].
This reduction works roughly as follows. Firstly, we produce 3CNF formulas \(\psi _1,\dotsc ,\psi _v\) where each \(\psi _i\) is 1-in-3-satisfiableFootnote 15 if and only if there exists a satisfying assignment of \(\psi \) that sets at least i variables to true. Then, for each i, we transform \(\psi _i\) to an agenda \(\Phi _i\) and a profile \({\varvec{J}}_i\) such that there is a judgment with equal Hamming distance to each \(J \in {\varvec{J}}_i\) if and only if \(\psi _i\) is 1-in-3-satisfiable. Finally, we put the agendas \(\Phi _i\) and profiles \({\varvec{J}}_i\) together into a single agenda \(\Phi \) and a single profile \({\varvec{J}}\) such that we can—from the outcomes selected by the MaxEq rule—read off the largest i for which \(\psi _i\) is 1-in-3-satisfiable, and thus, the maximum number of variables set to true in any truth assignment satisfying \(\psi \). This last step involves duplicating issues in \(\Phi _1,\dotsc ,\Phi _v\) different numbers of times, and creating logical dependencies between them. Moreover, we do this in such a way that from any outcome selected by the MaxEq rule, we can reconstruct a truth assignment satisfying \(\psi \) that sets a maximum number of variables to true. \(\square \)
The result of Theorem 3 means that the computational complexity of computing outcomes for the MaxEq rule lies at the \(\Theta ^{\text { \textsf {p}}}_{2}\)-level of the Polynomial Hierarchy. This is in line with previous results on the computational complexity of the outcome determination problem for the MaxHam rule—De Haan and Slavkovik [40] showed that a decision variant of the outcome determination problem for the MaxHam rule is \(\Theta ^{\text { \textsf {p}}}_{2}\)-complete.
Interestingly, we found that the problem of deciding if there exists a judgment \(J^{*} \in {\mathcal {J}}(\Phi )\) that has the exact same Hamming distance to each judgment in the profile is NP-hard, even when the agenda consists of logically independent issues.
Proposition 6
Given an agenda \(\Phi \) and a profile \({\varvec{J}}\), the problem of deciding whether there is some \(J^{*} \in {\mathcal {J}}(\Phi )\) with \(\max _{J',J'' \in {\varvec{J}}} |H(J^{*},J') - H(J^{*},J'')| = 0\) is NP-complete. Moreover, NP-hardness holds even for the case where \(\Phi \) consists of logically independent issues—i.e., the case where \({\mathcal {J}}(\Phi ) = \{0,1\}^m\) for some m.
This is also in line with previous results for the MaxHam rule—De Haan [39] showed that computing outcomes for the MaxHam rule is computationally intractable even when the agenda consists of logically independent issues.
Next, we turn our attention to the problem of strategic manipulation. Specifically, we show that—for the case of decisive preferences over sets of judgments—the problem of deciding if an agent i can strategically manipulate is in the complexity class \(\Sigma ^{\text { \textsf {p}}}_{2}\).
Proposition 7
Let \({\succeq }\) be a preference relation over judgments that is polynomial-time computable, and let \({\mathrel {\mathring{\succeq }}}\) be a decisive extension over sets of judgments. Then the problem of deciding if a given agent i can strategically manipulate under the MaxEq rule—i.e., given \(\Phi \) and \({\varvec{J}}\), deciding if there exists some \({\varvec{J}}' =_{-i} {\varvec{J}}\) with \(\text {MaxEq}({\varvec{J}}') \mathrel {\mathring{\succ }}_i \text {MaxEq}({\varvec{J}})\)—is in the complexity class \(\Sigma ^{\text { \textsf {p}}}_{2}\).
Proof
To show membership in \(\Sigma ^{\text { \textsf {p}}}_{2} = \textsf {NP}^{ \textsf {NP}}\), we describe a nondeterministic polynomial-time algorithm with access to an NP oracle that solves the problem. The algorithm firstly guesses a new judgment \(J'_i\) for agent i in the new profile \({\varvec{J}}'\), and guesses a truth assignment \(\alpha \) for the variables in \(\Phi \). It then checks that \(J'_i\) is consistent—that is, that \(\alpha \) satisfies every formula in \(J'_i\).
Next, the algorithm needs to check whether \(\text {MaxEq}({\varvec{J}}') \mathrel {\mathring{\succ }}_i \text {MaxEq}({\varvec{J}})\)—that is, whether there is some \(J' \in \text {MaxEq}({\varvec{J}}')\) and some \(J \in \text {MaxEq}({\varvec{J}})\) such that \(J' \succ _i J\) and \(\{ J, J' \} \not \subseteq \text {MaxEq}({\varvec{J}}) \cap \text {MaxEq}({\varvec{J}}')\). It does so as follows. It first (1) computes the values \(k = \min _{J_0 \in {\mathcal {J}}(\Phi )} \max _{J_1,J_2 \in {\varvec{J}}} |H(J_0,J_1) - H(J_0,J_2)|\) and \(k' = \min _{J_0 \in {\mathcal {J}}(\Phi )} \max _{J_1,J_2 \in {\varvec{J}}'} |H(J_0,J_1)- H(J_0,J_2)|\). Then, (2) it nondeterministically guesses appropriate sets \(J,J' \in {\mathcal {J}}(\Phi )\), and using these values k and \(k'\) it verifies whether the sets J and \(J'\) satisfy the requirements. We will describe these two steps (1) and (2) in more detail.
For step (1), the algorithm uses the NP oracle to decide, for various values of u, whether there is some \(J_0 \in {\mathcal {J}}(\Phi )\) such that \(\max _{J_1,J_2 \in {\varvec{J}}} |H(J_0,J_1) - H(J_0,J_2)| \le u\). This is an NP problem, because one can nondeterministically guess the set \(J_0\), together with a truth assignment witnessing its consistency, and then in polynomial deterministic time verify that \(\max _{J_1,J_2 \in {\varvec{J}}} |H(J_0,J_1) - H(J_0,J_2)| \le u\). By querying the NP oracle for all relevant values of u—or more efficiently: for a logarithmic number of values of u, by using binary search—the algorithm can identify \(k = \min _{J_0 \in {\mathcal {J}}(\Phi )} \max _{J_1,J_2 \in {\varvec{J}}} |H(J_0,J_1) - H(J_0,J_2)|\). In an entirely similar fashion, the algorithm can also compute the value \(k' = \min _{J_0 \in {\mathcal {J}}(\Phi )} \max _{J_1,J_2 \in {\varvec{J}}'} |H(J_0,J_1) - H(J_0,J_2)|\) in polynomial time using the NP oracle.
Then, for step (2), the algorithm nondeterministically guesses judgments \(J,J'\) together with two truth assignments \(\alpha ,\alpha '\) and it verifies that \(J,J' \in {\mathcal {J}}(\Phi )\) by checking that \(\alpha \) satisfies J and that \(\alpha '\) satisfies \(J'\). What remains is to check that \(J' \in \text {MaxEq}({\varvec{J}}')\), that \(J \in \text {MaxEq}({\varvec{J}})\), that \(J' \succ _i J\) and that \(\{ J, J' \} \not \subseteq \text {MaxEq}({\varvec{J}}) \cap \text {MaxEq}({\varvec{J}}')\). For both \(J^{*} \in \{ J,J' \}\) and for both \({\varvec{J}}^{*} \in \{ {\varvec{J}}, {\varvec{J}}' \}\), the algorithm can compute \(\max _{J_1,J_2 \in {\varvec{J}}^{*}} |H(J^{*},J_1) - H(J^{*},J_2)|\) in polynomial time, and compare it with the appropriate value among k and \(k'\), thereby deciding if \(J^{*} \in \text {MaxEq}({\varvec{J}}^{*})\). Thus, the algorithm can in polynomial time check whether J and \(J'\) are appropriate witnesses for \(\text {MaxEq}({\varvec{J}}') \mathrel {\mathring{\succ }}_i \text {MaxEq}({\varvec{J}})\). It accepts the input if and only if this is the case. \(\square \)
For no-show manipulation and antipodal manipulation, we obtain an upper bound of \(\Theta ^{\text { \textsf {p}}}_{2}\)-membership for the MaxEq rule, under similar restrictions for the preference relation \({\succeq }\) and its decisive extension \({\mathrel {\mathring{\succeq }}}\)—essentially by the same argument, observing that the choice of manipulating judgment set \(J'_i\) is determined by the problem input, and thus does not need to be nondeterministically chosen.
Corollary 1
Let \({\succeq }\) be a preference relation over judgments that is polynomial-time computable, and let \({\mathrel {\mathring{\succeq }}}\) be a decisive extension over sets of judgments. Then the problems of deciding if a given judgment aggregation scenario is susceptible to no-show manipulation or to antipodal manipulation under the MaxEq rule (for a given agent i)—is in the complexity class \(\Theta ^{\text { \textsf {p}}}_{2}\).
Proof (sketch). The proof is entirely analogous to that of Proposition 7, with the only difference that the relevant judgment set \(J'_i\) can be computed in polynomial-time from the input. Therefore, the resulting algorithm is a deterministic polynomial-time algorithm with access to an NP oracle, leading to membership in \(\Theta ^{\text { \textsf {p}}}_{2}\). \(\square \)
These \(\Sigma ^{\text { \textsf {p}}}_{2}\)-membership and \(\Theta ^{\text { \textsf {p}}}_{2}\)-membership results can straightforwardly be extended to other preferences, as well as to the MaxHam rule. Due to space constraints, we omit further details on this. Still, we shall mention that results demonstrating that strategic manipulation is very complex are generally more welcome than analogous ones regarding outcome determination. If manipulation is considered a negative side-effect of the agents’ strategic behaviour, knowing that it is hard for the agents to materialise it is good news.Footnote 16 In Sect. 5.2 we will revisit these concerns from a different angle.
5.2 ASP encoding for the MaxEq rule
The complexity results in Sect. 5.1 leave no doubt that applying our egalitarian rules is computationally difficult. Nevertheless, they also indicate that a useful approach for computing outcomes of the MaxEq rule in practice would be to encode this problem into the paradigm of Answer Set Programming (ASP; [35]), and to use ASP solving algorithms.
ASP offers an expressive automated reasoning framework that typically works well for problems at the \(\Theta ^{\text { \textsf {p}}}_{2}\) level of the Polynomial Hierarchy.
In this section, we will show how this encoding can be done—similarly to an ASP encoding for the MaxHam rule [41]. We refer to the literature for details on the syntax and semantics of ASP—e.g., [33, 35].
Our aim in the current section and in the subsequent section (Sects. 5.2 and 5.3 ) is to complement the work of De Haan and Slavkovik [41] by providing (i) an encoding of the MaxEq rule, and (ii) a generic, readable and easily understandable method of encoding the problem of strategic manipulation (for arbitrary judgment aggregation rules). Especially the latter involves a non-trivial encoding. This paves the way for an extensive and thorough experimental analysis of the performance of ASP solvers on computing outcomes and determining manipulability of judgment aggregation scenarios. Such an experimental analysis is beyond the scope of this paper, and we leave this for future research.
We use the same basic setup that De Haan and Slavkovik [41] use to represent judgment aggregation scenarios—with some simplifications and modifications for the sake of readability. In particular, we use the predicate voter/1 to represent individuals, we use issue/1 to represent issues in the agenda, and we use js/2 to represent judgments—both for the individual voters and for a dedicated agent col that represents the outcome of the rule.
With this encoding of judgment aggregation scenarios, one can add further constraints on the predicate js/2 that express which judgments are consistent, based on the logical relations between the issues in the agenda \(\Phi \)—as done by De Haan and Slavkovik [41]. We refer to their work for further details on how this can be done.
Now, we show how to encode the MaxEq rule into ASP, similarly to the encoding of the MaxHam rule by De Haan and Slavkovik [41]. We begin by defining a predicate dist/2 to capture the Hamming distance D between the outcome and the judgment set of an agent A.

Then, we define predicates maxdist/1, mindist/1 and inequity/1 that capture the maximum Hamming distance from the outcome to any judgment in the profile, the minimum such Hamming distance, and the difference between the maximum and minimum (or inequity), respectively.

Finally, we add an optimization constraint that states that only outcomes should be selected that minimize the inequity.Footnote 17

For any answer set program that encodes a judgment aggregation setting, combined with Lines 2–6, it then holds that the optimal answer sets are in one-to-one correspondence with the outcomes selected by the MaxEq rule.
Interestingly, we can readily modify this encoding to capture refinements of the MaxEq rule. An example of this is the refinement that selects (among the outcomes of the MaxEq rule) the outcomes that minimize the maximum Hamming distance to any judgment in the profile. We can encode this example refinement by adding the following optimization statement that works at a lower priority level than the optimization in Line 6.

5.3 Encoding strategic manipulation
We now show how to encode the problem of strategic manipulation into ASP. The value of this section’s contribution should be viewed from the perspective of the modeller rather than from that of the agents. That is, even if we do not wish for the agents to be able to easily check whether they can be better off by lying, it may be reasonable, given a profile of judgments, to externally determine whether a certain agent can benefit from being untruthful.
We achieve this with the meta-programming techniques developed by Gebser et al. [34]. Their meta-programming approach allows one to additionally express optimization statements that are based on subset-minimality, and to transform programs with this extended expressivity to standard (disjunctive) answer set programs. We use this to encode the problem of strategic manipulation.
Due to space reasons, we will not spell out the full ASP encoding needed to do so. Instead, we will highlight the main steps, and describe how these fit together.
We will use the example of MaxEq, but the exact same approach would work for any other judgment aggregation rule that can be expressed in ASP efficiently using regular (cardinality) optimization constraints—in other words, for all rules for which the outcome determination problem lies at the \(\Theta ^{\text { \textsf {p}}}_{2}\) level of the Polynomial Hierarchy. Moreover, we will use the example of a decisive preference \(\mathrel {\mathring{\succ }}\) over sets of judgments that is based on a polynomial-time computable preference \(\succ \) over judgments. The approach can be modified to work with other preferences as well.
We begin by guessing a new judgment \(J'_i\) for the individual i that is trying to manipulate—and we assume, w.l.o.g., that \(i = 1\).

Then, we express the outcomes of the MaxEq rule, both for the non-manipulated profile \({\varvec{J}}\) and for the manipulated profile \({\varvec{J}}'\), using the dedicated agents col (for \({\varvec{J}}\)) and prime(col) (for \({\varvec{J}}'\)). This is done exactly as in the encoding of the problem of outcome determination (so for the case of MaxEq, as described in Sect. 5.2)—with the difference that optimization is expressed in the right format for the meta-programming method of Gebser et al. [34].
We express the following subset-minimality minimization statement (at a higher priority level than all other optimization constraints used so far). This will ensure that every possible judgment \(J'_i\) will be considered as a subset-minimal solution.

To encode whether or not the guessed manipulation was successful, we have to define a predicate successful/0 that is true if and only if (i) \(J' \succ _i J\) and (ii) J and \(J'\) are not both selected as outcome by the MaxEq rule for both \({\varvec{J}}\) and \({\varvec{J}}'\), where \(J'\) is the outcome encoded by the statements js(prime(col),X) and J is the outcome encoded by the statements js(col,X). Since we assume that \(\succ _i\) is computable in polynomial time, and since we can efficiently check using statements in the answer set whether J and \(J'\) are selected by the MaxEq rule for \({\varvec{J}}\) and \({\varvec{J}}'\), we know that we can define the predicate successful/0 correctly and succinctly in our encoding. For space reasons, we omit further details on how to do this.
Then, we express another minimization statement (at a lower priority level than all other optimization statements used so far), that states that we should make successful true whenever possible. Intuitively, we will use this to filter our guessed manipulations that are unsuccessful.

Finally, we feed the answer set program P that we constructed so far into the meta-programming method, resulting in a new (disjunctive) answer set program \(P'\) that uses no optimization statements at all, and whose answer sets correspond exactly to the (lexicographically) optimized answer sets of our program P. Since the new program \(P'\) does not use optimization, we can add additional constraint to \(P'\) to remove some of the answer sets. In particular, we will filter out those answer sets that correspond to an unsuccessful manipulation—i.e., those containing the statement unsuccessful. Effectively, we add the following constraint to \(P'\):

As a result the only answer sets of \(P'\) that remain correspond exactly to successful manipulations \(J'_i\) for agent i.
The meta-programming technique that we use uses the full disjunctive answer set programming language. For this full language, finding answer sets is a \(\Sigma ^{\text { \textsf {p}}}_{2}\)-complete problem [21]. This is in line with our result of Proposition 7 where we show that the problem of strategic manipulation is in \(\Sigma ^{\text { \textsf {p}}}_{2}\).
The encoding that we described can straightforwardly be modified for various variants of strategic manipulation (e.g., antipodal manipulation). To make this work, one needs to express additional constraints on the choice of the judgment \(J'_i\). To adapt the encoding for other preference relations \(\mathrel {\mathring{\succ }}\), one needs to adapt the definition of successful/0, expressing under what conditions an act of manipulation is successful.
Our encoding using meta-programming is relatively easily understandable, since we do not need to tinker with the encoding of complex optimization constraints in full disjunctive answer set programming ourselves—this we outsource to the meta-programming method. If one were to do this manually, there is more space for tailor-made optimizations, which might lead to a better performance of ASP solving algorithms for the problem of strategic manipulation. It is an interesting topic for future research to investigate this, and possibly to experimentally test the performance of different encodings, when combined with ASP solving algorithms.
6 Conclusion
We have introduced the concept of egalitarianism into the framework of judgment aggregation and have presented how egalitarian and strategyproofness axioms interact in this setting. Importantly, we have shown that the two main interpretations of egalitarianism give rise to rules with differing levels of protection against manipulation. In addition, we have looked into computational aspects of the egalitarian rules that arise from our axioms—regarding both outcome determination and manipulability—in a twofold manner: First, we have provided worst-case complexity results; second, we have shown how to solve the relevant hard problems using Answer Set Programming.
While we have formalised two prominent egalitarian principles in terms of axioms, it remains to be seen whether other egalitarian axioms can provide stronger barriers against manipulation. For example, in parallel to majoritarian rules, one could define rules that minimise the distance to some egalitarian ideal. Moreover, as is the case in judgment aggregation, there is an obvious lack of voting rules designed with egalitarian principles in mind. We hope this paper opens the door for similar explorations in voting theory.
Finally, this paper brings up more concrete technical questions too: Can full axiomatisations be provided for more refined egalitarian rules in judgment aggregation (similarly to that of the leximin rule based on the Sen-Hammond principle by Hammond, [42])? Can the agenda structures that cause the incompatibility of our different axioms be characterised, and do our results extend to more general utility functions beyond those based on Hamming distance? All these are intriguing directions for future work.
Notes
In the latter problem, the teacher may notably choose a collection of toys that violates the Pareto principle, e.g., there may be a different collection that increases the satisfaction of one kid more than the satisfaction of the remaining kids; this unbalance would arguaby create undesirable competition and tension amongst humans of a young age. More generally, the Pareto principle is not always as attractive in egalitarian contexts as it is in utilitarian ones—in particular, it will not be necessarily fulfilled by the equity rule we will define later.
For an exposition of the similarities and differences between the frameworks of belief merging and judgment aggregation, consult the work of Everaere et al. [29].
Note that the direct proofs that we provide in this paper hold for all agendas and all numbers of agents. On the other hand, each of our counterexamples relies on the construction of a specific agenda, but can be extended to any number of agents. Importantly, our counterexamples fail for some rich agendas that are natural, such as the preference agenda [18] or the agenda that contains logically independent formulas. Overall, characterising the exact conditions on the agenda for which suitable counterexamples exist is an intriguing but rather demanding task, which we do not tackle here.
Various approaches have been taken within the area of social choice theory in order to extend preferences over objects to preferences over sets of objects—see Barberà et al. [2] for a review.
A central problem in judgment aggregation concerns the fact that the issue-wise majority is not always logically consistent [52].
Of course, several natural refinements of these rules can be defined, with respect to various other axiomatic properties that we may find desirable. Identifying and studying such rules is an interesting direction for future research.
Another egalitarian property in belief merging is the arbitration postulate. We do not go into detail on this postulate, but refer the reader to Konieczny and Pérez [45].
The original definition of Dietrich and List [19] concerned single-judgment collective outcomes, and a type of preferences that covers Hamming-distance ones.
This agrees with [10], studying the minimax rule in approval voting.
cf. the no-show paradox in voting [30].
For other agendas we can simply take the rules to be constant.
Note also that the first case of the example demonstrates antipodal manipulation, while the second case demonstrates no-show manipulation.
Note that antipodal strategyproofness is not so weak a requirement that is immediately satisfied by all “utilitarian” aggregation rules. For example, the Copeland voting rule fails the analogous axiom of half-way monotonicity [66].
Let \(\psi \) be a propositional logic formula in 3CNF, i.e., \(\psi = c_1 \wedge \cdots \wedge c_m\), where each \(c_i\) is a clause containing exactly three literals. Then \(\psi \) is 1-in-3-satisfiable if there exists a truth assignment \(\alpha \) that satisfies exactly one of the three literals in each clause \(c_i\).
Note though that hardness results regarding manipulation of our egalitarian rules remain an open question.
The expression “@30” in Line 6 indicates the priority level of this optimization statement (we used the arbitrary value of 30, and priority levels lexicographically).
References
Amanatidis, G., Birmpas, G., & Markakis, E. (2016). On truthful mechanisms for maximin share allocations. In Proceedings of the 25th international joint conference on artificial intelligence (IJCAI).
Barberà, S., Bossert, W., & Pattanaik, P. K. (2004). Ranking sets of objects. Handbook of utility theory (pp. 893–977). Springer.
Baum, S. D. (2017). Social choice ethics in artificial intelligence. AI & Society 1–12.
Baumeister, D., Erdélyi, G., Erdélyi, O. J., & Rothe, J. (2013). Computational aspects of manipulation and control in judgment aggregation. In Proceedings of the 3rd international conference on algorithmic decision theory (ADT).
Baumeister, D., Erdélyi, G., Erdélyi, O. J., & Rothe, J. (2015). Complexity of manipulation and bribery in judgment aggregation for uniform premise-based quota rules. Mathematical Social Sciences, 76, 19–30.
Baumeister, D., Rothe, J., & Selker, A. -K. (2017). Strategic behavior in judgment aggregation. In Trends in computational social choice (pp. 145–168). Lulu. com.
Botan, S., de Haan, R., Slavkovik, M., & Terzopoulou, Z. (2021). Egalitarian judgment aggregation. In Proceedings of the 20th international conference on autonomous agents and multiagent systems (AAMAS).
Botan, S. & Endriss, U. (2020). Majority-strategyproofness in judgment aggregation. In Proceedings of the 19th international conference on autonomous agents and multiagent systems (AAMAS).
Brams, S. J., Jones, M. A., & Klamler, C. (2008). Proportional pie-cutting. International Journal of Game Theory, 36(3–4), 353–367.
Brams, S. J., Kilgour, D. M., & Sanver, M. R. (2007). A minimax procedure for electing committees. Public Choice, 132(3), 401–420.
Budish, E. (2011). The combinatorial assignment problem: Approximate competitive equilibrium from equal incomes. Journal of Political Economy, 119(6), 1061–1103.
Caragiannis, I., Kalaitzis, D., & Markakis, E. (2010). Approximation algorithms and mechanism design for minimax approval voting. In Proceedings of the 24th AAAI conference on artificial intelligence (AAAI).
Chen, Y., Lai, J. K., Parkes, D. C., & Procaccia, A. D. (2013). Truth, justice, and cake cutting. Games and Economic Behavior, 77(1), 284–297.
Chen, Z.-Z., & Toda, S. (1995). The complexity of selecting maximal solutions. Information and Computation, 119, 231–239.
Conitzer, V., Sinnott-Armstrong, W., Borg, J. S., Deng, Y., & Kramer, M. (2017). Moral decision making frameworks for artificial intelligence. In Proceedings of the 31st AAAI conference on artificial intelligence (AAAI).
Cook, S. A. (1971). The complexity of theorem-proving procedures. In Proceedings of the 3rd annual ACM symposium on theory of computing (pp. 151–158). Shaker Heights.
Dalton, H. (1920). The measurement of the inequality of incomes. Economic Journal, 30(119), 348–461.
Dietrich, F., & List, C. (2007). Arrow’s theorem in judgment aggregation. Social Choice and Welfare, 29(1), 19–33.
Dietrich, F., & List, C. (2007). Strategy-proof judgment aggregation. Economics & Philosophy, 23(3), 269–300.
Duggan, J., & Schwartz, T. (2000). Strategic manipulability without resoluteness or shared beliefs: Gibbard-Satterthwaite generalized. Social Choice and Welfare, 17(1), 85–93.
Eiter, T., & Gottlob, G. (1995). On the computational cost of disjunctive logic programming: Propositional case. Annals of Mathematics and Artifficial Intelligence, 15(3–4), 289–323.
Endriss, U. (2016). Judgment aggregation. In F. Brandt, V. Conitzer, U. Endriss, J. Lang, & A. D. Procaccia (Eds.), Handbook of computational social choice. Cambridge University Press.
Endriss, U. (2016). Judgment aggregation. In F. Brandt, V. Conitzer, U. Endriss, J. Lang, & A. D. Procaccia (Eds.), Handbook of computational social choice. Cambridge University Press.
Endriss, U. & de Haan, R. (2015). Complexity of the winner determination problem in judgment aggregation: Kemeny, Slater, Tideman, Young. In Proceedings of the 14th international conference on autonomous agents and multiagent systems (AAMAS).
Endriss, U., de Haan, R., Lang, J., & Slavkovik, M. (2020). The complexity landscape of outcome determination in judgment aggregation. Journal of Artificial Intelligence Research.
Endriss, U., Grandi, U., de Haan, R., & Lang, J. (2016). Succinctness of languages for judgment aggregation. In Proceedings of the 15th international conference on the principles of knowledge representation and reasoning (KR).
Endriss, U., Grandi, U., & Porello, D. (2012). Complexity of judgment aggregation. Journal of Artificial Intelligence Research, 45, 481–514.
Everaere, P., Konieczny, S., & Marquis, P. (2014). On egalitarian belief merging. In Proceedings of the 14th international conference on the principles of knowledge representation and reasoning (KR).
Everaere, P., Konieczny, S., & Marquis, P. (2017). Belief merging and its links with judgment aggregation. In U. Endriss (Ed.), Trends in computational social choice (pp. 123–143). AI Access Foundation.
Fishburn, P. C., & Brams, S. J. (1983). Paradoxes of preferential voting. Mathematics Magazine, 56(4), 207–214.
Foley, D. K. (1967). Resource allocation and the public sector. Yale Economic Essays, 7(1), 45–98.
Gärdenfors, P. (1976). Manipulation of social choice functions. Journal of Economic Theory, 13(2), 217–228.
Gebser, M., Kaminski, R., Kaufmann, B., & Schaub, T. (2012). Answer set solving in practice. Synthesis lectures on artificial intelligence and machine learning. Morgan & Claypool Publishers.
Gebser, M., Kaminski, R., & Schaub, T. (2011). Complex optimization in answer set programming. Theory and Practics of Logic Programming, 11(4–5), 821–839.
Gelfond, M. (2006). Answer sets. In F. van Harmelen, V. Lifschitz, & B. Porter (Eds.), Handbook of knowledge representation. Elsevier.
Goldreich, O. (2010). P, NP, and NP-completeness: The basics of complexity theory. Cambridge University Press.
Grandi, U. & Endriss, U. (2010). Lifting rationality assumptions in binary aggregation. In Proceedings of the 24th AAAI conference on artificial intelligence (AAAI).
Grossi, D. & Pigozzi, G. (2014). Judgment aggregation: A primer, volume 8 of synthesis lectures on artificial intelligence and machine learning. Morgan & Claypool Publishers.
de Haan, R. (2018). Hunting for tractable languages for judgment aggregation. In Proceedings of the 16th international conference on the principles of knowledge representation and reasoning (KR).
de Haan, R. & Slavkovik, M. (2017). Complexity results for aggregating judgments using scoring or distance-based procedures. In Proceedings of the 16th conference on autonomous agents and MultiAgent systems, AAMAS.
de Haan, R. & Slavkovik, M. (2019). Answer set programming for judgment aggregation. In Proceedings of the 28th international joint conference on artificial intelligence (IJCAI).
Hammond, P. J. (1976). Equity, arrow’s conditions, and rawls’ difference principle. Econometrica, 44(4), 793–804.
Kelly, J. S. (1977). Strategy-proofness and social choice functions without singlevaluedness. Econometrica, 45(2), 439–446.
Köbler, J. & Thierauf, T. (1990). Complexity classes with advice. In Proceedings of the 5th annual structure in complexity theory conference.
Konieczny, S., & Pérez, R. P. (2011). Logic based merging. Journal of Philosophical Logic, 40(2), 239–270.
Krajicek, J. (1995). Bounded arithmetic, propositional logic and complexity theory. Cambridge University Press.
Krentel, M. W. (1988). The complexity of optimization problems. Journal of Computer and System Sciences, 36(3), 490–509.
Kruger, J. & Terzopoulou, Z. (2020). Strategic manipulation with incomplete preferences: Possibilities and impossibilities for positional scoring rules. In Proceedings of the 19th international conference on autonomous agents and multiagent systems (AAMAS).
Lackner, M. & Skowron, P. (2018). Approval-based multi-winner rules and strategic voting. In Proceedings of the 27th international joint conference on artificial intelligence (IJCAI).
Lang, J., Pigozzi, G., Slavkovik, M., & van der Torre, L. (2011). Judgment aggregation rules based on minimization. In Proceedings of the 13th conference on theoretical aspects of rationality and knowledge (TARK).
Lang, J. & Slavkovik, M. (2014). How hard is it to compute majority-preserving judgment aggregation rules? In Proceedings of the 21st European conference on artificial intelligence (ECAI).
List, C., & Pettit, P. (2002). Aggregating sets of judgments: An impossibility result. Economics and Philosophy, 18(1), 89–110.
Miller, M. K., & Osherson, D. (2009). Methods for distance-based judgment aggregation. Social Choice and Welfare, 32(4), 575–601.
Mossel, E. & Tamuz, O. (2010). Truthful fair division. In Proceedings of the 3rd international symposium on algorithmic game theory (SAGT).
Moulin, H. (1988). Axioms of cooperative decision making, volume 15 of econometric society monographs. Cambridge University Press.
Nehring, K., Pivato, M., & Puppe, C. (2014). The condorcet set: Majority voting over interconnected propositions. Journal of Economic Theory, 151, 268–303.
Noothigattu, R., Gaikwad, S. S., Awad, E., Dsouza, S., Rahwan, I., Ravikumar, P., & Procaccia, A. D. (2018). A voting-based system for ethical decision making. In Proceedings of the 32nd AAAI conference on artificial intelligence (AAAI).
Peters, D. (2018). Proportionality and strategyproofness in multiwinner elections. In: Proceedings of the 17th international conference on autonomous agents and multiagent systems (AAMAS).
Pigozzi, G. (2006). Belief merging and the discursive dilemma: An argument-based account to paradoxes of judgment aggregation. Synthese, 152(2), 285–298.
Rawls, J. (1971). A theory of justice. Belknap Press.
Sanver, M. R., & Zwicker, W. S. (2009). One-way monotonicity as a form of strategy-proofness. International Journal of Game Theory, 38(4), 553–574.
Schaefer, T. J. (1978). The complexity of satisfiability problems. In Conference record of the 10th annual ACM symposium on theory of computing. ACM.
Sen, A. (1997). Choice, welfare and measurement. Harvard University Press.
Terzopoulou, Z. & Endriss, U. (2018). Modelling iterative judgment aggregation. In Proceedings of the 32nd AAAI conference on artificial intelligence (AAAI).
Wagner, K. W. (1990). Bounded query classes. SIAM Journal on Computing, 19(5), 833–846.
Zwicker, W. S. (2016). Introduction to the theory of voting. In F. Brandt, V. Conitzer, U. Endriss, J. Lang, & A. D. Procaccia (Eds.), Handbook of computational social choice. Cambridge University Press.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This paper extends and corrects the version appearing in the AAMAS-2021 proceedings. We are grateful to the anonymous AAMAS and JAAMAS reviewers for their valuable feedback.
Appendix
Appendix
In this section we delve deeper into the proofs of our complexity results.
1.1 Appendix 1: Hardness of outcome determination for the MaxEq rule
In this appendix, we will show that the outcome determination problem for the MaxEq rule boils down to a \(\Theta ^{\text { \textsf {p}}}_{2}\)-complete problem. In particular, we will show that the outcome determination problem for the MaxEq rule, when seen as a search problem, is complete (under polynomial-time Levin reductions) for \( \textsf {FP}^{\textsf {NP}}\textsf {[log,wit]}{}\)—which is a search variant of \(\Theta ^{\text { \textsf {p}}}_{2}\). Then, we show that the problem of finding the minimum difference between two agents’ satisfaction, and deciding if this value is divisible by 4, is a \(\Theta ^{\text { \textsf {p}}}_{2}\)-complete problem.
Along the way, we show that deciding if there is a judgment \(J^{*} \in {\mathcal {J}}(\Phi )\) that has the same Hamming distance to each judgment in a given profile \({\varvec{J}}\) is NP-hard, even in the case where the agenda consists of logically independent issues.
We begin, in Sect. 2, by recalling some notions from computational complexity theory—in particular, notions related to search problems. In Sect. 3, we establish the computational complexity results mentioned above.
1.2 Appendix 2: Additional complexity-theoretic preliminaries
We will consider search problems. Let \(\Sigma \) be an alphabet. A search problem is a binary relation R over strings in \(\Sigma ^*\). For any input string \(x \in \Sigma ^{*}\), we let \(R(x) = \{\ y \in \Sigma ^{*} \ |\ (x,y) \in R \ \}\) denote the set of solutions for x. We say that a Turing machine T solves R if on input \(x \in \Sigma ^*\) the following holds: if there exists at least one y such that \((x,y) \in R\), then T accepts x and outputs some y such that \((x,y) \in R\); otherwise, T rejects x.
With any search problem R we associate a decision problem \(S_R\), defined by \(S_R = \{\ x \in \Sigma ^{*} \ |\ \text {there exists some } y \in \Sigma ^{*} \text { such that } (x,y) \in R \ \}\). We will use the following notion of reductions for search problems. A polynomial-time Levin reduction from one search problem \(R_1\) to another search problem \(R_2\) is a pair of polynomial-time computable functions \((g_1,g_2)\) such that:
-
The function \(g_1\) is a many-one reduction from \(S_{R_1}\) to \(S_{R_2}\), i.e., for every \(x \in \Sigma ^{*}\) it holds that \(x \in S_{R_1}\) if and only if \(g_1(x) \in S_{R_2}\).
-
For every string \(x \in S_{R_1}\) and every solution \(y \in R_2(g_1(x))\) it holds that \((x,g_2(x,y)) \in R_1\).
One could also consider other types of reductions for search problems, such as Cook reductions (an algorithm that solves \(R_1\) by making one or more queries to an oracle that solves the search problem \(R_2\)).
For more details, we refer to textbooks on the topic—e.g., [36].
We will use complexity classes that are based on Turing machines that have access to an oracle. Let C be a complexity class with decision problems. A Turing machine T with access to a yes-no C oracle is a Turing machine with a dedicated oracle tape and dedicated states \(q_{\text {oracle}}\), \(q_{\text {yes}}\) and \(q_{\text {no}}\). Whenever T is in the state \(q_{\text {oracle}}\), it does not proceed according to the transition relation, but instead it transitions into the state \(q_{\text {yes}}\) if the oracle tape contains a string x that is a yes-instance for the problem C, i.e., if \(x \in C\), and it transitions into the state \(q_{\text {no}}\) if \(x \not \in C\).
Let C be a complexity class with search problems. Similarly, a Turing machine with access to a witness C oracle has a dedicated oracle tape and dedicated states \(q_{\text {oracle}}\), \(q_{\text {yes}}\) and \(q_{\text {no}}\). Also, whenever T is in the state \(q_{\text {oracle}}\) it transitions into the state \(q_{\text {yes}}\) if the oracle tape contains a string x such that there exists some y such that C(x, y), and in addition the contents of the oracle tape are replaced by (the encoding of) such an y; it transitions into the state \(q_{\text {no}}\) if there exists no y such that C(x, y). Such transitions are called oracle queries.
We consider the following complexity classes that are based on oracle machines.
-
The class \( \textsf {P}^{\textsf {NP}}\textsf {[log]}\) consists of all decision problems that can be decided by a deterministic polynomial-time Turing machine that has access to a yes-no NP oracle, and on any input of length n queries the oracle at most \(O(\log n)\) many times. This class coincides with the class
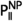 (spoken: “parallel access to NP”), and is also known as \(\Theta ^{\text { \textsf {p}}}_{2}\). Incidentally, allowing the algorithms access to a witness FNP oracle instead of access to a yes-no NP oracle leads to the same class of problems, i.e., the class \( \textsf {P}^{\textsf {NP}}\textsf {[log,wit]}\) that coincides with \( \textsf {P}^{\textsf {NP}}\textsf {[log]}\) (cf. [46, Corollary 6.3.5]).
(spoken: “parallel access to NP”), and is also known as \(\Theta ^{\text { \textsf {p}}}_{2}\). Incidentally, allowing the algorithms access to a witness FNP oracle instead of access to a yes-no NP oracle leads to the same class of problems, i.e., the class \( \textsf {P}^{\textsf {NP}}\textsf {[log,wit]}\) that coincides with \( \textsf {P}^{\textsf {NP}}\textsf {[log]}\) (cf. [46, Corollary 6.3.5]). -
The class \( \textsf {FP}^{\textsf {NP}}\textsf {[log,wit]}\) consists of all search problems that can be solved by a deterministic polynomial-time Turing machine that has access to a witness FNP oracle, and on any input of length n queries the oracle at most \(O(\log n)\) many times. In a sense, it is the search variant of \( \textsf {P}^{\textsf {NP}}\textsf {[log]}\). This complexity class happens to coincide with the class \( \textsf {FNP}/\!\!/\textsf {OptP[log]}\), which is defined as the set of all search problems that are solvable by a nondeterministic polynomial-time Turing machine that receives as advice the answer to one “NP optimization” computation [14, 44].
1.3 Appendix 3: Complexity proofs for the MaxEq rule
We define the search problem of outcome determination for a judgment aggregation rule F as follows. The input for this problem consists of an agenda \(\Phi \), a profile \({\varvec{J}}= (J_1,\dotsc ,J_n) \in {\mathcal {J}}(\Phi )^{n}\). The problem is to output some judgment \(J^{*} \in F({\varvec{J}})\). In other words, the problem is the relation R that consists of all pairs \(((\Phi ,{\varvec{J}}),J^{*})\) such that \({\varvec{J}}\in {\mathcal {J}}(\Phi )^{n}\) is a profile and \(J^{*} \in F({\varvec{J}})\). We will show that the outcome determination problem for the MaxEq rule is complete for the complexity class \( \textsf {FP}^{\textsf {NP}}\textsf {[log,wit]}{}\) under polynomial-time Levin reductions.
In order to do so, we begin with establishing a lemma that will be useful for the \( \textsf {FP}^{\textsf {NP}}\textsf {[log,wit]}{}\)-hardness proof.
This lemma uses the notion of 1-in-3-satisfiability. Let \(\psi \) be a propositional logic formula in 3CNF, i.e., \(\psi = c_1 \wedge \cdots \wedge c_m\), where each \(c_i\) is a clause containing exactly three literals. Then \(\psi \) is 1-in-3-satisfiable if there exists a truth assignment \(\alpha \) that satisfies exactly one of the three literals in each clause \(c_i\).
Lemma 1
Let \(\psi \) be a 3CNF formula with clauses \(c_1,\dotsc ,c_b\) that are all of size exactly 3 and with n variables \(x_1,\dotsc ,x_n\), such that
(1) no clause of \(\psi \) contains complementary literals, and (2) there exists some \(x^{*} \in \{ x_1,\dotsc ,x_n \}\) and a partial truth assignment \(\beta : \{ x_1,\dotsc ,x_n \} \setminus \{ x^{*} \} \rightarrow \{0,1\}\) that satisfies exactly one literal in each clause where \(x^{*}\) or \(\lnot x^{*}\) occurs, and satisfies no literal in each clause where \(x^{*}\) or \(\lnot x^{*}\) occurs. We can, in polynomial time given \(\psi \), construct an agenda \(\Phi \) on m issues such that \({\mathcal {J}}(\Phi ) = \{ 0,1 \}^{m}\) and a profile \({\varvec{J}}\) over \(\Phi \), such that:
-
\(\Phi = \{\ y_i, y'_i\ |\ 1 \le i \le n\ \} \cup \{ z_1,\dotsc ,z_5 \}\);
-
There exists a judgment \(J \in {\mathcal {J}}(\Phi )\) that has the same Hamming distance to each \(J' \in {\varvec{J}}\) if and only if \(\psi \) is 1-in-3-satisfiable;
-
if \(\psi \) is not 1-in-3-satisfiable, then for each judgment set \(J \in {\mathcal {J}}(\Phi )\) it holds that \(\max _{J',J'' \in {\varvec{J}}} |H(J,J') - H(J,J'')| \ge 2\), and there exists some \(J \in {\mathcal {J}}(\Phi )\) such that \(\max _{J',J'' \in {\varvec{J}}} |H(J,J') - H(J,J'')| = 2\);
-
The above two properties hold also when restricted to judgment sets J that contain exactly one of \(y_i\) and \(y'_i\) for each \(1 \le i \le n\), and that contain \(\lnot z_1,\dotsc ,\lnot z_4, z_5\); and
-
The number of judgments in the profile \({\varvec{J}}\) only depends on n and b.
Proof
We let the agenda \(\Phi \) consist of the \(2n+5\) issues \(y_1,\dotsc ,y_n\), \(y'_1,\dotsc ,y'_n,z_1,\dotsc ,z_5\). It follows directly that \({\mathcal {J}}(\Phi ) = \{0,1\}^{2n+5}\). Then, we start by constructing 2n judgments \(J_1,\dotsc ,J_{2n}\) over these issues, defined as depicted in Fig. 2.
Construction of the judgments \(J_1,\dotsc ,J_{2n}\) in the proof of Lemma 1
Then, for each clause \(c_k\) of \(\psi \), we introduce three judgments \(J_{k,1}\), \(J_{k,2}\), and \(J_{k,3}\) that are defined as follows. The judgment \(J_{k,1}\) contains \(y_i, \lnot y'_i\) for each positive literal \(x_i\) occurring in \(c_k\), and contains \(y'_i, \lnot y_i\) for each negative literal \(\lnot x_i\) occurring in \(c_k\). Conversely, the judgments \(J_{k,2},J_{k,3}\) contain \(y'_i, \lnot y_i\) for each positive literal \(x_i\) occurring in \(c_k\), and contain \(y_i, \lnot y'_i\) for each negative literal \(\lnot x_i\) occurring in \(c_k\). For each variable \(x_j\) that does not occur in \(c_k\), all three of \(J_{k,1},J_{k,2},J_{k,3}\) contain \(\lnot y_j, \lnot y'_j\). Finally, the judgment \(J_{k,1}\) contains \(\lnot z_1,\dotsc ,\lnot z_4,z_5\), the judgment \(J_{k,2}\) contains \(\lnot z_1,\lnot z_2,z_3,z_4,z_5\), and the judgment \(J_{k,3}\) contains \(z_1,z_2,\lnot z_3,\lnot z_4,z_5\).
This is illustrated in Fig. 3 for the example clause \((x_1 \vee \lnot x_2 \vee x_3)\).
Illustration of the construction of the judgments \(J_{k,1},J_{k,2},J_{k,3}\) for the example clause \(c_k = (x_1 \vee \lnot x_2 \vee x_3)\) in the proof of Lemma 1
The profile \({\varvec{J}}\) then consists of the judgments \(J_1,\dotsc ,J_{2n}\), as well as the judgments \(J_{k,1},J_{k,2},J_{k,3}\) for each \(1 \le k \le b\).
In order to prove that \({\varvec{J}}\) has the required properties, we consider the following observations and claims (and prove the claims).
Observation 1
If a judgment J contains exactly one of \(y_i\) and \(y'_i\) for each i, then the Hamming distance from J to each of \(J_1,\dotsc ,J_{2n}\)—restricted to the issues \(y_1,\dotsc ,y_n,y'_1,\dotsc ,y'_n\)—is exactly n.
Claim 2
If a judgment J contains both \(y_i\) and \(y'_i\) for some i, or neither \(y_i\) nor \(y'_i\) for some i, then there are at least two judgments among \(J_1,\dotsc ,J_{2n}\) such that the Hamming distance from J to these two judgments differs by at least 2.
Proof of Claim 2
We argue that this is the case for \(y_1\) and \(y'_1\), i.e., for the case of \(i = 1\). For other values of i, an entirely similar argument works.
Picking both \(y_1\) and \(y'_1\) to be part of a judgment J adds to the Hamming distances between J, on the one hand, and \(J_1,\dotsc ,J_{2n}\), on the other hand, according to the vector \(v^{+}_{1}\):
Picking both \(\lnot y_1\) and \(\lnot y'_1\) to be part of the set J adds to the Hamming distances between J and \(J_1,\dotsc ,J_{2n}\) according to the vector \(v^{-}_{1}\):
Picking exactly one of \(y_1\) and \(y'_1\) and exactly one of \(\lnot y_1\) and \(\lnot y'_1\) to be part of J corresponds to the all-ones vector \(\varvec{1} = (1,\dotsc ,1)\). More generally, both \(y_i\) and \(y'_i\) to be part of J adds to the Hamming distances according to the vector \(v^{+}_{i}\):
picking both \(\lnot y_i\) and \(\lnot y'_i\) corresponds to the vector \(v^{-}_{i}\):
and picking exactly one of \(y_i\) and \(y'_i\) and exactly one of \(\lnot y_i\) and \(\lnot y'_i\) to be part of J corresponds to the all-ones vector \(\varvec{1} = (1,\dotsc ,1)\). For each \(1 \le i \le n\), the vectors \(v^{-}_{1},\dotsc ,v^{-}_{n}\) and \(v^{+}_{i}\) are linearly independent, and the vectors \(v^{+}_{1},\dotsc ,v^{+}_{n}\) and \(v^{-}_{i}\) are linearly independent.
Suppose now that we pick J to contain both \(y_1\) and \(y'_1\). Suppose, moreover, to derive a contradiction, that the Hamming distance from J to each of the judgments \(J_1,\dotsc ,J_{2n}\) is the same. This means that there is some way of choosing \(s_2,\dotsc ,s_n\) such that \(v^{-}_{1} = \sum _{1 < i \le n} v^{s_i}_{i}\), which contradicts the fact that \(v^{+}_{1},\dotsc ,v^{+}_{n}\) and \(v^{-}_{i}\) are linearly independent—since each \(v^{-}_{j}\) can be expressed as \(v^{-}_{j} = v^{+}_{i} + v^{-}_{i} - v^{+}_{j}\). Thus, we can conclude that there exist at least two judgments among \(J_1,\dotsc ,J_{2n}\) such that the Hamming distance from J to these two judgments differs. Moreover, since all vectors contain only even numbers, and the coefficients in the sum are integers (in fact, either 0 or 1), we know that the difference must be even and thus at least 2.
An entirely similar argument works for the case where we pick J to contain both \(\lnot y_1\) and \(\lnot y'_1\). \(\dashv \)
Observation 3
Let \(\alpha : \{ x_1,\dotsc ,x_n \} \rightarrow \{0,1\}\) be a truth assignment that satisfies exactly one literal in each clause of \(\psi \). Consider the judgment \(J_{\alpha } = \{\ y_i, \lnot y'_i\ |\ 1 \le i \le n, \alpha (x_i) = 1\ \} \cup \{\ y'_i, \lnot y_i\ |\ 1 \le i \le n, \alpha (x_i) = 0\ \} \cup \{ \lnot z_1,\dotsc ,\lnot z_4,z_5 \}\). Then the Hamming distance from \(J_{\alpha }\) to each judgment in the profile \({\varvec{J}}\) is exactly \(n+1\).
Claim 4
Suppose that \(\psi \) is not 1-in-3-satisfiable. Then for each judgment J that contains exactly one of \(y_i\) and \(y'_i\) for each i, there is some clause \(c_k\) of \(\psi \) such that the difference in Hamming distance from J to (two of) \(J_{k,1},J_{k,2},J_{k,3}\) is at least 2.
Proof of Claim 4
Take an arbitrary judgment J that contains exactly one of \(y_i\) and \(y'_i\) for each i. This judgment J corresponds to the truth assignment \(\alpha _{J} : \{ x_1,\dotsc ,x_n \} \rightarrow \{0,1\}\) defined such that for each \(1 \le i \le n\) it is the case that \(\alpha (x_i) = 1\) if \(y_i \in J\) and \(\alpha (x_i) = 0\) if \(y_i \not \in J\). Since \(\psi \) is not 1-in-3-satisfiable, we know that there exists some clause \(c_{\ell }\) such that \(\alpha _{J}\) does not satisfy exactly one literal in \(c_{\ell }\). We distinguish several cases: either (i) \(\alpha _{J}\) satisfies no literals in \(c_{\ell }\), or (ii) \(\alpha _{J}\) satisfies two literals in \(c_{\ell }\), or (iii) \(\alpha _{J}\) satisfies three literals in \(c_{\ell }\). In each case, the Hamming distances from J, on the one hand, and \(J_{k,1},J_{k,2},J_{k,3}\), on the other hand, must differ by at least 2. This can be verified case by case—and we omit a further detailed case-by-case verification of this. \(\dashv \)
Claim 5
If \(\psi \) is not 1-in-3-satisfiable, then there exists a judgment J such that \(\max _{J',J'' \in {\varvec{J}}} |H(J,J') - H(J,J'')| = 2\).
Proof of Claim 5
Suppose that \(\psi \) is not 1-in-3-satisfiable. We know that there exists a variable \(x^{*} \in \{ x_1,\dotsc ,x_n \}\) and a partial truth assignment \(\beta : \{ x_1,\dotsc ,x_n \} \setminus \{ x^{*} \} \rightarrow \{0,1\}\) that satisfies exactly one literal in each clause where \(x^{*}\) or \(\lnot x^{*}\) does not occur, and satisfies no literal in each clause where \(x^{*}\) or \(\lnot x^{*}\) occurs. Without loss of generality, suppose that \(x^{*} = x_1\). Now consider the judgment \(J_{\beta } = \{ \lnot y_1, \lnot y'_1 \} \cup \{\ y_i, \lnot y'_i\ |\ 1< i \le n, \beta (x_i) = 1\ \} \cup \{\ y'_i, \lnot y_i\ |\ 1 < i \le n, \beta (x_i) = 0\ \} \cup \{ \lnot z_1,\dotsc ,\lnot z_4,z_5 \}\).
One can verify that the Hamming distances from \(J_{\beta }\), on the one hand, and \(J' \in {\varvec{J}}\), on the other hand, differ by at most 2—and for some \(J',J'' \in {\varvec{J}}\) it holds that \(|H(J,J') - H(J,J'')| = 2\). \(\dashv \)
We now use the above observations and claims to show that \(\Phi \) and \({\varvec{J}}\) have the required properties. If \(\psi \) is 1-in-3-satisfiable, by Observation 3, there is some \(J \in {\mathcal {J}}(\Phi )\) that has the same Hamming distance to each \(J' \in {\varvec{J}}\). Suppose, conversely, that \(\psi \) is not 1-in-3-satisfiable. Then by Claims 2 and 4 , there exist two judgments \(J',J'' \in {\varvec{J}}\) such that \(H(J,J')\) and \(H(J,J'')\) differ (by at least 2). Thus, \(\psi \) is 1-in-3-satisfiable if and only if there exists a judgment set \(J \in {\mathcal {J}}(\Phi )\) that has the same Hamming distance to each judgment in the profile \({\varvec{J}}\).
Suppose that \(\psi \) is not 1-in-3-satisfiable. Then by Claims 2 and 4 , we know that for each \(J \in {\mathcal {J}}(\Phi )\) it holds that \(\max _{J',J'' \in {\varvec{J}}} |H(J,J') - H(J,J'')| \ge 2\). Moreover, by Claim 5, there exists a judgment \(J \in {\mathcal {J}}(\Phi )\) such that \(\max _{J',J'' \in {\varvec{J}}} |H(J,J') - H(J,J'')| = 2\).
We already observed that that \({\mathcal {J}}(\Phi ) = \{0,1\}^{m}\) for some m. Moreover, one can straightforwardly verify that the statements after the first two bullet points in the statement of the lemma also hold when restricted to judgment sets J that contain exactly one of \(y_i\) and \(y'_i\) for each \(1 \le i \le n\) and that contain \(\lnot z_1,\dotsc ,\lnot z_4, z_5\). This concludes the proof of the lemma. \(\square \)
Now that we have established the lemma, we continue with the \( \textsf {FP}^{\textsf {NP}}\textsf {[log,wit]}{}\)-completeness proof.
Theorem 3
The problem of outcome determination for the MaxEq rule is \( \textsf {FP}^{\textsf {NP}}\textsf {[log,wit]}{}\)-complete under polynomial-time Levin reductions.
Proof
To show membership in \( \textsf {FP}^{\textsf {NP}}\textsf {[log,wit]}\), we describe an algorithm with access to a witness FNP oracle that solves the problem in polynomial time by making at most a logarithmic number of oracle queries. This algorithm will use an oracle for the following FNP problem: given some \(k \in {\mathbb {N}}\) and given the agenda \(\Phi \) and the profile \({\varvec{J}}\), compute a judgment \(J \in {\mathcal {J}}(\Phi )\) such that \(\max _{J',J'' \in {\varvec{J}}} |H(J,J') - H(J,J'')| \le k\), if such a J exists, and return “none” otherwise. By using \(O(\log |\Phi |)\) queries to this oracle, one can compute the minimum value \(k_{\text {min}}\) of \(\max _{J',J'' \in {\varvec{J}}} |H(J,J') - H(J,J'')|\) where the minimum is taken over all judgments \(J \in {\mathcal {J}}(\Phi )\). Then, with a final query to the oracle, using \(k = k_{\text {min}}\), one can use the oracle to produce a judgment \(J^{*} \in \text {MaxEq}({\varvec{J}})\).
We will show \( \textsf {FP}^{\textsf {NP}}\textsf {[log,wit]}{}\)-hardness by giving a polynomial-time Levin reduction from the \( \textsf {FP}^{\textsf {NP}}\textsf {[log,wit]}{}\)-complete problem of finding a satisfying assignment for a (satisfiable) propositional formula \(\psi \) that sets a maximum number of variables to true (among any satisfying assignment of \(\psi \)) [14, 44, 47, 65].
Let \(\psi \) be an arbitrary satisfiable propositional logic formula with v variables. Without loss of generality, assume that v is even and that there is a satisfying truth assignment for \(\psi \) that sets at least one variable to true. We will construct an agenda \(\Phi \) and a profile \({\varvec{J}}\), such that the minimum value of \(\max _{J',J'' \in {\varvec{J}}} |H(J^{*},J') - H(J^{*},J'')|\), for any \(J^{*} \in {\mathcal {J}}(\Phi )\), is divisible by 4 if and only if the maximum number of variables set to true in any satisfying assignment of \(\psi \) is odd. Moreover, we will construct \(\Phi \) and \({\varvec{J}}\) in such a way that from any \(J^{*} \in \text {MaxEq}(\Phi )\) we can construct, in polynomial time, a satisfying assignment of \(\psi \) that sets a maximum number of variables to true.
This—together with the fact that \(\Phi \) and \({\varvec{J}}\) can be constructed in polynomial time—suffices to exhibit a polynomial-time Levin reduction, and thus to show \( \textsf {FP}^{\textsf {NP}}\textsf {[log,wit]}{}\)-hardness.
We proceed in several stages (i–iv).
-
(i)
We begin, in the first stage, by constructing a 3CNF formula \(\psi _i\) with certain properties, for each \(1 \le i \le v\).
Claim 6
We can construct in polynomial time, for each \(1 \le i \le v\), a 3CNF formula \(\psi _i\), that is 1-in-3-satisfiable if and only if there is a truth assignment that satisfies \(\psi \) and that sets at least i variables in \(\psi \) to true. Moreover, we construct these formulas \(\psi _i\) in such a way that they all contain exactly the same variables \(x_1,\dotsc ,x_n\) and exactly the same number b of clauses, and such that each formula \(\psi _i\) has the properties:
-
That it contains no clause with complementary literals, and
-
That it contains a variable \(x^{*}\) for which there exists a partial truth assignment \(\beta : \{ x_1,\dotsc ,x_n \} \setminus \{ x^{*} \} \rightarrow \{0,1\}\) that satisfies exactly one literal in each clause where \(x^{*}\) or \(\lnot x^{*}\) does not occur, and satisfies no literal in each clause where \(x^{*}\) or \(\lnot x^{*}\) occurs.
Proof of Claim 6
Consider the problems of deciding if a given truth assignment \(\alpha \) to the variables in \(\psi \) satisfies \(\psi \), and deciding if \(\alpha \) satisfies at least i variables, for some \(1 \le i \le v\). These problems are both polynomial-time solvable. Therefore, by using standard techniques from the proof of the Cook-Levin Theorem [16], we can construct in polynomial time a propositional formula \(\chi \) in 3CNF containing (among others) the variables \(t_1,\dotsc ,t_v\), the variable \(x^{\dagger }\) and the variables in \(\psi \) such that any truth assignment to the variables \(x^{\dagger },t_1,\dotsc ,t_v\) and the variables in \(\psi \) can be extended to a satisfying truth assignment for \(\chi \) if and only if either (i) it sets \(x^{\dagger }\) to true, or (ii) it satisfies \(\psi \) and for each \(1 \le i \le v\) it sets \(t_i\) to false if and only if it sets at least i variables among the variables in \(\psi \) to true.
Then, we can transform this 3CNF formula \(\chi \) to another 3CNF formula \(\chi '\) with a similar property—namely that any truth assignment to the variables \(x^{\dagger },t_1,\dotsc ,t_v\) and the variables in \(\psi \) can be extended to a truth assignment that satisfies exactly one literal in each clause of \(\chi \) if and only if either (i) it sets \(x^{\dagger }\) to true, or (ii) it satisfies \(\psi \) and for each \(1 \le i \le v\) it sets \(t_i\) to false if and only if it sets at least i variables among the variables in \(\psi \) to true. We do so by using the the polynomial-time reduction from 3SAT to 1-IN-3-SAT given by Schaefer [62].
Then, for each particular value of i, we add two clauses that intuitively serve to ensure that variable \(t_i\) must be set to false in any 1-in-3-satisfying truth assignment. We add \((s_0 \vee s_1 \vee t_i)\) and \((\lnot s_0 \vee \lnot s_1 \vee t_i)\), where \(s_0\) and \(s_1\) are fresh variables—the only way to satisfy exactly one literal in both of these clauses is to set exactly one of \(s_0\) and \(s_1\) to true, and to set \(t_i\) to false.
Moreover, we add the clauses \((r_0 \vee r_1 \vee x^{\dagger })\), \((\lnot r_0 \vee r_2 \vee \lnot x^{\dagger })\), \((x^{*} \vee r_3 \vee r_0)\), and \((\lnot x^{*} \vee r_4 \vee r_0)\), where \(r_0,\dotsc ,r_4\) and \(x^{*}\) are fresh variables. These clauses serve to ensure the property that there always exists a partial truth assignment \(\beta : \{ x_1,\dotsc ,x_n \} \setminus \{ x^{*} \} \rightarrow \{0,1\}\) that satisfies exactly one literal in each clause where \(x^{*}\) or \(\lnot x^{*}\) does not occur, and satisfies no literal in each clause where \(x^{*}\) or \(\lnot x^{*}\) occurs. Moreover, these added clauses preserve 1-in-3-satisfiability if and only if there exists a 1-in-3-satisfying truth assignment for the formula without these added clauses that sets \(x^{\dagger }\) to true.
Putting all this together, we have constructed a 3CNF formula \(\chi ''\)—consisting of \(\chi '\) with the addition of the six clauses mentioned in the above two paragraphs—that has the right properties mentioned in the statement of the claim. In particular, \(\chi ''\) is 1-in-3-satisfiable if and only if there is a truth assignment that satisfies \(\psi \) and that sets at least i variables in \(\psi \) to true. Moreover, the constructed formula \(\chi ''\) has the same variables and the same number of clauses, regardless of the value of i chosen in the construction. \(\dashv \)
Since the formulas \(\psi _i\), as described in Claim 6, satisfy the requirements for Lemma 1, we can construct agendas \(\Phi _1,\dotsc ,\Phi _v\) and profiles \({\varvec{J}}_1,\dotsc ,{\varvec{J}}_v\) such that for each \(1 \le i \le v\), the agenda \(\Phi _i\) and the profile \({\varvec{J}}_i\) satisfy the conditions mentioned in the statement of Lemma 1. Moreover, we can construct the agendas \(\Phi _1,\dotsc ,\Phi _v\) in such a way that they are pairwise disjoint. For each \(1 \le i \le v\), let \(y_{i,1},\dotsc ,y_{i,n},y'_{i,1},\dotsc ,y'_{i,n}, z_{i,1},\dotsc ,z_{i,5}\) denote the issues in \(\Phi _i\) and let \({\varvec{J}}_i = (J_{i,1},\dotsc ,J_{i,u})\).
-
(ii)
Then, in the second stage, we will use the profiles \(\Phi _1,\dotsc ,\Phi _v\) and the profiles \({\varvec{J}}_1,\dotsc ,{\varvec{J}}_v\) to construct a single agenda \(\Phi \) and a single profile \({\varvec{J}}\).
We let \(\Phi \) contain the issues \(y_{i,j}\), \(y'_{i,j}\) and \(z_{i,1},\dotsc ,z_{i,5}\), for each \(1 \le i \le v\) and each \(1 \le j \le n\), as well as issues \(w_{i,\ell ,k}\) for each \(1 \le i \le v\), each \(1 \le \ell \le u\) and each \(1 \le k \le n\). We let \({\varvec{J}}\) contain judgments \(J'_{i,\ell }\) for each \(1 \le i \le v\) and each \(1 \le \ell \le u\), that we will define below. Intuitively, for each i, the sets \(J'_{i,\ell }\) will contain the judgments \(J_{i,1},\dotsc ,J_{i,u}\) from the profile \({\varvec{J}}_i\).
Take an arbitrary \(1 \le i \le v\), and an arbitrary \(1 \le \ell \le u\). We let \(J'_{i,\ell }\) agree with \(J_{i,\ell }\) (from \({\varvec{J}}_i\)) on all issues from \(\Phi _i\)—i.e., the issues \(y_{i,j}\), \(y'_{i,j}\) for each \(1 \le j \le n\) and \(z_{i,1},\dotsc ,z_{i,5}\). On all issues \(\varphi \) from each \(\Phi _{i'}\), for \(1 \le i' \le v\) with \(i' \ne i\), we let \(J'_{i,\ell }(\varphi ) = 0\). Then, we let \(J'_{i,\ell }(w_{i',\ell ',k}) = 1\) if and only if \(i = i'\) and \(\ell = \ell '\).
In other words, \(J'_{i,\ell }\) agrees with \(J_{i,\ell }\) on the issues from \(\Phi _i\), it sets every issue from each other \(\Phi _{i'}\) to false, it sets all the issues \(w_{i,\ell ,k}\) to true, and it sets all other issues \(w_{i',\ell ',k}\) to false.
-
(iii)
In the third stage, we will replace the logically independent issues in \(\Phi \) by other issues, in order to place restrictions on the different judgments that are allowed.
We start by describing a constraint—in the form of a propositional logic formula \(\Gamma \) on the original (logically independent) issues in \(\Phi \)—and then we describe how this constraint can be used to produce replacement formulas for the issues in \(\Phi \). We define \(\Gamma = \Gamma _{1} \vee \Gamma _{2}\) by:
In other words, \(\Gamma \) requires that either (1) for some \(i,\ell \) all issues \(w_{i,\ell ,k}\) are set to true, and all other issues \(w_{i',\ell ',k}\) are set to false, or (2) all issues \(w_{i,\ell ,k}\) are set to false and for each i, j exactly one of \(y_{i,j}\) and \(y'_{i,j}\) is set to true.
Because we can in polynomial time compute a satisfying truth assignment for \(\Gamma \), we know that we can also in polynomial time compute a replacement \(\varphi '\) for each \(\varphi \in \Phi \), resulting in an agenda \(\Phi '\), so that the logically consistent judgments \(J \in {\mathcal {J}}(\Phi ')\) correspond exactly to the judgments \(J \in {\mathcal {J}}(\Phi )\) that satisfy the constraint \(\Gamma \) [26, Proposition 3].
In the remainder of this proof, we will use \(\Phi \) (with the restriction that judgment sets should satisfy \(\Gamma \)) interchangeably with \(\Phi '\).
-
(iv)
Finally, in the fourth stage, we will duplicate some issues \(\varphi \in \Phi \) a certain number of times, by adding semantically equivalent (yet syntactically different) issues to the agenda \(\Phi \), and by updating the judgments in the profile \({\varvec{J}}\) accordingly.
For each \(1 \le i \le v\), we will define a number \(c_i\) and will make sure that there are \(c_i\) (syntactically different, logically equivalent) copies of each issue in \(\Phi \) that originated from the agenda \(\Phi _i\). In other words, we duplicate each agenda \(\Phi _i\) a certain number of times, by adding \(c_i - 1\) copies of each issue that originated from \(\Phi _i\). For each \(1 \le i \le v\), we let \(c_i = (v-i)\). This concludes the description of our reduction—i.e., of the profile \(\Phi \) and the profile \({\varvec{J}}\). What remains is to show that the minimum value of \(\max _{J',J'' \in {\varvec{J}}} |H(J^{*},J') - H(J^{*},J'')|\), for any \(J^{*} \in {\mathcal {J}}(\Phi )\), is divisible by 4 if and only if the maximum number of variables set to true in any satisfying assignment of \(\psi \) is odd. To do so, we begin with stating and proving the following claims.
Claim 7
For any judgment \(J^{*} \in {\mathcal {J}}(\Phi )\) that satisfies \(\Gamma _1\), the value of \(\max _{J',J'' \in {\varvec{J}}} |H(J^{*},J') - H(J^{*},J'')|\) is at least 2n.
Proof of Claim 7
Take some \(J^{*}\) that satisfies \(\Gamma _{1}\). Then there must exist some \(i,\ell \) such that J sets all \(w_{i,\ell ,k}\) to true and all other \(w_{i',\ell ',k}\) to false. Therefore, \(|H(J^{*},J'_{i,\ell }) - H(J^{*},J_{i',\ell '})|\) is at least 2n, for any \(i',\ell '\) such that \((i,\ell ) \ne (i',\ell ')\). \(\dashv \)
Claim 8
For any judgment \(J^{*} \in {\mathcal {J}}(\Phi )\) that satisfies \(\Gamma _2\), the value of \(\max _{J',J'' \in {\varvec{J}}} |H(J^{*},J') - H(J^{*},J'')|\) is strictly less than 2v.
Proof of Claim 8
Take some \(J^{*}\) that satisfies \(\Gamma _{2}\). Then \(J^{*}\) sets each \(w_{i,\ell ,k}\) to false, and for each \(1 \le i \le v\) the judgment J contains \(\lnot z_{i,1},\dotsc ,\lnot z_{i,4},z_{i,5}\) and contains exactly one of \(y_{i,j}\) and \(y'_{i,j}\) for each \(1 \le j \le n\). Moreover, without loss of generality, we may assume that \(J^{*}\), for each \(1 \le i \le v\), assigns truth values to the issues originating from \(\Phi _i\) in a way that corresponds either (a) to a truth assignment to the variables in \(\psi _i\) witnessing that \(\psi _i\) is 1-in-3-satisfiable, or (b) to a partial truth assignment \(\beta : \text {var}(\psi _i) \setminus \{ x_1 \} \rightarrow \{0,1\}\) that satisfies exactly one literal in each clause where \(x_1\) or \(\lnot x_1\) occurs, and satisfies no literal in each clause where \(x_1\) or \(\lnot x_1\) occurs.
If this were not the case, we could consider another \(J^{*}\) instead that does satisfy these properties and that has a value of \(\max _{J',J'' \in {\varvec{J}}} |H(J^{*},J') - H(J^{*},J'')|\) that is at least as small.
Then, by the construction of \({\varvec{J}}\)—and the profiles \({\varvec{J}}_i\) used in this construction—for each \(J'_{i,j}\) it holds that \(H(J^{*},J'_{i,j}) = \sum \nolimits _{1 \le i \le v}c_i(n+1) + n \pm d_i\), where \(d_i = 0\) if \(\psi _i\) is 1-in-3-satisfiable and \(d_i = (v-i)\) otherwise. From this it follows that the value of \(\max _{J',J'' \in {\varvec{J}}} |H(J^{*},J') - H(J^{*},J'')|\) is strictly less than 2v, since \(\psi _1\) is 1-in-3-satisfiable. \(\dashv \)
By Claims 7 and 8 , and because we may assume without loss of generality that \(n \ge v\), we know that any judgment \(J^{*} \in {\mathcal {J}}(\Phi )\) that minimizes \(\max _{J',J'' \in {\varvec{J}}} |H(J^{*},J') - H(J^{*},J'')|\) must satisfy \(\Gamma _2\). Moreover, by a straightforward modification of the arguments in the proof of Claim 8, we know that the minimal value, over judgments \(J^{*} \in {\mathcal {J}}(\Phi )\), of \(\max _{J',J'' \in {\varvec{J}}} |H(J^{*},J') - H(J^{*},J'')|\) is \(2(v-i)\) for the smallest value of i such that \(\psi _i\) is not 1-in-3-satisfiable, which coincides with \(2(v+1-i)\) for the largest value of i such that \(\psi _i\) is 1-in-3-satisfiable. Since v is even (and thus \(v+1\) is odd), we know that \(2(v+1-i)\) is divisible by 4 if and only if i is odd. Therefore, the minimal value of \(\max _{J',J'' \in {\varvec{J}}} |H(J^{*},J') - H(J^{*},J'')|\) is divisible by 4 if and only if the maximum number of variables set to true in any satisfying assignment of \(\psi \) is odd.
Moreover, it is straightforward to show that from any \(J^{*} \in \text {MaxEq}(\Phi )\) we can construct, in polynomial time, a satisfying assignment of \(\psi \) that sets a maximum number of variables to true.
This concludes our description and analysis of the polynomial-time Levin reduction, and thus of our hardness proof. \(\square \)
Proposition 6
Given an agenda \(\Phi \) and a profile \({\varvec{J}}\), the problem of deciding whether there is some \(J^{*} \in {\mathcal {J}}(\Phi )\) with \(\max _{J',J'' \in {\varvec{J}}} |H(J^{*},J') - H(J^{*},J'')| = 0\) is NP-complete. Moreover, NP-hardness holds even for the case where \(\Phi \) consists of logically independent issues—i.e., the case where \({\mathcal {J}}(\Phi ) = \{0,1\}^m\) for some m.
Proof
We show that the problem is in NP by giving a nondeterministic polynomial-time algorithm that solves the problem. Given an agenda \(\Phi \) and a profile \({\varvec{J}}\), the algorithm guesses a binary vector \(J^{*}\), together with a truth assignment \(\alpha \) witnessing that \(J^{*}\) is consistent. The algorithm first checks that \(J^{*} \in {\mathcal {J}}(\Phi )\), by checking that \(\alpha \) satisfies all formulas in \(J^{*}\). Then it iterates over all \(J' \in {\varvec{J}}\), and computes \(H(J^{*},J')\). This provides enough information to compute \(\max _{J',J'' \in {\varvec{J}}} |H(J^{*},J') - H(J^{*},J'')|\). The algorithm accepts if and only if this value equals 0.
We continue with showing NP-hardness. We give a polynomial-time reduction from the problem of deciding if there exists a truth assignment that satisfies a given 3CNF formula \(\psi \) and that sets at least 3 variables among the variables of \(\psi \) to true. It is straightforward to show that this problem is NP-complete. NP-hardness of this problem can be shown by a reduction from the problem of satisfiability of propositional logic formulas in 3CNF. Take an arbitrary 3CNF formula \(\chi \) with variables \(x_1,\dotsc ,x_n\), and construct the formula \(\chi ' = \chi \wedge (x_{n+1} \vee x_{n+2} \vee x_{n+3})\). Then \(\chi \) is satisfiable if and only if \(\chi '\) is satisfiable by setting at least 3 of its variables to true.
We proceed with our hardness proof. Take an arbitrary 3CNF formula \(\psi \). By Claim 6 in the proof of Theorem 3, we can in polynomial time construct a 3CNF formula \(\psi '\) with variables \(x_1,\dotsc ,x_n\) that is 1-in-3-satisfiable if and only if \(\psi \) is satisfiable by a truth assignment that sets at least 3 of its variables to true. Moreover, we know that \(\psi '\) contains no clause with complementary literals, and that \(\psi '\) contains a variable \(x^{*}\) for which there exists a partial truth assignment \(\beta : \{ x_1,\dotsc ,x_n \} \setminus \{ x^{*} \} \rightarrow \{0,1\}\) that satisfies exactly one literal in each clause of \(\psi '\) where \(x^{*}\) or \(\lnot x^{*}\) does not occur, and satisfies no literal in each clause of \(\psi '\) where \(x^{*}\) or \(\lnot x^{*}\) occurs. Then, by Lemma 1, we can construct from \(\psi '\) an agenda \(\Phi \) with logically independent issues and a profile \({\varvec{J}}\) over \(\Phi \) with the property that there is some \(J^{*} \in {\mathcal {J}}(\Phi )\) with \(\max _{J',J'' \in {\varvec{J}}} |H(J^{*},J') - H(J^{*},J'')| = 0\) if and only if \(\psi '\) is 1-in-3-satisfiable—which is the case if and only if the original formula \(\psi \) is satisfiable.
Therefore, the problem of deciding—for a given agenda \(\Phi \) and a given profile \({\varvec{J}}\) over \(\Phi \)—whether there is some \(J^{*} \in {\mathcal {J}}(\Phi )\) with \(\max _{J',J'' \in {\varvec{J}}} |H(J^{*},J') - H(J^{*},J'')| = 0\) is NP-hard, even for the case where \(\Phi \) consists of logically independent issues. \(\square \)
Notably, the proof of Theorem 3 brings out an intriguing fact about a problem that is at first glance simpler than outcome determination for MaxEq: Given an agenda \(\Phi \) and a profile \({\varvec{J}}\), deciding whether the minimum value of \(\max _{i,j\in N} |H(J_i,J)-H(J_j,J)|\) for \(J \in {\mathcal {J}}(\Phi )\)—the value that the MaxEq rule minimizes—is divisible by 4, is \(\Theta ^{\text { \textsf {p}}}_{2}\)-complete (Proposition 8). Intuitively, merely computing the minimum value that is relevant for MaxEq is \(\Theta ^{\text { \textsf {p}}}_{2}\)-hard.
Proposition 8
Given an agenda \(\Phi \) and a profile \({\varvec{J}}\), deciding whether the minimal value of \(\max _{J',J'' \in {\varvec{J}}} |H(J^{*},J') - H(J^{*},J'')|\) for \(J^{*} \in {\mathcal {J}}(\Phi )\), is divisible by 4, is a \(\Theta ^{\text { \textsf {p}}}_{2}\)-complete problem.
Proof
This follows from the proof of Theorem 3. The proof of membership in \( \textsf {FP}^{\textsf {NP}}\textsf {[log,wit]}{}\) for the outcome determination problem for the MaxEq rule can directly be used to show membership in \(\Theta ^{\text { \textsf {p}}}_{2}\) for this problem.
Moreover, the polynomial-time Levin reduction used in the \( \textsf {FP}^{\textsf {NP}}\textsf {[log,wit]}{}\)-hardness proof can be seen as a polynomial-time (many-to-one) reduction from the \(\Theta ^{\text { \textsf {p}}}_{2}\)-complete problem of deciding if the maximum number of variables set to true in any satisfying assignment of a (satisfiable) propositional formula \(\psi \) is odd [47, 65]. \(\square \)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Botan, S., de Haan, R., Slavkovik, M. et al. Egalitarian judgment aggregation. Auton Agent Multi-Agent Syst 37, 16 (2023). https://doi.org/10.1007/s10458-023-09598-6
Accepted:
Published:
DOI: https://doi.org/10.1007/s10458-023-09598-6







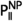 (spoken: “parallel access to NP”), and is also known as
(spoken: “parallel access to NP”), and is also known as 
