Towards explainable interactive multiobjective optimization: R-XIMO

Abstract

In interactive multiobjective optimization methods, the preferences of a decision maker are incorporated in a solution process to find solutions of interest for problems with multiple conflicting objectives. Since multiple solutions exist for these problems with various trade-offs, preferences are crucial to identify the best solution(s). However, it is not necessarily clear to the decision maker how the preferences lead to particular solutions and, by introducing explanations to interactive multiobjective optimization methods, we promote a novel paradigm of explainable interactive multiobjective optimization. As a proof of concept, we introduce a new method, R-XIMO, which provides explanations to a decision maker for reference point based interactive methods. We utilize concepts of explainable artificial intelligence and SHAP (Shapley Additive exPlanations) values. R-XIMO allows the decision maker to learn about the trade-offs in the underlying problem and promotes confidence in the solutions found. In particular, R-XIMO supports the decision maker in expressing new preferences that help them improve a desired objective by suggesting another objective to be impaired. This kind of support has been lacking. We validate R-XIMO numerically, with an illustrative example, and with a case study demonstrating how R-XIMO can support a real decision maker. Our results show that R-XIMO successfully generates sound explanations. Thus, incorporating explainability in interactive methods appears to be a very promising and exciting new research area.

1 Introduction

Real-life optimization problems seldom consist of only a single objective to be optimized. Instead, multiple conflicting objectives are to be considered simultaneously. These problems are known as multiobjective optimization problems and many solutions, known as Pareto optimal solutions, exist with various trade-offs between the objectives. The characteristics that define the best solution to be implemented in practice depend on the problem and subjective information. This information can be obtained from a human domain expert, known as a decision maker (DM). If the DM provides their preferences, we can find the DM’s best (i.e., most preferred) solution.

The type of preferences a DM can provide varies a lot (see, e.g., [1,2,3]). When the preferences are incorporated into the solution process also matters. The DM can provide preferences before the optimization, but they can be too optimistic or pessimistic. Alternatively, a representative set of Pareto optimal solutions can be generated for the DM to choose from, but this can be both computationally and cognitively demanding. In contrast to these, in interactive multiobjective optimization methods [4, 5], preferences are incorporated iteratively during the solution process [1]. Interactive methods are many and vary in various aspects, such as the type of preference information required from the DM and how preferences are incorporated in the optimization process [4, 6, 7].

Moreover, the course of an interactive solution process can be divided into a learning and a decision phase [5]. Roughly speaking, as the name suggests, in the learning phase, the DM learns about the trade-offs and the feasibility of one’s preferences to identify a region of interest and, in the decision phase, one converges to the most preferred solution in that region. Unfortunately, interactive methods typically offer little support to the DM during the learning phase making it hard for the DM to learn. This lack of support is an open issue in interactive multiobjective optimization [8, 9], which we will address in our work.

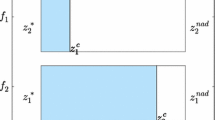
An example of preference information is a reference point consisting of desirable objective function values. We propose an approach to support the DM in applying interactive reference point based methods [10, 11], where explanations are provided to the DM about why an interactive method has mapped their preferences to certain solutions. Reference point based methods are classified, e.g., in [12], as ad hoc methods arguing that they do not support the DM in directing the solution process to provide preferences for the next iteration. Thus, these methods may seem like black-boxes to DMs. Therefore, explanations can help the DM learn about the trade-offs between the objectives in the problem, for instance. The general concept of an iteration of a reference point based interactive methods is illustrated in Fig. 1. The DM provides a reference point per iteration to get desirable values for objective functions. There are many ways a solution can be computed based on a reference point, e.g., by minimizing an appropriate scalarizing function that maps the reference point to the closest Pareto optimal solution. Thus, by modifying the reference point, different solutions can be found.

In addition, by utilizing the explanations, we can also support the DM by deriving suggestions from the explanations that provide information about how preferences can be modified to achieve some desired results, such as improving a certain objective function value in a solution of the next iteration. An example of the second iteration where we want to support the DM is illustrated in Fig. 1. There, the DM wishes to improve Objective 2 in the initial solution and wonders how the initial reference point should be modified to achieve this goal. Indeed, according to the advice given in [13], we consider two central questions in interactive multiobjective optimization which can arise in the mind of the DM:

• 1. Why preferences have been mapped to the computed solution(s)?

• 2. How can preferences be changed to affect the computed solution(s)?

Fig. 1

The general concept of reference point based interactive multiobjective optimization methods illustrated with a problem with two objectives to be minimized. The questions of why a reference point has been mapped to a specific solution and how the reference point could be changed to achieve a desired result are highlighted

We borrow ideas from the field of explainable artificial intelligence (XAI) [14]. We do not attempt to create a new interactive multiobjective optimization method. Instead, we present a method that is able to explain the behavior of reference point based methods and support the DM in learning about the multiobjective optimization problem and providing preference information. There are methods in the field of XAI that can be used to formulate explanations for the predictions made by black-box machine learning models. Most of these methods have the advantage of being model agnostic, which means that they can be applied to any kind of (machine learning) model [15]. We show in our work that these methods can be applied in interactive multiobjective optimization methods as well and used to successfully formulate explanations.

Our main contribution is developing the concept of explainable interactive multiobjective optimization (XIMO) by exploring reference point based interactive multiobjective optimization methods. The ideas introduced in this paper are applicable to other interactive methods as well. XIMO is a very broad topic and our paper will, hopefully, lead to more follow-up research exploring the application of the concept of explainability in multiobjective optimization. Our proposed method, R-XIMO, derives explanations and supports a DM in providing a reference point to reflect desired changes in the objective functions. This method is also ideal to be incorporated as an agent in a multi-agent system supporting the DM in an interactive multiobjective solution process as discussed in [16].

Our paper is structured as follows. In Sect. 2, we introduce the background concepts required to understand the ideas discussed in the paper. Then, we introduce our proposed method R-XIMO in Sect. 3. In Sect. 4, we give an illustrative example on how R-XIMO can support a DM in practice, and we also present a case study with a real DM solving a multiobjective optimization problem in Finnish forest management. We validate R-XIMO further numerically and present the results in Sect. 5. We discuss the results of Sects. 4 and 5, as well as future research perspectives of R-XIMO, and XIMO in general, in Sect. 6. Lastly, we conclude our work in Sect. 7.

2 Background

2.1 Concepts of multiobjective optimization

Multiobjective optimization [1] consist of multiple conflicting objective functions to be optimized simultaneously. Such problems can be mathematically formulated as follows:

$$\begin{aligned} \begin{aligned}&\text {minimize}&\mathbf {F}(\mathbf {x})=\left( f_1(\mathbf {x}), \dots , f_k(\mathbf {x})\right) \\&\text {subject to}&\mathbf {x}\in S, \\ \end{aligned} \end{aligned}$$

(1)

where $f_i(\mathbf {x})$, $i=1, \dots , k$ are objective functions (with $k\ge 2$), and $\mathbf {x}= (x_1,..., x_n)^T$ is a vector of n decision variables belonging to the feasible set $S \subset \mathbb {R}^n$. For every decision vector $\mathbf {x}$, there is a corresponding objective vector $\mathbf {F}(\mathbf {x})$. In the rest of this article, we refer only to minimization problems, but the conversion of a function to maximization is trivial (i.e., multiplying by -1).

Because of the conflict between the objective functions, not all of them can achieve their optimal values simultaneously. Given two feasible solutions $\mathbf {x}^1, \mathbf {x}^2 \in S$, $\mathbf {x}^1$ dominates $\mathbf {x}^2$ if and only if $f_{i}(\mathbf {x}^1) \le f_{i}(\mathbf {x}^2)$ for all $i=1, \dots k$, and $f_{j}(\mathbf {x}^1) < f_{j}(\mathbf {x}^2)$ for at least one index $j=1, \dots , k$. A solution $\mathbf {x}^* \in S$ is Pareto optimal if and only if there is no solution $\mathbf {x} \in S$ that dominates it. The set of all Pareto optimal solutions is called a Pareto optimal set, and the corresponding objective vectors constitute a Pareto optimal front. A feasible solution $\mathbf {x}^* \in S$ and the corresponding objective vector $\mathbf {F}(\mathbf {x}^*)$ in the objective space are weakly Pareto optimal if there does not exist another feasible solution $\mathbf {x} \in S$ such that $f_{i}(\mathbf {x}) < f_{i}(\mathbf {x}^*)$ for all $i= 1, \dots , k$.

The ideal point $\mathbf {z}^*$ and nadir point $\mathbf {z}^{nad}$ represent the lower and upper bounds of the objective function values among Pareto optimal solutions, respectively. The ideal point is calculated by minimizing each objective function separately. The nadir point represents the worst objective function values in the Pareto optimal set. Obtaining its value is not straightforward, as it requires computing the Pareto optimal set. However, it can be approximated [1]. The components of a utopian point $\mathbf {z}^{**}$ are derived by improving the components of the ideal point with a small positive $\varepsilon$.

As mentioned, typically, solving a multiobjective optimization problem involves a DM who has deeper knowledge of the problem. The DM is responsible for finding the most preferred solution among the conflicting objectives.

There are different types of methods for solving multiobjective optimization problems, for example, scalarization based and population based (like evolutionary) methods [17]. Scalarizing functions convert a multiobjective optimization problem into a single objective one [1, 11]. They usually also incorporate the preference information of the DM. Problem (1) can be converted into a scalarized one as

$$\begin{aligned} \begin{aligned}&\text {minimize} \quad s(\mathbf {F(\mathbf {x}); \, \mathbf {p}}) \\&\text {subject to}\quad \mathbf {x}\in S, \end{aligned} \end{aligned}$$

(2)

where $\mathbf {p}$ is a set of parameters required by the scalarizing function s. Several scalarizing functions have been proposed in the literature [1, 11]. We are interested in scalarizing functions [18] that consider a reference point $\varvec{\bar{z}}$ provided by the DM. As mentioned, a reference point consists of desirable objective function values, also known as aspiration levels. As examples, we utilize scalarizing function from different methods (for more information about reference point based scalarizing functions, see [10, 11]).

The scalarizing function of the GUESS method [19] is the following

$$\begin{aligned} \begin{aligned} \text {GUESS}(\varvec{\bar{z}};\, \mathbf {F}, \mathbf {z}^\text {nad})=\, \min _{\mathbf {x}\in S}\,\max _{i=1,...,k} \left[ \frac{f_i(\mathbf {x}) - {z}^\text {nad}_i}{z^\text {nad}_i - \bar{z}_i} \right] . \end{aligned} \end{aligned}$$

(3)

From the STOM method [20], we get

$$\begin{aligned} \text {STOM}(\varvec{\bar{z}};\, \mathbf {F}, \mathbf {z}^{**})=\, \min _{\mathbf {x}\in S}\,\max _{i=1,...,k} \left[ \frac{f_i(\mathbf {x}) - {z}^{**}_i}{\bar{z}_i - z^{**}_i} \right] + \rho \sum _{i=1}^k\frac{f_i(\mathbf {x})}{\bar{z}_i - z^{**}_i}, \end{aligned}$$

(4)

and from the reference point method (RPM) [18, 21] we get

$$\begin{aligned} \text {RPM}(\varvec{\bar{z}}; \mathbf {F}, \mathbf {z}^{**}, \mathbf {z}^\text {nad})=\, \min _{\mathbf {x}\in S}\,\max _{i=1,...,k} \left[ \frac{f_i(\mathbf {x}) - \bar{z}_i}{{z}^\text {nad}_i - z^{**}_i} \right] + \rho \sum _{i=1}^k\frac{f_i(\mathbf {x})}{{z}^\text {nad}_i - z^{**}_i}. \end{aligned}$$

(5)

Scalarizing functions (4) and (5) contain an augmentation term with a small, positive multiplier $\rho$. This term guarantees that the solution will not be weakly Pareto optimal, as can be the case for (3). Actually, the solutions of (4) and (5) are properly Pareto optimal (for further information, see [1]). For the three scalarizing functions, the denominator must not equal zero. In fact, it is positive when $z_i^*< \bar{z}_i < z_i^\text {nad}$ for all $i=1, \dots , k$.

As mentioned in the introduction, we consider reference point based methods, where in each iteration, the DM provides a reference point and the method generates one or some Pareto optimal solutions reflecting the preferences. Depending on the method, the scalarizing function used to generate the solution(s) varies (it can, e.g., be one of the three functions above). The DM can iteratively compare the obtained solutions and provide new reference points until the most preferred solution is found.

2.2 Explainable artificial intelligence and SHAP values

The central goal of machine learning methods [22] is to approximate, or predict, new information based on past observations. State-of-the-art machine learning methods, such as deep neural networks, have shown vast potential for various applications across many fields, see, e.g., [23,24,25,26]. It is typical for the most accurate machine learning models, which are often the most complex ones, to be also the most opaque [27], but not necessarily always [28]. These models are often employed in high-stakes domains, such as healthcare [29] and self-driving cars [30], where their opaque black-box nature can become problematic, see, e.g., [31, 32].

Because the true value of a prediction of a machine learning model is often unknown, the validity of the predictions cannot be checked by comparing it to the true value. Therefore, the viability of the prediction needs to be validated in some other way. An example is to provide some explanation justifying the prediction. Based on this explanation, a human, or humans, can then decide whether the prediction is sound or not.

XAI [14] sheds light on black-box models to understand how they make predictions. Many different XAI methods exist [33]. Usually, they try to explain the predictions made by black-box models, which have already been trained, as is done by LIME [34], for instance. The explanations are therefore not a result of the model itself, but an external tool. This kind of explanation is known as post-hoc. Another typical approach is to come up with new, inherently explainable, machine learning models, such as Bayesian rule lists [35]; or to simply tap into the explainability inherently found in interpretable models, such as decision trees [36]. Explanation models that do not depend on the type of machine learning model are known as model agnostic ones. Typically, these models can explain any machine learning model. For example, they are able to explain the prediction of an individual input for some previously trained model. And as we will later see in our work, some model agnostic explanation models can also be utilized to explain black-boxes that are not machine learning models at all. For reviews on the recent advancements in XAI, see, e.g., [15, 37].

Typically, a machine learning model g is trained on input–output training set pairs consisting of vectors with M features (also known as attributes) $\mathbf {a}$ and output values y. Training consists of finding internal parameter values for g so that when g is evaluated with some new observation $\mathbf {a}^*$, which was not present in the training set, the output of g, $g(\mathbf {a}^*) = y^*$, would be as close as possible to the true output value, i.e., $y^*\approx y^\text {true}$, which is often unknown. The output of the model g is also known as a prediction.

In our work, we focus on ad-hoc explanation methods unified by the SHAP framework [38]. The reason for this is that the SHAP framework guarantees certain theoretically sound properties (local accuracy, missingness, consistency, and uniqueness; see [38] for an in-depth discussion on their implications). By utilizing the SHAP framework, so-called SHAP values can be computed. SHAP values are based on Shapley values [39], which in turn are based on game theory [40].

Shapley values can be used to assign a value to the contribution of a single player to the payout in an n-player game. In other words, Shapley values can be used to characterize the contribution of a single entity (i.e., an attribute in an input to a machine learning model) when multiple entities collaborate to achieve a common goal (i.e., make a prediction). Thus, Shapley values can be used akin to sensitivity analysis to explore how a prediction made by a machine learning model changes when certain combinations of attributes are present or missing in the input, but with the added value of also having the four properties listed above. For instance, for some input $\mathbf {a}$ and prediction $g(\mathbf {a})$, a positive value for a Shapley value $\phi _i$ would indicate that the value of the attribute $a_i \in \mathbf {a}$ has overall contributed positively (i.e., increasingly) to the output value $g(\mathbf {a})$, and vice versa for a negative value for $\phi _i$, and when $\phi _i$ is zero, attribute i has not contributed to the output value. With this kind of information, it is possible to come up with plausible explanations on how the machine learning method has made some particular prediction for a given input.

However, a typical machine learning model is not able to work with missing attributes; at least not without retraining the model, which in most cases can be very time-consuming. This makes Shapley values not directly applicable when generating explanations for some arbitrary machine learning model. That is why SHAP values are used, instead. In particular, kernel SHAP [38], which combines the idea behind Shapley values and LIME [34], is of particular interest because it is a model agnostic approach for computing SHAP values. Kernel SHAP requires so-called missing data, which is used to replace attributes in the input to a machine learning model to simulate missing attributes when explaining its predictions. In this way, the input to the machine learning model has always the same number of attributes, and the model does not have to be retrained when computing SHAP values. We use kernel SHAP to compute SHAP values in R-XIMO, proposed in Sect. 3, when it is validated in Sect. 5.

2.3 Explainability in multiobjective optimization

In what follows, we provide a brief literature review on explainable multiobjective optimization. The emphasis here is not on studies that use multiobjective optimization methods to generate explanations, but rather on studies that apply the existing explainable methods (or propose new ones) for multiobjective optimization.

A diversified recommendation framework based on a decomposition-based evolutionary algorithm was proposed in [9]. The authors modeled the recommender system as a multiobjective optimization problem and applied MOEA/D [41] to generate explainable recommendation lists for each user while maintaining a high recommendation accuracy.

A method explaining the reasoning behind the solution found for a multiobjective probabilistic planning problem was proposed in [42]. Their method generates verbal explanations about why it chose a specific solution among the other alternatives and also about the trade-off made between conflicting objectives in the final solution. Explaining trade-offs among various objectives was also studied in [43] via reinforcement learning by utilizing a correlation matrix that represents the relative importance between objectives.

There are some recent initiatives in the literature that incorporate explanations into interactive methods. For the sake of explainability, the interactive method called INFRINGER [44] utilized belief-rule-based systems to learn and model the DM’s preferences. Similarly, in [45], the authors modeled the DM’s preferences by using “if..., then...” decision rules, which were then used to explain the impact of the DM’s preferences on the obtained solutions. They proposed a method called XIMEA-DRSA, which uses the decision rules as a preference model to guide the search in the solution process.

3 R-XIMO

In this section, we introduce the method proposed in this paper, R-XIMO, to explain how reference point based interactive multiobjective optimization methods map preference information into solutions. We start by describing the setting and general assumptions made in Sect. 3.1. In Sect. 3.2, we describe in detail how SHAP values are used to interpret a black-box that maps reference points to the Pareto optimal front. Finally, in Sect. 3.3, we discuss how the SHAP values are used to generate explanations and suggestions for a DM to allow them to make meaningful trade-offs regarding the preferences they have expressed.

3.1 Setting and assumptions

In general, a DM has domain expertise about the multiobjective optimization problem, allowing them to understand the existence of conflicts among the objectives (i.e., gaining in one objective in a Pareto optimal solution will result in a loss in at least one other objective). Assuming that a DM acts rationally (see, e.g., [46] for a discussion on rationality), they are only interested in Pareto optimal solutions. But a DM does not necessarily understand how the interactive method transforms the preference information into solution candidates during the solution process. According to these characteristics of DMs, we will assume that they perceive interactive multiobjective optimization methods as black-boxes.

Let us consider black-boxes mapping reference points $\varvec{\bar{z}}$ to objective vectors $\mathbf {z}$ on the Pareto optimal front for a problem (1) with k objectives. We define such a black-box as

$$\begin{aligned} \mathfrak {B}(\varvec{\bar{z}}):\,\mathbb {R}^k \rightarrow \mathbb {R}^k_{\text {Pareto}}, \end{aligned}$$

(6)

where the subterm Pareto means that the objective vectors and the reference points are mapped to solutions that lie on the Pareto optimal front.

In particular, we use black-boxes, which minimize reference point based scalarizing functions [1, 11]. As mentioned, as examples, we consider the scalarizing functions (3), (4) and (5), and the DM provides preferences as a reference point. We assume that the DM is informed of the values for the ideal and nadir points when providing reference points, as it was originally assumed in [21]. This will allow the DM to provide more realistic reference points. Depending on the type of black-box (6) considered, it may also be necessary to assume that each aspiration level in the reference point is between the objective’s respective components in the ideal and nadir points. Lastly, we assume the DM to be interacting with an interactive method that acts like the black-box defined in (6) over the course of a few iterations until they find a most preferred solution.

3.2 Using SHAP values to explain reference point based black-box models

The idea behind SHAP values discussed in Sect. 2.2 can also be applied to other types of black-boxes, not necessarily related to machine learning models. We apply the idea to an interactive multiobjective optimization method explaining its behavior to a DM. We limit the discussion to a simple case of an interactive method (6), where a DM is only required to provide a reference point over the course of a few iterations. Then, the input to the model is the reference point provided by the DM and the prediction is the result of solving problem (2) with some scalarizing function s.

We can use SHAP values to formulate explanations for models adherent with (6). Since the reference point provided by a DM and the output of (6) have $k\ge 2$ dimensions, the SHAP values computed are represented by a $k\times k$ square matrix $\Phi$ with elements $\phi _{ij}$, $i,j= 1, \dots , k$:

$$\begin{aligned} \Phi = \begin{pmatrix} \phi _{11}, &{}\phi _{12}, &{}\dots , &{}\phi _{1k} \\ \phi _{21}, &{}\phi _{22}, &{}\dots , &{}\phi _{2k} \\ \vdots &{}\vdots &{}\vdots &{}\vdots \\ \phi _{k1}, &{}\phi _{k2}, &{}\dots , &{}\phi _{kk} \\ \end{pmatrix}. \end{aligned}$$

(7)

The average effect of a reference point on a solution is represented by (7). How the ith component in the resulting objective vector has been affected by the jth component in the reference point, is represented by the value of the element $\phi _{ij}$ in (7). Thus, the SHAP values in (7) can be used to induce how, on average, the input $\varvec{\bar{z}}$ has affected the output $\mathbf {z}$. Expanding on the discussion given for the interpretation of Shapley values in Sect. 2.2, a positive value for $\phi _{ij}$ means that on average, the jth component in the reference point had an increasing effect on the value of objective i in the solution, and vice versa for negative values. A value of zero for $\phi _{ij}$ means that there was no effect between the two. When objectives are minimized, an increasing effect means impairing, and a decreasing effect means improving.

We know that in multiobjective optimization, the objectives are conflicting. Therefore, we can say that when two objectives have an increasing effect on each other (i.e., both $\phi _{ij}$ and $\phi _{ji}$ are positive for some i, j) the aspiration levels set by the DM in the reference point are not simultaneously achievable on the Pareto optimal front. This is because in the specific region of the front the reference point was mapped to, objectives i and j are conflicting. Note that in case $i=j$, the value of $\phi _{ij}$ is understood as the objective’s effect upon itself. It is important to mention that not all objectives need be always conflicting, and that the conflict can be between more than two objectives, but in our work, we only consider conflicts between pairs of objectives for the sake of simplicity. Therefore, the exact conflicting nature of two considered objectives depends on which region of the Pareto optimal front is observed.

Because of the properties mentioned in Sect. 2 for SHAP values, we know that the values are local and unique. Especially, the local nature of the SHAP values is important because it guarantees that the SHAP values computed describe the conflicts among objectives in a local region of the Pareto optimal front. Moreover, a direct consequence of the uniqueness of the SHAP values warrants that the explanations derived from the SHAP values can be assumed to be unique (albeit the way the values are interpreted can lead to different explanations, but any reasoning based solely of the actual numerical values should lead to the same conclusions). This is why we have decided in our work to utilize SHAP values.

We use SHAP values (7) to deduce how a component in a given reference point affects the solution computed by a black-box (6). Particularly, we can gather information about the conflict between two objectives. We can then communicate this information to the DM giving them support in formulating new reference points. Thus, an explainable support system can be created to support the DM in achieving their goals in an interactive solution process utilizing SHAP values. How this kind of system can be realized, is discussed in the next subsection.

3.3 Utilizing explanations and suggestions to aid a decision maker

We choose to demonstrate the plausibility of utilizing SHAP values for explaining interactive multiobjective optimization methods with a simple application as follows. Consider a DM has provided a reference point $\varvec{\bar{z}}$ to a black-box (6) and has been presented with a solution $\mathbf {z}$. Now the DM wishes to see an improvement in the value of the ith objective in $\mathbf {z}$. We designate this objective as the target and define its index as $i_\text {target}$. We can then use the computed SHAP values to find the component in $\bar{\mathbf {z}}$, which had the most impairing effect on the target in $\mathbf {z}$ (i.e., $\phi _{i_\text {target}j} = \max _{\phi _{ij}, i = i_\text {target}}\Phi$). We name this objective with the most impairing effect as the rival with index $j_\text {rival}$. Therefore, we can formulate explanations for the DM on how the solution $\mathbf {z}$ relates to the given reference point $\varvec{\bar{z}}$ from the perspective of the target, and how the DM can change the reference point for the next iteration to achieve a better value in the target.

The general idea of our proposed method is depicted in Fig. 2. Since our method enhances reference point based interactive methods with explanations, we call it R-XIMO.

Fig. 2

Illustration on how R-XIMO interacts with the interactive method and the DM. R-XIMO is aware of both the reference point provided by the DM and the solution computed by the interactive method. After the DM selects a target, R-XIMO can provide a suggestion and explanation with information on the rival. In the figure, a single iteration of an interactive method combined with R-XIMO is depicted

The details of the procedure to compute the rival and generate an explanation in R-XIMO are given in Algorithm 1. The input to Algorithm 1 are the black-box $\mathfrak {B}$ (6), a reference point $\varvec{\bar{z}}$, the solution $\mathbf {z}$ computed utilizing the black-box and the reference point, missing data $Z_\text {missing}$ needed in computing SHAP values, and the index of the target objective $i_\text {target}$ provided by the DM. The missing data is used by the routine shap_values in Algorithm 1 to calculate the SHAP values. The routine shap_values can be any routine able to compute SHAP values like in (7) (e.g., kernel SHAP). The output of Algorithm 1 is the index of the rival objective $j_\text {rival}$ and an explanation explanation on how the reference point $\varvec{\bar{z}}$ given has affected the solution $\mathbf {z}$ computed.

When choosing the missing data $Z_\text {missing}$ to be used in R-XIMO, it is important that such data is available in the vicinity of the reference point being explained to assure the locality of the explanations. Therefore, missing data should be generated as evenly as possible in the domain space of (6), but since we assume a DM to provide reference points with component values bounded by the respective components of the ideal and nadir points, it is enough for the generated missing data to be bound in a similar way. However, when experimenting, we found that we could use a representation of the Pareto optimal front of the original multiobjective optimization problem as the missing data without any loss in performance of R-XIMO. This, we believe, is because the Pareto optimal front characterizes the trade-offs among the objectives in the problem, which is what we are primarily interested in.

For computing the index of the rival $j_\text {rival}$ in Algorithm 1, the general idea is to find the element $\phi _{i_\text {target}j} \in \Phi$ with the largest positive value. If this value exists and it is not the target itself, then the index j of the element found is defined as worst_effect. Otherwise worst_effect is set to be $-1$ indicating that it does not exist. Likewise, we can also find the element $\phi _{i_\text {target}j}$ with the smallest negative value and define its j index as best_effect. The routine why_objective_i in Algorithm 1 computes both of these values. In cases where worst_effect does not exist, we can find the element $\phi _{i_\text {target}j}$ with the largest negative value and set its j index as least_negative as is done in Algorithm 1. Lastly, if worst_effect $= i_\text {target}$, we can find the element $\phi _{i_\text {target}j}$ with the second largest value and define second_worst to be equal to j. The value of $j_\text {rival}$ returned by Algorithm 1 is therefore always either worst_effect, second_worst, or least_negative. An implementation of Algorithm 1 is discussed in Sect. 5.1.

The nine possible explanations (indexed by $\texttt {n}=1, \dots , 9$) returned by Algorithm 1 are listed in Table 1. From each of the explanations, a suggestion is derived to support the DM in achieving their goal of improving the value of the target in the solution. The explanations tell the DM how the given reference point $\varvec{\bar{z}}$ is related to the solution $\mathbf {z}$, and how the components of $\varvec{\bar{z}}$ have affected the value of the target in $\mathbf {z}$. In supporting the DM, the suggestion derived from the explanation is most relevant. However, the explanation can help the DM gain additional insight related to the multiobjective optimization problem, and it can help the DM build confidence in the suggestion given as well. Therefore, in practice, the explanation should be shown to the DM only when they request to see it. The suggestion should be always provided to the DM. Examples of utilizing R-XIMO are given in Sect. 4.

The first four explanations in Table 1 are relevant in cases where the components of the given reference point are either worse in regard to every objective value when compared to the solution ($\texttt {n}=1,2$), or the components in the reference point are all better than in the solution ($\texttt {n}=3,4$). Such reference points can be expected to arise when the DM is still in an early stage of the interactive solution process and is therefore still learning about the problem. In case of $\texttt {n}=2$, the suggestion still prompts the DM to improve the target component in the reference point despite the target having the most impairing effect on the target objective in the solution. This can feel counter intuitive, but it is done because worsening the rival component in the reference point can lead to a situation where some other objective than the target improves, if the target component is left unchanged. By still improving the target component in the reference point, we try to guarantee that the DM will see an improvement in the target objective in the solution.

The following two explanations in Table 1 arise when none of the components in the reference point had an improving effect on the target ($\texttt {n}=5$), or when none of the components had an impairing effect on the target ($\texttt {n}=6$). In the first case, the DM may want to be careful when improving the value of the target in the next reference point since in the area of the Pareto optimal front the solution resides, the other objectives seem to be all in conflict with the target objective. In the second case, the DM may want to experiment with improving the value of the target objective in the next reference point since none of the other objectives had any impairing effects on the target.

The seventh explanation in Table 1 ($\texttt {n}=7$) is the explanation that one can expect to arise in most cases after the DM has gained some insight about the problem and its trade-offs. In this case, some component in the reference point had an improving effect on the target objective in the solution and some other component had an impairing effect. In this case, neither best_effect nor worst_effect is the target objective.

Table 1 Explanations explanation_n returned by Algorithm 1 for indices $\texttt {n} = 1, \dots , 9$

The last two explanations in Table 1 ($\texttt {n}=8,9$) arise when the condition of the first four explanations are not met and the most impairing or improving effect on the target objective’s value in the solution was due to the target objective’s component in the reference point. The eighth explanation $(\texttt {n}=8)$ is something the DM does not probably desire to see when they care about the target objective, and could therefore be a reason for the DM to mistrust the interactive method. On the other hand, the last explanation ($\texttt {n}=9$) is probably the one a DM would expect to see as they deem the target objective to be the most important, when providing a reference point.

We can think of impairing a component of the reference point as a way to gain more room in terms of improving some other objective value in the solution. This is why the suggestion in Table 1 always prompts the DM to improve the target component in the reference point. In this way, we can assume that the room gained in impairing the rival is reflected in the improvement on the target. We can justify this on basis of the objectives being in conflict in multiobjective optimization problems.

Validating the explanations in Table 1 (i.e., how useful the explanation and suggestion is to a human DM) is impossible without either human participants or advanced artificial DMs. To our knowledge, no artificial DMs exist that could help validate the explanations. In Sect. 4.1 we provide an illustrative example how the explanations (and suggestions) generated by R-XIMO, can support a hypothetical DM. In Sect. 4.2, we demonstrate R-XIMO in a case study with a real DM. We also validate the suggestions derived from the explanations in Sect. 5 numerically—i.e., does improving the target and impairing the rival computed by R-XIMO lead to an improvement in the value of the target in the solution? As we will see, the suggestions generated by R-XIMO can reveal to the DM the best component to be impaired in a reference point when a given target objective is to be improved. This alone can be very valuable information to a DM.

4 Example and case study

In this section, we show how R-XIMO can be applied in solving multiobjective optimization problems interactively. We demonstrate this both with an illustrative example in Sect. 4.1, and a case study involving a real DM in Sect. 4.2.

4.1 Illustrative example

In this subsection, we demonstrate with an example how R-XIMO supports a DM by providing explanations and suggestions (Table 1) in an interactive solution process. An analyst (one of the authors) acted as the DM to illustrate the support R-XIMO provides in solving a real-world multiobjective optimization problem. The problem considered was originally proposed in [47] and modified in [48]. A Python notebook with the described solution process is available online.¹

4.1.1 Problem description

The problem describes a (hypothetical) pollution of a river. There is a fishery company and a city in a valley along the river. The company is located near the head of the valley, and it causes industrial pollution on the river. The city is located downstream from the fishery and is the source of municipal waste pollution on the river. Water quality is measured in terms of dissolved oxygen level (DO), while industrial and municipal pollution is quantified in pounds of biochemical oxygen demanding material (BOD). There are some existing treatment facilities that reduce the BOD in the water, and their costs are paid by the company and the city. To deal with the water pollution, additional water treatment facilities should be built, which would incur higher costs, raising the city’s tax rate and decreasing the company’s return on investment.

The two decision variables, $x_1$ and $x_2$, control the amount of BOD removed from water in two treatment plans located in the company and in the city, respectively. The original problem had four objectives; $f_1$ maximizing DO in the city, $f_2$ maximizing DO at the state line downstream from the city, $f_3$ maximizing percent return on investment at the company, and $f_4$ minimizing the additional tax rate in the city. We use the modified version of the problem [48], in which the fifth objective ($f_5$) is added to describe the functionality of the treatment facilities. Thus, the multiobjective optimization problem has five objectives and two decision variables (we consider it as a minimization problem by multiplying the first three objectives by -1), as follows:

$$\begin{aligned} \begin{array}{rll} &{}\text {minimize}\quad f_1({\mathbf {x}}) =&{} - 4.07 - 2.27 x_1 \\ &{}\text {minimize}\quad f_2({\mathbf {x}}) =&{} - 2.60 - 0.03 x_1 - 0.02 x_2 \\ &{}&{}\quad - \frac{0.01}{1.39 - x_1^2} - \frac{0.30}{1.39 - x_2^2} \\ &{}\text {minimize}\quad f_3({\mathbf {x}}) =&{} - 8.21 + \frac{0.71}{1.09 - x_1^2} \\ &{}\text {minimize}\quad f_4({\mathbf {x}}) =&{} - 0.96 + \frac{0.96}{1.09 - x_2^2} \\ &{}\text {minimize}\quad f_5({\mathbf {x}}) =&{} \max \{|x_1 - 0.65 |, |x_2 - 0.65 |\} \\ &{}&{}\\ &{}\text {subject to} &{} 0.3 \le x_1, x_2 \le 1.0. \\ \end{array} \end{aligned}$$

(8)

4.1.2 Solution process

We can now describe the interactive solution process using R-XIMO with a DM. To scalarize (8), we used STOM (4) and an approximation of the Pareto optimal front of (8) computed utilizing evolutionary methods (NSGA-III [49], MOEA/D [41], and RVEA [50]). The scalarized version of (8) was solved by finding the objective vector that minimizes (2) in the Pareto optimal front. At the beginning of the solution process, the ideal $(-\,6.34, -3.44, -\,7.5, 0, 0)$ and nadir $(-\,4.75, -\,2.85, -\,0.32, 9.70, 0.35)$ points were calculated based on the approximation of the Pareto optimal front and shown to the DM.

Iteration 1. First, the DM set the ideal point as the reference point to see how difficult it is to achieve these promising values. The obtained result was $(-\,5.75, -\,2.91, -\,6.91, 0.20, 0.13)$. The DM desired to improve the water quality in the city ($f_1$) and R-XIMO returned the following suggestion: “ Try improving the 1st component and impairing the 3rd component.”

Iteration 2. Since the reference point had been too optimistic, and the DM realized that to improve $f_1$, he needed to impair $f_3$ (the return on investments). Therefore, he adjusted all aspiration levels accordingly but most impairments were made in the 3rd one, and he set the next reference point as $(-\,6.00, -\,3.20, -\,6.00, 0.10, 0.10)$. As a consequence, the following solution was obtained: $(-6.00, -2.92, -6.26, 0.21, 0.20)$. He was happy with the return on investments ($f_3$), the addition to the tax ($f_4$), and the efficiency of the treatment facilities ($f_5$). However, the water quality after the city ($f_2$) was inadequate, so he wanted to improve that objective with the support of R-XIMO, which made the following suggestion: “ Try improving the 2nd component and impairing the 4th component. ”

Iteration 3. Based on the given suggestion, the DM realized the trade-off between $f_2$ and $f_4$. He followed the suggestion and impaired the 4th aspiration level, set the reference point $(-6.00, -3.20, -6.00, 1.00, 0.10)$ and obtained the corresponding solution $(-5.90, -3.06, -6.60, 1.21, 0.16)$. There was a good improvement on $f_2$, but the DM wished to improve it even further, if possible. R-XIMO provided the following suggestion in response to the DM’s request of improving the value of $f_2$: “ Try improving the 2nd component and impairing the 5th component.”

Iteration 4. To improve $f_2$, the DM needed to impair the aspiration level for $f_5$ and kept the same aspiration levels for the other objectives as in the previous reference point: $(-\,6.00, -\,3.20, -\,6.00, 1.00, 0.20)$. As a consequence, the following solution was obtained: $(-6.09, -3.09, -5.79, 1.44, 0.24)$. As can be observed, the water quality in and after the city ($f_1$ and $f_2$) improved, while the economic objectives ($f_3$ and $f_4$) and facility efficiency ($f_5$) deteriorated. The DM was not satisfied with the last three objectives, particularly the last one. He wished to improve it, and the following suggestion was made to achieve his purpose: “ Try improving the 5th component and impairing the 3rd component.”

Iteration 5. Therefore, he reduced his economic expectations ($f_3$) and improved the efficiency ($f_5$) in his reference point: $(-6.00, -3.20, -5.50, 1.00, 0.12)$. The DM was almost happy with the returned solution $(-\,5.94, -\,3.08, -\,6.49, 1.38, 0.17)$ since he nearly obtained what he desired without sacrificing the third objective. However, he wanted to ensure that the addition to the tax rate ($f_4$) could be decreased without jeopardizing other objectives. To understand whether this is possible, the DM requested an explanation in addition to the suggestion for improving the tax rate. R-XIMO returned the following: “ None of the components in the reference point had an impairing effect on objective $f_4$ in the solution. The 1st component of the reference point had the least improving effect on objective $f_4$ in the solution. Try improving the 4th component and impairing the 1st component.”

Iteration 6. The DM improved his aspiration level for the fourth objective based on the suggestion and kept the others the same as before: $(-6.00, -3.20, -5.50, 0.80, 0.12)$, because none of the components had an impairing effect on objective $f_4$ based on the given explanation. The solution obtained was $(-\,5.95, -\,3.06, -\,6.45, 1.25, 0.18)$. As can be seen, the return on investments ($f_3$) was relatively higher than his aspiration level for that objective, he obtained sufficient water quality for the city ($f_1$), and after the city ($f_3$), the addition to tax ($f_4$) was slightly improved from the previous solution, and the efficiency of the facilities was nearly identical. The DM was satisfied with this solution and decided to stop the solution process.

4.1.3 Observations

Clearly, the suggestions made by R-XIMO assisted the DM in recognizing the trade-offs among the objectives and efficiently providing his preference information to get more preferred solutions. Having the option to request an explanation was also beneficial to the DM; for example, in iteration 5, the DM benefited from the explanation provided by R-XIMO. At that point, the DM gained sufficient insight into the problem and was mostly aware of the existing conflicts among the objectives. He was almost satisfied but wanted to improve one specific objective further, if possible. That is why he requested an explanation from R-XIMO whether he missed some other existing conflicts or not. Based on the given explanation, he understood that there were no other objectives impairing his target objective. Therefore, he followed the first part of the suggestion (improving the target objective) but not the second part, which suggested impairing some other objective having the least improving effect on the target objective (which he learned from the explanation). As experienced, the DM was not forced to follow the suggestions but benefited from the explanations.

4.2 Real case study

As a proof of concept, we consider a multiobjective optimization problem with a domain expert as the DM in a case study in Finnish forest management. We first briefly outline the problem and then describe the setting and solution process with the DM. We also report the DM’s opinions and feedback regarding R-XIMO and the support it provides.

4.2.1 Problem description

Finnish forests are divided into managerial areas known as stands. In a forest management problem, for each stand, a particular management strategy is to be chosen to be employed over a certain time period. Some examples of available strategies are, for instance, that trees in a stand are cut down or thinned out, or the stand is left untouched. Depending on which strategy is employed for a stand, corresponding consequences will ensue. These consequences can be regarded as objectives, and by considering multiple consequences at the same time, the forest management problem can be modeled as a multiobjective optimization problem.

In our case, we have three objectives to be maximized simultaneously over the considered time period: income from sold timber (Income), carbon dioxide stored in the trees (Stored CO$_2$), and the combined habitat suitability index indicating how habitable the forest is for fauna (CSHI). Solutions to the problem will be represented by objective vectors of the form (Income, Stored CO$_2$, CSHI). These objectives are in conflict; for instance, cutting down trees and selling the timber for increased profit will release stored carbon dioxide and make the stand inhabitable for the fauna; or thinning out a stand can increase its combined suitable habitat index, but it will also release stored carbon, and it can be financially unprofitable; or leaving the stand as it is will maximize the stored carbon dioxide and provide zero income.

The objective values for each stand in the considered forest (consisting of multiple stands) are aggregated, which means that the objectives represent the whole forest instead of single stands. Therefore, a solution to the multiobjective optimization problem consists of choosing a managerial strategy for each individual stand, and then summing each objective over all available stands, i.e., for the whole forest. We have computed a representative set of Pareto optimal solutions based on simulated data. For details on the problem and how the solutions have been generated, see Chapter 5 in [51] and [44]. The representation of the Pareto front used in the case study is available online.²

4.2.2 Setting

The forest management problem was solved utilizing a simple interactive method, where the DM provides a reference point in each iteration. R-XIMO was used to generate suggestions and explanations. Based on the reference point, a new solution was then computed utilizing a scalarizing function (5). Prior to the experiment, the DM was already familiar with this kind of interactive multiobjective optimization process. Before the solution process, the DM was informed about the support R-XIMO offers, namely, that after a solution is computed based on a provided reference point, he may express whether he would like to improve any of the objective function values computed based on the reference point. Before starting to solve the problem, the DM was asked whether he would like to see the explanations generated by R-XIMO in addition to the suggestions, to which he agreed.

Overall, the forest management problem was solved twice by the DM (with different strategies behind the preferences). All the information related to the solution processes shown to the DM was in textual or tabulated formats. No visualizations were used. After the two solution processes, the DM was asked some additional questions. In what follows, we describe the two solution processes, followed by the answers to the presented questions and some general observations. Two Python notebooks are available online with the contents of the two optimization processes described next.³,⁴

4.2.3 First solution process

Table 2 The solutions and reference points of the first solution process

Table 3 The solutions and reference points of the second solution process. See the caption of Table 2 for additional details

Iteration 1. First, the DM was shown the ideal and nadir points shown in Table 2. With the first reference point, the DM wished to achieve a solution with a moderate amount of income and a moderate CSHI, with “quite a bit” of stored carbon dioxide. This reference point is shown in Table 2.

Iteration 2. The solution with the objective function values shown in Table 2 was computed based on the reference point given in the first iteration. The first thing the DM noted was how close the objective function values were to the reference point given. He then wished to improve either the stored carbon dioxide or the CSHI value by lowering the income. He decided that he would like to improve the CHSI value. Therefore, CHSI was chosen as the target in R-XIMO, which produced the following suggestion: Try improving the CSHI and impairing the Stored CO$_2$. In formulating a new reference point, the DM did not, however, wish to improve CHSI any further. The reference point given by the DM in the second iteration is shown in Table 2.

Iteration 3. After seeing the newly computed solution shown in Table 2, the DM wondered what should be changed to improve the income. R-XIMO provided the following suggestion: Try improving the Income and impairing the Stored CO$_2$. But the DM did not wish to impair the stored carbon dioxide anymore. Instead, he wanted to improve the stored carbon dioxide next, which was set as the target in R-XIMO. The provided suggestion by R-XIMO was: Try improving the Stored CO$_2$ and impairing the Income. The DM thought that the suggestion was what he expected and proceeded as suggested. The reference point given by the DM is shown in Table 2.

Iteration 4. The solution in Table 2 was shown to the DM. After seeing the solution, the DM thought it was a “good and reasonable solution”, was happy with it and stopped the solution process.

4.2.4 Second solution process

Iteration 1. After the DM completed the first solution process, he wished to solve the problem once more from a more ecological point of view. Thus, he preferred high values for the stored carbon dioxide and CSHI. The nadir and ideal points were naturally the same as earlier. He provided the first reference point shown in Table 3.

Iteration 2. The computed solution in Table 3 was shown to the DM. He was quite happy with it, but wished to still improve CSHI, which was set as the target. R-XIMO provided the following suggestion: Try improving the CSHI and impairing the Stored CO$_2$. The DM did as suggested and provided the reference point shown in Table 3.

Iteration 3. The first thing the DM noticed once he saw the computed solution shown in Table 3 was that the income also improved in addition to CSHI. The DM was happy with this solution and decided to stop the solution process.

4.2.5 Questions and answers

After the two solution processes, the DM was asked a few questions regarding R-XIMO and the support it provides. Below, we present the questions and the DM’s answers. The answers have been slightly paraphrased to improve comprehensibility.

How useful did you find the suggestions? “I really liked them. I liked how easy they were to understand. The fact that something was to be improved and something was to be impaired was nice. I liked that a lot. But I did not always understand why one [of the objectives] was highlighted over another.”

How easy were the suggestions to understand? “Generally, quite easy. Could be still simpler.”

Did you pay any attention to the explanations? “No, they were too long. I did not want to read them.” (At this point, the DM went back to the explanations to read them out of curiosity.)

Did you find the explanations and suggestions supporting during the interactive solution process? “Yes, I think so. The suggestions sort of highlighted where I should put my attention. Normally, I would just randomly change things until I get to where I want to go. I think I got where I wanted to be with fewer iterations.”

Did you find the suggestions too repetitive or otherwise frustrating? “No, because I did not have to iterate very often. Normally, I would find it frustrating to go back and forth [between iterations], but this time it was not frustrating because the suggestions were highlighting where I should focus, which made finding a solution a little bit easier.”

Would you have preferred the suggestions or explanations, or both, to be visualized? “I do not think so. If I had provided the reference points in a visual way, then yes.”

4.2.6 Observations

The suggestions generated by R-XIMO were well received by the DM. It was also observed that each suggestion, when followed, led to an improvement in the target objective expressed by the DM. Even though in the second iteration of the first solution process (Table 2) the DM did not improve the target component in the reference point, but instead only impaired the rival, the computed solution had a better value for the target objective when compared to the previous solution. It was also interesting to note that in the third iteration in the first solution process, the first suggestion given by R-XIMO was not preferable in the opinion of the DM, which prompted him to change his preferences regarding how he would like to improve the solution. While the suggestions were well received by the DM, the explanations were practically ignored. The main reason for this was their length according to the DM. Nevertheless, the support R-XIMO provided to the DM decreased the number of iterations needed to reach a preferred solution, according to the DM. Saving the DM’s time is naturally desirable.

5 Validation and results

In this section, we discuss how we have numerically validated R-XIMO. We begin with a general description of the validation setting, assumptions made, and give an example of a possible implementation of R-XIMO in Sect. 5.1. Then, we describe the numerical validation process to study how well and how often the suggestions generated by R-XIMO lead to desirable outcomes in Sect. 5.2. After that, we discuss the results of the validations and the observations made in Sects. 5.3 and 5.4, respectively.

5.1 Setting and implementation

In the numerical validation, R-XIMO is utilized according to the following pattern:

• 1. An initial reference point $\varvec{\bar{z}}_0$ is randomly generated.

• 2. An initial solution $\mathbf {z}_0$ is computed by utilizing $\varvec{\bar{z}}_0$ and the black-box $\mathfrak {B}$ (6).

• 3. An objective $i_\text {target}$ is selected. Details about selecting the target are given later.

• 4. According to Algorithm 1, objective $j_\text {rival}$ is computed and an explanation provided.

• 5. In the next iteration, a new reference point $\varvec{\bar{z}}_1$ is provided, where the component $i_\text {target}$ is changed by a value $\delta$; and the component $j_\text {rival}$ is impaired by the same value $\delta$. The value $\delta$ is a constant scalar value relative to the range of the respective objective function (i.e., the difference of components of the ideal and nadir points).

• 6. A new solution $\mathbf {z}_1$ is then computed with $\varvec{\bar{z}}_1$ and $\mathfrak {B}$.

Our goal is to compare $\mathbf {z}_0$ with $\mathbf {z}_1$. The expected result is that objective $i_\text {target}$ should have a better value in $\mathbf {z}_1$ when compared to $\mathbf {z}_0$ in cases where the component $i_\text {target}$ is improved and the component $j_\text {rival}$ is impaired in $\varvec{\bar{z}}_1$ relative to $\varvec{\bar{z}}_0$. The value $\delta$ represents the change the DM makes in the components corresponding to the target and the rival in the reference point. We have limited the value $\delta$ to affect just $i_\text {target}$ and $j_\text {rival}$ since R-XIMO generates suggestions only concerning these two.

In the validation, we deal with two multiobjective optimization problems, the river pollution problem [47] (river problem, also considered in Sect. 4) and the vehicle crash-worthiness design problem [52] (car problem, described in more detail in the Appendix). Both problems have all objectives to be minimized. The river problem has five objectives and two decision variables, while the car problem has three objectives and five decision variables. In both problems, variables are subject to box constraints.

We consider three black-boxes (6) defined with the scalarizing functions (3), (4), and (5). We are only interested in whether the solutions computed by the considered black-boxes can be improved by utilizing the suggestions generated by R-XIMO or not. Thus, we are not comparing the performances of the scalarizing functions. We have chosen these scalarizing functions because they can generate different solutions [11]. Therefore, using them to validate R-XIMO shows how well it works for different black-boxes.

The version of R-XIMO utilized in the validations was implemented in Python utilizing the DESDEO software framework [53] for defining and solving multiobjective optimization problems. The SHAP library [38] was used to compute SHAP values. The kernel SHAP method was selected because it can be applied to any kind of black-box models to generate SHAP values.

The source code of the R-XIMO implementation is available online on GitHub.⁵ Likewise, the numerical data generated during the validation is also available online.⁶

5.2 Validation

We generated approximations of the Pareto optimal fronts for both problems considered utilizing evolutionary multiobjective optimization methods (NSGA-III [49], MOEA/D [41], and RVEA [50]). Following the discussion in Sect. 3.3, we utilized the fronts as the missing data $Z_\text {missing}$ (referred to in Algorithm 1) in the kernel SHAP method to compute the SHAP values for the considered black-boxes. The ideal and nadir points were calculated for both problems based on the approximations of their Pareto optimal fronts.

When calculating the SHAP values, the missing data was also used as an approximation to the original multiobjective optimization problem. This is because kernel SHAP requires evaluating the original black-box many times over the course of computing the SHAP values. However, the solutions $\mathbf {z}_0$ and $\mathbf {z}_1$ were computed using the original (analytical) formulations of the underlying multiobjective optimization problems. This was done to get more accurate solutions. In other words, the approximation of the Pareto optimal fronts were used only when calculating SHAP values.

During the course of the validations, many experiments were conducted. One experiment consisted of running R-XIMO 200 times (a single batch) for each objective. This amount of runs was empirically found to give statistically enough data, while taking a moderate amount of time to compute. In each batch, one of the objectives was always set as the target. For the river problem, this meant a total of 1000 iterations, and for the car crash problem, this meant a total of 600 iterations. The initial reference point $\varvec{\bar{z}}_0$ was generated randomly and resided in the objective space bounded by the ideal and nadir points for each problem. Between the experiments, the problem, the value $\delta$, and the scalarizing function, were varied. Four different $\delta$ values were considered: 5%, 10%, 15%, and 20%. These values were relative to the distance between the ideal and nadir points of the considered problem and respective component being changed. Therefore, the $\delta$ values were constant and depended only on the range of the objective being changed. We decided to choose four different $\delta$ values to test how much the amount the components in the initial reference point are changed affects the change seen in the solution $\mathbf {z}_1$ when compared to $\mathbf {z}_0$. The reason for choosing these four values for $\delta$ is based on empirical testing; we found that increasing $\delta$ to be greater than 20% of the range of the respective objective, started to yield wildly varying results. In the numerical validations conducted, we found the chosen four values to give the best insight on the effect the value of $\delta$ has on the performance of R-XIMO, at least for two problems considered.

In the validation, we considered five possible ways a reference point may be changed in respect to the target and rival. These ways are characterized by the following strategies: A) the target is improved and the rival is impaired in the reference point $\varvec{\bar{z}}_0$; B) only the target is improved; C) the target is improved while some other component than the rival or the target is impaired; D) the target is not improved and the rival is impaired; and E) the target is not improved while some other component than the rival or the target is impaired. These strategies have been listed in Table 4.

Strategy A is equivalent to following the suggestion of R-XIMO fully. Strategy B represent the naive, or business-as-usual, course of action of only improving the target. Strategies B-D represent scenarios where the suggestions of R-XIMO are followed only in part. These strategies are included to check how the suggestions provided by R-XIMO work if followed only partly, and especially to check if the provided suggestion really is the best course of action if the target is to be improved. Partly following the suggestions is also a realistic behavior that can be expected from a real DM. The last strategy, strategy E, represents the case of not following the suggestion at all. This strategy has been included purely for validation purposes. Comparing how the target objective’s value varies between solutions $\mathbf {z}_0$ and $\mathbf {z}_1$ when employing different strategies, gives a good indication on the performance of R-XIMO (strategy A) when compared to alternative courses of action (strategies B-E) in respect to the target and rival. Especially, the comparison of strategy A to strategy B gives a fair idea of the added value of R-XIMO to the DM, since strategy B represents the naive course of action a DM would take without the support provided by R-XIMO.

Table 4 The five strategies employed in the validation of R-XIMO

Each experiment with its variations was repeated for each strategy (Table 4). This resulted in 60 experiments performed for each problem. In each experiment, the reference points $\varvec{\bar{z}}_0$ and $\varvec{\bar{z}}_1$, the solutions $\mathbf {z}_0$ and $\mathbf {z}_1$, the index of the rival $j_\text {rival}$ and the index of the target $i_\text {target}$, and the type of the explanation and suggestion (Table 1) generated, were recorded.

5.3 Results

The main results of the numerical validation runs are shown in Tables 5 and 6. All the numerical values shown in the tables are percentages. In what follows, change refers to the relative change of the target objective in $\mathbf {z}_0$ when compared to $\mathbf {z}_1$. Since all the objectives in the experiments are to be minimized, a negative change means an improvement in the target and a positive change indicates an impairement of the target.

The first three columns (Delta, SF, Strategy) in Tables 5 and 6 show the value $\delta$, the scalarizing function (SF) used, and the strategy employed (Table 4), respectively. For each experiment, the overall rates of success (target was improved in $\mathbf {z}_1$ compared to $\mathbf {z}_0$), neutral (target was the same in $\mathbf {z}_1$ and $\mathbf {z}_0$), and failures (target was impaired in $\mathbf {z}_1$ compared to $\mathbf {z}_0$) are recorded in the columns Success, Neutral, and Failure, respectively.

To indicate how much the target objective’s value was changed after the reference point was modified, in each experiment the median of the change was computed. To show the variation in the change, the mean absolute deviation (MAD) was used. These values are listed in the columns median and MAD, respectively. The median was used because the target’s change had some very small and large values in the experiments making the mean an inaccurate measure. These values can be seen in the tables in the columns min and max, respectively. The MAD was used instead of the standard deviation for the same reason the median was used. In other words, the median and the MAD were used because they are more resilient to outliers when compared to the mean and the standard deviation.

Table 5 Numerical validation results for the river problem. All listed values are percentages

Utilizing the MAD and assuming the changes of the target in the experiments would follow a normal distribution, a standard deviation $\sigma _\text {MAD}$ was computed for the changes observed in each experiment and recorded in the last column of Tables 5 and 6. Again, assuming a standard distribution, the median, and the computed standard deviation $\sigma _\text {MAD}$ (centered on the median) were used to introduce a cut−off, where the values of change residing inside the $2\sigma _\text {MAD}$ confidence interval were used to compute a mean $\mu _{95}$ recorded in the penultimate column in each table. The parentheses following the values listed on this column show, in percentages, how many samples were cut−off in each experiment when calculating $\mu _{95}$. The purposes of the last two columns are to give the reader quantities that are perhaps more familiar and easier to interpret than the median and MAD. The quantities $\mu _\text {95}$ and $\sigma _\text {MAD}$ are less accurate than the median and MAD, respectively. The $\mu _\text {95}$ and $\sigma _\text {MAD}$ should therefore be considered with some care.

Table 6 Numerical validation results for the car problem. All listed values are percentages

5.4 Observations

Some observations of the results in Tables 5 and 6 are worth mentioning. The average rates for a success, neutral, and failure for each strategy across all the experiments are shown in the stacked bar graphs in Fig. 3 for the river and car problem. We can see that the average rates are very similar for strategies A, B, C and D for the river problem; and for strategies A, B and C for the car problem, while for strategy D the success rate seems a little lower, yet notably higher than strategy E. Strategy E seems to have the lowest success rate and highest failure rate for both problems. Looking just at the success rates, it seems that the desired result of improving the target can be achieved by just improving the target component in the reference point $\varvec{\bar{z}}_0$; it does not seem to matter which component is impaired, or if another component is impaired at all. If we do not improve the target and impair a component, which is not the rival (strategy E), then the success rates seem to be the worst for both problems. Lastly, the rate for a neutral outcome is very low for the river problem and significantly higher for the car problem across all strategies.

Fig. 3

Average of the success, neutral, and failure rates observed for each strategy for the river (left) and car (right) problems. The error bars show the standard error for each rate

The average median of the changes observed for each value $\delta$ is grouped by strategy for both problems and shown as grouped bar charts in Fig. 4. It is evident that, on average, the greatest negative changes in the target objective can be achieved by employing strategy A in both problems. The changes observed for strategy E seem to average out at zero for both problems. While strategies B, C, and D seem to yield somewhat similar results for the river problem, for the car problem, strategy D is clearly inferior to strategies B and C, while strategy C seems to be better than strategy B. Looking at Fig. 5, we can see similar results to what we see in Fig. 4—the average values of the medians are very close to the respective values of the average means. With the cut-off introduced, the mean values are close to the medians.

Fig. 4

The average of the median changes observed in the target for each strategy and $\delta$ value for the river (left) and car (right) problems

Fig. 5

The average of the $\mu _{95}$ means observed in the change of the target for each strategy and $\delta$ value for the river and car problems

Looking at the average values of the MADs of the changes observed in the target shown in Fig. 6, we can observe the greatest variation for strategies A and C, for both problems. For the river problem, the variations for strategies B and E seem similar, while the variations for strategy D are a little bit higher than for B and E. For the car problem, the variations for strategies B, D, and E are more similar, with the variations in strategy B being still the highest. We can see a similar pattern for the average of the $\sigma _\text {MAD}$ deviations shown in Fig. 7. However, the values of the $\sigma _\text {MAD}$ variations are noticeably larger than the medians across both problems.

Fig. 6

The average of the median absolute deviation of changes in the target for each strategy and $\delta$ value for the river and car problems

Fig. 7

The average of the $\sigma _\text {MAD}$ deviations of changes in the target for each strategy and $\delta$ value for the river and car problems

In all Figs. 4, 5, 6, and 7, we can clearly see that the average changes and deviations of the changes increase systematically as the value of $\delta$ increases. The average changes seem to be best for strategy A, but also the deviations seem to be greatest for strategy A. This means that while the best average improvement of the target can be observed by employing strategy A, it can also yield very varying results. The overall worst strategy seems to be strategy E, which results, on average, in no observed change in the target. The deviations for strategy E are also small, indicating that the average changes observed in the target are not just zero-centered but also very small. It is also evident that looking just at the success rates in Fig. 3 is not enough. For instance, just looking at the success rates for strategy A would indicate that it is no different from strategy B, while the average changes clearly indicate that a better result can be achieved by employing strategy A.

In summary, the results indicate that employing strategy A, that is, improving the target and impairing the rival, as suggested by R-XIMO, has the best chance of achieving the desirable result of improving the target and in the greatest amount. The choice of the rival objective seems to also matter, otherwise strategies A and C should be similar. Moreover, it also seems that strategy D (only impairing the rival and not improving the target) can yield improvements in the target objective. Overall, the improvement of the target component in the reference point seems to be a sound course of action to be always taken when the target objective is to be improved in the solution.

6 Discussion

In this section, we discuss the validity of R-XIMO. In Sect. 6.1, we consider the results of the illustrative example given in Sect. 4.1, and in Sect. 6.2 we consider the results of the case study with a real DM conducted in Sect. 4.2. Likewise, in Sect. 6.3, we discuss the results of the numerical validations of Sect. 5. Lastly, in Sect. 6.4, we outline the overall potential of R-XIMO, its future prospects and XIMO in general.

6.1 On the example

In Sect. 4.1, the usefulness of R-XIMO was demonstrated with the river problem and an analyst as the DM. R-XIMO generated explanations and suggestions at each iteration. The most important benefit for the DM was understanding the trade-offs among the conflicting objectives with the assistance of R-XIMO. The DM was able to learn about the conflicts between the objectives and the feasibility of their preferences, thanks to the explanations and suggestions. The DM noted that the assistance increased his confidence in the final solution because he gained enough insight into the problem throughout the solution process. Moreover, this assistance made it easier for the DM to provide preference information.

When we pondered on the interactive solution process, we noticed that the DM was not aware of how strong the conflict degrees among the objectives were. This emphasizes the necessity of providing not just the trade-offs among the objectives, but also the degrees of conflict between them. Furthermore, we need to underline the importance of providing these explanations visually. We did not work on visualization perspectives of explanations because our aim was to demonstrate the benefits of explanations in interactive methods. However, this needs attention in the future.

6.2 On the case study

We utilized R-XIMO in the case study in Sect. 4.2 with a real DM. While the suggestions clearly supported the DM in the solution processes, it was also evident that the explanations were too convoluted for a real DM, which led the DM to completely ignore the explanations. Based on the DM’s answers to the questions presented, the suggestions generated by R-XIMO were valuable and aided the DM in both gaining a sense of direction on what to change in the reference point to achieve a desirable result and by reducing the number of required iterations. The DM did, however, state that the suggestions could be still simpler.

It is obvious that if explanations are to be presented to the DM, further studies are needed to make this information palatable for real DMs. However, this does not mean the explanations generated by R-XIMO are completely useless since the suggestions, which were found to be very useful, are derived from the explanations. Moreover, as seen in the example given in Sect. 4.1, the explanations can be useful to an analyst. We think the most valuable lesson from the case study is the observation that future studies on how the suggestions and explanations are presented to the DM are definitely needed. We believe the right direction to pursue is the exploration of new visualizations and graphical user interfaces that better support conveying the explanations and suggestions to human DMs in a graphical format.

6.3 On the numerical validations

From the success rates shown in Fig. 3, we notice that when the target component chosen by the DM is improved or the rival computed by R-XIMO is impaired in the reference point (strategies A-D in Table 4), the target is improved most of the time (around 70–80% of the time). When neither the target is improved nor the rival is impaired (strategy E in Table 4), the success rates are clearly the worst with a failure at around 50% of the time. Therefore, improving the target in the solution requires improving it in the reference point or impairing the rival. A combination of these, improving the target and impairing the rival (strategy A in Table 4), seems to yield the best results when compared to the other strategies. Lastly, the higher rates of neutral outcomes observed for the car problem can stem from the more challenging shape of the Pareto optimal front of the problem, which may have been more challenging for the underlying optimization method used to minimize the scalarizing functions considered. Thus, there may have been local minima that multiple different reference points were mapped to. However, the results of the numerical validations do not seem to have suffered from this in any major fashion.

The above has two important implications. First, improving the target in the reference point has a clear effect on the value of the target in the solution (strategies A-D). This is expected since the black-box considered in (6) finds a solution close to the given reference point. Secondly, because the success rates for strategy E are clearly worse than for strategy D (not improving the target but impairing the rival) implies that the rival computed is indeed, on average, the best component to be impaired in the reference point. If this was not the case, then there should be no significant differences in the success rates between strategies D and E. Based on the success rates alone, we claim that the proposed method suggests a rival, which when impaired in the reference point, will yield better results for the target in the solution. This means that R-XIMO is able to capture (local) conflicts between the target and some other objective (the rival in our case).

Success rates alone do not give strong evidence that improving the target and impairing the rival (strategy A) in the reference point would be significantly better than strategies B-D, but the results show that improving the target in the reference point is always a sound action if the value of the target is to be improved. As said, this is an expected result and gives us confidence in the numerical validations.

The results for the relative improvements of the target objective’s value in the solution (Figs. 4 and 5) indicate clearly that improving the target and impairing the rival in the reference point is the best strategy (strategy A). The results for strategies B, C, and D indicate that smaller improvements can be observed in the target’s value in the solution when either the target is improved or the rival is impaired in the reference point. Lastly, not improving the target and not impairing the rival in the reference point leads to almost no improvement in the target’s value in the solution (strategy E), and is therefore the worst course of action to be taken, which is expected.

The above observations are also confirmed when looking at Tables 5 and 6. We clearly notice from the median columns that the best improvements of the target’s value in the solution are achieved in almost all cases across both problems when strategy A is employed. The best success rates (in the column Success) are also found to belong to strategy A in most cases, but not as often as the best improvement of the target.

Interestingly, strategies B (only improving the target) and C (improving the target and impairing something else than the rival) yield similar results for the river problem, while for the car problem, strategy C is somewhat better, when it comes to the relative improvement of the target objective’s value in the solution (Figs. 4 and 5). One conclusion from this is that with more objectives, impairing some objective in addition to improving the target, is more important when compared to a problem with less objectives.

If we compare strategies A (improving the target and impairing the rival) and C (improving the target and impairing something else than the rival) in Figs. 4 and 5, we can see that the actual choice of the rival does also matter when the target component is improved. The results of strategy A in the river problem are clearly better than for strategy C, while for the car problem, the difference is less, but still notable. Again, this can be an indication that with less objectives, the actual choice of the rival is not as important when compared to a problem with more objectives.

Therefore, in the river problem, it is important to choose a rival, and choose it correctly for the best result, while in the car problem, the choice of the rival is not that critical and only improving the target (strategy B) can yield good results as well. This observation on the importance of choosing the rival correctly, with more objective functions present, is further confirmed by the results for strategy D (not improving the target and impairing the rival). With more objectives, in the river problem impairing only the rival will yield better results when compared to the same results for the car problem. It is also clear that impairing at least some component in the reference point is always better than just improving the target, which is confirmed by the improvements for strategy C (improving the target and impairing something else than the rival) being always better than for strategy B (only improving the target), for both problems. Again, this kind of behavior is expected with trade-offs existing among the objectives.

From all of this, we conclude that the rival computed by R-XIMO is, on average, the best component to be impaired in the reference point when a DM wishes to improve the target in the solution. The correct choice of the rival seems to be more important in problems with more objective functions. For the best result, the target should be improved in the reference point as well. To make more general assumptions on how important the choice of the rival is when the number of objective functions varies, further numerical studies are required.

The results for the deviations of the relative improvement of the target in the solution (Figs. 6 and 7) indicate that the best performing strategy (strategy A) is also the most volatile because of the high values of deviation when compared to the other strategies. However, for strategy A, the average absolute values of the improvement of the target in the solution (in Figs. 4 and 5) are close to the deviations. This indicates that when the target fails to improve, its new value is probably closer to its original value in the previous solution. This is assuring because it means that if the explanations provided to the DM fail helping the DM reach the desired result, the magnitude of failure is small (i.e., the target has only a slightly worse value). Interestingly, improving the target and impairing a random component in the reference point (strategy C) is as volatile as strategy A. Strategy C is also the only other strategy, apart from A, where two components are changed in the reference point. This means that changing more components in the reference point yields more varying solutions, which is an expected behavior from the black-boxes considered (6). The variations of strategy D in the river problem are clearly greater than the variations of strategies B and E, while in the car problem, the variations of strategy B are greater than strategies D and E. It seems that the rival has a greater effect of the volatility of the results depending on the number of objectives at hand. Overall, when the average improvements and the average deviations are compared to each other, there are no conflicts with the success rates (Fig. 3).

Comparing the case study to the numerical validations conducted in Sect. 5, the changes in the components of the reference point expressed by the DM varied between $\delta$ values of $2.3\%$ and $9.0\%$. If the actions taken by the DM are compared to the strategies A-E, the DM pursued actions described by strategy A most of the time, with pursuing an action described by strategy D once. Based on these observations alone, any specific conclusions are hard to make. But if it is generally true that $\delta$ values around $15-20\%$ lead to greater improvements in the target objective, then some way of communicating the amount the DM should change the target and rival components in the reference point is worth exploring in the future. In conclusion, the numerical validations have shown that the suggestions generated by R-XIMO can help the DM reach the desired outcome of improving the target in the solution.

6.4 Potential of R-XIMO and future prospects

Explainability clearly provides support to the DM, as discussed in Sects. 6.1 and 6.2, and R-XIMO is able to generate sound explanations (and therefore suggestions), as discussed in Sect. 6.3. R-XIMO supports the DM in learning about the multiobjective optimization problem and helps them in formulating new preferences in reference point based interactive multiobjective optimization methods. These issues have been seldom addressed in past research, as mentioned in Sect. 1.

The importance of providing explanations to the DM in interactive multiobjective optimization methods is emphasized when they are used to make real-life decisions affecting humans. Incidentally, in the member nations of the European Union, when decisions affect humans, individuals should have a right to an explanation on why, and on which basis, such decisions have been made [54]. Therefore, R-XIMO, and the concept of XIMO in general, has important societal implications.

Making trade-offs in decision making is challenging, as discussed in [55]. R-XIMO supports the DM in this regard as well by suggesting trade-offs directly to the DM. Therefore, the cognitive load on the DM is lower in reference point based interactive multiobjective optimization methods with the support of R-XIMO. Moreover, not much research has been done on studying the local conflicts in multiobjective optimization as discussed in [56]. Because SHAP values are local, as discussed in Sect. 2.2, the interactions of the objectives represented by SHAP values reflect the local conflicts among them. Thus, R-XIMO can give insight to the DM about the trade-offs local to the current solution.

In our work, we did not utilize the SHAP values computed in R-XIMO to convey to the DM any information about the actual magnitude of the conflicts among the objectives in a multiobjective optimization problem. Moreover, no support was provided to the DM on how much the target and rival should be perturbed. We made the deliberate choice to only communicate simple and easy to understand ideas to the DM with the explanations generated by R-XIMO to not overburden the DM with additional information.

If we chose to numerically show the SHAP values to the DM, we run a risk of the DM starting to compare the SHAP values to each other, or to the objectives, instead of comparing the objectives. This would greatly reduce the actual support provided to the DM by R-XIMO. Therefore, it is important that information is communicated to the DM is an easily understood way, and in a way that minimizes the possibility for the DM to confuse different types of information. By keeping the suggestions and explanations textual, we at least have made a clear distinction between objectives (numerical information) and the suggestions and explanations (textual information).

To further minimize the additional cognitive load on the DM imposed by R-XIMO, we decided to only show the suggestions derived from the explanations (Table 1) by default, and give the DM the option to see the more detailed explanation, if they so desire. The detailed explanations were formulated in a causal tone since it has been demonstrated previously that such explanations have high cognitive value to DMs [57]. Moreover, by separately providing a suggestion to the DM, we provide them with actionable insights (mentioned in [57]) on how they may reach their goal of improving a specific objective. However, the SHAP values can portray valuable information to the DM and can further help them in deciding how much the components of the reference points should change. This is something R-XIMO does not provide support for. We believe this information should be communicated to the DM graphically, but to find the actual best way of communication, further studies with human participants are required. The graphical communication of explanations in multiobjective optimization is also yet to be explored.

We argue that R-XIMO could help the DM in avoiding some cognitive biases as well, such as anchoring. Indeed, as argued in [58], a common reason for the anchoring effect in interactive methods is that DMs do not have time to spend in a long interactive process. R-XIMO can speed up an interactive process by eliminating some of the time required for a DM to think about trade-offs and possibly help the DM away from a previous solution aided by the suggestions. However, based solely on our work, we cannot make any definitive claims regarding the cognitive support offered to DMs by R-XIMO.

R-XIMO can be readily scaled up to convey suggestions and explanations to the DM about the interaction between other components of the reference point and solution than the target and rival. For instance, the second order effects, i.e., the components in the reference point with the second greatest improving or impairing effect on the target in the solution. This information is already available in R-XIMO and remains only to be exploited. However, we believe that further research should be conducted on how to best convey explanations to DMs in the context of multiobjective optimization before R-XIMO is scaled up. This is also the reason why we decided to keep the suggestions and explanations simple and focused only on the most significant effects (i.e., the target and the rival).

As mentioned in the introduction, R-XIMO can be implemented as an agent to support a DM in various ways. A generic multiagent architecture for any type of interactive methods was proposed in [16], which allows more efficient and reliable interactive solution processes through the use of specialized agents. Moreover, the architecture enables a DM to select the most suited interactive methods based on their needs in different phases during the interactive solution process. In the aforementioned architecture, a preference agent that interacts with a DM constructs their preference model by actively observing and learning the preferences. The preference agent notifies a DM whenever they provide uncertain or contradictory preferences with the help of constructed preference model. R-XIMO does not currently keep a history of the DM’s preferences, but it clearly has the potential to be implemented as a preference agent as part of the said architecture and can be extended to provide not only trade-offs among objectives, but also to explain uncertainties and/or contradictions in the provided preference information. This may enable a DM to provide more accurate and reliable preference information.

7 Conclusions

We proposed the R-XIMO method to be applied with reference point based interactive multiobjective optimization methods to explain to a DM why their preferences have lead to solutions shown and how the reference point may be modified to achieve a more preferred solution. Our method can be used with any reference point based interactive method. We have incorporated multiobjective optimization with ideas from explainable artificial intelligence, and utilized SHAP values to generate the explanations. We have demonstrated the usefulness of R-XIMO in practice with an illustrative example and a case study, and we validated it numerically. We can safely say that R-XIMO has a high potential as a decision support tool clearly augmenting the insight offered by the existing reference point based interactive methods. Nevertheless, in its current state, our work should still be regarded as a proof-of-concept. Future studies are needed to explore what kind of explanations best serve the needs of DMs in finding preferred solutions in multiobjective optimization problems. In the case study, we considered the opinion of only one DM, which is clearly a limitation. To properly assess the usefulness of explanations to humans in multiobjective optimization, studies with more DMs are still required.

In the future, other tools and methods apart from SHAP values should be explored in XIMO, and implementing new interactive methods with inherent explainability should be considered as well considering also different types of preference information. Some promising methods to explore in this regard are, for instance, individual conditional expectations [59], belief rule-based systems [60] (as already preliminarily explored in [44]), and scoped rules [61], just to name a few.

By supporting the DM in providing reference points and learning about the underlying multiobjective optimization problem, we provide answers to open questions in interactive multiobjective optimization. In addition, we also advance the field of explainable interactive multiobjective optimization, or XIMO, to new horizons. Our work can be regarded as pioneering and the first of its kind for explaining scalarization-based interactive multiobjective optimization methods. Our work investigates and proposes ideas that have a strong potential to inspire a plethora of various future works exploring the concept of explainability in multiobjective optimization.

Appendix

The crash-worthiness design of vehicles problem [52] is a real-world engineering problem in which the frontal structure of vehicles is designed for crash safety. The vehicle’s frontal structure absorbs the energy created by the crash, increasing passenger safety. Improving a vehicle’s energy absorption capacity often increase the overall vehicle mass. On the other hand, lightweight designs are required to minimize a vehicle’s mass and, as a result, its fuel consumption. Therefore, higher energy absorption and lightweight design conflict with each other, and we must find a compromise between the two to achieve a proper design.

As design variables in this problem, the thickness of five reinforced components surrounding the frontal structure affecting crash safety is chosen. The mass of a vehicle ($f_1$), deceleration during the full-frontal crash ($f_2$, which influences passenger injuries), and toe board intrusion in the offset-frontal crash ($f_3$, which affects the vehicle’s structural integrity) are all defined as objectives to be minimized. Mathematical formulation of the multiobjective optimization problem is as follows:

$$\begin{aligned} \begin{array}{rll} &{}\text {minimize} &{}F(\mathbf {x}) = (f_1({\mathbf {x}}), f_2({\mathbf {x}}), f_3({\mathbf {x}}))\\ \\ &{}\text {subject to} &{}1 \le x_j \le 3,\quad \text {where}\, j = 1,\dots ,5\\ \end{array} \end{aligned}$$

where $f_i$ $(i = 1,2,3)$ represents the relevant objectives and the decision variable $x_j$ $(j = 1, \dots , 5)$ represents the thickness of five components of the frontal structure. Objectives have the following formulations:

$$\begin{aligned} \begin{aligned} f_1({\mathbf {x}}) = {}&1640.2823 + 2.3573285 x_1 + 2.3220035 x_2 + 4.5688768 x_3\\&+ 7.7213633 x_4 + 4.4559504 x_5 \end{aligned} \\ \begin{aligned} f_2({\mathbf {x}}) ={}&6.5856 + 1.15 x_1 - 1.0427 x_2 + 0.9738 x_3 + 0.8364 x_4 \\ {}&- 0.3695 x_1x_4 + 0.086 1x_1x_5 + 0.3628x_2x_4 \\ {}&- 0.1106x_1^2 - 0.3437x_3^2 + 0.1764x_4^2 \end{aligned}\\ \begin{aligned} f_3({\mathbf {x}}) = {}&- 0.0551 + 0.0181x_1 + 0.1024x_2 + 0.0421x_3 - 0.0073x_1x_2 \\ {}&+ 0.024x_2x_3 - 0.0118x_2x_4 - 0.0204x_3x_4 - 0.008x_3x_5 \\ {}&- 0.0241x_2^2 + 0.0109x_4^2 \end{aligned} \end{aligned}$$

More details about the crash-worthiness design of vehicles problem can be found in the original study [52].