Abstract
Generalization is a major challenge for multi-agent reinforcement learning. How well does an agent perform when placed in novel environments and in interactions with new co-players? In this paper, we investigate and quantify the relationship between generalization and diversity in the multi-agent domain. Across the range of multi-agent environments considered here, procedurally generating training levels significantly improves agent performance on held-out levels. However, agent performance on the specific levels used in training sometimes declines as a result. To better understand the effects of co-player variation, our experiments introduce a new environment-agnostic measure of behavioral diversity. Results demonstrate that population size and intrinsic motivation are both effective methods of generating greater population diversity. In turn, training with a diverse set of co-players strengthens agent performance in some (but not all) cases.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
An emerging theme in single-agent reinforcement learning research is the effect of environment diversity on learning and generalization [26, 27, 45]. Reinforcement learning agents are typically trained and tested on a single level, which produces high performance and brittle generalization. Such overfitting stems from agents’ capacity to memorize a mapping from environmental states observed in training to specific actions [48]. Single-agent research has counteracted and alleviated overfitting by incorporating environment diversity into training. For example, procedural generation can be used to produce larger sets of training levels and thereby encourage policy generality [5, 6].
In multi-agent settings, the tendency of agents to overfit to their co-players is another large challenge to generalization [31]. Generalization performance tends to be more robust when agents train with a heterogeneous set of co-players. Prior studies have induced policy generality through population-based training [3, 24], policy ensembles [35], the application of diverse leagues of game opponents [44], and the diversification of architectures or hyperparameters for the agents within the population [21, 36].
Of course, the environment is still a major component of multi-agent reinforcement learning. In multi-agent games, an agent’s learning is shaped by both the other co-players and the environment [34]. Despite this structure, only a handful of studies have explicitly assessed the effects of environmental variation on multi-agent learning. Jaderberg et al. [24] developed agents for Capture the Flag that were capable of responding to a variety of opponents and match conditions. They argued that this generalizability was produced in part by the use of procedurally generated levels during training. Other multi-agent experiments using procedurally generated levels (e.g., [14, 32]) stop short of rigorously measuring generalization. It thus remains an open question whether procedural generation of training levels benefits generalization in multi-agent learning.
Here we build from prior research and rigorously characterize the effects of environment and population diversity on multi-agent reinforcement learning. Specifically, we use procedural generation and population play to investigate performance and generalization in four distinct multi-agent environments drawn from prior studies: HarvestPatch, Traffic Navigation, Overcooked, and Capture the Flag. These experiments make three contributions to multi-agent reinforcement learning research:
-
1.
Agents trained with greater environment diversity exhibit stronger generalization to new levels. However, in some environments and with certain co-players, these improvements come at the expense of performance on an agent’s training set.
-
2.
Expected action variation—a new, domain-agnostic metric introduced here—can be used to assess behavioral diversity in a population.
-
3.
Behavioral diversity tends to increase with population size, and in some (but not all) environments is associated with increases in performance and generalization.
2 Environments
2.1 Markov games and multi-agent reinforcement learning
This paper aims to explore the influence of diversity on agent behavior and generalization in n-player Markov games [34]. A partially observable Markov game \({\mathcal {M}}\) is played by n players within a finite set of states \({\mathcal {S}}\). The game is parameterized by an observation function \(O: {\mathcal {S}} \times \{1,\dots ,n\} \rightarrow {\mathbb {R}}^d\), sets of available actions for each player \({\mathcal {A}}_1,\dots ,{\mathcal {A}}_n\), and a stochastic transition function \({\mathcal {T}}: {\mathcal {S}} \times {\mathcal {A}}_1 \times \cdots \times {\mathcal {A}}_n \rightarrow \varDelta ({\mathcal {S}})\), mapping from joint actions at each state to the set of discrete probability distributions over states.
Each player i independently experiences the game and receives its own observation \(o_i = O(s,i)\). The observations of the n players in the game can be represented jointly as \(\vec {o} = (o_1,\dots , o_n)\). Following this notation, we can also refer to the vector of player actions \(\vec {a} = (a_1,\dots ,a_n) \in {\mathcal {A}}_1,\dots ,{\mathcal {A}}_n\) for convenience. Each agent i independently learns a behavior policy \(\pi (a_i|o_i)\) based on its observation \(o_i\) and its extrinsic reward \(r_i(s,\vec {a})\). Agent i learns a policy which maximizes a long-term \(\gamma\)-discounted payoff defined as:
where \(U_i(s_t, \vec {o}_t, \vec {a}_t)\) is the utility function for agent i. In the absence of reward sharing [23] or instrinsic motivation [22, 40], the utility function maps directly to the extrinsic reward provided by the environment.
A key source of diversity in Markov games is the environment itself. To this end, we train agents on distributions of environment levels produced by procedural generators. Our investigation explores four distinct environments drawn from prior studies: HarvestPatch (a mixed-motive game), Traffic Navigation (a coordination game), Overcooked (a common-payoff game), and Capture the Flag (a competitive game). The following subsections provide an overview of the game rules for each of these games. All environments were implemented with the open-source engine DeepMind Lab2D [2]. Full details on the environments and the procedural generation methods are available in the Supplementary file.
2.2 HarvestPatch
HarvestPatch [36] (Fig. 1a) is a mixed-motive game, played by \(n = 6\) players in the experiments here (see also [22, 25, 30, 38]).
Players inhabit a gridworld environment containing harvestable apples. Players can harvest apples by moving over them, receiving a small reward for each apple collected (\(+1\) reward). Apples regrow after being harvested at a rate determined by the number of unharvested apples within the regrowth radius r. An apple cannot regrow if there are no apples within its radius. This property induces a social dilemma for the players. The group as a whole will perform better if its members are abstentious in their apple consumption, but in the short term individuals can always do better by harvesting greedily.
We investigate the influence of environment and population diversity on agent performance across four distinct n-player Markov games: a HarvestPatch (a six-player mixed-motive game), b Traffic Navigation (an eight-player coordination game), c Overcooked (a two-player common-payoff game), and d Capture the Flag (a four-player team-competition game)
Levels are arranged with patches of apples scattered throughout the environment in varying densities. Every step, players can either stand still, move around the level, or fire a short tag-out beam. If another player is hit by the beam, they are removed from play for a number of steps. Players also observe a partial egocentric window of the environment.
2.3 Traffic navigation
Traffic Navigation [33] (Fig. 1b) is a coordination game, played by \(n = 8\) players.
Players are placed at the edges of a gridworld environment and tasked with reaching specific goal locations within the environment. When a player reaches their goal, they receive a reward and a new goal location. If they collide with another player, they receive a negative reward. Consequently, each player’s objective is to reach their goal locations as fast as possible while avoiding collisions with other players.
To make coordinated navigation more challenging, blocking walls are scattered throughout the environment, creating narrow paths which limit the number of players that can pass at a time. On each step of the game, players can either stand still or move around the level. Players observe both a small egocentric window of the environment and their relative offset to their current goal location.
2.4 Overcooked
Overcooked [3] (Fig. 1c) is a common-payoff game, played in the experiments here by \(n = 2\) players (see also [4, 29, 47]).
Players are placed in a kitchen-inspired gridworld environment and tasked with cooking as many dishes of tomato soup as possible. Cooking a dish is a sequential task: players must deposit three tomatoes into a cooking pot, let the tomatoes cook, remove the cooked soup with a dish, and then deliver the dish. Both players receive a reward upon the delivery of a plated dish.
Environment levels contain multiple cooking pots and stations. Players can coordinate their actions to maximize their shared reward. On each step, players can stand still, move around the level, or interact with the entity the object are facing (e.g., pick up tomato, place tomato onto counter, or deliver soup). Players observe a partial egocentric window of the level.
2.5 Capture the flag
Capture the Flag (Fig. 1d) is a competitive game. Jaderberg et al. [24] studied Capture the Flag using the Quake engine. Here, we implement a gridworld version of Capture the Flag played by \(n = 4\) players.
Players are split into red and blue teams and compete to capture the opposing team’s flag by strategically navigating, evading, and tagging members of the opposing team. The team that captures the greater number of flags by the end of the episode wins.
Walls partition environment levels into rooms and corridors, generating strategic spaces for players to navigate and exploit to gain an advantage over the other team. On each step, players can stand still, move around the level, or fire a tag-out beam. If another player is hit by the tag-out beam three times, they are removed from play for a set number of steps. Each player observes a partial egocentric window oriented in the direction they are facing, as well as whether each of the two flags is held by its opposing team.
3 Agents
We use a distributed, asynchronous framework for training, deploying a set of “arenas” to train each population of N reinforcement learning agents. Arenas run in parallel; each arena instantiates a copy of the environment, running one episode at a time. To begin an episode, an arena selects a population i of size \(N_i\) with an associated set of \(L_i\) training levels. The arena samples one level l from the population’s training set and n agents from the population (with replacement). The episode lasts T steps, with the resulting trajectories used by the sampled agents to update their weights. Agents are trained until episodic rewards converge. After training ends, we run various evaluation experiments with agents sampled after the convergence point.
For the learning algorithm of our agents, we use V-MPO [41], an on-policy variant of Maximum a Posteriori Policy Optimization (MPO). In later experiments, we additionally endow these agents with the Social Value Orientation (SVO) component, encoding an intrinsic motivation to maintain certain group distributions of reward [36]. These augmented agents act as a baseline for our behavioral diversity analysis, following suggestions from prior research that imposing variation in important hyperparameters can lead to greater population diversity. More details on the algorithm (including hyperparameters) are available in Supplementary file.
4 Methods
4.1 Investigating environment diversity
To assess how environment diversity (i.e., the number of unique levels encountered during training) affects an agent’s ability to generalize, we follow single-agent work on quantifying agent generalization in procedurally generated environments [5, 6, 48].
Specifically, we train multiple populations of \(N = 1\) agents with different sets of training levels. We procedurally generate training levels in sets of size \(L \in \{1, {1}\mathrm {e}{1}, {1}\mathrm {e}{2}, {1}\mathrm {e}{3}, {1}\mathrm {e}{4}\}\), where each training set is a subset of any larger sets. We also procedurally generate a separate test set containing 100 held-out levels. These held-out levels are not played by agents during training. For each training set of size L, we launch ten independent training runs and train each population until their rewards converge.
Generalization Gap. Following prior work, we compare the performance of populations on the levels from their training set with their performance on the 100 held-out test levels. We focus on the size of the generalization gap, defined as the absolute difference between the population’s performance on the test-set levels and training-set levels.
Cross-Play Evaluation. We also assess population performance through cross-play evaluation—that is, by evaluating agents in groups formed from two different training populations. We evaluate populations in cross-play both on the level(s) in their training set and on the held-out test levels. Specifically, for every pair of populations A and B, the training-level evaluation places agents sampled from population A (e.g., trained on \(L = 1\) level) with agents sampled from population B (e.g., trained on \(L = {1}\mathrm {e}{1}\) levels) in a level from the intersection of the populations’ training sets. The held-out evaluation similarly samples agents from populations A and B, but uses a level not found in either of the populations’ training sets.
As each environment requires a different number of players, we group agents from populations A and B as shown in Table 1. For HarvestPatch, Traffic Navigation, and Overcooked, we report the individual rewards achieved by the agents sampled from population A. For Capture the Flag, we analogously report the win rate for the agents from population A.
4.2 Investigating population diversity
We run a second set of experiments to investigate how population diversity affects generalization. Measuring and optimizing for agent diversity are established challenges in reinforcement learning research. In single-agent domains, diversity is often estimated over behavioral trajectories or state-action distributions [10, 18]. Prior multi-agent projects have largely focused on two-player zero-sum games [1, 37]. In these environments, the diversity of a set of agent strategies can be directly estimated from the empirical payoff matrix, rather than behavioral trajectories.
Given the varied environments used in our experiments (and particularly the cooperative and competitive natures of their payoff structures), we draw inspiration from the former approach, focusing on heterogeneity in agent behavior. This paper uses the term “population diversity” to refer to variation in the set of potential co-player policies that a new individual joining a population might face [36]. High policy diversity maximizes coverage over the set of all possible behaviors in an environment (including potentially suboptimal or useless behaviors) [15], while low policy diversity consistently maps a given state to the same behavior, regardless of the agents involved.
In multi-agent research, the increasing prevalence of population play and population-based training make population size a commonly tuned feature of experimental design. Prior studies suggest that larger population sizes can increase policy diversity [8, 39]. We directly examine how varying population size affects diversity by training agents in populations of size \(N \in \{1, 2, 4, 8\}\) for each environment. For Capture the Flag experiments, we additionally train populations with \(N = 16\).
Expected Action Variation. Researchers should ideally be able to estimate population diversity in a task-agnostic manner, but in practice diversity is often evaluated using specific knowledge about the environment (e.g., unit composition in StarCraft II [44]).
To address this challenge, we introduce a new method of measuring behavioral diversity in a population that we call expected action variation (EAV; Algorithm 1 in Supplementary file). Intuitively, this metric captures the probability that two agents sampled at random from the population will select different actions when provided the same state (Fig. 2). At a high level, we compute expected action variation by simulating a number of rollouts for each policy in the population and calculating the total variational distance between the resulting action distributions. One of the key advantages of this metric is that it can be naïvely applied to a set of stochastic policies generated in any environment.
Expected action variation ranges in value from 0 to 1: a value of 0 indicates that the population is behaviorally homogeneous (all agents select the same action for any given agent state), whereas a value of 1 indicates that the population is maximally behaviorally diverse (all agents select different actions for any given agent state). An expected action variation of 0.5 indicates that if two agents are sampled at random from the population and provided a representative state, they are just as likely to select the same action as they are to select different actions.
This procedure is designed to help compare diversity across populations and to reason about the way a focal agent’s experience of the game might change as a function of which co-players are encountered. Expected action variation is affected by stochasticity in policies, since such stochasticity can affect the state transitions that a focal agent experiences. Expected action variation is not intended to test whether the behavioral diversity of a population is significantly different from zero (or from 1), since such a difference could emerge for trivial reasons.
We leverage expected action variation to assess the effect of population size on behavioral diversity. We also include additional baselines to help explore the dynamics of co-player diversity. Specifically, we train several \(N = 4\) populations parameterized with an intrinsic motivation module [40] on \(L = {1}\mathrm {e}{3}\) levels. In particular, we use the SVO component to motivate agents in these populations to maintain target distributions of reward [36]. Each population is parameterized with either a homogeneous or heterogeneous distribution of SVO targets (see Supplementary file).
Cross-Play Evaluation. We employ a cross-play evaluation procedure to measure the performance resulting from varying population sizes, following Sect. 4.1. Specifically, we group agents sampled from populations A and B and then evaluate group performance on a level from the intersection of the populations’ training sets. We use the same grouping and reporting procedure as before.
4.3 Quantifying performance
For the majority of our environments, we quantify and analyze the individual rewards earned by the agents. In Capture the Flag, we evaluate agents in team competition. Consequently, we record the result of each match from which we calculate win rates and skill ratings. To estimate each population’s skill, we use the Elo rating system [13], an evaluation metric commonly used in games such as chess (see Supplementary file for details).
4.4 Statistical analysis
In our experiments, we launch multiple independent training runs for each value of L and each value of N being investigated. Critically, we match the training sets of these independent runs across values of L and N. For example, the first run of the \(N = 1\) HarvestPatch experiment trains on the exact same training set as the first runs of the \(N \in \{2, 4, 8\}\) experiments. Similarly, the second runs for each of the \(N = 1\) to \(N = 8\) experiments use the same training set, and so on. This allows us to avoid confounding the effects of N with those of L and vice versa.
For our statistical analyses, we primarily leverage the Analysis of Variance (ANOVA) method [16]. The ANOVA allows us to test whether changing the value of an independent variable (e.g., environment diversity) significantly affects the value of a specified dependent variable (e.g., individual reward). Each ANOVA is summarized with an F-statistic and a p-value. In cases where we repeat ANOVAs for each environment, we apply a Holm–Bonferroni correction to control the probability of false positives [20].
5 Results
5.1 Environment diversity
To begin, we assess how environment diversity (i.e., the number of unique levels used for training) affects generalization. Agents are trained on \(L \in \{1, {1}\mathrm {e}{1}, {1}\mathrm {e}{2}, {1}\mathrm {e}{3}, {1}\mathrm {e}{4}\}\) levels in populations of size \(N = 1\).
5.1.1 Generalization gap analysis
As shown in Fig. 3, for all environments generalization improves as the number of levels used for training increases. Performance on the test set increases as L increases, while performance on the training set tends to decrease with greater values of L (Fig. 3, top row).
Top row: Effect of training set size L on group performance on train vs. test levels for each environment. Error bands reflect 95% confidence intervals calculated over 10 independent runs (nine for Capture the Flag). Bottom row: Effect of training set size L on the generalization gap between training and test levels for each environment. Error bars correspond to 95% confidence intervals calculated over 10 independent runs (nine for Capture the Flag). Result: As environment diversity increases, test performance tends to improve. Training performance and the generalization gap experience concomitant decreases
Performance on the training set experiences a minor decrease from low to high values of L. In contrast, the variance in training-set performance declines considerably as environment diversity increases. The variance in training-set performance is notably large for HarvestPatch and Capture the Flag when \(L = 1\). This variability likely results from the wide distribution of possible rewards in the generated levels (e.g., due to varying apple density in HarvestPatch or map size in Capture the Flag). For Capture the Flag, the observed variance may also stem from the inherent difficulty of learning navigation behaviors on a singular large level where the rewards are sparse (i.e., without the availability of a natural curriculum).
To avoid ecological fallacy [17], we directly quantify and analyze the generalization gap with the procedure outlined in Sect. 4.1. As environment diversity increases, the generalization gap between the training and test sets decreases substantially (Fig. 3, bottom row). The trend is sizeable, materializing even in the shift from \(L = 1\) to \(L = {1}\mathrm {e}{1}\). Across the environments considered here, the generalization gap approaches zero around values of \(L={1}\mathrm {e}{3}\). A set of ANOVAs confirm that L has a statistically significant effect on generalization in HarvestPatch, \(F(4,45) = 4.8\), \(p = 2.5 \times 10^{-3}\), Traffic Navigation, \(F(4,45) = 314.9\), \(p = 1.1 \times 10^{-31}\), Overcooked, \(F(4,45) = 106.8\), \(p = 6.9 \times 10^{-22}\), and Capture the Flag, \(F(4,40) = 12.8\), \(p = 1.6 \times 10^{-6}\) (p-values adjusted for multiple comparisons with a Holm–Bonferroni correction).
5.1.2 Cross-Play evaluation
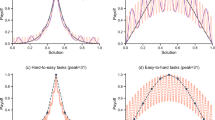
Next, we conduct cross-play evaluations of all populations following the procedure outlined in Sect. 4.1. We separately evaluate populations on the single level included in the training set for all populations (Fig. 4, top row) and the held-out test levels (Fig. 4, bottom row).
Top row: Cross-play evaluation of agent performance for each environment, using levels drawn from their training set. Bottom row: Cross-play evaluation of agent performance for each environment, using held-out test levels. Result: Environment diversity exerts strong effects on agent performance, though the exact pattern varies substantially across environments
Overall, the effects of environment diversity vary substantially across environments.
HarvestPatch. We observe the highest level of performance for the agents playing with a group trained on a large number of levels (column \(L = {1}\mathrm {e}{4}\)) after themselves training on a small number of levels (row \(L = 1\)). In contrast, the worst-performing agents play with a group trained on a small number of levels (column \(L = 1\)) after themselves training on a large number of levels (row \(L = {1}\mathrm {e}{4}\)). These patterns emerge in both the training-level and test-level evaluations.
Traffic Navigation. Agents perform equally well on their training level across all values for their training set size and for the training set size of the group’s other members. In contrast, when evaluating agents on held-out test levels, an agent’s performance strongly depends on how many levels the agent and its group were trained on. Average rewards increase monotonically from column \(L = 1\) to column \(L = {1}\mathrm {e}{4}\), and increase near-monotonically from row \(L = 1\) to row \(L = {1}\mathrm {e}{4}\). Navigation appears more successful with increasing experience of various level layouts and with increasingly experienced groupmates.
Overcooked. In the held-out evaluations, we observe a consistent improvement in rewards earned from the bottom left (\(L=1\) grouped with \(L=1\)) to the top right (\(L={1}\mathrm {e}{4}\) grouped with \(L={1}\mathrm {e}{4}\)). An agent benefits both from playing with a partner with diverse training and from itself training with environment diversity.
A different pattern emerges in the training-level evaluation. Team performance generally decreases when one of the two agents trains on just \(L = 1\) levels. However, when both agents train on \(L = 1\), they collaborate fairly effectively. The highest scores occur at the intermediate values \(L = {1}\mathrm {e}{2}\) and \(L = {1}\mathrm {e}{3}\), rather than at \(L = {1}\mathrm {e}{4}\). Population skill on training levels declines with increasing environment diversity.
Capture the Flag. Team performance is closely tied to environment diversity. A team’s odds of winning are quite low when they train on a smaller level set than the opposing team, and the win rate tends to jump considerably as soon as a team’s training set is larger than their opponents’. However, echoing the results in Overcooked, agents trained on an intermediate level-set size achieve the highest performance on training levels. Population skill actually decreases above \(L = {1}\mathrm {e}{2}\) on these levels (Table 2, middle column). In contrast, in held-out evaluation, environment diversity consistently strengthens performance; Elo ratings monotonically increase as L increases (Table 2, right column).
5.2 Population diversity
We next delve into the effects of population diversity on agent policies and performance. Agents are trained in populations of size \(N \in \{1, 2, 4, 8\}\) on \(L = 1\) levels. In Capture the Flag, a set of additional populations are trained with size \(N = 16\).
5.2.1 Expected action variation analysis
We investigate the behavioral diversity of each population by calculating their expected action variation (see Sect. 4.2).
As shown in Fig. 5, population size positively associates with behavioral diversity among agents trained in each environment. A set of ANOVAs confirm that N has a statistically significant effect on expected action variation in HarvestPatch, \(F(3,16) = 367.7\), \(p = 1.7 \times 10^{-14}\), Traffic Navigation, \(F(3,16) = 70.5\), \(p = 1.9 \times 10^{-9}\), Overcooked, \(F(3,16) = 126.7\), \(p = 4.6 \times 10^{-11}\), and Capture the Flag, \(F(4,20) = 634.6\), \(p = 3.7 \times 10^{-20}\) (p-values adjusted for multiple comparisons with a Holm–Bonferroni correction). Increasing population size amplifies co-player diversity, without requiring any explicit optimization for variation. Multiple sources likely contribute to this diversity, including random initialization for agents and independent exploration and learning.
Effect of variation in intrinsic motivation on behavioral diversity on HarvestPatch. Error bands reflect 95% confidence intervals calculated over five independent runs. Result: Populations with a heterogeneous distribution of intrinsic motivation exhibit significantly greater behavioral diversity than populations with no intrinsic motivation or with a homogeneous distribution
Intrinsic Motivation and Behavioral Diversity. Prior studies demonstrate that parameterizing an agent population with heterogeneous levels of intrinsic motivation can induce behavioral diversity, as measured through task-specific, hard-coded metrics [36]. These agent populations benefited from the resulting diversity in social dilemma tasks, including HarvestPatch. We run an experiment to confirm that this behavioral diversity can be detected through the measurement of expected action variation. Following prior work on HarvestPatch, we endow several \(N = 4\) populations with SVO, an intrinsic motivation for maintaining a target distribution of reward among group members, and then train them on \(L = {1}\mathrm {e}{3}\) levels. We parameterize these populations with either a homogeneous or heterogeneous distribution of SVO (see Supplementary file for details).
As seen in Fig. 6, populations with heterogeneous intrinsic motivation exhibit significantly greater behavioral diversity than populations without intrinsic motivation, \(p = 4.9 \times 10^{-4}\). In contrast, behavioral diversity does not differ significantly between populations of agents lacking intrinsic motivation and those parameterized with homogeneous intrinsic motivation, \(p = 0.99\). These results help baseline the diversity induced by increasing population size and demonstrate that expected action variation can be used to assess established sources of behavioral heterogeneity.
5.2.2 Cross-Play evaluation
We next conduct a cross-play evaluation of all populations following the procedure outlined in Sect. 4.2. As before, we test whether observed patterns are statistically significant using a set of ANOVAs (with a Holm–Bonferroni correction to account for multiple comparisons).
Population diversity does not significantly affect agent rewards for HarvestPatch, \(F(3,16) = 0.06\), \(p = 1.0\) (Fig. 7a), and Traffic Navigation, \(F(3,16) = 0.22\), \(p = 1.0\) (Fig. 7b). Agents trained through self-play (\(N = 1\)) perform equivalently to agents from the largest, most diverse populations (\(N = 8\)). Training in a diverse population thus appears to neither advantage nor disadvantage agents in these environments.
In contrast, agents trained in diverse populations outperform those trained in lower-variation populations for Overcooked, \(F(3,76) = 5.2\), \(p = 7.7 \times 10^{-3}\) (Fig. 7c) and Capture the Flag (Fig. 7d). For both environments, we observe a substantial jump in performance from \(N = 1\) to \(N = 2\) and diminishing increases thereafter. The diminishing returns of diversity resemble the relationship between environment diversity and performance observed for Overcooked and Capture the Flag in Sect. 5.1.2.
Effect of population size N on agent performance. Error bars indicate 95% confidence intervals calculated over five independent runs (20 for Overcooked). Result: Training population size has no influence on the rewards of agents for HarvestPatch and Traffic Navigation. For Overcooked and Capture the Flag, larger populations produced stronger agents. The increase in performance is especially salient moving from \(N = 1\) to \(N = 2\), with diminishing returns as N increases further.
6 Discussion
In summary, this paper makes several contributions to multi-agent reinforcement learning research. Our experiments extend single-agent findings on environment diversity and policy generalization to the multi-agent domain. We find that applying a small amount of environment diversity can lead to a substantial improvement in the generality of agents. However, this generalization reduces performance on agents’ training set for certain environments and co-players.
The expected action variation metric demonstrates how population size and the diversification of agent hyperparameters can influence behavioral diversity. As with environmental diversity, we find that training with a diverse set of co-players strengthens agent performance in some (but not all) cases.
Expected action variation measures population diversity by estimating the heterogeneity in a population’s policy distribution. As recognized by hierarchical and options-based frameworks [42], the mapping of lower-level actions to higher-level strategic outcomes is imperfect; in some states, different actions may lead to identical outcomes. Higher levels of expected action variation may capture greater strategic diversity. Nonetheless, future work could aim to directly measure variation in a population’s strategy set.
These findings may prove useful for the expanding field of human-agent cooperation research. Human behavior is notoriously variable [7, 12]. Interindividual differences in behavior can be a major difficulty for agents intended to interact with humans [11]. This variance thus presents a major challenge stymying the development of human-compatible reinforcement learning agents. Improving the generalizability of our agents could advance progress toward human compatibility, especially for cooperative domains [9].
Future work could seek to develop more sophisticated approaches for quantifying diversity. For example, here we use the “number of unique levels” metric as a proxy of environment diversity, and therefore increased L leads to monotonically increasing environment diversity. However, these levels may be unique in ways which are irrelevant to the agents. Scaling existing approaches to these settings, such as those that study how the environment influences agent behaviour [46], may help determine which features correspond to meaningful diversity.
The experiments presented here employ a rigorous statistical approach to test the consistency and significance of the effects in question. Consequently, they help scope the benefits of environment and population diversity for multi-agent reinforcement learning. Overall, we hope that these findings can improve the design of future multi-agent studies, leading to more generalized agents.
References
Balduzzi, D., Garnelo, M., Bachrach, Y., Czarnecki, W., Perolat, J., Jaderberg, M., Graepel, T. (2019). Open-ended learning in symmetric zero-sum games. In: International Conference on Machine Learning, pp. 434–443. PMLR.
Beattie, C., Köppe, T., Duéñez-Guzmán, E.A., Leibo, J.Z. (2020). DeepMind Lab2D. arXiv preprint arXiv:2011.07027.
Carroll, M., Shah, R., Ho, M.K., Griffiths, T., Seshia, S., Abbeel, P., Dragan, A. (2019). On the utility of learning about humans for human-AI coordination. In: Advances in Neural Information Processing Systems, pp. 5175–5186.
Charakorn, R., Manoonpong, P., Dilokthanakul, N. (2020). Investigating partner diversification methods in cooperative multi-agent deep reinforcement learning. In: International Conference on Neural Information Processing, pp. 395–402. Springer.
Cobbe, K., Hesse, C., Hilton, J., Schulman, J. (2019). Leveraging procedural generation to benchmark reinforcement learning. arXiv preprint arXiv:1912.01588.
Cobbe, K., Klimov, O., Hesse, C., Kim, T., Schulman, J. (2019). Quantifying generalization in reinforcement learning. In: International Conference on Machine Learning, pp. 1282–1289.
Cronbach, L. J. (1957). The two disciplines of scientific psychology. American Psychologist, 12(11), 671.
Czarnecki, W. M., Gidel, G., Tracey, B., Tuyls, K., Omidshafiei, S., Balduzzi, D., & Jaderberg, M. (2020). Real world games look like spinning tops. Advances in Neural Information Processing Systems, 33, 17443–17454.
Dafoe, A., Hughes, E., Bachrach, Y., Collins, T., McKee, K.R., Leibo, J.Z., Larson, K., Graepel, T. (2020). Open problems in cooperative AI. arXiv preprint arXiv:2012.08630.
Dai, T., Du, Y., Fang, M., & Bharath, A. A. (2022). Diversity-augmented intrinsic motivation for deep reinforcement learning. Neurocomputing, 468, 396–406.
Egan, D. E. (1988). Individual differences in human-computer interaction. In: Handbook of Human-Computer Interaction, (pp. 543–568). Netherlands: Elsevier.
Eid, M., & Diener, E. (1999). Intraindividual variability in affect: Reliability, validity, and personality correlates. Journal of Personality and Social Psychology, 76(4), 662.
Elo, A. E. (1978). The Rating of Chessplayers Past and Present. New York: Arco Publishing.
Everett, R., Cobb, A., Markham, A., Roberts, S. (2019). Optimising worlds to evaluate and influence reinforcement learning agents. In: Proceedings of the 18th International Conference on Autonomous Agents and Multiagent Systems, pp. 1943–1945. International Foundation for Autonomous Agents and Multiagent Systems.
Eysenbach, B., Gupta, A., Ibarz, J., Levine, S. (2019). Diversity is all you need: Learning skills without a reward function. In: International Conference on Learning Representations.
Fisher, R. A. (1928). Statistical Methods for Research Workers. United Kingdom: Oliver & Boyd.
Freedman, D. A. (1999). Ecological inference and the ecological fallacy. International Encyclopedia of the Social and Behavioral Sciences, 6(4027–4030), 1–7.
Haarnoja, T., Tang, H., Abbeel, P., Levine, S. (2017). Reinforcement learning with deep energy-based policies. In: International Conference on Machine Learning, pp. 1352–1361. PMLR.
Hessel, M., Soyer, H., Espeholt, L., Czarnecki, W., Schmitt, S., van Hasselt, H. (2019). Multi-task deep reinforcement learning with PopArt. In: Proceedings of the AAAI Conference on Artificial Intelligence, vol. 33, pp. 3796–3803.
Holm, S. (1979). A simple sequentially rejective multiple test procedure. Scandinavian Journal of Statistics pp. 65–70.
Hu, H., Lerer, A., Peysakhovich, A., Foerster, J. (2020). ‘Other-play’ for zero-shot coordination. arXiv preprint arXiv:2003.02979.
Hughes, E., Leibo, J.Z., Phillips, M., Tuyls, K., Dueñez-Guzman, E., Castañeda, A.G., Dunning, I., Zhu, T., McKee, K.R., Koster, R., Roff, H., Graepel, T. (2018). Inequity aversion improves cooperation in intertemporal social dilemmas. In: Advances in Neural Information Processing Systems, pp. 3326–3336.
Ibrahim, A., Jitani, A., Piracha, D., Precup, D. (2020). Reward redistribution mechanisms in multi-agent reinforcement learning. In: Adaptive Learning Agents Workshop at the International Conference on Autonomous Agents and Multiagent Systems.
Jaderberg, M., Czarnecki, W. M., Dunning, I., Marris, L., Lever, G., Castañeda, A. G., Beattie, C., Rabinowitz, N. C., Morcos, A. S., Ruderman, A., Sonnerat, N., Green, T., Deason, L., Leibo, J. Z., Silver, D., Hassabis, D., Kavukcuoglu, K., & Graepel, T. (2019). Human-level performance in 3D multiplayer games with population-based reinforcement learning. Science, 364(6443), 859–865.
Jaques, N., Lazaridou, A., Hughes, E., Gulcehre, C., Ortega, P.A., Strouse, D., Leibo, J.Z., De Freitas, N. (2019). Intrinsic social motivation via causal influence in multi-agent RL. In: International Conference on Learning Representations.
Juliani, A., Khalifa, A., Berges, V.P., Harper, J., Teng, E., Henry, H., Crespi, A., Togelius, J., Lange, D. (2019). Obstacle tower: A generalization challenge in vision, control, and planning. arXiv preprint arXiv:1902.01378.
Justesen, N., Torrado, R.R., Bontrager, P., Khalifa, A., Togelius, J., Risi, S. (2018). Illuminating generalization in deep reinforcement learning through procedural level generation. arXiv preprint arXiv:1806.10729.
Kingma, D.P., Ba, J., Adam (2014). A method for stochastic optimization. arXiv preprint arXiv:1412.6980.
Knott, P., Carroll, M., Devlin, S., Ciosek, K., Hofmann, K., Dragan, A., Shah, R. (2021). Evaluating the robustness of collaborative agents. arXiv preprint arXiv:2101.05507.
Kramár, J., Rabinowitz, N., Eccles, T., Tacchetti, A. (2020). Should I tear down this wall? Optimizing social metrics by evaluating novel actions. arXiv preprint arXiv:2004.07625.
Lanctot, M., Zambaldi, V., Gruslys, A., Lazaridou, A., Tuyls, K., Pérolat, J., Silver, D., Graepel, T. (2017). A unified game-theoretic approach to multiagent reinforcement learning. In: Advances in Neural Information Processing Systems, pp. 4190–4203.
Leibo, J.Z., Perolat, J., Hughes, E., Wheelwright, S., Marblestone, A.H., Duéñez-Guzmán, E., Sunehag, P., Dunning, I., Graepel, T. (2019). Malthusian reinforcement learning. In: Proceedings of the 18th International Conference on Autonomous Agents and Multiagent Systems, pp. 1099–1107. International Foundation for Autonomous Agents and Multiagent Systems.
Lerer, A., Peysakhovich, A. (2019). Learning existing social conventions via observationally augmented self-play. In: Proceedings of the 2019 AAAI/ACM Conference on AI, Ethics, and Society, pp. 107–114.
Littman, M. L. (1994). Markov games as a framework for multi-agent reinforcement learning. In: Machine Learning Proceedings 1994 (pp. 157–163). Elsevier.
Lowe, R., Wu, Y., Tamar, A., Harb, J., Abbeel, P., Mordatch, I. (2017). Multi-agent actor-critic for mixed cooperative-competitive environments. In: Advances in Neural Information Processing Systems, pp. 6382–6393.
McKee, K.R., Gemp, I., McWilliams, B., Duéñez-Guzmán, E.A., Hughes, E., Leibo, J.Z. (2020). Social diversity and social preferences in mixed-motive reinforcement learning. In: Proceedings of the 19th International Conference on Autonomous Agents and Multiagent Systems. International Foundation for Autonomous Agents and Multiagent Systems.
Nieves, N.P., Yang, Y., Slumbers, O., Mguni, D.H., Wen, Y., Wang, J. (2021). Modelling behavioural diversity for learning in open-ended games. arXiv preprint arXiv:2103.07927.
Perolat, J., Leibo, J.Z., Zambaldi, V., Beattie, C., Tuyls, K., Graepel, T. (2017). A multi-agent reinforcement learning model of common-pool resource appropriation. In: Advances in Neural Information Processing Systems, pp. 3643–3652.
Sanjaya, R., Wang, J., Yang, Y. (2021). Measuring the non-transitivity in chess. arXiv preprint arXiv:2110.11737.
Singh, S.P., Barto, A.G., Chentanez, N. (2005). Intrinsically motivated reinforcement learning. In: Advances in Neural Information Processing Systems.
Song, H.F., Abdolmaleki, A., Springenberg, J.T., Clark, A., Soyer, H., Rae, J.W., Noury, S., Ahuja, A., Liu, S., Tirumala, D., Heess, N., Belov, D., Riedmiller, M., Botvinick, M.M. (2019). V-MPO: On-policy maximum a posteriori policy optimization for discrete and continuous control. arXiv preprint arXiv:1909.12238.
Sutton, R. S., Precup, D., & Singh, S. (1999). Between MDPs and semi-MDPs: A framework for temporal abstraction in reinforcement learning. Artificial Intelligence, 112(1–2), 181–211.
Tukey, J.W. (1949). Comparing individual means in the analysis of variance. Biometrics pp. 99–114.
Vinyals, O., Babuschkin, I., Czarnecki, W. M., Mathieu, M., Dudzik, A., Chung, J., Choi, D. H., Powell, R., Ewalds, T., Georgiev, P., Oh, J., Horgan, D., Kroiss, M., Danihelka, I., Huang, A., Sifre, L., Cai, T., Agapiou, J. P., Jaderberg, M., … Silver, D. (2019). Grandmaster level in StarCraft II using multi-agent reinforcement learning. Nature, 575(7782), 350–354.
Wang, R., Lehman, J., Clune, J., Stanley, K.O. (2019). Paired open-ended trailblazer (POET): Endlessly generating increasingly complex and diverse learning environments and their solutions. arXiv preprint arXiv:1901.01753.
Wang, R., Lehman, J., Rawal, A., Zhi, J., Li, Y., Clune, J., Stanley, K. (2020). Enhanced POET: Open-ended reinforcement learning through unbounded invention of learning challenges and their solutions. In: International Conference on Machine Learning, pp. 9940–9951. PMLR.
Wang, R.E., Wu, S.A., Evans, J.A., Tenenbaum, J.B., Parkes, D.C., Kleiman-Weiner, M. (2020). Too many cooks: Bayesian inference for coordinating multi-agent collaboration. In: Cooperative AI Workshop at the Conference on Neural Information Processing Systems.
Zhang, C., Vinyals, O., Munos, R., Bengio, S. (2018). A study on overfitting in deep reinforcement learning. arXiv preprint arXiv:1804.06893.
Acknowledgements
We thank Ian Gemp, Edgar Duéñez-Guzmán, and Thore Graepel for their support and feedback during the preparation of this manuscript. We are also indebted to Mary Cassin for designing and creating the sprite art for the DeepMind Lab2D implementation of Overcooked.
Author information
Authors and Affiliations
Corresponding authors
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
McKee, K.R., Leibo, J.Z., Beattie, C. et al. Quantifying the effects of environment and population diversity in multi-agent reinforcement learning. Auton Agent Multi-Agent Syst 36, 21 (2022). https://doi.org/10.1007/s10458-022-09548-8
Accepted:
Published:
DOI: https://doi.org/10.1007/s10458-022-09548-8