Using informative behavior to increase engagement while learning from human reward

Abstract

In this work, we address a relatively unexplored aspect of designing agents that learn from human reward. We investigate how an agent’s non-task behavior can affect a human trainer’s training and agent learning. We use the TAMER framework, which facilitates the training of agents by human-generated reward signals, i.e., judgements of the quality of the agent’s actions, as the foundation for our investigation. Then, starting from the premise that the interaction between the agent and the trainer should be bi-directional, we propose two new training interfaces to increase a human trainer’s active involvement in the training process and thereby improve the agent’s task performance. One provides information on the agent’s uncertainty which is a metric calculated as data coverage, the other on its performance. Our results from a 51-subject user study show that these interfaces can induce the trainers to train longer and give more feedback. The agent’s performance, however, increases only in response to the addition of performance-oriented information, not by sharing uncertainty levels. These results suggest that the organizational maxim about human behavior, “you get what you measure”—i.e., sharing metrics with people causes them to focus on optimizing those metrics while de-emphasizing other objectives—also applies to the training of agents. Using principle component analysis, we show how trainers in the two conditions train agents differently. In addition, by simulating the influence of the agent’s uncertainty–informative behavior on a human’s training behavior, we show that trainers could be distracted by the agent sharing its uncertainty levels about its actions, giving poor feedback for the sake of reducing the agent’s uncertainty without improving the agent’s performance.

1 Introduction

Autonomous agents (such as robots, software agents, etc.) have the potential to assist people in their daily lives, e.g., help them do the laundry at home, clean the house, perform individualized customer service, etc. As such, agents enter into human-oriented environments where people themselves are full of untapped knowledge. To adapt to novel situations, they need to be able to learn new skills from any ordinary person who has much task knowledge but little expertise in autonomous agents or technology in general. Intuitively, how well these agents can learn from human users will depend heavily on how efficiently such agents can interact with them. Therefore, to effectively transfer task knowledge from ordinary people to agents, we need to understand how to develop interfaces that facilitate the interaction between them while learning occurs.

Many approaches for agent learning by interacting with a human teacher have been proposed. The feedback that the human teacher provides during such interaction can take many forms, e.g., advice [27], guidance [35], or critiques [2], etc. One popular method based on reinforcement learning (RL)—an area of machine learning concerned with how to map situations to actions so as to maximize a numerical reward signal [31]—incorporates the real-time human reward that reflects the human trainer’s judgement of the quality of the agent’s actions supplied by a trainer who observes the agent’s behavior [14, 18, 29]. In the TAMER framework [18], one solution proposed for learning from human reward, the agent learns from this feedback by directly creating a predictive model of the human trainer’s feedback and myopically choosing the action at each time step that it predicts will receive the highest feedback value. Just like any agent that learns from a human, a TAMER agent’s performance depends critically on the efficiency of the interaction between the human trainer and the agent, which means the effort or cost per unit used by the trainer to train the agent to perform a task well.

In this article, we propose an extension to TAMER that allows the agent to give the trainer feedback about its learning state to improve the efficiency of this interaction by better engaging the human trainer. Here, engagement is defined as the depth of participation measured by the duration of training, the number of feedback given and the frequency of feedback. We use TAMER as our learning algorithm because it succeeds in many domains including Tetris, Mountain Car, Cart Pole, Keepaway Soccer, Interactive Robot Navigation, etc. [17], thus enabling our approach to transfer to other domains.

The key idea behind our approach is that, similar to a human student and teacher, the interactions between an agent and its human trainer should ideally be bi-directional. For example, the teacher gives the student lessons and grades her performance to guide the student’s learning, while the student informs the teacher about her confusion by asking questions. Therefore, the teacher can adjust her teaching to meet the needs of the student at different learning stages. Similarly, in the human–agent situation, not only should the human teach the agent how to complete the task, the agent should also influence the human to teach it as efficiently as possible. Therefore, in addition to the human giving reward to the agent, the agent should also give feedback to the human to inform her about its progress and indicate the kind of human feedback that would be most useful. Our goal is to allow the agent to provide responsive feedback to the trainer’s training. We expect this could help the human trainer to understand how her feedback affects the agent’ s learning and to adjust her training to make the training process more efficient.

Specifically, in this article, we propose two interfaces with which we investigate the influence of the agent’s feedback on the human trainer’s training behavior and its learning via TAMER. In the first, the uncertainty–informative interface, the agent informs the human of its uncertainty about the actions it selects with a bar graph, in the hope that this motivates the human to reduce that uncertainty by focusing feedback on the most needed states. In the second, the performance–informative interface, the agent informs the human about its current performance in the task relative to its earlier performance also with a bar graph, which we expect will motivate the human to give the feedback needed to further improve performance. We hypothesize that the agent’s informative feedback will cause the human to train longer, give more feedback and that the agent’s performance will improve as a result.

To test these hypotheses, we conducted a user study with 51 subjects and compared the agents trained with these informative interfaces to the original TAMER agent. We found that the agent’s informative feedback can significantly increase the duration of training and the amount of feedback provided by the trainer, with the uncertainty–informative interface generating the most feedback. As we expected, our results show that the performance–informative feedback led to substantially better agent performance. Surprisingly, the uncertainty–informative feedback led to worse agent performance although much more human feedback was elicited.

Altogether, these results not only provide insights into TAMER, they also highlight the importance of interface design—a previously under-emphasized aspect of agent training using humans—by providing evidence of its influence on human training behavior. Furthermore, the results that measuring performance increased performance, and measuring uncertainty reduced uncertainty, also fit with a pattern observed in organizational behavior research that follows from the adage “you get what you measure” [7]—sharing behavior-related metrics will tend to make people attempt to improve their scores with respect to that metric. To our knowledge, our work is the first to observe this phenomenon in the context of humans training artificial agents. This provides a potentially powerful guiding principle for human–agent interface design in general.

Furthermore, using principle component analysis, we show how trainers in the two conditions train agents differently. In addition, by simulating the influence of the agent’s uncertainty–informative behavior on a human’s training behavior, we show that trainers could be distracted by the agent sharing its uncertainty levels about its actions, which may explain the performance discrepancy between the uncertainty–informative condition and the control condition.

2 Related work

Many approaches have been proposed for enabling agents to learn with human assistance, including learning from demonstration [1, 2, 33], giving advice to reinforcement learners [15, 26, 27], and learning from human feedback [5, 18, 34, 35]. In this section, we discuss the research most related to our work, namely learning from demonstration and learning from human reward.

2.1 Learning from demonstration

In learning from demonstration, the agent learns from sequences of state-action pairs provided by a human trainer who demonstrates the desired behavior [3]. For example, apprenticeship learning [1] together with inverse reinforcement learning [28], are a form of learning from demonstration in which an expert’s demonstrations are used to estimate a hidden reward function.

In learning from demonstration systems, the agent’s performance is limited by the information provided in the demonstration. Most agents passively receive the demonstrations from the trainer, neither actively gathering data nor providing feedback information to affect the learning process. To improve what is learned from the trainer’s demonstrations, Argall et al. [2] propose an approach wherein learning from demonstration is coupled with critiques by the human of the agent’s performance. In addition, some approaches that acquire new demonstrations by making the agent active in the learning process have also been proposed. For example, an agent, based on its confidence in what it has learned, can request a specific demonstration from the human [9, 10, 13]. The human can then correct the agent’s mistakes.

These approaches are similar in motivation to ours, in that they seek human–agent interfaces that aid agent learning. In addition, the approach of Chernova and Veloso [10] is related to the uncertainty–informative interface we propose in Sect. 4.1, in that the agent’s uncertainty is used to guide this interaction. However, the focus of these methods is different but complementary to ours. While these studies are concerned with the impact of enabling the agent to query the trainer and of enabling the trainer to give corrective feedback after observing behavior learned from demonstration, our work investigates how trainer behavior—and resultant agent performance—is influenced by the specific stream of information that the agent shares with the trainer.

2.2 Learning from human reward

An agent can also learn from feedback that a human provides about the agent’s behavior. In this learning scenario, feedback can be restricted to express various intensities of approval and disapproval; such feedback is mapped to numeric “reward” that the agent uses to revise its behavior [14, 18, 29, 30, 34]. Compared to learning from demonstration, learning from human reward requires only a simple task-independent interface and may require less expertise and place less cognitive load on the trainer [20].

One of the earliest attempts to train artificial agents in this way is based on clicker training [5, 16]. This is a form of animal training in which the sound of an audible device such as a clicker or whistle is associated with a primary reinforcer such as food and then used as a reward signal to guide the agent towards desired behavior. Isbell et al. [14] apply reinforcement learning in an online text-based virtual world where people interact by allowing the agent to learn to take proactive actions from multiple sources of human reward, which are ‘reward and punish’ text-verbs invoked by multiple users.

While most of the work treats the human reward as indistinguishable from other feedback in the environment, the TAMER framework [18] allows an agent to learn from human reward signals provided by a human trainer who observes and evaluates the agent’s behavior without a predefined reward function as in traditional reinforcement learning. The primary differences between the TAMER framework and other algorithms for learning from human feedback are that TAMER creates a predictive model of human reward, explicitly addresses delay in the delivery of human reward signals, and chooses actions that its human model predicts will elicit maximal reward through fully myopic valuation, considering only reward caused by its immediate action. In reinforcement learning, myopia is defined as discounting the value of future reward with a discount factor $\gamma$. General myopia is a feature of all past algorithms for learning from human feedback and received empirical support in recent work [20], but TAMER is unique in that it is fully myopic (in reinforcement learning terminology, it does not value future reward at all because a trainer’s reward signal carries an assessment of the behavior itself, with a model of its long-term consequences in mind).

In the TAMER+RL framework [19, 21], the agent learns from both human and environmental feedback, which can lead to better performance than learning from either alone. This can be done sequentially (i.e., the agent first learns from human feedback and then environmental feedback) [19] or simultaneously (i.e., the agent learns from both at the same time), allowing the human trainer to provide feedback at any time during the learning process [21].

Thomaz and Breazeal [37] also distinguish the human reward from the other environmental feedback, but also claim that there are different intents in the communication from the human trainer. In addition to use the human reward to train the agent, they use guidance, which allows the user to recommend actions for the agent to perform, to bias the agent’s action selection. Their results showed an improvement in agent’s learning with guidance intention. While Thomaz and Breazeal addressed the human-side of the interaction by investigating what kinds of intentions people try to communicate in their teaching behavior, we are interested in the effect of specific streams of information that the agent shares with the trainer on the training behavior.

Similar to our approach, Thomaz and Breazeal [37] also claim that the transparency of an agent’s behavior can improve its learning environment using gaze behavior to reveal the agent’s uncertainty and potential next actions. Their results show that the gaze behavior reduces the redundancy of guidance from the human trainer but does not further improve the agent’s learning. In addition, Knox et al. [23] also examine how human trainers respond to changes in their perception of the agent and to certain changes in the agent’s behavior and find that the agent can induce the human trainer to give more feedback but with lower performance when the quality of the agent’s behavior is deliberately reduced whenever the rate of human feedback decreases.

The approach of Knox et al. investigates how an agent’s task-focused behavior affects trainer’s training behavior, and Thomaz and Breazeal’s transparent approach is conceptually similar to ours. However, in this work, we are interested in how specific stream of information that the agent shares with the trainer affect the trainer’s training and agent’s performance. Ultimately, we believe that it will be helpful for facilitating the interaction between the trainer and the agent if the agent provides information (such as facial expressions, body language etc.) to indicate something about its learning state and solicit feedback from a human [8, 36, 38].

Our work builds on the TAMER framework but focuses on how to improve training through the interface design. In particular, in past work on TAMER and TAMER+RL, the agent communicates only its action and environmental state to the trainer and does not empirically analyze what agent information should be communicated to elicit training of higher efficiency or longer duration. In this article, we frame the information sharing of an agent’s interactive interface as a form of communicative behavior. Unlike the transparent learning mechanism described above, our work is the first to consider this within the TAMER framework and provides the first analysis of how manipulating the information the agent provides can affect the trainer’s behavior. Furthermore, our empirical user study provides evidence that such informative behavior increases the trainer’s feedback quantity and greatly affects the agent’s learning.

Our preliminary work on this topic was presented in [25]. This article significantly extends upon our initial work by providing a more extensive analysis of the reason for the performance discrepancy between our uncertainty–informative condition and control condition by simulating the influence of an agent’s uncertainty–informative behavior on a trainer’s behavior. Our results show that the trainer may be distracted by an agent’s shared uncertainty levels by trying to reduce the uncertainty level of the agent regardless of the quality of the feedback they give.

3 Background

This section briefly introduces the TAMER framework and the Tetris platform used in our experiment.

3.1 TAMER framework

An agent implemented according to the TAMER framework learns from real-time evaluations of its behavior, provided by a human trainer. From these evaluations, which we refer to as “reward”, the TAMER agent creates a predictive model of future human reward and chooses actions it predicts will elicit the greatest human reward. Unlike in traditional reinforcement learning, a reward function is not predefined.

A TAMER agent strives to maximize the reward caused by its immediate action, which also contrasts with traditional reinforcement learning, in which the agent seeks the largest discounted sum of future rewards. The intuition for why an agent can learn to perform tasks using such a myopic valuation of reward is that human feedback can generally be delivered with small delay—the time it takes for the trainer to assess the agent’s behavior and deliver feedback—and the evaluation that creates a trainer’s reward signal carries an assessment of the behavior itself, with a model of its long-term consequences in mind. Until recently [22], general myopia was a feature of all algorithms involving learning from human feedback and has received empirical support [20]. Built to solve a variant of a Markov decision processes, (i.e., a specification of a sequential decision-making problem commonly addressed through reinforcement learning [31]) in which there is no reward function encoded before learning, the TAMER agent learns a function $\hat{H}(s, a)$ that approximates the expectation of experienced human reward, $H: S \times A \rightarrow \mathfrak {R}$. Given a state s, the agent myopically chooses the action with the largest estimated expected reward, $\mathrm{arg}\,\mathrm{max}\,_{a}\hat{H}(s, a)$. The trainer observes the agent’s behavior and can give reward corresponding to its quality.

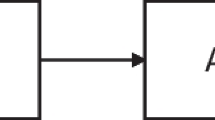
The TAMER agent treats each observed reward signal as part of a label for the previous (s, a), which is then used as a supervised learning sample to update the estimate of $\hat{H}(s, a)$. In this article, the update is performed by incremental gradient descent; i.e., the weights of the function approximator specifying $\hat{H}(s, a)$ are updated to reduce the error $|r - \hat{H}(s, a)|$, where r is the sum of reward instances observed shortly after taking action a in state s. Figure 1 illustrates interaction in the TAMER framework.

In TAMER, feedback is given via keyboard input and attributed to the agent’s most recent action. Each press of one of the feedback buttons registers as a scalar reward signal (either $-1$ or $+1$). This signal can also be strengthened by pressing the button multiple times and the label for a sample is calculated as a delay-weighted aggregate reward based on the probability that a human reward signal targets a specific time step [17]. The TAMER learning algorithm repeatedly takes an action, senses reward, and updates $\hat{H}$. Note that unlike [17], when no feedback is received from the trainer, learning is suspended until the next feedback instance is received.

Fig. 1

Interaction in the TAMER framework (reproduced from [17])

3.2 Experimental Platform: Tetris

Tetris is a fun and popular game that is familiar to most people, making it an excellent platform for investigating how humans and agents interact during agent learning. We use an adaptation of the RL-Library implementation of Tetris.¹

Tetris is played on a $w \times h$ game board, in which seven different shapes of Tetris piece, called tetrominos, composed of multiple configurations of four blocks are selected randomly and fall from the top of the game board. A player can configure the horizontal placement of consecutive blocks at the base of the board or on top of previously placed pieces. When a row is completely filled with blocks, all the blocks in that row are cleared, and the remaining blocks above this row fall to fill the cleared line. The game ends when the blocks stack beyond the top of the grid. During this task, the player’s goal is to arrange the pieces so as to clear as many lines as possible before the game ends.

Although Tetris has simple rules, it is a challenging problem for agent learning because the number of states required to represent all possible configurations of the Tetris board is extremely large [11]. In the TAMER framework, the agent uses 46 state features—including the 10 column heights, 9 differences in consecutive column heights, the maximum column height, the number of holes, the sum of well depths, the maximum well depth, and the 23 squares of the previously described 23 features [17]—to represent the state observation. The input to $\hat{H}$ is 46 corresponding state-action features, the difference between state features before a placement and after the placement and clearing any resulting solid rows.

Like other implementations of Tetris learning agents (e.g., [4, 6, 32]), the TAMER agent only chooses an action from a set of possible final placements of a piece on the stack of previously placed pieces. That is, for a given action, the combination of atomic rotations and left/right movements of a piece to place it in the chosen position are determined independently by the agent and not learned via trainer feedback. Even with this simplification, playing Tetris remains a complex and highly stochastic task.

4 Informative interfaces

In this section, we propose two variations on the baseline TAMER interface described above that each display additional information about the agent’s performance history or internal processes. These variations are motivated by the notion that the interaction between the trainer and the agent should be consciously designed to be bi-directional, where the agent gives the trainer informative and/or motivating feedback about its learning process. Our intuition is that such feedback will help keep the trainer involved in the training process and empower her to offer more useful feedback. More objectively, we hypothesize that doing so will increase the quantity of the trainer’s feedback and improve the agent’s task performance.

4.1 Uncertainty–informative behavior

The first variation is the uncertainty–informative interface, in which the agent indicates to the trainer its uncertainty about the action it selects. We hypothesize that doing so will motivate the trainer to reduce uncertainty by giving more feedback and enable her to focus that feedback on the states where it is most needed. To implement this interface, we added a dynamic bar graph above the Tetris board that shows the agent’s uncertainty, as shown in Fig. 2.

Fig. 2

The uncertainty–informative interface: a the uncertainty graph window, b the current uncertainty (pink bar), and c the uncertainty of past actions (dark blue bar) (Color figure online)

Many methods are possible for measuring the agent’s confidence of action selection. For example, the confidence execution algorithm in [10] uses the nearest neighbor distance from demonstrated states to classify unfamiliar, ambiguous states. Since we are primarily interested in how a trainer’s perception of the agent’s uncertainty of an action affects training behavior, we applied a simple uncertainty metric that we expected to maximize the amount of feedback given. While more sophisticated uncertainty metrics could also be used, optimizing this metric is not the focus of our study.

Our approach considers an agent to be more certain about its action in a state if it has received feedback for a similar state. So the best way for a trainer to reduce an agent’s uncertainty and improve agent learning at the same time is to give as much feedback to as many states as possible. We calculate the weighted sum of the distance in feature space from the current state to the k nearest states that previously received feedback, yielding a coarse measure of the agent’s uncertainty about the current action. Thus, we define the uncertainty U of the current state $s_c$ as

$$\begin{aligned} U(s_c)= \sum _{i=1}^{k}w_{i}d_{i}, \end{aligned}$$

(1)

where $d_{i}$ is the Euclidean distance between the current state $s_{c}$ and the i-th closest state $s_i$ in the set of all states wherein the agent received feedback:

$$\begin{aligned} d_{i} = \sqrt{\sum _{j=1}^{n}(s_{ij}-s_{cj})^{2}}, \end{aligned}$$

(2)

where $s_{ij}$ is the value of the j-th state feature of state $s_i$, $s_{cj}$ is the value of the j-th state feature of the current state $s_c$ and n is the dimension of the state feature vector. We chose the weights $w_i$ (where $\Sigma _{i=1}^{k}w_{i} =1$) to approximate an exponential decay in the ranking of farther neighbors. In our experiments, $k=3$ and $(w_1,w_2,w_3) = (0.55, 0.3,0.15)$.

While the human is training the agent, the graph shows both the uncertainty of the current state (pink rightmost bar) and past states (dark blue bars), as illustrated in Fig. 2. In the graph window, the uncertainty at each time step (each time a piece is placed) is shown from left to right chronologically. For the first game, no bar is shown until the agent has received feedback three times. Then, before each piece is placed, the agent shows its current uncertainty for the action it is about to make. If the trainer gives feedback, the value of the current uncertainty is modified according to Eq. 1 and the new uncertainty is visualized as a dark blue bar after the piece is placed. Meanwhile, a new pink bar appears to the right of it, showing the uncertainty of the new placement. Since the graph window can only show up to 60 time steps, it is cleared when the current time step is a multiple of 60, and the bar showing the new uncertainty is shown from the left side again. The vertical axis is labeled only with “high” and “low” so that trainers focus on relative differences in uncertainty, not absolute values. To keep the changes in uncertainty visible, the interface starts with a fixed maximum uncertainty value; if the height of the bar exceeds this maximum, the ceiling value of the vertical axis is correspondingly adjusted. When the height of the bar exceeds the ceiling value of the vertical axis, the ceiling value is automatically adjusted to fully show the highest bar.

4.2 Performance–informative behavior

The second variation is the performance–informative interface, in which the agent indicates to the trainer its performance over past and current games. We hypothesize that explicitly displaying performance history will increase the trainer’s motivation to improve the agent’s performance, thus leading to more and higher quality feedback. To implement this interface, we again added a dynamic bar graph above the Tetris board, as shown in Fig. 3. In this case, however, each bar indicates the agent’s performance in a whole Tetris game. Since clearing a line reduces the stack height and in turn gives the agent the opportunity to clear more lines, we quantified the performance of the agent by the number of lines cleared. This metric is both intuitive for the trainer to understand and fits with past work on agents that learn to play Tetris [6, 32]. The interface was designed to look very similar to the uncertainty–informative interface to avoid confounding factors. However, the vertical axes in the two interfaces were labeled according to the different metrics, to display the information as clearly as possible. During training, the graph shows the agent’s performance (i.e., lines cleared per game) during past and current games, ordered chronologically from left to right, so the trainer can keep track of the agent’s progress.

During the first game, after the first line is cleared, the graph shows a pink bar at the left side of the graph window, representing the number of lines cleared so far. When a game ends, its corresponding bar becomes dark blue and any new lines cleared in the new game are visualized by a pink bar to its right. As in the uncertainty–informative interface, the window is cleared after it is filled with 60 bars—games in this case—and new bars appear from the left. The vertical axis is labeled ‘Lines Cleared’ and is initially bounded between 0 and 10. When the number of lines cleared exceeds the axis’s upper bound, the limit is increased by 25 while all prior performance is in the range [0, 100] and the height of all bars are adjusted accordingly. Subsequently, the upper bound is increased by 50 for the range (100, 1000], 100 for the range (1000, 10000], and 1000 for greater than 10000.

Fig. 3

The performance–informative interface: a performance graph window, b current game performance, and c performance of past games

5 Experiment

The purpose of the experiment is to understand what information the agent should share with the trainer and how this specific stream of information affects the trainer’s training and resultant agent’s learning. Using Tetris and proposed informative interfaces as tools, we conducted an experiment and analyzed the result in this section.

5.1 Experimental design

To maximize the diversity of subject recruitment, we deployed the Tetris game on the internet. 70 participants from more than 10 countries were recruited by email, a Facebook page and flyer and poster advertisements. Their ages ranged from 19 to 63 and included both males and females. Some had backgrounds in AI or related fields while others had little knowledge of computer science; at least 8 had no programming skills. Of the 38 subjects who filled in the post-experiment questionnaire, 9 were from the Netherlands, 8 from China, 7 from Austria, 3 from Germany, 2 each from the USA, Italy, and Greece, and one each from the UK, Belgium, Japan, Canada, and Turkey.

In the experiment, all the participants were told “In this experiment you will be asked to train an agent to play Tetris by giving positive and negative feedback” in the instructions. The instructions also described how to give feedback and, for the appropriate conditions, explained the agent’s informative behavior. The subjects were divided evenly and randomly into the three conditions. However, data from 19 of the recruited subjects was removed because the subjects registered but never started training or used the wrong ID when returning to train their agents (so they trained multiple agents). Thus, the rest of this paper analyzes the results from the remaining 51 participants. The experimental details of each condition are described below:

• Control condition 16 participants trained the agent without seeing any informative behaviors using the baseline TAMER interface described in Sect. 3.1.

• Uncertainty–informative condition 19 participants trained the agent using the interface described in Sect. 4.1.

• Performance–informative condition 16 participants trained the agent using the interface described in Sect. 4.2.

The participants in the three conditions trained the agents by pressing two buttons on the keyboard to give positive and/or negative feedback. Similar to the baseline TAMER interface described in Sect. 3.1, they could also strengthen their feedback by pressing each button multiple times. A training session was turned on automatically when any button was pressed and turned off when no feedback was provided. They were encouraged to train the agent as many times as they liked during 7 days. We recorded the state observation, actions, human rewards, lines cleared, the absolute start time, speed of each time step, lines cleared per game, and number of training sessions.

We also investigated the correlation between the trainer’s training behavior and certain characteristics of the trainer’s personality. We hypothesized that for the uncertainty–informative and performance–informative conditions, a respectively empathetic or competitive trainer would spend more time on training, leading to higher performing agents.

To validate these hypotheses, we designed a questionnaire to measure the trainer’s feelings about the agent, the training process, and the personalities of the trainer. We used a 5-point scale composed of bipolar adjective pairs: 7 to test the trainer’s feelings about the agent, and 10 for the training process. Participants were also given a self-report scale including 13 items from the Empathy Quotient (EQ) [24] to measure the trainers’ willingness to interpret the informative behavior and 14 items as a measure of competitiveness, which were adapted from the Sport Orientation Questionnaire [12]. Eight filler items were also included to minimise potential bias that can be caused by the trainers second-guessing what the questionnaire was about (four of them were from the Introversion-Extroversion Scale and another four from EQ [24]).

Table 1 Pearson’s correlation test between trainer’s training behavior, agent’s offline performance and trainer’s self-report competitiveness and empathy regardless of condition, in the control, performance–informative and uncertainty–informative conditions, respectively

Table 1 shows a Pearson’s correlation test between trainer’s training behavior, agent’s offline performance and trainer’s self-report competitiveness and empathy. We observed that, regardless of the experimental condition, the trainers who score highly on empathy tended to give more feedback instances ($r = 0.31, p = 0.056$). Trainers in the performance–informative condition who scored highly on empathy also tended to give more feedback instances ($r = 0.60, p = 0.024$) and give feedback on more time steps ($r = 0.63, p = 0.016$); trainers in the uncertainty–informative condition who scored highly on empathy trained agents that performed worse ($r = -0.73, p = 0.004$). However, there are no significant correlations found between a trainer’s self-reported competitiveness and that trainer’s training behavior or agent performance, which gives further evidence that at least for the performance metric, the differences in feedback quality between conditions are influenced more by the condition itself.

5.2 Results and discussion

Below we present and analyze the results of our human-user study. All reported p values were computed via a two-sample t test. Since each hypothesis specifies a one-directional prediction, a one-tailed test was used. Additionally, an F-test was used to assess whether the dependent variables for each condition have equal variances, since the two-sample t test is calculated differently if the difference in variance for the two samples is significant (i.e., $p < 0.05$).

5.2.1 Influence of agent’s informative behavior on engagement

a. Training time

We hypothesized that both conditions would increase the time spent on training compared to the control condition. We found that both informative behaviors did engage the trainers for longer, in terms of both absolute time and number of time steps. In terms of mean absolute time spent on training, trainers in the performance–informative condition spent 2.2 times more time on training ($t(17)=1.74, p < 0.02$), as did trainers in the uncertainty–informative condition, who spent 1.3 times longer ($t(21)=1.72, p = 0.05$), as shown in Fig. 4a. In terms of mean number of time steps trained by the trainers—a metric unaffected by the player’s chosen falling speed—for the performance–informative and uncertainty–informative conditions, the number of time steps spent training the agent were 5.7 times ($t(16)=1.75, p <0.01$) and 2.7 times ($t(19)=1.73, p =0.076$) more than for the control condition, as shown in Fig. 4b.

b. Amount of feedback

To measure the amount of feedback given, we counted the number of times a feedback button was pressed, comparing each experimental condition to the control. As shown in Fig. 5a, in the performance–informative condition, 1.7 times more feedback is given ($t(17)=1.74, p = 0.03$), whereas in the uncertainty–informative condition, 3.9 times more feedback than in the control condition ($t(19)=1.73, p < 0.02$). In addition, the number of time steps with feedback (irrespective of the number of feedback instances at each time step) for both informative conditions was significantly more than the control condition (performance–informative: $t(19)=1.73,$ $p <0.02$; uncertainty–informative: $t(19)=1.73, p < 0.03$), as shown in Fig. 5b.

Fig. 4

Mean absolute time trained (a), number of time steps trained (b). Control condition: blue (left), performance–informative condition: red (middle), uncertainty–informative condition: green (right). Note that error bars represent standard error of the mean (Color figure online)

Fig. 5

Number of feedback instances during training (a), number of time steps with feedback (b). Control condition: blue (left), performance–informative condition: red (middle), uncertainty–informative condition: green (right). Note that error bars represent standard error of the mean (Color figure online)

c. Feedback frequency

Figure 6 shows how feedback was distributed per 200 time steps over the first 6000 time steps. The longest training time is about 20,000 time steps; for the sake of brevity, we show only the first 6000 time steps. After 6000 time steps, only the subjects in the uncertainty–informative condition still continued to give more feedback. Trainers in both informative conditions gave feedback for much longer than those in the control condition. Most notably, trainers in the uncertainty–informative condition gave a strikingly large amount of feedback, even during later training process, with a much slower fall-off than the other conditions.

Fig. 6

Number of feedback instances per 200 time steps over the first 6000 time steps. Control condition: blue (left), performance–informative condition: red (middle), uncertainty–informative condition: green (right) (Color figure online)

Fig. 7

Offline performance per cumulative 200 time steps for the three conditions. Control condition: blue (middle), performance–informative condition: red (top), uncertainty–informative condition: green (bottom) (Color figure online)

Thus, our results clearly suggest that informative behavior can significantly increase the amount of feedback given and time spent training, suggesting better involvement.

5.2.2 Influence of agent’s informative behavior on performance

We also hypothesized that the trainers’ increased involvement would lead to improved performance by the agents. To test this, we first examined how the agents’ performances varied over time. Because the duration of a game varies significantly depending on the quality of the trained policy, we saved each agent’s policy every 200 time steps. We used the agent’s performance over a window of 200 time steps to get a sense of the temporal evolution of the agents’ learning progress at a reasonable resolution. Then, we tested the saved policy of each agent offline for 20 games. Figure 7 shows the resulting mean performance averaged across games, and then agents, for the first 2800 time steps, as well as the final offline performance, after all training was complete. If an agent’s training stopped before others in the same condition, then in later policy testings its final average offline performance was used to compute the average for that condition.

Compared with the control condition (average final off-line performance is 926.5 lines), agents in the performance–informative condition learned best (1241.8 lines, $t(30)=1.70, p=0.27$), while those in the uncertainty–informative condition learned worst (645.1 lines, $t(33)=1.69, p=0.24$). While the differences are not significant (perhaps due to insufficient samples), Fig. 7 shows that the uncertainty–informative condition performs consistently worse than the other conditions while the performance–informative condition performs consistently better.

Our results show that the agent’s informative behaviors have great effect on agent’s performance. The performance–informative behavior allows the trainers to train the agent better, while the uncertainty–informative behavior worsens the agent’s learning.

5.2.3 Influence of agent’s informative behavior on distribution of feedback given by trainer

The main surprise in the results presented in Sects. 5.2.1 and 5.2.2 is that, while the uncertainty–informative condition elicited the most feedback, the resulting agents performed substantially worse. This result is especially puzzling given that the performance–informative condition also elicited more feedback than the control condition but generated agents with better performance. The differences in performance between the performance–informative and uncertainty–informative conditions did not always match our hypotheses. Note that the learning algorithm had no access to uncertainty or performance metrics, and the interfaces differ only in their feedback to the trainer. Therefore, differences in agent performance result only from the feedback given by the agent.

Fig. 8

Distribution of states along the first (horizontal axis) and second (vertical axis) principal components (PC), with (colored according to corresponding conditions) and without (colored black) feedback. The three rows from top to bottom show the control (C), performance–informative (PI) and uncertainty–informative (UI) conditions respectively. The columns show three sections of the training process: time steps 1–600, 601–1200, and 1201–2800, from left to right, respectively. Note that these graphs were generated by first plotting the states without feedback and then overlaying the colored states where feedback was received (Color figure online)

We hypothesized that this discrepancy could be because the trainers in the performance–informative condition were influenced by the agent’s feedback that was better aligned with the goal of the game. In other words, because they were shown the agent’s performance, they were more motivated to train the agent to maximize performance. In contrast, we suspect that trainers in the uncertainty–informative condition were distracted from this goal by the agent’s informative behavior. That is, while they trained for longer and gave more feedback than trainers in the control condition, they were more focused on giving feedback that would reduce the uncertainty bar, rather than giving feedback that would maximize performance.

In an effort to test this hypothesis, we analyzed how the state of the game itself might have influenced the feedback given using principal component analysis (PCA) with the state features of all the states visited by all of the agents in every condition. Then, within the feature space created by the first two principal components, we examined how the distribution over states in which feedback was given by trainers differed across time and across the three conditions.

a. Distribution of state space along the whole training process

As shown in Fig. 8, we divided the training process in each condition into 4 sections chronologically: time steps 1–600, 601–1200, 1201–2800, and 2801 and higher. For brevity, we do not show plots for time steps 2801 and greater; at this point, all trainers in the control condition had stopped; plots for the other two conditions are qualitatively similar to those for time steps 1201–2800. From top to bottom, the three rows show the control, performance- and uncertainty–informative conditions. We plotted the projection of the visited states onto the first two principal components of the data. Since there were many more states without feedback (shown in black), for visualization, they were overlaid with those that received feedback, which were colored according to their corresponding condition: control in blue, performance–informative in red and uncertainty–informative in green. The proportion of variance explained by the first and second components are 45.01 and 9.49 %, respectively.

Figure 8 shows that, in the initial stage (time steps 1–600), informative behaviors seem to have little influence on the distribution of states with feedback. However, in all sections thereafter, the performance–informative behavior appears to keep the trainer focused on giving feedback in states in the center of the second principal component (around 0), while the uncertainty–informative behavior receives feedback in a much wider range of states along the second principal component. Note that in the uncertainty–informative condition, not all trainers exhibited the broader feedback behavior; trainers that gave more focused feedback (like the performance–informative users) had the better performing agents. On closer inspection of the distribution of states with and without feedback, we observed that, in all cases, the distributions were unimodal.

Fig. 9

Example stacks of the Tetris board along the first and second principal components in the section of 1201 to 2800 time steps in the uncertainty–informative condition. These boards illustrate that the first principal component corresponds roughly with the height of the stack, and the second to whether the stack is ‘u’ or ‘n’ shaped

Inspecting the coefficients of the principal eigenvectors, we observed that the state features corresponding to the height of the stack and the number of holes contributed most to the first principal component, and so the narrow point at the far right of the space is representative of the start of each game when the stack height is 0. For the second principal component, negative weights were found for columns 1, 2, 9, and 10, of the Tetris board, while the features representing the column heights 4, 5, 6, and 7 were positively correlated. This is seen more clearly in Fig. 9, where along the first principal component from right to left, the overall height of the Tetris board is gradually increasing while keeping roughly flat. For the second principal component, the contour of the Tetris board is changing from n-shaped to u-shaped from the top to the bottom. Combining with Fig. 8, we observe that, in the uncertainty–informative condition, a lot of feedback (including positive and negative feedback) was given to n-shaped states, especially in time steps 1201–2800.

b. Influence of informative behavior starts at the early training stage

After further checking the data, we suspected that trainers in the uncertainty–informative condition already started training the agent differently in the early training stage (during the first section in Fig. 8). This is also the time when all performance improvement takes place, after which performance stagnates, as shown in Fig. 7. Therefore, zooming in on the first section in Fig. 8, within the sub-space created by the first two principal components, we examined how the distribution over states in cases with and without feedback differed across time and across the three conditions.

As shown in Fig. 10, we divided the first 600 time steps into 6 subsections chronologically in each condition: time steps 1–100, 101–200, 201–300, 301–400, 401–500, and 501–600. From top to bottom, the three rows are control, performance–informative and uncertainty–informative conditions respectively. Similar to Fig. 8, the projection of the visited states were plotted onto the first two principal components. The states without feedback were colored black and plotted first; then the states with feedback were plotted and colored according to the condition: control condition (blue), performance–informative condition (red) and uncertainty–informative condition (green).

Fig. 10

More detailed visualisation of the data from the first column of Fig. 8 at a finer temporal resolution. Distribution of states along the first (horizontal axis) and second (vertical axis) principal components (PC), with (colored according to corresponding conditions) and without (colored black) feedback for the first 600 time steps during the training process. The three rows from top to bottom show the control (C), performance–informative (PI) and uncertainty–informative (UI) conditions respectively. The columns show time steps 1–100, 101–200, 201–300, 301–400, 401–500, and 501–600, from left to right, respectively (Color figure online)

Figure 10 shows that, for the first three subsections (time steps 1–300), the distributions of states with feedback are very similar in the three conditions. After that, however, the distributions of states with feedback in the uncertainty–informative condition is quite different from the other conditions, especially the control condition. Thus, while Figs. 8 and 9 show trainers in the uncertainty–informative condition providing feedback in a much larger range of states after the performance has stagnated, Fig. 10 shows that this kind of trainer behavior in the uncertainty–informative condition starts much sooner in the agent’s learning trajectory and interestingly, in the early stages when the agent’s performance is still improving (Fig. 7). This observation further highlights that the condition itself was already having a significant effect on the trainer’s behavior even in the early stages of learning where the the agent’s policy had yet to mature and hence the types of states visited and the corresponding actions taken would have been very similar across all three conditions.

5.2.4 Effect of uncertainty–informative behavior

The analysis in Sect. 5.2.3 reveals qualitative differences between how trainers trained the agent in the performance–informative (PI) and the uncertainty–informative (UI) conditions. While we know from Sects. 5.2.2 and 5.2.3 that UI leads to worse performance and UI trainers gave feedback to a wider range of states, we wondered why UI trainers behave in this way and how it affected the agent’s learning.

We hypothesized that the trainer might be distracted from the main task by the agent’s uncertainty–informative behavior and therefore sometimes give feedback just to reduce the agent’s uncertainty, regardless of whether she thinks that feedback will improve the agent’s performance. A simple model of such behavior is as follows. When the trainer evaluates the agent’s behavior as positive or negative, she gives the appropriate positive or negative feedback. However, when she evaluates the agent’s behavior as neutral, then with probability $\varepsilon$, she gives random feedback (to reduce uncertainty) and with probability $1-\varepsilon$, she gives no feedback.

To test this hypothesis, we simulated the behavior of a trainer acting according to this model. Since the trainer’s behavior in the control condition is not affected by the agent’s informative behavior, we started with the training data collected in this condition, and then with $\varepsilon$ probability we added positive or negative feedback randomly to states without feedback. We tested several values of $\varepsilon$ and, for each $\varepsilon$ and each trainer in the control condition dataset, we repeated this stochastic process ten times. TAMER was then used to learn a new policy for each altered trainer (ten for each original trainer). Finally to see how well our simulated user fits with the behaviour of someone in the uncertainty–informative condition, we measured the uncertainty of the agent’s actions (as it was in the UI condition; see Eq. 1) and the average offline performance of the learned policies.

Figures 11 and 12 show the average uncertainty and final offline performance, respectively, of the policies learned from these simulated trainers for different $\varepsilon$’s and compares it to the original control and UI conditions. In general, as $\varepsilon$ increases, the agent’s average uncertainty and final offline performance decrease. When $\varepsilon$ is 0.25, the final offline performance and overall average uncertainty are very close to the original UI condition.

Fig. 11

Overall average uncertainty across subjects for different $\varepsilon$ values and original Control and UI conditions. Note that error bars stand for standard error of the mean

Fig. 12

Final offline learning performance for different $\varepsilon$ values and original control and UI conditions. Note that error bars stand for standard error of the mean

Fig. 13

Average uncertainty per 200 time steps across subjects during the training process for different $\varepsilon$ values and original Control and UI conditions. Note that from left to right, each bar represents the corresponding value for the original Control condition, $\varepsilon = 0.1$, $\varepsilon = 0.2$, $\varepsilon = 0.25$, $\varepsilon = 0.3$, $\varepsilon = 0.4$, $\varepsilon = 0.5$ and the original UI condition, respectively (Color figure online)

However, looking at the uncertainty across time, as shown in Fig. 13, reveals a more nuanced picture. While $\varepsilon = 0.25$ best matches the average uncertainty of UI in the first 400 time steps, it substantially overestimates it thereafter, with $\varepsilon = 0.5$ being the best match. However, $\varepsilon = 0.5$ substantially underestimates uncertainty in the first 400 time steps and, as shown in Figs. 11 and 12, is a poor predictor of overall uncertainty and final offline performance.

Since the first 400 time steps roughly correspond to the period in which the agent’s performance was improving (see Fig. 7), these results suggest that the UI trainers may have become even more distracted after learning plateaued. In other words, once performance plateaued, the trainers were even more likely to give feedback for the sake of reducing uncertainty, rather than in an effort to further improve performance. Since $\varepsilon = 0.25$ overestimates uncertainty only after performance has plateaued, it can nonetheless accurately model final offline performance.

Overall, these results shed some light on the performance discrepancy between the control and UI conditions. In particular, they show that UI trainers’ behavior is consistent with a model in which the trainer sometimes gives random feedback instead of neutral feedback in an effort to reduce the agent’s uncertainty irrespective of its effect on performance. The behavior of the UI trainers is most consistent with a model in which neutral feedback is replaced with random feedback 25 % of the time.

6 Discussion

Our user study with two informative interfaces shows that the agent’s informative feedback can significantly affect the trainer’s training, in terms of the duration of training, the number of feedback instances and the frequency of feedback. Moreover, the performance–informative feedback led to substantially better agent performance, whereas the uncertainty–informative feedback led to worse agent performance. In addition, our PCA analysis shows that trainers in the uncertainty–informative condition provide feedback in a much wider range of states than those in the performance–informative condition, which is caused by the agent’s informative feedback—the only difference between these two conditions.

Furthermore, the results of simulating UI trainers’ behaviors suggest that in the initial training stage, such trainers’ behavior is consistent with that of trainers who are distracted by the agent’s uncertainty–informative behavior and thus aim to reduce uncertainty by sometimes (with probability 0.25) giving close to random feedback when they evaluate the agent’s behavior to be neutral. After the agent’s learning performance plateaued, this probability increases. These results also point out that encouraging trainers to give more feedback only helps agent learning if they know that their feedback has a positive effect on the agent’s performance.

Finally, our results align with what could be expected from the maxim, “you get what you measure”; i.e., people often try to optimize the metrics you show them while de-emphasizing others. In our case, measuring (i.e., informing users about) performance increased performance, and measuring uncertainty reduced uncertainty, through increased feedback, but reduced performance, as shown in Figs. 7, 11 and 13. The notion that “you get what you measure” has been discussed extensively in organizational literature (e.g., metrics for software development teams [7]), but we believe our work is the first to find evidence that suggests the concept applies to the design of interactive interfaces for training agents. Consequently, understanding the influence of metric-sharing on human behavior could be a powerful guiding principle in the design of interactive interfaces for training agents, though more investigation is needed to judge its general applicability.

7 Conclusion

This article studies the proposed bi-directional approach between the agent and the trainer with two novel informative interfaces, and provides an analysis of the trainer’s training behavior and agent performance. Our empirical user study showed that the agent’s informative feedback can significantly increase the trainer’s engagement. The agent’s performance, however, increases only in response to the addition of performance-oriented information, not by sharing uncertainty levels. Further investigation of our experimental data using PCA suggested that trainers trained the agents differently in the performance–informative and uncertainty–informative condition. Subsequent analysis suggests that trainers in the uncertainty–informative condition could be distracted by the agent’s shared uncertainty levels and thus aim to reduce uncertainty by sometimes giving close to random feedback, which may explain the performance discrepancy between the uncertainty–informative and control conditions. Our results also align with the notion “you get what you measure”, providing a powerful guiding principle for human–agent interface design in general.

Our work contributes to the design of human–agent systems that facilitates the agent to learn more efficiently and be easier to teach. To our knowledge, we are the first to provide the analysis of how manipulating the information the agent shares with the trainer can affect the trainer’s behavior. We demonstrate that an understanding of how to design the interaction between the agent and the trainer allows for the design of the algorithms that support how people can teach effectively and be actively engaged in the process at the same time. Our results also point out that encouraging trainers to give more feedback only helps if they do not feel forced to give feedback even to states where they do not have any strong positive or negative feedback to give. Our approach can also apply to other interactive learning algorithms, e.g., learning from demonstration.