Abstract
We investigate the Lax equation in the context of infinite-dimensional Lie algebras. Explicit solutions are discussed in the sequentially complete asymptotic estimate context, and an integral expansion (sums of iterated Riemann integrals over nested commutators with correction term) is derived for the situation that the Lie algebra is inherited by an infinite-dimensional Lie group in Milnor’s sense. In the context of Banach Lie groups (and Lie groups with suitable regularity properties), we generalize the Baker–Campbell–Dynkin–Hausdorff formula to the product integral (with additional nilpotency assumption in the non-Banach case). We combine this formula with the results obtained for the Lax equation to derive an explicit representation of the product integral in terms of the exponential map. An important ingredient in the non-Banach case is an integral transformation that we introduce. This transformation maps continuous Lie algebra-valued curves to smooth ones and leaves the product integral invariant. This transformation is also used to prove a regularity statement in the asymptotic estimate context.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
We investigate regularity properties of Lie groups in Milnor’s sense [3, 19] and extend the Baker–Campbell–Dynkin–Hausdorff formula for the exponential map to the product integral. The product integral generalizes the Riemann integral (for curves in Hausdorff locally convex vector spaces) to Lie groups, so that Lie algebra-valued curves are “integrated” to Lie group elements. The results are based on a deeper analysis of the Lax equation in the context of asymptotic estimate and sequentially complete Lie algebras. A further ingredient is an integral transformation that we introduce. This transformation maps continuous Lie algebra-valued curves to smooth ones and leaves the product integral invariant.
Explicitly, let G be a Lie group in Milnor’s senseFootnote 1 [3, 19] that is modeled over the Hausdorff locally convex vector space E. We denote the Lie algebra of G by \((\mathfrak {g},\varvec{[}\cdot , \cdot \varvec{]})\), the adjoint action by \(\text {Ad} :G\times \mathfrak {g}\rightarrow \mathfrak {g}\), and set \(\text {Ad} _g:=\text {Ad} (g,\cdot )\) for each \(g\in G\). The left and the right translation by some \(g\in G\) is denoted by \(\text {L} _g\) and \(\text {R} _g\), respectively. For \(a<b\), we set
The evolution map is the inverse of the right logarithmic derivativeFootnote 2 (\(a<b\))

and is denoted by

The product integral is defined by

and for \(k\in \mathbb {N}\cup \{\text {lip} ,\infty \}\), we set

We equip \(C^k([0,1],\mathfrak {g})\) for \(k\in \mathbb {N}\cup \{\text {lip} ,\infty \}\) with the \(C^k\)-topology, as well as \(\mathfrak {D}\cap C^k([0,1],\mathfrak {g})\) with the corresponding subspace topologyFootnote 3:
-
We say that G is \(C^k\)-semiregular if \(C^k([0,1],\mathfrak {g})\subseteq \mathfrak {D}\) holds.
-
We say that G is weakly \(C^k\)-regular if G is \(C^k\)-semiregular and \({\text {evol} }_k\) is differentiable.
-
We say that G is \(C^k\)-regular if G is \(C^k\)-semiregular and \({\text {evol} }_k\) is smooth.
We briefly want to report on the continuity problem (under which circumstances is \({\text {evol} }_k\) continuous w.r.t. the \(C^k\)-topology):
-
In [8], this problem had been solved for the case \(k=0\). Specifically, it was shown that \(C^0\)-continuity of \({\text {evol} }_0\) on its domain (also if \(C^0\)-semiregularity is not assumed) is equivalent to local \(\mu \)-convexity of G [4, 8]. Roughly speaking, local \(\mu \)-convexity is a generalized triangle inequality for the Lie group multiplication.
-
In [9], the continuity problem was completely solved in the asymptotic estimate context that we also consider in this paper (simply put, Theorem 1 in [9] states that all continuity notions are equivalent in the asymptotic estimate context).
A Lie group is said to be asymptotic estimate if its Lie algebra is asymptotic estimate. More generally, we have the following definitions for an infinite-dimensional Lie algebra \((\mathfrak {q},\varvec{[}\cdot , \cdot \varvec{]})\)Footnote 4
-
A subset \(\text {M} \subseteq \mathfrak {q}\) is said to be an \(\text {AE} \)-set if for each \(\textsf {v} \in \textsf {Sem}(\mathfrak {q})\), there exists \(\textsf {v} \le \textsf {w} \in \textsf {Sem}(\textsf {q} )\) with
$$\begin{aligned} \textsf {v} (\varvec{[}X_1,\varvec{[}X_2,\varvec{[}\dots ,\varvec{[}X_n,Y\varvec{]}{\dots }\varvec{]}\varvec{]}])\le \textsf {w} (X_1)\cdot {\dots }\cdot \textsf {w} (X_n)\cdot \textsf {w} (Y) \end{aligned}$$for all \(X_1,\dots ,X_n,Y\in \text {M} \), and \(n\ge 1\).
-
The Lie algebra \((\mathfrak {q},\varvec{[}\cdot , \cdot \varvec{]})\) is said to be asymptotic estimate if \(\mathfrak {q}\) is an \(\text {AE} \)-set.
For instance, abelian Lie groups are asymptotic estimate, and the same is true for Lie groups with nilpotent Lie algebras. Also Banach Lie groups are asymptotic estimate, because their Lie bracket is submultiplicative. Notably, the class of asymptotic estimate Lie algebras has good permanence properties, as it is closed under passage to subalgebras, Hausdorff quotient Lie algebras, as well as closed under arbitrary Cartesian products (hence, e.g., under projective limits).
As already indicated above, Theorem 1 in [9] states that if G is asymptotic estimate, then G is locally \(\mu \)-convex if and only if \({\text {evol} }_k\) is \(C^k\)-continuous for some (and then each) \(k\in \mathbb {N}\cup \{\text {lip} ,\infty \}\). Based on the semiregularity results obtained in [8], this statement was used in [9] to prove that \(C^\infty \)-regularity implies \(C^k\)-regularity for each \(k\in \mathbb {N}\cup \{\text {lip} ,\infty \}\), whereby for \(k=0\) additional completeness assumptions (on the Lie group not the Lie algebra) are required. Complementary to that, we prove the following theorem in the weakly regular context (cf. Theorem 2):
Theorem I
Assume that \((\mathfrak {g},\varvec{[}\cdot , \cdot \varvec{]})\) is asymptotic estimate and sequentially complete. If G is weakly \(C^\infty \)-regular, then G is weakly \(C^k\)-regular for each \(k\in \mathbb {N}\cup \{\text {lip} ,\infty \}\).
This theorem is obtained by a comprehensive analysis of the Lax equation in the sequentially complete asymptotic estimate context, as well as by application of an integral transformation that we introduce. As a by-product of these investigations, we obtain a generalization of the Baker–Campbell–Dynkin–Hausdorff formula (BCDH formula) in the Banach case (Proposition 4) as well as in the nilpotent weakly \(C^k\)-regular case (Theorem 1). In particular, this yields an explicit formula for the product integral in terms of the exponential map that involves iterated Riemann integrals over nested commutators (see Point (a)). More explicitly:
Given an infinite-dimensional Lie algebra \((\mathfrak {q},\varvec{[}\cdot , \cdot \varvec{]})\) (not necessarily the Lie algebra of a Lie group), we denote its completion by \(\widehat{\mathfrak {q}}\) and set
for each \(Z\in \mathfrak {q}\). For \(\psi \in C^0([a,b],\mathfrak {q})\) and \(X\in \mathfrak {q}\), we define the maps (\(\ell \ge 1\))
and set
We have the following results:
-
(a)
Let G be a Banach Lie group such that the norm on \(\mathfrak {g}\) fulfills \(\Vert [X,Y]\Vert \le \Vert X\Vert \cdot \Vert Y\Vert \) for all \(X,Y\in \mathfrak {g}\). Then, there exists \(\mathfrak {r}>0\) such that (Corollary 9 in Sect. 4.1)
 (2)
(2)holds for all \(a<b\) and \(\phi \in C^0([a,b],\mathfrak {g})\) with \(\int _a^b \Vert \phi (s)\Vert \, \text {d} s< \mathfrak {r}\).
The same formula is proven in the nilpotent weakly \(C^k\)-regular context (see Corollary 10 in Sect. 4.2.1), whereby the occurring sums are finite. For instance, if G is abelian and weakly \(C^k\)-regular for some \(k\in \mathbb {N}\cup \{\text {lip} ,\infty \}\), then (2) specializes to the well-known formula [18]

Note that (2) provides an explicit formula for holonomies in principal bundles, as such holonomies are locally given by product integrals of curves that are pairings of (smooth) connections with derivatives of (smooth) curves in the base manifold of the principal bundle.
-
(b)
The maps (1) are the elementary building blocks of solutions to the Lax equation
$$\begin{aligned} {\dot{\alpha }}=\varvec{[}\psi , \alpha \varvec{]}\qquad \quad \text {with initial condition}\qquad \quad \alpha (a)=X, \end{aligned}$$(3)where \(X\in \mathfrak {q}\), \(\psi \in C^0([a,b],\mathfrak {q})\) (\(a<b\)) are fixed parameters, and \(\alpha \in C^1([a,b],\mathfrak {q})\) is the solution.
-
Assume that \((\mathfrak {q},\varvec{[}\cdot , \cdot \varvec{]})=(\mathfrak {g},\varvec{[}\cdot , \cdot \varvec{]})\) is the Lie algebra of a Lie group G:
-
For \(\psi \in \mathfrak {D}_{[a,b]}\), the unique solution to (3) is given by
 (cf. Corollary 7).
(cf. Corollary 7). -
For \(\psi \in \mathfrak {D}_{[a,b]}\) and \(\ell \ge 1\), define

A straightforward induction shows (cf. Lemma 13)

In particular, if \(\text {M} \) is an \(\text {AE} \)-set with \(\text {im} [\psi ]\subseteq \text {M} \), then we have (cf. Corollary 8)
 (4)
(4)Notably, for \(\psi :[0,1]\ni t\mapsto Y\in \mathfrak {g}\) constant, (4) reproduces the well-known formula

-
-
Assume that \((\mathfrak {q},\varvec{[}\cdot , \cdot \varvec{]})\) is sequentially complete and asymptotic estimate:
Mimicking (4), for \(\psi \in C^0([a,b],\mathfrak {q})\) and \(X\in \mathfrak {q}\), we define
$$\begin{aligned} \textstyle {\textbf {Ad}} _\psi [X]:[a,b]\rightarrow \mathfrak {q},\qquad t\mapsto \sum _{\ell =0}^\infty \varvec{\lambda }_{\ell ,\psi }[X](t). \end{aligned}$$(5)-
It is straightforward to see that \(\alpha :={\textbf {Ad}} _\psi [X]\) solves the Lax equation (3)—and is of class \(C^{k+1}\) if \(\psi \) is of class \(C^k\) for \(k\in \mathbb {N}\cup \{\infty \}\).
-
It is ad hoc not clear that this solution is unique. To prove uniqueness, one basically has to show that for each \(t\in [a,b]\) one has
$$\begin{aligned} \textsf {Aut} (\mathfrak {q})\ni {\textbf {Ad}} _\psi [t]:\mathfrak {q}\rightarrow \mathfrak {q},\qquad X\mapsto {\textbf {Ad}} _\psi [X](t). \end{aligned}$$Indeed, it is not hard to see that \({\textbf {Ad}} _\psi [t]\) admits a left inverse; but, to prove the existence of a right inverse some effort is necessary.
-
In this paper, we use the solutions (5) to prove Theorem I. We combine them with an integral transformation that we introduce, and that is also used to prove Formula (2) in the nilpotent weakly \(C^k\)-regular situation. It naturally arises in the context of semiregular Lie groups:
-
Let G be \(C^k\)-semiregular for \(k\in \mathbb {N}\cup \{\text {lip} , \infty \}\). Then, the integral transformation
 (6)
(6)is defined for all \(a<b\) (cf. Proposition 1) and has the invariance property

-
Let \((\mathfrak {q},\varvec{[}\cdot , \cdot \varvec{]})\) be sequentially complete and asymptotic estimate. Motivated by (6), we consider the integral transformation (defined by Lemma 24)
$$\begin{aligned} \textstyle \mathfrak {T}:C^0([a,b],\mathfrak {q}) \rightarrow&~ C^\infty ([0,1],\mathfrak {q})\nonumber \\ \phi \mapsto&~\textstyle \big [ [0,1]\ni t \mapsto \int _a^b {\textbf {Ad}} _{t\cdot \phi |_{[s,b]}}[b](\phi (s)) \,\text {d} s\,\big ], \end{aligned}$$(7)for which we have (Corollary 19)
 (8)
(8)If G is weakly \(C^\infty \)-semiregular and \(\phi \in C^0([0,1],\mathfrak {q})\), then

is of class \(C^1\), whereby (8) implies
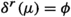 which establishes Theorem I.
which establishes Theorem I.
This paper is organized as follows. In Sect. 2, we fix the notations and provide some basic facts and definitions concerning locally convex vector spaces, Lie groups, Lie algebras, and mappings. We furthermore discuss some elementary properties of power series that we need in the main text. Section 3 contains some preliminary results. We discuss the integral transformation (6), and provide an integral expansion for the adjoint action. We furthermore prove a differentiation result for the product integral in the weakly regular context. In Sect. 4, we generalize the Baker–Campbell–Dynkin–Hausdorff formula to the product integral and give some applications to it. In particular, we prove formula (2). In Sect. 5, we discuss the Lax equation for asymptotic estimate and sequentially complete Lie algebras. We also investigate the elementary properties of the integral transformation (7) that we finally use to prove Theorem I.
2 Preliminaries
In this section, we fix the notations and provide definitions and elementary facts concerning Lie groups, Lie algebras, and locally convex vector spaces that we shall need in the main text.
2.1 Conventions
Given sets X, Y, the set of all mappings \(X\rightarrow Y\) is denoted by \(\textsf {Maps} (X,Y)\equiv Y^X\). Let Z be a topological space, and \(S\subseteq Z\) a subset:
-
We denote the closure of S in Z by \(\textsf {clos} _{Z}(S)\), or simply by \(\textsf {clos} (S)\) if it is clear from the context which topological space Z is meant.
-
We denote the interior of S in Z by \(\textsf {int} _{Z}(S)\), or simply by \(\textsf {int} (S)\) if it is clear from the context which topological space Z is meant.
The class of Hausdorff locally convex vector spaces is denoted by \(\textsf {hlcVect}\). Given \(F\in \textsf {hlcVect}\), the system of continuous seminorms on F is denoted by \(\textsf {Sem}(F)\). We define
for each \(\textsf {q} \in \textsf {Sem}(F)\) and \(\varepsilon >0\). The completion of F is denoted by \(\widehat{F}\in \textsf {hlcVect}\). For each \(\textsf {q} \in \textsf {Sem}(F)\), we let \(\widehat{\textsf {q} }:\widehat{F}\rightarrow [0,\infty )\) denote the continuous extension of \(\textsf {q} \) to \(\widehat{F}\). Given \(F_1,\dots ,F_n\in \textsf {hlcVect}\), we have \(F_1\times {\dots }\times F_n\in \textsf {hlcVect}\) via the Tychonoff topology generated by the seminorms
with \(\textsf {q} _k\in \textsf {Sem}(F_k)\) for \(k=1,\dots ,n\). If \(\Phi :F_1\times {\dots }\times F_n\rightarrow F\) is a continuous n-multilinear map, then \(\widehat{\Phi }:\widehat{F}_1\times {\dots }\times \widehat{F}_n\rightarrow \widehat{F}\) denotes its continuous n-multilinear extension.
In this paper, manifolds and Lie groups are always understood to be in the sense of [3], i.e., smooth, Hausdorff, and modeled over a Hausdorff locally convex vector space.Footnote 5 If \(f:M\rightarrow N\) is a \(C^1\)-map between the manifolds M and N, then \(\text {d} f:TM \rightarrow TN\) denotes the corresponding tangent map between their tangent manifolds, and we write \(\text {d} _xf\equiv \text {d} f(x,\cdot ):T_xM\rightarrow T_{f(x)}N\) for each \(x\in M\). An interval is a non-empty, non-singleton connected subset \(D\subseteq \mathbb {R}\). A curve is a continuous map \(\gamma :D\rightarrow M\) for an interval and a manifold M. If \(D\equiv I\) is open, then \(\gamma \) is said to be of class \(C^k\) for \(k\in \mathbb {N}\cup \{\infty \}\) if it is of class \(C^k\) when considered as a map between the manifolds I and M. If D is an arbitrary interval, then \(\gamma \) is said to be of class \(C^k\) for \(k\in \mathbb {N}\cup \{\infty \}\) (we write \(\gamma \in C^k(D,M)\)) if \(\gamma =\gamma '|_D\) holds for a \(C^k\)-curve \(\gamma ':I\rightarrow M\) that is defined on an open interval I containing D. If \(\gamma :D\rightarrow M\) is of class \(C^1\), then we denote the corresponding tangent vector at \(\gamma (t)\in M\) by \({\dot{\gamma }}(t)\in T_{\gamma (t)}M\). The above conventions also hold if \(M\equiv F\in \textsf {hlcVect}\) is a Hausdorff locally convex vector space.
Throughout this paper, G denotes an infinite-dimensional Lie group in the sense of [3] that is modeled over \(E\in \textsf {hlcVect}\). We fix a chart \(\Xi :G\supseteq \mathcal {U}\rightarrow \mathcal {V}\subseteq E\), with \(\mathcal {V}\) convex, \(e\in \mathcal {U}\), and \(\Xi (e)=0\). We denote the Lie algebra of G by \((\mathfrak {g}, \varvec{[} \cdot , \cdot \varvec{]})\), and setFootnote 6
We let \(\textsf {m} :G\times G\rightarrow G\) denote the Lie group multiplication, \(\text {R} _g:=\textsf {m} (\cdot , g)\) the right translation by \(g\in G\), \(\textsf {inv} :G\ni g\mapsto g^{-1}\in G\) the inversion, and \(\text {Ad} :G\times \mathfrak {g}\rightarrow \mathfrak {g}\) the adjoint action. We have
for each \(g\in G\) and \(X\in \mathfrak {g}\), as well as
We recall the Jacobi identity (cf. also Example 5)
as well as the product rule
2.2 Locally convex vector spaces
In this section, we collect some elementary facts and definitions concerning locally convex vector spaces that we shall need in the main text.
2.2.1 Sets of curves
Let \(F\in \textsf {hlcVect}\) be given. For each \(X\in F\), we let \(\mathcal {C}_X:\mathbb {R}\ni t\mapsto X \in F\) denote the constant curve X. Let \(a<b\) be given. We set \(C^\text {c} ([a,b],F):=\{\mathcal {C}_X|_{[a,b]}\,|\, X\in F\}\); and let \(C^\text {lip} ([a,b],F)\) denote the set of all Lipschitz curves on [a, b], i.e., all curves \(\gamma :[a,b]\rightarrow F\) with
We define \(\text {c} +1:=\infty \), \(\infty +1:=\infty \), \(\text {lip} +1:=1\); as well as

for \(\textsf {q} \in \textsf {Sem}(F)\), \(k\in \mathbb {N}\cup \{\infty ,\text {c} \}\), \(0\le \text {s} \preceq k\). Here, the notation \(s\preceq k\) means
-
\(\text {s} = \text {lip} \) for \(k= \text {lip} \),
-
\(\mathbb {N}\ni \text {s} \le k\) for \(k\in \mathbb {N}\),
-
\(\text {s} \in \mathbb {N}\) for \(k=\infty \),
-
\(\text {s} =0\) for \(k= \text {c} \).
Given \(k\in \mathbb {N}\cup \{\text {lip} ,\infty ,\text {c} \}\), the \(C^k\)-topology on \(C^k([a,b],F)\) is the Hausdorff locally convex topology that is generated by the seminorms \(\textsf {q} _\infty ^\text {s} \) for \(\textsf {q} \in \textsf {Sem}(F)\) and \(0\le \text {s} \preceq k\).
By an element in \(\text {CP} ^0([a,b],F)\) (piecewise continuous curves), we understand a decomposition \(a= t_0<{\dots }<t_n=b\) (for \(n\ge 1\)) together with a collection \(\gamma \equiv \{\gamma [p]\}_{0\le p\le n-1}\) of curves \(\gamma [p]\in C^0([t_p,t_{p+1}],F)\) for \(0\le p\le n-1\). Linear combinations as well as restrictions to compact intervals of elements in \(\text {CP} ^0([a,b],F)\) are defined in the obvious way. We equip \(\text {CP} ^0([a,b],F)\) with the \(C^0\)-topology, i.e., the Hausdorff locally convex topology that is generated by the seminorms
for \(\textsf {q} \in \textsf {Sem}(F)\), and \(\gamma \equiv \{\gamma [p]\}_{0\le p\le n-1}\) as above.
2.2.2 Mackey convergence
Let \(F\in \textsf {hlcVect}\). A subsystem \(\mathfrak {H}\subseteq \textsf {Sem}(F)\) is said to be a fundamental system if \(\{\text {B} _{\textsf {h} ,\,\varepsilon }(0)\}_{\textsf {h} \in \mathfrak {H},\varepsilon >0}\) is a local base of zero in F. We recall the following standard result [17]:
Lemma 1
Let \(\mathfrak {H}\subseteq \textsf {Sem}(F)\) be a fundamental system, and \(\mathfrak {S}\subseteq \textsf {Sem}(F)\) a subsystem. Then, \(\mathfrak {S}\) is a fundamental system if and only if to each \(\textsf {h} \in \mathfrak {H}\) there exist \(c>0\) and \(\textsf {s} \in \mathfrak {S}\) with \(\textsf {h} \le c\cdot \textsf {s} \).
Proof
Confer, e.g., Lemma 20 in [11]. \(\square \)
Let \(\mathfrak {H}\subseteq \textsf {Sem}(F)\) be a fundamental system. We write  for \(\{X_n\}_{n\in \mathbb {N}}\subseteq F\), \(X\in F\) if
for \(\{X_n\}_{n\in \mathbb {N}}\subseteq F\), \(X\in F\) if
holds for certain \(\{\mathfrak {c}_\textsf {h} \}_{\textsf {h} \in \mathfrak {H}}\subseteq \mathbb {R}_{\ge 0}\), and \(\mathbb {R}_{> 0}\supseteq \{\lambda _{n}\}_{n\in \mathbb {N}}\rightarrow 0\). In this case, \(\{X_n\}_{n\in \mathbb {N}}\) is said to be Mackey convergent to X.
Remark 1
-
It is immediate from Lemma 1 that the definition made in (12) does not depend on the explicit choice of the fundamental system \(\mathfrak {H}\subseteq \textsf {Sem}(F)\).
-
Since we will make use of the differentiability results obtained in [8], we explicitly mention that in [8] an equivalent definition of Mackey convergence (more suitable for the technical argumentation there) was used. Specifically, (12) is equivalent to require that
$$\begin{aligned} \textsf {h} (X-X_n)\le \mathfrak {c}_\textsf {h} \cdot \lambda _{n} \qquad \quad \forall \, n\ge \mathfrak {l}_\textsf {h} ,\,\,\textsf {h} \in \mathfrak {H}\end{aligned}$$(13)holds for certain \(\{\mathfrak {c}_\textsf {h} \}_{\textsf {h} \in \mathfrak {H}}\subseteq \mathbb {R}_{\ge 0}\), \(\{\mathfrak {l}_\textsf {h} \}_{\textsf {h} \in \mathfrak {H}}\subseteq \mathbb {N}\), and \(\mathbb {R}_{\ge 0}\supseteq \{\lambda _{n}\}_{n\in \mathbb {N}}\rightarrow 0\).
In other words, the indices \(\{\mathfrak {l}_\textsf {h} \}_{\textsf {h} \in \mathfrak {H}}\) in (13) can be circumvented (can be set equal to zero) if \(\{\lambda _n\}_{n\in \mathbb {N}}\subseteq \mathbb {R}_{>0}\) instead of \(\{\lambda _n\}_{n\in \mathbb {N}}\subseteq \mathbb {R}_{\ge 0}\) is required. \(\square \)
Assume now \(F= C^k([a,b],\mathfrak {g})\) for \(k\in \mathbb {N}\cup \{\text {lip} ,\infty ,\text {c} \}\) and \(a<b\). We write

if \(\{\phi _n\}_{n\in \mathbb {N}}\) is Mackey convergent to \(\phi \) w.r.t. to the \(C^k\)-topology.
2.2.3 The Riemann integral and completeness
Let \(F\in \textsf {hlcVect}\). The Riemann integral of \(\gamma \in C^0([a,b],F)\) for \(a<b\) is denoted by \(\int \gamma (s) \,\text {d} s\in \widehat{F}\).
Remark 2
The Riemann integral in complete Hausdorff locally convex vector spaces can be defined exactly as in the finite-dimensional case; namely, as the limit of Riemann sums (which form a Cauchy sequence in F), confer Sect. 2 in [16]. In particular, the following assertions hold:
-
If F is sequentially complete, then \(\int \gamma (s) \,\text {d} s\in F\) holds for \(\gamma \in C^0([a,b],F)\).
-
For \(\gamma \in C^0([a,b],F)\) and \(\gamma _-:[a,b]\ni t\mapsto \gamma (a+b-t)\), we have \(\int \gamma _-(s)\,\text {d} s=\int \gamma (s)\, \text {d} s\). \(\square \)
Given \(x<y\) and \(\gamma \in C^0([x,y],F)\), then for \(x\le a<b\le y\) and \(x\le c\le y\), we set
Clearly, the Riemann integral is linear with
The Riemann integral admits the following additional properties:
-
For \(a<b\), we have
$$\begin{aligned} \qquad \textstyle \gamma -\gamma (a)\textstyle =\int _a^\bullet {\dot{\gamma }}(s)\,\text {d} s&\qquad \,\,\quad \forall \, \gamma \in C^1([a,b],F), \end{aligned}$$(17)$$\begin{aligned} \textsf {q} (\gamma -\gamma (a))\textstyle \le \int _a^\bullet \textsf {q} ({\dot{\gamma }}(s))\, \text {d} s&\qquad \quad \forall \, \gamma \in C^1([a,b],F),\, \textsf {q} \in \textsf {Sem}(F), \end{aligned}$$(18)$$\begin{aligned} \textstyle \widehat{\textsf {q} }\big (\int _a^\bullet \gamma (s)\,\text {d} s\big )\textstyle \le \int _a^\bullet \textsf {q} (\gamma (s))\,\text {d} s&\qquad \quad \forall \, \gamma \in C^0([a,b],F),\, \textsf {q} \in \textsf {Sem}(F). \end{aligned}$$(19) -
For \(a<b\) and \(\gamma \in C^0([a,b],F)\), we have
$$\begin{aligned} \textstyle C^1([a,b],\widehat{F})\ni \Gamma :[a,b]\ni t\mapsto \int _a^t \gamma (s)\,\text {d} s \in \widehat{F}\qquad \quad \text {with}\qquad \quad {\dot{\Gamma }}=\gamma . \end{aligned}$$(20) -
For \(a<b\), \(a'<b'\), \(\gamma \in C^1([a,b],F)\), \(\varrho :[a',b'] \rightarrow [a,b]\) of class \(C^1\), and \(t\in [a',b']\), we have the substitution formula
$$\begin{aligned} \textstyle \int _a^{\varrho (t)} \gamma (s)\, \text {d} s=\int _{a'}^t {\dot{\varrho }}(s)\cdot (\gamma \circ \varrho )(s)\,\text {d} s + \int _a^{\varrho (a')} \gamma (s)\,\text {d} s. \end{aligned}$$(21) -
Let \(\tilde{F}\in \textsf {hlcVect}\), \(a<b\), and \(\mathcal {L}:F\rightarrow \tilde{F}\) a continuous and linear map. Then, the following implication holds:
$$\begin{aligned}&\textstyle \int _a^b \gamma (s)\,\text {d} s\in F \quad \text {for}\quad \gamma \in C^0([a,b],F)\nonumber \\&\qquad \Longrightarrow \qquad \textstyle \mathcal {L}\big (\int _a^b \gamma (s)\,\text {d} s\big )=\int _a^b \mathcal {L}(\gamma (s)) \, \text {d} s. \end{aligned}$$(22)
Next, let us recall the following definitions:
-
We say that F is Mackey complete if \(\int _0^1 \gamma (s)\,\text {d} s \in F\) exists for each \(\gamma \in C^\infty ([0,1],F)\).
This is equivalent to require that \(\int _a^b \gamma (s)\,\text {d} s \in F\) exists for each \(\gamma \in C^\text {lip} ([a,b],F)\) and \(a<b\), confer Theorem 2.14 in [16] or Corollary 6 in [8].
-
We say that F is integral complete if \(\int _a^b \gamma (s)\,\text {d} s \in F\) exists for all \(a<b\) and \(\gamma \in C^0([a,b],F)\).
Evidently, F is Mackey complete if F is integral complete. Moreover, Remark 2 implies that F is integral complete (hence, Mackey complete) if F is sequentially complete.
Finally, for \(\gamma \equiv \{\gamma [p]\}_{0\le p\le n-1}\in \text {CP} ^0([a,b],F)\) (\(n\ge 1\)), we define
Clearly, the so-extended Riemann integral is linear, and \(C^0\)-continuous—specifically, (19) yields
For \(x<y\) and \(\gamma \in \text {CP} ^0([x,y],F)\), we define \(\int _a^b\gamma (s)\, \text {d} s\), \(\int _b^a\gamma (s)\, \text {d} s\), \(\int _c^c \gamma (s)\, \text {d} s\) for \(x\le a<b\le y\) and \(x\le c\le y\) as in (15). Clearly, then (16) also holds for the extended Riemann integral. We furthermore note that \([a,b]\ni t\mapsto \int _a^t \gamma (s)\,\text {d} s\in F\) is continuous for each \(x\le a<b\le y\), as well as of class \(C^1\) if \([a,b]\subseteq [t_p,t_{p+1}]\) holds for some \(0\le p\le n-1\).
2.2.4 Extensions and completeness
Let \(F\in \textsf {hlcVect}\) be given. In this subsection, we collect some statements that we shall need in Sect. 5. We recall the following result.Footnote 7
Lemma 2
Let \(D\subseteq \mathbb {R}\) be an interval, \(k\in \mathbb {N}\cup \{\infty \}\), and \(\gamma \in C^k(J,F)\) for \(J:=\textsf {int} _{\mathbb {R}}(D)\). Let \(\{\gamma _\ell \}_{0\le \ell \preceq k}\subseteq C^0(D,F)\) be given such that \(\gamma ^{(\ell )}=\gamma _\ell |_{J}\) holds for all \(0\le \ell \preceq k\). Then, there exists an open interval \(I\subseteq \mathbb {R}\) with \(D\subseteq I\) as well as \(\tilde{\gamma }\in C^k(I,F)\) such that \(\tilde{\gamma }|_D=\gamma \) holds.
Proof
This is immediate from Theorem 1 in [12]. \(\square \)
Lemma 3
If F is sequentially complete, then \(C^k([a,b],F)\) is sequentially complete w.r.t. the \(C^k\)-topology for each \(k\in \mathbb {N}\cup \{\infty \}\) and \(a<b\).
Proof
Let \(k\in \mathbb {N}\cup \{\infty \}\) be fixed; and let \(\{\gamma _n\}_{n\in \mathbb {N}}\subseteq C^k([a,b],F)\) be a Cauchy sequence w.r.t. the \(C^k\)-topology. Then, \(\{(\gamma _n)^{(\ell )}\}_{n\in \mathbb {N}}\subseteq C^0([a,b],F)\) is a Cauchy sequence w.r.t. the \(C^0\)-topology for \(0\le \ell \preceq k\), and a standard \(\frac{\varepsilon }{3}\)-argument shows that it converges w.r.t. the \(C^0\)-topology to some \(\gamma _\ell \in C^0([a,b],F)\). Let \(\gamma :=\gamma _0|_{(a,b)}\). By Lemma 2, it suffices to show
Since the Riemann integral is \(C^0\)-continuous by (19), we have for \(0\le \ell < k\) and \(t\in [a,b]\)
Then, (20) shows \(\gamma _\ell |_{(a,b)}\in C^1((a,b),F)\) with \((\gamma _\ell |_{(a,b)})^{(1)}=\gamma _{\ell +1}|_{(a,b)}\) for \(0\le \ell < k\).
Now, since \(\gamma =\gamma _0|_{(a,b)}\) holds by definition, we can assume that there exists some \(0\le q< k\) such that (24) holds for \(k\equiv q\). We obtain
hence \(\gamma \in C^{q+1}((a,b),F)\). \(\square \)
Corollary 1
Assume that F is sequentially complete, and let \(\mathfrak {H}\subseteq \textsf {Sem}(F)\) be a fundamental system. Let \(k\in \mathbb {N}\cup \{\infty \}\), \(a<b\), and \(\{\gamma _p\}_{p\in \mathbb {N}}\subseteq C^k([a,b],F)\) be given with
Then, \(\textstyle \gamma := \sum _{p=0}^\infty \gamma _p\in C^k([a,b],F)\) converges w.r.t. the \(C^k\)-topology, i.e., \(\gamma ^{(\ell )}=\sum _{p=0}^\infty (\gamma _p)^{(\ell )}\) converges w.r.t. the \(C^0\)-topology for each \(0\le \ell \preceq k\).
Proof
The assumptions imply that \(\{\sum _{p=0}^n\gamma _p\}_{n\in \mathbb {N}}\subseteq C^k([a,b],F)\) is Cauchy w.r.t. the \(C^k\)-topology. The rest is clear from Lemma 3. \(\square \)
Corollary 2
Assume that F is sequentially complete, and let \(\mathfrak {H}\subseteq \textsf {Sem}(F)\) be a fundamental system. Let \(\{X_p\}_{p\in \mathbb {N}}\subseteq F\) and \(\delta >0\) be given, such that
is defined for each \(\textsf {q} \in \mathfrak {H}\). Define \(\gamma _p:(-\delta ,\delta )\ni t\mapsto t^p\cdot X_p\in F\) for each \(p\in \mathbb {N}\).
-
(a)
Let \(-\delta<a<b<\delta \). Then, \(\textstyle \gamma [a,b]:= \sum _{p=0}^\infty \gamma _p|_{[a,b]}\in C^\infty ([a,b],F)\) converges w.r.t. the \(C^\infty \)-topology, with
$$\begin{aligned} \textstyle \gamma [a,b]^{(\ell )}=\sum _{p=0}^\infty (\gamma _p|_{[a,b]})^{(\ell )}:[a,b]\ni t\mapsto \sum _{p=\ell }^\infty \frac{p !}{(p-\ell )!}\cdot t^{p-\ell }\cdot X_p\in F\qquad \quad \forall \, \ell \in \mathbb {N}. \end{aligned}$$ -
(b)
We have \(\gamma :=\sum _{p=0}^\infty \gamma _p\in C^\infty ((-\delta ,\delta ),F)\) with
$$\begin{aligned} \textstyle \gamma ^{(\ell )}=\sum _{p=0}^\infty (\gamma _p)^{(\ell )}:(-\delta ,\delta )\ni t\mapsto \sum _{p=\ell }^\infty \frac{p !}{(p-\ell )!}\cdot t^{p-\ell }\cdot X_p\in F \qquad \quad \forall \, \ell \in \mathbb {N}. \end{aligned}$$
Proof
Point b) is clear from Point a). To prove Point a), we observe that \(\gamma [\textsf {q} ]\) is smooth for each \(\textsf {q} \in \mathfrak {H}\), with
This implies \(\sum _{p=0}^\infty \textsf {q} _\infty ^\text {s} (\gamma _p|_{[a,b]})<\infty \) for all \(\textsf {q} \in \mathfrak {H}\), \(\text {s} \in \mathbb {N}\), \(a<b\), so that the claim is clear from Corollary 1. \(\square \)
2.2.5 Lie Algebras
Let \((\mathfrak {q},\varvec{[}\cdot , \cdot \varvec{]})\) be a fixed Lie algebra (not necessarily the Lie algebra of a Lie group), i.e.,
-
\(\mathfrak {q}\in \textsf {hlcVect}\),
-
\(\varvec{[}\cdot , \cdot \varvec{]}:\mathfrak {q}\times \mathfrak {q}\rightarrow \mathfrak {q}\) is bilinear, antisymmetric, and continuous, with (Jacobi identity)
$$\begin{aligned} \varvec{[}Z, \varvec{[}X, Y \varvec{]} \varvec{]}= \varvec{[}\varvec{[}Z, X \varvec{]}, Y \varvec{]} + \varvec{[}X, \varvec{[}Z, Y \varvec{]} \varvec{]}\qquad \quad \forall \, X,Y,Z\in \mathfrak {q}. \end{aligned}$$(25)
We shall need the following definitions:
-
Given \(X\in \mathfrak {q}\), we denote \(\text {ad} _{X}^1\equiv \text {ad} _{X}:\mathfrak {q}\ni Y\mapsto \varvec{[}X, Y \varvec{]}\in \mathfrak {q}\),Footnote 8 and define inductively
$$\begin{aligned} \text {ad} _{X}^0:=\text {id} _\mathfrak {q}\qquad \quad \text {as well as}\qquad \quad \text {ad} _{X}^n:=\text {ad} _{X}\circ \text {ad} _{X}^{n-1}\qquad \forall \, n\ge 1. \end{aligned}$$ -
Given a subset \(S\subseteq \mathfrak {q}\), then \(\varvec{\langle } S\varvec{\rangle } \subseteq \mathfrak {q}\) denotes the linear subspace that is generated by S. We define inductively
$$\begin{aligned} \mathcal {V}_1(S):=\varvec{\langle } S\varvec{\rangle } \qquad \quad \text {as well as}\qquad \quad \mathcal {V}_{n+1}(S):=\varvec{\langle } \varvec{[}\mathcal {V}(S), \mathcal {V}_n(S) \varvec{]}\varvec{\rangle } \qquad \forall \, n\ge 1; \end{aligned}$$and set \(\textstyle \mathcal {G}_n(S):= \varvec{\langle } \bigcup _{\ell = n}^{\infty } \mathcal {V}_\ell (S)\varvec{\rangle } \) for each \(n\ge 1\).
A straightforward induction involving (25) shows (confer Appendix A.2 or Exercise 5.2.7 in [13])
For \(n\ge 1\), we set \(\overline{\mathcal {V}}_n:=\textsf {clos} _{\mathfrak {q}}(\mathcal {V}_n)\) as well as \(\overline{\mathcal {G}}_n:=\textsf {clos} _{\mathfrak {q}}(\mathcal {G}_n)\). Since \(\varvec{[}\cdot , \cdot \varvec{]}\) is continuous, (26) implies
We observe that \(\overline{\mathcal {G}}_{n+\ell }(S)\subseteq \overline{\mathcal {G}}_{n}(S)\) holds for all \(n,\ell \in \mathbb {N}\). We shall need the following definitions: Footnote 9
-
A subset \(\text {M} \subseteq \mathfrak {q}\) is said to be an \(\text {AE} \)-set if to each \(\textsf {v} \in \textsf {Sem}(\mathfrak {q})\), there exist \(\textsf {v} \le \textsf {w} \in \textsf {Sem}(\textsf {q} )\) with
$$\begin{aligned} \textsf {v} (\varvec{[}X_1,\varvec{[}X_2,\varvec{[}\dots ,\varvec{[}X_n,Y\varvec{]}{\dots }\varvec{]}\varvec{]}])\le \textsf {w} (X_1)\cdot {\dots }\cdot \textsf {w} (X_n)\cdot \textsf {w} (Y) \end{aligned}$$(28)for all \(X_1,\dots ,X_n,Y\in \text {M} \), and \(n\ge 1\). We say that \((\mathfrak {q},\varvec{[}\cdot , \cdot \varvec{]})\) is asymptotic estimate if \(\mathfrak {q}\) is an \(\text {AE} \)-set.
-
A subset \(\text {N} \subseteq \mathfrak {q}\) is said to be a \(\text {Nil} _{q}\)-set for \(q\ge 2\) if
$$\begin{aligned} \varvec{[}X_1,\varvec{[}X_2,\varvec{[}\dots ,\varvec{[}X_{q-1},X_q\varvec{]}{\dots }\varvec{]}\varvec{]}\varvec{]}=0 \qquad \quad \forall \, X_1,\dots ,X_q\in \text {N} . \end{aligned}$$(29)Evidently, each \(\text {Nil} _{q}\)-set (for \(q\ge 2\)) is an \(\text {AE} \)-set. We say that \((\mathfrak {q},\varvec{[}\cdot , \cdot \varvec{]})\) is nilpotent if \(\mathfrak {q}\) is a \(\text {Nil} _{q}\)-set for some \(q\ge 2\).
In view of Sect. 4.2 (the proof of Lemma 16), we observe the following.
Remark 3
Let \(\text {N} \subseteq \mathfrak {q}\) be a \(\text {Nil} _{q}\)-set for some \(q\ge 2\). Then,
-
1)
\(\overline{\mathcal {G}}_{q+n}(\text {N} )=\{0\}\) holds for each \(n\in \mathbb {N}\).
-
2)
\(\varvec{[}\overline{\mathcal {G}}_m(\text {N} ), \overline{\mathcal {G}}_n(\text {N} ) \varvec{]}\subseteq \overline{\mathcal {G}}_{m+n}(\text {N} )\) holds for \(m,n\ge 1\), by (27).
-
3)
\(\overline{\mathcal {G}}_n(\text {N} )\) is a \(\text {Nil} _{q}\)-set for each \(n\ge 1\), by the previous points 1) and 2).
-
4)
Let \(k\in \mathbb {N}\cup \{\text {lip} ,\infty \}\) be given; and assume that \(\mathfrak {q}\) is Mackey complete for \(k\in \mathbb {N}_{\ge 1}\cup \{\text {lip} ,\infty \}\), as well as integral complete for \(k\equiv 0\). Then, for \(n\in \{1,\dots ,q\}\) and \(\phi \in C^k([a,b],\mathfrak {q})\) with \(\text {im} [\phi ]\subseteq \overline{\mathcal {G}}_n(\text {N} )\), we have
$$\begin{aligned} \textstyle \int _s^t \phi (s)\,\text {d} s \in \overline{\mathcal {G}}_n(\text {N} )\qquad \quad \forall \, a\le s<t\le b. \qquad \qquad \quad \end{aligned}$$\(\square \)
2.2.6 Some properties of maps
Let \(F_1,\dots ,F_n,F,E\in \textsf {hlcVect}\) be given.
Lemma 4
Let X be a topological space; and let \(\Phi :X\times F_1\times {\dots }\times F_n\rightarrow F\) be continuous, such that \(\Phi (x,\cdot )\) is n-multilinear for each \(x\in X\). Then, to each compact \(\text {K} \subseteq X\) and each \(\textsf {q} \in \textsf {Sem}(F)\), there exist \(\textsf {q} _1\in \textsf {Sem}(F_1),\dots ,\textsf {q} _n\in \textsf {Sem}(F_n)\) as well as \(O\subseteq X\) open with \(\text {K} \subseteq O\), such that
Proof
Confer, e.g., Corollary 1 in [8]. \(\square \)
Lemma 5
Let \(V\subseteq F\) be open with \(0\in V\). Let furthermore \(\Psi :V\times E\rightarrow E\) be smooth with \(\Psi (0,\cdot )=\text {id} _{E}\), such that \(\Psi (x,\cdot )\) is linear for each \(x \in V\). Then, to each \(\textsf {p} \in \textsf {Sem}(E)\), there exist \(\textsf {q} \in \textsf {Sem}(F)\) and \(\textsf {w} \in \textsf {Sem}(E)\) with
Proof
Confer Appendix A.3. \(\square \)
Lemma 6
Let \(F_1,F_2\in \textsf {hlcVect}\), and \(f:F_1\supseteq U\rightarrow F_2\) of class \(C^{2}\). Assume that \(\gamma :D\rightarrow F_1\) is continuous at \(t\in D\), such that \(\lim _{h\rightarrow 0} 1/h \cdot (\gamma (t+h)-\gamma (t))=:X\in \widehat{F}_1\) exists. Then, we have
Proof
Confer, e.g., Lemma 7 in [8]. \(\square \)
We close this subsection with the following convention concerning differentiable maps with values in Lie groups.
Convention 1
Let \(F\in \textsf {hlcVect}\), \(U\subseteq F\), G a Lie group modeled over \(E\in \textsf {hlcVect}\). A map \(f:U\rightarrow G\) is said to be
-
differentiable at \(x\in U\) if there exists a chart \((\Xi ',\mathcal {U}')\) of G with \(f(x)\in \mathcal {U}'\), such that
$$\begin{aligned} \textstyle (D^{\Xi '}_v f)(x):=\lim _{h\rightarrow 0} 1/h\cdot ((\Xi '\circ f)(x+h\cdot v)-(\Xi '\circ f)(x))\in E \end{aligned}$$(30)exists for all \(v \in F\). Lemma 6 applied to coordinate changes shows that (30) holds for one chart around f(x) if and only if it holds for each chart around f(x), and that
$$\begin{aligned} \text {d} _x f(v):= \big (\text {d} _{\Xi '(f(x))}\Xi '^{-1} \circ (D^{\Xi '}_v f)\big )(x)\in T_{f(x)}G \qquad \quad \forall \, v\in F \end{aligned}$$is independent of the explicit choice of \((\Xi ',U')\).
-
differentiable if f is differentiable at each \(x\in U\). \(\square \)
2.3 Power series
In this subsection, we collect some statements concerning power series in (Banach) algebras that we shall need to work informally in Sect. 4.1. We set
and let \(\mathbb {K}\in \{\mathbb {R},\mathbb {C}\}\) be fixed.
-
Let \((\mathcal {N},*_\mathcal {N},1_\mathcal {N})\) be a unital \(\mathbb {K}\)-algebra, and let \(\mathcal {N}_q:=\{\mathfrak {n}\in \mathcal {N}\,|\, \mathfrak {n}^{q+1}=0\}\) for \(q\ge 1\). Set furthermore \(\mathfrak {n}^0:=1_\mathcal {N}\) and \(\mathfrak {n}^1:=\mathfrak {n}\) for each \(\mathfrak {n}\in \mathcal {N}\).
-
Let \((\mathcal {A},*_\mathcal {A},1_\mathcal {A},\Vert \cdot \Vert _\mathcal {A})\) be a unital submultiplicative Banach algebra over \(\mathbb {K}\), and set \(\mathfrak {a}^0:=1_\mathcal {A}\) as well as \(\mathfrak {a}^1:=\mathfrak {a}\) for each \(\mathfrak {a}\in \mathcal {A}\).
Let \(f:U_{R}(0)\ni z\mapsto \sum _{n=0}^\infty a_n\cdot z^n\in \mathbb {C}\) for \(\{a_n\}_{n\in \mathbb {N}}\subseteq \mathbb {K}\) be a power series with radius of convergence \(R >0\). We define
and set \(\textstyle f_p:U_{R}(0)\ni z\mapsto \sum _{n=0}^p a_n\cdot z^n\in \mathbb {C}\) for each \(p\in \mathbb {N}\). We furthermore let
Let \(g:U_{S}(0)\ni z\mapsto \sum _{n=0}^\infty b_n\cdot z^n\in \mathbb {C}\) be a power series with radius of convergence \(S>0\).
-
Assume \(S=R\). The Cauchy product formula yields
$$\begin{aligned} \textstyle f *g:U_R\ni z\mapsto \sum _{n=0}^\infty \big (\sum _{\ell =0}^n a_\ell \cdot b_{n-\ell }\big ) \cdot z^n=f(z)\cdot g(z)\in \mathbb {C}. \end{aligned}$$
- \(\circ \):
-
For \(\mathfrak {n}\in \mathcal {N}_q\) with \(q\ge 1\), we evidently have
$$\begin{aligned} \textstyle f(\mathfrak {n})*_\mathcal {N}g(\mathfrak {n}) = \sum _{n=0}^q \big (\sum _{\ell =0}^n a_\ell \cdot b_{n-\ell }\big ) \cdot \mathfrak {n}^n = (f*g)(\mathfrak {n})\in \mathcal {N}. \end{aligned}$$ - \(\circ \):
-
For \(\mathfrak {a}\in \mathcal {A}\) with \(\Vert \mathfrak {a}\Vert _\mathcal {A}< R\), we obtain
$$\begin{aligned} \textstyle f(\mathfrak {a})*_\mathcal {A}g(\mathfrak {a}) = \sum _{n=0}^\infty \big (\sum _{\ell =0}^n a_\ell \cdot b_{n-\ell }\big ) \cdot \mathfrak {a}^n = (f*g)(\mathfrak {a})\in \mathcal {A}. \end{aligned}$$(Apply, e.g., Exercise 3.1.3 in [13], with \(X,Y,Z\equiv \mathcal {A}\) and \(\beta \equiv *_\mathcal {A}\) there.)
-
Assume \(|g|_s=\sum _{n=0}^\infty |b_n|\cdot s^n < R\) for all \(0\le s< S\), thus \(g(U_{S})\subseteq U_{R}(0)\). By analyticity, we have

The following statements are verified in Appendix A.4:
- \(\circ \):
-
Assume \(b_0=0\), and let \(\mathfrak {n}\in \mathcal {N}_q\) with \(q\ge 1\). We have \(g(\mathfrak {n})\in \mathcal {N}_q\) with
$$\begin{aligned} \textstyle f(g(\mathfrak {n}))= \sum _{n=0}^q c_n \cdot \mathfrak {n}^n = (f\diamond g)(\mathfrak {n})\in \mathcal {N}. \end{aligned}$$(31) - \(\circ \):
-
For \(\mathfrak {a}\in \mathcal {A}\) with \(\Vert \mathfrak {a}\Vert _\mathcal {A}< S\), we have
$$\begin{aligned} \textstyle f(g(\mathfrak {a}))= \sum _{n=0}^\infty c_n \cdot \mathfrak {a}^n = (f\diamond g)(\mathfrak {a})\in \mathcal {A}. \end{aligned}$$(32)
Example 1
Let \(\mathbb {K}=\mathbb {R}\), and define the power series

In the context of the above notations, we have \(b_0=0\), \(R=1\), \(S=\ln (2)\), with \(|g|_s<\text {e} ^{S}-1=R\) for \(0\le s<S\) as well as
We consider the power seriesFootnote 10

and obtain for \(t\in (-\ln (2),\ln (2))\) that
Let now \(Z\in \mathfrak {g}\) be fixed, and assume that one of the following situations hold:
-
A)
Let \(\text {N} \subseteq \mathfrak {g}\) be a \(\text {Nil} _{q}\)-set for \(q\ge 1\). We define \(V:=\overline{\mathcal {G}}_1(\text {N} )\), and let \(\text {End} (V)\) denote the set of all linear maps \(V\rightarrow V\). Then, \((\mathcal {N},*_\mathcal {N},1_\mathcal {N})\equiv (\text {End} (V),\circ ,\text {id} _{V})\) is a unital \(\mathbb {R}\)-algebra, with \(\text {ad} _{Z}\in \mathcal {N}_{q-1}\) for each \(Z\in V\) by Remark 3.3).
-
B)
G is a Banach Lie group with
$$\begin{aligned} \Vert \varvec{[}X, Y \varvec{]}\Vert \le \Vert X\Vert \cdot \Vert Y\Vert \qquad \quad \forall \, X,Y\in \mathfrak {g}, \end{aligned}$$and we have \(\Vert Z\Vert <\ln (2)\). We define \(V:=\mathfrak {g}\), and let \(\text {End} ^{\textrm{c}}(V)\) denote the set of all continuous linear maps \(V\rightarrow V\). Then, \((\mathcal {A},*_\mathcal {A},1_\mathcal {A},\Vert \cdot \Vert _\mathcal {A})\equiv (\text {End} ^{\textrm{c}}(V),\circ ,\text {id} _{V},\Vert \cdot \Vert _\text {op} )\) is a unital submultiplicative Banach algebra over \(\mathbb {R}\), and we have \(\text {ad} _{Z}\in \text {End} ^{\textrm{c}}(V)\) with \(\Vert \text {ad} _{Z}\Vert _\text {op} < \ln (2)\).
In both situations A) and B), the above discussions together with (33) and (34) show
for \(Z\in V\). This can be rewritten as
for each \(Y\in V\), whereby for maps \(\xi ,\zeta :\mathfrak {g}\rightarrow \mathfrak {g}\) and \(X\in \mathfrak {g}\) we set (convergence presumed)
Equation (35) will be relevant for our discussions in Sect. 4.1. \(\square \)
2.4 The evolution map
The subject of this section is the evolution map. We recall its elementary properties (confer also [8]), as well as the differentiability results obtained in [11]. We furthermore introduce the notion of weak \(C^k\)-regularity (confer Definition 1).
2.4.1 Elementary definitions
The right logarithmic derivative is given by

for each interval \(D\subseteq \mathbb {R}\). Notably, for \(\mu \in C^1(D,G)\), \(g\in G\), an interval \(D'\subseteq D\), and \(\varrho :D''\rightarrow D\) of class \(C^1\) for \(D''\subseteq \mathbb {R}\) an interval, we have

Moreover, for \(\mu ,\nu \in C^1(D,G)\), it follows from the product rule (11) that

holds. For \(a<b\) and \(k\in \mathbb {N}\cup \{\text {lip} ,\infty ,\text {c} \}\), we define

Now,  restricted to the set
restricted to the set
is injective for \(a<b\) (confer, e.g., Lemma 9 in [8]). We thus obtain a map
if for \(a<b\) we define

Notably, for \(a<b\) and \(k\in \mathbb {N}\cup \{\text {lip} ,\infty ,\text {c} \}\), we have (confer, e.g., Lemma 10 in [8])
Moreover, for \(a<b\) and \(\phi \in \mathfrak {D}_{[a,b]}^k\), we have
by the second equality in (36) as well as Lemma 10 in [8].
Remark 4
Given \(X\in \mathfrak {g}\), there exist \(\varepsilon >0\) and \(\phi _X\in \mathfrak {D}^\infty _{[0,\varepsilon ]}\) with \(\phi _X(0)=X\). In fact, fix \(\varepsilon >0\) with \((-2\varepsilon ,2\varepsilon )\cdot \text {d} _e\Xi (X)\subseteq \mathcal {V}\), and define
Then, \(\mu _X\) is of class \(C^\infty \), and  has the desired properties. \(\square \)
has the desired properties. \(\square \)
Example 2
(The Riemann Integral) Assume \((G,\cdot )\equiv (F,+)\) equals the additive group of some \(F\in \textsf {hlcVect}\). We have  for each \(a<b\), hence
for each \(a<b\), hence
as well as \(\text {Evol} (\gamma ):[a,b]\ni t\mapsto \int _a^t \gamma (s)\,\text {d} s\) for each \(\gamma \in \mathfrak {D}_{[a,b]}\). \(\square \)
2.4.2 The product integral
The product integral is defined by

We set  as well as
as well as  for \(a<b\), \(\phi \in \mathfrak {D}_{[a,b]}\), \(c\in [a,b]\), and define
for \(a<b\), \(\phi \in \mathfrak {D}_{[a,b]}\), \(c\in [a,b]\), and define

We let \({\text {evol} }_\text {k} \equiv {\text {evol} }_{[0,1]}^k\) as well as \(\text {D} _\text {k} \equiv \mathfrak {D}^k_{[0,1]}\) for each \(k\in \mathbb {N}\cup \{\text {lip} ,\infty ,\text {c} \}\). We furthermore let
The following elementary identities hold for \(a<b\), confer [4, 15] or Sect. 3.5.2 in [8]:
-
(a)
For each \(\phi ,\psi \in \mathfrak {D}_{[a,b]}\), we have
 with
with 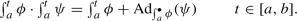
-
(b)
For each \(\phi ,\psi \in \mathfrak {D}_{[a,b]}\), we have
 with
with 
-
(c)
For each \(\phi \in \mathfrak {D}_{[a,b]}\), we have
 with
with 
-
(d)
For \(a=t_0<{\dots }<t_n=b\) and \(\phi \in \mathfrak {D}_{[a,b]}\), we have

-
(e)
For \(\varrho :[a',b']\rightarrow [a,b]\) of class \(C^1\) and \(\phi \in \mathfrak {D}_{[a,b]}\), we have \({\dot{\varrho }}\cdot (\phi \circ \varrho )\in \mathfrak {D}_{[a',b']}\) with
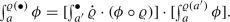
-
(f)
For each homomorphism \(\Psi :G\rightarrow H\) between Lie groups G and H that is of class \(C^1\), we have

Remark 5
Let \(k\in \mathbb {N}\cup \{\text {lip} ,\infty \}\) and \(a<b\) be given. We have by (a), (c), and Lemma 13 in [8] (confer also Lemma 8) that

holds for each \(\phi ,\psi \in \mathfrak {D}^k_{[a,b]}\). It is then not hard to see that \((\mathfrak {D}^k_{[a,b]},\star ,\cdot ^{-1},0)\) is a group:
-
We have \((\psi ^{-1})^{-1}=\psi \) for each \(\psi \in \mathfrak {D}^k_{[a,b]}\). In fact, applying (c) twice, we obtain

The claim is thus clear from injectivity of
 .
. -
We have \(\psi \star \psi ^{-1} =0=\psi ^{-1}\star \psi \) for each \(\psi \in \mathfrak {D}^k_{[a,b]}\). In fact, it is clear that
$$\begin{aligned} \psi \star \psi ^{-1} =0\qquad \quad \forall \, \psi \in \mathfrak {D}^k_{[a,b]}. \end{aligned}$$Then, we obtain from the previous point that
$$\begin{aligned} \psi ^{-1}\star \psi =\psi ^{-1}\star (\psi ^{-1})^{-1}=0\qquad \quad \forall \, \psi \in \mathfrak {D}^k_{[a,b]}. \end{aligned}$$ -
We have \(\phi \star (\psi \star \chi ) = (\phi \star \psi )\star \chi \) for all \(\phi ,\psi ,\chi \in \mathfrak {D}^k_{[a,b]}\). In fact, we obtain from (a) that

The claim is thus clear from injectivity of
 .
.
We will reconsider this group structure in Sects. 4.2.1 and 5. \(\square \)
Example 3
(The Riemann Integral) Assume we are in the situation of Example 2. Then,

holds; and, the identities (a), (d), (e), and (f) encode (in the given order) the additivity of the Riemann integral, (16), (21), and (22) (for if in (f), \((H,\cdot )\equiv (\tilde{F},+)\) is the additive group of some further \(\tilde{F}\in \textsf {hlcVect}\)), respectively. \(\square \)
Example 4
For \(a<b\), we define
Let \(a<b\) be fixed. Then, \({\mathfrak {inv}}|_{C^0([a,b],\mathfrak {g})}\) is linear. Moreover, for \(\phi \in C^0([a,b],\mathfrak {g})\) and \(\varrho :[a,b]\ni t\mapsto a +b -t\in [a,b]\), we have \({\mathfrak {inv}(\phi )}={\dot{\varrho }}\cdot \phi \circ \varrho \). Then, (e) shows that \({\mathfrak {inv}(\phi )}\in \mathfrak {D}^k_{[a,b]}\) holds for each \(\phi \in \mathfrak {D}^k_{[a,b]}\) and \(k\in \mathbb {N}\cup \{\text {lip} ,\infty \}\), with

For instance, in the situation of Example 3, the right side of (39) reads
which is in line with the second point in Remark 2. The relation  will be useful for our argumentation in Sect. 3.2. \(\square \)
will be useful for our argumentation in Sect. 3.2. \(\square \)
Example 5
(The Lie bracket and Homomorphisms) Assume that we are in the situation of (f), and let \((\mathfrak {h},\varvec{[}\cdot , \cdot \varvec{]}_\mathfrak {h})\) denote the Lie algebra of H. Then, we have
Proof of Equation (40)
Let \(X,Y\in \mathfrak {g}\) be fixed, and choose \(\phi _{X}:[0,\varepsilon _1]\rightarrow \mathfrak {g}\) as well as \(\phi _{Y}:[0,\varepsilon _2]\rightarrow \mathfrak {g}\) as in Remark 4. We obtain

which shows (40). \(\square \)
For instance, let \(\Psi \equiv \text {Conj} _g:G\rightarrow H= G\) with \(g\in G\). We obtain
Then, given \(X,Y,Z\in \mathfrak {g}\), fix \(\mu :(-\varepsilon ,\varepsilon )\rightarrow G\) (\(\varepsilon >0\)) of class \(C^1\), with \(\mu (0)=e\) and \({\dot{\mu }}(0)=Z\). We obtain from (41) and the parts b), d), e) of Proposition A.1 that
holds, which is the Jacobi identity (10). \(\square \)
2.4.3 Weak regularity
In this section, we recall certain differentiation results from [11] and introduce the notion of weak \(C^k\)-regularity for \(k\in \mathbb {N}\cup \{\text {lip} ,\infty \}\) (cf. Definition 1). We say that G is \(C^k\)-semiregular [4, 8, 11] for \(k\in \mathbb {N}\cup \{\text {lip} ,\infty ,\text {c} \}\) if \(\text {D} _\text {k} =C^k([0,1],\mathfrak {g})\) holds.
Remark 6
It follows from (e) when applied to affine transformations that G is \(C^k\)-semiregular if and only if \(\mathfrak {D}^k_{[a,b]}=C^k([a,b],\mathfrak {g})\) holds for all \(a<b\) (confer, e.g., Lemma 12 in [8]).\(\square \)
We write \(\lim ^\infty _{n}\mu _n=\mu \) for \(\{\mu _n\}_{n\in \mathbb {N}}\subseteq C^0([a,b],G)\) and \(\mu \in C^0([a,b],G)\) if \(\{\mu _n\}_{n\in \mathbb {N}}\) converges uniformly to \(\mu \), i.e., if to each open \(U\subseteq G\) with \(e\in U\), there exists \(N_U\in \mathbb {N}\) with
We recall (14), and say that G is Mackey k-continuous for \(k\in \mathbb {N}\cup \{\text {lip} ,\infty \}\) if

Lemma 13 in [11] shows:
Lemma A
G is Mackey k-continuous for \(k\in \mathbb {N}\cup \{\text {lip} ,\infty \}\) if and only if for each \(a<b\) the following implication holds:

Theorem 1 in [11] states:
Theorem B
If G is \(C^k\)-semiregular for \(k\in \mathbb {N}\cup \{\text {lip} ,\infty \}\), then G is Mackey k-continuous.
Theorem 3 in [11] (in particular) states:
Theorem C
Assume that G is Mackey k-continuous for \(k\in \mathbb {N}\cup \{\text {lip} ,\infty \}\). Let \(\Phi :I\times [a,b]\rightarrow \mathfrak {g}\) (\(I\subseteq \mathbb {R}\) open) be given with \(\Phi (z,\cdot )\in \mathfrak {D}^k_{[a,b]}\) for each \(z\in I\). Then, for \(x\in I\) we have

provided that the following conditions hold:
-
(i)
We have \((\partial _1 \Phi )(x,\cdot )\in C^k([a,b],\mathfrak {g})\).
-
(ii)
To \(\textsf {p} \in \textsf {Sem}(E)\) and \(\text {s} \preceq k\), there exists \(L_{\textsf {p} ,\text {s} }\ge 0\) as well as \(I_{\textsf {p} ,\text {s} }\subseteq I\) open with \(x\in I_{\textsf {p} ,\text {s} }\), such that
$$\begin{aligned} \textstyle \textsf {p} ^\text {s} _\infty (\Phi (x+h,\cdot )-\Phi (x,\cdot ))\le |h|\cdot L_{\textsf {p} ,\text {s} }\qquad \quad \forall \, h\in \mathbb {R}_{\ne 0}\,\text { with }\, x+h\in I_{\textsf {p} ,\text {s} }. \end{aligned}$$
In particular, we have (recall Convention 1)

if and only if the Riemann integral on the right side exists in \(\mathfrak {g}\).
Recall from the end of Sect. 2.2.3 that the last condition in Theorem C concerning the Riemann integral is always fulfilled
-
for \(k\in \mathbb {N}_{\ge 1}\cup \{\text {lip} ,\infty \}\) if \(\mathfrak {g}\) is Mackey complete,
-
for \(k=0\) if \(\mathfrak {g}\) integral complete for \(k=0\).
In particular, this implies the following statement (cf. Theorem 2 in [11] and Corollary 3 in [11]):
Proposition D
Assume that G is \(C^k\)-semiregular for \(k\in \mathbb {N}\cup \{\text {lip} , \infty \}\). Then, \({\text {evol} }_\text {k} \) is differentiable if and only if \(\mathfrak {g}\) is Mackey complete for \(k\in \mathbb {N}_{\ge 1}\cup \{\text {lip} ,\infty \}\) as well as integral complete for \(k=0\). In this case, \({\text {evol} }^k_{[a,b]}\) is differentiable for each \(a<b\), with

Moreover, for \(a<b\) and \(\phi ,\psi \in C^k([a,b],\mathfrak {g})\), we have

Proof
Clear from Theorem 2 in [11] and Corollary 3 in [11]. \(\square \)
Proposition D motivates the following definitionFootnote 11:
Definition 1
G is said to be weakly \(C^k\)-regular for \(k\in \mathbb {N}\cup \{\text {lip} ,\infty \}\) if G is \(C^k\)-semiregular, and \(\mathfrak {g}\) is Mackey complete for \(k\in \mathbb {N}_{\ge 1}\cup \{\text {lip} ,\infty \}\) as well as integral complete for \(k=0\). \(\square \)
Remark 7
Apart from \(C^k\)-semiregularity, the (standard) notion of \(C^k\)-regularity involves smoothness (and continuity) of the evolution map w.r.t. the \(C^k\)-topology. These additional assumptions, however, are unnecessarily strong for our purposes. This is because, due to the results stated above, the usual differentiability properties of the evolution map are already available in the weakly \(C^k\)-regular context. \(\square \)
Remark 8
Theorem C will in particular be applied to the situation in Example 2, i.e., where \((G,\cdot )\equiv (F,+)\) equals the additive group of some given \(F\in \textsf {hlcVect}\). For this observe that  is \(C^0\)-continuous, hence Mackey 0-continuous. Moreover, \(G\equiv F\) is
is \(C^0\)-continuous, hence Mackey 0-continuous. Moreover, \(G\equiv F\) is
-
\(C^0\)-semiregular if F is integral complete,
-
\(C^\text {lip} \)-semiregular if F is Mackey complete.\(\square \)
For instance, we obtain the following statements that we shall need in Sect. 3.1.
Corollary 3
Let \(F\in \textsf {hlcVect}\), \(k\in \mathbb {N}\), \(a<b\), and \(I\subseteq \mathbb {R}\) an open interval. Let furthermore \(\Theta ^0:I\times [a,b] \rightarrow F\) be a map with \(\alpha _x:=\Theta ^0(\cdot ,x)\in C^k(I,F)\) for each \(x\in [a,b]\), and assume that for \(0\le \ell \le k\) the map
is continuous such that
is defined. Then, \(\varvec{\gamma }:=\varvec{\gamma }^0\in C^k(I,F)\) holds with \(\varvec{\gamma }^{(\ell )}=\varvec{\gamma }^\ell \) for \(0\le \ell \le k\).
Proof
For each \(0\le \ell \le k\), we have by (19), compactness of [a, b], and continuity of \(\Theta ^\ell \) that \(\varvec{\gamma }^\ell \in C^0(I,F)\) holds. Let now \(0\le \ell < k\) be given, and set \(\Phi \equiv \Theta ^\ell \). We observe the following:
-
For \(t\in I\), we have \(\Phi (t,\cdot )=\Theta ^\ell (t,\cdot )\in C^0([a,b],F)\).
-
For \(t\in I\), we have \(\partial _1\Phi (t,\cdot )\in C^0([a,b],F)\), as
$$\begin{aligned} \partial _1\Phi (t,x)=\partial _1\Theta ^\ell (t,x)=\alpha _x^{(\ell +1)}(t)=\Theta ^{\ell +1}(t,x)\qquad \quad \forall \, t\in I,\, x\in [a,b]. \end{aligned}$$ -
For \(\textsf {q} \in \textsf {Sem}(F)\), \(x\in [a,b]\), \(t\in I\), and \(\tau >0\) with \(t+[-\tau ,\tau ]\subseteq I\), we have by (18)
$$\begin{aligned} \textstyle 1/|h|\cdot \textsf {q} (\Phi (t+h,x)&-\Phi (t,x))\\&\textstyle = 1/|h|\cdot \textsf {q} \big (\alpha ^{(\ell )}_x(t+h)-\alpha _x^{(\ell )}(t)\big )\\&\le \sup \big \{-\tau \le s\le \tau \,|\, \textsf {q} \big (\alpha _x^{(\ell +1)}(t+s)\big )\big \}\\&\le \sup \big \{-\tau \le s\le \tau ,\,a\le y\le b\,|\, \textsf {q} \big (\Theta ^{\ell +1}(t+s,y)\big )\big \} \end{aligned}$$for each \(-\tau \le h\le \tau \).
Theorem C (Remark 8) shows that for each \(t\in I\), we have
Since this holds for each \(0\le \ell <k\), the claim follows from \(\varvec{\gamma }^{(0)}=\varvec{\gamma }=\varvec{\gamma }^{0}\) by induction. \(\square \)
Lemma 7
Let \(F\in \textsf {hlcVect}\) be Mackey complete, \(a<b\), \(I\subseteq \mathbb {R}\) an open interval, \(\Theta ^0:I\times [a,b] \rightarrow F\) continuous, and \(\Omega :F\times F\rightarrow F\) smooth. Assume that the following two conditions are fulfilled:
-
(a)
\(\Theta ^0(t,\cdot )~~\in C^1([a,b],F)\) holds for each \(t\in I\).
-
(b)
\(\alpha _x:=\Theta ^0(\cdot ,x)\in C^1(I,F)\) holds for each \(x\in [a,b]\), with
$$\begin{aligned} \textstyle {\dot{\alpha }}_x(t)=\Omega \big (\int _x^b\alpha _y(t)\,\text {d} y,\alpha _x(t)\big )\qquad \quad \forall \, t\in I. \end{aligned}$$
Then, \(\varvec{\gamma }[z]:I\ni t\mapsto \int _z^b \Theta ^0(t,x)\,\text {d} x\in F\) is smooth for each \(z\in [a,b]\).
Proof
It suffices to prove the following statement. \(\square \)
Statement 1
Let \(k\in \mathbb {N}\) be given. Then, \(\alpha _x\in C^k(I,F)\) holds for each \(x\in [a,b]\). Moreover,
is continuous for \(0\le \ell \le k\), with \(\Theta ^\ell (t,\cdot )\in C^1([a,b],F)\) for each \(t\in I\).
In fact, let \(k\in \mathbb {N}\) be given. Since F is Mackey complete, it follows from Statement 1 that
exists for each \(z\in [a,b]\) and \(0\le \ell \le k\). Moreover, Corollary 3 shows that \(\varvec{\gamma }[z]\in C^k(I,F)\) holds for each \(z\in [a,b]\), with
Since \(k\in \mathbb {N}\) was arbitrary, Lemma 7 follows.
It thus remains to prove Statement 1:
Proof of Statement 1 We first discuss the cases \(k\in \{0,1\}\) and then argue by induction:
-
\(k=0\): Clear from the assumptions.
-
\(k=1\): By (b), we have \(\alpha _x\in C^1(I,F)\) for each \(x\in [a,b]\). Since \(\Theta ^0\) is continuous,
$$\begin{aligned} \textstyle \Gamma ^0:I\times [a,b]\ni (t,z) \mapsto \int _z^b \Theta ^0(t,x)\,\text {d} x\in F \end{aligned}$$is continuous. It is clear that \(\Gamma ^0(t,\cdot )\in C^1([a,b],F)\) holds for each \(t\in I\); and we have \(\Theta ^0(t,\cdot )\in C^1([a,b],F)\) for each \(t\in I\) by (a). Now, (b) yields
$$\begin{aligned} \textstyle \Theta ^1(t,x)={\dot{\alpha }}_x(t)=\Omega (\Gamma ^0(t,x),\Theta ^0(t,x))\qquad \quad \forall \, t\in I,\, x\in [a,b]. \end{aligned}$$Since \(\Omega \) is smooth, \(\Theta ^1\) is continuous with \(\Theta ^1(t,\cdot )\in C^1([a,b],F)\) for each \(t\in I\).
Assume now that Statement 1 holds for some \(k\ge 1\). We observe the following:
-
(i)
\(\Theta ^\ell \) is continuous for \(0\le \ell \le k\), hence
$$\begin{aligned} \textstyle \Gamma ^\ell :I\times [a,b]\ni (t,z) \mapsto \int _z^b \Theta ^\ell (t,x)\,\text {d} x\in F \end{aligned}$$is continuous for \(0\le \ell \le k\).
-
(ii)
For \(z\in [a,b]\), we have \(\alpha _z,\varvec{\gamma }[z]\in C^k(I,F)\), with
$$\begin{aligned} \textstyle \alpha _z^{(\ell )}=\Theta ^\ell (\cdot ,z)\qquad \text {and}\qquad \varvec{\gamma }[z]^{(\ell )}\textstyle {\mathop {=}\limits ^{(42)}} \Gamma ^\ell (\cdot ,z)\qquad \text {for}\qquad 0\le \ell \le k. \end{aligned}$$(43)Then, i) implies that the following maps are continuous:
$$\begin{aligned} \begin{aligned} I\times [a,b]\ni (t,z)&\mapsto ~~\alpha ^{(\ell )}_z(t)\in F\\ I\times [a,b]\ni (t,z)&\mapsto \varvec{\gamma }[z]^\ell (t)\in F \end{aligned} \end{aligned}$$(44)for \(0\le \ell \le k\)
-
(iii)
For \(t\in I\) and \(0\le \ell \le k\), the maps
$$\begin{aligned} \begin{aligned} {[}a,b]\ni z&\mapsto ~~\alpha _z^{(\ell )}(t)\in F\\ {[}a,b]\ni z&\mapsto \varvec{\gamma }[z]^{(\ell )}(t)\in F \end{aligned} \end{aligned}$$(45)are of class \(C^1\) (use (43)).
Then, by (b) we have
Together with ii), this shows \(\alpha _x\in C^{k+1}(I,F)\) for all \(x\in [a,b]\). Moreover, set \(\gamma [x]_1:=\alpha _x\) and \(\gamma [x]_2:=\varvec{\gamma }[x]\) for each \(x\in [a,b]\). It follows from (46) thatFootnote 12
is a sum of maps of the form
for certain \(0\le \ell _1,\dots ,\ell _m\le k\), \(1\le i_1,\dots ,i_m \le 2\), \(m\ge 2\), where \(\Psi :F^{m}\rightarrow F\) is smooth. Then, (44) implies that \(\Theta ^{k+1}\) is continuous, and (45) implies that \(\Theta ^{k+1}(t,\cdot )\in C^1([a,b],F)\) holds for each \(t\in I\). This establishes the claim for \(k+1\), so that Statement 1 follows by induction. \(\square \)
This proves the Lemma 7. \(\square \)
2.4.4 The exponential map
We let \(\mathfrak {i}:\mathfrak {g}\ni X\rightarrow \mathcal {C}_X|_{[0,1]}\in C^\text {c} ([0,1],\mathfrak {g})\), hence
The exponential map is given by

-
Instead of saying that G is \(C^\text {c} \)-semiregular, in the following we rather say that G admits an exponential map.
-
The relation (e) implies \(\mathbb {R}\cdot \text {dom} [\exp ]\subseteq \text {dom} [\exp ]\), as well as that \(t\mapsto \exp (t\cdot X)\) is a 1-parameter group for each \(X\in \text {dom} [\exp ]\) with
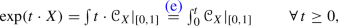 (48)
(48)confer, e.g., Remark 2.1) in [8].
Finally, Theorem 1 in [11] (cf. Theorem B), Corollary 6 in [11], and Remark 9.1 in [11] provide the following statement.
Corollary 4
Let \(\mathfrak {X}:I\rightarrow \text {dom} [\exp ]\subseteq \mathfrak {g}\) (\(I\subseteq \mathbb {R}\) an open interval) be of class \(C^1\), and set \(\alpha :=\exp \circ \,\mathfrak {X}\). Assume that G is weakly \(C^\infty \)-regular, or that \(\exp :\mathfrak {g}\rightarrow G\) is defined and of class \(C^1\). Then, \(\alpha \) is of class \(C^1\), with
Proof
If G is weakly \(C^\infty \)-regular, then the claim is clear from Theorem 1 in [11] and Corollary 6 in [11]. Assume now that \(\exp \) is of class \(C^1\). Then, Remark 9.1 in [11] shows that
holds, so that the claim is clear from Part d of Proposition A.1. \(\square \)
3 Preliminary results
In this section, we derive some elementary results from Theorem C (Proposition 1 in Sect. 3.1 and Proposition 2 in Sect. 3.2) and provide an integral expansion for the adjoint action (Lemma 13 in Sect. 3.3). Proposition 1 and Lemma 13 will be used in Sect. 4.2 to investigate the product integral of nilpotent curves. Also, Proposition 2 was supposed to be applied in this paper, but eventually turned out not to be necessary for our argumentation. We kept this result for academic reasons, and because it certainly will play a role in future applications. Our considerations in Sects. 3.1 and 3.2 furthermore serve as motivations for the constructions made in Sect. 5.
3.1 An integral transformation
Let \(\mathfrak {R}:=\{\phi \in \mathfrak {D}\,|\, [0,1]\cdot \phi \subseteq \mathfrak {D}\}\). We define \(\mathfrak {T}:\mathfrak {R}\rightarrow \textsf {Maps} ([0,1],\widehat{\mathfrak {g}})\) by

for each \(a<b\). In view of Sect. 4.2 (the proof of Lemma 16), for \(a<b\) and \(\phi \in \mathfrak {R}\cap \mathfrak {D}_{[a,b]}\), we define
In this section, we proof the following proposition.
Proposition 1
Assume that G is weakly \(C^k\)-regular for \(k\in \mathbb {N}\cup \{\text {lip} ,\infty \}\). Then, for \(a<b\) and \(\phi \in C^k([a,b],\mathfrak {g})\), we have \(\mathfrak {T}(\phi )\in C^\infty ([0,1],\mathfrak {g})\) with

In particular,  holds, and
holds, and  is smooth by (37).
is smooth by (37).
Example 6
Assume that G is abelian, as well as weakly \(C^k\)-regular for \(k\in \mathbb {N}\cup \{\text {lip} ,\infty \}\). Then, Proposition 1 recovers the well-known formula [18]

for each \(a<b\) and \(\phi \in C^k([a,b],\mathfrak {g})\). \(\square \)
Remark 9
Assume that G is weakly \(C^k\)-regular for \(k\in \mathbb {N}\cup \{\text {lip} ,\infty \}\); and recall the group structure discussed in Remark 5, as well as the map (38) introduced in Example 4. It is straightforward from Proposition 1 and the properties of the product integral that
holds for \(a<c<b\), \(\psi \in C^k([a,b],\mathfrak {g})\), as well as \(\varrho :[a',b']\rightarrow [a,b]\) (\(a'<b'\)) of class \(C^1\) with \({\dot{\varrho }}|_{(a',b')}>0\), \(\varrho (a')=a\), \(\varrho (b')=b\):
-
By (a) (first step), Proposition 1 (second step), and (39) (fourth step), we have
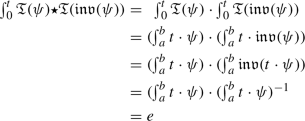
for each \(t\in [0,1]\). Then, injectivity of
 implies \(\mathfrak {T}(\psi )\star \mathfrak {T}({\mathfrak {inv}(\psi )})=0\), which proves the first line in (52).
implies \(\mathfrak {T}(\psi )\star \mathfrak {T}({\mathfrak {inv}(\psi )})=0\), which proves the first line in (52). -
By Proposition 1 (first and third step), (d) (second step), and (a) (fourth step), we have

for each \(t\in [0,1]\). The second line in (52) now follows from injectivity of
 .
. -
Since \({\dot{\varrho }}|_{(a',b')}>0\) holds, the substitution formula (e) applies to \(\varrho |_{[x',y']}\) and \(t\cdot \psi |_{[\varrho (x'),\varrho (y')]}\) for all \(a'\le x'< y'\le b'\) and \(t\in [0,1]\). We obtain

where we have applied (21) in the third step. This proves the third line in (52). \(\square \)
Remark 10
The smoothness statement in Proposition 1, in particular, ensures that \(\mathfrak {T}\) can be applied iteratively. We will use this fact in Sect. 4.2 to prove an identity for the product integral in the nilpotent context.\(\square \)
For the proof of Proposition 1, we shall need the following statements.
Lemma 8
Let \(k\in \mathbb {N}\cup \{\text {lip} ,\infty \}\), \(a<b\), \(\mu \in C^{k+1}([a,b],G)\), and \(\phi \in C^k([a,b],\mathfrak {g})\). Then, we have \(\text {Ad} _\mu (\phi )\in C^k([a,b],\mathfrak {g})\).
Proof
Confer, e.g., Lemma 13 in [8]. \(\square \)
Lemma 9
Assume that G is weakly \(C^k\)-regular for \(k\in \mathbb {N}\cup \{\text {lip} ,\infty \}\), and let \(\phi \in C^k([a,b])\) (\(a<b\)) be given. Then,  is continuous.
is continuous.
Proof
Confer Appendix A.5. \(\square \)
Lemma 10
Assume that G is weakly \(C^k\)-regular for \(k\in \mathbb {N}\cup \{\text {lip} ,\infty \}\), and let \(a<b\) as well as \(\phi \in C^k([a,b])\) be given. Then,  is smooth.
is smooth.
Proof
We consider the map

and observe the following:
-
Lemma 9 shows that \(\Theta ^0\) is continuous, as we have (with \(\kappa \) as in Lemma 9)
$$\begin{aligned} \Theta ^0(t,x)= \text {Ad} _{\kappa (t,x)}(\phi (x))\qquad \quad \forall \, t\in \mathbb {R}, \, x\in [a,b]. \end{aligned}$$ -
Given \(t\in \mathbb {R}\), we have \(\Theta ^0(t,\cdot )\in C^k([a,b],\mathfrak {g})\subseteq C^1([a,b],\mathfrak {g})\) by Lemma 8, (37), and

-
Given \(x\in [a,b]\), Proposition D yields

Then, Lemma 8 shows
$$\begin{aligned} \textstyle C^1(\mathbb {R},\mathfrak {g})\ni \alpha _x:= \Theta ^0(\cdot ,x) :\mathbb {R}\ni t \mapsto \text {Ad} _{\mu _x(t)}(\phi (x))\in \mathfrak {g}. \end{aligned}$$(53)Moreover, for \(t,h\in \mathbb {R}\) we have
 (54)
(54)By Proposition D, the map
 is of class \(C^1\) for \(t\in \mathbb {R}\) (recall that \(\Theta ^0(t,\cdot )\in C^k([a,b],\mathfrak {g})\) holds by the second point above), with
is of class \(C^1\) for \(t\in \mathbb {R}\) (recall that \(\Theta ^0(t,\cdot )\in C^k([a,b],\mathfrak {g})\) holds by the second point above), with  (55)
(55)We obtain for \(t\in \mathbb {R}\) that
 (56)
(56)
The claim is now clear from Lemma 7 (with \(I=\mathbb {R}\), \(\Omega =\varvec{[}\cdot , \cdot \varvec{]}\), and \(z=b\) there). \(\square \)
We are ready for the proof of Proposition 1.
Proof of Proposition 1
By Lemma 10, we have \(\mathfrak {T}(\phi )\in C^\infty ([0,1],\mathfrak {g})\). By Proposition D, we have  with
with

In the third step, we have applied (22) with \(\mathcal {L}\equiv \text {Ad} _{\mu (t)}\). This shows that  holds, with \(\mu (0)=e\). We obtain
holds, with \(\mu (0)=e\). We obtain

which proves the claim. \(\square \)
The following corollary verifies the guess made in Remark 8.2) in [11].
Corollary 5
Assume that G is weakly \(C^k\)-regular for \(k\in \mathbb {N}\cup \{\text {lip} ,\infty \}\), and let \(\phi ,\psi \in C^k([a,b],\mathfrak {g})\) be given. Then,  is smooth.
is smooth.
Proof
We have

By Lemma 8, it thus suffices to prove the claim for \(\phi =0\) and arbitrary \(\psi \in C^k([a,b],\mathfrak {g})\). Let thus \(\psi \in C^k([a,b],\mathfrak {g})\) be given. Then, we have

By Lemma 8, it thus suffices to prove smoothness of the map  for each \(\chi \in C^k([a,b],\mathfrak {g})\), so that the claim is clear from (the last statement in) Proposition 1. \(\square \)
for each \(\chi \in C^k([a,b],\mathfrak {g})\), so that the claim is clear from (the last statement in) Proposition 1. \(\square \)
3.2 Differentiation of parameter-dependent integrals
In this section, we prove the following differentiation result.
Proposition 2
Assume that G is Mackey k-continuous for \(k\in \mathbb {N}\cup \{\text {lip} ,\infty \}\). Let \(a<b\), \(\sigma >0\), \(I\subseteq \mathbb {R}\) an open interval with \([a-\sigma ,b+\sigma ]\subseteq I\), as well as \(\Phi :I\times [a-\sigma ,b+\sigma ]\rightarrow \mathfrak {g}\) a map with \(\Phi (z,\cdot )\in \mathfrak {D}^k_{[a-\sigma ,b+\sigma ]}\) for each \(z\in I\). Let \(x\in [a,b]\) be given, such that the following conditions hold:
-
(i)
We have \((\partial _1 \Phi )(x,\cdot )\in C^k([a,b],\mathfrak {g})\) with
 .
. -
(ii)
To \(\textsf {p} \in \textsf {Sem}(E)\) and \(\text {s} \preceq k\), there exists \(L_{\textsf {p} ,\text {s} }\ge 0\) as well as \(I_{\textsf {p} ,\text {s} }\subseteq I\) open with \(x\in I_{\textsf {p} ,\text {s} }\), such that
$$\begin{aligned} \textsf {p} ^\text {s} _\infty (\Phi (x+h,\cdot )-\Phi (x,\cdot ))\le |h|\cdot L_{\textsf {p} ,\text {s} }\qquad \quad \forall \, h\in \mathbb {R}_{\ne 0}\,\text { with }\, x+h\in I_{\textsf {p} ,\text {s} }. \end{aligned}$$
Then, we have

For the proof of Proposition 2, we shall need the following statements.
Lemma 11
To \(\textsf {p} \in \textsf {Sem}(E)\), there exist \(\textsf {p} \le \textsf {q} \in \textsf {Sem}(E)\) and \(U\subseteq G\) open with \(e\in U\), such that for each \(a<b\) and \(\chi \in \mathfrak {D}_{[a,b]}\) with  we have
we have

Proof
Confer Lemma 4 in [11]. \(\square \)
Corollary 6
For each compact \(\text {C} \subseteq G\) and each \(\textsf {q} \in \textsf {Sem}(E)\), there exists some \(\textsf {q} \le \textsf {m} \in \textsf {Sem}(E)\), such that \(\textsf {q} \circ \text {Ad} _g\le \textsf {m} \) holds for each \(g\in \text {C} \).
Proof
This is clear from Lemma 4, because \(\text {Ad} :G\times \mathfrak {g}\ni (g,X)\mapsto \text {Ad} _g(X)\in \mathfrak {g}\) is smooth as well as linear in the second argument. \(\square \)
Proof of Proposition 2
We consider the maps

and obtain

We furthermore observe the following:
- (1):
-
The maps \(\nu _+,\eta _-\) are continuous at \(h=0\), with \(\nu _+(0)=e=\eta _-(0)\). To show this, it suffices to prove the same property for the maps

First, it is clear that \(\alpha _\pm \) is continuous (in particular at \(h=0\)) with \(\alpha _\pm (0)=e\), as we have

Second, Condition ii) implies that for each sequence \([-\sigma ,0)\cup (0,\sigma ]\supseteq \{h_n\}_{n\in \mathbb {N}}\rightarrow 0\), we have
 . Since G is Mackey k-continuous, Lemma A yields the following:
. Since G is Mackey k-continuous, Lemma A yields the following:
-
For each sequence \((0,\sigma ]\supseteq \{h_n\}_{n\in \mathbb {N}}\rightarrow 0\), we have

This implies \(\lim _{h\rightarrow 0}\beta _+(h) = e\).
-
For each sequence \([-\sigma ,0)\supseteq \{h_n\}_{n\in \mathbb {N}}\rightarrow 0\), we have

This implies \(\lim _{h\rightarrow 0}\beta _-(h) = e\), as we have

- (2):
-
We have
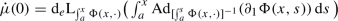 (58)$$\begin{aligned} {\dot{\nu }}_-(0)&=\Phi (x,x) \end{aligned}$$(59)$$\begin{aligned} {\dot{\eta }}_+(0)&=\Phi (x,x). \end{aligned}$$(60)
(58)$$\begin{aligned} {\dot{\nu }}_-(0)&=\Phi (x,x) \end{aligned}$$(59)$$\begin{aligned} {\dot{\eta }}_+(0)&=\Phi (x,x). \end{aligned}$$(60)In fact, (60) is evident, (58) is clear from Theorem C, and (59) is obtained as follows:
\(\square \)
Proof of Equation (59). Given \(-\sigma \le h<0\), we define \(\varrho _h:[x,x-h]\ni t\mapsto t+h \in [x + h,x]\), and obtain

According to Example 4 (with \(\varrho :[x+h,x]\ni t\mapsto 2x+h -t\in [x+h,x]\) there), we have

We obtain

which proves (59). \(\square \)
- (3):
-
By 1), there exists \(0<\delta \le \sigma \), such that the following maps are defined:
$$\begin{aligned} \Delta _+:(0,\delta ]\ni h\mapsto \textstyle \frac{1}{h}\cdot \Xi (\nu _+(h))\qquad \quad \text {and}\qquad \quad \Delta _-:[-\delta ,0)\ni h\mapsto \textstyle \frac{1}{h}\cdot \Xi (\eta _-(h)). \end{aligned}$$Then, to establish the proof, it suffices to show
$$\begin{aligned} \textstyle \lim _{0<h\rightarrow 0}\Delta _+(h)=0\qquad \quad \text {as well as}\qquad \quad \lim _{0>h\rightarrow 0}\Delta _-(h)=0. \end{aligned}$$(62)In fact, let \((\Xi ',\mathcal {U}')\) be a chart around \(\mu (0)\). Let furthermore \(O\subseteq \mathcal {U}\) and \(O'\subseteq \mathcal {U}'\) be open with \(e\in O\) and \(\mu (0)\in O'\), such that \(O\cdot O\cdot O'\subseteq \mathcal {U}'\) holds. We set \(W:=\Xi (O)\), \(W':=\Xi '(O')\), \(\mathcal {V}':=\Xi '(\mathcal {U}')\). We furthermore define
$$\begin{aligned} f:W\times W\times W'&\rightarrow \mathcal {V}'\\ (X,Y,Z)&\mapsto \Xi '(\Xi ^{-1}(X)\cdot \Xi ^{-1}(Y)\cdot \Xi '^{-1}(Z)), \end{aligned}$$as well as (shrink \(\delta >0\) if necessary, to ensure \(\text {im} [\eta _\pm ]\subseteq O\), \(\text {im} [\nu _\pm ]\subseteq O\), \(\text {im} [\mu ]\subseteq O'\))

Then, Lemma 6 (with \(F_1\equiv E\times E\times E\), \(F_2\equiv E\), and \(\gamma \equiv \gamma _\pm \) there) together with Part e) of Proposition A.1 (cf. also (11)), (57), (58), (59), (60), (62) implies the claim.
Finally, to prove (62), let \(\textsf {p} \in \textsf {Sem}(E)\) be fixed, and choose \(\textsf {p} \le \textsf {q} \in \textsf {Sem}(E)\) as well as \(U\subseteq G\) as in Lemma 11. Since both \(\nu _+,\eta _-\) are continuous by 1), there exists \(0<\delta _U\le \delta \) (\(\delta \) as in 3)) with \(\nu _+([0,\delta _U])\subseteq U\) and \(\eta _-([-\delta _U,0]))\subseteq U\). We observe that

holds by (b), and obtain from Lemma 11 that
Let \(\textsf {q} \le \textsf {m} \in \textsf {Sem}(E)\) be as in Corollary 6, for \(\text {C} \equiv \textsf {inv} (\text {im} [\alpha _+])\cup \textsf {inv} (\text {im} [\beta _-])\) there. We shrink \(0<\delta _U\le \delta \) such that \(x+ (-\delta _U,\delta _U)\subseteq I_{\textsf {m} ,0}\) holds, for \(I_{\textsf {m} ,0}\) as in Condition ii) (with \(\text {s} =0\) there). Then, Condition ii) yields the following:
-
For \(0< h<\delta _U\), we have
$$\begin{aligned} \textstyle \textsf {p} (\Delta _+(h))&\textstyle \le \frac{1}{|h|}\cdot \int _x^{x+h}\textsf {q} \big (\text {Ad} _{\alpha _+(\cdot )^{-1}}(\Phi (x+h,s)-\Phi (x,s)\big )\,\text {d} s \\&\textstyle \le \sup \{x\le s\le x+h\,|\,\textsf {m} (\Phi (x+h,s)-\Phi (x,s))\} \\&\textstyle \le |h|\cdot L_{\textsf {m} ,0}. \end{aligned}$$ -
For \(-\delta _U< h<0\), we have
$$\begin{aligned} \textstyle \textsf {p} (\Delta _-(h))&\textstyle \le \frac{1}{|h|}\cdot \int _{x+h}^{x}\textsf {q} \big (\text {Ad} _{\beta _-(\cdot )^{-1}}(\Phi (x,s)-\Phi (x+h,s)\big )\,\text {d} s \\&\textstyle \le \sup \{x+h\le s\le x\,|\, \textsf {m} (\Phi (x,s)-\Phi (x+h,s))\} \\&\textstyle \le |h|\cdot L_{\textsf {m} ,0}. \end{aligned}$$
This proves (62), hence the claim. \(\square \)
3.3 An integral expansion for the adjoint action
Let \(a<b\) and \(\psi \in \mathfrak {D}_{[a,b]}\) be given. For \(X\in \mathfrak {g}\), we define

We furthermore define
For \(\chi \in C^0([a,b],\mathfrak {g})\), we set
The following assertions are immediate from the definitions:
-
We have \(\varvec{\eta }^\pm (\psi ,\chi )\in C^{k+1}([a,b],\mathfrak {g})\) for \(k\in \mathbb {N}\cup \{\infty \}\), for each \(\psi \in \mathfrak {D}^k_{[a,b]}\) and \(\chi \in C^{k+1}([a,b],\mathfrak {g})\) (by (37) and smoothness of the group operations).
-
We have \(\varvec{\eta }^\pm (\psi ,\varvec{\eta }^\mp (\psi ,\chi ))=\chi \) for each \(\psi \in \mathfrak {D}_{[a,b]}\) and \(\chi \in C^0([a,b],\mathfrak {g})\).
We furthermore observe the following:
Lemma 12
Let \(a<b\), \(\psi \in \mathfrak {D}_{[a,b]}\), and \(X\in \mathfrak {g}\) be given. Then, \({\textbf {Ad}} ^\pm _\psi [X]\in C^1([a,b],\mathfrak {g})\) holds, with \({\textbf {Ad}} ^\pm _\psi [X](a)=X\) as well as
for each \(t\in [a,b]\). In particular, for \(\chi \in C^1([a,b],\mathfrak {g})\), we have
Proof
Equation (64) is verified in Appendix A.6; and (65) is clear from (64) as well as the parts b), d), e) of Proposition A.1. \(\square \)
For the sake of completeness, we want to mention the following well-known result:
Corollary 7
Let \(a<b\), \(\psi \in \mathfrak {D}_{[a,b]}\), \(X\in \mathfrak {g}\). Then, \({\textbf {Ad}} ^+_\psi [X]\) is the unique solution \(\alpha \in C^1([a,b],\mathfrak {g})\) to the differential equation (Lax equation) \({\dot{\alpha }}=\varvec{[}\psi , \alpha \varvec{]}\), with the initial condition \(\alpha (a)=X\).
Proof
By Lemma 12, it remains to show uniqueness. Let thus \(\alpha \in C^1([a,b],\mathfrak {g})\) be given, with \({\dot{\alpha }}=\varvec{[}\psi , \alpha \varvec{]}\) and \(\alpha (a)=X\). Then, \({\dot{\varvec{\eta }}}^-(\psi ,\alpha )=0\) holds by (65), with \(\varvec{\eta }^-(\psi ,\alpha )(a)=X\). Then, (17) yields \(\varvec{\eta }^-(\psi ,\alpha )=X\), hence
This proves the claim. \(\square \)
Let \(\widehat{\mathfrak {g}}\) denote the completion of \(\mathfrak {g}\). Let \(\psi \in C^0([a,b],\mathfrak {g})\), \(X\in \mathfrak {g}\), \(n\in \mathbb {N}\) be given. We set
and define for \(\ell \ge 1\)

For \(\ell \ge 1\), we set

To simplify the notations, we define

We obtain the following statement.
Lemma 13
Let \(\psi \in \mathfrak {D}_{[a,b]}\), \(X\in \mathfrak {g}\), and \(n\in \mathbb {N}\) be given. Then, for \(t\in [a,b]\) we have
Proof
We thus can assume that the claim holds for some \(n\in \mathbb {N}\). We obtain from (22) (third steps) that
as well as
The claim now follows by induction. \(\square \)
We recall the definition of an \(\text {AE} \)-set in (28), and obtain the following corollary.
Corollary 8
Let \(\text {M} \subseteq \mathfrak {g}\) be an \(\text {AE} \)-set, \(a<b\), and \(\psi \in \mathfrak {D}_{[a,b]}\) with \(\text {im} [\psi ]\subseteq \text {M} \) be given. Then,
converges uniformly for each fixed \(X\in \text {M} \). In particular, the following assertions hold:
-
(1)
For \(\textsf {v} \le \textsf {w} \) as in (28), we have
$$\begin{aligned} \textsf {v} \circ {\textbf {Ad}} ^\pm _\psi [X]\le \textsf {w} (X)\cdot \text {e} ^{\int _a^\bullet \textsf {w} (\psi (s))\,\text {d} s}\qquad \quad \forall \, X\in \text {M} . \end{aligned}$$ -
(2)
By (48), for \(Z\in \text {dom} [\exp ]\cap \text {M} \) we have
$$\begin{aligned} \textstyle \text {Ad} _{\exp (t\cdot Z)^{\pm 1}}(X)={\textbf {Ad}} ^\pm _{\mathcal {C}_Z|_{[0,1]}}[X](t)= \sum _{\ell =0}^\infty \frac{t^\ell }{\ell !}\cdot \text {ad} _{\pm Z}^\ell (X)\qquad \quad \forall \, X\in \text {M} ,\, t\in [0,1]. \end{aligned}$$
Proof
Equation (68) is clear from the following two estimates:
-
Let \(\textsf {v} \le \textsf {w} \) be as in (28), as well as \(\textsf {w} \le \textsf {m} \) be as in Corollary 6 for \(\textsf {q} \equiv \textsf {w} \) and
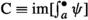 there. We obtain from Lemma 13 that $$\begin{aligned} \textstyle \textsf {v} \big ({\textbf {Ad}} ^+_\psi [X](t)\textstyle -\sum _{\ell =0}^n \varvec{\lambda }^+_{\ell ,\psi }[X](t)\big )&\textstyle =\textsf {v} \big (\varvec{\mathfrak {R}}^+_{n+1,\psi }[X](t)\big )\\&\textstyle \le \frac{(b-a)^{n+1}}{(n+1)!}\cdot \textsf {w} _\infty (\psi )^{n+1}\cdot \textsf {w} _\infty ({\textbf {Ad}} ^+_\psi [X])\\&\textstyle \le \frac{(b-a)^{n+1}}{(n+1)!}\cdot \textsf {w} _\infty (\psi )^{n+1}\cdot \textsf {m} (X) \end{aligned}$$
there. We obtain from Lemma 13 that $$\begin{aligned} \textstyle \textsf {v} \big ({\textbf {Ad}} ^+_\psi [X](t)\textstyle -\sum _{\ell =0}^n \varvec{\lambda }^+_{\ell ,\psi }[X](t)\big )&\textstyle =\textsf {v} \big (\varvec{\mathfrak {R}}^+_{n+1,\psi }[X](t)\big )\\&\textstyle \le \frac{(b-a)^{n+1}}{(n+1)!}\cdot \textsf {w} _\infty (\psi )^{n+1}\cdot \textsf {w} _\infty ({\textbf {Ad}} ^+_\psi [X])\\&\textstyle \le \frac{(b-a)^{n+1}}{(n+1)!}\cdot \textsf {w} _\infty (\psi )^{n+1}\cdot \textsf {m} (X) \end{aligned}$$holds for each \(t\in [a,b]\), \(X\in \mathfrak {g}\), and \(n\in \mathbb {N}\).
-
Let \(\textsf {q} \le \textsf {m} \) be as in Corollary 6 for
 there. Let furthermore \(\textsf {m} \le \textsf {w} \) be as in (28) for \(\textsf {v} \equiv \textsf {m} \) there. We obtain from Lemma 13 that $$\begin{aligned} \textstyle \textsf {q} \big ({\textbf {Ad}} ^-_\psi [X](t)\textstyle -\sum _{\ell =0}^n \varvec{\lambda }^-_{\ell ,\psi }[X](t)\big ) \textstyle =\textsf {q} \big ( \varvec{\mathfrak {R}}^-_{n+1,\psi }[X](t) \big )\le \frac{(b-a)^{n+1}}{(n+1)!}\cdot \textsf {w} _\infty (\psi )^{n+1}\cdot \textsf {w} (X) \end{aligned}$$
there. Let furthermore \(\textsf {m} \le \textsf {w} \) be as in (28) for \(\textsf {v} \equiv \textsf {m} \) there. We obtain from Lemma 13 that $$\begin{aligned} \textstyle \textsf {q} \big ({\textbf {Ad}} ^-_\psi [X](t)\textstyle -\sum _{\ell =0}^n \varvec{\lambda }^-_{\ell ,\psi }[X](t)\big ) \textstyle =\textsf {q} \big ( \varvec{\mathfrak {R}}^-_{n+1,\psi }[X](t) \big )\le \frac{(b-a)^{n+1}}{(n+1)!}\cdot \textsf {w} _\infty (\psi )^{n+1}\cdot \textsf {w} (X) \end{aligned}$$holds for each \(t\in [a,b]\), \(X\in \mathfrak {g}\), and \(n\in \mathbb {N}\).
Now, Part 2) is just clear from (68), and Part 1) is clear from (68) as well as
for each \(\ell \ge 1\). (The equality in the second step just follows by induction over \(\ell \ge 1\), via taking the derivative of both expressions.) \(\square \)
Example 7
Let \(\text {N} \subseteq \mathfrak {g}\) be a \(\text {Nil} _{q}\)-set for some \(q\ge 2\). Then, \(\text {N} \) is an \(\text {AE} \)-set, and Corollary 8 shows
for each \(X\in \text {N} \) and \(\psi \in \mathfrak {D}\) with \(\text {im} [\psi ]\subseteq \text {N} \). In particular, we have
for each \(X\in \text {N} \) and \(Z\in \text {dom} [\exp ]\cap \text {N} \). \(\square \)
4 A generalized BCDH formula
In the first part of this section, we generalize the Baker–Campbell–Dynkin–Hausdorff formula (for the exponential map) to the product integral (cf. Proposition 3). In the second part, we apply this formula (together with the integral transformation introduced in Sect. 3.1) to express the product integral of nilpotent curvesFootnote 13 (cf. Theorem 1) via the exponential map. Various applications of the derived formula are discussed in Sect. 4.2.1.
4.1 A BCDH formula for the product integral
Let \(\mathfrak {X}\in C^1([a,b],\mathfrak {g})\) for \(a<b\) be given, with \(\text {im} [\mathfrak {X}]\subseteq \text {dom} [\exp ]\). In this section, we consider the following two situations:
-
A) G is a Banach Lie group with \(\Vert [X,Y]\Vert \le \Vert X\Vert \cdot \Vert Y\Vert \) for all \(X,Y\in \mathfrak {g}\), and we have \(\Vert \mathfrak {X}\Vert _\infty <\ln (2)\). We set \(V:=\mathfrak {g}\) as well as \({\textbf {I}} ,{\textbf {J}} :=\infty \), and observe the following:
-
− \((\mathfrak {g},\varvec{[}\cdot , \cdot \varvec{]})\) is asymptotic estimate.
-
− \(\exp :\mathfrak {g}\rightarrow \mathfrak {g}\) is defined and smooth, and a local diffeomorphism. In particular, there exists an identity neighborhood \(\mathcal {O}\subseteq G\) on which \(\exp \) is a diffeomorphism, such that \(\Vert \exp ^{-1}(g)\Vert <\ln (2)\) holds for each \(g\in \mathcal {O}\).
-
− G is \(C^0\)-regular (even \(L^1\)-regular by Theorem C in [5]). In particular, there exists some \(\mathfrak {r}>0\), such that for all \(\phi \in C^0([a,b],\mathfrak {g})\) (\(a<b\)) and \(\psi \in C^0([a',b'],\mathfrak {g})\) (\(a'<b'\)) with \(\int _a^b \Vert \phi (s)\Vert \, \text {d} s + \int _{a'}^{b'} \Vert \psi (s)\Vert \, \text {d} s< \mathfrak {r}\), we haveFootnote 14
 (69)
(69)
-
-
B) G is weakly \(C^\infty \)-regular, or \(\exp :\mathfrak {g}\rightarrow G\) is defined (\(\text {dom} [\exp ]=\mathfrak {g}\)) and of class \(C^1\). Moreover, \(\text {N} :=\text {im} [\mathfrak {X}]\cup \text {im} [{\dot{\mathfrak {X}}}]\) is a \(\text {Nil} _{q}\)-set for some \(q\ge 2\). We set \(V:=\overline{\mathcal {G}}_1(\text {N} )\) as well as \({\textbf {I}} :=q-1\) and \({\textbf {J}} :=q-2\), and recall that V is a \(\text {Nil} _{q}\)-set by Remark 3.3).
In both situations, the presumptions in Corollary 4 are fulfilled. Moreover, by Example 1, for \(t\in [a,b]\) and \(Y\in V\), we have
with \(\Phi (\text {ad} _{\mathfrak {X}(t)})(Y)\in V\) (by Remark 3 in the situation of B)). Here, for maps \(\xi ,\zeta :\mathfrak {g}\rightarrow \mathfrak {g}\) as well as \(X\in \mathfrak {g}\), we set (convergence presumed)
We obtain the following proposition:
Proposition 3
Let \(\phi \in \mathfrak {D}_{[a,b]}\), \(g\in G\), \(\mathfrak {X}\in C^1([a,b],\mathfrak {g})\) be given, with \(\text {im} [\mathfrak {X}]\subseteq \text {dom} [\exp ]\) as well as

Assume furthermore that we are in the situation of A) or B). Then, we have \(\text {im} [\phi ]\subseteq V\), and the following identities hold for each \(t\in [a,b]\):



Proof
We observe the following:
-
For \(t\in [a,b]\), we have by Corollary 8.2) (and Example 7)
$$\begin{aligned} \textstyle \text {Ad} _{\exp (\lambda \cdot \mathfrak {X}(t))^{\pm 1}}|_V \textstyle = \sum _{n=0}^{\textbf {J}} \frac{\lambda ^n}{n!}\cdot \text {ad} _{\pm \mathfrak {X}(t)}^n|_V. \end{aligned}$$(76) -
For \(t\in [a,b]\), we have
$$\begin{aligned} \Phi (\text {ad} _{\mathfrak {X}(t)})(\dot{\mathfrak {X}}(t))&\textstyle = \sum _{n=0}^{{\textbf {J}} } \frac{1}{(n+1)!} \cdot \text {ad} _{\mathfrak {X}(t)}^n(\dot{\mathfrak {X}}(t))\in V. \end{aligned}$$(77) -
For \(t\in [a,b]\), we have by (70), (71), and (77) that
$$\begin{aligned} \begin{aligned} \dot{\mathfrak {X}}(t)&= \textstyle \Psi \big (\sum _{n=0}^\infty \frac{1}{n!}\cdot \text {ad} _{\mathfrak {X}(t)}^n\big )(\Phi (\text {ad} _{\mathfrak {X}(t)})(\dot{\mathfrak {X}}(t)))\\&= \textstyle \widetilde{\Psi }\big (\sum _{n=0}^\infty \frac{1}{n!}\cdot \text {ad} _{-\mathfrak {X}(t)}^n\big )(\Phi (\text {ad} _{\mathfrak {X}(t)})(\dot{\mathfrak {X}}(t))). \end{aligned} \end{aligned}$$(78)
Set \(\alpha :=\exp \circ \mathfrak {X}\in C^1([a,b],\mathfrak {g})\). Then, given \(t\in [a,b]\), we obtain from (72) (first step), Corollary 4 (second step), (22) (third step), (76) (fourth step), \(C^0\)-continuity of the Riemann integral in the situation of A) (fifth step), as well as (77) (fifth step) that
Together with (77), this shows
We obtain from (17), (78), (79), and (76) the following identities for each \(t\in [a,b]\):
Together with (72), this implies (73) and (74). We now finally have to prove (75):
-
Assume that we are in the situation of B). Since \(\text {im} [\phi ]\subseteq V\) holds by (79), we obtain from (17), (78), (79) (first step), \(\text {im} [\phi ]\subseteq V\) (second step), linearity of the Riemann integral (third step), (76) (fourth step), and (72) (fifth step) that
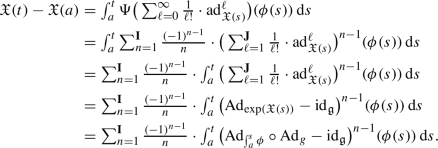
-
Assume that we are in the situation of A). Then, (76) (first step) together with \(\Vert \mathfrak {X}\Vert _\infty <\ln (2)\) (last step) implies
$$\begin{aligned} \begin{aligned} \textstyle \Vert (\text {Ad} _{\exp (\mathfrak {X}(t))}-\text {id} _\mathfrak {g})^k(\phi (t))\Vert&\textstyle \le (\Vert \sum _{\ell =1}^\infty \frac{1}{\ell !}\cdot \text {ad} _{\mathfrak {X}(t)}^\ell \Vert _\text {op} )^k\cdot \Vert \phi \Vert _\infty \\&\textstyle \le (\sum _{\ell =1}^\infty \frac{1}{\ell !}\cdot \Vert \text {ad} _{\mathfrak {X}(t)}^\ell \Vert _\text {op} )^k \cdot \Vert \phi \Vert _\infty \\&\textstyle \le \big (\text {e} ^{\Vert \mathfrak {X}\Vert _\infty }-1\big )^k \cdot \Vert \phi \Vert _\infty \\&\textstyle <\Vert \phi \Vert _\infty \end{aligned} \end{aligned}$$(81)for each \(t\in [a,b]\) and \(k \ge 1\). We obtain from (80) (first step), \(C^0\)-continuity of the Riemann integral and (81) (third step), as well as (72) (fourth step) that

holds for each \(t\in [a,b]\).\(\square \)
Proposition 4
Assume that G is a Banach Lie group, and let \(\mathfrak {r}>0\) be as in A). Let \(\phi \in C^0([a,b],\mathfrak {g})\) (\(a<b\)) and \(\psi \in C^0([a',b'])\) (\(a'<b'\)) be given, with \(\int _a^b \Vert \phi (s)\Vert \, \text {d} s+ \int _{a'}^{b'} \Vert \psi (s)\Vert \, \text {d} s< \mathfrak {r}\). Then, we have

provided that for \(t'\in [a',b']\) and \(t\in [a,b]\) we set
Proof
By definition, there exist open intervals \(I,I'\subseteq \mathbb {R}\) with \([a,b]\subseteq I\) and \([a',b']\subseteq I'\), as well as \(\mu \in C^1(I,G)\) and \(\nu \in C^1(I',G)\), with  and
and  . We make the following modifications to these curves:
. We make the following modifications to these curves:
-
We replace \(\mu \) by \(\mu \cdot \mu (a)^{-1}\) to ensure
 .
. -
We replace \(\nu \) by \(\nu \cdot \nu (a')^{-1}\) to ensure
 .
. -
We define \(\alpha :=\mu \cdot \nu (b')\), and observe
 .
. -
We shrink I around [a, b] and \(I'\) around \([a',b']\), to ensure \(\mu (I)\cdot \nu (I')\subseteq \mathcal {O}\) (recall (69)).
Then, the maps
are defined and of class \(C^1\), with

We conclude the following:
-
Equation (75) in Proposition 3 for \(g\equiv e\) there, together with Corollary 8 shows \(\mathfrak {X}'=\mathfrak {X}_\psi \).
-
Equation (75) in Proposition 3 for
 there, together with Corollary 8 and the previous point shows $$\begin{aligned} \mathfrak {X}-\mathfrak {X}_\psi (b')=\mathfrak {X}-\mathfrak {X}'(b')=\mathfrak {X}-\mathfrak {X}(a)=\mathfrak {X}_{\phi ,\psi }, \end{aligned}$$
there, together with Corollary 8 and the previous point shows $$\begin{aligned} \mathfrak {X}-\mathfrak {X}_\psi (b')=\mathfrak {X}-\mathfrak {X}'(b')=\mathfrak {X}-\mathfrak {X}(a)=\mathfrak {X}_{\phi ,\psi }, \end{aligned}$$which proves the claim. \(\square \)
Corollary 9
Assume that G is a Banach Lie group, and let \(\mathfrak {r}>0\) be as in A). Then, for \(\phi \in C^0([a,b],\mathfrak {g})\) (\(a<b\)) with \(\int _a^b \Vert \phi (s)\Vert \, \text {d} s< \mathfrak {r}\), we have

Proof
Apply Proposition 4 with \(\psi =0\). \(\square \)
Example 8
(The BCDH Formula) Assume that we are in the situation of Proposition 3, with
for certain \(X,Y\in \mathfrak {g}\) and \(\mathfrak {X}\in C^1([0,1],\mathfrak {g})\). We obtain the well-knownFootnote 15 integral representation of the Baker–Campbell–Dynkin–Hausdorff formula:
Proof of Equation (83)
By (48), we have  for each \(t\in [0,1]\), hence
for each \(t\in [0,1]\), hence

Then, (74) in Proposition 3 shows

for each \(t\in [0,1]\), from which the claim follows. \(\square \)
For instance, the assumptions in (82) are fulfilled in the following situations:
-
G is a Banach Lie group, with \(\Vert X\Vert +\Vert Y\Vert <\mathfrak {r}\). Indeed, by A), then there exists \(\mathfrak {X}\in C^1([0,1],\mathfrak {g})\) with \(\mathfrak {X}(0)=-X\), such that (72) holds for \(\phi \) and g as in (82).
-
G is weakly \(C^k\)-regular for \(k\in \mathbb {N}\cup \{\text {lip} ,\infty \}\), and \(\{X,Y\}\) is a \(\text {Nil} _{q}\)-set for some \(q\ge 2\). Indeed, we will reconsider this situation in Corollary 11 in Sect. 4.2. There, we construct some \(\mathfrak {X}\in C^1([0,1],\mathfrak {g})\) with \(\mathfrak {X}(0)=-X\), such that (72) holds for \(\phi \) and g as in (82). \(\square \)
4.2 The product integral of nilpotent curves
Assume that G is weakly \(C^k\)-regular for \(k\in \mathbb {N}\cup \{\text {lip} ,\infty \}\), and let \(\phi \in C^k([a,b],\mathfrak {g})\) for \(a<b\) as well as \(\psi \in C^k([a',b'],\mathfrak {g})\) for \(a'<b'\) be given.
-
If \(\text {im} [\psi ]\) is a \(\text {Nil} _{q}\)-set for some \(q\ge 2\), then for each \(t\in [a',b']\) we set
 (84)
(84) -
If \(\text {im} [\phi ]\cup \text {im} [\psi ]\) is a \(\text {Nil} _{q}\)-set for some \(q\ge 2\), then for each \(t\in [a,b]\) we set
 (85)
(85)
Notably, both maps take values in \(\mathfrak {g}\) by Lemma 8 and are thus of class \(C^1\) by (20). In this section, we combine Proposition 3 with the integral transformation introduced in Sect. 3.1 to prove the following statement.
Theorem 1
Assume that G is weakly \(C^k\)-regular for \(k\in \mathbb {N}\cup \{\text {lip} ,\infty \}\), and let \(\phi \in C^k([a,b],\mathfrak {g})\), \(\psi \in C^k([a',b'],\mathfrak {g})\) be given, such that \(\text {N} :=\text {im} [\phi ]\cup \text {im} [\psi ]\) is a \(\text {Nil} _{q}\)-set for some \(q\ge 2\). Then,

The proof of Theorem 1 is given in Sect. 4.2.2. We now first want to discuss some consequences.
4.2.1 Some consequences
Setting \(\psi =0\) in Theorem 1, we immediately obtain the following statement.
Corollary 10
Assume that G is weakly \(C^k\)-regular for \(k\in \mathbb {N}\cup \{\text {lip} ,\infty \}\), and let \(\phi \in C^k([a,b],\mathfrak {g})\) be given such that \(\text {im} [\phi ]\) is a \(\text {Nil} _{q}\)-set for some \(q\ge 2\). Then, we have

Example 9
Let G be abelian, as well as weakly \(C^k\)-regular for some \(k\in \mathbb {N}\cup \{\text {lip} ,\infty \}\). Then, \(\mathfrak {g}\) is a \(\text {Nil} _{2}\)-set, and Corollary 10 recovers formula (51) in Example 6. \(\square \)
Moreover, combining Theorem 1 with Example 8, we obtain the BCDH formula:
Corollary 11
Assume that G is weakly \(C^k\)-regular for \(k\in \mathbb {N}\cup \{\text {lip} ,\infty \}\). Let furthermore \(X,Y\in \mathfrak {g}\) be given, such that \(\{X,Y\}\) is a \(\text {Nil} _{q}\)-set for some \(q\ge 2\). Then, we have
Proof
Set \(\phi :=-\mathcal {C}_Y|_{[0,1]}\) as well as \(\psi := -\mathcal {C}_X|_{[0,1]}\), and let \(\mathfrak {X}_\psi ,\mathfrak {X}_{\phi ,\psi }\) be as in (84),(85). Then, \(\mathfrak {X}:[0,1]\ni t\mapsto \mathfrak {X}_\psi (1) + \mathfrak {X}_{\phi ,\psi }(t) \in \mathfrak {g}\) is of class \(C^1\), with \(\mathfrak {X}(0)=\mathfrak {X}_\psi (1)=-X\), as well as

by Theorem 1. The claim is thus clear from Example 8. \(\square \)
Next, we define
We observe the following:
Lemma 14
If G is weakly \(C^\infty \)-regular, then \(G^\infty _{\textrm{Nil}}=\text {im} [\exp ]\) holds.
Proof
Obviously, have \(\mathfrak {i}(\text {dom} [\exp ])\subseteq \Gamma ^\infty _{\textrm{Nil}}\), hence \(\text {im} [\exp ]\subseteq G^\infty _{\textrm{Nil}}\). Moreover, Corollary 10 shows \(G^\infty _{\textrm{Nil}}\subseteq \text {im} [\exp ]\), which proves the claim. \(\square \)
Lemma 15
Assume that G is connected. Then, \({\text {evol} }_\infty \) is surjective.
Proof
Let \(\mathcal {A}\subseteq G\) denote subgroup of all \(g\in G\), such that there exist \(\mu _1,\dots ,\mu _n\in C^\infty ([0,1],G)\) (\(n\in \mathbb {N}\)), with \(g=\mu _n(1)\cdot {\dots }\cdot \mu _1(1)\) as well as \(\mu _\ell (0)=e\) for \(\ell =1,\dots ,n\). Set furthermore \(\mathcal {O}:= \mathcal {U}\cap \textsf {inv} (\mathcal {U})\). Since G is connected, we have \(G=\bigcup _{n\ge 1} \mathcal {O}^n\). Since \(\mathcal {O}\subseteq \mathcal {U}\subseteq \mathcal {A}\) holds,Footnote 16 we obtain \(G=\mathcal {A}\). Let now \(g\in G\) be fixed, and choose \(\mu _1,\dots ,\mu _n\in C^\infty ([0,1],\mathfrak {g})\) with \(\mu _1(0),\dots ,\mu _n(0)=e\) and \(g=\mu _n(1)\cdot {\dots }\cdot \mu _1(1)\). We set  for \(\ell =1,\dots ,n\), and observe
for \(\ell =1,\dots ,n\), and observe

Applying (a) inductively, we obtain (recall Remark 5)

which proves the claim. \(\square \)
Combining Lemma 14 with Lemma 15, we obtain the following proposition.
Proposition 5
Assume that G is weakly \(C^\infty \)-regular and connected. If \(\Gamma ^\infty _{\textrm{Nil}}= C^\infty ([0,1],\mathfrak {g})\) holds, then \(\exp :\mathfrak {g}\rightarrow G\) is surjective.
Proof
Lemma 14 shows \(\text {im} [\exp ]=G^\infty _{\textrm{Nil}}={\text {evol} }_\infty (\Gamma ^\infty _{\textrm{Nil}})\), with \({\text {evol} }_\infty (\Gamma ^\infty _{\textrm{Nil}})={\text {evol} }_\infty (C^\infty ([0,1],\mathfrak {g}))\) by assumption. Since \({\text {evol} }_\infty \) is surjective by Lemma 15, the claim follows. \(\square \)
Proposition 5 immediately implies the following statement.
Corollary 12
Assume that G is weakly \(C^\infty \)-regular and connected. If \((\mathfrak {g},\varvec{[}\cdot , \cdot \varvec{]})\) is nilpotent, then \(\exp \) is surjective.
Remark 11
-
(1)
The statement in Corollary 12 follows from Theorem IV.2.6 in [21] provided we replace “weakly \(C^\infty \)-regular” by “\(\mathfrak {g}\) is Mackey complete and \(\exp \) is smooth”.
-
(2)
Let \(\mathfrak {g}\) be finite-dimensional. Then, the hypothesis \(\Gamma ^\infty _{\textrm{Nil}}= C^\infty ([0,1],\mathfrak {g})\) in Proposition 5 is equivalent to nilpotency of \(\mathfrak {g}\).
In fact, the one implication is evident. Assume thus that \(\Gamma ^\infty _{\textrm{Nil}}= C^\infty ([0,1],\mathfrak {g})\) holds, and let \(\{X_0,\dots ,X_{n-1}\}\subseteq \mathfrak {g}\) be a base of \(\mathfrak {g}\). Let furthermore \(\rho :[0,1/n]\rightarrow [0,\infty )\) be a bump function, i.e., \(\rho \) is smooth with
$$\begin{aligned} \rho |_{(0,1/n)}>0\qquad \quad \text {as well as}\qquad \quad \rho ^{(\ell )}(0)=0=\rho ^{(\ell )}(1/n)\qquad \forall \,\ell \in \mathbb {N}. \end{aligned}$$We define \(\phi :[0,1]\rightarrow \mathfrak {g}\) by \(\phi (0):=0\) and
$$\begin{aligned} \phi |_{(\ell /n,(\ell +1)/n]}:(\ell /n,(\ell +1)/n]\ni t \mapsto \rho (t-\ell /n)\cdot X_\ell \in \mathfrak {g}\qquad \quad \forall \, \ell =0,\dots ,n-1. \end{aligned}$$Then, \(\phi \) is easily seen to be smooth (for details confer, e.g., Lemma 24 and Appendix B.2 in [8]). By assumption, there exists some \(q\ge 2\), such that \(\text {N} :=\text {im} [\phi ]\) is a \(\text {Nil} _{q}\)-set. Then, \(\mathcal {V}_1(\text {N} )\) is a \(\text {Nil} _{q}\)-set by Remark 3, with \(\{X_0,\dots ,X_{n-1}\}\subseteq \mathcal {V}_1(\text {N} )\), hence \(\mathfrak {g}=\mathcal {V}_1(\text {N} )\). \(\square \)
We finally want to mention that Proposition 5 also provides an easy proof of the following well-known result in the finite-dimensional context.
Corollary 13
If G is compact and connected, then \(\exp \) is surjective.
Proof
Let \(T\subseteq G\) be a maximal torus with Lie algebra \(\mathfrak {t}\). Since T is abelian, Corollary 12 shows that \(\exp |_\mathfrak {t}:\mathfrak {t}\rightarrow T\) is surjective. Since G is covered by maximal tori (confer, e.g., Theorem 12.2.2.(iii) in [13]), the claim follows. \(\square \)
Remark 12
The proof of Corollary 13 can be simplified. Specifically, surjectivity of \(\exp |_\mathfrak {t}:\mathfrak {t}\rightarrow T\) also follows from Lemma 15 and formula (51) (as T is abelian). Notably, in finite dimensions, (51) follows easily from smoothness of the exponential map:
Proof of (51) in the finite-dimensional case
Let G be abelian and finite-dimensional, and let \(\phi \in C^0([a,b],\mathfrak {g})\) be given. Let \(\psi \in C^0([a,b+\varepsilon ),\mathfrak {g})\) for \(\varepsilon >0\) be a continuous extension of \(\phi \). Then,
is of class \(C^1\) as \(\exp \) is smooth. Since G is abelian, we have
Since \(\text {d} _e\exp =\text {id} _\mathfrak {g}\) holds, we obtain  , hence
, hence

by injectivity of  . \(\square \)
. \(\square \)
4.2.2 The proof of Theorem 1
In this subsection, we prove Theorem 1. Our argumentation is based on the following (straightforward but technical) lemma that is proven in Sect. 4.2.3.
Lemma 16
Let G be weakly \(C^k\)-regular for \(k\in \mathbb {N}\cup \{\text {lip} ,\infty \}\), and let \(\phi \in C^k([a,b],\mathfrak {g})\) be given such that \(\text {im} [\phi ]\) is a \(\text {Nil} _{q}\)-set for some \(q\ge 2\). Then, the following assertions hold:
-
We have \(\mathfrak {T}^{q-1}(\phi |_{[a,\tau ]})\in C^\text {c} ([0,1],\mathfrak {g})\) for each \(\tau \in [a,b]\), hence the map (recall (47))
$$\begin{aligned} \mathfrak {X}:[a,b]\ni \tau \mapsto \mathfrak {i}^{-1}(\mathfrak {T}^q(\phi |_{[a,\tau ]}))\in \mathfrak {g}\end{aligned}$$is defined.
-
We have \(\mathfrak {X}\in C^1([a,b],\mathfrak {g})\), and \(\text {im} [\mathfrak {X}]\cup \text {im} [{\dot{\mathfrak {X}}}]\) is a \(\text {Nil} _{q}\)-set.
In particular, iterated application of Proposition 1 yields

Proof
Confer Sect. 4.2.3. \(\square \)
Remark 13
Let \(\psi \in C^0([x,y],\mathfrak {g})\) with \(x<y\) be given. Let \(\varrho :[x',y']\rightarrow [x,y]\) (\(x'<y'\)) be of class \(C^1\), with \(\varrho (x')=x\) and \(\varrho (y')=y\). We set \(\phi := {\dot{\varrho }}\cdot (\psi \circ \varrho )\) and obtain inductively from (21) that
holds for each \(\ell \in \mathbb {N}\). \(\square \)
We are ready for the proof of Theorem 1.
Proof of Theorem 1
Let \(\varrho _1:[0,1]\rightarrow [a',b']\) and \(\varrho _2:[1,2]\rightarrow [a,b]\) be smooth, such that \(\rho _{j}:={\dot{\varrho }}_j\) is a bump function for \(j=1,2\), i.e., we haveFootnote 17
Define \(\chi :[0,1]\rightarrow \mathfrak {g}\) by
Then, \(\chi \) is easily seen to be of class \(C^k\) (confer, e.g., Lemma 24 and Appendix B.2 in [8]), with \(\text {im} [\chi ]\subseteq \mathcal {V}_1(\text {N} )\subseteq \overline{\mathcal {G}}_1(\text {N} )\) (a \(\text {Nil} _{q}\)-set by Remark 3). Then, for \(\tau \in [0,1]\) and \(t\in [1,2]\), we have

Now, Lemma 16 provides some \(\tilde{\mathfrak {X}}\in C^1([0,2],\mathfrak {g})\) with  , such that \(\text {im} [\tilde{\mathfrak {X}}]\cup \text {im} [\dot{\tilde{\mathfrak {X}}}]\) is a \(\text {Nil} _{q}\)-set. In particular, we have
, such that \(\text {im} [\tilde{\mathfrak {X}}]\cup \text {im} [\dot{\tilde{\mathfrak {X}}}]\) is a \(\text {Nil} _{q}\)-set. In particular, we have

and obtain from Proposition 3 (specifically from (75) with \(g\equiv e\) and \(\mathfrak {X}\equiv \tilde{\mathfrak {X}}|_{[0,1]}\) there) and (68) in Corollary 8 (first step), as well as Remark 13 (second step) that
holds. Moreover, (75) in Proposition 3 applied with  , \(\phi \equiv \chi |_{[1,2]}\), \(\mathfrak {X}\equiv \tilde{\mathfrak {X}}|_{[1,2]}\) there (first step) yields for \(t\in [1,2]\) that
, \(\phi \equiv \chi |_{[1,2]}\), \(\mathfrak {X}\equiv \tilde{\mathfrak {X}}|_{[1,2]}\) there (first step) yields for \(t\in [1,2]\) that

We obtain

From this, the claim follows, because \(\varrho _2\) is strictly increasing on (1, 2), thus strictly increasing on [1, 2], hence bijective. \(\square \)
4.2.3 The proof of Lemma 16
Let \(\text {N} \subseteq \mathfrak {g}\) and \(\ell \ge 1\) be given:
We let \(\mathcal {H}_\ell (\text {N} )\) denote the set of all maps \(\alpha :[a,b]\times [0,1]\rightarrow \mathfrak {g}\) that admit the following properties:
- (1):
-
We have \(\text {im} [\alpha ]\subseteq \overline{\mathcal {G}}_{\ell +1}(\text {N} )\).
- (2):
-
There exists a continuous map \(L:[a,b]\times [0,1]\rightarrow \overline{\mathcal {G}}_1(\text {N} )\subseteq \mathfrak {g}\), as well as a map \(\tilde{\alpha }:I\times [0,1]\rightarrow \mathfrak {g}\) for \(I\subseteq \mathbb {R}\) an open interval with \([a,b]\subseteq I\), such that the following conditions hold:
- (a):
-
\(\tilde{\alpha }\) is continuous, with \(\tilde{\alpha }|_{[a,b]\times [0,1]}=\alpha \).
- (b):
-
To each \(\tau \in [a,b]\), there exist \(\delta _{\tau }>0\) as well as \(\epsilon _\tau :(-\delta _\tau ,\delta _\tau )\times [0,1]\rightarrow \mathfrak {g}\) continuous with \(\lim _{h\rightarrow 0}\textsf {p} _\infty (\epsilon _\tau (h,\cdot ))=0\) for each \(\textsf {p} \in \textsf {Sem}(E)\), such that
$$\begin{aligned} \tilde{\alpha }(\tau +h,t)= \tilde{\alpha }(\tau ,t) + h\cdot L(\tau ,t) + h\cdot \epsilon _\tau (h,t)\qquad \quad (h,t)\in (-\delta _\tau ,\delta _\tau )\times [0,1]. \end{aligned}$$In particular, \(\Phi \equiv \tilde{\alpha }\) fulfills the assumptions in Theorem C for \((G,\cdot )\equiv (\mathfrak {g},+)\) there (recall Remark 8), i.e., we have
$$\begin{aligned} \textstyle \frac{\text {d} }{\text {d} h}\big |_{h=0}\int _0^1\alpha (\tau +h,s)\,\text {d} s= \int _0^1 L(\tau ,s)\,\text {d} s\qquad \quad \forall \, \tau \in [a,b]. \end{aligned}$$(89)
We let \(\mathcal {K}_{\ell }(\text {N} )\) denote the set of all (continuous) maps of the form
for \(\mathfrak {z}\in C^1([a,b],\mathfrak {g})\) with \(\text {im} [\mathfrak {z}]\cup \text {im} [{\dot{\mathfrak {z}}}]\subseteq \overline{\mathcal {G}}_1(\text {N} )\), and \(\alpha \in \mathcal {H}_\ell (\text {N} )\) (in particular, \(\text {im} [\eta ]\subseteq \overline{\mathcal {G}}_1(\text {N} )\)).
We recall Convention (50), and are ready for the proof of Lemma 16.
Proof of Lemma 16
Set \(\text {N} :=\text {im} [\phi ]\). We prove by induction that
holds. Evaluating this for \(\ell =q-1\), the claim follows because:
-
For \(\alpha \in \mathcal {H}_{q-1}(\text {N} )\), we have \(\text {im} [\alpha ]\subseteq \overline{\mathcal {G}}_q(\text {N} )=\{0\}\) by Condition 1) and Remark 3.1).
-
\(\overline{\mathcal {G}}_1(\text {N} )\) is a \(\text {Nil} _{q}\)-set by Remark 3.3).
To perform the induction, we fix \(\varepsilon >0\) and \(\tilde{\phi }\in C^k([a-\varepsilon ,b+\varepsilon ],\mathfrak {g})\) with \(\tilde{\phi }|_{[a,b]}=\phi \). We observe that for each \(\psi \in \mathfrak {D}_{[a,b]}\) with \(\text {im} [\psi ]\) a \(\text {Nil} _{q}\)-set, and \(\lambda ,t\in [a,b]\) we have (confer Example 7)

Induction Basis: Let \(\ell =1\). By (91), for \(\tau \in [a,b]\) and \(t\in [0,1]\) we have

with
-
\(\mathfrak {z}\in C^1([a,b],\mathfrak {g})\) by (20), and \(\text {im} [\mathfrak {z}]\cup \text {im} [{\dot{\mathfrak {z}}}]\subseteq \overline{\mathcal {G}}_1(\text {N} )\) by Remark 3.4).
-
\(\text {im} [\alpha ]\subseteq \overline{\mathcal {G}}_2(\text {N} )\) (hence Condition 1) for \(\ell \equiv 1\) there) by Remark 3.4).
To verify Condition 2), for \(\tau _1,\tau _2\in I:= (a-\varepsilon ,b+\varepsilon )\) and \(t\in [0,1]\), we set
and define \(\tilde{\alpha }(\tau ,t):= \tilde{\beta }(\tau ,\tau ,t) - \tilde{\beta }(a,\tau ,t)\) for \(\tau \in I\) and \(t\in [0,1]\). Then, \(\tilde{\alpha }\) is continuous, with \(\tilde{\alpha }|_{[a,b]\times [0,1]}=\alpha \), hence fulfills Condition 2).a). Moreover, for \(\tau \in I\), \(t\in [0,1]\), and \(|h|>0\) suitably small, we have
We define \(L:[a,b]\times [0,1]\rightarrow \overline{\mathcal {G}}_1(\text {N} )\subseteq \mathfrak {g}\) (recall Remark 3.4)) by
for all \(\tau \in [a,b]\) and \(t\in [0,1]\). Clearly, L is continuous; and it follows from (19) as well as continuity of the involved maps that
holds, which verifies Condition 2).b). We thus have shown (90) for \(\ell = 1\). In particular, this proves the claim for \(q=2\).
Induction Step: Assume that (90) holds for some \(1\le \ell \le q-1\) (with \(q\ge 3\)), hence we have
for some \(\mathfrak {z}_\ell \in C^1([a,b],\mathfrak {g})\) with \(\text {im} [\mathfrak {z}_\ell ]\cup \text {im} [{\dot{\mathfrak {z}}}_\ell ]\subseteq \overline{\mathcal {G}}_1(\text {N} )\), as well as \(\alpha _\ell \in \mathcal {H}_{\ell }(\text {N} )\). Let \(I\subseteq \mathbb {R}\) be as in Condition 2) for \(\alpha \equiv \alpha _\ell \) there. We can shrink I around [a, b] in such a way that \(\mathfrak {z}_\ell \) extends to a \(C^1\)-curve \(\tilde{\mathfrak {z}}_\ell \in C^1(I,\mathfrak {g})\), and set
Now, (91) for \(\psi \equiv \eta _\ell (\tau ,\cdot )\) and \(\lambda \equiv 1\) yields for \(\tau \in [a,b]\) and \(t\in [0,1]\) that

We obtain from (92) that \(\mathfrak {z}_{\ell +1}=\mathfrak {z}_{\ell }+ \int _0^1 \alpha _\ell (\cdot ,s) \, \text {d} s\) holds, and conclude the following:
-
Let \(L:[a,b]\times [0,1]\rightarrow \overline{\mathcal {G}}_1(\text {N} )\subseteq \mathfrak {g}\) be as in Condition 2).b) for \(\alpha \equiv \alpha _\ell \) there (induction hypothesis). Then, we have
$$\begin{aligned} \textstyle {\dot{\mathfrak {z}}}_{\ell +1}(\tau ){\mathop {=}\limits ^{(89)}}{\dot{\mathfrak {z}}}_{\ell }(\tau ) + \int _0^1 L(\tau ,s)\, \text {d} s\in \overline{\mathcal {G}}_1(\text {N} ) \qquad \quad \forall \, \tau \in [a,b]. \end{aligned}$$Since L is continuous, this implies \(\mathfrak {z}_{\ell +1}\in C^1([a,b],\mathfrak {g})\) with \(\text {im} [\mathfrak {z}_{\ell +1}]\cup \text {im} [{\dot{\mathfrak {z}}}_{\ell +1}]\subseteq \overline{\mathcal {G}}_1(\text {N} )\).
-
We have \(\text {im} [\alpha _{\ell +1}]\subseteq \overline{\mathcal {G}}_{\ell +2}(\text {N} )\) by Remark 3.2), Remark 3.4), bilinearity of \(\varvec{[}\cdot , \cdot \varvec{]}\), and
-
\((\text {ad} _{\mathfrak {z}_\ell (\tau )}\circ \dots \circ \text {ad} _{\mathfrak {z}_\ell (\tau )})(\mathfrak {z}_\ell (\tau ))=0\) for all \(\tau \in [a,b]\),
-
\(\text {im} [\mathfrak {z}_\ell ]\subseteq \overline{\mathcal {G}}_1(\text {N} )\),
-
\(\text {im} [\alpha _\ell ]\subseteq \overline{\mathcal {G}}_{\ell +1}(\text {N} )\),
which verifies Condition 1) (for \(\alpha \equiv \alpha _{\ell +1}\) there).
-
It remains to verify Condition 2) (for \(\alpha \equiv \alpha _{\ell +1}\) there). For this, we set (recall (93))
for \(\tau \in I\) and \(t\in [0,1]\). Clearly, \(\tilde{\alpha }_{\ell +1}\) fulfills Condition 2).a) (for \(\alpha \equiv \alpha _{\ell +1}\) there). Moreover, since \(\mathfrak {z}_\ell \) is of class \(C^1\) with \(\text {im} [\mathfrak {z}]\cup \text {im} [{\dot{\mathfrak {z}}}]\subseteq \overline{\mathcal {G}}_1(\text {N} )\), by (93), and Condition 2).b) for \(\alpha \equiv \alpha _\ell \) (induction hypothesis), there exists a continuous map \(L:[a,b]\times [0,1]\rightarrow \overline{\mathcal {G}}_1(\text {N} )\subseteq \mathfrak {g}\), as well as to each fixed \(\tau \in [a,b]\) some \(\delta _{\tau }>0\) and \(\epsilon _\tau :(-\delta _\tau ,\delta _\tau )\times [0,1]\rightarrow \mathfrak {g}\) continuous with \(\lim _{h\rightarrow 0}\textsf {p} _\infty (\epsilon _\tau (h,\cdot ))=0\) for each \(\textsf {p} \in \textsf {Sem}(E)\), such that
holds. We define for \(\tau \in I\) and \(t\in [0,1]\)
where for \(1\le p\le q-2\) and \(0\le s_1,\dots ,s_p,s\le 1\), we set
as well as for \(1\le k\le p\)
It follows from continuity and bilinearity of \(\varvec{[}\cdot , \cdot \varvec{]}\), (94), and (19) that
holds, which verifies Condition 2).b) for \(\alpha \equiv \alpha _{\ell +1}\) there. \(\square \)
5 Asymptotic estimate Lie algebras
Throughout this section, \((\mathfrak {q},\varvec{[}\cdot , \cdot \varvec{]})\) denotes a fixed sequentially complete and asymptotic estimate Lie algebra, i.e., the following conditions are fulfilled:
-
\(\mathfrak {q}\in \textsf {hlcVect}\) is sequentially complete.
-
\(\varvec{[}\cdot , \cdot \varvec{]}:\mathfrak {q}\times \mathfrak {q}\rightarrow \mathfrak {q}\) is bilinear, antisymmetric, continuous, and fulfills the Jacobi identity (25). Moreover, to each \(\textsf {v} \in \textsf {Sem}(\mathfrak {q})\), there exist \(\textsf {v} \le \textsf {w} \in \textsf {Sem}(\mathfrak {q})\) with
$$\begin{aligned} \textsf {v} (\varvec{[}X_1,\varvec{[}X_2,\varvec{[}\dots ,\varvec{[}X_n,Y\varvec{]}{\dots }\varvec{]}\varvec{]}\varvec{]})\le \textsf {w} (X_1)\cdot {\dots }\cdot \textsf {w} (X_n)\cdot \textsf {w} (Y) \end{aligned}$$(95)for all \(X_1,\dots ,X_n,Y\in \mathfrak {q}\) and \(n\ge 1\).
The first part of this section (Sect. 5.1) is dedicated to a comprehensive analysis of the Lax equation
for \(X\in \mathfrak {q}\) and \(\psi \in C^0([a,b],\mathfrak {q})\) (\(a<b\)) fixed, and \(\alpha \in C^1([a,b],\mathfrak {q})\). We first show the existence and uniqueness of solutions and discuss their elementary properties (Sect. 5.1.1 and Sect. 5.1.2). More specifically, let \({\textbf {Ad}} ^\pm _\psi [X]\) be defined by the right hand side of (68). We show that the unique solution to the above equation is given by \(\alpha ={\textbf {Ad}} _\psi ^+[X]\). We also showFootnote 18
with \({\textbf {Ad}} ^\pm _\psi [t]^{-1}={\textbf {Ad}} ^\mp _\psi [t]\) (both statements are proven in Proposition 6). This allows to define a group structure on \(C^k([a,b],\mathfrak {q})\) for \(k\in \mathbb {N}\cup \{\infty \}\) (in analogy to Remark 5 and Sect. 1.14 in [2]) by
for \(\phi ,\psi \in C^k([a,b],\mathfrak {q})\). The group axioms are verified in Sect. 5.1.3.
Remark 14
(A Lie Group Construction) Let \(k\in \mathbb {N}\cup \{\infty \}\) and \(a<b\) be given; and set
As already mentioned, we will show that the maps

are defined (confer Lemma 17), and that \((G_k,\textsf {m} _k,\textsf {inv} _k,e_k)\) is a group (confer Lemma 22). Expectably, the group operations (96) are smooth w.r.t. the \(C^k\)-topology; hence give rise to a Lie group \(G_k\) with global chart \(\Xi _k\), and sequentially complete Lie algebra \(\mathfrak {g}_k\) (recall Lemma 3). It is furthermore to be expected that the corresponding Lie bracket \(\varvec{[}\cdot , \cdot \varvec{]}_k:\mathfrak {g}_k\times \mathfrak {g}_k\rightarrow \mathfrak {g}_k\) is given by
for \(\phi ,\psi \in \mathfrak {g}_k\), just as in Sect. 1.14 in [2] (confer Proposition 1.14.1 in [2]). Presumably, \((\mathfrak {g}_k,\varvec{[}\cdot , \cdot \varvec{]}_k)\) is asymptotic estimate, and \(G_k\) is \(C^0\)-regular. The technical details will be worked out in a separate paper. This serves as a preparation for a possible extension of Lie’s third theorem to the infinite-dimensional asymptotic estimate case—just by performing the same (a similar) construction made in Sect. 1.14 in [2] to prove this theorem (Theorem 1.14.3 in [2]) in the finite-dimensional context. Notably, this construction had already been used in [1], to prove Lie’s third theorem in the context of Lie algebroids. \(\square \)
In the last part of Sect. 5.1, we use the proven statements to investigate the properties of the following integral transformation that mimics (49) in Sect. 3.1:
The investigations serve as a preparation for the discussions in Sect. 5.2. There, the above transformation is applied to the situation where \((\mathfrak {q},\varvec{[}\cdot , \cdot \varvec{]})\equiv (\mathfrak {g},[\cdot ,\cdot ])\) equals the Lie algebra of a given Lie group G. Specifically, we prove the following regularity result (cf. Theorem I):
Theorem 2
Assume that \((\mathfrak {g},\varvec{[}\cdot , \cdot \varvec{]})\) is asymptotic estimate and sequentially complete. If G is weakly \(C^\infty \)-regular, then G is weakly \(C^k\)-regular for each \(k\in \mathbb {N}\cup \{\text {lip} ,\infty \}\).
Remark 15
Note that in the situation of Theorem 2, G is weakly \(C^k\)-regular for \(k\in \mathbb {N}\cup \{\text {lip} ,\infty \}\) if and only if G is \(C^k\)-semiregular, just because \(\mathfrak {g}\) is assumed to be sequentially complete. \(\square \)
This result complements Theorem 2 in [9] that essentially states that \(C^\infty \)-regularityFootnote 19 implies \(C^k\)-regularity for each \(k\in \mathbb {N}\cup \{\text {lip} ,\infty \}\), where for \(k=0\) additionally sequentially completeness of the Lie group has to be assumed.Footnote 20 Hence, in a certain sense, the assumption in Theorem 2 in [9] that G is sequentially complete, had been replaced in Theorem 2 by the assumption that \(\mathfrak {g}\) is sequentially complete. The key result proven in [9] (Theorem 1 in [9]) states that in the asymptotic estimate context, \(C^\infty \)-continuity of the product integral is equivalent to its \(C^0\)-continuity (local \(\mu \)-convexity of G), which makes the semiregularity results obtained in [8] applicable—Basically, in analogy to the definition of the Riemann integral as a limit over Riemann sums, in [8] the product integral is obtained as a limit over product integrals of piecewise integrable curves (under certain assumptions on the Lie group that are automatically fulfilled in the asymptotic estimate context). The proof of Theorem 2 works differently: For some given \(\phi \in C^0([a,b],\mathfrak {g})\), we show that (this is defined by \(C^\infty \)-semiregularity of G, as well as \(\text {im} [\mathfrak {T}]\subseteq C^\infty ([0,1],\mathfrak {g})\))

is of class \(C^1\), with  .
.
Remark 16
We will tacitly use throughout this section that sequentially completeness of \(\mathfrak {q}\) implies (recall Remark 2)
We will also use that \(\varvec{[}\cdot , \cdot \varvec{]}\) is smooth (apply, e.g., the parts b), e) of Proposition A.1). \(\square \)
Theorem 2, together with Theorem 4 in [8] and Theorem 1 in [9], yields the following statement:
Corollary 14
If \((\mathfrak {g},\varvec{[}\cdot , \cdot \varvec{]})\) is asymptotic estimate and sequentially complete, then the following assertions are equivalent:
-
(a)
G is \(C^k\)-semiregular for some \(k\in \mathbb {N}\cup \{\infty \}\), and \({\text {evol} }_\text {k} \) is of class \(C^\ell \) for some \(\ell \in \mathbb {N}\cup \{\infty \}\).
-
(b)
G is \(C^0\)-semiregular, and \({\text {evol} }_0\) is \(C^0\)-continuous ( G is locally \(\mu \)-convex ).
-
(c)
G is \(C^k\)-regular for all \(k\in \mathbb {N}\cup \{\infty \}\).
Proof
The implication c) \(\Rightarrow \) a) is evident. Moreover:
a) \(\Rightarrow \) b): If the assertion b) holds, then
-
G is \(C^\infty \)-semiregular, as \(C^\infty ([0,1],\mathfrak {g})\subseteq C^k([0,1],\mathfrak {g})\) holds. Hence, G is weakly \(C^\infty \)-regular by Remark 15; thus, G is \(C^0\)-semiregular by Theorem 2.
-
\({\text {evol} }_\text {k} \) is \(C^k\)-continuous, as of class \(C^\ell \) (with \(\ell \ge 0\)). Hence, \({\text {evol} }_0\) is \(C^0\)-continuous (G is locally \(\mu \)-convex) by Theorem 1 in [9].
b) \(\Rightarrow \) c): Assume that the assertion b) holds, and let \(k\in \mathbb {N}\cup \{\infty \}\) be given. Then,
-
G is \(C^k\)-semiregular, as \(C^k([0,1],\mathfrak {g})\subseteq C^0([0,1],\mathfrak {g})\) holds.
-
\({\text {evol} }_\text {k} ={\text {evol} }_0|_{C^k([0,1],\mathfrak {g})}\) is \(C^k\)-continuous, as even \(C^0\)-continuous.
Since \(\mathfrak {g}\) is sequentially complete (hence, integral complete and Mackey complete), Theorem 4 in [8] shows that \({\text {evol} }_\text {k} \) is smooth. \(\square \)
5.1 The Lax equation
Let \(a<b\) and \(\psi \in \text {CP} ^0([a,b],\mathfrak {q})\) be given.Footnote 21 Motivated by Sect. 3.3, for \(X\in \mathfrak {q}\) we set
as well as (recall (23))

for each \(\ell \ge 1\). We furthermore define (definedness is covered by Lemma 17)
and let
To simplify the notations, we define
5.1.1 Elementary properties
In this section, we discuss the elementary properties of the objects defined in the beginning of Sect. 5.1. We start with the following lemma.
Lemma 17
Let \(\psi \in C^0([a,b],\mathfrak {q})\) be given. Then, the following assertions hold:
- (1):
-
The maps \(\varvec{\Lambda }_\psi ^\pm \) are defined and of class \(C^1\), and we have
$$\begin{aligned} \partial _1 \varvec{\Lambda }_\psi ^+(t,X)&\textstyle =\partial _t{\textbf {Ad}} _\psi ^+[X](t)=\varvec{[}\psi (t), {\textbf {Ad}} ^+_\psi [X](t) \varvec{]}\\ \partial _1 \varvec{\Lambda }^-_\psi (t,X)&\textstyle =\partial _t{\textbf {Ad}} _\psi ^-[X](t)=-{\textbf {Ad}} ^-_\psi [\varvec{[}\psi (t), X \varvec{]}](t) \end{aligned}$$for all \(t\in [a,b]\) and \(X\in \mathfrak {q}\).
- (2):
-
\(\varvec{\Lambda }^\pm _\psi (t,\cdot )={\textbf {Ad}} _\psi ^\pm [t]\) is linear and continuous for each \(t\in [a,b]\).
- (3):
-
If \(\psi \in C^k([a,b],\mathfrak {q})\) holds for \(k\in \mathbb {N}\cup \{\infty \}\), then \(\varvec{\Lambda }_\psi ^\pm \) is of class \(C^{k+1}\).
Proof
The proof is straightforward but technical. It is provided in Appendix A.7. \(\square \)
Remark 17
The substitution formula (21) yields the following:
-
Let \(a<b\), \(a'<b'\), \(\psi \in C^0([a,b],\mathfrak {q})\), as well as \(\varrho :[a',b']\rightarrow [a,b]\) be of class \(C^1\) with \(\varrho (a')=a\) and \(\varrho (b')=b\). We set \(\phi := {\dot{\varrho }}\cdot (\psi \circ \varrho )\) and obtain inductively from (21) that
$$\begin{aligned} \textstyle \varvec{\lambda }^\pm _{\ell ,\phi }[t]=\varvec{\lambda }^\pm _{\ell ,\psi }[\varrho (t)]\qquad \quad \forall \, t\in [a',b'] \end{aligned}$$holds for all \(\ell \in \mathbb {N}\). Hence, we have \( {\textbf {Ad}} ^\pm _{{\dot{\varrho }}\,\cdot \, (\psi \,\circ \,\varrho )}[\cdot ]={\textbf {Ad}} ^\pm _{\psi }[\varrho (\cdot )]\). In particular, if additionally \({\dot{\varrho }}|_{(a,b)}>0\) holds, then we have
$$\begin{aligned} {\textbf {Ad}} ^\pm _{({\dot{\varrho }}\,\cdot \, (\psi \,\circ \,\varrho ))|_{[x',y']}}[\cdot ]={\textbf {Ad}} ^\pm _{\psi |_{[\varrho (x'),\varrho (y')]}}[\varrho (\cdot )]\qquad \quad \forall \, a'\le x'<y\le b'. \end{aligned}$$(97) -
The previous point applied to affine transformations yieldsFootnote 22
$$\begin{aligned} {\textbf {Ad}} ^\pm _\chi [b]={\textbf {Ad}} ^\pm _{\chi (\cdot -x)}[b+x] \end{aligned}$$for \(a<b\), \(\chi \in C^0([a,b],\mathfrak {q})\), and \(x\in \mathbb {R}\).\(\square \)
Corollary 15
For \(\psi \in C^0([a,b],\mathfrak {q})\) and \(t\in [a,b]\), we have \({\textbf {Ad}} _\psi ^-[t]\circ {\textbf {Ad}} _\psi ^+[t]=\text {id} _\mathfrak {q}\).
Proof
Let \(Z\in \mathfrak {q}\) be given, and define
Then, Lemma 17 shows \(\alpha _Z\in C^1([a,b],\mathfrak {q})\); and the parts b), b), e) of Proposition A.1 yield
hence \(\alpha _Z(t)=Z+ \int _a^t {\dot{\alpha }}_Z(s) \,\text {d} s=Z\) for each \(t\in [a,b]\) by (17). \(\square \)
Lemma 18
For \(\psi \in \text {CP} ^0([a,b],\mathfrak {q})\) and \(a< c< b\), we have \({\textbf {Ad}} ^+_\psi ={\textbf {Ad}} ^+_{\psi |_{[c,b]}}\circ {\textbf {Ad}} ^+_{\psi |_{[a,c]}}\).
Proof
Let \(X\in \mathfrak {q}\) be fixed. We first prove by induction that
holds for each \(\ell \in \mathbb {N}\). It is clear from the definitions that
We thus can assume that (98) holds for some \(\ell \in \mathbb {N}\), and obtain for \(c<s\le b\) that

holds, so that (98) follows by induction. Then, for \(n\ge 1\) we have
For \(\textsf {v} \le \textsf {w} \) as in (95), we obtain from (100) and the binomial theorem that
holds, which yields

It thus remains to show \(\lim _n \beta _n={\textbf {Ad}} ^+_{\psi |_{[c,b]}}({\textbf {Ad}} ^+_{\psi |_{[a,c]}}(X))\). For this, we observe that

holds for each \(n\in \mathbb {N}\); and choose \(\textsf {w} \le \textsf {m} \) as in (95) for \(\textsf {v} \equiv \textsf {w} \) and \(\textsf {w} \equiv \textsf {m} \) there. We obtain
hence \(\lim _n \textrm{T}_1(n)=0\). We furthermore obtain
hence \(\lim _n \textrm{T}_2(n)=0\). It follows that \(\lim _n\widetilde{\Delta }_n=0\) holds, which proves the claim. \(\square \)
Remark 18
Lemma 18, together with the second point in Remark 17 shows
for \(a<b\), \(\psi \in \text {CP} ^0([a,b],\mathfrak {q})\), and \(x\in \mathbb {R}\). \(\square \)
Lemma 19
Let \(\psi \in \text {CP} ^0([a,b],\mathfrak {q})\) and \(\{\psi _n\}_{n\in \mathbb {N}}\subseteq \text {CP} ^0([a,b],\mathfrak {q})\) be given, with \(\{\psi _n\}_{n\in \mathbb {N}}\rightarrow \psi \) w.r.t. the \(C^0\)-topology. Then, for each \(X\in \mathfrak {q}\), we have \(\{{\textbf {Ad}} ^\pm _{\psi _n}[X]\}_{n\in \mathbb {N}} \rightarrow {\textbf {Ad}} _\psi ^\pm [X]\) w.r.t. the \(C^0\)-topology.
Proof
For each \(\ell \ge 1\) and \(X_1,\dots ,X_\ell ,Y_1,\dots ,Y_\ell ,X\in \mathfrak {q}\), we have
Let \(\textsf {v} \le \textsf {w} \) be as in (95). For \(N\in \mathbb {N}\) suitably large, we have \(\textsf {w} _\infty (\psi _n)\le 2\cdot \textsf {w} _\infty (\psi )\) for each \(n\ge N\). We obtain for \(n\ge N\) from (101) (second step) that
holds for each \(t\in [a,b]\), which proves the claim. \(\square \)
5.1.2 Uniqueness of the solution
For \(\psi \in C^0([a,b],\mathfrak {q})\) with \(a<b\), we define \({\mathfrak {inv}(\psi )}\in C^0([a,b],\mathfrak {q})\) as in Example 4 by
Notably, we have \({\mathfrak {inv}({\mathfrak {inv}(\psi )})}=\psi \). In this section, we prove the following proposition.Footnote 23
Proposition 6
Let \(\psi \in C^0([a,b],\mathfrak {q})\) be given. Then, the following assertions hold:
-
(1)
We have \({\textbf {Ad}} ^\pm _\psi [t]\in \textsf {Aut} (\mathfrak {q})\) for each \(t\in [a,b]\), with \({\textbf {Ad}} ^\pm _\psi [t]^{-1}={\textbf {Ad}} ^\mp _\psi [t]={\textbf {Ad}} ^\pm _{{\mathfrak {inv}(\psi |_{[a,t]})}}\).
-
(2)
Let \(X\in \mathfrak {q}\) be given. Then, \({\textbf {Ad}} ^+_\psi [X]\) is the unique solution \(\alpha \in C^1([a,b],\mathfrak {q})\) to the differential equation (Lax equation)
$$\begin{aligned} {\dot{\alpha }}=\varvec{[}\psi , \alpha \varvec{]}\qquad \,\,\text {with initial condition}\qquad \,\, \alpha (a)=X. \end{aligned}$$
We obtain the following corollaries.
Corollary 16
For each \(\psi \in C^0([a,b],\mathfrak {q})\), we have
Proof
Let \(X,Y\in \mathfrak {g}\) and \(\psi \in C^0([a,b],\mathfrak {q})\) be given. Lemma 17 shows
with \(\alpha (a)=\varvec{[}X, Y \varvec{]}\). The parts b), e) of Proposition A.1 (first step), and the Jacobi identity (25) (second step) show that
holds for each \(t\in [a,b]\). Proposition 6.2) yields \(\alpha ={\textbf {Ad}} ^+_\psi [\varvec{[}X, Y \varvec{]}]\), which proves the one part of the statement. Then, Proposition 6.1) shows
for each \(t\in [a,b]\) and \(X,Y\in \mathfrak {q}\), which establishes the claim. \(\square \)
Corollary 17
For \(\psi \in C^0([a,b],\mathfrak {q})\) and \(\varrho :[a',b']\rightarrow [a,b]\) of class \(C^1\), we have
Proof
For \(Z\in \mathfrak {q}\), define
Proposition 6 shows \(\alpha _Z\in C^1([a',b'],\mathfrak {q})\), with \(\alpha _Z(a')=Z\) and (additionally apply b) in Proposition A.1)
The uniqueness statement in Proposition 6 (second identity) yields
Given \(X\in \mathfrak {q}\), we set \(Z:={\textbf {Ad}} _\psi ^+[\varrho (a')](X)\) and obtain from Proposition 6.1) that
holds, from which the claim is clear. \(\square \)
Remark 19
Let \(\mathcal {L}:\mathfrak {q}\rightarrow \mathfrak {q}\) be linear and continuous, with
It follows by iterated application of (102) and (22) that
holds. This equality alternatively follows from Proposition 6:
Proof of Equation (103)
Given \(\psi \in C^0([a,b],\mathfrak {q})\) and \(Z\in \mathfrak {q}\), define \(\alpha :=\mathcal {L}\circ {\textbf {Ad}} ^+_{\psi }[Z]\in C^1([a,b],\mathfrak {q})\). Then, we have \(\alpha (a)=\mathcal {L}(Z)\), with
Proposition 6.2) shows \(\alpha ={\textbf {Ad}} ^+_{\mathcal {L}\,\circ \, \psi }[\mathcal {L}(Z)]\), which establishes the “\(+\)”-case in (103). Together with Proposition 6.1), we obtain
for \(a<t\le b\) and \(\psi \in C^0([a,b],\mathfrak {q})\), which establishes the “−”-case in (103). \(\square \)
For the proof of Proposition 6, we shall need the following facts and definitions:
-
For \(\phi \equiv \{\phi [p]\}_{0\le p\le n-1}\in \text {CP} ^0([a,b],\mathfrak {q})\), we define \({\mathfrak {inv}(\phi )}\in \text {CP} ^0([a,b],\mathfrak {q})\) by
$$\begin{aligned} {\mathfrak {inv}(\phi )}:= \{{\mathfrak {inv}(\phi [(n-1)-p])}\}_{0\le p\le n-1}. \end{aligned}$$ -
Let \(\phi \equiv \{\phi [p]\}_{0\le p\le n-1}\in \text {CP} ^0([a,b],\mathfrak {q})\) (\(a<b\), \(n\ge 1\)) and \(\phi '\equiv \{\phi '[q]\}_{0\le q\le n'-1}\in \text {CP} ^0([a',b'],\mathfrak {q})\) (\(a'<b'\), \(n'\ge 1\)) be given. We set
$$\begin{aligned} \psi [\ell ]:= {\left\{ \begin{array}{ll} \phi [\ell ] &{}\text {for}\quad 0\le \ell \le n-1\\ \phi '[\ell -n] &{}\text {for}\quad n\le \ell \le n+n'-1, \end{array}\right. } \end{aligned}$$and define \(\phi \triangleright \phi '\in \text {CP} ^0([a,b+(b'-a')],\mathfrak {q})\) by
$$\begin{aligned} \phi \triangleright \phi ':= \{\psi [\ell ]\}_{0\le \ell \le n+n'-1}. \end{aligned}$$Lemma 18 together with Remark 18 shows
$$\begin{aligned} {\textbf {Ad}} ^+_{\phi \,\triangleright \, \phi '}\textstyle ={\textbf {Ad}} ^+_{\phi \,\triangleright \, \phi '}|_{[b,b + (b'-a')]}\circ {\textbf {Ad}} ^+_{\phi \,\triangleright \, \phi '}|_{[a,b]} = {\textbf {Ad}} ^+_{\phi '}\circ {\textbf {Ad}} ^+_{\phi }. \end{aligned}$$(104) -
We have \({\mathfrak {inv}({\mathfrak {inv}(\psi )})}=\psi \) for each \(\psi \in C^0([a,b],\mathfrak {q})\).
-
For \(a<b\) and \(Z\in \mathfrak {q}\), we have (observe \({\mathfrak {inv}(\mathcal {C}_Z|_{[a,b]})}=-\mathcal {C}_Z|_{[a,b]}\))
$$\begin{aligned} \textstyle {\textbf {Ad}} ^+_{\mathcal {C}_Z|_{[a,b]}}[b]\textstyle =\sum _{\ell =0}^\infty \, \frac{(b-a)^\ell }{\ell !}\cdot \text {ad} _{Z}^\ell ={\textbf {Ad}} ^-_{{\mathfrak {inv}(\mathcal {C}_Z|_{[a,b]})}}[b]. \end{aligned}$$(105)Corollary 15 (second step) yields
$$\begin{aligned} {\textbf {Ad}} ^+_{\mathcal {C}_Z|_{[a,b]}}[b]\circ {\textbf {Ad}} ^+_{{\mathfrak {inv}(\mathcal {C}_Z|_{[a,b]})}}[b]{\mathop {=}\limits ^{(105)}}{\textbf {Ad}} ^-_{{\mathfrak {inv}(\mathcal {C}_Z|_{[a,b]})}}[b]\circ {\textbf {Ad}} ^+_{{\mathfrak {inv}(\mathcal {C}_Z|_{[a,b]})}}[b]=\text {id} _\mathfrak {q}. \end{aligned}$$(106)
We obtain the following statement.
Lemma 20
For \(\psi \in C^0([a,b],\mathfrak {q})\), we have \({\textbf {Ad}} ^+_\psi \circ {\textbf {Ad}} ^+_{{\mathfrak {inv}(\psi )}}=\text {id} _\mathfrak {q}\).
Proof
For \(n\ge 1\) and \(p=0,\dots ,n\), we define \(t_{n,p}:=a+ \frac{p}{n}\cdot (b-a)\) and \(Z_{n,p}:=\psi (t_{n,p})\). We set
For \(n\ge 1\), we define \(\psi ^\pm _n\equiv \{\psi _n^\pm [p]\}_{0\le p\le n-1}\in \text {CP} ^0([a,b],\mathfrak {q})\) by
(hence \(\psi _n^-={\mathfrak {inv}(\psi _n^+)}\). Obviously, we have \(\{\psi ^+_n\}_{n\ge 1}\rightarrow \psi \) as well as \(\{\psi ^-_n\}_{n\ge 1}\rightarrow {\mathfrak {inv}(\psi )}\) w.r.t. the \(C^0\)-topology. Moreover, for \(n\ge 1\), we have by Lemma 18 and (106) that
holds. We define \(\phi :={\mathfrak {inv}(\psi )}\triangleright \psi \), as well as \(\phi _n:=\psi ^-_n\triangleright \psi ^+_n\) for each \(n\ge 1\). Then, \(\{\phi _n\}_{n\ge 1}\rightarrow \phi \) converges w.r.t. the \(C^0\)-topology; and we obtain from Lemma 19 (second step) that
holds for each \(X\in \mathfrak {q}\), which proves the claim. \(\square \)
We are ready for the proof of Proposition 6.
Proof of Proposition 6
-
(1)
The claim is clear for \(t=a\). Then, it suffices to prove the statement for \(t=b\), as then we can apply it to the restriction \(\psi |_{[a,t]}\) for each \(a<t<b\). By Lemma 20 (first step), and Corollary 15 (third step), we have
$$\begin{aligned} {\textbf {Ad}} _\psi ^-[b]&={\textbf {Ad}} _\psi ^-[b]\circ ({\textbf {Ad}} _\psi ^+[b]\circ {\textbf {Ad}} ^+_{{\mathfrak {inv}(\psi )}}[b])\\&=({\textbf {Ad}} _\psi ^-[b]\circ {\textbf {Ad}} _\psi ^+[b])\circ {\textbf {Ad}} ^+_{{\mathfrak {inv}(\psi )}}[b] ={\textbf {Ad}} ^+_{{\mathfrak {inv}(\psi )}}[b]. \end{aligned}$$Applying \({\textbf {Ad}} _\psi ^+\) from the left, Lemma 20 yields (Corollary 15 in the second equality)
$$\begin{aligned} {\textbf {Ad}} _\psi ^+[b]\circ {\textbf {Ad}} _\psi ^-[b]=\text {id} _\mathfrak {q}={\textbf {Ad}} _\psi ^-[b]\circ {\textbf {Ad}} _\psi ^+[b]. \end{aligned}$$Together, we have shown the following properties:
-
\({\textbf {Ad}} ^\pm _{\psi }[b]\in \textsf {Aut} (\mathfrak {q})\) with \({\textbf {Ad}} ^\pm _{\psi }[b]^{-1}={\textbf {Ad}} ^\mp _{\psi }[b]\),
-
\({\textbf {Ad}} _\psi ^-[b]={\textbf {Ad}} ^+_{{\mathfrak {inv}(\psi )}}[b]\).
Applying the third property to \(\widetilde{\psi }:={\mathfrak {inv}(\psi )}\) (second step), we obtain from \({\mathfrak {inv}({\mathfrak {inv}(\psi )})}=\psi \) (third step) that
holds, which completes the proof.
-
(2)
By Lemma 17, for \(\alpha \equiv {\textbf {Ad}} ^+_\psi [X]\), we have \(\alpha \in C^1([a,b],\mathfrak {q})\) with \(\alpha (a)=X\) and \({\dot{\alpha }}=\varvec{[}\psi , \alpha \varvec{]}\). This shows the solution property. For uniqueness, let \(\alpha \in C^1([a,b],\mathfrak {q})\) be given, such that \(\alpha (a)=X\) and \({\dot{\alpha }}=\varvec{[}\psi , \alpha \varvec{]}\) holds. By Lemma 17, we have \(\beta :=\varvec{\Lambda }_\psi ^-(\cdot ,\alpha (\cdot ))\in C^1([a,b],\mathfrak {q})\) with (use Part e) of Proposition A.1 on the left side, as well as (20) on the right side)
$$\begin{aligned}&{\dot{\beta }}=-\varvec{\Lambda }_\psi ^-(\cdot ,\varvec{[}\psi (\cdot ), \alpha (\cdot ) \varvec{]})+ \varvec{\Lambda }_\psi ^-(\cdot ,\varvec{[}\psi (\cdot ), \alpha (\cdot ) \varvec{]})=0\\&\quad \textstyle \Longrightarrow \qquad \,\,\, \beta =\beta (a)+ \int _a^\bullet {\dot{\beta }}(s) \,\text {d} s=X. \end{aligned}$$Applying Part 1), we obtain
$$\begin{aligned} {\textbf {Ad}} ^+_\psi [X](t)={\textbf {Ad}} _\psi ^+[t](\beta (t))=({\textbf {Ad}} _\psi ^+[t]\circ {\textbf {Ad}} _\psi ^-[t])(\alpha (t))=\alpha (t)\qquad \quad \forall \, t\in [a,b], \end{aligned}$$which proves the claim.\(\square \)
5.1.3 A group structure
For \(\phi ,\psi \in C^0([a,b],\mathfrak {q})\) with \(a<b\), we define
We observe the following.
Lemma 21
Let \(\phi ,\psi \in C^0([a,b],\mathfrak {q})\) be fixed. Then, the following assertions hold:
-
(1)
We have \({\textbf {Ad}} ^+_{\psi ^{-1}}[t]={\textbf {Ad}} _\psi ^-[t]\) for each \(t\in [a,b]\).
-
(2)
We have \({\textbf {Ad}} ^+_{\phi \,\star \,\psi }[t]={\textbf {Ad}} ^+_\phi [t]\circ {\textbf {Ad}} ^+_\psi [t]\) for each \(t\in [a,b]\).
Proof
-
(1)
Let \(X\in \mathfrak {q}\) be given, and set \(\alpha _X:= {\textbf {Ad}} _\psi ^-[X]\in C^1([a,b],\mathfrak {q})\). We have \(\alpha _X(a)=X\); and Lemma 17 shows \(\alpha _X:= {\textbf {Ad}} _\psi ^-[X]\in C^1([a,b],\mathfrak {q})\) with (for the second step use Corollary 16)
$$\begin{aligned} {\dot{\alpha }}_X(t)\textstyle = -{\textbf {Ad}} _\psi ^-[t](\varvec{[}\psi (t), X \varvec{]})=\varvec{[}-{\textbf {Ad}} _\psi ^-[t](\psi (t)), {\textbf {Ad}} _\psi ^-[X](t) \varvec{]}=\varvec{[}\psi ^{-1}(t), \alpha _X(t) \varvec{]} \end{aligned}$$for each \(t\in [a,b]\). Then, Proposition 6.2) gives \(\alpha _X={\textbf {Ad}} ^+_{\psi ^{-1}}[X]\).
-
(2)
For \(X\in \mathfrak {q}\), we define
$$\begin{aligned} \alpha _X:[a,b]\ni t\mapsto ({\textbf {Ad}} ^+_\phi [t]\circ {\textbf {Ad}} ^+_\psi [t])(X) = \varvec{\Lambda }^+_\phi (t,{\textbf {Ad}} ^+_\psi [X](t))\in \mathfrak {q}. \end{aligned}$$We have \(\alpha _X(a)=X\); and Lemma 17 shows \(\alpha _X\in C^1([a,b],\mathfrak {q})\) with (for the first step additionally apply the parts b) and e) of Proposition A.1; and for the second step apply Corollary 16)
$$\begin{aligned} {\dot{\alpha }}_X(t)&\textstyle = \varvec{[}\phi (t), \alpha _X(t) \varvec{]}+ {\textbf {Ad}} ^+_\phi [t](\varvec{[}\psi (t), {\textbf {Ad}} ^+_\psi [t](X) \varvec{]})\\&\textstyle = \varvec{[}\phi (t), \alpha _X(t) \varvec{]} + \varvec{[}{\textbf {Ad}} ^+_{\phi }[t](\psi (t)), \alpha _X(t) \varvec{]} \\&\textstyle = \varvec{[}(\phi \star \psi )(t), \alpha _X(t) \varvec{]}. \end{aligned}$$Proposition 6.2) yields \(\alpha _X={\textbf {Ad}} ^+_{\phi \,\star \,\psi }[X]\), which proves the claim. \(\square \)
Lemma 22
Given \(\phi ,\psi ,\chi \in C^0([a,b],\mathfrak {q})\), then we have
Proof
We have \({\textbf {Ad}} ^+_0[t]=\text {id} _\mathfrak {q}\) and \({\textbf {Ad}} ^+_\psi [t](0)=0\) for each \(t\in [a,b]\); hence,
Next, Proposition 6.1) yields
Moreover, Lemma 21.1) shows
for each \(t\in [a,b]\). Finally, we obtain from Lemma 21.2) that
holds for each \(t\in [a,b]\), which establishes the proof. \(\square \)
Corollary 18
For \(\phi ,\psi \in C^0([a,b],\mathfrak {q})\) and \(t\in [a,b]\), we have
Proof
By Lemma 22, we have
for each \(t\in [a,b]\). Lemma 21.2) (first step) and Lemma 21.1) (third step) yield
for each \(t\in [a,b]\). Applying \({\textbf {Ad}} ^+_\phi [t]\) to both hand sides, the claim follows from Lemma 21.2), Lemma 22, as well as \({\textbf {Ad}} ^+_0[t]=\text {id} _\mathfrak {q}\) for each \(t\in [a,b]\). \(\square \)
5.1.4 An integral transformation
In analogy to (49), for \(a<b\) and \(\phi \in C^0([a,b],\mathfrak {q})\), we set
as well as \(\mathfrak {T}(\phi |_{[a,a]}):[0,1]\ni t \mapsto 0\in \mathfrak {q}\). Observe that (108) is defined as the integrand is continuous; because, by Lemma 18 and Proposition 6 we have
Continuity of the integrand also implies the following statement.
Remark 20
Let \(a<b\) and \(\psi \in C^0([a,b],\mathfrak {q})\). Let \(\varrho :[a',b']\rightarrow [a,b]\) (\(a'<b'\)) be of class \(C^1\), with \({\dot{\varrho }}|_{(a',b')}>0\) as well as \(\varrho (a')=a\) and \(\varrho (b')=b\). Then, (97) in Remark 17 (second step) shows
where we have applied the substitution formula (21) in the third step. \(\square \)
In this section, we investigate the elementary properties of this map, and provide some statements that we shall need in Sect. 5.2. We start with some technical properties:
Lemma 23
Let \(a<b\), \(\psi \in C^0([a,b],\mathfrak {q})\), and \(X\in \mathfrak {q}\) be given. Then, \(\eta _{\psi ,X}:\mathbb {R}\ni t \mapsto {\textbf {Ad}} ^+_{t\cdot \psi }[b](X)\in \mathfrak {q}\) is smooth, with
Proof
It follows from the definitions that \(\eta _{\psi ,X}(t)=\sum _{p=0}^\infty t^p\cdot \varvec{\lambda }^+_{p,\psi }[b](X)\) holds for each \(t\in \mathbb {R}\). Now, for \(\textsf {v} \le \textsf {w} \) as in (95), we have
Consequently, \(\textstyle \gamma [\textsf {q} ]:\mathbb {R}\ni t\mapsto \sum _{p=0}^\infty t^p\cdot \textsf {q} (\varvec{\lambda }^+_{p,\psi }[b](X))\in [0,\infty )\) is defined for each \(\textsf {q} \in \textsf {Sem}(\mathfrak {q})\), so that the claim is clear from Corollary 2. \(\square \)
Next, let \(a<b\) and \(\psi \in C^0([a,b],\mathfrak {q})\) be given:
-
For \(a\le s< z\le b\), we define \(\mathcal {Y}_0(\psi ,s,z):=\psi (s)\), as well as
$$\begin{aligned} \textstyle \mathcal {Y}_p(\psi ,s,z):= \int _s^{z}\text {d} s_1\int _s^{s_1}\text {d} s_2 \, {\dots } \int _s^{s_{p-1}}\text {d} s_p \, (\text {ad} _{\psi (s_1)}\circ \dots \circ \text {ad} _{\psi (s_{p})})(\psi (s))\qquad \quad \forall \, p \ge 1. \end{aligned}$$For each \(t\in [0,1]\) and \(a<z\le b\), we have
$$\begin{aligned} \mathfrak {T}(\psi |_{[a,z]})(t)= \textstyle \int _a^z \sum _{p=0}^\infty \varvec{\lambda }^+_{p,\, t\cdot \psi |_{[s,z]}}(\psi (s))\, \text {d} s=\textstyle \int _a^z \sum _{p=0}^\infty t^p \cdot \mathcal {Y}_p(\psi ,s,z)\, \text {d} s. \end{aligned}$$(109) -
We define
$$\begin{aligned} \textstyle \mathcal {T}_p(\psi ,z,t):= \textstyle t^p\cdot \int _a^z \mathcal {Y}_p(\psi ,s,z)\, \text {d} s \qquad \quad \forall \, p\in \mathbb {N},\,\, t\in [0,1],\,\, z\in [a,b]. \end{aligned}$$(110)
We have the following statement.
Lemma 24
For each \(a<b\), we have \(\mathfrak {T}:C^0([a,b],\mathfrak {q})\rightarrow C^\infty ([0,1],\mathfrak {q})\). Moreover,
converges w.r.t. the \(C^\infty \)-topology for each \(\psi \in C^0([a,b],\mathfrak {q})\) and \(a<z\le b\); and we have
Proof
Let \(\psi \in C^0([a,b],\mathfrak {q})\) be given, and let \(\textsf {v} \le \textsf {w} \) be as in (95). Then, we have
It follows that \(\textstyle \{\sum _{p=0}^\ell t^p\cdot \mathcal {Y}_p(\psi ,\cdot ,z)\}_{\ell \in \mathbb {N}}\rightarrow \sum _{p=0}^\infty t^p\cdot \mathcal {Y}_p(\psi ,\cdot ,z)\) converges uniformly on [a, b], for each fixed \(t\in [0,1]\) and \(a< z\le b\). Since the Riemann integral is \(C^0\)-continuous, we obtain

Now, for each \(p\in \mathbb {N}\) and \(a<z\le b\), we have
Consequently, \(\textstyle \gamma [\textsf {q} ]:\mathbb {R}\ni t\mapsto \sum _{p=0}^\infty t^p\cdot \textsf {q} (X_p(z))\in [0,\infty )\) is defined for each \(\textsf {q} \in \textsf {Sem}(\mathfrak {q})\) and \(a<z\le b\), so that the claim is clear from Corollary 2. \(\square \)
Lemma 25
For \(\psi \in C^0([a,b],\mathfrak {q})\), we have
Proof
Let \(X\in \mathfrak {q}\) be given. Lemma 23 yields the following:
-
We have \(C^\infty (\mathbb {R},\mathfrak {q})\ni \eta _{\psi ,X}:\mathbb {R}\ni t \mapsto {\textbf {Ad}} ^+_{t\cdot \psi }[b](X)\in \mathfrak {q}\).
-
By Lemma 17, we have
$$\begin{aligned} \chi _t:={\textbf {Ad}} ^-_{t\cdot \psi }[\cdot ](\psi (\cdot ))\in C^0([a,b],\mathfrak {q})\qquad \quad \forall \, t\in \mathbb {R}. \end{aligned}$$Lemma 23 shows that \(\eta _{\chi _t,X}:\mathbb {R}\ni h\mapsto {\textbf {Ad}} ^+_{h\cdot \chi _t}[b](X)\in \mathfrak {q}\) is smooth for each \(t\in \mathbb {R}\), with
$$\begin{aligned} {\dot{\eta }}_{\chi _t,X}(0)\textstyle = \varvec{\lambda }^+_{1,\chi _t}[b](X){\mathop {=}\limits ^{(22)}}\varvec{[}\int _a^b \chi _t(s)\,\text {d} s, X \varvec{]}. \end{aligned}$$(112)
By Lemma 18 (second step) and Proposition 6.1) (third step), we have
This yields (second step), together with Corollary 16 and (112) (first step) that
holds for each \(t\in [0,1]\). Now, Corollary 18 (second step) shows
for \(t,h\in \mathbb {R}\). Hence, (113), together with Lemma 17 and Part b) of Proposition A.1 yields
with \(\eta _{\psi ,X}(0)=X\). Then, Proposition 6.2) ( second step) shows
Since \(X\in \mathfrak {q}\) was arbitrary, the claim follows. \(\square \)
We obtain the following statement.
Lemma 26
Let \(\psi \in C^0([a,b+\varepsilon ],\mathfrak {q})\) with \(a< b\) and \(\varepsilon >0\) be given. Then, we have
Proof
Let \(a< z\le b\) and \(0< h\le \varepsilon \) be fixed. For \(t\in [0,1]\), we have

Now, Lemma 18 and (22) (first step), as well as Lemma 25 (third step) yield
for each \(t\in [0,1]\). We obtain
for each \(t\in [0,1]\), which proves the claim. \(\square \)
We obtain the following statement (in analogy to Remark 9).
Proposition 7
Let \(a<c<b\), \(\psi \in C^k([a,b],\mathfrak {q})\), and \(\varrho :[a',b']\rightarrow [a,b]\) (\(a'<b'\)) be of class \(C^1\) with \({\dot{\varrho }}|_{(a',b')}>0\), \(\varrho (a')=a\), \(\varrho (b')=b\). Then, we have
Proof
Lemma 26 shows (115), and Remark 20 shows (116). To prove (114), let \(\varrho _1:[a,b]\rightarrow [a,b]\) with \(\varrho _1(a)=a\), \(\varrho _1(b)=b\), as well as \(\varrho _2:[b,2b+a]\rightarrow [a,b]\) with \(\varrho _2(b)=a\), \(\varrho _2(2b+a)=b\) both be of class \(C^1\), such that \({\dot{\varrho }}_1|_{(a,b)}>0\) as well as \({\dot{\varrho }}_2|_{(b,2b+a)}>0\) holds with
We set \(\chi _1:={\dot{\varrho }}_1\cdot (\psi \circ \varrho _1)\in C^0([a,b],\mathfrak {q})\) as well as \(\chi _2:={\dot{\varrho }}_2\cdot ({\mathfrak {inv}(\psi )}\circ \varrho _2)\in C^0([b,2b+a],\mathfrak {q})\), and define \(\phi \in C^0([a,2b+a],\mathfrak {q})\) by
for each \(t\in [a,2b+a]\). Then, we have
Let now \(t\in [0,1]\) and \(X\in \mathfrak {q}\) be given (and observe \(t\cdot {\mathfrak {inv}(\psi )}={\mathfrak {inv}(t\cdot \psi )}\)).
-
For \(s\in [a,b]\), we have by Lemma 18 (first step), (97) in Remark 17 (third step), as well as Lemma 18 and Proposition 6.1) (fourth step) that
$$\begin{aligned} \begin{aligned} {\textbf {Ad}} ^+_{t\cdot \phi |_{[s,2b+a]}}(X)&={\textbf {Ad}} ^+_{t\cdot \phi |_{[b,2b+a]}}\big ({\textbf {Ad}} ^+_{t\cdot \phi |_{[s,b]}}(X)\big )\\&={\textbf {Ad}} ^+_{t\cdot \chi _2}\big ({\textbf {Ad}} ^+_{t\cdot \chi _1|_{[s,b]}}(X)\big )\\&={\textbf {Ad}} ^+_{ {\mathfrak {inv}(t\cdot \psi )}}\big ({\textbf {Ad}} ^+_{t\cdot \psi |_{[\varrho _1(s),b]}}(X)\big )\\&={\textbf {Ad}} ^-_{t\cdot \psi |_{[a,\varrho _1(s)]}}(X). \end{aligned} \end{aligned}$$(118) -
For \(s\in [b,2b+a]\), we define
$$\begin{aligned} \chi :[\varrho _2(s),b]\ni z \mapsto {\mathfrak {inv}(t\cdot \psi |_{[a,a+b-\varrho _2(s)]})}(z-(\varrho _2(s)-a)) \in \mathfrak {q}. \end{aligned}$$We observe the following:
-
(i)
We have \(\chi ={\mathfrak {inv}(t\cdot \psi )}|_{[\varrho _2(s),b]}\) as
$$\begin{aligned} \chi (z)&=t\cdot \psi (2a+b-\varrho _2(s)- (z-(\varrho _2(s)-a)))=t\cdot \psi (a+b-z)\\&={\mathfrak {inv}(t\cdot \psi )}|_{[\varrho _2(s),b]}(z) \end{aligned}$$holds for each \(z\in [\varrho _2(s),b]\).
-
(ii)
By the second point in Remark 17 (second step), we have
$$\begin{aligned} {\textbf {Ad}} ^+_{\chi }&={\textbf {Ad}} ^+_{\chi }[b]\\&= {\textbf {Ad}} ^+_{\chi (\cdot -(a-\varrho _2(s)))}[b+(a-\varrho _2(s))]\\&={\textbf {Ad}} ^+_{{\mathfrak {inv}(t\cdot \psi |_{[a,a+b-\varrho _2(s)]})}}[b+(a-\varrho _2(s))]\\&={\textbf {Ad}} ^+_{{\mathfrak {inv}(t\cdot \psi |_{[a,a+b-\varrho _2(s)]})}}. \end{aligned}$$
We obtain from (97) in Remark 17 (second step), Point i) (third step), Point ii) (fourth step), as well as Proposition 6.1) (fifth step) that
We obtain from (118) and (119) (third step), (21) (fourth step), as well as the second point in Remark 2 (sixth step) that
holds for each \(t\in [0,1]\). Together with (117), this proves (116). \(\square \)
Moreover, applying Lemma 26 to the situation where \((\mathfrak {q},\varvec{[}\cdot , \cdot \varvec{]})\equiv (\mathfrak {g},\varvec{[}\cdot , \cdot \varvec{]})\) is an asymptotic estimate and sequentially complete Lie algebra that is inherited by a Lie group G, we obtain the following statement.
Corollary 19
Let G be weakly \(C^\infty \)-regular, with sequentially complete and asymptotic estimate Lie algebra \((\mathfrak {g},\varvec{[}\cdot , \cdot \varvec{]})\). Then, for \(\psi \in C^0([a,b+\varepsilon ])\) with \(a< b\) and \(\varepsilon >0\), we have

Proof
Let \(a< z\le b\) and \(0< h\le \varepsilon \) be fixed. Corollary 8 showsFootnote 24

We thus obtain from (a) (first step) as well as Lemma 26 (last step) that

holds, which proves the claim. \(\square \)
5.2 Weak regularity
In this section, we prove Theorem 2. In the following, let thus G be weakly \(C^\infty \)-regular, with asymptotic estimate and sequentially complete Lie algebra \((\mathfrak {g},\varvec{[}\cdot , \cdot \varvec{]})\).
Let \(a\le b\), \(0<\varepsilon <1\), and \(\psi \in C^0([a,b+\varepsilon ],\mathfrak {g})\) be given.
-
We define \(\Phi _\psi :(a-1,b+\varepsilon )\times [0,1]\rightarrow \mathfrak {g}\) by
$$\begin{aligned} \begin{aligned} \Phi _\psi (z,t) := {\left\{ \begin{array}{ll} (z-a)\cdot \psi (a) &{}\text {for}\quad z\in (a-1,a)\\ \mathfrak {T}(\psi |_{[a,z]})(t) &{}\text {for}\quad z\in [a,b+\varepsilon ) \end{array}\right. } \end{aligned} \end{aligned}$$(120)for each \(t\in [0,1]\). Lemma 24 yields the following:
-
For \(z\in (a-1,b+\varepsilon )\), we have \(\Phi _\psi (z,\cdot )\in C^\infty ([0,1],\mathfrak {g})\).
-
For \(z\in [a,b+\varepsilon )\), we have
$$\begin{aligned} \textstyle \Phi _\psi (z,t)=\int _a^z {\textbf {Ad}} ^+_{\, t\cdot \psi |_{[s,z]}}[\psi (s)] \,\text {d} s =\sum _{\ell =0}^\infty \mathcal {T}_\ell (\psi ,z,t)\qquad \quad \forall \, t\in [0,1], \end{aligned}$$where \(\Phi _\psi (z,\cdot ) =\sum _{\ell =0}^\infty \mathcal {T}_\ell (\psi ,z,\cdot )\) converges w.r.t. the \(C^\infty \)-topology.
-
For \(\textsf {p} \in \textsf {Sem}(E)\) and \(\text {s} \in \mathbb {N}\), we have
$$\begin{aligned} \sup \{a-1\le z\le b+\varepsilon \,|\, \textsf {p} _\infty ^\text {s} (\Phi _\psi (z,\cdot ))\}<\infty . \end{aligned}$$(121)
-
-
For each \(t\in [0,1]\), we define the map
 (122)
(122)We observe the following:
-
We have
 (123)
(123) -
We have
$$\begin{aligned} \Phi _\psi (a,\cdot )=\mathfrak {T}(\psi |_{[a,a]})(\cdot )=0 \qquad \text {hence}\qquad \mu _{t,\psi }(a)=e\qquad \text {for each}\qquad t\in [0,1]. \end{aligned}$$(124)
-
We obtain the following lemma.
Lemma 27
Let \(a\le b\), \(0<\varepsilon <1\), and \(\psi \in C^0([a,b+\varepsilon ],\mathfrak {g})\) be given. We define \(\varvec{\psi }\in C^0((a-1,b+\varepsilon ),\mathfrak {g})\) by
and set
Then, the following assertions hold:
-
(1)
For \(z\in (a-1,b+\varepsilon )\), \(\textsf {p} \in \textsf {Sem}(E)\), and \(\text {s} \in \mathbb {N}\), we have
$$\begin{aligned} \textstyle \lim _{ h\rightarrow 0}\frac{1}{|h|}\cdot \textsf {p} ^\text {s} _\infty \big (\Phi _\psi (z+h,\cdot )-\Phi _\psi (z,\cdot )- h\cdot \mathcal {D}(z,\cdot )\big )=0. \end{aligned}$$(125) -
(2)
The following assertions hold:
-
(a)
We have \(\partial _1\Phi _\psi (z,\cdot )=\mathcal {D}(z,\cdot )\in C^\infty ([0,1],\mathfrak {g})\) for each \(z\in (a-1,b+\varepsilon )\).
-
(b)
To each \(\textsf {p} \in \textsf {Sem}(E)\), \(\text {s} \preceq k\), and \(z\in (a-1,b+\varepsilon )\), there exists \(L_{\textsf {p} ,\text {s} }\ge 0\) as well as \(I_{\textsf {p} ,\text {s} }\subseteq (a-1,b+\varepsilon )\) open with \(z\in I_{\textsf {p} ,\text {s} }\), such that
$$\begin{aligned} \textstyle \textsf {p} ^\text {s} _\infty (\Phi (z+h,\cdot )-\Phi (z,\cdot ))\le |h|\cdot L_{\textsf {p} ,\text {s} }\qquad \quad \forall \, h\in \mathbb {R}_{\ne 0}\,\text { with }\, z+h\in I_{\textsf {p} ,\text {s} }. \end{aligned}$$ -
(c)
\(\Phi _\psi \) is continuous.
-
(a)
-
(3)
We have \(\mu _{t,\psi }\in C^1((a-1,b+\varepsilon ),G)\) for each \(t\in [0,1]\), with
$$\begin{aligned}&\textstyle {\dot{\mu }}_{t,\psi }(z)\textstyle =\text {d} _e\text {L} _{\mu _{t,\psi }(z)}\big (\int _0^t \text {Ad} _{\mu _{s,\psi }(z)^{-1}}\big (\varvec{\psi }(z)+s\cdot \varvec{[}\varvec{\psi }(z), \Phi _\psi (z,s) \varvec{]}\big )\,\text {d} s\,\big )\\&\qquad \forall \,z\in (a-1,b+\varepsilon ). \end{aligned}$$In particular, for each \(t\in [0,1]\) and \(z\in [a,b+\varepsilon )\), we have
$$\begin{aligned} \textstyle {\dot{\mu }}_{t,\psi }(z)\textstyle =\text {d} _e\text {L} _{\mu _{t,\psi }(z)}\big (\int _0^t \text {Ad} _{\mu _{s,\psi }(z)^{-1}}(\psi (z)+s\cdot \varvec{[}\psi (z), \mathfrak {T}(\psi |_{[a,z]})(s) \varvec{]})\,\text {d} s\,\big ). \end{aligned}$$(126)
Proof
-
(1)
For \(t\in [0,1]\), \(z\in (a-1,a]\) and \(h\ne 0\) with \(z+h\in (a-1,a]\), we have
$$\begin{aligned} \Phi _\psi (z+h,t)\,&-\Phi _\psi (z,t)- h\cdot \mathcal {D}(z,t)\\&\textstyle =(z+h-a)\cdot \psi (a)- (z-a)\cdot \psi (a) \\&\quad -h\cdot (\psi (a) + t\cdot \varvec{[}\psi (a), (z-a)\cdot \psi (a) \varvec{]})\\&=0. \end{aligned}$$Hence, (125) holds for each \(z\in (a-1,a)\), and we have
$$\begin{aligned}&\textstyle \lim _{0> h\rightarrow 0}\frac{1}{|h|}\cdot \textsf {p} ^\text {s} _\infty \big (\Phi _\psi (a+h,\cdot )-\Phi _\psi (a,\cdot )- h\cdot \mathcal {D}(a,\cdot )\big )=0 \nonumber \\&\qquad \quad \forall \, \textsf {p} \in \textsf {Sem}(E),\, \text {s} \in \mathbb {N}. \end{aligned}$$(127)For the remaining cases, we need the following observations:
-
For \(t\in [0,1]\) and \(z\in [a,b+\varepsilon )\), we define \(L_0(z,t):=\psi (z)\) as well as (recall (110))
$$\begin{aligned}&\textstyle L_\ell (z,t):=\,\textstyle t\cdot \varvec{[}\psi (z), \mathcal {T}_{\ell -1}(\psi ,z,t) \varvec{]}\\&\quad \textstyle =t\cdot \varvec{[}\psi (z), t^{\ell -1}\cdot \int _a^z \mathcal {Y}_{\ell -1}(\psi ,s,z)\, \text {d} s \varvec{]} \\&\quad \textstyle =t^\ell \cdot \int _a^{z}\text {d} s \int _s^{z}\text {d} s_2 \, {\dots } \int _s^{s_{\ell -1}}\text {d} s_\ell \, (\text {ad} _{\psi (z)}\circ \text {ad} _{\psi (s_2)}\circ \dots \circ \text {ad} _{\psi (s_{\ell })})(\psi (s)) \end{aligned}$$for \(\ell \ge 1\). Since \((\mathfrak {g},\varvec{[}\cdot , \cdot \varvec{]})\) is asymptotic estimate and sequentially complete, Corollary 2 shows that the map
$$\begin{aligned} \textstyle L:[a,b+\varepsilon )\times [0,1]\rightarrow \mathfrak {g},\qquad (z,t)\mapsto \sum _{\ell =0}^\infty L_\ell (z,t) \end{aligned}$$(128)is defined, such that \(C^\infty ([0,1],\mathfrak {g})\ni L(z,\cdot )=\sum _{\ell =0}^\infty L_\ell (z,t)\) converges w.r.t. the \(C^\infty \)-topology for each \(z\in [a,b+\varepsilon )\).
-
Let \(t\in [0,1]\), \(z\in [a,b+\varepsilon )\), and \(h>0\) be fixed.
-
If \(z+h<b\) holds, we have \(\mathcal {T}_0(\psi ,z+h,t)-\mathcal {T}_0(\psi ,z,t)=\int _z^{z+h} \psi (s)\, \text {d} s\), as well as for \(\ell \ge 1\)
$$\begin{aligned}&\mathcal {T}_\ell (\psi ,z+h,t) -\mathcal {T}_\ell (\psi ,z,t)\\&\quad \textstyle =t^\ell \cdot \int _a^{z} \text {d} s \textstyle \int _z^{z+h}\text {d} s_1\int _s^{s_1}\text {d} s_2 \, {\dots } \int _s^{s_{\ell -1}}\text {d} s_\ell \, (\text {ad} _{\psi (s_1)}\circ \dots \circ \text {ad} _{\psi (s_{\ell })})(\psi (s))\\&\qquad \textstyle + t^\ell \cdot \int _z^{z+h}\text {d} s \textstyle \int _s^{z+h}\text {d} s_1\int _s^{s_1}\text {d} s_2 \, {\dots } \int _s^{s_{\ell -1}}\text {d} s_\ell \, (\text {ad} _{\psi (s_1)}\circ \dots \circ \text {ad} _{\psi (s_{\ell })})(\psi (s))\\&\quad \textstyle = t^\ell \cdot \int _a^{z} \text {d} s \textstyle \int _z^{z+h}\text {d} s_1\int _s^{z}\text {d} s_2 \, {\dots } \int _s^{s_{\ell -1}}\text {d} s_\ell \, (\text {ad} _{\psi (s_1)}\circ \dots \circ \text {ad} _{\psi (s_{\ell })})(\psi (s))\\&\qquad \textstyle +t^\ell \cdot \int _a^{z} \text {d} s \textstyle \int _z^{z+h}\text {d} s_1\int _z^{s_1}\text {d} s_2 \, {\dots } \int _s^{s_{\ell -1}}\text {d} s_\ell \, (\text {ad} _{\psi (s_1)}\circ \dots \circ \text {ad} _{\psi (s_{\ell })})(\psi (s))\\&\qquad \textstyle + t^\ell \cdot \int _z^{z+h}\text {d} s \textstyle \int _s^{z+h}\text {d} s_1\int _s^{s_1}\text {d} s_2 \, {\dots } \int _s^{s_{\ell -1}}\text {d} s_\ell \, (\text {ad} _{\psi (s_1)}\circ \dots \circ \text {ad} _{\psi (s_{\ell })})(\psi (s)). \end{aligned}$$(In the second step, we have split the third integral in the first summand at z.)
-
If \(a<z-h\) holds, we have \(\mathcal {T}_0(\psi ,z,t)-\mathcal {T}_0(\psi ,z-h,t)=\int _{z-h}^{z} \psi (s)\, \text {d} s\), as well as for \(\ell \ge 1\)
$$\begin{aligned}&\mathcal {T}_\ell (\psi ,z,t)-\mathcal {T}_\ell (\psi ,z-h,t)\\&\quad \textstyle = t^\ell \cdot \int _a^{z-h} \text {d} s \textstyle \int _{z-h}^{z}\text {d} s_1\int _s^{s_1}\text {d} s_2 \, {\dots } \int _s^{s_{\ell -1}}\text {d} s_\ell \, (\text {ad} _{\psi (s_1)}\circ \dots \circ \text {ad} _{\psi (s_{\ell })})(\psi (s))\\&\qquad \textstyle + t^\ell \cdot \int _{z-h}^{z}\text {d} s \textstyle \int _s^{z}\text {d} s_1\int _s^{s_1}\text {d} s_2 \, {\dots } \int _s^{s_{\ell -1}}\text {d} s_\ell \, (\text {ad} _{\psi (s_1)}\circ \dots \circ \text {ad} _{\psi (s_{\ell })})(\psi (s))\\&\quad \textstyle =t^\ell \cdot \int _a^{z-h} \text {d} s \textstyle \int _{z-h}^{z}\text {d} s_1\int _s^{z-h}\text {d} s_2 \, {\dots } \int _s^{s_{\ell -1}}\text {d} s_\ell \, (\text {ad} _{\psi (s_1)}\circ \dots \circ \text {ad} _{\psi (s_{\ell })})(\psi (s))\\&\qquad \textstyle + t^\ell \cdot \int _a^{z-h} \text {d} s \textstyle \int _{z-h}^{z}\text {d} s_1\int _{z-h}^{s_1}\text {d} s_2 \, {\dots } \int _s^{s_{\ell -1}}\text {d} s_\ell \, (\text {ad} _{\psi (s_1)}\circ \dots \circ \text {ad} _{\psi (s_{\ell })})(\psi (s))\\&\qquad \textstyle + t^\ell \cdot \int _{z-h}^{z}\text {d} s \textstyle \int _s^{z}\text {d} s_1\int _s^{s_1}\text {d} s_2 \, {\dots } \int _s^{s_{\ell -1}}\text {d} s_\ell \, (\text {ad} _{\psi (s_1)}\circ \dots \circ \text {ad} _{\psi (s_{\ell })})(\psi (s)). \end{aligned}$$(In the second step, we have split the third integral in the first summand at \(z-h\).)
-
Let \(\textsf {v} \le \textsf {w} \) be as in (95), and set
Let \(z\in [a,b+\varepsilon )\) be fixed, and set
For \(\text {s} \in \mathbb {N}\), \(\ell \ge 1\), and \(h\in D_z\), we obtain
Now, the maps (with \(h\in D\))
converge w.r.t. the \(C^\infty \)-topology; and continuity of \(\psi \) implies \(\lim _{h\rightarrow 0}\Delta (\textsf {w} ,z,h)=0\). The triangle inequality thus yields
Together with (127) this proves the claim, because for \(z\in [a,b+\varepsilon )\) and \(t\in [0,1]\), we have
by continuity of \(\varvec{[}\cdot , \cdot \varvec{]}\).
-
(2)
Point (a) is clear from Part 1). For the points (b) and (c), we observe the following:
-
For \(\textsf {p} \in \textsf {Sem}(E)\), \(\text {s} \in \mathbb {N}\), \(z\in (a-1,b+\varepsilon )\), and \(h\in \mathbb {R}\) with \(z+h\in (a-1,b+\varepsilon )\), we have
$$\begin{aligned} \begin{aligned}&\textsf {p} ^\text {s} _\infty (\Phi _\psi (z+h,\cdot )-\Phi _\psi (z,\cdot ))\\&\quad \le \textsf {p} ^\text {s} _\infty (\Phi _\psi (z+h,\cdot )-\Phi _\psi (z,\cdot )-h\cdot \mathcal {D}(z,\cdot )) + |h|\cdot \textsf {p} ^\text {s} _\infty ( \mathcal {D}(z,\cdot )). \end{aligned} \end{aligned}$$(129) -
Since \(\varvec{[}\cdot , \cdot \varvec{]}\) is continuous and bilinear, there exists \(\textsf {q} \in \textsf {Sem}(E)\) with
$$\begin{aligned} \textsf {p} (\varvec{[}X, Y \varvec{]})\le \textsf {q} (X)\cdot \textsf {q} (Y) \qquad \quad \forall \, X,Y\in \mathfrak {g}. \end{aligned}$$Consequently, (121) implies
$$\begin{aligned} \sup \{a-1\le z\le b+\varepsilon \,|\, \textsf {p} _\infty ^\text {s} (\mathcal {D}(z,\cdot ))\}<\infty \qquad \quad \forall \, \textsf {p} \in \textsf {Sem}(E). \end{aligned}$$(130)
Point (b) is now clear from Part 1), (129), and (130). For point (c), we set \(\text {s} :=0\). Then, by Part 1) and (130), both summands in (129) tend to zero if h tends to zero. Point (c) now follows from the triangle inequality, as well as continuity of \(\Phi _\psi (z,\cdot )\) for each \(z\in (a-1,b+\varepsilon )\).
-
(3)
Let \(z\in (a-1,b+\varepsilon )\) and \(\mathbb {R}_{\ne 0}\supseteq \{h_n\}_{n\in \mathbb {N}}\rightarrow 0\) be given. Then, Part 2).(b) implies that
 holds (recall (14)). Theorem B and Lemma A yield
holds (recall (14)). Theorem B and Lemma A yield 
It follows that the map
 (131)
(131)is continuous. In particular, \(\mu _{t,\psi }\) is continuous for each \(t\in [0,1]\).
Let now \(t\in [0,1]\) be fixed. The points (a) and (b) in Part 2) show that the map \(\Phi _\psi |_{(a-1,b+\varepsilon )\times [0,t]}\) fulfills the assumptions in Theorem C. We obtain (apply Part 2).(a) in the third step)

for each \(z\in (a-1,b+\varepsilon )\). It follows from smoothness of the group operations, continuity of (131), and continuity of \(\Phi _\psi \) (by Part 2).(c)) that \({\dot{\mu }}_{t,\psi }\) is continuous. This shows that \(\mu _{t,\psi }\) is of class \(C^1\), which proves the claim. \(\square \)
We are ready for the proof of Theorem 2.
Proof of Theorem 2
Since \(\mathfrak {g}\) is sequentially complete, \(\mathfrak {g}\) is both Mackey complete and integral complete. To prove the claim, it thus suffices to show that G is \(C^0\)-semiregular. For this, let \(\phi \in C^0([0,1],\mathfrak {g})\) be given, and fix a continuous extension \(\psi :[0,1+\varepsilon ]\rightarrow \mathfrak {g}\) for some \(\varepsilon >0\). We define \(\mu _{1,\psi }:(-1,1+\varepsilon )\rightarrow G\) as in (122) (for \(a\equiv 0\) and \(b\equiv 1\) there). Lemma 27.2) shows that \(\mu _{1,\psi }\) is of class \(C^1\), so that it remains to verify  . For this, let \(z\in [0,1]\) be fixed. Corollary 19 shows (\(\Phi _\psi \) is defined as in (120))
. For this, let \(z\in [0,1]\) be fixed. Corollary 19 shows (\(\Phi _\psi \) is defined as in (120))

for each \(h\in [0,\varepsilon )\). Set \(\widehat{\psi }:=\psi |_{[z,z+\varepsilon ]}\). Then,

holds by definition, so that we have
Lemma 27.2) shows \(\mu _{1,\widehat{\psi }}\in C^1((z-1,z+\varepsilon ),G)\), and Equation (126) in Lemma 27.2) together with both sides of (124) (first step) yields
Then, (133) shows  , which proves the claim. \(\square \)
, which proves the claim. \(\square \)
Data availability
The data that support the findings of this study are included in this paper.
Notes
Throughout this paper, we work in the slightly more general setting introduced by Glöckner in [3]. Specifically, this means that any completeness presumption on the modeling space is dropped. Moreover, Milnor’s definition of an infinite-dimensional manifold M involves the requirement that M is a regular topological space, i.e., fulfills the separation axioms \(T_2, T_3\). Deviating from that, in [3] only the \(T_2\) property of M is explicitly assumed. This, however, makes no difference in the Lie group case, because topological groups are automatically \(T_3\). We also refer to [21, 22] for introductions into this topic.
Injectivity of
 is easily verified, confer, e.g., Lemma 9 in [8].
is easily verified, confer, e.g., Lemma 9 in [8].Specifically, \(\mathfrak {q}\) is a Hausdorff locally convex vector space; and \(\varvec{[}\cdot , \cdot \varvec{]}:\mathfrak {q}\times \mathfrak {q}\rightarrow \mathfrak {q}\) is bilinear, antisymmetric, continuous, and fulfills the Jacobi identity \(\varvec{[}Z, \varvec{[}X, Y \varvec{]} \varvec{]}= \varvec{[}\varvec{[}Z, X \varvec{]}, Y \varvec{]} + \varvec{[}X, \varvec{[}Z, Y \varvec{]} \varvec{]}\) for all \(X,Y,Z\in \mathfrak {q}\).
In other words, we equip \(\mathfrak {g}\) with the Hausdorff locally convex topology that is generated by the system of seminorms \(\{\textsf {p} \circ \text {d} _e\Xi \,|\, \textsf {p} \in \textsf {Sem}(E)\}\). It is then not hard to see that \(\textsf {Sem}(\mathfrak {g})=\{\textsf {p} \circ \text {d} _e\Xi \,|\, \textsf {p} \in \textsf {Sem}(E)\}\) holds, hence \(\textsf {Sem}(\mathfrak {g})\cong \textsf {Sem}(E)\).
We note that if \((\mathfrak {q},\varvec{[}\cdot , \cdot \varvec{]})\) is the Lie algebra of a Lie group Q, then one usually defines \(\text {ad} _{X}:\mathfrak {q}\ni Y\mapsto \text {d} _e\text {Ad} (Y)(X)\in \mathfrak {q}\) for \(X\in \mathfrak {g}\). According to our definition (9) of the commutator, this is consistent with our notation in the general case (i.e., where \((\mathfrak {q},\varvec{[}\cdot , \cdot \varvec{]})\) is not necessarily the Lie algebra of a Lie group).
Note that the first definition is recalled from Sect. 1.
More specifically, \(\tilde{f}=p*f\) for \(p:(-1,1)\ni t\mapsto (1+t)\in \mathbb {R}\), and \(\tilde{g}:(-\ln (2),\ln (2))\ni t\mapsto \sum _{n=1}^\infty \frac{1}{n!}\cdot (-t)^n \in (-1,1)\).
Specifically, such \(\mathfrak {g}\)-valued curves whose image is a \(\text {Nil} _{q}\)-set for some \(q\ge 2\), recall (29).
For the finite-dimensional case, confer, e.g., Proposition 3.4.4 in [13], with \(\Psi \equiv \widetilde{\Psi }\) there.
For \(g \in \mathcal {U}\), consider \(C^\infty ([0,1],G)\ni \mu _1:[0,1]\ni t\mapsto \Xi ^{-1}(t\cdot \Xi (g))\in G\).
Confer, e.g., Sect. 4.3 in [8] for explicit constructions of such bump functions.
Although it might be obvious, we explicitly mention at this point that in contrast to the finite-dimensional case, in the context considered it not suffices to show the existence of a left- or right inverse of \({\textbf {Ad}} _\psi ^\pm [t]\) but both. Basically, this is the reason for the necessity of the investigations made in Sect. 5.1.2.
We recall that in contrast to the definition of weak \(C^k\)-regularity for \(k\in \mathbb {N}\cup \{\text {lip} ,\infty \}\), the definition of \(C^k\)-regularity additionally involves continuity of the product integral w.r.t. the \(C^k\)-topology.
Sequentially completeness of a Lie group and sequentially completeness of its Lie algebra are ad hoc different properties; details can be found in [8].
We consider \(C^0([a,b],\mathfrak {q})\subseteq \text {CP} ^0([a,b],\mathfrak {q})\) as a subset in the obvious way.
Specifically, in the previous point set \(\psi :=\chi (\cdot -x):[a+x,b+x]\rightarrow \mathfrak {q}\) as well as \(\varrho :[a,b]\ni t\mapsto t+x\in [a+x,b+x]\).
For \(a<b\) and \(\chi \in C^0([a,b],\mathfrak {q})\), set \({\textbf {Ad}} ^\pm _{\chi |_{[a,a]}}:=\text {id} _\mathfrak {q}\).
Recall that in Sect. 3.3, \({\textbf {Ad}} ^+_\psi [X]\) had been defined in Equation (63) by
 , for \(\psi \in \mathfrak {D}_{[0,1]}\supseteq C^\infty ([0,1],\mathfrak {g})\) and \(X\in \mathfrak {g}\). Furthermore, observe that the right side of (68) in Corollary 8 obviously equals the definition of \({\textbf {Ad}} ^\pm _\psi [X]\) in the beginning of Sect. 5.1.
, for \(\psi \in \mathfrak {D}_{[0,1]}\supseteq C^\infty ([0,1],\mathfrak {g})\) and \(X\in \mathfrak {g}\). Furthermore, observe that the right side of (68) in Corollary 8 obviously equals the definition of \({\textbf {Ad}} ^\pm _\psi [X]\) in the beginning of Sect. 5.1.Apply the triangle inequality in the form \(\Vert f(g(\mathfrak {a}))-f_p(g_p(\mathfrak {a}))\Vert _\mathcal {A}\le \Vert f(g(\mathfrak {a}))-f(g_p(\mathfrak {a}))\Vert _\mathcal {A}+\Vert f(g_p(\mathfrak {a}))-f_p(g_p(\mathfrak {a}))\Vert _\mathcal {A}\).
References
Crainic, M., Fernandes, R.L.: Integrability of Lie brackets. Ann. Math. 157, 575–602 (2003)
Duistermaat, J.J., Kolk, J.A.C.: Lie Groups. Universitext. Springer, Berlin (2000)
Glöckner, H.: Infinite-dimensional Lie groups without completeness restrictions. In: Geometry and Analysis on Finite- and Infinite-dimensional Lie Groups (Bȩdlewo 2000), Banach Center Publ. 55, Polish Academy of Sciences, Warsaw, pp 43–59 (2002)
Glöckner, H.: Regularity properties of infinite-dimensional Lie groups, and semiregularity, preprint (2012), arXiv:1208.0715
Glöckner, H.: Measurable regularity properties of infinite-dimensional Lie groups, preprint (2015), arXiv:1601.02568
Glöckner, H., Neeb, K.-H.: When unit groups of continuous inverse algebras are regular Lie groups. Studia Math. 211(2), 95–109 (2012)
Hamilton, R.: The inverse function theorem of Nash and Moser. Bull. Amer. Math. Soc. (N. S.) 7(1), 65–222 (1982)
Hanusch, M.: Regularity of Lie groups. Commun. Anal. Geom. 30(1), 53–152 (2022)
Hanusch, M.: The Regularity Problem for Lie Groups with Asymptotic Estimate Lie Algebras. Indag. Math. 31(1), 152–176 (2020)
Hanusch, M.: The strong Trotter property for locally \(\mu \)-convex Lie Groups. J. Lie Theory 30(1), 025–032 (2020)
Hanusch, M.: Differentiability of the Evolution Map and Mackey Continuity. Forum Math. 31(5), 1139–1177 (2019)
Hanusch, M.: A \(\cal{C}^k\)-seeley-extension-theorem for Bastiani’s differential calculus. Can. J. Math. 75(1), 170–201 (2023)
Hilgert, J., Neeb, K.-H.: Structure and Geometry of Lie Groups. Springer, New York (2012)
Jarchow, H.: Locally Convex Spaces. B.G. Teubner, Stuttgart (1981)
Kriegl, A., Michor, P.W.: Regular infinite-dimensional Lie groups. J. Lie Theory 7(1), 61–99 (1997)
Kriegl, A., Michor, P.W.: The Convenient Setting of Global Analysis, Math. Surveys Monogr. 53, American Mathematical Society, Providence (1997)
Meise, R., Vogt, D.: Introduction to Functional Analysis, Oxf. Grad. Texts Math. 2, Oxford University, New York (1997)
Michor, P.W., Teichmann, J.: Description of infinite dimensional abelian regular Lie groups. J. Lie Theory 9(2), 487–489 (1999)
Milnor, J.: Remarks on infinite-dimensional Lie groups. In: Relativity, Groups and Topology. II (Les Houches 1983), North-Holland, Amsterdam, pp. 1007–1057 (1984)
Neeb, K.-H.: Infinite-dimensional groups and their representations. In: Infinite Dimensional Kähler Manifolds (Oberwolfach 1995), DMV Sem. 31, Birkhäuser, Basel (2001), 131-178
Neeb, K.-H.: Towards a Lie theory of locally convex groups. Jpn. J. Math. 1(2), 291–468 (2006)
Neeb, K.-H.: Infinite-Dimensional Lie Groups. 3rd cycle. Monastir (Tunisie), (2005), pp.76. cel-00391789
Omori, H., Maeda, Y., Yoshioka, A., Kobayashi, O.: On regular Fréchet-Lie groups. IV. Definition and fundamental theorems. Tokyo J. Math. 5(2), 365–398 (1982)
Omori, H.: Infinite-Dimensional Lie Groups, Translations of Math. Monographs 158, Amer. Math. Soc. (1997)
Seeley, R.T.: Extension of \(C^\infty \) functions defined in a half space. Proc. Amer. Math. Soc. 15, 625–626 (1964)
Walter, B.: Weighted diffeomorphism groups of Banach spaces and weighted mapping groups. Diss. Math. 484, 1–126 (2012)
Acknowledgements
The author thanks Stefan Waldmann for drawing his attention to the construction made by Duistermaat and Kolk [2] to prove Lie’s third theorem in the finite-dimensional context. This research was supported by the Deutsche Forschungsgemeinschaft, DFG, Project Number HA 8616/1-1.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
1.1 Bastiani’s Differential Calculus
In this appendix, we recall Bastiani’s differential calculus, confer also [3, 7, 19,20,21,22]. Let \(E,F\in \textsf {hlcVect}\) be given. A map \(f:U\rightarrow F\), with \(U\subseteq E\) open, is said to be differentiable if
exists for each \(x\in U\) and \(v\in E\). The map f is said to be k-times differentiable for \(k\ge 1\) if
is defined for all \(v_1,\dots ,v_k\in E\). Implicitly, this means that f is p-times differentiable for each \(1\le p\le k\), and we set
for \(p=1,\dots ,k\). We furthermore define \(\text {d} f:= \text {d} ^1 f\), as well as \(\text {d} _x f:= \text {d} ^1_x f\) for each \(x\in U\). The map \(f:U\rightarrow F\) is said to be
-
of class \(C^0\) if it is continuous. In this case, we define \(\text {d} ^0 f:= f\).
-
of class \(C^k\) for \(k\ge 1\) if it is k-times differentiable, such that
$$\begin{aligned} \text {d} ^p f:U\times E^p\rightarrow F,\qquad (x,v_1,\dots ,v_p)\mapsto D_{v_p,\dots ,v_1}f(x) \end{aligned}$$is continuous for \(p=0,\dots ,k\). In this case, \(\text {d} ^p_x f\) is symmetric and p-multilinear for each \(x\in U\) and \(p=1,\dots ,k\), cf. [3].
-
of class \(C^\infty \) if it is of class \(C^k\) for each \(k\in \mathbb {N}\).
Remark
Assume that E, F are normed spaces. Let \(U\subseteq E\) be non-empty open, as well as \(k\in \mathbb {N}\cup \{\infty \}\). Let \(\mathcal {F}C^k(U,F)\) denote the set of all k-times Fréchet differentiable maps \(U\rightarrow F\). Then, \(C^{k+1}(U,F)\subseteq \mathcal {F}C^k(U,F)\subseteq C^k(U,F)\) holds [20, 26], hence \(C^\infty (U,F)=\mathcal {F}C^\infty (U,F)\). \(\square \)
We have the following differentiation rules [3].
Proposition A.1
-
(a)
A map \(f:E\supseteq U\rightarrow F\) is of class \(C^k\) for \(k\ge 1\) if and only if \(\text {d} f\) is of class \(C^{k-1}\) when considered as a map \(E \times E \supseteq U\times E \rightarrow F\).
-
(b)
Let \(f:E\rightarrow F\) be linear and continuous. Then, f is smooth, with \(\text {d} ^1_xf=f\) for each \(x\in E\), as well as \(\text {d} ^pf=0\) for each \(p\ge 2\).
-
(c)
Let \(F_1,\dots ,F_m\) be Hausdorff locally convex vector spaces, and \(f_q:E\supseteq U\rightarrow F_q\) be of class \(C^k\) for \(k\ge 1\) and \(q=1,\dots ,m\). Then,
$$\begin{aligned} f:=f_1\times {\dots }\times f_m :U\rightarrow F_1\times {\dots }\times F_m,\qquad x\mapsto (f_1(x),\dots ,f_m(x)) \end{aligned}$$if of class \(C^k\), with \(\text {d} ^p f=\text {d} ^pf_1{\times } \dots \times \text {d} ^pf_m\) for \(p=1,\dots ,k\).
-
(d)
Let \(F,\bar{F},\bar{\bar{F}}\in \textsf {hlcVect}\), \(1\le k\le \infty \), as well as \(f:F\supseteq U\rightarrow \bar{U}\subseteq \bar{F}\) and \(\bar{f}:\bar{F}\supseteq \bar{U}\rightarrow \bar{\bar{U}}\subseteq \bar{\bar{F}}\) be of class \(C^k\). Then, \(\bar{f}\circ f:U\rightarrow \bar{\bar{F}}\) is of class \(C^k\), with
$$\begin{aligned} \text {d} _x(\bar{f}\circ f)=\text {d} _{f(x)}\bar{f}\circ \text {d} _x f\qquad \quad \forall \, x\in U. \end{aligned}$$ -
(e)
Let \(F_1,\dots ,F_m,E\in \textsf {hlcVect}\), and \(f:F_1\times {\dots } \times F_m\supseteq U\rightarrow E\) be of class \(C^0\). Then, f is of class \(C^1\) if and only if for \(p=1,\dots ,m\), the partial derivatives
$$\begin{aligned}&\partial _p f :U\times F_p\ni ((x_1,\dots ,x_m),v_p)\mapsto \lim _{t\rightarrow 0} 1/t\\&\quad \cdot (f(x_1,\dots , x_p+t\cdot v_p,\dots ,x_m)-f(x_1,\dots ,x_m)) \end{aligned}$$exist in E and are continuous. In this case, we have
$$\begin{aligned} \textstyle \text {d} f((x_1,\dots ,x_m),v_1,\dots ,v_m)&\textstyle =\sum _{p=1}^m\partial _p f((x_1,\dots ,x_m),v_p)\\ \big (\!&\textstyle = \sum _{p=1}^m ~~\text {d} f((x_1,\dots ,x_m),(0,\dots ,0, v_p,0,\dots ,0))\,\big ) \end{aligned}$$for each \((x_1,\dots ,x_m)\in U\), and \(v_p\in F_p\) for \(p=1,\dots ,m\).
1.2 Proof of Equation (26)
The claim is clear for \(m=1\) and \(n\ge 1\). Assume now that (26) holds for some \(m\ge 1\), as well as each \(n\ge 1\). For \(X\in \mathcal {V}_1(S)\), \(\alpha \in \mathcal {V}_m(S)\), and \(\beta \in \mathcal {V}_n(S)\) with \(n\ge 1\), we obtain from (25) and antysimmetry of \(\varvec{[}\cdot , \cdot \varvec{]}\) that
holds. Since \(\varvec{[}\cdot , \cdot \varvec{]}\) is bilinear, this implies \(\varvec{\langle } \varvec{[}\mathcal {V}_{m+1}(S), \mathcal {V}_n(S) \varvec{]}\varvec{\rangle } \subseteq \mathcal {V}_{(m+1)+n}(S)\) for each \(n\ge 1\), so that the claim follows inductively.
1.3 Proof of Lemma 5
Lemma 5
Let \(V\subseteq F\) be open with \(0\in V\). Let furthermore \(\Psi :V\times E\rightarrow E\) be smooth with \(\Psi (0,\cdot )=\text {id} _{E}\), such that \(\Psi (x,\cdot )\) is linear for each \(x \in V\). Then, to each \(\textsf {p} \in \textsf {Sem}(E)\), there exist \(\textsf {q} \in \textsf {Sem}(F)\) and \(\textsf {w} \in \textsf {Sem}(E)\) with
Proof of Lemma 5
We consider the continuous map
that is linear in the last two arguments. Then, for \(\textsf {p} \in \textsf {Sem}(E)\) fixed, by Lemma 4 there exist \(\textsf {q} \in \textsf {Sem}(F)\) and \(\textsf {p} \le \textsf {w} \in \textsf {Sem}(E)\) with
For \(x\in \text {B} _{\textsf {q} ,1}\), we let \(\gamma :[0,1]\ni t\mapsto t\cdot x \in \text {B} _{\textsf {q} ,1}\), and define
Then, the parts b) and e) of Proposition A.1 yield \({\dot{\alpha }}_Y=\Phi ((\gamma ,Y),{\dot{\gamma }})=\Phi ((\gamma ,Y),x)\), and we obtain
for all \(x\in \text {B} _{\textsf {q} ,1}\) and \(Y\in E\). \(\square \)
1.4 Appendix to Sect. 2.3
For combinatorial reasons, there exist \(c[p]_0,\dots ,c[p]_{p^2}\in \mathbb {K}\) with
Set \(c[p]_n:=0\) for \(n\ge p^2+1\). Since \(\{f_p\circ g_p\}_{p\in \mathbb {N}}\rightarrow f\circ g\) converges compactly on \(U_{S}(0)\), the Weierstrass convergence theorem yields
Proof of Equation (31)
Since \(b_0=0\) holds, we have \(c[q+\ell ]_{n}=c[q]_{n}\) for \(n=0,\dots ,q\) and \(\ell \in \mathbb {N}\), hence \(c[q]_n=c_n\) for \(n=0,\dots ,q\) by (135). We obtain
which proves (31). \(\square \)
Proof of Equation (32)
Fix \(\Vert \mathfrak {a}\Vert _\mathcal {A}< s <S\), and set \(M:=|f|_{|g|_s}\). Then, \(|(f_p\circ g_p)(z)|\le M\) holds for all \(p\in \mathbb {N}\) and \(z\in \mathbb {C}\) with \(|z|\le s\). Cauchy’s estimate yields \(\textstyle |c[p]_n|\le \frac{M}{s^n}\) for all \(p,n\in \mathbb {N}\), hence
for all \(N,p\in \mathbb {N}\). Given \(\varepsilon >0\), there thus exists \(N_\varepsilon \in \mathbb {N}\) with
By (135), there exists \(m\in \mathbb {N}\) with
Increasing m if necessary, we can additionally assumeFootnote 25
Set \(p:= m\). Then, we have

with
by (136) and (137).\(\square \)
1.5 Proof of Lemma 9
Lemma 9
Assume that G is weakly \(C^k\)-regular for \(k\in \mathbb {N}\cup \{\text {lip} ,\infty \}\), and let \(\phi \in C^k([a,b])\) (\(a<b\)) be given. Then,  is continuous.
is continuous.
Proof
Let \(z\in [a,b]\), \(t\in \mathbb {R}\), and \(U\subseteq G\) be an open neighborhood of e. We fix \(W\subseteq G\) open with \(e\in W\) and \(W\cdot W\subseteq U\), and observe that

is continuous. Since [a, b] is compact, there exists some open \(V\subseteq G\) with \(e\in V=V^{-1}\), such that

Theorem B together with Lemma 15 in [11] implies that there exists \(\delta >0\) with

For \(a\le x\le b\) and \(|h|<\delta \), we obtain

Since \(\kappa (t,\cdot )\) is continuous, we can shrink \(\delta >0\) such that for each \(x\in (z-\delta ,z+\delta ) \cap [a,b]\), we have  . We obtain
. We obtain

for \(|h|<\delta \) and \(x\in (z-\delta ,z+\delta ) \cap [a,b]\). \(\square \)
1.6 Proof of Equation (64)
Proof of Equation (64)
By definition, we have  for certain \(\mu \in C^1((a-\varepsilon ,b+\varepsilon ),G)\) and \(\varepsilon >0\). Replacing \(\mu \) by \(\mu \cdot \mu (a)^{-1}\) if necessary, we can assume that \(\mu (a)=e\) holds, hence
for certain \(\mu \in C^1((a-\varepsilon ,b+\varepsilon ),G)\) and \(\varepsilon >0\). Replacing \(\mu \) by \(\mu \cdot \mu (a)^{-1}\) if necessary, we can assume that \(\mu (a)=e\) holds, hence

Then, \(\alpha ^\pm := \text {Ad} _{\mu ^\pm }(X)\in C^1((a-\varepsilon ,b+\varepsilon ))\) holds by Lemma 8, with \(\alpha ^\pm |_{[a,b]}={\textbf {Ad}} ^\pm _\psi [X]\). This shows \({\textbf {Ad}} _\psi ^\pm [X]\in C^1([a,b],\mathfrak {g})\), with \({\textbf {Ad}} ^\pm _\psi [X](a)=\text {Ad} _e(X)=X\). Let now \(t\in [a,b]\) and \(0<h<\varepsilon \) be given. We observe

and obtain from (d) that

Differentiating both hand sides and then applying (9), we obtain (64). \(\square \)
1.7 The Proof of Lemma 17
Lemma 17
Let \(\psi \in C^0([a,b],\mathfrak {q})\) be given. Then, the following assertions hold:
-
(1)
The maps \(\varvec{\Lambda }_\psi ^\pm \) are defined and of class \(C^1\), and we have
$$\begin{aligned} \partial _1 \varvec{\Lambda }_\psi ^+(t,X)&\textstyle =\partial _t{\textbf {Ad}} _\psi ^+[X](t)=\varvec{[}\psi (t), {\textbf {Ad}} ^+_\psi [X](t) \varvec{]}\\ \partial _1 \varvec{\Lambda }^-_\psi (t,X)&\textstyle =\partial _t{\textbf {Ad}} _\psi ^-[X](t)=-{\textbf {Ad}} ^-_\psi [\varvec{[}\psi (t), X \varvec{]}](t) \end{aligned}$$for all \(t\in [a,b]\) and \(X\in \mathfrak {q}\).
-
(2)
\(\varvec{\Lambda }^\pm _\psi (t,\cdot )={\textbf {Ad}} _\psi ^\pm [t]\) is linear and continuous for each \(t\in [a,b]\).
-
(3)
If \(\psi \in C^k([a,b],\mathfrak {q})\) holds for \(k\in \mathbb {N}\cup \{\infty \}\), then \(\varvec{\Lambda }_\psi ^\pm \) is of class \(C^{k+1}\).
Proof
Let \(X\in \mathfrak {q}\) be fixed. Then, \(\varvec{\lambda }^\pm _{\ell ,\psi }[X]\) is of class \(C^1\) for each \(\ell \in \mathbb {N}\) by (20); with \(\partial _t\varvec{\lambda }^\pm _{0,\psi }[X]=0\) as well as
for each \(\ell \ge 1\) and \(t\in [0,1]\). For \(\textsf {v} \le \textsf {w} \) as in (95), we have
Corollary 1 thus implies \(\varvec{\Lambda }^\pm (\cdot ,X)={\textbf {Ad}} _\psi ^\pm [X]\in C^1([a,b],\mathfrak {q})\), with
for each \(t\in [a,b]\), which establishes Part 1). Now, it is clear from the definitions that \(\varvec{\Lambda }^\pm _\psi (t,\cdot )\) is linear for each \(t\in [a,b]\); and we furthermore observe that
holds for all \(t,t'\in [a,b]\) and \(X\in \mathfrak {q}\). We obtain from (138) and (139) that
for all \(t,t'\in [a,b]\) and \(X,X'\in \mathfrak {q}\). This shows that \(\varvec{\Lambda }_\psi ^\pm \) is continuous, which establishes Part 2). We furthermore conclude that the partial derivatives
are continuous. Part e) of Proposition A.1 thus shows that the maps \(\varvec{\Lambda }_\psi ^\pm \) are of class \(C^1\), with
Finally, assume that \(\psi \in C^k([a,b],\mathfrak {q})\) holds for \(k \ge 1\). Then, (140) together with the parts a), c), d) of Proposition A.1 imply that given \(1\le \ell \le k\), then \(\varvec{\Lambda }_\psi ^\pm \) is of class \(C^{\ell +1}\) if \(\varvec{\Lambda }_\psi ^\pm \) is of class \(C^\ell \), which establishes Part 3). It thus follows by induction that \(\varvec{\Lambda }_\psi ^\pm \) is of class \(C^{k+1}\). \(\square \)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Hanusch, M. The Lax equation and weak regularity of asymptotic estimate Lie groups. Ann Glob Anal Geom 63, 21 (2023). https://doi.org/10.1007/s10455-023-09888-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10455-023-09888-y





 (cf. Corollary
(cf. Corollary 







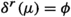 which establishes Theorem
which establishes Theorem 
 with
with 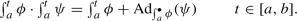
 with
with 
 with
with 

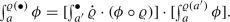


 .
.
 .
.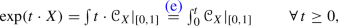
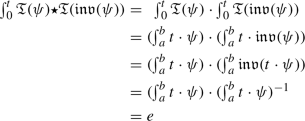
 implies
implies 
 .
.



 is of class
is of class 

 .
.

 . Since G is Mackey k-continuous, Lemma
. Since G is Mackey k-continuous, Lemma 


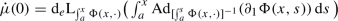

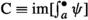 there. We obtain from Lemma
there. We obtain from Lemma  there. Let furthermore
there. Let furthermore 
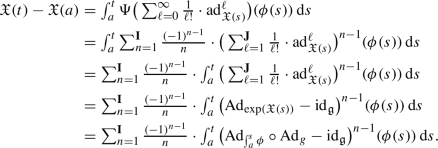

 .
. .
. .
. there, together with Corollary
there, together with Corollary 



 holds (recall (
holds (recall (


 is easily verified, confer, e.g., Lemma 9 in [
is easily verified, confer, e.g., Lemma 9 in [ , for
, for