Generalised Bianchi permutability for isothermic surfaces

Abstract

Isothermic surfaces are surfaces which allow a conformal curvature line parametrisation. They form an integrable system, and Darboux transforms of isothermic surfaces obey Bianchi permutability: for two distinct spectral parameters, the corresponding Darboux transforms have a common Darboux transform which can be computed algebraically. In this paper, we discuss two-step Darboux transforms with the same spectral parameter, and show that these are obtained by a Sym-type construction: All two-step Darboux transforms of an isothermic surface are given, without further integration, by parallel sections of the associated family of the isothermic surface, either algebraically or by differentiation against the spectral parameter.

1 Introduction

First defined by Bour in [3] as surfaces which admit conformal curvature lines, isothermic surfaces have enjoyed massive interest in the late 19th and early 20th century. Darboux showed in [11] that given an isothermic surface $f: M \rightarrow \mathbb { R}^3$ from a Riemann surface M into the 3-sphere, one can construct a second isothermic surface via a Ribaucour sphere congruence that depends on a spectral parameter, a transformation which we refer to as Darboux transformation.

Then Bianchi, [1], showed that Darboux transformations admit permutability: starting from an isothermic surface f and constructing two Darboux transforms $f_1$ and $f_2$ using spectral parameters $\varrho _1$ and $\varrho _2$, respectively, one can always find a fourth surface $f_{12}$ that is both a Darboux transform of $f_1$ and $f_2$ with respect to spectral parameters $\varrho _2$ and $\varrho _1$. Demoulin further showed in [12] that these four surfaces in the permutability enjoy a relationship characterised by cross-ratios:

$$\begin{aligned} \mathrm {cr}(f, f_1, f_{12}, f_2) = \frac{\varrho _2}{\varrho _1}. \end{aligned}$$

(1.1)

Generally, one needs integration to find Darboux transforms of a given isothermic surface; however, the cross-ratio equation (1.1) coming from permutability enables one to find successive Darboux transforms algebraically after an initial integration. The cross-ratio equation (1.1) shows that the fourth surface $f_{12}$ is identical to the given starting surface f if the spectral parameters are equal. Therefore, permutability gives algebraic methods to find non-trivial successive Darboux transforms as long as the spectral parameters are pairwise distinct.

Note however that one can always integrate twice to find non-trivial two-step Darboux transforms: the condition in Bianchi permutability that the spectral parameters need to be distinct is only essential to obtain non-trivial successive Darboux transforms algebraically.

The aim of this paper is to eliminate the assumption in Bianchi permutability and obtain all successive Darboux transforms without further integration, even in the case when the spectral parameters are equal. Rather than using Bianchi permutability, we obtain two-step Darboux transforms with the same spectral parameter by a Sym-type method, [22], that is, by differentiation with respect to the spectral parameter.

The existence of spectral parameters, transformations, and permutability suggested that the class of isothermic surfaces constitutes an integrable system, an approach taken in [10] which renewed modern interest in isothermic surfaces. Various characterisations of Darboux transformations have been obtained since Darboux transformation can be described in terms of a Riccati-type equation [18]; Darboux pairs of isothermic surfaces can be viewed as a curved flat using the Minkowski model [9] or using the quaternionic model [15] of conformal geometry. In fact, isothermic surfaces can be characterised via the existence of a closed 1-form or, equivalently, a one-parameter family of flat connections [5, 14, 19], and one can view Darboux transformations as the parallel sections of the flat connections [16, 17]. In addition, many of the aforementioned works have investigated the various transformations of isothermic surfaces and their relationships: for example, the T-transforms, also known as Calapso transforms, can be obtained algebraically from the Darboux transforms, while the Christoffel dual can be obtained via a Sym-type formula from either the T-transforms or the Darboux transforms.

In this paper, we use the quaternionic model and describe Darboux transform by parallel sections of the associated family of flat connections of the isothermic surface. A short review of isothermic surfaces, the associated family $d_\lambda$ and Bianchi permutability in this setting, is given in Sect.  2 to setup the notations and tools for our main result.

Then, we tackle the problem to eliminate the need for a second integration for finding two-step Darboux transforms in Sect.  3. For this, we use the fact that Darboux transforms of isothermic surfaces are indeed given by a simple factor dressing. In particular, the associated family of flat connections $d^1_\lambda$ of a Darboux transform $f_1$ with spectral parameter $\varrho$ is given by an explicit gauge $r_\lambda$, which depends smoothly on the spectral parameter and has a simple pole at $\varrho$, of the associated family $d_\lambda$ of f. Although the gauge has a pole, the family $d^1_\lambda =r_\lambda \cdot d_\lambda$ extends into $\varrho$, and we give an explicit form of the associated family.

With this at hand, we obtain the parallel sections $\varphi _1 =r_\lambda (\varphi )$ of $f_1$ by applying the gauge matrix to parallel sections $\varphi$ given by the isothermic surface f, for spectral parameter away from the pole $\varrho$ of $r_\lambda$. This way, we recover the parallel sections used for Bianchi permutability, the Bianchi-type parallel sections, explicitly as projections of parallel sections $\varphi$. In the case when the spectral parameter coincide, there is a quaternionic one-dimensional space arising from this construction: To obtain further parallel sections, we have to consider limits of parallel sections for spectral parameter $\lambda$ when $\lambda$ tends to the pole $\varrho$. We show that these limits, the Sym-type parallel sections, are given by differentiation of a family of $d_\lambda$-parallel sections with respect to the spectral parameter.

Indeed, we can conclude that all parallel sections of the associated family of a Darboux transform are either Bianchi- or Sym-type. In particular, we obtain all non-trivial two-step Darboux transforms with same spectral parameter without need for a second integration, a principle we call generalised Bianchi permutability.

Given an isothermic surface $f: M\rightarrow \mathbb { R}^3$, the Darboux transformation is initially a local construction: the used parallel sections exist globally only on the universal cover of the Riemann surface M. Since all two-step parallel sections are given algebraically or by a Sym-type method, we discuss closing conditions for one- and two-step Darboux transforms by investigating the holonomy of the family of flat connections $d_\lambda$ of f only.

We conclude the paper by demonstrating our construction in the explicit example of the round cylinder. In particular, we give explicit formulae for all parallel sections and obtain a complete description of the set of all closed Darboux transforms of a cylinder. Depending on the spectral parameter, four cases can occur: there is exactly one closed Darboux transform, which is the cylinder, there are two distinct Darboux transforms, which are again cylinders, there is a $\mathbb { C}\mathbb { P}^1$-worth of Darboux transforms which are rotation surfaces, or there is a $\mathbb { H}\mathbb { P}^1$-worth of (possibly singular) Darboux transforms which are rotation surfaces or isothermic bubbletons. We then use the parallel sections to give explicit formulae for Sym-type Darboux transforms, including two-step bubbletons.¹

Since the main ingredients for our construction are the associated family and the simple factor dressing, we expect our results to be templates for similar results for other surface classes allowing simple factor dressing, such as CMC surfaces in space forms, and completely integrable differential equations. This should allow to construct new surfaces and, more generally, new solutions to differential equations given by complete integrability.

2 Background

In this section, we will give a short summary of results and methods used in this paper. For details on the quaternionic formalism and isothermic surfaces, we refer to [4, 8, 13, 16, 18].

2.1 Conformal immersions and quaternions

In this paper, we will identify 4-space by the quaternions $\mathbb { R}^4=\mathbb { H}$, and 3-space by the imaginary quaternions $\mathbb { R}^3={{\,\mathrm{Im}\,}}\mathbb { H}$ where $\mathbb { H}={{\,\mathrm{span}\,}}_\mathbb { R}\{1, i, j, k\}$ and $i^2=j^2=k^2=ijk=-1$. For imaginary quaternions, the product in the quaternions links to the inner product $\langle \cdot , \cdot \rangle$ and the cross-product in $\mathbb { R}^3$ by

$$\begin{aligned} ab =-\langle a,b\rangle +a\times b, \quad a, b\in {{\,\mathrm{Im}\,}}\mathbb { H}\,. \end{aligned}$$

Here, we identify $\mathbb { H}=\mathrm {Re}\,\mathbb { H}\oplus {{\,\mathrm{Im}\,}}\mathbb { H}=\mathbb { R}\oplus \mathbb { R}^3$. In particular, we see

$$\begin{aligned} S^2 =\{ n\in {{\,\mathrm{Im}\,}}\mathbb { H}\mid n^2=-1\}\,. \end{aligned}$$

Thus, if $f: M \rightarrow \mathbb { R}^3$ is an immersion then its Gauss map $N: M \rightarrow S^2$ is a complex structure $N^2=-1$ on $\mathbb { R}^4=\mathbb { H}$. Moreover, if $(M, J_{TM})$ is a Riemann surface, then $f: M \rightarrow \mathbb { R}^3$ is conformal if and only if

$$\begin{aligned} *df = N df = -df N\,, \end{aligned}$$

where $*$ denotes the negative Hodge star operator, that is, $*\omega (X) = \omega (J_{TM}X)$ for $X\in TM$, $\omega \in \Omega ^1(M)$. More generally, if $f: M \rightarrow \mathbb { R}^4$ is a conformal immersion from a Riemann surface into 4-space, the Gauss map is given by a pair of complex structures

$$\begin{aligned} (N, R): M \rightarrow S^2\times S^2 =\mathrm {Gr}_2(\mathbb { R}^4) \end{aligned}$$

such that

$$\begin{aligned} *df = Ndf = -df R\,. \end{aligned}$$

Note that $N=R$ in the case when f is a surface in 3-space.

Since the theory of isothermic surfaces is conformal, it is useful to also consider conformal immersions into the 4-sphere by identifying $S^4=\mathbb { H}\mathbb { P}^1$. Then, a map $f: M\rightarrow S^4=\mathbb { H}\mathbb { P}^1$ can be identified with a line subbundle $L\subset \underline{\mathbb { H}}^{2} =M\times \mathbb { H}^2$ of the trivial $\mathbb { H}^2$-bundle over M via

$$\begin{aligned} f(p) = L_p\,. \end{aligned}$$

Therefore, the group of oriented Möbius transformations is in this setup given by ${{\,\mathrm{GL}\,}}(2,\mathbb { H})$. The derivative of L is given by $\delta = \pi _L d$ where $\pi _L: \underline{\mathbb { H}}^{2} \rightarrow \underline{\mathbb { H}}^{2}/L$ denotes the canonical projection. Then, an immersion f is conformal if and only if there are complex structures $J_L$ on L and $J_{V/L}$ on $\underline{\mathbb { H}}^{2}/L$ such that

$$\begin{aligned} *\delta = J_{V/L} \delta = \delta J\,. \end{aligned}$$

In particular, if $f: M\rightarrow \mathbb { R}^k$, $k=3,4$, is an immersion from a Riemann surface into 3- or 4-space we will consider f as a map into the 4-sphere by setting

$$\begin{aligned} L = \psi \mathbb { H}, \quad \psi = \begin{pmatrix} f \\ 1 \end{pmatrix}\,. \end{aligned}$$

We will identify $e\mathbb { H}=\underline{\mathbb { H}}^{2}/L$ via the isomorphism $\pi _L|_{e\mathbb { H}}: e\mathbb { H}\rightarrow \underline{\mathbb { H}}^{2}/L$ where $e\mathbb { H}=\infty$ is the point at infinity with

$$\begin{aligned}e=\begin{pmatrix} 1\\ 0 \end{pmatrix}\,. \end{aligned}$$

Then, $N, R: M \rightarrow S^2$ induce the complex structures $J_L$ on the line bundles L and $J_{V/L}$ on $\underline{\mathbb { H}}^{2}/L$ by setting $J_L\psi =-\psi R$ and $J_{V/L} e = e N$: since $\delta \psi = e df$, we obtain indeed

$$\begin{aligned} *\delta \psi = J_{V/L}\delta \psi = \delta J_L \psi \,. \end{aligned}$$

2.2 Isothermic surfaces and Darboux transforms

Classically, an isothermic surface is considered as a surface in 3-space which allows a conformal curvature line parametrisation (away from umbilic points). In our setting, it is convenient to view an isothermic surface as a quaternionic line bundle with an associated closed 1-form ( [4, Theorem 2.3], [16, §5.3.19], [19, Definition 3.1]):

Definition 2.1

A conformal immersion $f: M \rightarrow S^4$ is called isothermic if there exists a non-trivial closed 1-form $\eta \in \Omega ^1({{\,\mathrm{End}\,}}(\mathbb { H}^2))$, the retraction form, such that

$$\begin{aligned} \mathrm {Im}\,\eta \subset L \subset \ker \eta \,. \end{aligned}$$

Remark 2.2

This definition immediately shows that the notion of isothermicity is conformally invariant, that is, if $f: M \rightarrow S^4$ is isothermic so are its Möbius transforms: given the line bundle L corresponding to f, ${\tilde{L}} =AL$ for $A\in {{\,\mathrm{GL}\,}}(2,\mathbb { H})$ is isothermic with 1-form ${\tilde{\eta }} = A\eta A^{-1}$.

This definition links with the Christoffel transformation of an isothermic surface when f is a surface in 3- or 4-space: since ${{\,\mathrm{im}\,}}\eta \subset L \subset \ker \eta$ we can write

$$\begin{aligned} \eta =\begin{pmatrix} f\omega &{} -f\omega f\\ \omega &{} -\omega f \end{pmatrix} \end{aligned}$$

(2.1)

for a 1-form $\omega$ with values in $\mathbb { H}$. But then $d\eta = 0$ shows that $d\omega =0$, so locally there exists a (possibly branched) immersion $f^d$ with $df^d=\omega$. Additionally, we see from $df \wedge \omega =\omega \wedge df= 0$ that $f^d$ is conformal with Gauss map $(N^d, R^d)= (-R, -N)$: $f^d$ is indeed a Christoffel transform or dual surface of f. If $z=x+i y$ is an isothermic coordinate (and f does not map into the round sphere), then up to scaling, $df^d = f_x^{-1}dx - f_y^{-1}dy$. Conversely, away from umbilics the isothermic coordinate can be constructed from $\eta$ (see [4, p. 28]).

In particular, the definition we are using immediately allows to introduce a spectral parameter $\varrho \in \mathbb { R}$, see e.g. [5, Theorem 15.4], [6, Proposition 3.6], and we obtain an associated family of flat connections: since $d_\lambda =d+ \lambda \eta , \lambda \in \mathbb { R}$, has curvature

$$\begin{aligned} R_\lambda = R+ \lambda d\eta + \lambda ^2\eta \wedge \eta =0\end{aligned}$$

we see that the associated family $d_\lambda$ of f is flat for all $\lambda \in \mathbb { R}$. The converse holds as well:

Theorem 2.3

If $\eta \in \Omega ^1({{\,\mathrm{End}\,}}(\underline{\mathbb { H}}^{2}))$ is non-trivial with $\eta ^2=0$ and

$$\begin{aligned} d_\lambda = d+ \lambda \eta \end{aligned}$$

is flat for all $\lambda \in \mathbb { R}$ then $\ker \eta$ can be extended to a quaternionic line bundle L and L is isothermic with retraction form $\eta$.

Proof

We follow the arguments in [7, Theorem 3.1], and only give a short outline how the argument there can be adapted to our situation. Let I be the complex structure on $\mathbb { H}^2$ which is given by right multiplication by the quaternion i. Let $\eta ^{1,0}$ be the (1, 0)-part of $\eta$ and $E =\ker \eta ^{1,0}$. Since $\eta$ is quaternionic, $\ker \eta = E \oplus E j$. In [7, Theorem 3.1] it is shown that d induces a holomorphic structure on $\Gamma (K {{\,\mathrm{End}\,}}(\underline{\mathbb { C}^4}))$ when identifying sections in $\Gamma ({\bar{K}} K)$ with 2-rforms in $\Omega ^2(M)$. Since $d_\lambda$ is flat we see that $d\eta =0$, so that also $d\eta ^{1,0}=0$. Thus, $\eta ^{1,0}$ is holomorphic and $E=\ker \eta ^{1,0}$ extends holomorphically across the zeros of $\eta ^{1,0}$, and so does $\ker \eta = E\mathbb { H}$. $\square$

Recall that an isothermic surface $f: M \rightarrow \mathbb { R}^3$ can be locally characterised as a surface which allows a sphere congruence that conformally envelops f and a second surface ${\hat{f}}$ where $f(p) \not = {\hat{f}}(p)$ for all p. Then, ${\hat{f}}$ is called a Darboux transform of f.

In the framework we set up, the Darboux transformation can be formulated in terms of parallel sections of $\underline{\widetilde{\mathbb { H}}}^{2}$ of the associated family of flat connections, see e.g. [16, §5.4.8]. Here, $\underline{\widetilde{\mathbb { H}}}^{2}$ denotes the trivial $\mathbb { H}^2$ bundle $\underline{\widetilde{\mathbb { H}}}^{2} = {\tilde{M}} \times \mathbb { H}^2$ over the universal cover ${\tilde{M}}$ of M. In this situation, the resulting Darboux transform is in general an isothermic surface in the 4-sphere and is defined on the universal cover of M, and is a surface in the 3-sphere only for suitable initial conditions. We will identify, in abuse of notation, a surface $f: M \rightarrow S^4$ with the canonical lift $f: {\tilde{M}} \rightarrow S^4$.

Definition 2.4

Let $f: M \rightarrow S^4$ be isothermic. Then, ${\hat{f}}: {\tilde{M}} \rightarrow S^4$ is called a Darboux transform of f with respect to the parameter $\varrho \in \mathbb { R}_*=\mathbb { R}\setminus \{0\}$ if ${\hat{L}} = \varphi ^\varrho \mathbb { H}$, where $\varphi ^\varrho \in \Gamma (\underline{\widetilde{\mathbb { H}}}^{2})$ is a $d_\varrho$-parallel section, and $L(p)\not = {\hat{L}}(p)$ for all $p\in {\tilde{M}}$.

Remark 2.5

In the case when the assumption $L(p)\not ={\hat{L}}(p)$ is not satisfied for all $p\in M$, the surface ${\hat{f}}$ is called a singular Darboux transform of f, see [2]. If $f, {\hat{f}}: M \rightarrow \mathbb { R}^3$ are surfaces in 3-space, this means that the enveloping sphere congruence degenerates to a point for $p\in M$ with ${\hat{f}}(p) = f(p)$ and ${\hat{f}}$ becomes a branched conformal immersion.

To simplify notations, we will abbreviate $\varphi =\varphi ^\varrho$ if it is clear from the context that $\varphi$ is a $d_\varrho$-parallel section, and use the superscript only if we want to emphasise the parameter in the family of flat connections that we use. Similarly, we will call the associated surface a Darboux transform, and only refer to it as $\varrho$-Darboux transform or Darboux transform with respect to the parameter $\varrho$ for emphasis of a specific spectral parameter.

We now investigate the closing conditions for Darboux transforms, see [2]. Let us recall the notion of sections with multiplier.

Definition 2.6

Given a parallel section $\varphi \in \Gamma (\underline{\widetilde{\mathbb { H}}}^{2})$ a multiplier is a group homomorphism $h: \pi _1(M) \rightarrow \mathbb { H}_*$ such that

$$\begin{aligned} \gamma ^*\varphi = \varphi \circ \gamma _\sharp = \varphi h_\gamma , \quad \text { for all } \quad \gamma \in \pi _1(M) \end{aligned}$$

where $\gamma _\sharp$ is the deck transformation of ${\tilde{M}}$ associated to $\gamma$. A section with multiplier is a parallel section for which multipliers exist. A spectral parameter $\varrho \in \mathbb { R}_*$ is called a resonance point if every $d_\varrho$-parallel section is a section with multiplier.

Since a Darboux transform of an isothermic surface $f: M \rightarrow S^4$ is given by ${\hat{f}} =\varphi \mathbb { H}$ where $\varphi =\varphi ^ \varrho$ is a parallel section of $d_\varrho$ for some $\varrho \in \mathbb { R}_*$, we see that ${\hat{f}}$ is closed if and only if $\varphi$ is a section with multiplier. In this paper, we consider the “closure condition” to mean that the Darboux transform is defined on the same Riemann surface of the original immersion.

Since for $h\in \mathbb { H}_*$ there exists $m\in \mathbb { H}_*$ with $m^{-1}h m\in \mathbb { C}_*$ we can assume without loss of generality that $h_\gamma \in \mathbb { C}_*$ by changing $\varphi$ to $\varphi m$ in case of an abelian fundamental group. Note that since $d_\varrho$ is quaternionic, we see that if $\varphi$ is $d_\varrho$-parallel with multiplier h then $\varphi j$ is $d_\varrho$-parallel with multiplier ${\bar{h}}$, so that multipliers come in pairs $(h, {\bar{h}})$ which give both rise to the same surface ${\hat{f}}$. In particular, in the case when h is real, the corresponding space of parallel sections with multiplier h is at least quaternionic one-dimensional, whereas in the case of $h\not \in \mathbb { R}$, the space of parallel sections with multiplier h is not quaternionic.

Example 2.7

In the case of a surface of revolution $f: M \rightarrow \mathbb { R}^3$, the holonomy of $d_\varrho$ is for all spectral parameter $\varrho \in \mathbb { R}\setminus \{0, \varrho _0\}$ diagonalisable and has at most two distinct multipliers, h and $h^{-1}$, see [20] and Proposition 4.4 in the case of a round cylinder. The spectral parameter $\varrho _0\in \mathbb { R}_*$ is determined by the choice of dual surface: scaling of $f^d$ by some factor will result in a scale of $\varrho _0$. In the case when $f(x,y)= ip(x)+ j q(x) e^{-iy}$ with smooth real-valued functions p, q satisfying $p'^2+q'^2=q^2$ is a conformally parameterised surface of revolution in the conformal coordinate $z=x+iy$ and $df^d = f^{-1}_xdx-f^{-1}_y dy$ we have $\varrho _0 = -\frac{1}{4}$.

With such choices, for the unique spectral parameter $\varrho =-\frac{1}{4}$ with non-diagonalisable holonomy there is exactly one parallel section with multiplier h (up to quaternionic scaling), which indeed is $h=-1$, and the corresponding Darboux transform is a rotation of f, see Theorem 4.5 in the case when f is a round cylinder and Remark 4.6 for the general case.

For $\varrho <-\frac{1}{4}$, there are exactly two distinct real multipliers $h, h^{-1}\in \mathbb { R}$, and two $\mathbb { H}$-linearly independent $d_\varrho$-parallel sections $\varphi _1^\varrho , \varphi _2^\varrho$ with multiplier h and $h^{-1}$, respectively. These give two distinct Darboux transforms of f which are both rotations of f. Since $\varphi _1^\varrho j, \varphi _2^\varrho j$ have the same real multipliers as $\varphi _1^\varrho$ and $\varphi _2^\varrho$, respectively, there are no further Darboux transforms, see Theorem 4.5 and Remark 4.6.

For $\varrho >-\frac{1}{4}, \varrho \not =\frac{k^2-1}{4}, k\in \mathbb { Z}, k\ge 1,$ there are exactly two complex multipliers $h\in S^1\setminus \{\pm 1\}$, and two $\mathbb { H}$-linearly independent $d_\varrho$-parallel sections $\varphi _1^\varrho , \varphi _2^\varrho$ with multiplier h. Since any complex linear combination $\varphi ^\varphi = \varphi _1^\varrho m_1 + \varphi _2^\varrho m_2$, $m_1, m_2\in \mathbb { C}$, is a $d_\varrho$-parallel section with multiplier h, we obtain a $\mathbb { C}\mathbb { P}^1$ family of closed (possibly singular) Darboux transforms, giving in case of the round cylinder general rotation surfaces, see Theorem 4.5 and Remark 4.6. Since $\varphi ^\varrho j$ has multiplier ${\bar{h}} = h^{-1}$ and $\varphi ^\varrho \mathbb { H}= \varphi ^\varrho j\mathbb { H}$, we obtain no further Darboux transforms in this case.

Fig. 1

Darboux transforms of an unduloid for $\varrho \in \mathbb { R}_*, \varrho \not =\frac{k^2-1}{4}, k>1, k\in \mathbb { Z},$ are rotation surfaces

In the case of a surface of revolution, the only other case which can occur is that the spectral parameter is a resonance point: every $d_{\varrho _r}$-parallel section $\varphi ^{\varrho _r}$ is a section with multiplier, that is, every Darboux transform with parameter $\varrho _r$ is a closed Darboux transform.

Put differently, given a basis $\{\varphi _1^{\varrho _r}, \varphi _2^{\varrho _r}\}$ of $d_{\varrho _r}$-parallel sections at a resonance point $\varrho _r$ every $d_{\varrho _r}$-parallel section, and thus, every (possibly singular) $\varrho _r$-Darboux transform, is given by $\varphi ^{\varrho _r} = \varphi _1^{ \varrho _r} m_1 + \varphi _2^{\varrho _r} m_2$, $m_1, m_2\in \mathbb { H}$:

Note that this shows that all $d_\varrho$-parallel sections at a resonance point $\varrho \in \mathbb { R}_*$ have the same multiplier h, and since multipliers appear as pairs $(h, {\bar{h}})$, we also see that $h\in \mathbb { R}$.

The corresponding Darboux transforms in case of a surface of revolution are rotation surfaces or isothermic bubbletons: in this case resonance points $\varrho _r = \frac{k^2-1}{4}$ are parametrised by positive integers $k\in \mathbb { Z}, k>1,$ such that the corresponding Darboux transforms have k lobes. Special initial conditions give, in the case of a Delaunay surface, again Delaunay surfaces and CMC bubbletons, see Proposition 4.4 for the case of a round cylinder.

Fig. 2

Darboux transforms in 3-space of an unduloid at a resonance point for $k=2,3$ are unduloids, CMC bubbletons, surfaces of revolution or isothermic bubbletons

Given two Darboux transforms $f_1, f_2$ of f with respect to parameter $\varrho _1, \varrho _2\in \mathbb { R}$, there is a common Darboux transform of both $f_1, f_2$ which can be computed from the parallel sections without further integration.

Theorem 2.8

(Bianchi permutability, [1, 16, §5.6.6], [21]) Let $f: M \rightarrow S^4$ be an isothermic surface. Let $\varrho _1, \varrho _2\in \mathbb { R}_*$ and $f_i$ be the Darboux transforms given by $d_{\varrho _i}$-parallel sections $\varphi _{i} =\varphi _i^{\varrho _i}\in \Gamma (\underline{\widetilde{\mathbb { H}}}^{2})$. If $f_1(p)\not =f_2(p)$ for all $p\in M$ then

$$\begin{aligned} \varphi _{12} =\varphi _{2}- \varphi _{1}\chi \end{aligned}$$

gives a $\varrho _2$-Darboux transform of $f_1$ and a $\varrho _1$-Darboux transform of $f_2$ on the universal cover ${\tilde{M}}$ of M by

$$\begin{aligned} f_{12} = \varphi _{12}\mathbb { H}\,. \end{aligned}$$

Here $\chi : {\tilde{M}} \rightarrow \mathbb { H}$ is given by $d\varphi _{2} = d\varphi _{1}\chi$.

Remark 2.9

Note that the condition $d_{\varrho _i}\varphi _{i}=0$ shows that $d\varphi _{i}\in \Omega ^1(L)$, and thus $\chi : {\tilde{M}} \rightarrow \mathbb { H}$ is well-defined. The classical case can be extended to allow $\varrho _1=\varrho _2$ in which case the parallel section $\varphi _{12}\in \Gamma (L)$ is a section in $L =\ker \eta$: since $d\varphi _2 =d\varphi _1\chi$ and $d_\varrho \varphi _{i}=0$, we see that $\eta \varphi _2 = \eta \varphi _1\chi$ and thus $\eta \varphi _{12} =0$.

In particular, the Darboux transform $f_{12}$ is f: in contrast to the case when $\varrho _1\not =\varrho _2$, we do not get all Darboux transforms of $f_1$ with parameter $\varrho _1=\varrho _2$ by this construction. We will discuss how to obtain all Darboux transforms by a Sym-type argument in the next section.

We also know [20] that $\varphi _{12}=\varphi _{12}^{\varrho _2}$ is a parallel section of the family of flat connections of $f_1$ for spectral parameter $\varrho _2$, and $\varphi _{21}= \varphi _{21}^{\varrho _1}:= \varphi _{12}\chi ^{-1}$ is a parallel section of the family of flat connections of $f_2$ at $\varrho _1$. In particular, $f_{12} =\varphi _{12}\mathbb { H}= \varphi _{21}\mathbb { H}= f_{21}$:

Fig. 3

Common Darboux transforms of two bubbletons

3 Generalised Bianchi permutability

Given an isothermic surface f with associated family $d_\lambda$ and a Darboux transform $f_1$ given by spectral parameter $\varrho _1\in \mathbb { R}$ and $d_{\varrho _1}$-parallel section $\varphi _1 = \varphi _1^{\varrho _1}$, Bianchi permutability allows to compute Darboux transforms of $f_1$ for all spectral parameter $\varrho _2\not =\varrho _1$ by solely knowing the parallel sections of the family of flat connections of f and performing an algebraic operation. However, in the case when $\varrho :=\varrho _1=\varrho _2$ we only obtain one Darboux transform of $f_1$ via Bianchi permutability, namely $f_{12}=f$. In this section, we show that we still obtain all Darboux transforms of $f_1$ without integration by the parallel sections of the associated family of f. The Darboux transform in this case is not given algebraically but by a Sym-type argument: we will differentiate parallel sections with respect to the spectral parameter.

3.1 Simple factor dressing

Let $f: M \rightarrow S^4$ be an isothermic surface with associated family $d_\lambda$ and let ${\hat{f}}=f_1$ be a Darboux transform given by a $d_\varrho$-parallel section $\varphi$. To find all parallel sections of the associated family ${\hat{d}}_\lambda =d^1_\lambda$ of ${\hat{f}}$ at $\lambda =\varrho$ in terms of parallel sections of $d_\lambda$ we need to understand ${\hat{d}}_\lambda$ at $\varrho$. To this end, we recall the so-called simple factor dressing: it is known that a suitable $\lambda$-dependent gauge matrix $r_\lambda$ with a simple pole given by $\varrho$ gives via gauging the associated family ${\hat{d}}_\lambda = r_\lambda \cdot d_\lambda$ of a $\varrho$-Darboux transform.

Theorem 3.1

(Simple Factor Dressing, [6, Definition 3.7]) Let $f: M \rightarrow S^4$ be isothermic with associated family $d_\lambda = d+ \lambda \eta$, $\lambda \in \mathbb { R}$. Let $\varrho \in \mathbb { R}_*$ and let $\varphi \in \Gamma (\underline{\widetilde{\mathbb { H}}}^{2})$ be a $d_\varrho$-parallel section with corresponding Darboux transform ${\hat{f}}: {\tilde{M}} \rightarrow \mathbb { H}$ given by ${\hat{L}} =\varphi \mathbb { H}$. Denote by ${\hat{\pi }}$ and $\pi$ the projections onto ${\hat{L}}$ and L, respectively, along the splitting $\underline{\mathbb { H}}^{2}= {\hat{L}}\oplus L$ and define

$$\begin{aligned} r(\lambda ) = r_\varrho ^{{\hat{L}}}(\lambda )= {\hat{\pi }}+ \sigma _\varrho (\lambda )\pi \end{aligned}$$

(3.1)

with

$$\begin{aligned} \sigma _\varrho (\lambda )=\frac{\varrho }{\varrho - \lambda }\,. \end{aligned}$$

Then, ${\hat{d}}_\lambda = r(\lambda )\cdot d_\lambda$ is the family of flat connections of the Darboux transform ${\hat{f}}$. Moreover, ${\hat{d}}_\lambda = d+\lambda {\hat{\eta }}$ with

$$\begin{aligned} {\hat{\eta }} =-{\hat{\pi }} \circ d \circ \pi \frac{1}{\varrho }\,. \end{aligned}$$

Proof

Since the Darboux transform ${\hat{L}} =\varphi \mathbb { H}$ is an isothermic surface, we can consider its family of flat connections ${\hat{d}}_\lambda = d+ \lambda {\hat{\eta }}$, $\lambda \in \mathbb { R}$, with ${{\,\mathrm{im}\,}}{\hat{\eta }}=\ker {\hat{\eta }} ={\hat{L}}$. We first show that

$$\begin{aligned} r_\lambda \cdot d_\lambda ={\hat{d}}_\lambda \quad \text {for all} \quad \lambda \in \mathbb { R}\setminus \{\varrho \}\,. \end{aligned}$$

Since L is a Darboux transform of ${\hat{L}}$ with parameter $\varrho$, there exists a ${\hat{d}}_\varrho$-parallel section ${\hat{\varphi \in \Gamma }}(L)$. Since $\underline{\mathbb { H}}^{2}=L \oplus {\hat{L}} = {\hat{\varphi \mathbb { H}}} \oplus \varphi \mathbb { H}$ it is enough to show that the connections $r_\lambda \cdot d_\lambda$ and ${\hat{d}}_\lambda$ coincide on $\varphi$ and ${\hat{\varphi }}$.

Since $r_\lambda ^{-1}= {\hat{\pi }} + \pi \sigma _\varrho (\lambda )^{-1}$, $d_\varrho \varphi =0$ and ${\hat{\eta \varphi }}=0$ we have

$$\begin{aligned} (r_\lambda \cdot d_\lambda )\varphi&= r_\lambda (d\varphi + \eta \varphi \lambda ) = r_\lambda (\eta \varphi (\lambda - \varrho )) =-\eta \varphi \varrho = d\varphi = {\hat{d}}_\lambda \varphi \,. \end{aligned}$$

Similarly, we see that ${\hat{d}}_\varrho {\hat{\varphi }}=0$ and $\eta {\hat{\varphi }}=0$ give

$$\begin{aligned} (r_\lambda \cdot d_\lambda ){\hat{\varphi }}&= r_\lambda (d_\lambda \hat{\varphi }\frac{\varrho -\lambda }{\varrho }) =r_\lambda (d {\hat{\varphi }} \frac{\varrho -\lambda }{\varrho }) =r_\lambda ({\hat{\eta {\hat{\varphi }}}})(\lambda -\varrho ) = {\hat{\eta {\hat{\varphi }}}}(\lambda -\varrho ) = {\hat{d}}_\lambda {\hat{\varphi }},. \end{aligned}$$

Thus, $r_\lambda \cdot d_\lambda =d+ \lambda {\hat{\eta }}$ for $\lambda \not =\varrho$ and $r_\lambda \cdot d_\lambda$ extends to $\lambda =\varrho$. We observe that

$$\begin{aligned} r_\lambda \cdot d= {\hat{\pi \circ }} d \circ {\hat{\pi }} + \pi \circ d \circ \pi + {\hat{\pi }} \circ d \circ \pi \frac{\varrho -\lambda }{\varrho }+ \pi \circ d\circ {\hat{\pi }} \frac{\varrho }{\varrho -\lambda } \end{aligned}$$

and

$$\begin{aligned} {{\,\mathrm{Ad}\,}}(r_\lambda )\eta = \pi \circ \eta \circ {\hat{\pi }} \frac{\varrho }{\varrho -\lambda } \end{aligned}$$

since $\eta |_L =0, {{\,\mathrm{im}\,}}\eta \subset L$. Therefore, the claim now follows from

$$\begin{aligned} {\hat{\eta }} =\lim _{\lambda \rightarrow \infty } \frac{1}{\lambda }r_\lambda \cdot d_\lambda = -{\hat{\pi }} \circ d \circ \pi \frac{1}{\varrho }\,. \end{aligned}$$

Note that indeed ${\hat{\eta }}^2=0$ and ${{\,\mathrm{im}\,}}{\hat{\eta }} =\ker \hat{\eta }= {\hat{L}}$. $\square$

In particular, the family of flat connections ${\hat{d}}_\lambda =r_\lambda \cdot d_\lambda$ extends into the pole $\varrho$ of $r_\lambda$. We will now investigate parallel sections of ${\hat{d}}_\lambda$ at $\lambda = \varrho$ and their corresponding Darboux transforms in terms of parallel sections of $d_\lambda$.

3.2 Bianchi-type and Sym-type parallel sections

Let $f_1$ be the Darboux transform of an isothermic surface $f: M \rightarrow S^4$ which is given by $\varrho \in \mathbb { R}_*$ and a $d_\varrho$-parallel section $\varphi _1=\varphi _1^\varrho$, and $d^1_\lambda$ its associated family of flat connections. For $\lambda \not =\varrho$ all parallel sections of $d^1_\lambda$ are given by Bianchi permutability. We are now investigating parallel sections of $d^1_\lambda$ at $\lambda =\varrho$.

Proposition 3.2

Assume that $\varphi _2 = \varphi _2^\varrho$ is $d_\varrho$-parallel and independent of $\varphi _1$ over $\mathbb { H}$. Then,

$$\begin{aligned} \varphi _{12} = \pi \varphi _2\, \end{aligned}$$

is a parallel section of the flat connection

$$\begin{aligned} d_\varrho ^1 =d - \pi _1 \circ d \circ \pi \end{aligned}$$

of $f_1$. Here, $\pi$ and $\pi _1$ are the projections onto L and $L_1$ respectively along the splitting $\underline{\mathbb { H}}^{2}= L_1 \oplus L$. We call $\varphi _{12}$ a Bianchi-type section. The associated Darboux transform of $f_1$ is $f_{12}=f$.

Proof

Consider the $d_\varrho ^1$-parallel section ${\tilde{\varphi }}$ given by Bianchi permutability by

$$\begin{aligned} {\tilde{\varphi }}= \varphi _2-\varphi _1\chi \end{aligned}$$

with $d\varphi _2 = d\varphi _1\chi$. By Remark 2.9, we know that ${\tilde{\varphi }}\in \Gamma (L)$ is a section in L. Therefore,

$$\begin{aligned} {\tilde{\varphi }} = \pi (\varphi _2-\varphi _1\chi ) = \pi \varphi _2 =\varphi _{12}\,. \end{aligned}$$

$\square$

Since all $d^1_\varrho$-parallel sections arising from Bianchi permutability are sections in L and therefore quaternionic multiples of $\varphi _{12}$, we know that there exist $d^1_\varrho$-parallel sections on the universal cover ${\tilde{M}}$ of M which do not arise from Bianchi permutability since $d^1_\varrho$ is a flat connection on $\underline{\mathbb { H}}^{2}$. We now investigate these.

Recall that away from $\lambda =\varrho$, we have $d^1_\lambda = r_\lambda \cdot d_\lambda$ where

$$\begin{aligned} r_\lambda = \pi _1 + \sigma _\varrho (\lambda )\pi , \quad \sigma _\varrho (\lambda ) = \frac{\varrho }{\varrho -\lambda } \end{aligned}$$

is the simple factor dressing matrix given by the bundle $L_1$ and the pole $\varrho$.

Moreover, if $\varphi _1^\lambda$ are $d_\lambda$-parallel sections with $\varphi _1 = \varphi _1^{\lambda =\varrho }$, which depend smoothly on $\lambda$, then $\varphi _{11}^\lambda = r_\lambda \varphi _1^\lambda$ is $d^1_\lambda$-parallel away from $\lambda =\varrho$. At $\lambda =\varrho$, the dressing matrix $r_\lambda$ has a pole. However, by L’Hôpital’s rule the limit $\varphi _{11} = \lim _{\lambda \rightarrow \varrho } \varphi _{11}^\lambda$ at $\varrho$ exists since $\lim _{\lambda \rightarrow \varrho } \pi \varphi _1^\lambda =0$, and we obtain

$$\begin{aligned} \varphi _{11}= \varphi _1 - \varrho \pi (\frac{\partial }{\partial \lambda }\varphi _1^\lambda )|_{\lambda =\varrho }\,. \end{aligned}$$

Indeed, $\varphi _{11}$ is parallel with respect to $d^1_\varrho = d-{\hat{\pi }} \circ d\circ \pi$: since $d_\lambda \varphi _1^\lambda =0$, we first have

$$\begin{aligned} 0= \frac{\partial }{\partial \lambda } (\pi d_\lambda \varphi _1^\lambda )|_{\lambda =\varrho } = \pi \frac{\partial }{\partial \lambda }(d\varphi _1^\lambda + \lambda \eta \varphi _1^\lambda )|_{\lambda =\varrho } = \pi (d_\varrho (\frac{\partial }{\partial \lambda }\varphi _1^\lambda )|_{\lambda =\varrho }+ \eta \varphi _1)\,, \end{aligned}$$

so that

$$\begin{aligned} \eta \varphi _1 =- \pi (d_\varrho (\frac{\partial }{\partial \lambda }\varphi _1^\lambda )|_{\lambda =\varrho })=- \pi (d_\varrho \pi (\frac{\partial }{\partial \lambda }\varphi _1^\lambda )|_{\lambda =\varrho })\,. \end{aligned}$$

Here, we used that ${{\,\mathrm{im}\,}}\eta \in L$ and that $L_1$ is $d_\varrho$-stable so that $\pi \circ d_\varrho \circ \pi = \pi \circ d_\varrho$. Together with $\eta |_L=0$ and $\pi \varphi _1=0$, we now see that

$$\begin{aligned} d^1_\varrho \varphi _{11}&= d\varphi _1 - \varrho d \pi ((\frac{\partial }{\partial \lambda }\varphi _1^\lambda )|_{\lambda =\varrho }) +\varrho \pi _1 d \pi (\frac{\partial }{\partial \lambda }\varphi _1^\lambda )|_{\lambda =\varrho }= d\varphi _1-\varrho \pi d\pi ((\frac{\partial }{\partial \lambda }\varphi _1^\lambda )|_{\lambda =\varrho })\\&= d\varphi -\varrho \pi d_\varrho \pi ((\frac{\partial }{\partial \lambda }\varphi _1^\lambda )|_{\lambda =\varrho }) =d_\varrho \varphi _1 =0\,. \end{aligned}$$

Thus, we have shown that $\varphi _{11}$ gives a Darboux transform $f_{11}$ of $f_1$. Since $\pi _1\varphi _{11} = \varphi _1\not =0$, we see that $f_{11}\not =f$, and thus, $f_{11}$ is not a Darboux transform given by Bianchi permutability. We summarise:

Theorem 3.3

Let $f: M \rightarrow S^4$ be isothermic and $d_\lambda$ its associated family of flat connections. Let $\varrho \in \mathbb { R}_*$ be fixed, $\varphi _1=\varphi _1^\varrho \in \Gamma (\underline{\widetilde{\mathbb { H}}}^{2})$ a $d_\varrho$-parallel section, and $f_1$ the corresponding Darboux transform. Given $d_\lambda$-parallel sections $\varphi _1^\lambda$ near $\varrho$ which depend smoothly on $\varrho$ with $\varphi _1^{\lambda =\varrho }=\varphi _1$, the section

$$\begin{aligned} \varphi _{11} = \varphi _1^{\lambda =\varrho }-\varrho \pi (\frac{\partial }{\partial \lambda }\varphi _1^\lambda )|_{\lambda =\varrho }\end{aligned}$$

is $d^1_\varrho$-parallel where $d^1_\lambda = d- \frac{\lambda }{\varrho }\pi _1\circ d \circ \pi$ is the family of flat connections of $f_1$. We call the $\varphi _{11}$ as Sym-type (parallel) section and its associated Darboux transform $f_{11}$ a Sym-type (two-step) Darboux transform of f.

Remark 3.4

Note that the Sym-type parallel section $\varphi _{11}$, and thus the Sym-type Darboux transform $f_{11}$ depends on the choice of the extension $\varphi ^\lambda _1$.

Fig. 4

Sym-type Darboux transform of an unduloid f. In the first case the one-step Darboux transform $f_1$ of f is a surface of revolution, in the second case $f_1$ is a CMC bubbleton

3.3 A generalisation of Bianchi permutability

Combining previous results, we are now in the position to give a generalisation of Bianchi permutability: we obtain for all $\varrho \in \mathbb { R}_*$ all two-step Darboux transforms of an isothermic surface $f: M \rightarrow S^4$ by parallel sections of the associated family of f without further integration.

Theorem 3.5

Let $f: M \rightarrow S^4$ be an isothermic surface and let $d_\lambda$ be the associated family of f. Let $\varrho \in \mathbb { R}_*$ be a spectral parameter and $f_1$ be a Darboux transform of f given by a $d_\varrho$-parallel section $\varphi _1 = \varphi _1^\varrho \in \Gamma (\underline{\widetilde{\mathbb { H}}}^{2})$. Then any parallel section of the flat connection $d^1_\varrho$ in the associated family of $f_1$ is either a Sym-type or a Bianchi-type parallel section.

Proof

Choose a smooth extension $\varphi _1^\lambda$ of $\varphi _1$ near $\lambda =\varrho$ and let $\varphi _{11}=\varphi _1-\varrho \pi (\frac{\partial }{\partial \lambda }\varphi _1^\lambda )|_{\lambda =\varrho }$ be the corresponding Sym-type parallel section. Moreover, let $\varphi _2$ be a $d_\varrho$-parallel section with $\varphi _{12} = \pi \varphi _2\not =0$. Since $\pi _1\varphi _{11} =\varphi _1\not =0$, we see that $\varphi _{11}, \varphi _{12}$ are $\mathbb { H}$-independent parallel sections of $d_\varrho ^1$.

Now let ${\hat{\varphi }}\in \Gamma (\underline{\widetilde{\mathbb { H}}}^{2})$ be an arbitrary $d^1_\varrho$-parallel section. We first show that ${\hat{\varphi }}$ is a Bianchi-type parallel section if $\pi _1 {\hat{\varphi }}=0$. In this case, ${\hat{\varphi \in \Gamma }}(L)$ and since both ${\hat{\varphi }}$ and $\varphi _{12}$ are non-vanishing $d^1_\varrho$-parallel sections of the line bundle L, we have

$$\begin{aligned} {\hat{\varphi }} = \varphi _{12} m, \quad m\in \mathbb { H}_*\,, \end{aligned}$$

But then ${\hat{\varphi }} =\pi (\varphi _2m)$ is a Bianchi-type parallel section. We can therefore now assume that $\pi _1{\hat{\varphi }}\not =0$ so that

$$\begin{aligned} \pi _1 {\hat{\varphi }} = \varphi _1 m, m\in \mathbb { H}_*\,.\end{aligned}$$

We aim to show that ${\hat{\varphi }}$ is a Sym-type Darboux transform of f. Therefore, we have to find a smooth extension ${\tilde{\varphi }}_1^\lambda$ near $\lambda =\varrho$ so that ${\hat{\varphi }}$ is its associated Sym-type parallel section, that is,

$$\begin{aligned} {\hat{\varphi }} = {\tilde{\varphi }}_{11} = {\tilde{\varphi }}_1^{\lambda =\varrho } -\varrho \pi (\frac{\partial }{\partial \lambda }{\tilde{\varphi }}_1^\lambda )|_{\lambda =\varrho } \,. \end{aligned}$$

Since $\varphi _{11}, \varphi _{12}$ are linearly independent over $\mathbb { H}$, we can write

$$\begin{aligned} {\hat{\varphi }} = \varphi _{11} m_1 + \varphi _{12} m_2, \quad m_1, m_2\in \mathbb { H}\,. \end{aligned}$$

Since $\pi {\hat{\varphi }}=\varphi _1m$ and $\pi \varphi _{11} = \varphi _1$ we see that $m_1=m$. Extend $\varphi _2$ to $d_\lambda$-parallel sections $\varphi _2^\lambda$ which depend smoothly on $\lambda$ near $\lambda =\varrho$ and put

$$\begin{aligned} {\tilde{\varphi }}_1^\lambda = \varphi _1^\lambda m+ \varphi _2^\lambda m_2\frac{\varrho -\lambda }{\varrho }\,. \end{aligned}$$

Then, ${\tilde{\varphi }}_1^\lambda$ depends smoothly on $\lambda$ near $\lambda =\varrho$. Moreover, since $\varphi _1^\lambda , \varphi _2^\lambda$ are $d_\lambda$-parallel and $\frac{\varrho -\lambda }{\varrho }\in \mathbb { C}$ is constant for fixed $\lambda$, we see that ${\tilde{\varphi }}_1^\lambda$ is $d_\lambda$-parallel. At $\lambda =\varrho$, we have

$$\begin{aligned} {\tilde{\varphi }}_1^\varrho = \varphi _1 m \end{aligned}$$

and the associated Sym-type parallel section is

$$\begin{aligned} {\tilde{\varphi }}_{11}&= {\tilde{\varphi }}_1^{\lambda =\varrho } -\varrho \pi (\frac{\partial }{\partial \lambda }{\tilde{\varphi }}_1^\lambda )|_{\lambda =\varrho } \\&=\varphi _1m - \varrho \pi \Big ( (\frac{\partial }{\partial \lambda }\varphi _1^\lambda )|_{\lambda =\varrho }m - \varphi _2m_2\frac{1}{\varrho } + (\frac{\partial }{\partial \lambda }\varphi _2^\lambda )m_2\frac{\varrho -\lambda }{\varrho }|_{\lambda =\varrho }\Big ) \\&= \Big (\varphi _1^{\lambda =\varrho } - \varrho \pi (\frac{\partial }{\partial \lambda }\varphi _1^\lambda )|_{\lambda =\varrho }\Big ) m + \pi \varphi _2m_2 = \varphi _{11}m + \varphi _{12}m_2\\&= {\hat{\varphi }}. \end{aligned}$$

This concludes the proof. $\square$

This immediately gives a generalisation of Bianchi permutability, Theorem 2.8:

Theorem 3.6

(generalised Bianchi permutability) Let $f: M\rightarrow S^4$ be isothermic and $f_1$ be a Darboux transform of f given by the spectral parameter $\varrho _1\in \mathbb { R}_*$ and the $d_{\varrho _1}$-parallel section $\varphi _1\in \Gamma (\underline{\widetilde{\mathbb { H}}}^{2})$. Then, all Darboux transforms of $f_1$ are either Sym-type or Bianchi-type two-step Darboux transforms of f.

In particular, all Darboux transforms are given by parallel sections $\varphi ^\lambda \in \Gamma (\underline{\widetilde{\mathbb { H}}}^{2})$ of the associated family $d_\lambda$ of f via algebraic operations and differentiation with respect to the spectral parameter $\lambda$.

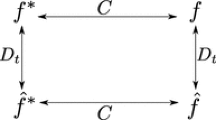
Denoting by $f_{11}$ the Sym–Darboux transform given by a Sym-type parallel section $\varphi _{11}$ and by $f_{12}$ a Darboux transform given by Bianchi permutability by a Bianchi-type parallel section $\varphi _{12}$, we see the following picture:

Remark 3.7

Note that the previous theorem now allows to construct all Darboux transforms (of any order) of an isothermic surface f from parallel sections of the associated family $d_\lambda$ of f without further integration.

3.4 Closing conditions

We now investigate the closing condition for a two-step Darboux transform of an isothermic surface $f: M \rightarrow S^4$.

For $\varrho _i\in \mathbb { R}, i=1,2,$ let $\varphi _i=\varphi _i^{\varrho _i}$ be $d_{\varrho _i}$-parallel sections of the associated family of flat connections $d_\lambda$ of f. Assume that $\varphi _i$ have multipliers $h_i\in \mathbb { C}$, that is, $\gamma ^*\varphi _i = \varphi _i h_i(\gamma )$ for all $\gamma \in \pi _1(M)$. Then, both associated Darboux transforms $f_i: M \rightarrow S^4$ are closed surfaces. The function $\chi$ defined by $d\varphi _2 = d\varphi _1\chi$ satisfies $\chi ^*=h_1^{-1}\chi h_2$ so that

$$\begin{aligned} \varphi _{12} = \varphi _2-\varphi _1\chi \end{aligned}$$

has multiplier $h_2$. In particular, we see that the two-step Darboux transforms, which are obtained by Bianchi permutability from closed Darboux transforms, are closed too.

Proposition 3.8

Let $f: M \rightarrow S^4$ be an isothermic surface and $f_i: M \rightarrow S^4$, $i=1, 2$, be closed Darboux transforms of f, with $f_1(p)\not =f_2(p)$ for all p. Then, the common Darboux transform of $f_1$ and $f_2$ is closed too.

Remark 3.9

This result holds trivially when $\varrho _1=\varrho _2$: in this case the Bianchi-type two-step Darboux transforms are $f = f_{12} = f_{21}$.

Consider now the remaining case when $\varrho :=\varrho _1=\varrho _2$ and the Darboux transform $f_{11}$ of $f_1$ is given by a Sym-type parallel section, that is, it is given by $\varphi _{11}= \varphi _1 - \varrho \pi (\frac{\partial }{\partial \lambda }\varphi _1^\lambda )|_{\lambda =\varrho }$ where $\varphi _1^\lambda$ is $d_\lambda$-parallel near $\lambda =\varrho$ and $\varphi _1^{\lambda =\varrho } =\varphi _1$. If $\varphi _1^\lambda$ is a section with multiplier $h_1^\lambda$ for all $\lambda$ near $\varrho$ then

$$\begin{aligned} \gamma ^*\pi (\frac{\partial }{\partial \lambda }\varphi _1^\lambda )|_{\lambda =\varrho }= \pi ((\frac{\partial }{\partial \lambda }\varphi _1^\lambda )|_{\lambda =\varrho }h_1^{\lambda =\varrho } + \varphi _1 (\frac{\partial }{\partial \lambda }h_1^\lambda )|_{\lambda =\varrho }) = \pi (\frac{\partial }{\partial \lambda }\varphi _1^\lambda )|_{\lambda =\varrho }h_1 \end{aligned}$$

and thus $\varphi _{11} = \varphi _1 - \pi (\frac{\partial }{\partial \lambda }\varphi _1^\lambda )|_{\lambda =\varrho }$ has the same multiplier $h_1$ as $\varphi _1$. In particular, the resulting Darboux transform $f_{11}$ of $f_1$ is closed.

We summarise:

Theorem 3.10

Let $f: M \rightarrow S^4$ be isothermic and $f_1: M \rightarrow S^4$ a Darboux transform given by the $d_\varrho$-parallel section $\varphi _1$. A Sym-type Darboux transform $f_{11}$ given by an extension $\varphi _1^\lambda$ of $\varphi _1$ is closed if $\varphi _1^\lambda$ is a section with multiplier near $\lambda =\varrho$.

We now investigate cases where we can guarantee existence of closed two-step Darboux transforms in terms of the behaviour of the holonomy of $d_\lambda$.

Corollary 3.11

Let $f: M \rightarrow S^4$ be isothermic and $d_\lambda$ its associated family of flat connections. If $\varrho \in \mathbb { R}_*$ is a spectral parameter such that there are four distinct complex multipliers of the holonomy of $d_\varrho$, then every closed Darboux transform $f_1$ has exactly two closed Darboux transforms with parameter $\varrho$.

Remark 3.12

Homogeneous tori are examples of isothermic surfaces which have exactly four distinct complex multipliers: we will return to this topic in a future paper.

Proof

If one of the multipliers is real, then there exist two complex independent parallel sections $\varphi , \varphi _j$ with the same multiplier which contradicts the assumption that the holonomy has four distinct eigenvalues with complex one-dimensional eigenspaces.

Since complex multipliers appear as pairs of conjugate complex multipliers, we have exactly two $d_\varrho$-parallel sections $\varphi _1, \varphi _2$ with complex multiplier $h_1$ and $h_2$, $h_1\not =h_2$, respectively, which are $\mathbb { H}$-independent. Thus, all multipliers are given by $\{h_1, {\bar{h}}_1, h_2, {\bar{h}}_2\}$.

Since $f_1$ is closed, it is given by one of these parallel sections, say $\varphi _1$. The multipliers depend smoothly on the spectral parameter and since there are four distinct multipliers for $\lambda$ near $\varrho$, we can extend $\varphi _1$ around $\varrho$ to a smooth family of $d_\lambda$-parallel sections $\varphi _1^\lambda$ with multipliers $h_1^\lambda$ . Then, the Sym-type formula shows that $\varphi _{11}$ is a section with multiplier $h_1$ and $f_{11}$ is closed. Since $f_{11} \not = f$, we obtain the second closed Darboux transform from Bianchi permutability and the parallel section $\varphi _2$. Since $h_1\not =h_2$, we cannot have further closed Darboux transforms of $f_1$. $\square$

Corollary 3.13

Let $f: M \rightarrow S^4$ be isothermic and $d_\lambda$ its associated family of flat connections. Assume that there are two $\mathbb { H}$-independent $\varphi _1^\lambda , \varphi _2^\lambda$ with multipliers $h^\lambda =h_1^\lambda = h_2^\lambda \in \mathbb { C}\setminus \mathbb { R}$ for $\lambda$ near $\varrho \in \mathbb { R}_*$. Then, every closed Darboux transform $f_1$ of f with parameter $\varrho$ has a $\mathbb { C}\mathbb { P}^1$-worth of closed Darboux transforms.

Proof

Since $h=h^{\lambda =\varrho }\not \in \mathbb { R}$, we see that $\varrho$ is not a resonance point. Let $\varphi _1$ be a $d_\varrho$-parallel section with multiplier and $f_1$ the Darboux transform given by $\varphi _1$. Since multipliers come in pairs of complex conjugates, we know that the holonomy of $d_\lambda$ is diagonalisable with complex two-dimensional, $d_\lambda$-stable eigenspaces $E^\lambda ={{\,\mathrm{span}\,}}_\mathbb { C}\{\varphi _1^\lambda , \varphi _2^\lambda \}$ and $E^\lambda j$ with multipliers h and ${\bar{h}}$. Therefore, we can assume without loss of generality that the $d_\varrho$-parallel section $\varphi _1$ has multiplier h by replacing $\varphi _1$ by $\varphi _1j$ if necessary. Moreover, we can write $\varphi _1 = \varphi _1^{\lambda =\varrho } m_1 + \varphi _2^{\lambda =\varrho }m_2$, $m_1, m_2\in \mathbb { C}$, and thus can also assume without loss of generality that $\varphi _1 =\varphi _1^{\lambda =\varrho }$ by replacing $\varphi _1^\lambda$ by $\varphi _1^\lambda m_1 + \varphi _2^\lambda m_2$ if necessary.

The Sym-type parallel section

$$\begin{aligned} \varphi _{11} = \varphi _1 - \varrho \pi (\frac{\partial }{\partial \lambda }\varphi _1^\lambda )|_{\lambda =\varrho }\end{aligned}$$

has multiplier h since $\gamma ^* (\frac{\partial }{\partial \lambda }\varphi _1^\lambda )|_{\lambda =\varrho }= (\frac{\partial }{\partial \lambda }\varphi _1^\lambda )|_{\lambda =\varrho }h + \varphi _1 (\frac{\partial }{\partial \lambda } h^\lambda )|_{\lambda =\varrho }$. Here, $\pi$ is the projection onto L along the splitting $\underline{\mathbb { H}}^{2}= L \oplus L_1$.

On the other hand, the Bianchi-type Darboux transform $f_{12}$ of $f_1$ is given $\varphi _{12} = \pi \varphi _2^{\lambda =\varrho }$ which is also a section with multiplier h. Thus, any $\mathbb { C}$-linear combination of $\varphi _{11} , \varphi _{12}$ is a $d_\varrho$-parallel section with multiplier h, and thus we have a $\mathbb { C}\mathbb { P}^1$ worth of closed Darboux transforms. Since $\varrho$ is not a resonance point, parallel sections with multipliers ${\bar{h}}$ give the same surfaces. $\square$

Example 3.14

This case appears for surfaces of revolution in 3-space: If $\varrho >-\frac{1}{4}, \varrho \not =0,$ is not a resonance point, then a closed Darboux transform $f_1$ with parameter $\varrho$ in 3-space is a surface of revolution and so is every Darboux transform with parameter $\varrho$ of $f_1$ in 3-space.

Fig. 5

Closed Sym-type Darboux transforms of an unduloid for a non-resonance spectral parameter $\varrho >-\frac{1}{4}$

At resonance points $\varrho _r$, it is possible that a Darboux transform $f_1$ has $\varrho _r$ as a resonance point.

Theorem 3.15

Let $\varrho _r\in \mathbb { R}_*$ is a resonance point of an isothermic surface f and $f_1$ be a closed Darboux transform of f given by a $d_{\varrho _r}$-parallel section $\varphi _1$ with multiplier $h_1$. If $\varphi _1$ extends to $d_\lambda$-parallel sections $\varphi _1^\lambda$ with multiplier $h_1^\lambda$ near $\lambda =\varrho _r$, then $\varrho _r$ is a resonance point of $f_1$.

Proof

By Theorem 3.5, every parallel section of the family of flat connections of $f_1$ is either a Sym-type or a Bianchi-type parallel section. Every Bianchi-type parallel section $\varphi _{12}$ gives rise to the Darboux transform $f_{12} = f$ and is given by a parallel section $\varphi _2$ with real multiplier $h_2 = h_1$ since $\varrho _r$ is a resonance point.

By Theorem 3.10, we know that a Sym-type Darboux transform is closed if $\varphi _1$ can be extended by a $d_\lambda$-parallel sections $\varphi _1^\lambda$ with multiplier $h_1^\lambda$. In this case, $\varphi _{11}$ has multiplier $h_1$ and $\varphi _{12}$ and $\varphi _{11}$ have the same real multiplier. Since any parallel section ${\hat{\varphi }}$ is a linear combination

$$\begin{aligned} {\hat{\varphi }} = \varphi _{11} m_1 + \varphi _{12}m_2 \end{aligned}$$

with $m_1, m_2\in \mathbb { H}$ we see that every parallel section has multiplier $h_1$. Thus, $\varrho _r$ is a resonance point of $f_1$. $\square$

Example 3.16

Surfaces of revolution $f: M \rightarrow \mathbb { R}^3$ are examples of isothermic surfaces with resonance points. All Darboux transforms $f_1$ with respect to a resonance point $\varrho _r\in \mathbb { R}_*$ which are surfaces of revolution have $\varrho _r$ as a resonance point too and thus a $\mathbb { H}\mathbb { P}^1$-family of closed (possibly singular) Darboux transforms.

The only closed Darboux transforms $f_1$ of f which are not surfaces of revolution are (isothermic) bubbletons. In this case, the spectral parameter $\varrho _r$ gives only one closed Darboux transform of $f_1$, namely the original surface of revolution f.

Fig. 6

Sym-type Darboux transforms of an unduloid at resonance points $\varrho _k = \frac{k^2-1}{4}, k=2,3$

4 Sym-type Darboux transforms of the round cylinder

In this section, we will demonstrate explicitly the construction of Sym-type Darboux transforms in the example of a conformally parametrised round cylinder (referred to simply as cylinder, hereafter). We will first show that the Darboux transform of a real-analytic surface of revolution, which does not have constant mean curvature, has constant mean curvature if and only if the Darboux transform is again a surface of revolution. This will allow to rule out later that closed surfaces obtained by Sym-type Darboux transforms are constant mean curvature surfaces.

We then will give all Darboux transforms of a cylinder explicitly by computing all parallel sections of the family of flat connections. With this at hand, we will consider the case when the one-step Darboux transform is a surface of revolution but not CMC. In this case, we give two surprisingly explicit examples of Sym-type transforms, one which is a surface of revolution and one which is not.

4.1 Darboux transforms of a surface of revolution

We first discuss curvature properties of Darboux transforms of a surface of revolution which is not a Delaunay surface. Given an isothermic surface $f: M \rightarrow \mathbb { R}^3$ recall that the associated family $d_\lambda$ gives rise to a dual surface $f^d$ via (2.1) by $df^d = \omega$. Writing a $d_\varrho$-parallel section $\varphi = e\alpha + \psi \beta \in \Gamma (\underline{\widetilde{\mathbb { H}}}^{2})$, $\varrho \in \mathbb { R}_*$, where

$$\begin{aligned} e =\begin{pmatrix} 1 \\ 0 \end{pmatrix}, \quad \psi =\begin{pmatrix} f \\ 1 \end{pmatrix} \end{aligned}$$

we obtain the Riccati equation

$$\begin{aligned} dT = -df + T df^d\varrho T \end{aligned}$$

(4.1)

for $T=\alpha \beta ^{-1}$ in the case when $T: {\tilde{M}} \rightarrow \mathbb { R}^3$. In this case, the Darboux transform given by $\varphi$ can be written in affine coordinates as ${\hat{f}} = f + T$ so that $d{\hat{f}} = \varrho T df^d T$.

Next, we recall that for an isothermic surface $f: M \rightarrow \mathbb { R}^3$ the mean curvature of a Darboux transform ${\hat{f}} = f +T$ in 3-space is given in terms of the mean curvature of a dual surface $f^d$ of f.

Lemma 4.1

( [18, Eq. 58]) Let $f: M \rightarrow \mathbb { R}^3$ be an isothermic surface in 3-space with Gauss map N and dual surface $f^d$. Then, the mean curvature of a Darboux transform ${\hat{f}} = f+ T: {\tilde{M}} \rightarrow \mathbb { R}^3$ of f with parameter $\varrho$ is given by

$$\begin{aligned} {\hat{H}} = -\frac{1}{|T|^2}(\frac{H^d}{\varrho } - 2\langle T,N\rangle )\,, \end{aligned}$$

(4.2)

where $H^d$ is the mean curvature of the dual surface $f^d$ of f.

Similar to the case when f is CMC in [8], one can now derive a necessary condition for a Darboux transform of an isothermic surface to have constant mean curvature:

Lemma 4.2

Let $f: M \rightarrow \mathbb { R}^3$ be an isothermic surface and ${\hat{f}} = f+ T: {\tilde{M}} \rightarrow \mathbb { R}^3$ a Darboux transform of f. If ${\hat{f}}$ has constant mean curvature ${\hat{H}}$, then

$$\begin{aligned} (H - {\hat{H}})\langle df, T\rangle + \frac{dH^d}{2\varrho }=0\,, \end{aligned}$$

where H and $H^d$ are the mean curvatures of f and its dual surface $f^d$, respectively.

Proof

From $-Hdf = \frac{1}{2}(dN -N*dN)$, see [8, Sec. 7.2], and $N^d=-N$, we know that $dN = H^ddf^d - Hdf$. Since ${\hat{H}}$ is constant, we can differentiate Eq. (4.2)

$$\begin{aligned} \frac{1}{2}{\hat{H}} |T|^2 + \frac{H^d}{2\varrho } - \langle T,N\rangle =0 \end{aligned}$$

to obtain, using the Riccati equation, that

$$\begin{aligned} 0&={\hat{H}} \langle dT, T\rangle + \frac{dH^d}{2\varrho } -\langle dT, N\rangle -\langle T, dN\rangle \\&= {\hat{H}} \langle -df + Tdf^d\varrho T, T\rangle + \frac{dH^d}{2\varrho } -\langle Tdf^d\varrho T, N\rangle -\langle T, H^ddf^d - Hdf\rangle \\&= (H - {\hat{H}})\langle df, T\rangle + \frac{dH^d}{2\varrho } + \langle Tdf^d \varrho T, {\hat{H}} T-N\rangle -\langle T, H^d df^d\rangle \,. \end{aligned}$$

It remains to show that

$$\begin{aligned} 0=\langle Tdf^d \varrho T, {\hat{H}} T-N\rangle -\langle T, H^d df^d\rangle \,. \end{aligned}$$

Since $\langle a,b\rangle =- \frac{1}{2}(ab + ba)$ for $a, b\in {{\,\mathrm{Im}\,}}\mathbb { H}=\mathbb { R}^3$, we get

$$\begin{aligned} \langle Tdf^d \varrho T, T\rangle = -\varrho |T|^2\langle T,df^d\rangle \end{aligned}$$

so that

$$\begin{aligned} \langle Tdf^d \varrho T,&{\hat{H}} T-N\rangle -\langle T, H^d df^d\rangle \\&=-(\varrho |T|^2 {\hat{H}} + H^d)\langle T, df^d\rangle - \varrho \langle Tdf^dT, N\rangle \\&= -2\varrho \langle T,N\rangle \langle T, df^d\rangle - \varrho \langle Tdf^dT, N\rangle \\&=\frac{\varrho }{2}( -(TN + NT)df^dT - Tdf^d(TN + NT) + Tdf^dTN + NTdf^dT)\\&=0 \end{aligned}$$

where we used equation (4.2) and $Ndf^d =-df^dN$. $\square$

We can now use the previous lemma to discuss the mean curvature of Darboux transforms of surfaces of revolution.

Theorem 4.3

Let $f: M \rightarrow \mathbb { R}^3$ be a real-analytic conformal surface of revolution in 3-space. If a Darboux transform ${\hat{f}}: {\tilde{M}} \rightarrow \mathbb { R}^3$ of f has constant mean curvature in 3-space then ${\hat{f}}: M \rightarrow \mathbb { R}^3$ is a surface of revolution or f is CMC, that is, at least one of ${\hat{f}}$ or f is a Delaunay surface.

Proof

Since f is conformally parametrised, we can write $f(x,y)= ip(x)+ j q(x) e^{-iy}$ with smooth real-valued functions p, q satisfying $p'^2+q'^2=q^2$.

Let ${\hat{f}}: {\tilde{M}} \rightarrow \mathbb { R}^3$ be a Darboux transform in 3-space with parameter $\varrho$, that is ${\hat{f}} = f + T$ where T satisfies the Riccati equation (4.1). Since both f and its dual $f^d$ are surfaces of revolution the mean curvatures H and $H^d$ of both surfaces are independent of y. Thus, Lemma 4.2 gives

$$\begin{aligned} 0 = ({\hat{H}}- H) \langle f_y, T\rangle = ({\hat{H}} -H) \langle -ji q e^{-iy},T\rangle \,. \end{aligned}$$

If ${\hat{H}} = H$, then f has constant mean curvature, and we are done. Now, assume that ${\hat{H}} \not =H$. Since f is real-analytic so is H, and thus ${\hat{H}}-H$ has only isolated zeros. Then, $\langle f_y, T\rangle =0$ away from the isolated zeros of ${\hat{H}}-H$. Since f and T are smooth, we conclude that $\langle f_y, T\rangle =0$ on M. This shows that

$$\begin{aligned} T = i n + j m e^{-iy} \end{aligned}$$

where m, n are real valued functions. On the other hand, $H^d$ and thus also $H^d_x$ only depend on x, so that

$$\begin{aligned} \langle f_x, T\rangle = \langle ip' + jq' e^{-iy}, in + jm e^{-iy}\rangle = p'n + q'm \end{aligned}$$

only depends on x. Now, $dT = -df + Tdf^d\varrho T$ shows

$$\begin{aligned} T_y = - f_y - \frac{1}{|f_y|^2}Tf_y \varrho T\,. \end{aligned}$$

Since

$$\begin{aligned} Tf_y T = f_y|T|^2 - 2\langle T, f_y\rangle T = f_y|T|^2 \end{aligned}$$

we have $T_y = f_y(-1-\frac{\varrho |T|^2}{|f_y|^2})$. Therefore, $T_y=in_y + j(m_y-i m)e^{-iy}$ is a scale of $f_y=kq e^{-iy}$ by a real-valued function, and thus $n_y=0$. Since $\langle f_x, T\rangle , p', q'$ only depend on x this shows that also $m_y=0$. Therefore, we have shown that ${\hat{f}}$ is a surface of revolution if ${\hat{H}}\not =H$. $\square$

4.2 Darboux transforms of a cylinder

We will compute all Darboux transforms of a conformally parametrised cylinder, of constant mean curvature $H=1$

$$\begin{aligned} f(x,y) = \frac{1}{2}(ix + j e^{-iy})\,. \end{aligned}$$

Consider the dual surface $f^d$ given, up to translation, by $df^d = f_x^{-1}dx - f_y^{-1}dy$. We choose $f^d(x,y)= -2( ix - je^{-iy})$ and observe that the dual surface has constant mean curvature $H^d= -\frac{1}{4}$.

To find all $d_\varrho$-parallel sections, $\varrho \not =0$, we recall (2.1) that

$$\begin{aligned} d_\varrho = d+ \varrho \begin{pmatrix} fdf^d &{} - fdf^d f\\ df^d &{}- df^d f \end{pmatrix}\,. \end{aligned}$$

Since $L\oplus e\mathbb { H}= \underline{\mathbb { H}}^{2}$ where $L =\psi \mathbb { H}$,

$$\begin{aligned} \psi = \begin{pmatrix} f \\ 1 \end{pmatrix}, e= \begin{pmatrix} 1 \\ 0 \end{pmatrix}\,, \end{aligned}$$

we can write a $d_\varrho$-parallel section $\varphi =\varphi ^\varrho \in \Gamma (\underline{\widetilde{\mathbb { H}}}^{2})$ as

$$\begin{aligned} \varphi = e\alpha + \psi \beta \,, \end{aligned}$$

with $\alpha =\alpha ^\varrho , \beta =\beta ^\varrho : {\tilde{M}} \rightarrow \mathbb { H}$. If $\varphi =\varphi ^\varrho$ is $d_\varrho$-parallel, we thus see that

$$\begin{aligned} d\alpha =-df \beta , d\beta =-df^d\alpha \varrho \,. \end{aligned}$$

From this, we observe that $\varphi$ has complex multiplier h if and only if $\alpha$ has also multiplier h.

Differentiating the above equations again, we obtain in the isothermic coordinate $z=x+iy$, the differential equation

$$\begin{aligned} \alpha _{yy} - i\alpha _y +\alpha \varrho =0\,, \end{aligned}$$

(4.3)

which has, in the case $\varrho \not =-\frac{1}{4}$, the solutions

$$\begin{aligned} \alpha = e^{\frac{iy}{2}}(c^+e^{\frac{i t y}{2}} + c^- e^{-\frac{i t y}{2}}) \end{aligned}$$

where $c^\pm$ are $\mathbb { H}$-valued functions, independent of y, and $t= \sqrt{1+4\varrho }$.

Thus, for $\varrho \not =-\frac{1}{4}$ the section $\varphi = e\alpha + \psi \beta$ is a section with multiplier if and only if $c^+=0$, $c^-=0$ or $\varrho$ is a resonance point. In particular, the multiplier is $h^\pm = -e^{\pm i \pi t}$. Note that if $\varrho$ is a resonance point, that is, if $h^+ = h^-$, then $\varrho = \frac{k^2-1}{4}, k\in \mathbb { Z}, k>1$.

In the case when $\varrho =-\frac{1}{4}$, the general solution to the differential equation (4.3) is given by

$$\begin{aligned} \alpha = e^{\frac{iy}{2}}(c_1 + y c_2) \end{aligned}$$

with $c_1, c_2$ quaternionic valued functions depending on x only. From this, we see that $\varphi =e\alpha +\psi \beta$ is a section with multiplier if and only if $c_2=0$. Thus, to find sections with multipliers we can restrict to finding solutions $\alpha$ of the form $\alpha = e^{\frac{iy}{2}}(c^+e^{\frac{i t y}{2}} + c^- e^{-\frac{i t y}{2}})$ for $t=\sqrt{1+4\varrho }, \varrho \not =0$ .

We write $c^\pm =c_0^\pm + j c_1^\pm$ with complex valued function $c_0^\pm , c_1^\pm$. Then, $\beta =-f_y^{-1}\alpha _y$ gives

$$\begin{aligned} \beta = e^{\frac{iy}{2}}\left( \Big (c^+_1(t-1) + j c_0^+(1+t)\Big ) e^{\frac{i t y}{2}} - \Big (c^-_1(1+t) + jc_0^-(t-1)\Big ) e^{\frac{-i t y}{2}}\right) \,. \end{aligned}$$

It remains to find the complex-valued functions $c_i^\pm$. Since $d\alpha = -df \beta$, we see that $*d\alpha =Nd\alpha$ where $N = - je^{-iy}$ is the Gauss map of f. Therefore, we can find $c^\pm$ by solving the differential equation $\alpha _y = N\alpha _x$ which gives the linear system

$$\begin{aligned} (c_0^\pm )'&= -\frac{i(-1\pm t)}{2} c_1^\pm \\ (c_1^\pm )'&= \frac{i(1\pm t)}{2} c_0^\pm \,. \end{aligned}$$

The solutions of this system are given by

$$\begin{aligned} c_0^\pm (x)&= -2i\sqrt{\varrho }(m_0^\pm e^{\sqrt{\varrho }x} - m_1^\pm e^{-\sqrt{\varrho }x}) \\ c_1^\pm (x)&= (1\pm t) (m_0^\pm e^{\sqrt{\varrho }x} + m_1^\pm e^{-\sqrt{\varrho }x}) \end{aligned}$$

with $m_i^\pm \in \mathbb { C}$. Thus, we have now computed all parallel sections of a cylinder explicitly. We summarise:

Proposition 4.4

Let $f(x,y) = \frac{1}{2}(i x+ j e^{-iy})$ be the round cylinder and $\varrho \in \mathbb { R}_*$. Then, $\varphi ^\pm = e\alpha ^\pm + \psi \beta ^\pm \in \Gamma (\underline{\widetilde{\mathbb { H}}}^{2})$ are $d_\varrho$-parallel sections with multipliers $h^\pm = -e^{\pm i \pi t}$, where

$$\begin{aligned} \alpha ^\pm&= e^{\frac{iy}{2}}(c_0^\pm +jc_1^\pm )e^{\pm \frac{i t y}{2}} \\ \beta ^\pm&= e^{\frac{iy}{2}}\left( c_1^\pm (\pm t-1) + j c_0^\pm (1\pm t)\right) e^{\pm \frac{i t y}{2}} \end{aligned}$$

with $t=\sqrt{1+4 \rho }$ and

$$\begin{aligned} c_0^\pm (x)=c_0^\pm (x, m_0^\pm , m_1^\pm )&= -2i\sqrt{\varrho }(m_0^\pm e^{\sqrt{\varrho }x} - m_1^\pm e^{-\sqrt{\varrho }x}) \\ c_1^\pm (x) =c_1^\pm (x, m_0^\pm ,m_1^\pm )&= (1\pm t) (m_0^\pm e^{\sqrt{\varrho }x} + m_1^\pm e^{-\sqrt{\varrho }x})\,, \quad m_0^\pm , m_1^\pm \in \mathbb { C}\,. \end{aligned}$$

Moreover, every $d_\varrho$-parallel section, $\varrho \not =-\frac{1}{4}$, is given by $\varphi = \varphi ^++\varphi ^-\in \Gamma (\underline{\widetilde{\mathbb { H}}}^{2})$.

Finally, the resonance points of the cylinder are given by

$$\begin{aligned} \varrho _k = \frac{k^2-1}{4}, \qquad k\in \mathbb { Z}, k>1\,. \end{aligned}$$

In this case, every $d_{\varrho _k}$-parallel section has multiplier $h_k=(- 1)^{k+1}$.

From the explicit form of the parallel sections, we have now complete information about the set of closed Darboux transforms:

Theorem 4.5

Let $f: M \rightarrow \mathbb { R}^3$ be given by $f(x,y)= \frac{1}{2}(ix + je^{-iy})$. Then for $\varrho \in \mathbb { R}_*, \varrho \not =\frac{k^2-1}{4}, k\in \mathbb { Z},$ each multiplier $h^\pm =-e^{\pm i \pi \sqrt{1+4\varrho }}$ has a complex two-dimensional space $E_\pm$ of parallel sections with multiplier $h^\pm$. Moreover,

• if $\varrho =-\frac{1}{4}$, then there is exactly one closed Darboux transform, which is the rotation of f with angle $\theta =\pi$ in the jk-plane, i.e. ${\hat{f}}(x,y) = \frac{1}{2}(ix-je^{-iy})$ is a cylinder.

• If $\varrho <-\frac{1}{4}$, then there are exactly two closed Darboux transforms which are the rotations of f with the angles $\pm \theta$ in the jk-plane where $e^{i\theta } = -\frac{1+\sqrt{1+4\varrho }}{1-\sqrt{1+4\varrho }}$, i.e. both Darboux transforms are cylinders.

• If $\varrho >-\frac{1}{4}, \varrho \not =\frac{k^2-1}{4}, k\in \mathbb { Z}, k\ge 1,$ then there is a $\mathbb { C}\mathbb { P}^1$-worth of closed Darboux transforms which are rotation surfaces.

• If $\varrho =\frac{k^2-1}{4}, k\in \mathbb { Z}, k>1$, then $\varrho$ is a resonance point. In this case, all Darboux transforms are closed and are either rotation surfaces or isothermic “bubbletons” with k lobes.

Proof

We first show that the sections $\varphi ^\pm$ from Proposition 4.4 give closed (non-singular) Darboux transforms. If $\varphi ^\pm (p)\in \Gamma (L)$ for some $p\in M$ then

$$\begin{aligned} \alpha ^\pm (p) = 0 \end{aligned}$$

which implies $m_0^\pm = m_1^\pm =0$. Therefore, $\varphi ^\pm \not =0$ give Darboux transforms which are not singular and are closed since $\varphi ^\pm$ are sections with multipliers.

We now observe that each multiplier $h^\pm =-e^{\pm i \pi t}$, $t=\sqrt{1+4\varrho }$, has a complex two-dimensional space $E_\pm$ of parallel sections with multiplier $h^\pm$, parametrised by the pairs $(m_0^\pm , m_1^\pm )\in \mathbb { C}^2$.

For non-resonance points $\varrho >-\frac{1}{4}$, the multipliers $h_\pm =-e^{\pm i \pi t} \in S^1\setminus \{\pm 1\}$ are not real with $h_+ =\overline{h_-}$ and thus $E_+j = E_-$. Therefore, we obtain a $\mathbb { C}\mathbb { P}^1$-worth of closed Darboux transforms by

$$\begin{aligned} L_+=\varphi _+\mathbb { H}, \qquad \begin{pmatrix} m_0^+ \\ m_1^+ \end{pmatrix}\mathbb { C}\in \mathbb { C}\mathbb { P}^1\,, \end{aligned}$$

and every closed Darboux transform arises this way. Writing $\varphi _+ =e\alpha _++\psi \beta _+$ the corresponding Darboux transform ${\hat{f}} = f + T$ is given by our explicit formulae as

$$\begin{aligned} T= \alpha _+\beta _+^{-1}= i {\hat{p}} + j e^{-iy} {\hat{q}} \end{aligned}$$

where ${\hat{p}}$ (resp. ${\hat{q}}$) is complex-valued (resp. real-valued) function in x. Thus, every closed Darboux transform is a rotation surface for non-resonance points $\varrho >-\frac{1}{4}$.

In the case when $\varrho < -\frac{1}{4}$, the two parallel sections $\varphi _\pm$ have real multipliers $h_\pm \in \mathbb { R}$ and the eigenspaces of the multipliers $h_\pm$ are quaternionic. Therefore, in this case $\varphi _+\mathbb { H}$ and $\varphi _-\mathbb { H}$ give two closed Darboux transforms $f_\pm =f + T_\pm$. Our explicit expressions give

$$\begin{aligned} T_\pm = \alpha _\pm \beta _\pm ^{-1}=- j \frac{1}{1\mp t} e^{iy} \end{aligned}$$

and both surfaces $f_\pm = f + T_\pm = \frac{1}{2}(ix + j e^{\pm i\theta } e^{-iy})$ are cylinders where $e^{i\theta } =-\frac{1+t}{1-t} \in S^1$ since $t\in i\mathbb { R}$.

In the case when $\varrho =-\frac{1}{4}$, we have real multiplier $h_+ =h_-=-1$ and $\varphi _+\mathbb { H}= \varphi _-\mathbb { H}$ gives one closed Darboux transform. Since there is no other section with multiplier, there are no other closed Darboux transforms in this case. The same computation as in the case $\varrho <-\frac{1}{4}$ shows that the surface is a cylinder (with $t= \sqrt{1+4\rho } =0$).

Finally, if $\varrho =\frac{k^2-1}{4}, k\in \mathbb { Z}, k>1$, is a resonance point then $h_+ = h_-\in \mathbb { R}$ and every parallel section is a section with multiplier. The closed Darboux transforms given by $L_\pm =\varphi _\pm \mathbb { H}$ are non-singular and give rotation surfaces. The closed Darboux transforms with $\varphi = \varphi _+ + \varphi _-$, $\varphi _\pm \not =0$, give isothermic bubbletons which may be singular Darboux transforms. $\square$

Examples of all possible types of closed Darboux transforms in 3-space of a cylinder can be seen in the following figures:

Fig. 7

At non-resonance points all Darboux transforms are cylinders or more general rotation surfaces

Fig. 8

At a resonance point $\varrho _k = \frac{k^2-1}{4}$ additionally CMC bubbletons or isothermic bubbletons can occur, here for $k=2,3$ lobes

Remark 4.6

We should note that similar arguments as in Proposition 4.4 and Theorem 4.5 allow to investigate parallel sections with multiplier and Darboux transforms of surfaces of revolution, see [20]. Although in general, the differential equations for $c^\pm$ cannot be solved explicitly, the corresponding shape of the functions $\alpha , \beta$ is still enough to find all possible multipliers and to conclude that all Darboux transforms are surfaces of revolution.

4.3 Sym-type Darboux transforms of a cylinder

Since now all parallel sections of $d_\varrho$ are known, we can compute explicit examples of Sym-type Darboux transforms.

We will consider the case when the one-step Darboux transform of the cylinder is a surface of revolution but not CMC. Otherwise, the Darboux transform is again a cylinder, and all of its Darboux transforms are already known, or an (isothermic) bubbleton which has the original cylinder f as its only closed Darboux transform.

We will fix our spectral parameter as the resonance point $\varrho =\frac{3}{4}$ and choose, according to Proposition 4.4, the parameter $m_0^+=m_1^+=1$ and $m_0^-=m_1^-=0$. Then, the $d_\varrho$-parallel section is given by $\varphi = e\alpha +\psi \beta$ with

$$\begin{aligned} \alpha =\alpha ^+&=2 e^{\frac{iy}{2}}(-i \sqrt{3} \sinh \frac{\sqrt{3}x}{2}+3j \cosh \frac{\sqrt{3}x}{2})e^{iy} \\ \beta =\beta ^+&= 6e^{\frac{iy}{2}}\left( \cosh \frac{\sqrt{3}x}{2} -j i \sqrt{3} \sinh \frac{\sqrt{3}x}{2}\right) e^{iy}\,. \end{aligned}$$

The resulting Darboux transform

$$\begin{aligned} {\hat{f}} = f+ \alpha \beta ^{-1}= i {\hat{p}} + j {\hat{q}} e^{-iy} \end{aligned}$$

(4.4)

is a surface of revolution in 3-space where

$$\begin{aligned} {\hat{p}}(x)&= \frac{x}{2}+\frac{2 \sqrt{3} \sinh (\sqrt{3} x)}{3-6 \cosh (\sqrt{3} x)}\\ {\hat{q}}(x)&= \frac{1}{2 \cosh (\sqrt{3} x)-1}+\frac{1}{2}\,. \end{aligned}$$

Fig. 9

One-step Darboux transform ${\hat{f}}$ in 3-space

In particular, ${\hat{f}}$ is real-analytic, and we see by Theorem 4.3 that a Darboux transform of ${\hat{f}}$ can only have constant mean curvature if is a surface of revolution.

We now demonstrate in two examples how to explicitly construct Sym-type Darboux transforms of f. The first one is obtained by extending $\varphi$ near $\lambda =\varrho$ to $d_\lambda$-parallel sections $\varphi ^\lambda$. Here, $\varphi$ is the section which gives the above Darboux transform ${\hat{f}}$. To obtain the Sym-type parallel section, we then compute

$$\begin{aligned} {\hat{\varphi }} =\varphi - \pi (\frac{\partial }{\partial \lambda }\varphi ^\lambda )|_{\lambda =\varrho }\varrho \end{aligned}$$

where $\pi$ is the projection along the splitting $\underline{\mathbb { H}}^{2} = L\oplus {\hat{L}}$ , ${\hat{L}} =\varphi \mathbb { H}$.

Example 4.7

We choose $\varphi ^\lambda = e\alpha ^\lambda +\psi \beta ^\lambda$ where

$$\begin{aligned} \alpha ^\lambda&= e^{\frac{iy}{2}}(c_0+jc_1)e^{\frac{i t y}{2}} \\ \beta ^\lambda&= e^{\frac{iy}{2}}\left( c_1^\pm (t-1) + j c_0^\pm (1+ t)\right) e^{\frac{i t y}{2}} \end{aligned}$$

with $t=\sqrt{1+ 4\lambda }$ and

$$\begin{aligned} c_0^\lambda (x)&= -4i\sqrt{\lambda }\sinh (\sqrt{\lambda }x) \\ c_1^\lambda (x)&= 2(1+ t) \cosh (\sqrt{\lambda }x)\,, \end{aligned}$$

so that indeed $\varphi ^{\lambda =\varrho } = \varphi$. Abbreviating the $\lambda$-derivative evaluated at $\varrho$ by a dot, we have

$$\begin{aligned} {\dot{\varphi }} =(\frac{\partial }{\partial \lambda }\varphi ^\lambda )|_{\lambda =\varrho }= e{\dot{\alpha }} + \psi {\dot{\beta }}\,. \end{aligned}$$

We compute

$$\begin{aligned} \dot{c}_0&= - 2i\left( \frac{2\sqrt{3}}{3} \sinh (\frac{\sqrt{3}x}{2} ) + x \cosh (\frac{\sqrt{3}x}{2} ) \right) \\ \dot{c}_1&= 2\left( \cos (\frac{\sqrt{3}x}{2} ) + \sqrt{3} x\sinh (\frac{\sqrt{3}x}{2} )\right) \end{aligned}$$

and thus

$$\begin{aligned} {\dot{\alpha }}&=-\frac{i e^{\frac{3 i y}{2}}}{3} \left( 6 x \cosh (\frac{\sqrt{3} x}{2})+\sqrt{3} (4+3 i y) \sinh (\frac{\sqrt{3} x}{2})\right) \\&\quad + \frac{j}{2} e^{\frac{1}{2} (-\sqrt{3} x+i y)} \left( e^{\sqrt{3} x} \left( 2 \sqrt{3} x+3 i y+2\right) -2 \sqrt{3} x+3 i y+2\right) \\ {\dot{\beta }}&= \frac{1}{2} e^{\frac{1}{2} (-\sqrt{3} x+3 i y)} \left( e^{\sqrt{3} x} \left( 2 \sqrt{3} x+3 i y+8\right) -2 \sqrt{3} x+3 i y+8\right) \\&\quad -3 j i e^{\frac{i y}{2}} \left( 2 x \cosh (\frac{\sqrt{3} x}{2})+\sqrt{3} (2+i y) \sinh (\frac{\sqrt{3} x}{2})\right) \,. \end{aligned}$$

Since $e=\varphi \alpha ^{-1}-\psi \beta \alpha ^{-1}$, we obtain $\pi {\dot{\varphi }} = \psi ({\dot{\beta }}-\beta \alpha ^{-1}{\dot{\alpha }})$ so that

$$\begin{aligned} {\hat{\varphi }} = \varphi - \pi {\dot{\varphi }} \varrho = e\alpha + \psi \beta (1+ m) \end{aligned}$$

with

$$\begin{aligned} m&=(\alpha ^{-1}{\dot{\alpha }} - \beta ^{-1}{\dot{\beta }})\varrho \\&=-\tfrac{1}{4} \left( \tfrac{4 \sqrt{3} x \sinh (\sqrt{3} x)+3 \cosh (\sqrt{3} x)}{2 \cosh (2 \sqrt{3} x)+1}+2+j i \tfrac{e^{2 i y} \left( \sqrt{3} \sinh (\sqrt{3} x)-12 x \cosh (\sqrt{3} x)\right) }{2 \cosh (2 \sqrt{3} x)+1}\right) \,. \end{aligned}$$

Thus, using $(1+m)^{-1}= 1- m(1+m)^{-1}$, we obtain

which gives with

$$\begin{aligned}&{\hat{T}} = \tfrac{2 i \left( \sqrt{3} \sinh (\sqrt{3} x) \left( 48 x^2-8 \cosh (2 \sqrt{3} x)-7\right) +72 x \cosh (\sqrt{3} x)\right) }{3 \left( 2 \cosh (\sqrt{3} x)-1\right) \left( 48 x^2-16 \sqrt{3} x \sinh (\sqrt{3} x)-12 \cosh (\sqrt{3} x)+8 \cosh (2 \sqrt{3} x)+7\right) } \\&\quad + j\tfrac{e^{-i y} \left( -48 x^2+16 \sqrt{3} x \sinh (2 \sqrt{3} x)+4 \cosh (2 \sqrt{3} x)+5\right) }{\left( 2 \cosh (\sqrt{3} x)-1\right) \left( 48 x^2-16 \sqrt{3} x \sinh (\sqrt{3} x)-12 \cosh (\sqrt{3} x)+8 \cosh (2 \sqrt{3} x)+7\right) } \end{aligned}$$

In particular, is again a surface of revolution in 3-space.

Fig. 10

Sym-type Darboux transform of the round cylinder f

Since is not a Delaunay surface, we see that is isothermic but not CMC.

We now compute another Sym-type Darboux transform of the cylinder by using Theorem 3.5: all Darboux transforms of ${\hat{f}}$ are given by parallel sections which are quaternionic linear combinations of ${\hat{\varphi }}$ and of ${\hat{\varphi }}_2 =\pi \varphi _2$, where $\pi$ is the projection to L along the splitting $L\oplus {\hat{L}}$, ${\hat{L}} =\varphi \mathbb { H}$, and $\varphi _2$ is a $d_\varrho$-parallel section $\varphi _2$ which is $\mathbb { H}$-independent of $\varphi$.

Note that for the resonance point $\varrho =\frac{3}{4}$ all Darboux transforms obtained this way are closed surfaces. Moreover, if , then is a Sym-type Darboux transform of f: recall that by Theorem 3.6 a two-step Darboux transform is either Sym-type or Bianchi type; in the latter case, it is the original cylinder , whereas in the former .

Example 4.8

(Closed Sym-type Darboux transform is not a surface of revolution) Let $c_0^2 = c_0^+(x,i,-i)$ and consider the corresponding parallel section ${\tilde{\varphi }}$ which is quaternionic independent of $\varphi$ by construction. To obtain a CMC bubbleton, see [20], we put $\varphi ^2= \varphi + {\tilde{\varphi }} j = e\alpha ^2 + \psi \beta ^2$ with

$$\begin{aligned} \alpha ^2&= -2 i e^{-\frac{i y}{2}} \left( -3+\sqrt{3} e^{2 i y}\right) \sinh (\frac{\sqrt{3} x}{2})+ 2 j e^{-\frac{3 i y}{2}} \left( \sqrt{3}+3 e^{2 i y}\right) \cosh (\frac{\sqrt{3} x}{2}) \\ \beta ^2&= 6 e^{-\frac{i y}{2}} \left( -\sqrt{3}+e^{2 i y}\right) \cosh (\frac{\sqrt{3} x}{2})-6 j i e^{-\frac{3 i y}{2}} \left( 1+\sqrt{3} e^{2 i y}\right) \sinh (\frac{\sqrt{3} x}{2})\,. \end{aligned}$$

The resulting Darboux transform $f_2$ of f can be explicitly computed as

$$\begin{aligned} f_2(x,y)=\begin{pmatrix}\frac{x}{2}+\frac{2 \sinh \left( \sqrt{3} x\right) }{3 \cos (2 y)-2 \sqrt{3} \cosh \left( \sqrt{3} x\right) }\\ \frac{\cos (y)}{2}+\frac{3 \cos (y)-\cos (3 y)}{6 \cos (2 y)-4 \sqrt{3} \cosh \left( \sqrt{3} x\right) }\\ \frac{\sin y}{2} + \frac{\frac{1}{2} \sin y}{\frac{\sqrt{3} \cosh \left( \sqrt{3} x\right) +3}{\cos (2 y)+2}-\frac{3}{2}} \end{pmatrix}\,, \end{aligned}$$

and is indeed a CMC bubbleton.

Fig. 11

CMC bubbleton $f_2$

To obtain a surface in 3-space from linear combinations of the two parallel sections ${\hat{\varphi }}$ and ${\hat{\varphi }}_2 = \pi \varphi _2$, we need to satisfy an initial condition: if we use

$$\begin{aligned} {\hat{\varphi }} + {\hat{\varphi }}_2 i r \end{aligned}$$

where $r\in \mathbb { R}$ is a free parameter, the resulting Darboux transforms of ${\hat{f}} : M \rightarrow \mathbb { R}^3$ are surfaces in 3-space and Sym-type Darboux transforms of f since

$$\begin{aligned} {\hat{\pi }}({\hat{\varphi }} + {\hat{\varphi }}_2 i r) ={\hat{\varphi }} \not =0\,, \end{aligned}$$

that is .

The resulting Darboux transforms of ${\hat{f}}$ can be computed explicitly. For example, for $r=50$, we obtain with ${\hat{T}} = ({\hat{T}}_1, {\hat{T}}_2, {\hat{T}}_3)$ where

$$\begin{aligned} {\hat{T}}_1&= \frac{2}{d} \left( 2 \cosh (2 \sqrt{3} x)+1\right) \left( \sqrt{3} \sinh (\sqrt{3} x) 48 x^2-8 \cosh (2 \sqrt{3} x) \right. \\&\left. \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad + \ 639993+72 x \cosh (\sqrt{3} x)\right) \\ {\hat{T}}_2&= \frac{1}{d} \left( 4 \cosh ^2(\sqrt{3} x)-1\right) \left( - 3 A \cos y -3200 \sqrt{3} (2 \cosh (2 \sqrt{3} x)+1) \sin ^3 y \right) \\ {\hat{T}}_3&= -\frac{1}{d}\left( 2 \cosh (2 \sqrt{3} x)+1\right) \left( 3 A \sin y + 2400 \sqrt{3} (2 \cosh (2 \sqrt{3} x)+1) \cos y \right. \\&\left. \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad + \ 800 \sqrt{3} \left( 2 \cosh (2 \sqrt{3} x)+1\right) \cos (3 y)\right) \end{aligned}$$

where

$$\begin{aligned} A = 48 x^2 - 16 \sqrt{3} x \sinh (2 \sqrt{3} x) - 4 \cosh (2 \sqrt{3} x) + 639995 \end{aligned}$$

and

$$\begin{aligned} d&=3 \big (1-2 \cosh (\sqrt{3} x)\big )^2 \big (2 \cosh (\sqrt{3} x)+1\big ) \\&\quad \times \left( 48 x^2 -16 \sqrt{3} x \sinh (\sqrt{3} x) -12 \cosh (\sqrt{3} x) + 8 \cosh (2 \sqrt{3} x)\right. \\&\quad \left. +1600 \sqrt{3} \big (1-2 \cosh (\sqrt{3} x)\big ) \sin (2 y) + 640007\right) \,. \end{aligned}$$

Fig. 12

Sym-type Darboux transform of f

Despite the Sym-type Darboux transform having a similar shape to CMC bubbletons, the surface does not have constant mean curvature: for a Darboux transform of the surface of revolution ${\hat{f}}$ to have constant mean curvature, must be a surface of revolution.

Similarly, one can obtain other Sym-type Darboux transforms explicitly where k gives the number of lobes:

Fig. 13

Sym-type Darboux transforms of a cylinder at resonance points $\varrho _k = \frac{k^2-1}{4}, k=2,3$

To conclude this section, we observe that we also obtain all closed Darboux transform of higher order of the cylinder f by information on the multipliers of parallel sections of the associated family $d_\lambda$ of f, without further integration.

Fig. 14

Triple Darboux transforms at a resonance point: the first one is obtained as a Darboux transform of a Sym-type two-step transform surface of revolution at the resonance point $\varrho _2$, whereas the second one is obtained by Bianchi permutability from a non-rotational Sym-type Darboux transform, using the two different resonance points $\varrho _2, \varrho _3$