Abstract
Here, we present a community perspective on how to explore, exploit and evolve the diversity in aquatic ecosystem models. These models play an important role in understanding the functioning of aquatic ecosystems, filling in observation gaps and developing effective strategies for water quality management. In this spirit, numerous models have been developed since the 1970s. We set off to explore model diversity by making an inventory among 42 aquatic ecosystem modellers, by categorizing the resulting set of models and by analysing them for diversity. We then focus on how to exploit model diversity by comparing and combining different aspects of existing models. Finally, we discuss how model diversity came about in the past and could evolve in the future. Throughout our study, we use analogies from biodiversity research to analyse and interpret model diversity. We recommend to make models publicly available through open-source policies, to standardize documentation and technical implementation of models, and to compare models through ensemble modelling and interdisciplinary approaches. We end with our perspective on how the field of aquatic ecosystem modelling might develop in the next 5–10 years. To strive for clarity and to improve readability for non-modellers, we include a glossary.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
The societal niche for aquatic ecosystem models: developing short-term and long-term management strategies
Aquatic ecosystems provide a range of ecosystem services (Finlayson et al. 2005), in particular by being sources and sinks for natural resources and anthropogenic substances. For example, as a source, they provide water for drinking, irrigation, hydropower and industrial processes. Moreover, they provide many food products. More recently, their aesthetic and recreational value has been recognized with associated health benefits. Aquatic ecosystems also act as a sink for various substances, including sewage, agricultural run-off, discharge from impoundments, industrial waste and thermally polluted water. Equally important, they provide a critical habitat for organisms that form an important part of the biodiversity. Each of the anthropogenic and natural source functions puts specific requirements on the quality of the aquatic ecosystem (Postel and Richter 2003; Keeler et al. 2012). At the same time, these quality requirements can be hampered by both the source (through overexploitation) and the sink (through pollution) functions of the aquatic ecosystem. Aquatic ecosystem models (hereafter referred to as AEMs) frequently play a role in quantifying ecosystem services and developing strategies for water quality management (Jørgensen 2010; Mooij et al. 2010). The AEMs used for this purpose are often engineering-oriented based on accepted theory and methodology for routine applications. Engineering models may be complex and linked to one another, but components are always tested. Using projections and scenario analyses, engineering-oriented AEMs can assess the various source and sink functions to help optimize and understand aquatic ecosystem function in terms of human and conservation needs. For example, AEMs have been applied as management tools to evaluate the efficiency of eutrophication mitigation strategies, to understand oceanic dynamics (e.g. the global carbon cycle), and to predict biotic responses to climate change (Arhonditsis and Brett 2004). AEMs can also be used for near real-time modelling and forecasting to facilitate immediate management decisions on, for instance, the shutdown of drinking water intakes (Huang et al. 2012; Silva et al. 2014) or the suitability of water for swimming (Ibelings et al. 2003).
The scientific niche for AEMs: advancement of theory
A strong scientific motivation for the development of AEMs is to encapsulate and improve our understanding of aquatic ecosystems. For instance, scientific AEMs can help to close mass balances of essential elements such as carbon, nitrogen and phosphorus and thereby allow quantifying the role of aquatic systems in national and global carbon and nutrient budgets (Robson et al. 2008; Harrison et al. 2012). Keeping track of mass balances can also provide help in answering stoichiometric questions (Giordani et al. 2008; Li et al. 2014). Additionally, scientific AEMs can help untangle the feedbacks between aquatic biodiversity and aquatic ecosystem functioning (Bruggeman and Kooijman 2007), and also achieve an integrated ecosystem health assessment (Xu et al. 2001). Yet another timely research topic studied with models is assessing the resilience of ecosystems to changes in external forcing arising from nonlinear functional relationships between ecosystem components (Ludwig et al. 1997; Scheffer et al. 2001). This has been done by analysing the strength of various positive and negative feedback loops in the socio-ecological system (Van Der Heide et al. 2007; Downing et al. 2014). Such studies generate new hypotheses that can then be tested in laboratories or in the field. Models are therefore effective scientific tools because they allow undertaking ‘virtual experiments’ that would be too expensive or impractical to carry out in real-world systems (Meyer et al. 2009).
The methodological niche for AEMs: filling data gaps and inverse modelling
Another motivation to develop AEMs is to fill gaps in observations. For instance, some quantities (e.g. primary production) are measured at high spatial resolution, but at a low temporal resolution and vice versa. Modelling then allows for interpolation in space and time such as seen in climatology (Jeffrey et al. 2001). Other examples include interpolating through time between satellite images or across space to fill gaps caused by cloud cover (Hossain et al. 2015). Inverse modelling is another application within the methodological niche for AEMs, in which specific system parameters or process rates that are difficult to measure are estimated. In contrast to forward modelling, inverse modelling uses observations to estimate the processes or factors that created these observations (Tarantola 2005). Since inverse modelling in general lacks a unique solution, it is important to include all a priori information on model parameters and processes to reduce the uncertainty on the results (Tarantola 2005; Jacob 2007). Methods used for inverse modelling include Bayesian inference, often used with the Markov chain Monte Carlo technique (Press 2012; Gelman et al. 2014) and Frequentist inference (Press 2012). Different software packages for implementation of these methods exist (Vézina and Platt 1988; Reichert 1994; Lunn et al. 2000; Soetaert and Petzoldt 2010; Van Oevelen et al. 2010; Doherty 2015).
Existing diversity in AEMs
Due to numerous potential AEM applications (in an analogy to biodiversity, we refer to these as ‘model niches’), scientists began to develop these models in the 1960s, in tact with the availability of the necessary computing infrastructure to implement them (e.g. King and Paulik 1967). Since then, an array of AEMs has been developed around the world, with each development directed by a specific set of questions and hypotheses. In many cases, investigators and engineers implemented their own models rather than starting with an existing model. While this practice of creating one’s ‘own model’ can be criticized because it bears the inefficiency of ‘reinventing the wheel’ (Mooij et al. 2010), it has produced a great diversity in approaches, formulations, complexity and applications, which can be seen as an advantage. In addition, the extra investment is often compensated by a more efficient model application for the issue at hand and a better model understanding. Furthermore, the availability of modelling resources through the Internet provides new opportunities to explore and exploit this diversity and will most likely affect the evolution of model diversity in the near future.
A working definition of what constitutes an AEM
This paper aims to present a current perspective on how we can explore, exploit and evolve the existing diversity in AEMs as seen by a diverse and international community of aquatic scientists (the authors). We try to reach out to not only the skilled modellers, but also aquatic ecologists who are inexperienced in modelling. To make this study feasible, we need a definition of what constitutes an AEM. Here, we define an AEM as ‘a formal procedure by which the impact of external or internal forcing on aquatic ecosystem state(s) can be estimated’. In most cases, AEMs cover many processes and are spatially explicit, but both are not a prerequisite. According to our definition, a minimal model that qualitatively describes the ecosystem response to external forcing also qualifies as an AEM (Fig. 1). We exclude models that focus on one single component of an ecosystem (e.g. models that only deal with the population dynamics of a given species), but include models that zoom in on one part of the ecosystem (e.g. the fish or macrophyte community) while treating the remainder of the ecosystem in an aggregated way (typically through the use of carrying capacities or mortality rates). Two distinct classes of AEMs exist: those that formulate a direct mathematical relation between forcing and state (statistical models), and those that are formulated in terms of the processes underlying this relation (process-based models). Statistical models directly link forcing and state that can be derived from data with standard statistical techniques. Linking process-based models to data involves less standardized calibration and validation techniques. The advantage of process-based models is that they provide insight into the mechanisms underlying change and recovery. This study is primarily focussed on the diversity in process-based models, although we acknowledge the diversity and usefulness of statistical models that directly link forcing and state. AEMs, as defined here, combine elements from a number of scientific modelling disciplines (Fig. 2). In addition to defining what constitutes an AEM, we developed a glossary of terminology used in the field of aquatic ecosystem modelling (given in Text Box 1). The purpose of this glossary was to strive for clarity within the context of this study. This glossary may also be of help to newcomers in the modelling field. While working on the glossary, we noted that it is impossible to make a clear distinction between models (the mathematical description of a system), their implementation (e.g. software packages) and their applications (where model inputs/parameters are adapted to a specific ecosystem and confronted with data) because there is great diversity in how these components are perceived and combined by different modellers.
Example of output of a conceptual AEM showing a linear (a), catastrophic (b) and hysteretic (c) response of ecosystem state to external forcing. Modified after Scheffer et al. (2001)
How this study is structured
We first focus on exploring AEM diversity by discussing approaches to inventorize, categorize and document these models and finally present a more formal analysis of model diversity. To support our discussion, we compare a number of AEMs, hydrological and hydrodynamic drivers, relevant modelling approaches and supportive software for model implementation and model analyses that came about in a survey among modellers participating the third AEMON (Aquatic Ecosystem MOdelling Network) workshop held in February 2015. To put our analysis in perspective, we compare the number of AEMs, hydrological and hydrodynamic drivers, relevant modelling approaches and supportive software for model implementation and model analyses with published lists (Table 1). We cover both marine and freshwater AEMs, with a bias towards the latter group. All data can be found in Online Resource 1. It is remarkable that earlier attempts by Benz et al. (2001) have little overlap with our overview, which shows that there is a greater diversity than presented here. We then focus on exploiting diversity and ask several questions. How can we make use of the full breadth of expertise captured in existing AEMs, and how can we easily switch between spatial configurations or software packages to run and analyse the models using package-specific tools? We continue with stressing the potential of ensemble modelling, and we end this section with a discussion on how to exploit the full range of approaches used in aquatic ecosystem modelling. In the section on evolving diversity, we describe the origins of the current diversity in AEMs and discuss how model diversity could evolve in the future and how standardization can facilitate this process. In the final section, we discuss how we can learn from concepts and techniques in biodiversity research in our study on model diversity. Finally, we provide a list of practical recommendations and a perspective for the field of aquatic ecosystem modelling in the next decade.
Exploring diversity in AEMs
AEMs have been and are being developed independently in many places around the world. In this section, we explore model diversity.
Making an inventory of the diversity in AEMs
An exploratory survey among 42 modellers participating in the third AEMON workshop 2015 resulted in 133 different models, packages or programming languages in use in the field of aquatic ecosystem modelling (data presented in Online Resource 1, Datasheet 2). We performed a Redundancy Analysis (RDA, using the methods of Oksanen et al. 2014) on 39 AEMs from this list (results in Online Resource 2). This analysis demonstrates that the professional affiliation and country of origin played an important role in determining knowledge and usage of models. The driver behind this could be the research group’s background, but also the diverging needs that motivated the development of models, such as whether there are mainly shallow lakes or deep reservoirs in a specific country. Three approaches seem suited for developing a more formal and ongoing inventory of model diversity: (1) lists, (2) wikis and (3) code repositories. We are not aware of an up-to-date list of AEMs with a good coverage of the field. Laudable attempts to list ecological models are UFIS (Knorrenschild et al. 1996) and the ECOBAS initiative by Joachim Benz (http://www.ecobas.org, Benz et al. 2001). ECOBAS provides metadata on a wide range of models, including hydrological, hydrodynamic, meteorological and ecological models. However, the website has only rarely been updated since 2009; updating is a challenge for any top-down initiatives. An alternative could be an open community-based approach, such as wikis, where multiple editors independently contribute information. The obvious and overwhelmingly successful example of this approach is Wikipedia (http://www.wikipedia.org) which maintains many lists, for instance of programming languages (http://en.wikipedia.org/wiki/List_of_programming_languages). The potential lack of consistency of such community-based lists seems to be compensated by the scope and immediacy of the information provided and the commitment resulting from the community-based approach. The third option is code repositories, such as SourceForge (http://sf.net) and GitHub (http://github.com), which are increasingly popular platforms enabling open-source communities to develop software and distribute code.
Documenting diversity in AEMs
To preserve and communicate model diversity, proper documentation of models is crucial. There is no standard way of documenting AEMs, and different model developers have different methods to obtain and save their information. The existing ODD protocol (overview, design concepts and details) for individual-based models (Grimm et al. 2006), the Earth System documentation project (http://es-doc.org) or the TRACE approach (TRAnsparent and Comprehensive Ecological modelling documentation) might be adopted by aquatic ecosystem modellers in the future (Grimm et al. 2014). Models can be documented through model homepages, scientific publications or grey literature reports. Wikipedia is not an option because it has a strict policy of not being a primary source of documentation but instead only providing referenced information. To be useful in the current practice of scientific research, any type of documentation should be accessible through the Internet, preferably with open access. The majority (71 %) of the AEMs analysed in Online Resource 3 has a website that provides model documentation. Furthermore, for 86 % of the models, we could identify a primary publication; however, only three out of 42 AEMs analysed in Online Resource 3 have a page on Wikipedia (Ecopath, PCLake and PCDitch).
Categorizing diversity in AEMs
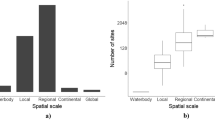
To cope with the diversity in models, some form of categorization is useful. ‘Bining’ models in clearly defined categories provide an overview for newcomers and experts, and help to identify what is missing. From the list of models in Online Resource 1, Datasheet 2, we selected those models that can be classified as an AEM according to our definition. This resulted in a list of 42 AEMs (see for data Online Resource 1, Datasheet 3). For these models, we were able to obtain metadata from experts to categorize them (see Online Resource 3 for all the details and see Text Box 1 for an explanation of all the technical terms used below). For the modelling approach, it was found that over 75 % of the models were qualified as being dynamic, process-based, biogeochemical, mass-balanced, compartmental or complex dynamical (Fig. 3a). Over 45 % of them were qualified as being stoichiometric or spatially explicit as well as being a competition, a consumer-resource, a food web or a community model. About 25 % of them were qualified as being of the NPZD type of model (nutrients, phytoplankton, zooplankton, detritus) as well as being a hydrodynamic model. One out of seven of these models contained individual-based approaches, more specifically being an individual-based community model, a trait-based model or a dynamic energy budget model. The 42 AEMs cover every aquatic habitat, with 22 % of models claiming global applicability (Fig. 3b). Eutrophication is an application domain of no less than 98 % of the analysed models (Fig. 3c). Next, in decreasing order of importance are climate change, carbon cycle, fisheries, biodiversity loss and adaptive processes. 90 % of the 42 models allow for dynamic simulations (Fig. 3e). The remaining models are based on statistical relations. About half of the models are implemented in frameworks that have tools for sensitivity analysis, calibration, validation and uncertainty analysis. Here, we define a framework as a software package that can be combined with user-written code to create a software application (for a more extensive definition, see Text Box 1). Tools for bifurcation analysis are less common. Over two-third of the models are implemented within an existing modelling framework, with the R/deSolve package (Soetaert et al. 2010) and the Framework for Aquatic Biogeochemical Models (FABM) (Bruggeman and Bolding 2014) being the most used of the 12 modelling frameworks that we encountered (Fig. 3d). One can rightfully say that the field of aquatic ecosystem modelling is quite scattered when it comes to the use of modelling frameworks. This notion was one of the incentives for developing Delft3D-Delwaq (Deltares 2014), FABM (Bruggeman and Bolding 2014) and the Database Approach to Modelling (DATM) (Mooij et al. 2014). With 50 %, FORTRAN is the dominant programming language for coding AEMs (Fig. 3f). Next comes C or C++ (together 26 %), Delphi (15 %) and R (15 %). The majority of AEMs are implemented as ordinary or partial differential equations (Fig. 3g).
Outcome of a categorization of 42 AEMs on six types of categorizations: a modelling approach (for all levels, see Online Resource 2), b environmental domain of the model, c model application domain, d modelling framework, e type of analysis available within the model’s framework, f programming language and g mathematical equation type. See text for explanation
Analysing diversity in AEMs
Analysing model diversity goes beyond the more descriptive approach mentioned above. Here, the aim was to identify whether we are dealing with true diversity or ‘pseudo-diversity’. Models are often related to each other. The MyLake model (Saloranta and Andersen 2007), for example, has characteristics that are also found in other lake models such as DYRESM-CAEDYM (Hamilton and Schladow 1997), MINLAKE (Riley and Stefan 1988), PROBE (Blenckner et al. 2002) and BELAMO (Omlin et al. 2001; Mieleitner and Reichert 2006). We aim for a more objective and in-depth analysis of a list of AEMs using a similarity index (for details on the analysis, see Online Resource 4 and for the data Online Resource 1, Datasheet 4). One approach is to compare state variables between models. We analysed 24 AEMs for which sufficient information was provided, which gave in total almost 550 unique state variables. The minimum number of state variables found in a model is 2 and the maximum is 118 (Fig. 4). It should be noted that in some (especially the larger and general) models, not all state variables are included simultaneously in each model application but rather subsets of variables are being used. Additionally, some models have state variables that can be duplicated by changing their parameters (e.g. cohorts of a species). A Sørensen similarity analysis (Sørensen 1948) using the state variables of 24 models (Online Resource 4) shows that models become more similar as their complexity increases. This is an expected result as the chance of similarities increases with increasing sampling size of a given pool. However, overall the dissimilarity is higher than the similarity since more than 80 % of the models have a similarity index of less than 0.25. Hence, many models benefit from predecessor models even though they are still unique with individual features not found in predecessor models. Most overlap can be found in general state variables such as phosphorus, ammonia and a generic group of phytoplankton or zooplankton. Three groups of models can be distinguished: general-purpose models with a relative high overlap, specialized models with low overlap and intermediate models with an intermediate level of overlap (see dendrogram in Online Resource 4). Interestingly, some models are significantly more dissimilar than would be statistically expected based on their number of state variables (red downward arrow, Fig. 4). This is because these models capture only a specific non-overlapping part of the aquatic ecosystem (e.g. the Guam Atlantis Coral Reef Ecosystem Model versus PCLake or CAEDYM). Other models are more similar than would be expected based on the number of state variables (upward green arrow); these models simulate the aquatic ecosystem in a more general way, such as CCHE and Mylake. A following step could be to compare the models for their mathematical process formulations, though this is beyond the scope of this paper. An educated guess is that this will reveal an even higher diversity, as endless combinations can be made with the available process formulations. For example, Tian (2006) counted 13 functions used to describe the effect of light forcing on phytoplankton growth. Using these light functions in combination with other functional relations, for instance, temperature forcing (10 different relations), zooplankton feeding (20 different relations), prey feeding (15 different relations) and mortality (8 different relations), lead to hundreds of thousands of combinations that give different results and are all ‘the best’, depending on the aim of the model (Gao et al. 2000).
Similarity matrix based on the Sørensen similarity index between the state variables considered in the models. Darker colours mean higher similarity. Models with a green upward arrow are significantly more similar to other models corrected for the maximum number of state variables (p < 0.05). Models with a red downward arrow are significantly more dissimilar to other models corrected for the number of state variables (p < 0.05). Grey bars on the right show the maximum number of state variables within a model. For detailed information on methods and results, see Online Resource 4. (Color figure online)
Exploiting diversity in AEMs
The inventory of the AEMs reveals a great diversity in model approaches, formulations and applications. Here, we ask whether and how this diversity could be exploited.
Exploiting the diversity in disciplines
One of the options is to exploit the diversity in contributing disciplines (see Fig. 2) and work in teams consisting of not only aquatic ecologists, but also social scientists, economists, climatologists, hydrologists, statisticians, mathematicians, etc. Working in an interdisciplinary setting helps one to look beyond the personal expert field and provides a more holistic view upon both models and aquatic ecosystems (Hamilton et al. 2015). Resulting interdisciplinary models have an increased complexity with the disadvantage that full understanding of the model by the individual modeller is lost (Scholten et al. 2007; Robson 2014a). The problem of inappropriate usage of complex models can be overcome by again working in interdisciplinary teams. In this way, team members are able to focus on their own area of expertise while the team as a whole is able to understand the full model. Statisticians and mathematicians can support interdisciplinary teams with their knowledge on mathematical formulations and their insight into model uncertainty. Especially within the scientific niche, understanding of the model is important since novel ideas need to be tested and understood. Within the engineering niche, there is less need to understand each model component in detail. Indeed, many people drive a car safely without having a detailed technical background on the engine’s functionality.
Exploiting the diversity in spatial explicitness of AEMs
Another way to exploit the diversity in AEMs is by using the full width of spatial explicitness, which varies from spatially homogenous (0D) and vertically or horizontally structured (1D) to fully 3D. Within these dimensions, a modeller can additionally choose between different structured grids (e.g. Cartesian grid, regular grid and curvilinear grid) and unstructured grids (e.g. finite elements). Following Occam’s razor, model complexity should be minimized and only increased if this increases the predictive performance of the model or its generality/universality (please note that, while mentioned here in the context of spatial explicitness, Occam’s razor applies to all aspects of complexity in AEMs). Therefore, to understand the basics of ecological processes in a well-mixed system, one should use a 0D model as its dynamics are often easier to understand. Additionally, 0D models are well suited for checking the internal consistency of the model functions. Spatially explicit models, however, are more realistic, as they account for the spatial heterogeneity of ecosystems, with the risk of getting lost in complexity when explaining model behaviour. Nonetheless, some research questions cannot be solved without taking spatial resolution into account [e.g. population dynamics of fish in Jackson et al. (2001), and spatial distribution of macrophytes and algae in Janssen et al. (2014)]. Recent advances facilitate the implementation of a model in different spatial settings. For example, with Delft3D-Delwaq, FABM and DATM, it is possible to switch between a 0D, 1D, 2D to 3D implementation of, for instance, PCLake (Van Gerven et al. 2015). However, these frameworks are currently implemented without accounting for feedbacks between ecology and hydrodynamics. Interfaces such as OpenMI (Gregersen et al. 2007) and FABM (Bruggeman and Bolding 2014) allow for such coupling and are designed to overcome the issues that emerge when integrating ecology and hydrodynamics. Examples of these issues are the different timescales and spatial schematization for ecology and hydrodynamics (e.g. Sachse et al. 2014) and feedbacks between ecology and hydrodynamics, such as the effects of water plants on the water flow (e.g. Berger and Wells 2008).
Exploiting diversity by having a given AEM implemented in multiple frameworks
Recent approaches such as DATM (Mooij et al. 2014), FABM (Bruggeman and Bolding 2014) and the open process library in Delft3D-Delwaq (Deltares 2014) make it possible to exploit model implementations in multiple frameworks without much overhead. Therefore, a myriad of tools for model analysis (e.g. sensitivity analysis, calibration, validation, uncertainty analysis, and bifurcation analysis) become easily available. The redundancy in tools among frameworks insists modellers to stick to the framework they are familiar with for most analyses, whereas the complementarity in tools is tempting to switch to other frameworks for alternative analyses (Van Gerven et al. 2015), including the switch between 0D and 3D. In this way, the strengths of frameworks (including run-time) can be exploited, and the underlying ecological question can be approached from different perspectives.
Exploiting diversity in dealing with uncertainty in AEMs
As a simplification of nature, AEMs suffer from uncertainty in their outcomes (Beck 1987; Chatfield 1995; Draper 1995). Sources of uncertainty are structural uncertainties, i.e. incomplete or imperfect process formulations, parameter uncertainty, uncertainty in forcing functions and initial values, uncertainty in validation data, and uncertainty due to the numerical methods used. A full coverage of the topic of uncertainty in AEMs is beyond the scope of this paper. For more information on this topic, we refer to the extensive literature available on this topic including Beck (1987), Chatfield (2006) and Doherty (2015). Below, we limit ourselves to presenting three different views on how to deal with uncertainty in parameters. First, a modeller measures the parameters’ magnitudes directly. The parameter values are then purely based on biologically, chemically or physically knowledge. Due to errors in the measurements (experimental uncertainty, Moffat 1988) and limited transferability (e.g. between laboratory and field conditions), these a priori parameter values have an uncertainty as well (Draper 1995). By repeating the measurements over and over, the experimental uncertainty can be reduced, thereby minimizing the parameter uncertainty, but this is often a costly measure (Chatfield 1995). A second option is to estimate the parameters using calibration data and statistics without the use of a priori knowledge. This method leads in many cases to multiple possible parameterizations of the model with equal fit (e.g. Beven 2006) and bears the risk of overfitting (Hawkins 2004). For this reason, a modeller may choose for the third option where the parameters are estimated based on calibration data, statistics and a priori knowledge (e.g. Janse et al. 2010). In this case, a realistic range of parameter values is defined, prior to the parameter estimation by statistics. Thereafter, using Bayesian statistics, the parameters can be estimated within the range of realism (Gelman et al. 2014).
Exploiting diversity by ensemble modelling with AEMs
One way to deal with the uncertainty is using the diversity of models in ensemble techniques [e.g. Ramin et al. (2012) or Trolle et al. (2014), see Fig. 5 for an example from the latter study]. A variety of ensemble techniques exists, each duplicating a certain aspect of the modelling process. In multi-model ensembles (MMEs), multiple models are applied to a given problem. Single-model ensembles use different model inputs (parameters, initial values, boundary conditions) to exploit the model’s sensitivity (e.g. Couture et al. 2014; Gal et al. 2014 or Nielsen et al. 2014). More ensemble techniques or combinations of techniques exist including multi-scheme ensembling (use of different numerical schemes) and hyper-ensembling (use of multiple physical processes). Ensemble modelling has become a standard in meteorological forecasting (e.g. Molteni et al. 1996) and climatic forecasting (e.g. IPCC 2014). There is an increasing number of applications in hydrology and hydrodynamics as well (e.g. Stepanenko et al. 2014; Thiery et al. 2014). In aquatic ecosystem modelling, the use of ensemble techniques is still rare (but see examples in, for instance, Lenhart et al. 2010; Ramin et al. 2012; Gal et al. 2014; Nielsen et al. 2014; Trolle et al. 2014). However, the relevance of MME for ecological modelling is large, as a strictly physically based description is not practically feasible and a unified, transferable set of equations is, therefore, not available. Additionally, we foresee that ensemble modelling will become common practice because of (1) the emergence of active communities of aquatic ecosystem modellers such as AEMON; (2) the increase in freely available papers, data and model code; and (3) the development of approaches such as Delft3D-Delwaq, FABM and DATM. Hence, the results of decades of individual model niche development can now be better utilized (Mooij et al. 2010; Trolle et al. 2012). The comparative list provided in Online Resource 1 (Datasheet 4) is a useful starting point of ensemble modelling with AEMs. When using a model to provide forecasts, MME have two major advantages over single-model approaches. First, the ensemble mean may be a better predictor than any of the sole ensemble members (Trolle et al. 2014). This is especially true when an aggregated performance measure over many diagnostics variables is considered (Hagedorn et al. 2005; Trolle et al. 2014). Second, the ensemble spread can serve as a convenient measure of predictive uncertainty if a spread–skill correlation exists. Although MMEs are attractive, their limitations need to be recognized. First, despite ever increasing computer power, they are time-consuming to put in place. More importantly, MME-based estimates of structural uncertainty can only be meaningful if the models involved differ substantially. Another more general limitation of ensembles is that the attainable estimate of uncertainty is inevitably incomplete, for example due to a limited number of suitable models and the requirement of each model to have its own set of—ideally standardized—parameters and initial values. Ensemble techniques therefore only quantify part of the total uncertainty in predictions (Krzysztofowicz 1999). In the context of ecological process-based modelling though, the integration of multiple models should not be viewed solely as an approach to improve our predictive devices, but also as an opportunity to compare alternative ecological structures, to challenge existing ecosystem conceptualizations, and to integrate across different (and often conflicting) paradigms (Ramin et al. 2012). Future research should also focus on the refinement of the weighting schemes and other performance standards to impartially synthesize the predictions of different models. Several interesting statistical post-processing methods presented in the field of ensemble weather forecasting will greatly benefit our attempts to develop weighting schemes suitable for the synthesis of multiple ecosystem models (Wilks 2002). Other outstanding challenges involve the development of ground rules for the features of the calibration and validation domain, the inclusion of penalties for model complexity that will allow building forecasts upon parsimonious models, and performance assessment that does not exclusively consider model endpoints but also examines the plausibility of the underlying ecosystem structures, i.e. biological rates, ecological processes or derived quantities (Arhonditsis and Brett 2004).
Example of a multi-model ensemble (MME). The shaded area shows the full width of predicting outcomes made by different models, the black line shows the mean of all models and the circles are the observations. Figure modified after Trolle et al. (2014) where the authors show that the prediction by the average model outcome is better than the prediction by individual models
Exploiting the diversity in fundamentally different approaches in aquatic ecosystem modelling
Finally, we could exploit the diversity in more fundamentally different model approaches, for example statistical- versus process-based models. The diversity in model approaches is the product of the numerous choices that can be made during model development, pursuing a certain trade-off between effort, model simplicity, realism, process details, boundary conditions, forcings and accuracy along various dimensions such as time and space (e.g. Weijerman et al. 2015). For example, minimal models aim to understand the response curve of ecosystems to disturbances, but they are generally too simple to allow for upscaling and process quantification. Complex models on the other hand can describe the cycling of nutrients through many compartments of an ecosystem as well as the flow of energy through the system. Therefore, they often allow for quantitative scenario evaluations, but their output is difficult to interpret as it is demanding to decipher the numerous interactions and feedback loops. More complexity also can be introduced by individual-based and trait-based models, which allow the inclusion of evolutionary processes. Thus, a higher diversity of model approaches permits addressing a higher number of different purposes, provided that they are sufficiently complementary. There is a great value in combining different modelling approaches, as insights gained by one model can be useful for the application of another, and we benefit from the strengths of different model types (Mooij et al. 2009). Combining modelling approaches helps to develop an integrative view on the functioning of aquatic systems and seems almost essential for the adaptive management of the source and sink functions of lake ecosystems, which require integrated thinking and decision support.
Evolving diversity in AEMs
We have explored and exploited diversity in AEMs. Before reflecting on possible future evolution of model diversity, it is interesting first to look back and see how the existing diversity came about.
A historical perspective on evolving diversity in AEMs
The field of AEMs started with great expectations when the first mainframe computers were installed at universities in the 1960s (Lavington 1975). But because of the adaptive nature of living systems, making predictive AEMs proved to be more difficult than predicting the trajectory of a rocket to the moon. This sparked the emergence of individual-based models sensu lato, including dynamic energy budget models (Kooijman 1993), structured population models (De Roos et al. 1992) and individual-based models sensu stricto (Mooij and Boersma 1996), that zoom in on a particular (group of) species in the ecosystem. In an opposite direction, minimal dynamical models of ecosystems zoomed out to detect dominant nonlinearities in ecosystem responses to external forcing (Scheffer et al. 2001). Renewed interest in large ecosystem models occurred in the past decades, not the least as a result of the increased and distributed computational power, but this time with the tendency to link the models with individual-based and trait-based approaches (DeAngelis and Mooij 2005) and compare their behaviour with minimal dynamical models (Mooij et al. 2009). In the past, region-specific questions have led to region-specific models; however, as a result of current globalization, the need for widely applicable models and models covering regional or continental aspects is rapidly increasing. The growing recognition of the importance anthropogenic stressors on ecosystems and the services provided by ecosystems asks for coupling of ecological models with socio-economics models (e.g. Downing et al. 2014). This can be realized by using output of one model as input for the other model, or run-time exchange of input and output between such models. The latter method is more complicated and only becomes necessary when there are strong feedbacks between ecology and socio-economics.
Arguments for reducing diversity
There are valid arguments why aquatic ecology as a whole could benefit from streamlining the diversity in AEMs. First, some formulations have been shown to be both less accurate and more complex than alternatives (Tian 2006). Second, some models are developed to answer one specific question and thus lose their functionality once this question has been addressed. It is likely that this kind of models has a high turnover rate, but such models could also be incorporated in large models as the results prove to be relevant. Finally, the presence of pseudo-diversity is an argument to reduce the number of models. For example, in climate studies, it has been shown that the performance of ensemble models significantly improved when pseudo-diversity was reduced (Knutti et al. 2013). Ideally, groups that work in parallel on similar models should have the incentives to join efforts, but these incentives are often not in place. Also at the level of the individual scientists, there seem to be few, if any, incentives to give up one’s own model, whereas there are many incentives to maintain it or even start yet another one. Only when the incentives that lead to fragmentation are overcome, or are outweighed by incentives to join forces, can we expect a healthy consolidation of the field to take place. Frameworks such as Delft3D-Delwaq (Deltares 2014), FABM (Bruggeman and Bolding 2014) and DATM (Mooij et al. 2014) facilitate this process, but also these frameworks have the risk to be duplicated, leading to yet another layer of fragmentation. The turnover rate of AEMs is hard to measure since publications on dropped models are rare, if they even exist. At the same time, the absence of publications on a specific model does not necessarily mean that a model became unused, as engineers, for example, might use the specific model on a daily basis without publishing the results. Furthermore, unlike extinct species that reduce biodiversity, ‘dead’ models can become ‘alive’ when a need for their existence emerges, thereby contributing again to model diversity.
Arguments for enlarging diversity
Because the field of aquatic ecosystem modelling can appear quite fragmented, arguments for enlarging diversity in AEMs are easily overlooked. Nevertheless, there should always be room for good ideas and new avenues. An interesting example is provided by minimal dynamical models. When these became prominent in the shallow lake literature about 25 years ago, they were met with considerable reservation and hardly perceived as a step forward. Nowadays, their ability to illustrate and communicate essential nonlinearity in the response of ecosystem (and many other dynamical systems) is broadly recognized (Scheffer et al. 2001). Another emerging approach with many applications in the aquatic domain is Dynamic Energy Budgets (DEB) (Kooijman 1993). The scope of current DEB models, however, is too limited to be qualified as ecosystem models as defined in this study.
Arguments for conserving diversity
With the first generation of aquatic ecosystem modellers about to retire, there can be serious concern about a loss of useful models and approaches, requiring active conservation effort by the community at large. Proper implementation of conservation schemes will help to prevent the proverbial ‘reinvention of the wheel’ (Mooij et al. 2010). Additionally, it can help future model developers to anticipate what models and formulations worked well and which did not. Obviously, this learning process is hampered at the lack of documentation of failures in the scientific literature. Conserving diversity would thus have a great educational value and would help understand the ‘genealogy’ of the existing models. Conservation of model diversity is important for science as well, as science builds on repetition which only can be complied with when code is conserved. However, model diversity conservation has to overcome ‘code rot’, which is the deterioration of software as a result of the ever evolving modelling environment, making the software invalid or unusable (Scherlis 1996). To prevent code rot, the code should be maintained. Another option is to conserve models in their purest mathematical form (e.g. like in the concept behind DATM, Mooij et al. 2010).
How to facilitate evolving diversity
One would like to have tools available and mechanisms in place that would allow diversity to evolve through a ‘natural selection’ of models. Natural selection is an emergent property of a system in which there is variation among agents; this variation is transferred to the offspring of the agents and has an impact on the survival of the agents. We have shown that there is ample diversity among AEMs, and there seems to be a healthy cross-fertilization of ideas leading to continued development of new versions and models. What may be hampering ‘natural selection’ among AEMs, however, are standardized methods to compare model ‘fitness’ within their niche and given the research question they address. Here, we point specifically to the research question since models might have a different purpose, and it only makes sense to compare the fitness of those models that are able to answer the same research question. To enhance selection and ‘gene transfer’, easy model accessibility is necessary in the first place. Easy accessibility not only includes freely available model software but also low time costs of, for instance, learning new modelling code or approaches. Additionally, data availability is very important for the improvement of models (Hipsey et al. 2015). As long as models are inaccessible, due to, for example, licence restrictions or inappropriate manuals, modellers will most likely choose the models in use by their colleagues (see Online Resource 2). These easily accessible models may not be the best suitable to answer their questions. Secondly, standard objective assessment criteria to calibrate and validate models are important (Refsgaard et al. 2005; Robson 2014b). These criteria are different for each modelling niche, as models that are suitable, for example, for forecasting of algal blooms require other criteria than models suitable for biodiversity assessments. It also implies providing a freely accessible set of data used as calibration or validation data (meteorology, hydrology, hydrodynamics, nutrient fluxes, etc.) of the models to be benchmarked. The application of the models to these common test data enables a direct comparison without interfering effects from differences in basin morphometry, hydrology, meteorology, and so on. The main idea behind this benchmarking is not to classify models into ‘good’ and ‘bad’ ones, but instead to characterize the dynamic behaviour and specific abilities of the separate models. Finally, we would like to point to the importance of the conservation and maintenance of expertise and experience for model evolution. Currently, project life cycles are generally short, and while mobility of people can help to spread models, the same mobility could lead to a local loss of expertise (Herrera et al. 2010; Parise et al. 2012).
Discussion
How can biodiversity research help us to interpret model diversity?
One could see the myriad of model purposes as niches that shape model diversity. Like biodiversity, model diversity can be organized in taxonomic structures to classify models. Using Wikipedia as a reference, such a taxonomic study has been done already for programming languages and showed a phylogenetic tree with new programming languages emerging from different elements of earlier programming languages (Valverde and Solé 2015). A similar study for AEMs is intriguing, but is beyond this study. Our analysis revealed a large diversity in the models. We argue that to fully exploit the niche, the tools for analysis provided in each modelling framework should be used. If we divide the AEMs in specialists or generalists, the majority of the AEMs seem to be specialists that address the research question that led to their development but with little application beyond. This can be attributed to the fact that models are often locked within frameworks which obstruct communication and cross-fertilization between the models (Mooij et al. 2014). For the same reason, we could question whether there is enough competition between the models to enable survival of the fittest and thus competitive exclusion. At present, most models seem to have the fingerprints of the resource group it is developed in, as if they were species that evolved in their island-specific supported niche. This has the disadvantage of reinventing the wheel, but surely has its advantage as well since the independently evolved models can be used for comparison as in ensemble modelling.
Recommendations
Our analysis of exploring, exploiting and evolving diversity in AEMs leads us to three types of recommendations related to (1) availability, (2) standardization and (3) coupling of AEMs.
Availability of AEMs
With respect to the availability of AEMs, it is important to continue the current trend of open-source policies for AEM models, tools for analysis and data. This will increase the transparency of model structure, assumptions and approaches. Besides that, there is an urgent need for a public overview of existing AEMs. This could be a Wikipedia list, with links to relevant (online) documentation or similar initiatives. Such a list could be complemented with an overview of the forces and niches that created the existing diversity in AEMs. Once there is an overview of the niches in which models are designed, the suitability of models for other applications is better assessed. Documentation of the available AEMs will create awareness of the full width of approaches in AEMs to avoid tunnel vision. We should also actively preserve AEMs to learn from the past and thereby avoid reinventing the wheel but also to identify and prevent pseudo-diversity in AEMs.
Standardization of AEM practices
We recommend developing standardization in the documentation of AEMs [comparable with, e.g. ODD for IBMs, Grimm et al. (2006)], terminology to categorize AEMs and the methods to analyse AEMs. Standardization of documentation and terminology is desirable for the communication on the different available models. Standardization of methods for parametrization, comparison, calibration, testing, structuring, conversion and interpolation in AEMs will lead to a common practice in model analysis.
Linking AEMs
In our analysis, we compared models by their state variables, while additional diversity is hidden in the process formulations. Here, we recommend fulfilling the next step by comparing models by their process formulations. Currently, this step is a time-consuming and difficult task as a result of lack in the availability of model definitions. Perhaps this step will be possible in the future due to the emerging linking approaches such as DATM. And linking has more benefits. We advocate linking AEMs with models from other disciplines to answer questions that require a holistic approach. We recommend running AEMs in more than one spatial setting to gain more insight into the effects within the spatial context and suggest running a given AEM in multiple frameworks to use the full set of tools for analysis and advice of the user community. Finally, we recommend ensemble modelling with AEMs in order to use the best out of multiple models. For example, statistical- and process-based AEMs should be used side by side because they have complementary strengths.
We anticipate that increasing model availability, standardization of model documentation, and various forms of linking will lead to an evolving diversity of AEMs in which the better performing models out-compete the poorer performing models. Given the large number of model niches, however, there will always remain a great diversity in AEMs.
Perspectives
We can only speculate where the field of aquatic ecosystem modelling will be heading in the coming five to 10 years. We expect that many new developments will be triggered and enabled by general trends in science, technology and society. Here, we list 10 of these possible trends. (1) We expect that wikis (e.g. Wikipedia), where users can either retrieve information or contribute information through standardized web interfaces, will gain in importance for the documentation and distribution of AEMs. While we recognize the inherent lack of quality control, we highly value the ease of access, the community effort and dynamic nature of this approach (the name ‘wiki’ is derived from the Hawaiian word for ‘quick’). (2) We recognize initiatives to develop e-infrastructures for the implementation of AEMs and other environmental models where users of different levels of experience share easy and secure access to models and data according to their needs. (3) We envision that current trends in the mandatory storage of scientific data in repositories will be extended to model code. (4) We envision that online databases of model parameters will be developed and become an important resource for the development and improvement of AEMs. (5) We see a change from the way consultancy companies earn money with AEMs. Formerly, their business model was based on copyrights of model code. Now, we see a switch to a business model emerging that is based on expertise in applying open-source models. (6) We hope for a further integration of the development, analysis and application of AEMs in fundamental research and applied science. It will be a challenge to develop models of intermediate complexity that are simple enough to be thoroughly analysed, yet complex enough to be applicable in real-life cases. (7) We hope for a better coverage of the mutual interaction of ecosystem dynamics and biodiversity in AEMs. (8) We expect that the domain of model application (e.g. type of water, climate zone and stress factors) of AEMs will increase. In the end, this will allow for global analysis of aquatic ecosystems exposed to multiple stressors. (9) We envision the implementation of AEMs in apps that run in a local context (e.g. using GPS information) on a smartphone or tablet computer. (10) Finally, we expect that various forms of ensemble modelling will gain importance. Through a comparative evaluation of model performance, ensemble modelling can contribute to a ‘natural selection’ of AEMs within their niches that are defined by questions from society and science.
References
Abbaspour KC (2007) User manual for SWAT-CUP, SWAT calibration and uncertainty analysis programs. Swiss Federal Institute of Aquatic Science and Technology, Eawag, Duebendorf
Abbaspour KC, Yang J, Maximov I, Siber R, Bogner K, Mieleitner J, Zobrist J, Srinivasan R (2007) Modelling hydrology and water quality in the pre-alpine/alpine Thur watershed using SWAT. J Hydrol 333:413–430
Aguilera DR, Jourabchi P, Spiteri C, Regnier P (2005) A knowledge-based reactive transport approach for the simulation of biogeochemical dynamics in Earth systems. Geochem Geophys Geosyst 6:1525–2027
Appelo CAJ, Postma D (2005) Geochemistry, groundwater and pollution. CRC Press, Boca Raton
Appendini CM, Torres-Freyermuth A, Oropeza F, Salles P, López J, Mendoza ET (2013) Wave modeling performance in the Gulf of Mexico and Western Caribbean: wind reanalyses assessment. Appl Ocean Res 39:20–30
Argent RM, Perraud J-M, Rahman JM, Grayson RB, Podger GM (2009) A new approach to water quality modelling and environmental decision support systems. Environ Model Softw 24:809–818
Arhonditsis GB, Brett MT (2004) Evaluation of the current state of mechanistic aquatic biogeochemical modeling. Mar Ecol Prog Ser 271:13–26
Arnold JG, Srinivasan R, Muttiah RS, Williams JR (1998) Large area hydrologic modeling and assessment part I: model development. J Am Water Resour Assoc 34:73–89
Baretta JW, Ebenhöh W, Ruardij P (1995) The European regional seas ecosystem model, a complex marine ecosystem model. Neth J Sea Res 33:233–246
Baumert H, Peters H (2004) Turbulence closure, steady state, and collapse into waves. J Phys Oceanogr 34:505–512
Baumert HZ, Benndorf J, Bigalke K, Goldmann D, Nöhren I, Petzoldt T, Post J, Rolinski S (2005) Das hydrophysikalisch-ökologische Talsperren-und Seenmodell SALMO-HR. Modelldokumentation und Leitfaden für den Anwender, Dresden
Beck MB (1987) Water quality modeling: a review of the analysis of uncertainty. Water Resour Res 23:1393–1442
Benndorf J, Recknagel F (1982) Problems of application of the ecological model SALMO to lakes and reservoirs having various trophic states. Ecol Model 17:129–145
Benz J, Hoch R, Legović T (2001) ECOBAS—modelling and documentation. Ecol Model 138:3–15
Berger CJ, Wells SA (2008) Modeling the effects of macrophytes on hydrodynamics. J Environ Eng 134:778–788
Bergström S (1976) Development and application of a conceptual runoff model for Scandinavian catchments. SMHI, Norrköping
Beusen AHW, de Vink PJF, Petersen AC (2011) The dynamic simulation and visualization software MyM. Environ Model Softw 26:238–240
Beven K (2006) A manifesto for the equifinality thesis. J Hydrol 320:18–36
Billen G, Garnier J, Hanset P (1994) Modelling phytoplankton development in whole drainage networks: the RIVERSTRAHLER model applied to the Seine river system. Hydrobiologia 289:119–137
Blenckner T, Omstedt A, Rummukainen M (2002) A Swedish case study of contemporary and possible future consequences of climate change on lake function. Aquat Sci 64:171–184
Bolaños R, Tornfeldt Sørensen JV, Benetazzo A, Carniel S, Sclavo M (2014) Modelling ocean currents in the northern Adriatic Sea. Cont Shelf Res 87:54–72
Booij N, Holthuijsen LH, Ris RC (1996) The “SWAN” wave model for shallow water. Coastal Engineering Proceedings, Orlando
Borrett SR, Osidele OO (2007) Environ indicator sensitivity to flux uncertainty in a phosphorus model of Lake Sidney Lanier, USA. Ecol Model 200:371–383
Brinkman AG, Ens BJ, Kersting K, Baptist M, Vonk M, Drent J, Janssen-Stelder BM, Van der Tol MWM (2001) Modelling the impact of climate change on the Wadden Sea ecosystems. National Institute of Public Health and the Environment, Bilthoven
Brown LC, Barnwell TO (1987) The enhanced stream water quality models QUAL2E and QUAL2E-UNCAS: documentation and user manual. US Environmental Protection Agency, Office of Research and Development. Environmental Research Laboratory, Medford
Bruce LC, Cook PLM, Teakle I, Hipsey MR (2014) Hydrodynamic controls on oxygen dynamics in a riverine salt wedge estuary, the Yarra River estuary, Australia. Hydrol Earth Syst Sci 18:1397–1411
Bruggeman J, Bolding K (2014) A general framework for aquatic biogeochemical models. Environ Model Softw 61:249–265
Bruggeman J, Kooijman SALM (2007) A biodiversity-inspired approach to aquatic ecosystem modeling. Limnol Oceanogr 52:1533–1544
Brunner GW (2001) HEC-RAS river analysis system: user’s manual. US Army Corps of Engineers, Institute for Water Resources, Hydrologic Engineering Center, Davis
Bryhn AC, Håkanson L (2007) A comparison of predictive phosphorus load-concentration models for lakes. Ecosystems 10:1084–1099
Burchard H, Bolding K, Villarreal MR (2004) Three-dimensional modelling of estuarine turbidity maxima in a tidal estuary. Ocean Dyn 54:250–265
Callies U, Plüß A, Kappenberg J, Kapitza H (2011) Particle tracking in the vicinity of Helgoland, North Sea: a model comparison. Ocean Dyn 61:2121–2139
Chapra S, Pelletier G, Tao H (2008) QUAL2 K: a modeling framework for simulating river and stream water quality (version 2.11) documentation. Civil and Environmental Engineering Department, Tufts University, Medford
Chatfield C (1995) Model uncertainty, data mining and statistical-inference. J R Stat Soc Series A 158:419–466
Chatfield C (2006) Model uncertainty. Encyclopedia of Environmetrics. Wiley-Blackwell, New York
Chavan PV, Dennett KE (2008) Wetland simulation model for nitrogen, phosphorus, and sediments retention in constructed wetlands. Water Air Soil Pollut 187:109–118
Chen C, Beardsley RC, Cowles G (2006) An unstructured grid, finite-volume coastal ocean model (FVCOM) system. Oceanography 19:78
Cheng RT, Casulli V, Gartner JW (1993) Tidal, residual, intertidal mudflat (TRIM) model and its applications to San Francisco Bay, California. Estuar Coast Shelf Sci 36:235–280
Chow S-N, Mallet-Paret J, Van Vleck ES (1996) Dynamics of lattice differential equations. Int J Bifurcat Chaos 6:1605–1621
Christensen V, Pauly D (1992) ECOPATH II—a software for balancing steady-state ecosystem models and calculating network characteristics. Ecol Model 61:169–185
Cole TM, Wells SA (2003) CE-QUAL-W2: A two-dimensional, laterally averaged, hydrodynamic and water quality model, version 3.1. US Army Engineering and Research Development Center, Vicksburg
Comber SDW, Smith R, Daldorph P, Gardner MJ, Constantino C, Ellor B (2013) Development of a chemical source apportionment decision support framework for catchment management. Environ Sci Technol 47:9824–9832
Couture R-M, Shafei B, Van Cappellen P, Tessier A, Gobeil C (2010) Non-steady state modeling of arsenic diagenesis in lake sediments. Environ Sci Technol 44:197–203
Couture R-M, Tominaga K, Starrfelt J, Moe SJ, Kaste Ø, Wright RF (2014) Modelling phosphorus loading and algal blooms in a Nordic agricultural catchment-lake system under changing land-use and climate. Environ Sci Process Impacts 16:1588–1599
Cugier P, Le Hir P (2002) Development of a 3D hydrodynamic model for coastal ecosystem modelling. Application to the plume of the Seine River (France). Estuar Coast Shelf Sci 55:673–695
De Hoop BJ, Herman PMJ, Scholten H, Soetaert K (1992) Seneca 2.0: a simulation environment for ecological application: manual. Netherlands Institute of Ecology, Centre for Estuarine and Coastal Ecology, Yerseke
De Roos AM, Persson L (2001) Physiologically structured models–from versatile technique to ecological theory. Oikos 94:51–71
De Roos AM, Diekmann O, Metz JAJ (1992) Studying the dynamics of structured population models: a versatile technique and its application to Daphnia. Am Nat 139:123–147
DeAngelis DL, Mooij WM (2005) Individual-based modeling of ecological and evolutionary processes. Annu Rev Ecol Evol Syst 36:147–168
Deltares (2014) Processes library description, detailed description of processes. Deltares, Delft
Doherty J (2015) Calibration and uncertainty analysis for complex environmental models. Watermark Numerical Computing, Brisbane
Downing AS, van Nes EH, Balirwa JS, Beuving J, Bwathondi POJ, Chapman LJ, Cornelissen IJM, Cowx IG, Goudswaard KPC, Hecky RE, Janse JH, Janssen ABG, Kaufman L, Kishe-Machumu MA, Kolding J, Ligtvoet W, Mbabazi D, Medard M, Mkumbo OC, Mlaponi E, Munyaho AT, Nagelkerke LAJ, Ogutu-Ohwayo R, Ojwang WO, Peter HK, Schindler DE, Seehausen O, Sharpe D, Silsbe GM, Sitoki L, Tumwebaze R, Tweddle D, van de Wolfshaar KE, van Dijk H, van Donk E, van Rijssel JC, van Zwieten PAM, Wanink J, Witte F, Mooij WM (2014) Coupled human and natural system dynamics as key to the sustainability of Lake Victoria’s ecosystem services. Ecol Soc 19:31
Draper D (1995) Assessment and propagation of model uncertainty. J R Stat Soc Series B Methodol 57:45–97
Eilola K, Meier HEM, Almroth E (2009) On the dynamics of oxygen, phosphorus and cyanobacteria in the Baltic Sea; a model study. J Mar Syst 75:163–184
Elliott JA, Irish AE, Reynolds CS (2010) Modelling phytoplankton dynamics in fresh waters: affirmation of the PROTECH approach to simulation. Freshw Rev 3:75–96
Fang X, Stefan HG (1996a) Development and validation of the water quality model MINLAKE96 with winter data. St. Anthony Falls Laboratory, Minneapolis
Fang X, Stefan HG (1996b) Long-term lake water temperature and ice cover simulations/measurements. Cold Reg Sci Technol 24:289–304
Finlayson CM, D’Cruz R, Davidson N, Assessment ME (2005) Ecosystems and human well-being: wetlands and water: synthesis. World Resources Institute, Washington
Fulton EA, Smith ADM, Smith DC (2007) Alternative management strategies for southeast Australian commonwealth fisheries: stage 2: quantitative management strategy evaluation. Commonwealth Scientific and Industrial Research Organisation (CSIRO), Hobart
Fulton EA, Jones T, Boschetti F, Sporcic M, De la Mare W, Syme GJ, Dzidic P, Gorton R, Little LR, Dambacher G (2011) A multi-model approach to stakeholder engagement in complex environmental problems. In: Conference Proceedings
Gal G, Makler-Pick V, Shachar N (2014) Dealing with uncertainty in ecosystem model scenarios: application of the single-model ensemble approach. Environ Model Softw 61:360–370
Gao H, Wei H, Sun W, Zhai X (2000) Functions used in biological models and their influences on simulations. Indian J Mar Sci 29:230–237
Gelman A, Carlin JB, Stern HS, Rubin DB (2014) Bayesian data analysis. Taylor & Francis, Boca Raton
Giordani G, Austoni M, Zaldivar JM, Swaney DP, Viaroli P (2008) Modelling ecosystem functions and properties at different time and spatial scales in shallow coastal lagoons: an application of the LOICZ biogeochemical model. Estuar Coast Shelf Sci 77:264–277
Gobeyn S (2012) Integrated modelling of the multifunctional ecosystem of the Drava river, Dissertation, Ghent University, Faculty of Bioscience Engineering, Ghent, Belgium
Goudsmit GH, Burchard H, Peeters F, Wuest A (2002) Application of k-epsilon turbulence models to enclosed basins: the role of internal seiches. J Geophys Res Oceans 107:23-21–23-13
Greenwood DJ, Karpinets TV, Stone DA (2001) Dynamic model for the effects of soil P and fertilizer P on crop growth, P uptake and soil P in arable cropping: model description. Ann Bot 88:279–291
Gregersen J, Gijsbers P, Westen S (2007) OpenMI: open modelling interface. J Hydroinform 9:175–191
Griffies SM, Gnanadesikan AWDK, Dixon KW, Dunne JP, Gerdes R, Harrison MJ, Rosati A, Russell JL, Samuels BL, Spelman MJ, Winton N, Zhang R (2005) Formulation of an ocean model for global climate simulations. Ocean Sci 1:45–79
Grimm V, Revilla E, Berger U, Jeltsch F, Mooij WM, Railsback SF, Thulke H-H, Weiner J, Wiegand T, DeAngelis DL (2005) Pattern-oriented modeling of agent-based complex systems: lessons from ecology. Science 310:987–991
Grimm V, Berger U, Bastiansen F, Eliassen S, Ginot V, Giske J, Goss-Custard J, Grand T, Heinz SK, Huse G (2006) A standard protocol for describing individual-based and agent-based models. Ecol Model 198:115–126
Grimm V, Augusiak J, Focks A, Frank BM, Gabsi F, Johnston ASA, Liu C, Martin BT, Meli M, Radchuk V (2014) Towards better modelling and decision support: documenting model development, testing, and analysis using TRACE. Ecol Model 280:129–139
Gurkan Z, Zhang J, Jørgensen SE (2006) Development of a structurally dynamic model for forecasting the effects of restoration of Lake Fure, Denmark. Ecol Model 197:89–102
Haasnoot M, Van de Wolfshaar KE (2009) Combining a conceptual framework and a spatial analysis tool, HABITAT, to support the implementation of river basin management plans. Int J River Basin Manag 7:295–311
Hagedorn R, Doblas-Reyes FJ, Palmer TN (2005) The rationale behind the success of multi-model ensembles in seasonal forecasting—I. Basic concept. Tellus A 57:219–233
Håkanson L, Boulion VV (2003) A general dynamic model to predict biomass and production of phytoplankton in lakes. Ecol Model 165:285–301
Håkanson L, Eklund JM (2007) A dynamic mass balance model for phosphorus fluxes and concentrations in coastal areas. Ecol Res 22:296–320
Håkanson L, Gyllenhammar A (2005) Setting fish quotas based on holistic ecosystem modelling including environmental factors and foodweb interactions—a new approach. Aquat Ecol 39:325–351
Hamilton DP, Schladow SG (1997) Prediction of water quality in lakes and reservoirs. Part I—model description. Ecol Model 96:91–110
Hamilton SH, ElSawah S, Guillaume JHA, Jakeman AJ, Pierce SA (2015) Integrated assessment and modelling: overview and synthesis of salient dimensions. Environ Model Softw 64:215–229
Hammrich A, Schuster D (2014) Fundamentals on ecological modelling in coastal waters including an example from the river Elbe. Die Küste 81:107–118
Hamrick JM, Wu TS (1997) Computational design and optimization of the EFDC/HEM3D surface water hydrodynamic and eutrophication models. In: Delic G, Wheeler MF (eds) Next generation environment models and computational methods. SIAM, Philadephia, pp 143–156
Harrison JA, Frings PJ, Beusen AH, Conley DJ, McCrackin ML (2012) Global importance, patterns, and controls of dissolved silica retention in lakes and reservoirs. Global Biogeochem Cycles 26:1–12
Hawkins DM (2004) The problem of overfitting. J Chem Inf Comp Sci 44:1–12
Heinle A, Slawig T (2013) Internal dynamics of NPZD type ecosystem models. Ecol Model 254:33–42
Henze M, Gujer W, Mino T, Matsuo T, Wentzel MC, Marais GvR, Van Loosdrecht MCM (1999) Activated sludge model No. 2D, ASM2D. Water Sci Technol 39:165–182
Herrera L, Muñoz-Doyague MF, Nieto M (2010) Mobility of public researchers, scientific knowledge transfer, and the firm’s innovation process. J Bus Res 63:510–518
Herzfeld M, Waring JR (2014) Sparse hydrodynamic ocean code V4985 user manual. CSIRO Marine Research, Hobart
Hes EMA, Niu R, Van Dam AA (2014) A simulation model for nitrogen cycling in natural rooted papyrus wetlands in East Africa. Wetl Ecol Manag 22:157–176
Hipsey MR, Romero JR, Antenucci JP, Hamilton DP (2006) Computational aquatic ecosystem dynamics model: CAEDYM V3. Centre for Water Research, University of Western Australia, Perth
Hipsey MR, Bruce LC, Hamilton DP (2013) GLM general lake model. Model overview and user information. The University of Western Australia, Perth
Hipsey MR, Hamilton DP, Hanson PC, Carey CC, Coletti JZ, Read JS, Ibelings BW, Valesini F, Brookes JD (2015) Predicting the resilience and recovery of aquatic systems: A framework for model evolution within environmental observatories. Water Resour Res 51
Hossain MS, Bujang JS, Zakaria MH, Hashim M (2015) Assessment of landsat 7 scan line corrector-off data gap-filling methods for seagrass distribution mapping. Int J Remote Sens 36:1188–1215
Hrennikoff A (1941) Solution of problems of elasticity by the framework method. J Appl Mech 8:169–175
Huang GH (2005) Model identifiability. John Wiley & Sons, Chichester
Huang JC, Gao JF, Hormann G, Mooij WM (2012) Integrating three lake models into a phytoplankton prediction system for Lake Taihu (Taihu PPS) with Python. J Hydroinform 14:523–534
Huang C-W, Lin Y-P, Chiang L-C, Wang Y-C (2014) Using CV-GLUE procedure in analysis of wetland model predictive uncertainty. J Environ Manag 140:83–92
Ibelings BW, Vonk M, Los HF, Van der Molen DT, Mooij WM (2003) Fuzzy modeling of cyanobacterial surface waterblooms: validation with NOAA-AVHRR satellite images. Ecol Appl 13:1456–1472
IPCC (2014) Climate change 2014: synthesis report. Contribution of working groups I, II and III to the fifth assessment report of the intergovernmental panel on climate change. IPCC, Geneva, Switzerland
Jackson DA, Peres-Neto PR, Olden JD (2001) What controls who is where in freshwater fish communities? the roles of biotic, abiotic, and spatial factors. Can J Fish Aquat Sci 58:157–170
Jacob DJ (2007) Inverse Modeling Techniques. In: Visconti G, Carlo P, Brune W, Wahner A, Schoeberl M (eds) Observing systems for atmospheric composition. Springer, New York, pp 230–237
Jamieson SR, Lhomme J, Wright G, Gouldby B (2012) A highly efficient 2D flood model with sub-element topography. In: Proceedings of the ICE-Water Management, pp 581–595
Janse JH, De Senerpont Domis LN, Scheffer M, Lijklema L, Van Liere L, Klinge M, Mooij WM (2008) Critical phosphorus loading of different types of shallow lakes and the consequences for management estimated with the ecosystem model PCLake. Limnologica 38:203–219
Janse J, Scheffer M, Lijklema L, Van Liere L, Sloot J, Mooij W (2010) Estimating the critical phosphorus loading of shallow lakes with the ecosystem model PCLake: sensitivity, calibration and uncertainty. Ecol Model 221:654–665
Janse J, Alkemade R, Meijer J, Jeuken MHJL (2014) Aquatic biodiversity. PBL Netherlands Environmental Assessment Agency, The Hague
Janse JH, Kuiper JJ, Weijters MJ, Westerbeek EP, Jeuken MHJL, Bakkenes M, Alkemade R, Mooij WM, Verhoeven JTA (2015) GLOBIO-Aquatic, a global model of human impact on the biodiversity of inland aquatic ecosystems. Environ Sci Policy 48:99–114
Janssen ABG, Teurlincx S, An S, Janse JH, Paerl HW, Mooij WM (2014) Alternative stable states in large shallow lakes? J Great Lakes Res 40:813–826
Jeffrey SJ, Carter JO, Moodie KB, Beswick AR (2001) Using spatial interpolation to construct a comprehensive archive of Australian climate data. Environ Model Softw 16:309–330
Jensen JP, Pedersen AR, Jeppesen E, Søndergaard M (2006) An empirical model describing the seasonal dynamics of phosphorus in 16 shallow eutrophic lakes after external loading reduction. Limnol Oceanogr 51:791–800
Jöhnk KD, Umlauf L (2001) Modelling the metalimnetic oxygen minimum in a medium sized alpine lake. Ecol Model 136:67–80
Jöhnk KD, Huisman JEF, Sharples J, Sommeijer B, Visser PM, Stroom JM (2008) Summer heatwaves promote blooms of harmful cyanobacteria. Glob Change Biol 14:495–512
Jørgensen SE (2009) The application of structurally dynamic models in ecology and ecotoxicology. In: Devillers J (ed) Ecotoxicology Modeling. Springer, New York, pp 377–393
Jørgensen SE (2010) The role of ecological modelling in ecosystem restoration. In: Comín FA (ed) Ecological restoration: a global challenge. Cambridge University Press, Cambridge, pp 245–263
Kaergaard K, Fredsoe J (2013) Numerical modeling of shoreline undulations part 1: constant wave climate. Coast Eng 75:64–76
Keeler BL, Polasky S, Brauman KA, Johnson KA, Finlay JC, O’Neill A, Kovacs K, Dalzell B (2012) Linking water quality and well-being for improved assessment and valuation of ecosystem services. PNAS 109:18619–18624
King CE, Paulik GJ (1967) Dynamic models and the simulation of ecological systems. J Theor Biol 16:251–267
Kishi MJ, Kashiwai M, Ware DM, Megrey BA, Eslinger DL, Werner FE, Noguchi-Aita M, Azumaya T, Fujii M, Hashimoto S, Huang D, Iizumi H, Ishida Y, Kang S, Kantakov GA, Kim H-c, Komatsu K, Navrotsky VV, Smith SL, Tadokoro K, Tsuda A, Yamamura O, Yamanaka Y, Yokouchi K, Yoshie N, Zhang J, Zuenko YI, Zvalinsky VI (2007) NEMURO—a lower trophic level model for the North Pacific marine ecosystem. Ecol Model 202:12–25
Knorrenschild M, Lenz R, Forster E, Herderich C (1996) UFIS: a database of ecological models. Ecol Model 86:141–144
Knutti R, Masson D, Gettelman A (2013) Climate model genealogy: generation CMIP5 and how we got there. Geophys Res Lett 40:1194–1199
Kooijman SALM (1993) Dynamic energy budgets in biological systems: theory and applications in ecotoxicology. Cambridge University Press, Cambridge
Kooijman SALM, Lika K (2014) Comparative energetics of the 5 fish classes on the basis of dynamic energy budgets. J Sea Res 94:19–28
Kramer MR, Scholten H (2001) The smart approach to modelling and simulation. In: EUROSIM 2001, shaping future with simulation, the 4th international EUROSIM congress, in which is incorporated the 2nd conference on modelling and simulation in biology, medicine and biomedical engineering Delft, the Netherlands, TU Delft
Krzysztofowicz R (1999) Bayesian theory of probabilistic forecasting via deterministic hydrologic model. Water Resour Res 35:2739–2750
Lavington SH (1975) A history of Manchester computers. British Computer Society, Swindon
Lemmen C, Wirtz KW (2014) On the sensitivity of the simulated European Neolithic transition to climate extremes. J Archaeol Sci 51:65–72
Lemmen C, Gronenborn D, Wirtz KW (2011) A simulation of the Neolithic transition in Western Eurasia. J Archaeol Sci 38:3459–3470
Lenhart H-J, Mills DK, Baretta-Bekker H, Van Leeuwen SM, Van Der Molen J, Baretta JW, Blaas M, Desmit X, Kühn W, Lacroix G (2010) Predicting the consequences of nutrient reduction on the eutrophication status of the North Sea. J Mar Syst 81:148–170
Li Y, Gal G, Makler-Pick V, Waite A, Bruce L, Hipsey M (2014) Examination of the role of the microbial loop in regulating lake nutrient stoichiometry and phytoplankton dynamics. Biogeosciences 11:2939–2960
Los FJ (1991) Mathematical simulation of algae blooms by the model BLOOM II: report on investigations. Delft Hydraulics, Delft
Ludwig D, Walker B, Holling CS (1997) Sustainability, stability, and resilience. Conserv Ecol 1:7
Lunn DJ, Thomas A, Best N, Spiegelhalter D (2000) WinBUGS—a Bayesian modelling framework: concepts, structure, and extensibility. Stat Comput 10:325–337
Madec G (2012) NEMO ocean engine, version 3.4. Institut Pierre-Simon Laplace Note du Pole de Modelisation, Paris, p 357
McIntyre NR, Wheater HS (2004) A tool for risk-based management of surface water quality. Environ Model Softw 19:1131–1140
McIntyre NR, Wagener T, Wheater HS, Chapra SC (2003) Risk-based modelling of surface water quality: a case study of the Charles River, Massachusetts. J Hydrol 274:225–247
Megrey BA, Rose KA, Klumb RA, Hay DE, Werner FE, Eslinger DL, Smith SL (2007) A bioenergetics-based population dynamics model of Pacific herring (Clupea harengus pallasi) coupled to a lower trophic level nutrient–phytoplankton–zooplankton model: description, calibration, and sensitivity analysis. Ecol Model 202:144–164
Ménesguen A (1991) Elise, an interactive software for modelling complex aquatic ecosystems. Computer Modelling in Ocean Engineering. Taylor & Francis, Boca Raton, pp 87–94
Meyer KM, Mooij WM, Vos M, Hol WHG, Van Der Putten WH (2009) The power of simulating experiments. Ecol Model 220:2594–2597
Mieleitner J, Reichert P (2006) Analysis of the transferability of a biogeochemical lake model to lakes of different trophic state. Ecol Model 194:49–61
Minor E, McDonald R, Treml E, Urban D (2008) Uncertainty in spatially explicit population models. Biol Conserv 141:956–970
Mironov DV (2008) Parameterization of lakes in numerical weather prediction. Part 1: Description of a lake model. Deutscher Wetterdienst, Offenbach am Main
Moffat RJ (1988) Describing the uncertainties in experimental results. Exp Therm Fluid Sci 1:3–17
Molteni F, Buizza R, Palmer TN, Petroliagis T (1996) The ECMWF ensemble prediction system: methodology and validation. Q J R Meteor Soc 122:73–119
Mooij WM, Boersma M (1996) An object-oriented simulation framework for individual-based simulations (OSIRIS): Daphnia population dynamics as an example. Ecol Model 93:139–153
Mooij WM, De Senerpont Domis LN, Janse JH (2009) Linking species-and ecosystem-level impacts of climate change in lakes with a complex and a minimal model. Ecol Model 220:3011–3020
Mooij WM, Trolle D, Jeppesen E, Arhonditsis G, Belolipetsky PV, Chitamwebwa DBR, Degermendzhy AG, DeAngelis DL, De Senerpont Domis LN, Downing AS, Elliott JA, Fragoso CR, Gaedke U, Genova SN, Gulati RD, Håkanson L, Hamilton DP, Hipsey MR, t’Hoen J, Hülsmann S, Los FH, Makler-Pick V, Petzoldt T, Prokopkin IG, Rinke K, Schep SA, Tominaga K, Van Dam AA, Van Nes EH, Wells SA, Janse JH (2010) Challenges and opportunities for integrating lake ecosystem modelling approaches. Aquat Ecol 44:633–667
Mooij WM, Brederveld RJ, De Klein JJM, DeAngelis DL, Downing AS, Faber M, Gerla DJ, Hipsey MR, t’Hoen J, Janse JH, Janssen ABG, Jeuken M, Kooi BW, Lischke B, Petzoldt T, Postma L, Schep SA, Scholten H, Teurlincx S, Thiange C, Trolle D, Van Dam AA, Van Gerven LPA, Van Nes EH, Kuiper JJ (2014) Serving many at once: how a database approach can create unity in dynamical ecosystem modelling. Environ Model Softw 61:266–273
Morée AL, Beusen AHW, Bouwman AF, Willems WJ (2013) Exploring global nitrogen and phosphorus flows in urban wastes during the twentieth century. Global Biogeochem Cycles 27:836–846
Neumann T (2000) Towards a 3D-ecosystem model of the Baltic Sea. J Mar Syst 25:405–419
Neumann T, Fennel W, Kremp C (2002) Experimental simulations with an ecosystem model of the Baltic Sea: a nutrient load reduction experiment. Global Biogeochem Cycles 16:7-1–7-19
Neumann D, Callies U, Matthies M (2014) Marine litter ensemble transport simulations in the southern North Sea. Mar Pollut Bull 86:219–228
Nielsen A, Trolle D, Bjerring R, Søndergaard M, Olesen JE, Janse JH, Mooij WM, Jeppesen E (2014) Effects of climate and nutrient load on the water quality of shallow lakes assessed through ensemble runs by PCLake. Ecol Appl 24:1926–1944
Nishat B, Rahman SM (2009) Water resources modeling of the Ganges–Brahmaputra–Meghna river basins using satellite remote sensing data1. J Am Water Resour Assoc 45:1313–1327
Oke PR, Cahill ML, Griffin DA, Herzfeld M (2013) Constraining a regional ocean model with climatology and observations: application to the Hawaiian Islands. CAWCR Research Letters, Hobard
Oksanen J, Guillaume Blanchet F, Kindt R, Legendre P, Minchin PR, O’Hara RB, Simpson GL, Solymos P, Stevens MHH, Wagner H (2014) Vegan: community ecology package. Software package
Omlin M, Reichert P, Forster R (2001) Biogeochemical model of Lake Zürich: model equations and results. Ecol Model 141:77–103
Parise S, Cross R, Davenport TH, Team LY (2012) Strategies for preventing a knowledge-loss crisis. Image 47:31–38
Park RA, Clough JS, Wellman MC (2008) AQUATOX: modeling environmental fate and ecological effects in aquatic ecosystems. Ecol Model 213:1–15
Passenko J, Lessin G, Erichsen AC, Raudsepp U (2008) Validation of hydrostatic and nonhydrostatic versions of hydrodynamical model MIKE 3 applied for the Baltic Sea. Est J Eng 14:255–270
Pelletier GJ, Chapra SC, Tao H (2006) QUAL2Kw—a framework for modeling water quality in streams and rivers using a genetic algorithm for calibration. Environ Model Softw 21:419–425
Petzoldt T, Siemens K (2002) Nutzung eines ökologischen Simulationsmodells im Entscheidungsfindungsprozess: Anwendung des Modells SALMO auf die Talsperre Bautzen: Seentherapie: Grundlagen, Methoden, Perpektiven. Wasser und Boden 54:42–48
Postel S, Richter B (2003) Rivers for life: managing water for people and nature. Island Press, Washington
Press SJ (2012) Applied multivariate analysis: using Bayesian and frequentist methods of inference. St. James Press, Mineola
Press WH, Teukolsky SA, Vetterling WT, Flannery BP (1986) Numerical recipes: the art of scientific computing. Cambridge Univ. Press, Cambridge
Ramin M, Labencki T, Boyd D, Trolle D, Arhonditsis GB (2012) A Bayesian synthesis of predictions from different models for setting water quality criteria. Ecol Model 242:127–145
Rasmussen EK, Sehested Hansen I, Erichsen A, Muhlenstein D, Dørge J (2000) 3D model system for hydrodynamics, eutrophication and nutrient transport. Environ Stud 43:291–300
Recknagel F, Cetin L, Zhang B (2008) Process-based simulation library SALMO-OO for lake ecosystems. Part 1: object-oriented implementation and validation. Ecol Inform 3:170–180
Refsgaard JC, Henriksen HJ (2004) Modelling guidelines—terminology and guiding principles. Adv Water Resour 27:71–82
Refsgaard JC, Henriksen HJ, Harrar WG, Scholten H, Kassahun A (2005) Quality assurance in model based water management—review of existing practice and outline of new approaches. Environ Model Softw 20:1201–1215
Refsgaard C, Storm B, Clausen T (2010) Système Hydrologique Europeén (SHE): review and perspectives after 30 years development in distributed physically-based hydrological modelling. Hydrol Res 41:355–377
Reichert P (1994) Aquasim—a tool for simulation and data-analysis of aquatic systems. Water Sci Technol 30:21–30
Reynolds CS, Irish AE, Elliott JA (2001) The ecological basis for simulating phytoplankton responses to environmental change (PROTECH). Ecol Model 140:271–291
Riley MJ, Stefan HG (1988) MINLAKE: a dynamic lake water quality simulation model. Ecol Model 43:155–182
Robson BJ (2014a) State of the art in modelling of phosphorus in aquatic systems: review, criticisms and commentary. Environ Model Softw 61:339–359
Robson BJ (2014b) When do aquatic systems models provide useful predictions, what is changing, and what is next? Environ Model Softw 61:287–296
Robson BJ, Hamilton DP (2004) Three-dimensional modelling of a Microcystis bloom event in the Swan River estuary, Western Australia. Ecol Model 174:203–222
Robson BJ, Bukaveckas PA, Hamilton DP (2008) Modelling and mass balance assessments of nutrient retention in a seasonally-flowing estuary (Swan River Estuary, Western Australia). Estuar Coast Shelf Sci 76:282–292
Sachse R, Petzoldt T, Blumstock M, Moreira S, Pätzig M, Rücker J, Janse JH, Mooij WM, Hilt S (2014) Extending one-dimensional models for deep lakes to simulate the impact of submerged macrophytes on water quality. Environ Model Softw 61:410–423
Saloranta TM, Andersen T (2007) MyLake—a multi-year lake simulation model code suitable for uncertainty and sensitivity analysis simulations. Ecol Model 207:45–60
Scheffer M, Carpenter S, Foley JA, Folke C, Walker B (2001) Catastrophic shifts in ecosystems. Nature 413:591–596
Scheffer M, Bascompte J, Brock WA, Brovkin V, Carpenter SR, Dakos V, Held H, van Nes EH, Rietkerk M, Sugihara G (2009) Early-warning signals for critical transitions. Nature 461:53–59
Scherlis B (1996) Beyond coding. ACM Comput Surv 28:201
Scholten H, Kassahun A, Refsgaard JC, Kargas T, Gavardinas C, Beulens AJM (2007) A methodology to support multidisciplinary model-based water management. Environ Model Softw 22:743–759
Shchepetkin AF, McWilliams JC (2005) The regional oceanic modeling system (ROMS): a split-explicit, free-surface, topography-following-coordinate oceanic model. Ocean Model 9:347–404
Silva CP, Marti CL, Imberger J (2014) Mitigating the effects of high biomass algal blooms on the drinking water intakes of the city of Buenos Aires, Argentina. J Hydraul Res 52:705–719
Skerratt J, Wild-Allen K, Rizwi F, Whitehead J, Coughanowr C (2013) Use of a high resolution 3D fully coupled hydrodynamic, sediment and biogeochemical model to understand estuarine nutrient dynamics under various water quality scenarios. Ocean Coast Manag 83:52–66
Soetaert K, Petzoldt T (2010) Inverse modelling, sensitivity and Monte Carlo analysis in R using package FME. J Stat Softw 33:1–28
Soetaert K, Herman PMJ, Middelburg JJ (1996) A model of early diagenetic processes from the shelf to abyssal depths. Geochim Cosmochim Acta 60:1019–1040
Soetaert K, deClippele V, Herman P (2002) FEMME, a flexible environment for mathematically modelling the environment. Ecol Model 151:177–193
Soetaert KER, Petzoldt T, Setzer RW (2010) Solving differential equations in R: package deSolve. J Stat Softw 33:1–25
Sørensen T (1948) A method of establishing groups of equal amplitude in plant sociology based on similarity of species and its application to analyses of the vegetation on Danish commons. Biol Skrif 5:1–34
Stepanenko VM, Machul’skaya EE, Glagolev MV, Lykossov VN (2011) Numerical modeling of methane emissions from lakes in the permafrost zone. Izv Atmos Ocean Phys 47:252–264
Stepanenko VM, Martynov A, Jöhnk KD, Subin ZM, Perroud M, Fang X, Beyrich F, Mironov D, Goyette S (2013) A one-dimensional model intercomparison study of thermal regime of a shallow, turbid midlatitude lake. Geosci Model Dev 6:1337–1352
Stepanenko V, Jöhnk KD, Machulskaya E, Perroud M, Subin Z, Nordbo A, Mammarella I, Mironov D (2014) Simulation of surface energy fluxes and stratification of a small boreal lake by a set of one-dimensional models. Tellus A 66
Sutanudjaja EH, Van Beek LPH, De Jong SM, Van Geer FC, Bierkens MFP (2014) Calibrating a large-extent high-resolution coupled groundwater-land surface model using soil moisture and discharge data. Water Resour Res 50:687–705
Tarantola A (2005) Inverse problem theory and methods for model parameter estimation. SIAM, Philadelphia
Thébault J-M (2004) Simulation of a mesotrophic reservoir (Lake Pareloup) over a long period (1983–1998) using ASTER2000 biological model. Water Res 38:393–403
Thiery WIM, Stepanenko VM, Fang X, Jöhnk KD, Li Z, Martynov A, Perroud M, Subin ZM, Darchambeau F, Mironov D, Van Lipzig NPM (2014) LakeMIP Kivu: evaluating the representation of a large, deep tropical lake by a set of one-dimensional lake models. Tellus A 66
Tian RC (2006) Toward standard parameterizations in marine biological modeling. Ecol Model 193:363–386
Trolle D, Hamilton DP, Hipsey MR, Bolding K, Bruggeman J, Mooij WM, Janse JH, Nielsen A, Jeppesen E, Elliott JA, Makler-Pick V, Petzoldt T, Rinke K, Flindt MR, Arhonditsis GB, Gal G, Bjerring R, Tominaga K, t’Hoen J, Downing AS, Marques DM, Fragoso CRJ, Søndergaard M, Hanson PC (2012) A community-based framework for aquatic ecosystem models. Hydrobiologia 683:25–34
Trolle D, Elliott JA, Mooij WM, Janse JH, Bolding K, Hamilton DP, Jeppesen E (2014) Advancing projections of phytoplankton responses to climate change through ensemble modelling. Environ Model Softw 61:371–379
Valverde S, Solé RV (2015) Punctuated equilibrium in the large-scale evolution of programming languages. J R Soc Interface 12:20150249
Van Beek LPH, Wada Y, Bierkens MFP (2011) Global monthly water stress: 1. Water balance and water availability. Water Resour Res 47
Van Dam AA, Dardona A, Kelderman P, Kansiime F (2007) A simulation model for nitrogen retention in a papyrus wetland near Lake Victoria, Uganda (East Africa). Wetl Ecol Manag 15:469–480
Van Der Heide T, Van Nes EH, Geerling GW, Smolders AJP, Bouma TJ, Van Katwijk MM (2007) Positive feedbacks in seagrass ecosystems: implications for success in conservation and restoration. Ecosystems 10:1311–1322
Van Gerven LPA, Brederveld RJ, De Klein JJM, DeAngelis DL, Downing AS, Faber M, Gerla DJ, ’t Hoen J, Janse JH, Janssen ABG, Jeuken M, Kooi BW, Kuiper JJ, Lischke B, Liu S, Petzoldt T, Schep SA, Teurlincx S, Thiange C, Trolle D, Van Nes EH, Mooij WM (2015) Advantages of concurrent use of multiple software frameworks in water quality modelling using a database approach. Fund Appl Limnol 186:5–20
Van Liere L, Janse JH, Arts GHP (2007) Setting critical nutrient values for ditches using the eutrophication model PCDitch. Aquat Ecol 41:443–449
Van Nes EH, Lammens EHRR, Scheffer M (2002a) PISCATOR, an individual-based model to analyze the dynamics of lake fish communities. Ecol Model 152:261–278
Van Nes EH, Scheffer M, Van den Berg MS, Coops H (2002b) Dominance of charophytes in eutrophic shallow lakes—when should we expect it to be an alternative stable state? Aquat Bot 72:275–296
Van Oevelen D, Van Den Meersche K, Meysman FJR, Soetaert K, Middelburg JJ, Vézina AF (2010) Quantifying food web flows using linear inverse models. Ecosystems 13:32–45
Vézina AF, Platt T (1988) Food web dynamics in the ocean. 1. Best-estimates of flow networks using inverse methods. Mar Ecol Prog Ser 42:269–287
Vollenweider RA (1975) Input–output models. Schweiz Z Hydrol 37:53–84
Wade AJ, Durand P, Beaujouan V, Wessel WW, Raat KJ, Whitehead PG, Butterfield D, Rankinen K, Lepisto A (2002) A nitrogen model for European catchments: INCA, new model structure and equations. Hydrol Earth Syst Sci 6:559–582
Weijerman M, Fulton EA, Janssen ABG, Kuiper JJ, Leemans R, Robson BJ (2015) How models can support ecosystem-based management of coral reefs. Prog Oceanogr. doi:10.1016/j.pocean.2014.12.017
Wijesekara GN, Farjad B, Gupta A, Qiao Y, Delaney P, Marceau DJ (2014) A comprehensive land-use/hydrological modeling system for scenario simulations in the Elbow River watershed, Alberta, Canada. Environ Manag 53:357–381
Wild-Allen K, Herzfeld M, Thompson PA, Rosebrock U, Parslow J, Volkman JK (2010) Applied coastal biogeochemical modelling to quantify the environmental impact of fish farm nutrients and inform managers. J Mar Syst 81:134–147
Wilks DS (2002) Smoothing forecast ensembles with fitted probability distributions. Q J R Meteor Soc 128:2821–2836
Wu TS, Hamrick JM, McCutcheon SC, Ambrose RB (1997) Benchmarking the EFDC/HEM3D surface water hydrodynamic and eutrophication models. In: Delic G, Wheeler MF (eds) Next generation environment models and computational methods. SIAM, Philadelphia, pp 157–161
Xiao Y, Friedrichs MAM (2014) Using biogeochemical data assimilation to assess the relative skill of multiple ecosystem models: effects of increasing the complexity of the planktonic food web. Biogeosciences 11:481–520
Xu F-L, Tao S, Dawson R, Li P-g, Cao J (2001) Lake ecosystem health assessment: indicators and methods. Water Res 35:3157–3167
Xu F, Yang ZF, Chen B, Zhao YW (2013) Impact of submerged plants on ecosystem health of the plant-dominated Baiyangdian Lake, China. Ecol Model 252:167–175
Yakushev E, Protsenko EA, Bruggeman J (2014) Bottom RedOx Model (BROM) general description and application for seasonal anoxia simulations. Norwegian Institute for water Research (NIVA), Oslo
Acknowledgments
This paper is the result of discussions at the 3rd AEMON workshop held on 18–21 February 2015, in Driebergen, the Netherlands. We are grateful of our four reviewers who provided us with very constructive comments and suggestions all from a different angle. ABGJ and WMM conceived the idea behind the paper, organized the workshop, contributed data, performed analysis, wrote a first version of the text and edited the manuscript. JJK and LPAVG participated in the workshop, contributed data and wrote sections of the text. BJR and ST participated in the workshop, contributed data, performed analysis and contributed to the text. All others except AD, MH and MW participated in the workshop, contributed data and contributed to the text. AD, MH and MW contributed data and contributed to the text. We thank Bob Brederveld, Jeroen De Klein, Valesca Harezlak, Michel Jeuken, Lilith Kramer, Egbert Van Nes and Michael Weber for their participation in the workshop and contribution to the data and Bas Van Der Wal for his contribution to the workshop. We are grateful to Piet Spaak, Editor-in-Chief of Aquatic Ecology, for inviting us to submit this paper to the journal. Collecting data and writing a manuscript with 39 authors was greatly enhanced by using Google Sheets and Docs. ABGJ is funded by the Netherlands Organisation for Scientific Research (NWO) Project No. 842.00.009. JJK and LPAVG are funded by the Netherlands Foundation for Applied Water Research (STOWA) Project No. 443237 and the Netherlands Environmental Assessment Agency (PBL). ST is funded by the Netherlands Organisation for Scientific Research (NWO) Project No. 841.11.009. TP and DK are funded by BMBF Grant No. 033W015EN (Nitrolimit 2). RS received funding from the 7th EU Framework Programme under grant agreement number 308393 (OPERAs). CL is funded by BMBF Grant No. 03F0667A (MOSSCO). DT, KB, FH and EJ were funded by CLEAR (a Villum Kann Rasmussen Centre of Excellence project) and MARS project (Managing Aquatic ecosystems and water Resources under multiple Stress) funded under the 7th EU Framework Programme, Theme 6 (Environment including Climate Change), Contract No.: 603378 (http://www.marsproject.eu). RMC is funded by Research Council of Norway (RCN) Project No. 244558/E50 (Lakes in Transition). This is publication 5936 of the Netherlands Institute of Ecology (NIOO-KNAW).
Author information
Authors and Affiliations
Corresponding author
Additional information
Handling Editor: Piet Spaak.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Janssen, A.B.G., Arhonditsis, G.B., Beusen, A. et al. Exploring, exploiting and evolving diversity of aquatic ecosystem models: a community perspective. Aquat Ecol 49, 513–548 (2015). https://doi.org/10.1007/s10452-015-9544-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10452-015-9544-1