Introduction

In a stratified reservoir, wind-induced currents and the structure of the thermocline mainly control the vertical distribution of heat, dissolved substances, and nutrients in the water column (Belolipetskii et al. 2002; Bonnet et al. 2000; Elci 2008; Holloway 1984; Gargett 1991; Patterson 1991; Belyaev 1992; MacIntyre 1993). Stratification in summer acts as a barrier restraining the mixing of the water column. The warm water in the epilimnion is unable to mix with the cold, dense water of the hypolimnion. As a result of the incomplete mixing of the water column and lack of light for the photosynthesis at the hypolimnion, the water column can become anoxic. It is shown (Imberger and Patterson 1990) that when stratification is established in small to medium lakes, transverse and longitudinal heterogeneities are negligible compared to those in the vertical direction. The need to manage the quality of the water stored in lakes and reservoirs has led to the continuing development of numerical models capable of predicting the dynamics of vertical stratification and mixing. Many such models have been constructed. To mention a few: SEEMOD (Zamboni et al. 1992), Minlake (Riley and Stefan 1987), LIMNMOD (Karagounis and Zamboni 1993), DYRESM (Imberger and Patterson 1981), PROBE (Svensson 1998; Elo et al. 1998), GOTM (Burchard et al. 1999), and others (Belolipetskii et al. 2002; Bonnet et al. 2000).

Meromixis is a condition of persistent chemical stratification with incomplete mixing over the course of a year; it usually results in anoxia and the accumulation of nutrients in the monimolimnion and reduced vertical mixing. Numerous saline lakes worldwide are known to be meromictic (Hammer 1986). The water in the upper mixed layer (the epilimnion) is characterized by strong turbulence, which usually leads to relatively constant temperature distribution. The mixed layer is separated from the deeper hypolimnetic waters by a region of increasing density. One of the main factors that determine the mixing status of Lake Shira is salinity. It is therefore important to note that from 1980 the average salinity has decreased approximately from 20 to 13‰ (Kalacheva et al. 2002). A gradient of salinity is formed in spring because of introducing fresh water due to melting of ice and snow. Later, this salinity gradient prevents the lake from being mixed by wind. In summer, the water is stratified because of both the temperature and the salinity gradients. In autumn, only the salinity gradient maintains the stratification. Therefore, if the water of Lake Shira were fresh, it would be mixed in autumn. Using the models documented in this paper, we have calculated the minimum value of salinity necessary to prevent Lake Shira from mixing by wind.

Earlier studies investigated the mathematical modeling of hydro-thermodynamic processes in Lake Shira (Belolipetskii et al. 2002). In this earlier study, the vertical distribution of salinity was not calculated and, mainly, summer stratification was investigated. The present study deals with the mathematical simulation of the hydrophysical processes in Lake Shira, including the lake thermal structure, wind and wind-induced currents, and the conditions for steady stratification in autumn have been investigated. Therefore, much attention has been given to the vertical salinity gradients.

Summarizing, there are two aims of this study. The first one is to develop, parameterize and compare a one-dimensional model and a two-dimensional model for Lake Shira, which can serve as the basis for an ecological water-quality model of the lake (Prokopkin et al. 2010). The second aim is to analyze, using both models, at which level of salinity meromixis is predicted to disappear.

Methods

Lake Shira

The lake is located in Siberia (54°29′N and 90°14′E) and is an inland lake, without islands. Lake Shira features unique therapeutic properties, which are largely determined by the specific chemical composition of the water (Lobova et al. 2002). The Son River flows into the lake from the south. As the inflowing volume of water is very small, the river only impacts the lake near its mouth. The lake has an oval shape and is 9.4 km long and about 5 km wide. The surface area of the lake is 34.7 km2, the maximal depth is 24 m, and the average depth of the middle part is 21 m. The underground water input constitutes about 9% of the total water input of the lake. The water temperatures are much higher in the epilimnion (15–20°C) than in the hypolimnion (2–3°C) in summer. The salinity is higher in the hypolimnion. The summer stratification is very stable because of the temperature stratification and the high salinity of the lake. The distinct density stratification is defined by both the decrease of the water temperature and increase of salinity with the lake depth. So mixing between the top and bottom layers is very low—this fact was repeatedly proved by measurements and was confirmed during simulations.

Equations for one-dimensional model

The formation of the temperature regime in a closed stratified water reservoir is dependent on the wind-induced flow and heat exchange with the atmosphere. The budget equation for temperature can be formulated as

$$ {\frac{\partial T}{\partial t}} = {\frac{\partial }{\partial z}}\left( {K_{T} {\frac{\partial T}{\partial z}}} \right) + \alpha \beta {\frac{{F_{I} {\text{e}}^{ - \beta z} }}{{c_{p} \rho_{0} }}}, $$
(1)

with the boundary conditions

$$ \begin{aligned} K_{T} {\frac{\partial T}{\partial z}} = & - {\frac{{F_{n} }}{{c_{p} \rho_{0} }}}\quad {\text{for}}\,z = 0, \\ K_{T} {\frac{\partial T}{\partial z}} = & 0\quad {\text{for}}\,z = H. \\ \end{aligned} $$
(2)

Here T is the water temperature, K T (z) is the coefficient of vertical turbulent exchange, F n is the complete heat flow through the free water surface, F I is incoming short-wave radiation, β is the coefficient of radiation absorption, α is the parameter defining the part of short-wave radiation penetrating to depth (0 ≤ α ≤ 1), c p is the specific heat of water, ρ 0 is the typical value of water density, H is the reservoir depth, z is the vertical coordinate.

There are various methods of calculation of short-wave radiation. In some of papers, penetrating radiation is taken into account only in the boundary conditions: α = 0 (see, for example Odrova 1979), in the other ones—in the right part of Eq. 1: α = 1 (see, for example Henderson-Sellers 1987).

The problem for the vertical distribution of salinity is posed similarly:

$$ \begin{array}{*{20}c} {{\frac{\partial S}{\partial t}} = {\frac{\partial }{\partial z}}\left( {K_{S} {\frac{\partial S}{\partial z}}} \right),} \\ \begin{gathered} K_{S} {\frac{\partial S}{\partial z}}\left| {_{z = 0} = 0,} \right. \hfill \\ K_{S} {\frac{\partial S}{\partial z}}\left| {_{z = H} = 0.} \right. \hfill \\ \end{gathered} \\ \end{array} $$
(3)

Here S is the water salinity, K S (z) is the coefficient of vertical turbulence for the salinity. Also, it is necessary to give the initial distributions of the temperature and salinity T(0, z) = T 0(z), S(0, z) = S 0(z).

Equations for two-dimensional model

The mathematical model of the wind-forced currents in the stratified reservoirs is based on the equations for turbulent currents of a non-uniform liquid in the Boussinesq and hydrostatic approaches (Belolipetskii and Belolipetsky 2006; Filatov 1983; Sarkisyan 1991):

$$ {\frac{{{\text{d}}U}}{{{\text{d}}t}}} = K_{x} {\frac{{\partial^{2} U}}{{\partial x^{2} }}} + {\frac{\partial }{\partial z}}K_{z} {\frac{\partial U}{\partial z}} + g{\frac{\partial \varsigma }{\partial x}} - g\int\limits_{0}^{z} {{\frac{{\partial \rho_{1} }}{\partial x}}{\text{d}}z} , $$
(4)
$$ {\frac{\partial }{\partial x}}\int\limits_{0}^{H} {U{\text{d}}z} = 0, $$
(5)
$$ {\frac{\partial U}{\partial x}} + {\frac{\partial W}{\partial z}} = 0, $$
(6)
$$ {\frac{{{\text{d}}T}}{{{\text{d}}t}}} = {\frac{\partial }{\partial x}}K_{xT} {\frac{\partial T}{\partial x}} + {\frac{\partial }{\partial y}}K_{yT} {\frac{\partial T}{\partial y}} + {\frac{\partial }{\partial z}}K_{zT} {\frac{\partial T}{\partial z}} + \alpha \beta {\frac{{F_{I} {\text{e}}^{ - \beta z} }}{{c_{p} \rho_{0} }}}, $$
(7)
$$ {\frac{{{\text{d}}S}}{{{\text{d}}t}}} = {\frac{\partial }{\partial x}}K_{xS} {\frac{\partial S}{\partial x}} + {\frac{\partial }{\partial y}}K_{yS} {\frac{\partial S}{\partial y}} + {\frac{\partial }{\partial z}}K_{zS} {\frac{\partial S}{\partial z}}, $$
(8)

Here U, W are the velocities of a current of water in the directions Ox, Oz, respectively. Axis Ox is directed left, axis Oz—down, t denotes time, ρ = ρ 0(1 + ρ 1(T, S)), where ρ is the density of the water, ρ 0 is the average value of the density of the water, g is the standard acceleration due to gravity, T is the temperature of water, S is the salinity of water, K x , K z , K xT , K zT , K xS , K zS —denote the factors of a turbulent exchange, \( {\frac{\text{d}}{{{\text{d}}t}}} = {\frac{\partial }{\partial t}} + U{\frac{\partial }{\partial x}} + W{\frac{\partial }{\partial z}} \) is the full derivative, FI is incoming short-wave radiation, β is the coefficient of radiation absorption, α is the parameter defining the part of short-wave radiation penetrating to depth (0 ≤ α ≤ 1), c p is the specific heat of the water. Equations 4–8 are supplemented with initial and boundary conditions.

The initial conditions:

$$ U = 0,\quad W = 0,\quad T = T_{0} (z),\quad S = S_{0} (z). $$
(9)

The boundary conditions:On the water surface, z = ς(t, x, y):

$$ K_{z} {\frac{\partial U}{\partial z}} = - {\frac{{\tau_{x} }}{{\rho_{0} }}},\quad K_{zT} {\frac{\partial T}{\partial z}} = - {\frac{{F_{n} }}{{c_{p} \rho_{0} }}},\quad K_{zS} {\frac{\partial S}{\partial z}} = 0, $$
(10)
$$ W = {\frac{\partial \varsigma }{\partial t}} + U{\frac{\partial \varsigma }{\partial x}} + V{\frac{\partial \varsigma }{\partial y}}, $$
(11)

On the bottom surface:

$$ U = 0,V = 0,{\frac{\partial T}{\partial n}} = 0,{\frac{\partial S}{\partial n}} = 0. $$
(12)

Here τ x , τ y denote the wind stress, F n is the full stream of heat through the water surface, n is the external normal for the bottom surface.

The factors of horizontal turbulent exchange K x , K xT , K xS are constants.

Numerical algorithm for one-dimensional model

In the one-dimensional case, we used a non-uniform grid on the spatial variables and a uniform grid on time: z j+1 = z j  + Δz j , t n+1 = t n  + Δt, T n j  = T(t n , z j ). Problems (1)–(3) are calculated by the implicit central finite-difference scheme:

$$ {\frac{{T_{j}^{n + 1} - T_{j}^{n} }}{\Updelta t}} = {\frac{1}{{(z_{j + 1} - z_{j - 1} )/2}}}\left( {{\frac{{K_{Tj + 1} + K_{Tj} }}{2}}{\frac{{T_{j + 1}^{n + 1} - T_{j}^{n + 1} }}{{z_{j + 1} - z_{j} }}} - {\frac{{K_{Tj} + K_{Tj - 1} }}{2}}{\frac{{T_{j}^{n + 1} - T_{j - 1}^{n + 1} }}{{z_{j} - z_{j - 1} }}}} \right) + F_{j}^{n} . $$
(13)

On the water surface:

$$ {\frac{{T_{0}^{n + 1} - T_{0}^{n} }}{\Updelta t}} = {\frac{1}{{(z_{1} - z_{0} )/2}}}\left( {{\frac{{K_{T1} + K_{T0} }}{2}}\;{\frac{{T_{1}^{n + 1} - T_{0}^{n + 1} }}{{z_{1} - z_{0} }}} - \beta_{1} } \right) + F_{0}^{n} , $$
(14)

On the bottom:

$$ {\frac{{T_{H}^{n + 1} - T_{H}^{n} }}{\Updelta t}} = {\frac{1}{{(z_{H} - z_{H - 1} )/2}}}\left( {\beta_{2} - {\frac{{K_{TH} + K_{TH - 1} }}{2}}\;{\frac{{T_{H}^{n + 1} - T_{H - 1}^{n + 1} }}{{z_{H} - z_{H - 1} }}}} \right). $$
(15)

The system of the linear algebraic equations obtained is solved by the sweep method. This algorithm is used for solving differential equations of the water-quality model, too (Prokopkin et al. 2010).

Numerical algorithm for two-dimensional model

In the two-dimensional case, we solve the model by the splitting method (Belotserkovskii 1984; Fletcher 1988), which was realized in (Belolipetsky 2005; Belolipetskii and Belolipetsky 2006). The numerical algorithm consists of several stages:

Stage 1:

$$ {\frac{{\tilde{U} - U^{n} }}{\Updelta t}} + U^{n} {\frac{{\partial U^{n} }}{\partial x}} + W^{n} {\frac{{\partial U^{n} }}{\partial z}} = 0. $$
(16)

Stage 2:

$$ {\frac{{U^{ \bullet } - \tilde{U}}}{\Updelta t}} = K_{x} {\frac{{\partial^{2} U^{ \bullet } }}{{\partial x^{2} }}} + {\frac{\partial }{\partial z}}K_{z} {\frac{{\partial U^{ \bullet } }}{\partial z}} - F_{1}^{n} ,\quad F_{1}^{n} = g\int\limits_{0}^{z} {{\frac{{\partial \rho^{n}_{1} }}{\partial x}}{\text{d}}z} , $$
(17)

Stage 3:

$$ {\frac{\partial \varsigma }{\partial x}} = - {\frac{1}{gH\Updelta t}}\int\limits_{0}^{H} {U^{ \bullet } {\text{d}}z} , $$
(18)

Stage 4:

$$ U^{n + 1} = U^{ \bullet } + g\Updelta {\kern 1pt} t{\frac{{\partial {\kern 1pt} \varsigma }}{\partial \,x}},\quad $$
(19)
$$ W^{n + 1} = - \int\limits_{0}^{z} {{\frac{{\partial U^{ \bullet } }}{\partial x}}{\text{d}}z} + \frac{z}{H}\int\limits_{0}^{H} {{\frac{{\partial U^{ \bullet } }}{\partial x}}{\text{d}}z} . $$
(20)

Stage 5:

$$ {\frac{{\tilde{T} - T^{n} }}{\Updelta t}} + U^{n} {\frac{{\partial T^{n} }}{\partial x}} + W^{n} {\frac{{\partial T^{n} }}{\partial z}} = 0, $$
(21)
$$ {\frac{{\tilde{S} - S^{n} }}{\Updelta t}} + U^{n} {\frac{{\partial S^{n} }}{\partial x}} + W^{n} {\frac{{\partial S^{n} }}{\partial z}} = 0. $$
(22)

Stage 6:

$$ {\frac{{T^{n + 1} - \tilde{T}}}{\Updelta t}} = K_{xT} {\frac{{\partial^{2} T^{n + 1} }}{{\partial x^{2} }}} + {\frac{\partial }{\partial z}}\left( {K_{zT} {\frac{{\partial T^{n + 1} }}{\partial z}}} \right), $$
(23)
$$ {\frac{{S^{n + 1} - \tilde{S}}}{\Updelta t}} = K_{xS} {\frac{{\partial^{2} S^{n + 1} }}{{\partial x^{2} }}} + {\frac{\partial }{\partial z}}\left( {K_{zS} {\frac{{\partial S^{n + 1} }}{\partial z}}} \right) $$
(24)

We also use boundary conditions (10)–(12). After obtaining the values T n+1, S n+1, we define the density of the water ρ n+1 using Eq. 28. Here ∆t is a time step.

Parameterization of vertical turbulent mixing

The turbulence exerts primary control over the heat and mass transfer. For the parameterization of the vertical turbulence mixing in the one-dimensional case, a formula based on the Prandtl–Obuchov formula and approximated solution for the wind-forced flow are applied (Belolipetsky and Genova 1998):

$$ K_{z} = \left\{ \begin{gathered} (0.05h_{1} )^{2} \sqrt B + K_{\min } \quad {\text{for}}\,\,B \ge 0, \hfill \\ K_{\min } \quad {\text{for}}\,\,B < 0, \hfill \\ \end{gathered} \right. $$
(25)

here \( \mathop {B = \left( {{\frac{\tau }{{\rho_{0} K_{0} }}}} \right)}\nolimits^{2} {\text{e}}^{ - 2\alpha z} - {\frac{g}{{\rho_{0} }}}\left( {{\frac{\partial \rho }{\partial z}}} \right),\tau = \sqrt {\tau_{x}^{2} + \tau_{y}^{2} } \) is the wind stress, \( K_{ \min } = 0.02\,{\frac{\text{sm}}{{{\text{s}}^{2} }}} \) is the minimal value of vertical turbulent exchange coefficient, \( K_{0} = {\frac{{(0.05\pi )^{2} \tau }}{{2\rho_{0} f}}}, \) \( \alpha = \sqrt {{\frac{f}{{2K_{0} }}}} , \) \( h_{1} = \pi \sqrt {{\frac{{K_{0} }}{2f}}} , \) f is the Coriolis parameter.

The factor of the vertical turbulent exchange in the two-dimensional case is calculated by the Prandtle–Obuhov formula (Belolipetskii et al. 2002; Belolipetskii and Belolipetsky 2006; Marchuk et al. 1980):

$$ K_{z} = \left\{ \begin{gathered} (0.05h)^{2} \sqrt B + K_{\min } \quad {\text{where}}\,B \ge 0, \hfill \\ K_{\min } \quad {\text{where}}\,B < 0, \hfill \\ \end{gathered} \right. $$
(26)

Here \( B = \left( {{\frac{\partial U}{\partial z}}} \right)^{2} + \left( {{\frac{\partial V}{\partial z}}} \right)^{2} - {\frac{g}{{\rho_{0} }}} \cdot {\frac{\partial \rho }{\partial z}} \), h is the depth of a quasi-homogeneous layer, determined by the first point from the surface in which the condition \( (0.05z_{k} )^{2} \sqrt {B|_{{z = z_{k} }} } \le K_{\min } \) is satisfied, K min is the minimal value of the vertical turbulent exchange.

In the monograph (Polezhaev et al. 1987), it is noticed that the diffusion coefficients of heat and salt in the water are less than the coefficient of viscosity. We suppose that

$$ K_{T} = K_{S} = \left\{ \begin{gathered} K_{z} \quad {\text{for}}\,z \le h, \hfill \\ K_{\min } /10\quad {\text{for}}\,(z > h\,{\text{and }}\,K_{z} = K_{\min } ). \hfill \\ \end{gathered} \right. $$
(27)

In the described procedure, the intensity of the vertical turbulent exchange is defined by the velocity gradient and stratification.

Parameterization of density

Chen and Millero (1986) presented an equation of the dependence of density on salinity and temperature. It is suitable for limnological systems based on the temperature effects of fresh water combined with seawater effects on salinity. But this equation does not consider the unique composition of Lake Shira. Based on the field measurements of density, the coefficients of this equation were corrected for Shira:

$$ \begin{aligned} \rho = & 0.9998395 + 6.7914 \times 10^{ - 5}\, T - 9.0894 \times 10^{ - 6} T^{2} \\ & + 1.0171 \times 10^{ - 7}\, T^{3} - 1.2846 \times 10^{ - 9} T^{4} \\ & + 1.592 \times 10^{ - 11} \,T^{5} - 5.0125 \times 10^{ - 14}\, T^{6} \\ & + S \cdot (1.32 \times 10^{ - 3} - 2 \times 10^{ - 5} T + 4.96 \times 10^{ - 8} T^{2} ), \\ \end{aligned} $$
(28)

Parameterization of heat flow

A strong positive relationship between water transparency and thermocline depth in both tropical and temperate lakes suggests that reductions in buoyant resistance to vertical mixing, caused by deeper penetration of solar radiation, are important in establishing the mixing depths in various lakes. Thus, in Eqs. 1 and 7, the coefficient of radiation absorption, β, (depending on the water transparency) was calibrated. Heat flows are important for the temperature regime of the reservoir. A complete heat flow through free water surface is defined by known relationships (Belolipetskii et al. 1994):

$$ F_{n} = (1 - \alpha )F_{\text{I}} - (F_{\text{ef}} + F_{\text{cn}} + F_{\text{ev}} ) , $$
(29)

Here F ef is the effective long-wave radiation, F ev is heat emission by evaporation, F cn is the convective heat emission, F I is the incoming short-wave radiation, α is a parameter defining a part of the incoming short-wave radiation permeating to depth (0 ≤ α ≤ 1). Several procedures (Odrova 1979; Ruan and Harleman 1973; Belolipetskii et al. 1994) are used for the definition of F n .

The short-wave radiation is calculated by the formula

$$ F_{\text{I}} = 0.94Q(h_{\text{c}} )(1 - 0.65N_{0}^{2} ) , $$
(30)

where

$$ Q(h_{\text{c}} ) = \left( {0.66 + 0.34{\frac{{\gamma - 0.9 + 0.4\sin h_{\text{c}} }}{{0.1 + 0.4\sin h_{\text{c}} }}}} \right){\frac{{\kappa_{n} \sin^{2} h_{\text{c}} }}{{\rho^{2} (\sin h_{\text{c}} + 0.107)}}}, $$
(31)
$$ h_{\text{c}} = \text{arc} { \sin }\left( {\sin \varphi_{k} \sin \gamma_{1} + \cos \varphi_{k} \cos \gamma_{1} \cos \left( {(t - t_{\text{n}} ){\frac{\pi }{12}}} \right)} \right), $$
(32)
$$ \gamma_{ 1} { = 0} . 4 { + 23} . 4\,{ \cos }\left( {{\frac{ 2\pi }{ 3 6 5}} (d{ + 192)}} \right) - 0. 4\,{ \cos }\left( {{\frac{ 2\pi }{ 3 6 5}} (d - 1 9 2 )} \right) , $$
(33)

κ n  = 1.11 – 1.23 depending on the atmosphere specific humidity, N 0 is the common cloud amount in the part of the unit, h c is the sun attitude in degrees, ρ is the air density, γ = 0.94, ϕ k is the latitude of the region (in degrees), t = 0, 1,…, 23 is the regional time, t n  = 12 is the time of the region, γ 1 is the sun declination, d is the number of days from the beginning of the year.

The long-wave radiation:

$$ F_{\text{ef}} = 4.46 \times 10^{ - 13} (1 + 0.17N_{0}^{2} )(T_{\text{a}} + 273.15)^{6} - 264 - 4.7T_{\text{s}}^{2} . $$
(34)

The turbulent exchange between the water surface and atmosphere:

$$ F_{\text{cn}} = 0.459f(W_{2} )(T_{\text{S}} - T_{\text{a}} ) $$
(35)

Heat emission by evaporation:

$$ F_{\text{ev}} = f(W_{2} )(e_{\text{S}} - e_{\text{a}} ), $$
(36)

where

$$ \begin{aligned} e_{\text{S}} & = & 25.4\exp \left( {17.62 - {\frac{5,278}\,{{T_{S} + 273.15}}}} \right), \\ e_{\text{a}} & = & 25.4\exp \left( {17.62 - {\frac{5,278}{{T_{d} + 273.15}}}} \right), \\ \end{aligned} $$
(37)
$$ \begin{aligned} T_{\text{d}} = & {\frac{{5,278(T_{\text{a}} + 273.15)}}{{5,278 - \ln \,\psi (T_{\text{a}} + 273.15)}}} - 273.15, \\ f(W_{2} ) = & 4.3W_{2} , \\ \end{aligned} $$
(38)

here T S is the temperature of the water surface (°C), T a is the air temperature (°C), N 0 is cloudiness (part of the unit), e S is the pressure of saturated vapor for the given water surface (millibar), e a is the pressure of saturated vapor in the atmosphere measurement on the same height with the temperature (millibar), W 2 is the wind velocity on the 2 m height (m/s), ψ is the relative air humidity.

Parametrization of wind stress

The wind stress on the water surface is defined by the formula (Sudolsky 1991):

$$ \overline{\tau } = \rho_{a} (0.69 + 0.107|\mathop {\overline{W} }\nolimits_{2} |) \times 10^{ - 3} |\mathop {\overline{W} }\nolimits_{2} |\mathop {\overline{W} }\nolimits_{2} , $$
(39)

here \( \rho_{a} = 1.25{\frac{\text{kg}}{{{\text{m}}^{ 3} }}} \) is the air density, \( \mathop {\overline{W} }\nolimits_{2} = (w_{x} ,w_{y} ) \) is the wind velocity vector on the 2 m height (m/s).

Implementation of the model and sources of meteorological data

The most important meteorological parameters affecting the variations in the water-quality parameters are the air temperature, lagged wind speed and humidity (Elci 2008). The meteorological data input into the model includes the cloud cover, air temperature, humidity, wind speed and direction. The meteorological data for the years 2002–2008 were taken from the server “Weather of Russia—weather archives” (http://meteo.infospace.ru/). These data were collected at a meteostation located 10 km west of Lake Shira.

Results

Comparison between the model results and the field data

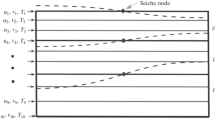
Both the one-dimensional and the two-dimensional model were used for the investigation of the vertical structure of Lake Shira. In particular, numerical experiments on estimating the spring–autumn thermal cycle dynamics in Lake Shira were carried out. The important elements of the vertical hydrophysical structure of Lake Shira are the thermocline and halocline, where the biggest gradients of the water temperature and salinity changes are observed. These layers separate the water mass with more similar characteristics. The thermocline and halocline are in the same depth in Lake Shira. The mathematical models allow for defining the position of the upper and lower quasi-homogeneous layers, which are divided by the thermocline and halocline, depending on the meteorological conditions. The calculated values were compared with the field measurements, obtained by the Institute of Biophysics of SB RAS. Figures 1 and 2 depict the vertical distributions of temperature and salinity obtained from the measurements and simulation for 2004. The profiles of temperature and salinity measured on May 25 were taken as the initial values. In both figures, the modeled temperatures (Fig. 1) and salinities (Fig. 2) are compared with measurements. Both the one-dimensional and two-dimensional numerical models allow for simulating these dynamics. In some years, the simulated thermocline is slightly higher than the observed one, in some other years it is slightly lower. Also, there are some differences in the absolute values. But, in general, the results of modeling coincide with the field data.

Fig. 1
figure 1

Temperature distributions. Shown are the measured values (dots) and the profiles calculated with the one-dimensional (solid line) and two-dimensional (dashed line) models in 2004 on May 25 (a), Aug 1 (b), Nov 5 (c)

Full size image
Fig. 2
figure 2

Salinity distributions. Shown are the measured values (dots) and profiles calculated by the one-dimensional (solid line) and two-dimensional (dashed line) models in 2004 on May 25 (a), Aug 1 (b), Nov 5 (c) 2004

Full size image

Analysis of salinity level influence on stability

Several numerical experiments were carried out with the aim to determine the critical level of salinity necessary to maintain stratification in autumn. The vertical distribution measured in spring was taken as the initial value for the temperature. But instead of taking the measured distribution of salinity in spring as our starting point, fresh water conditions were considered, or the measured distribution divided by 5, or divided by 10 was taken as the starting condition. Then, the measured and calculated vertical profiles in summer and autumn were compared for each year. In Figs. 3 and 4, the results of the calculations for 2004 are presented as an example. For other years, the results are comparable. As one can see in Fig. 3, in summer, Lake Shira is stratified, irrespective of the initial level of salinity. In autumn, however, the level of salinity determines the stability. With starting conditions of fresh water, the lake becomes fully mixed. If the observed initial distribution of salinity divided by 10 is taken as starting condition (this gives 1–2‰ gradient in summer), the two models give conflicting results: the two-dimensional model predicts the mixing of water, while the one-dimensional model predicts that the lake will still be stratified. If the observed initial distribution divided by 5 is taken as the starting condition (this gives 2–3‰ gradient at summer), both models show that the lake stays stratified.

Fig. 3
figure 3

Comparison of the measured temperature distributions (dots) with values calculated with the one-dimensional (solid line) and two-dimensional (dashed line) models in 2004 on Aug 1. The calculations were performed for the conditions of fresh water (a), the initial observed salinity distribution divided by 10 (b) and the initial observed salinity distribution divided by 5 (c)

Full size image
Fig. 4
figure 4

Comparison of the measured temperature distributions (dots) with profiles calculated with the one-dimensional (solid line) and two-dimensional (dashed line) models in 2004 Nov 5. The calculations were performed for the conditions of fresh water (a), the initial observed salinity distribution divided by 10 (b) and the initial observed salinity distribution divided by 5 (c)

Full size image

Discussion

Both the one-dimensional and two-dimensional numerical models allow for simulating dynamical changes in vertical stratification of Lake Shira. Although only the distributions for 2004 are presented (Figs. 1 and 2), they are illustrative for all years, because differences between years are small. The vertical gradients of salinity and temperature in the lake are formed in spring. The salinity profile is created because the inflow of fresh water from melting ice and snow onto the surface. The temperature profile is created by the heating of the surface water. Together these processes cause the formation of a thin upper layer (approximately 1 m) with low salinity (Fig. 2a) and high temperature (Fig. 1a). The density gradient is very large so the turbulent mixing and wind-forced currents cannot mix this thin upper with the lower layers. Subsequently, the energy of wind causes a deepening of the upper layer. Thus, the depth of the upper layer keeps growing until ice formation in late autumn. Also, the heating of the upper layer continues until midsummer while the temperature of the lower layer stays the same or changes only very slowly. So, at midsummer there are two processes contributing to stable stratification: the gradients of temperature (Fig. 1b) and salinity (Fig. 2b). Afterward, the water temperature does not change significantly for about a month. Then, in autumn, the upper layer is cooled and before ice formation, the temperatures of both layers become approximately equal (Fig. 1c). During these temperature transformations, the gradient of salinity is observed on the same depth as the gradient of temperature, and this depth is growing. Consequently, saltwater is added to the upper less saline mixed layer. Therefore, the salinity of the upper layer grows and that of the lower layer stays the same, and the gradient of salinity decreases but stays strong enough for preventing Lake Shira from mixing (Fig. 2c).

As it is mentioned, from 1980, the average salinity has decreased approximately from 20 to 13‰ (Kalacheva et al. 2002). What changes may cause the continuing decreasing salinity level? Is it possible that this may result in changing the mixing regime? An attempt was made to investigate this problem using our numerical models. If the water of Lake Shira were fresh, the summer stratification would not be very different (Fig. 3a). But in autumn, the lake would be fully mixed (Fig. 4a). From the salinities now observed in Shira (12–14‰) to the salinities in the range of 2–3‰, both the one-dimensional and two-dimensional models predict the stability of stratification (Figs. 3c and 4c). For the salinities in the range of 1–2‰, the two-dimensional model predicts the possibility of mixing while the one-dimensional model is still predicts the lake to be stratified (Figs. 3b and 4b). Using meteorological parameters near the common values, on basis of the two-dimensional model, it is concluded that Lake Shira will be stably stratified as long as the average salinity is higher than 3‰. The one-dimensional model predicts the possibility of mixing, again using the common meteorological parameters, only when the salinity is less than 1‰. We therefore conclude that the salinity in Lake Shira can be decreased greatly—from the average salinity of 13‰ to the average salinity of 3‰, and the lake will still stay meromictic. The reason is that the density changes associated with the salinity are very large in comparison with the changes in density associated with the temperature near 5°C. For example, the density difference between 4 and 5°C is approximately 100 times smaller than the density difference between 2 and 3‰ salinity.

The results of the one-dimensional model and two-dimensional model are in good agreement for the salinities higher than 3‰. When the salinity is smaller, the two-dimensional model predicts the possibility of mixing of Lake Shira, and in the one-dimensional model the lake is still stratified. The reason for the discrepancy in results between the one-dimensional and two-dimensional model at an average salinity of 3‰ is that the two-dimensional model, in addition to turbulent mixing, simulates transport processes caused by the wind-forced vertical circulation. When the density gradient is large, these wind-forced currents are not essential. But when the gradient is small, they become important and cause the observed differences between the results of the models. So, it is possible to use the simpler one-dimensional model for simulating the vertical dynamics in Lake Shira during the period free of ice only when the average salinity is higher than 3‰.

Conclusion

Two numerical models for the investigation of the vertical structure of a closed stratified lake were developed and analyzed. The model verification was carried out on the basis of the measured vertical temperature and salinity distributions in Lake Shira. The models show that for common meteorological parameters, Lake Shira will be stratified in autumn as long as the average salinity is higher than 3‰. The simpler one-dimensional model can be used for describing hydrophysical processes from spring until autumn as long as the average salinities in the lake are higher than 3‰.