Introduction

Vertical density stratification is of crucial importance for the space–time distribution of chemical components and ecology of plankton in deep lakes. In particular, vertical gradients of temperature, light, oxygen, salinity, redox potential, biogenic elements, and other components of an ecosystem being of ecological importance are formed in stratified water basins. Along gradients of physical and chemical characteristics, different ecological niches of planktonic microorganisms are formed, which leads to the formation of stable inhomogeneities in the vertical distribution of different bacterio-, phyto-, and protozooplankton species (Jorgensen et al. 1979; Montesinos et al. 1983; Baker et al. 1985; Overmann et al. 1991). In the light of climate change and other anthropogenic stress factors, the prediction of the dynamics of plankton biomass in space is among the most important research topics of aquatic ecology. In this field of research, mathematical modeling plays an important role. A prerequisite of for the construction of valid models for plankton populations in deep lakes obviously are models capable of calculating seasonal dynamics of the vertical gradients of the physico-chemical parameters such as temperature, salt content, and density in relation to weather conditions. Moreover, to make a valid ecological forecast for lakes located in the temperate zone, one should take into account the processes of ice formation and melting, again depending on weather conditions.

The basic components of a mathematical model of the ice thickness change are on the heat equations in the solid and liquid phases, the ice-atmosphere, ice-water, and water-bottom conditions (Maykut and Untersteiner 1971; Parkinson and Washington, 1979; Krass and Merzlikin 1990). When formulated in terms of the one-phase Stefan problem (Rubinstein 1967), the model involves the heat equation in the solid phase and boundary conditions on the upper and lower surfaces of an ice cover (Xu and Zhu 1985; Jeffries et al. 1996). In the quasi-stationary approximation, the temperature profile in the solid phase is linear, and the problem is reduced to the solution of an ordinary differential equation for the thickness of an ice cover (Belolipetskii et al. 1993; Belolipetskii and Genova 2008).

In this study, we focus on Lake Shira, which is a stratified lake in the south of Siberia (Khakasia, Russia). This lake experiences significant anthropogenic impact as it is a spa resort that is frequented by tourists in summer. At the same time, this economic use of the lake makes it very important to make a good ecological forecast for Lake Shira. Earlier, we constructed a one-dimensional model of the vertical distribution of plankton in Shira Lake in summer, but in this earlier model seasonal, variations are not taken into account (Degermendzhy et al. 2002). The next logical step was therefore to include seasonal variations, and in particular winter ones when timing and extend of ice cover has a strong impact on the dynamics of the lake. In this study, we developed such an extended model for calculating hydrophysical parameters in relation to seasonal variation. At this point, we do not yet take biotic factors into account. In summary, the purpose of this study is to construct a one-dimensional vertical model that describes yearly dynamics of the vertical distribution of water temperature and salinity, taking into account the processes of ice formation and melt, and to verify this model using field measurement data.

We propose to use a one-dimensional mathematical model to study the vertical hydrophysical structure in the central part of a saline lake. Taking only one-dimension (vertical) into account greatly simplifies the equations, compared with two-dimensional approaches. It also simplifies the recording and analysis of various environmental influences. These influences include wind stress, heat exchange with the atmosphere, the vertical turbulent mixing and, of course, ice formation. The proposed model allows for the determination and analysis of dynamics in vertical distributions of temperature, salinity, and density of water, while taking into account the processes of ice formation and melting depending on weather conditions.

Methods

Lake Shira

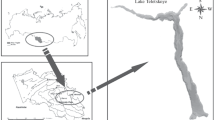
Lake Shira (90.11′ E, 54.30 N) is located in the north of the Republic of Khakasia (in the south of Siberia), 17 km away from the town of Shira. This is a large saline meromictic lake of area 39.5 km2; its maximum depth reaches about 24 m. The lake is closed, with the water inflow provided by the Son River and atmospheric, underground, and anthropogenic runoffs (Parnachev and Degermendzhy 2002). At a depth of 12–13 m and below, there is a stable anaerobic zone in the lake, with hydrogen sulfide concentration in the near-bottom layers varying from 15 to 20 mg/L. In summer, when density stratification is the most pronounced, mineral salt concentration of water in the mixolimnion is about 15 mg/L and that in the monimolimnion is about 19 mg/L (Rogozin et al. 2005). All measurements were performed at one central station, in the deepest part of the lake (90.11′350 E, 54.30.350 N). Vertical profiles of temperature and conductivity were measured using a Data-Sonde 4a submersible multi-channel probe (Hydrolab, USA) in calm weather, with the wave height not exceeding 5 cm, from an anchored boat. In winter, the measurements were performed from the ice, through a hole drilled into it. Mineral salt concentration of water was calculated as a function of specific conductivity, using the empirical equation that we obtained from the measurements of the ash content (Kalacheva et al. 2002) and conductivity for water of Lake Shira in August 2001. Specific conductivity of water was measured using a Data-Sonde 4a submersible multi-channel probe (Hydrolab, USA). Meteorological data were taken from “Russia’s Weather” (http://meteo.infospace.ru/) and “Weather’s record” (http://rp5.ru/) servers.

A one-dimensional model of the temperature and salinity conditions in a lake for the ice-free period

Temperature conditions of a closed stratified lake are formed due to wind-induced flows and the heat exchange with the atmosphere. The problem for the temperature is formulated as follows (Belolipetskii and Genova 2008):

$$ {\frac{\partial T}{\partial t}} = {\frac{\partial }{\partial z}}\left( {K_{T} {\frac{\partial T}{\partial z}}} \right) + \beta {\frac{{F_{I} e^{ - \beta z} }}{{c_{p} \rho_{0} }}}, $$
(1)

With the boundary conditions

$$ \begin{gathered} K_{T} {\frac{\partial T}{\partial z}} = - {\frac{{F_{n} }}{{c_{p} \rho_{0} }}}\quad {\text{for}}\;z = 0, \hfill \\ K_{T} {\frac{\partial T}{\partial z}} = {\frac{{F_{H} }}{{c_{p} \rho_{0} }}}\quad {\text{for}}\;z = H. \hfill \\ \end{gathered} $$
(2)

Here, T is water temperature, K z (z) is the coefficient of vertical turbulent mixing, F H is the heat exchange with bottom, F n is the total heat flow through a free surface, F I is incoming short-wave radiation, β is the radiation absorption coefficient; α is the parameter determining the portion of radiation penetrating into deep-water layers (0 ≤ α ≤ 1), c p is specific heat capacity of water, ρ 0 is typical water density, and H is depth of a lake.

The problem for determining the vertical distribution of salinity is formulated similarly:

$$ \begin{array}{*{20}c} {{\frac{\partial S}{\partial t}} = {\frac{\partial }{\partial z}}\left( {K_{S} {\frac{\partial S}{\partial z}}} \right),} \\ {K_{S} {\frac{\partial S}{\partial z}}\left| {_{z = 0} = - F_{S} ,} \right.\quad \quad \quad \quad K_{S} {\frac{\partial S}{\partial z}}\left| {_{z = H} = F_{SH} .} \right.} \\ \end{array} $$
(3)

Here, S is water salinity, K S (z) is the coefficient of vertical turbulent mixing for salinity, F SH is the mass exchange with bottom, and F S is flow across a free surface. It is also necessary to set the initial distributions of temperature and salinity: \( T(0,z) = T^{0} (z),\quad S(0,z) = S^{0} (z) \).

Schemes of the vertical hydrophysical structure of a saline lake in winter and spring

In autumn and winter, ice is formed on a water surface. On top of the ice surface, snow accumulates. Snow depth is taken into account when ice temperature is determined. As the ice is formed, salt is extruded, which leads to unstable density stratification and causes convective mixing directly below the ice.

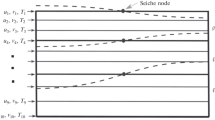
To construct a simplified mathematical model, we distinguish four horizontal layers of water under an ice cover (Fig. 1):

Fig. 1
figure 1

Scheme of the vertical distribution of temperature in snow layer, ice layer, and water column in winter

Full size image

  • ξ≤ z ≤ z 1—the convective mixed layer;

  • z1 ≤ z ≤ z2—the layer where convective mixed occurs;

  • z2 ≤ z ≤ z3—the inner layer;

  • z2 ≤ z ≤ H—the near-bottom layer of homogeneous liquid where \( {\frac{\partial T}{\partial z}} = 0, \, {\frac{\partial S}{\partial z}} = 0. \)

The distribution of temperature and salinity is supposed to be known at the n-th time step:

$$T^{n} (z) = \left\{ \begin{array}{ll} \beta_{{T_{1} }}^{n} +\gamma_{{T_{1}}}^{n} (z - z_{1} ) & {\text{for }}\; z_{1} < z <z_{2} , \\\beta_{{T_{2} }}^{n} + \gamma_{{T_{2} }}^{n} (z - z_{2}) & {\text{for}}\; \, z_{2} < z < z_{3} , \\\beta_{{T_{3} }}^{n} & {\text{for }}\; z_{3} < z < H.\\ \end{array} \right. $$
(4)
$$S^{n} (z) = \left\{ {\begin{array}{ll} \beta_{{S_{1} }}^{n} +\gamma_{{S_{1} }}^{n} (z - z_{1} )& {\text{for}}\; z_{1} < z < z_{2}, \\ \beta_{{S_{2} }}^{n} + \gamma_{{S_{2} }}^{n} (z - z_{2} )&{\text{for}}\; z_{2} < z < z_{3} , \\ \beta_{{S_{3} }}^{n} &{\text{for}}\; z_{3} < z < H. \\ \end{array} } \right.$$
(5)

z 1=h n is the depth to which convection spreads and H is depth of a lake. Initially (when ice cover formation begins), \( z_{1} = 0 \), \( \xi = 0 \), \( \beta_{T}^{0} = T_{ph} \), \( \beta_{{S_{1} }}^{0} = \bar{S} \) (salinity of a water surface). Further we assume that temperature and salinity vary in a convective mixed layer only.

In spring, heat flow and air temperature are increased. Ice melts from a top. Layer of water is formed in ice surface (Fig. 2). This is taken into account in the model. Our analysis shows that the above described schemes can approximately describe variation of ice thickness, depth of a convective mixed layer, the vertical distribution of temperature, salinity, and water density in Lake Shira.

Fig. 2
figure 2

Scheme of the vertical distribution of temperature in ice layer and water columns in spring

Full size image

A model of ice thickness variation

Dynamics of ice cover thickness is determined using a simplified model based on the quasi-stationary temperature conditions in a solidified domain (Belolipetskii et al. 1993; Krass and Merzlikin 1990). In this case, the balance of heat flows at a water–ice interface, taking into account latent heat of the phase transition, yields the following equation:

$$ L\rho_{ice} {\frac{{{\text{d}}\xi }}{{{\text{d}}t}}} =\lambda_{ice} {\frac{{T_{ph} - T_{ice} }}{\xi }} - F_{w - i} -F_{i}^{c} \cdot f(\xi ), $$
(6)
$$ f(\xi ) = {\frac{{2\left[ {1 - (1 + \kappa \sqrt \xi )} \right]\exp ( - \kappa \sqrt \xi )}}{{\kappa^{2} \xi }}} - \exp ( - \kappa \sqrt \xi ) $$

Heat flow F w–i at a water–ice interface is determined from the relation:

$$ F_{w - i} = \lambda_{w} {\frac{{T(h) - T_{ph} }}{h - \xi }} $$
(7)

Here, t is time, z is the vertical coordinate (the Oz axis is directed downwards, Fig. 1), ξ is ice thickness, ξ 0 is initial ice thickness, h is the depth to which convection spreads, H is the lake depth, λ w , λ ice are the heat conduction coefficients of water and ice, respectively, ρ ice is ice density, L is specific heat of ice melting, T is water temperature, T ice is ice temperature, T ph is water crystallization temperature depending on water salinity S, \( F_{i}^{c} = F_{i} \exp ( - 0.4\xi_{\text{sn}} ) \) , ξ sn is snow cover thickness, κ is the coefficient of attenuation of solar radiation in an ice cover.

The salt water crystallization temperature is determined from the formula (Vinnikov and Proskuryakov 1988):

$$ T_{ph} = - (3 \cdot 10^{ - 3} + 527 \cdot 10^{ - 4} \cdot S^{2} + 40 \cdot 10^{ - 6} \cdot S^{3} ). $$
(8)

Equation (5) is solved numerically using the difference scheme:

$$ 0.5 \cdot {\frac{{(\xi^{n + 1} )^{2} - (\xi^{n} )^{2} }}{\Updelta t}} = a^{n} - b^{n} - F_{i}^{c} \cdot \xi^{n} \cdot f(\xi^{n} )/(L\rho_{n} ) $$
(9)
$$ {\rm where} \quad a^{n} = {\frac{{\lambda_{ice} (T_{ph} - T_{ice} )}}{{L\rho_{ice} }}},b^{n} = {\frac{{F_{w - i} \xi^{n} }}{{L\rho_{ice} }}},\xi^{n} = \xi (t_{n} ),t_{n + 1} = t_{n} + \Updelta t. $$

If ice is covered with snow, the temperature T ice of an ice surface is expressed in terms of the temperature T sn of snow (Doronin 1981):

$$ T_{ice} = T_{sn} \cdot \mathop {\left[ {1 + {\frac{{\xi_{sn} \lambda_{ice} }}{{\xi \lambda_{sn} }}}} \right]}\nolimits^{ - 1} . $$
(10)

Here, ξ sn is snow cover thickness and λ sn is the coefficient of heat conduction of snow.

Estimation of the thickness of the convective mixed layer

Once a saline lake is covered with ice, the flow of salt that results from the crystallization of water as the ice cover further increases in thickness is the main determinant of the thickness of the convective mixed layer. Unstable density stratification arises, which leads to intensive vertical circulation and equalization of temperature and salinity in the convective layer. According to Doronin (1981), convective mixing propagates down when density of water becomes equal to that of the underlying water layer. This hypothesis is used as a basis for the numerical procedure presented here for determining the depth of propagation of convection and the values of temperature, salinity, and water density in a convective layer.

Let us determine the thickness (h–ξ) of a convective mixed layer step by step. Consider the first time step t 1=∆t. In the time ∆t, an ice cover of thickness ξ 1 is formed. As water freezes, salt is extracted (ice has by definition a very low salt content). In a water layer of thickness ξ 1, the amount of salt is:

$$ \int\limits_{0}^{{\xi^{1} }} (\overline{S} + \gamma_{S} z)dz = \overline{S} \xi^{1} + 0.5\gamma_{S} (\xi^{1} )^{2} . $$
(11)

Let γ S be the desalination coefficient, i.e., the parameter characterizing the part of salt which is extracted after freezing a water layer. Then

$$ \Updelta S^{1} = \alpha_{S} (\overline{S} \xi^{1} + 0.5\gamma_{S} (\xi^{1} )^{2} ). $$
(12)

The convection depth at the first time step is determined from

$$ \left. \rho \right|_{{\xi^{1} \le z \le h^{1} }} = \left. \rho \right|_{{z = h^{1} }} , $$
(13)

where \( \left. \rho \right|_{{\xi^{1} < z < h^{1} }} = \rho_{av}^{1} \) is density of a mixed layer: \( \rho_{av}^{1} = \rho (T_{av}^{1} ,S_{av}^{1} ). \)

The average temperature and salinity in a mixed layer are determined from the following equations:

$$ \begin{array}{ll} {S_{av}^{1} = {\frac{1}{{h^{1} - \xi^{1} }}}\int\limits_{{\xi^{1} }}^{{h^{1} }} \,Sdz + {\frac{{\Updelta S^{1} }}{{h^{1} - \xi^{1} }}} = S\left( {{\frac{{h^{1} + \xi^{1} }}{2}}} \right) + {\frac{{\Updelta S^{1} }}{{h^{1} - \xi^{1} }}},} \\ {T_{av}^{1} = {\frac{1}{{h^{1} - \xi^{1} }}}\int\limits_{{\xi^{1} }}^{{h^{1} }} \,Tdz = T\left( {{\frac{{h^{1} + \xi^{1} }}{2}}} \right).} \\ \end{array} $$
(14)

The Boussinesq approximation (Kochergin 1978):

$$ \rho = \rho_{0} \left(\varepsilon_{1} + \varepsilon_{2} {\frac{T}{{T_{0} }}} + \varepsilon_{3} {\frac{S}{{S_{0} }}}\right), $$
(15)

is taken as the equation of the state of salt water where ρ0 = 1.0254 g/cm3, ε1 = 0.9753, ε2 = – 0.00317, ε3 = 0.02737, T 0 = 17.5°C, S o = 35 ‰.

Taking into account (12) (14) (15) and the assumption that average density of a mixed layer is equal to density of the underlying water layer, we obtain the formula for determining h 1:

$$ h^{1} = \xi^{1} + \sqrt {{\frac{{2\varepsilon_{3} \Updelta S^{1} }}{{a_{1} S_{0} }}}} , $$
(16)

where \( a_{1} = {\frac{{\varepsilon_{2} \gamma_{T} }}{{T_{0} }}} + {\frac{{\varepsilon_{3} \gamma_{S} }}{{S_{0} }}} \).

The depth of propagation of convection at the (n + 1)-st time step is determined in a similar way:

$$ h^{n + 1} = \xi^{n + 1} + \sqrt {\left( {\xi^{n + 1} } \right)^{2} - 2a_{2} /a_{1} } , $$
(17)

Here

$$ \Updelta S^{n + 1} = \alpha_{S} S_{av}^{n} (\xi^{n + 1} - \xi^{n} ), $$
$$ a_{2} = - {\frac{{\varepsilon_{3} \Updelta S^{n + 1} }}{{S_{0} }}} - \left( {h^{n} - \xi^{n + 1} } \right)\left[ {{\frac{{\varepsilon_{2} }}{{T_{0} }}}\left( {T_{av}^{n} - T_{ph} } \right) + {\frac{{\varepsilon_{3} }}{{S_{0} }}}\left( {S_{av}^{n} - \bar{S}} \right)} \right] + a_{1} \left( {h^{n} } \right)^{2} , $$
$$ T_{av}^{n + 1} = {\frac{{T_{av}^{n} \left( {h^{n} - \xi^{n + 1} } \right) + T_{ph} \left( {h^{n + 1} - h^{n} } \right) + 0.5\gamma_{T} \left( {(h^{n + 1} )^{2} - (h^{n} )^{2} } \right)}}{{h^{n + 1} - \xi^{n + 1} }}}, $$
(18)
$$ S_{av}^{n + 1} = {\frac{{\Updelta S^{n + 1} + S_{av}^{n} \left( {h^{n} - \xi^{n + 1} } \right) + \bar{S}\left( {h^{n + 1} - h^{n} } \right) + 0.5\gamma_{s} \left( {(h^{n + 1} )^{2} - (h^{n} )^{2} } \right)}}{{h^{n + 1} - \xi^{n + 1} }}} $$

Thus, as long as thickness of an ice cover increases, thickness of a convective mixed layer increases as well.

A simplified model of ice cover melt in spring

In spring, the temperature of ice increases, reaching the temperature of the phase transition to water, and a heat flow from the top water layer under the ice leads to ice melt from below; this process is calculated using Equation (6). Simultaneously, ice melts from above. To evaluate this process, the following approach is proposed. The vertical structure is schematically shown in Fig. 2.

To estimate the water temperature profile, we use the stationary approximation. The process of ice melt from above is described by the following equation:

$$ \rho_{ice} L_{ice} {\frac{{d\xi_{w - t} }}{{{\text{d}}t}}} = K_{z} \left. {{\frac{{dT_{w - t} }}{dz}}} \right|_{{z = \xi_{w - t} }} $$
(19)

Here, T w–t (z) is the temperature of water formed on surface of ice.

$$ K_{z} {\frac{{d^{2} T_{w - t} }}{{dz^{2} }}} = \frac{d}{dz}F_{I} e^{{ - \beta (z - h_{w - t} )}} $$
(20)

Boundary conditions are as follows:

$$ K_{z} \left. {\frac{dT}{dz}} \right|_{{z = h_{t} }} = - {\frac{{\tilde{F}_{n} }}{c\rho }},\quad \left. {T_{w - t} } \right|_{{z = \xi_{w - t} }} = T_{ph} $$
(21)

Here \( \tilde{F}_{n} = F_{I} - F_{n} \), where F I is the radiation heat exchange, F n is the total heat flow through a water surface, and K z  = const.

The solution of the problem (20) (21) is given by:

$$ T_{w - t} = T_{a} + {\frac{1}{{c_{p} \rho_{0} K_{z} }}}\left[ {\left( {\tilde{F}_{n} - 2F_{I} } \right)\left( {z - \xi_{w - t} } \right) + {\frac{1}{\beta }}F_{I} e^{{\beta h_{w - t} }} \left( {e^{{ - \beta \xi_{w - t} }} - e^{ - \beta z} } \right)} \right] $$
(22)

To determine the position of the upper boundary of an ice cover, from (19) (22) we obtain the following equation:

$$ \rho_{ice} L_{ice} {\frac{{d\xi_{w - t} }}{dt}} = F_{n} + F_{I} \left( {1 - e^{{ - \beta (\xi_{w - t} - h_{w - t} )}} } \right) $$
(23)

The thickness of a water layer on an ice surface is calculated as follows:

$$ h_{w - t}^{n + 1} = h_{w - t}^{n} + {\frac{{\rho_{ice} }}{{\rho_{w} }}}\left( {\xi_{w - t}^{n + 1} - \xi_{w - t}^{n + 1} } \right) $$
(24)

For the equation (23), the following initial conditions are given:

$$ \begin{array}{*{20}c} {\left. {\xi_{w - t} } \right|_{t = 0} = \xi_{w - t}^{0} ,} & {\left. {h_{w - t} } \right|_{t = 0} = h_{w - t}^{0} } \\ \end{array} $$
(25)

Implementation of the model

Based on the above described set of equations, a computer program was written and calculations of ice thickness, depth of a convective mixed layer, the vertical distribution of salinity, temperature, and water density for Lake Shira Lake performed. Meteorological input data for 2002–2008 years taken from the “Russia’s Weather” (http://meteo.infospace.ru/) and “Weather’s record” (http://rp5.ru/) servers were used. A numerical algorithm for solving (1–3) was used that is based on an implicit scheme and the sweep method (Belolipetskii and Genova 2008). Going from the scheme 1 (Fig. 1) to the spring scheme 2 (Fig. 2) was carried out under the conditions: F n  > 0, T a  > 0. Calculations were performed for daily average air temperature, wind speed, humidity, and cloud cover.

Results

Modifications for the state equation of salt water for Shira Lake

According to field measurements, density of salt water for Shira Lake slightly differed from that calculated by the formula (15). Therefore, as a first result, the coefficients ε1, ε2, ε3 were refined to fit experimental data:

$$ \varepsilon_{ 1} = 0. 9 8 4 5 2 2,\varepsilon_{ 2} = -0.00 7 1 2,\varepsilon_{ 3} = 0.0 4 1 1 2 4 $$
(26)

For the winter period ε1 = 0.9825, ε2 = –0.0015.

Parameterization of the vertical turbulent exchange

The formation of a vertical structure of a reservoir with little inflow or outflow (i.e. almost stagnant water) occurs due to wind-induced turbulence. Turbulent flows can be described by the Reynolds equations involving turbulent transfer terms. To complete the system of equations, different turbulence models can be used: algebraic models, models with an equation for turbulent kinetic energy, models with the transfer equations for turbulence kinetic energy and velocity of dissipation of this energy, etc. (Mellor and Yamada 1974; Rodi 1980; Edinger and Buchak 1983).

Heat/mass transfer is considerably affected by turbulence. The vertical turbulent exchange is parametrized using a formula based on the Prandtl-Obukhov formula and the Ekman approximate solution for wind-induced flows (Belolipetskii and Genova 1998):

$$ K_{z} = \left\{ \begin{gathered} (0.05h_{1} )^{2} B + K_{\min } \quad {\text{for}}\quad B \ge 0, \hfill \\ K_{\min } \quad \quad \quad \quad \quad \quad {\text{ for}}\quad B < 0, \hfill \\ \end{gathered} \right. $$
(27)

here \( B = \sqrt {\left( {{\frac{\tau }{{\rho_{0} K_{0} }}}} \right)^{2} e^{{ - 2\tilde{a}z}} - {\frac{g}{{\rho_{0} }}}\left( {{\frac{d\rho }{dz}}} \right)} \), \( \tau = \sqrt {\tau_{x}^{2} + \tau_{y}^{2} } \) is wind friction stress, K min = 0.02 cm2/s is the minimal value of the coefficient of the vertical turbulent exchange, \( K_{0} = {\frac{{(0.05\pi )^{2} \tau }}{{2\rho_{0} f}}} \), \( \tilde{\alpha } = \sqrt {{\frac{f}{{2K_{0} }}}} \), \( h_{1} = \pi \sqrt {{\frac{{K_{0} }}{2f}}} \), f—the Coriolis parameter.

$$K_{T} = K_{S} = \left\{ \begin{gathered} K_{z} (T,S), \quad{\text{ for }}z \le h_{1} + \Updelta , \hfill \\ K_{{\min}} /10, \quad {\text{ for (}}z \ge h_{1} + \Updelta,\quad{\text{and}} \, K_{z} (T,S) = K_{{\min }} ). \hfill \\\end{gathered} \right. $$
(28)

Wind friction stress and heat flows

Wind friction stress is calculated using the following formula (Sudolsky 1991):

$$ \overline{\tau } = \rho_{a} (0.9 + 0.17|\mathop {\overline{W} }\nolimits_{2} |) \cdot 10^{ - 3} |\mathop {\overline{W} }\nolimits_{2} |\mathop {\overline{W} }\nolimits_{2} , $$
(29)

where ρα is air density and \( \mathop {\overline{W} }\nolimits_{2} = (w_{x} ,w_{y} ) \) is wind velocity vector at a height of 2 m (m/s).

Heat flows are significant parameters responsible for temperature conditions of a lake. The total heat flow across a free surface is determined by the known relations (Belolipetskii et al. 1993).

Calculated variations in ice thickness

Calculations of variations of ice thickness in the deepwater area of Lake Shira for different winters were performed and shown in Fig. 3. Measured starting data of ice cover in Lake Shira, as well as calculated ones, are different for different years: in 2002 it was on November 13, in 2004 it was on November 24, in 2007 it was on November 26 (Fig. 3). Table 1 shows air temperatures and snow depth averaged over winter, measured ice thickness and thickness of a convective mixed layer, and calculated depth of thermocline before the formation of an ice cover. The proposed model allows determining an ice thickness depending on air temperature and snow depth. The calculated values of ice thickness for different winters are different and are consistent with the measured data. Calculated and measured values of ice thickness for different winters are compared in Figs. 3. Solid lines show results of the calculations, and dots correspond to the measurement.

Fig. 3
figure 3

Calculated ice thickness based on the meteorological data for 2002–2008. Dots correspond to measured ice thickness

Full size image
Table 1 Air temperature, snow depth averaged over winter, ice thickness, and thickness of convective mixed layer and depth of the halocline before the start of ice formation for the three winters the were modeled
Full size table

Calculated variations in the depth of the convective mixed layer

Calculated values of depth of a convective mixed layer for different winters (2002–2003, 2004–2005, 2007–2008 years) are different and depend on air temperature, ice thickness, and halocline position in autumn. Thickness of a convective mixed layer varies from 10 to 16 m in the computed variants. Calculated and measured data are compared in Figs. 4. Solid lines show results of the calculations, and dots correspond to the measurement. The numerical results are in agreement with the measurement ones.

Fig. 4
figure 4

Calculated depth of a convective mixed layer based on the meteorological data for 2002–2008. Dots correspond to measured values

Full size image

Modeled and observed temperature profiles

The calculations of vertical profiles of water temperature in the deep area of Lake Shira in 2002–2004 are performed as shows in Fig. 5 (the calculated are solid lines and measured are dots). Without ice, a temperature regime is formed at the expense of the heat coming through the surface, deepening of thermocline is result from turbulent mixing. In summer, the water temperature in the upper layer of water increases to 22°C. In autumn, the thermocline depth increases, the temperature in the surface layer decreases until it reaches the phase transition temperature. A phase of ice formation and formation of a convective mixing starts. As the calculations show, the model adequately represents a change in the vertical distribution of temperature according to the seasons. The position of the thermocline in the different seasons of a year is determined with satisfactory accuracy.

Fig. 5
figure 5

Calculated (solid line) and measured (dots) temperature distributions

Full size image

Modeled and observed salinity profiles

The calculations of vertical profiles of water salinity in the deep area of Shira Lake in 2002–2004 are performed as shows in Fig. 6 (the calculated are solid lines and measured are dots). Qualitative and quantitative variations of the salinity profiles in different seasons are defined by meteorological data. In spring, a thin layer of lightly salted water is formed due to melting ice (Fig. 6: 24.05.2003). Halocline is formed due to turbulent mixing in the summer and convective mixing in winter. Calculated position of halocline qualitatively coincides with the measured data, which allows to assert about good agreement of model calculations and field data. Comparison of real and simulated data shows that the model profiles in general adequately represent seasonal variability of real stratification of the Lake Shira.

Fig. 6
figure 6

Calculated (solid line) and measured (dots) distributions of salinity

Full size image

Modeled density profiles

Water density is calculated from the obtained values of temperature and salinity by the equation of state (26) (Fig. 7). The position of thermocline and halocline (Fig. 5, 6) are similar. Because density is defined by temperature and salinity, position of picnocline coincides with position of thermocline and halocline and depends on variations of meteorological factors.

Fig. 7
figure 7

Calculated distributions of water density

Full size image

Discussion

To determine variation in thickness of sea ice, different mathematical models based on the heat equations for layers of water, ice, snow, and conditions on interfaces of layers are used (Maykut and Untersteiner 1971; Parkinson and Washington 1979; Krass and Merzlikin 1990). In a simplified formulation, the problem of ice formation is reduced to the solutions of ordinary differential equations for ice thickness (Belolipetskii et al. 1993; Belolipetskii and Genova 2008). In this paper, not only ice thickness but also thickness of a convective mixed layer for a salt water basin are modeled.

Seasonal vertical thermohaline stability of the water column in Lake Shira is provided by both thermal and salinity components in spring and summer, but only by salinity in autumn and winter. The thermal structure of salt Shira Lake is characterized by pronounced seasonal arrangement, due to the annual cycle of the heat exchange between the atmosphere and the lake surface. The warming up phase (May–August) and the cooling phase (September–March) are quite different. The typical summer vertical structure is formed in August, and the typical winter structure is formed in March.

Significant difference between winter distributions of different years can be completely explained by difference in meteorological conditions, which are taken into account in the model presented here. The winter distributions in the Shira Lake are apparently more sensitive to interannual variations of meteorological factors than the summer ones.

The use of the simplified, one-dimensional model allows for a simplified explanation and analysis of various environmental influences on the vertical structure of the reservoir. These effects include wind stress, the heat exchange with the atmosphere, the vertical turbulent mixing.

The thermocline (T), the halocline (S), and the pycnocline (ρ), where, respectively, the most dramatic variations of water temperature, salinity, and density in the vertical direction are observed, are important elements of the vertical hydrophysical structure of any saline lake. These layers separate water masses with more uniform parameters. Field observations show that the vertical positions of the thermocline, the halocline, and the pycnocline are practically the same; there position does depend, however, on the weather conditions and a season. Table 2 gives the positions of the pycnocline and the redox zone (the interface between oxygenated layers and those containing hydrogen sulfide). It follows from field measurement data that in Lake Shira the position of the redox zone coincides with a density step for autumn and winter. On the other hand, the position of a density step as calculated with the help of the hydrophysical model is the same as that obtained from the field measurement data. This implies that in winter and autumn the vertical coordinate of the redox zone in Shira Lake is mainly defined by density, which depends on weather factors. In summer and spring, the redox zone is significantly below the pycnocline.

Table 2 Measured depths at which the pycnocline and the redox zone are situated in the deep-water part of Shira Lake during 2002–2004
Full size table

It is particularly important to get an insight into the mechanisms responsible for the formation of the vertical structures of stratified lakes with hydrogen sulfide monimolimnions, such as Shira Lake. These zones of going from aerobic water layers to anaerobic ones (the chemocline, the redox zone) are special interest because usually they are characterized by hyperactivity of planktonic communities (Jorgensen et al. 1979) and, hence, by significant flows of carbon and biogenic elements.

A sufficient light level in the chemocline is a factor favoring the development of phototrophic anoxic bacteria, which perform photo-oxidation of the sulfide during anoxigenic photosynthesis. The community of phototrophic bacteria thus provides an “oxidative filter” that does not allow this toxic compound to ascend to the upper water layers. As the rate of anoxigenic photosynthesis is limited by light, the rate of sulfide photo-oxidation depends on light as well. The closer to a surface the chemocline is positioned, the more light penetrates into this zone, and vice versa. Therefore, the vertical position of the redox zone is a very important feature of a stratified lake, as it determines the amount of light that penetrates into this zone and, consequently, the rates of all microbial processes.

Moreover, there are studies showing that the quantitative and qualitative parameters of light penetrating into a redox zone determine the species composition of a bacterial community that is formed in this zone (Montesinos et al. 1983). Variations of lighting conditions in a chemocline may lead to variation of the species composition of phototrophic bacteria. For instance, until 2000, the chemocline of Lake Cadagno (Switzerland) was dominated by purple sulfur bacteria, which were subsequently replaced by green sulfur bacteria. The amount of light in the chemocline was considerably reduced after 2000 due to increased turbidity of overlying layers of water. Tonolla and co-authors (2005) suggested that elevated turbidity could be due to increase in phytoplankton biomass being a result of inflow of biogenic elements brought up from the deep and rich in biogenic elements monimolimnion when the lake was mixed too thoroughly. The green sulfur bacteria occupied the dominant position under impaired lighting conditions in the chemocline because the photosynthesizing pigments of green sulfur bacteria are better adapted to low levels of light and to the deep-water light spectrum (Montesinos et al. 1983). Increase in phytoplankton biomass caused by the inflow of biogenic elements from the monimolimnion, due to distruption of meromictic conditions, was also registered in Mono Lake (USA) (Melack and Jellison 1998). Similar events may hypothetically occur in other stratified lakes, including Shira Lake, suggesting the importance of the density stratification forecast.

The vertical distribution of hydrogen sulfide in each lake is certainly determined by the rates of sulfide production (bacterial sulfate reduction), its chemical and biological oxidation, and transfer, which depends on turbulence of water masses. In the general case, calculation of the profile of sulfide concentration in a given lake must be performed taking into account all the above-mentioned processes. However, in Shira Lake, the position of the redox zone estimated by field measurement data coincides with the density step for autumn and winter (Fig. 7, Table 2). At the same time, the position of the density step as calculated with the hydrophysical model that does not take into account biological and chemical processes is in good agreement with field measurement data. This implies that meteorological and hydrophysical factors are the main determinants of the vertical coordinate of the redox zone in Lake Shira.

Conclusions

In this paper, we present a parsimonious one-dimensional mathematical model of the vertical distribution of hydrophysical variables (temperature, salinity, and density of water, ice thickness, thickness of convective mixing under an ice cover) in water column of a saline lake. The calculations and their comparison with measurement data show the ability of the proposed model to reproduce vertical profiles of temperature, salinity, and density of water, to estimate variation of ice thickness and thickness of a convective mixed layer under an ice cover. The computer model can be used for the prediction of hydrophysical characteristics of a water column in a hypothetical scenarios of weather conditions and thereby contribute to the management of this economically important lake.