Low temperature adsorption of CO₂ in carbonaceous wedge pores: a Monte Carlo simulation study

Abstract

A systematic study of carbon dioxide in wedge pores under subcritical conditions were conducted with Grand Canonical Monte Carlo simulation. The effects of various factors: temperature, pore geometry (i.e., pore width, length, tilt angle and corrugation), on the formation of stepwise isotherms, were particularly investigated. The occurrence of this step-wise adsorption behaviour is correlated to the alternate packing between the commensurate and incommensurate along the pore axis direction. The steps faded with temperature, due to the adsorbates are less structured and gradually receded mainly from the wide end where the weakest potential exerted to the fluids. The number of steps on desorption branch depends on the number of junctions and domains formed. The particles accumulating at the narrow end in open wedge pore play a role analogy to the closed end. Moreover, having corrugation on the interior solid surface also results different mechanisms illustrated in the stepwise behaviour due to the change in the actual pore size distribution and the interference to the force field inside the pore.

1 Introduction

Carbon dioxide (CO₂) is widely known for its enormous effect on global warming and therefore its capture and removal have been extensively studied [1,2,3]. Compared to other porous materials such as zeolites [4, 5], molecular sieve [6, 7], silica [8, 9] and metal–organic frameworks [10, 11], carbonaceous materials are relatively easy to regenerate and inexpensive to prepare, have moderate heats of sorption, and are insensitive to water vapour as compared to the other materials [2].

Porous activated carbons (AC) having large pore volumes and surface areas are widely adopted [2, 12, 13]. Adsorption of CO₂ on AC near critical point or under supercritical conditions has been extensively studied experimentally [13,14,15] and by modelling [16,17,18]. In comparison with experimental technologies, the molecular simulation method is more time- and cost-efficient [12, 16, 17]. Among various molecular simulation methods, Grand Canonical Monte Carlo (GCMC) simulation is capable to mimic the volumetric adsorption that is widely used in practice [12, 17, 19].

In GCMC simulation, the AC is commonly simulated as a combination of uniform slit pores with varied sizes [12, 20, 21]. However, according to the X-ray analysis, the geometric structures of AC are rather complex and composed of crystallites that are stacked randomly and the confined spaces between the carbon stacks tend to be wedge shaped [22]. Thus, wedge pore is considered as a more realistic pore representation for the AC, which has non-uniform cross section [23,24,25,26]. The typical isotherm for a wedge pore possesses a Type C (in the de Boer classification) hysteresis loop, where its detailed shape depends on specific geometric configurations, including the range of pore widths, pore length and tilt angle. This Type C hysteresis is not commonly observed experimentally because the wedge configuration tends to be masked by other effects, such as closed ends and ink-bottle structures. A stepwise character of desorption branch can be realized on the isotherm of argon in a wedge pore at 70 K or 77 K [24, 25]. The hysteresis loop is stepped at the desorption boundary due to a transition between commensurate and incommensurate packing [25]. However, this feature is not exhibited at higher temperatures, e.g., 87 K (i.e., experimental boiling point of argon).

CO₂ adsorption in carbonaceous pore is not only important information for designing carbon adsorbents for carbon capture, but also a fundamental insight as CO₂ adsorption is intermediate between noble gases and molecules such as water and ammonia, with strong leading dipoles. Besides being the anthropogenic greenhouse gas, CO₂ is commonly used in characterizing the small pores of carbonaceous materials at 273 K as it has faster diffusion rates than other commonly used probe molecule at cryogenic temperatures [27, 28]. However, as most of the studies have been mainly focused on the CO₂ adsorption characters at or close to supercritical conditions [14, 29], limited attention was paid to CO₂ adsorption at low temperatures below the bulk triple point [30] and above the bulk triple point [1]. There has been no systematic study on the CO₂ adsorptive behavior using the more realistic pore model at temperatures below and above the bulk triple point. Also, the role of adsorbate intermolecular interactions, the adsorbate–adsorbent interactions and the temperature on CO₂ adsorptive behavior in carbonaceous wedge pore has not been quantified. Therefore, the main objective of this work is to evaluate systematically the behaviors of CO₂ adsorption in a wedge shaped pore in the temperature range from below the triple point to above it, considering the effects of geometric properties (pore length, angle). Moreover, pores in real porous materials do not always have homogeneous surfaces, but possess geometrical corrugations, which are either as a result of impurities or defects acquired during synthesis or arise naturally as a consequence of discrete atomic structure. We consider the presence of geometrical corrugations on pore walls, which possess different affinities from pure carbon. The occurrence and characters of hysteresis loop for CO₂ adsorption in both the smoothed wall and corrugated wedge pores are investigated by the GCMC simulation, to gain the insight of the mechanism of CO₂ adsorption in wedge pore at low temperatures and at molecular level. These insights can be useful information for carbon capture and removal process under subcritical conditions hence facilitate the designing and optimizing suitable carbon adsorbents.

2 Theory and simulation

2.1 Wedge pore model

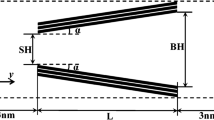
Figure 1 depicts a wedge pore with detailed structural parameters including pore size at small (SH) and large (BH) ends, pore length (L) and tilt angle (α). The pore walls consist of three homogeneous layers with a constant surface density ρ_s of 38.2 nm⁻² and a spacing ∆ = 0.3354 nm for representing a graphite surface. As shown in Fig. 1a, the wedge pore of SH = 2 nm, L = 10 nm and α = 5° with smooth walls was taken as the reference wedge pore for comparison purpose. The length of the simulation box in the x-direction is ten times the collision diameter of CO₂, σ_ff (Table 1) and a periodic boundary condition is applied in this direction. The dashed lines represent the boundaries of the simulation box in the y- and z-directions. The gas surrounding connected to each end of the pore has a length of 3 nm along the y-axis, and the dimensions in the x-direction and z-direction are the same as the pore walls in that direction. A corrugated wedge pore is constructed by grafting humps that composed of graphene-like layers in the same manner as the pore walls on the innermost graphene layers (see Fig. 1b). The configuration of the humps is included in the Sect. 3.5.

Fig. 1

Schematic diagrams of a a homogeneous and b corrugated wedge pore

Table 1 The molecular parameters of CO₂ and carbon atom

2.2 Potential models

The intermolecular potential energy of CO₂ is described by the 12-6 Lennard-Jones (LJ) equation and the solid (including the pore walls and the humps)–fluid interaction energy is calculated with the Bojan–Steele equation [33, 34]. The cross molecular parameters are calculated from the Lorentz–Berthelot combining rules. The molecular parameters of the selected CO₂ and carbon atom potential models utilized in this work are listed in Table 1.

2.3 Monte Carlo simulation details

The GCMC simulation was applied to determine adsorption and desorption isotherms, with at least 5 × 10⁵ cycles in both the equilibration and sampling stages. Each cycle consists of 1000 displacement moves and exchanges, which include insertion and deletion with equal probability. In the equilibration stage, the maximum displacement length is initially set as half of the largest dimension of the box and adjusted at the end of each cycle to give an acceptance ratio for displacement of 20% [35]. In the calculation of interaction energies, the cut-off radius is five times the collision diameter of the carbon atom of CO₂. The values of saturated vapour pressures at different temperatures, as tabulated in Table 2, are determined from vapour–solid equilibrium (VSE) or vapour–liquid equilibrium (VLE) simulations with Bin-Canonical Monte Carlo (Bin-CMC) scheme, details of which are given in Appendix 1.

Table 2 Saturated vapour pressures of CO₂ at various temperatures calculated with VLE/VSE simulations (simulated triple point = 172 K)

The absolute density of adsorbate in the pore is defined as below:

$${\rho }_{ad}=\frac{\langle N\rangle }{{V}_{acc}}$$

(1)

where $\left\langle {\text{N}} \right\rangle$ is the ensemble average of the number of molecules inside the pore, and V_acc is accessible volume. The total isosteric heat of adsorption, and the contributions from the fluid–solid (FS) and fluid–fluid (FF) interactions can be calculated with the equation that derived from fluctuation theory, details can be found in the work of Zeng et al. [36].

3 Results and discussion

3.1 CO₂ adsorption in the reference wedge pore at 150 K

The isotherm of CO₂ adsorption at 150 K in the reference wedge pore is presented in Fig. 2. A Type C (de Boer Classification) or Type H2(b) (IUPAC classification) hysteresis is observed with three distinct steps (i.e., sharp evaporation) occurring on the desorption branch. To shed further light on the underlying mechanisms, the snapshots tracking the evolution of adsorption and desorption processes are shown in Fig. 3, with A–J points as labelled in Fig. 2. All snapshots in this work are dimensionless units in the scale of collision diameter of CO₂, σ_ff (see Table 1).

Fig. 2

a Isotherm and b isosteric heat of CO₂ adsorption at 150 K in the reference wedge pore of SH = 2 nm, L = 10 nm and α = 5°, with the lines as guide to the eye

Fig. 3

Snapshots of evolution of CO₂ adsorption at 150 K in the reference wedge pore of SH = 2 nm, L = 10 nm and α = 5°: a adsorption and b desorption. The points from A to J are as labelled in Fig. 2

From the points A to C in Fig. 3a, the mass starts building on the pore walls via layering until the critical conditions are reached which triggered the condensation and the pore is filled at the point D with two menisci formed. The pore is then further filled through the proceeding of the menisci to the pore mouths. This adsorption process is also evidenced by the isosteric heat of adsorption presented in Fig. 2b; the main characters are summarized as below.

• (a) The linear monotonic increment of heats released during the formation of the first adsorption layer, with the feature of constant solid–fluid contribution.

• (b) After reaching the maximum, the heat drops which indicates molecules start to adsorb on the second layer, which is further from the pore walls compared to the first adsorption layer, therefore solid–fluid interaction decreased.

• (c) Constant heat is observed when condensation occurs, corresponding to the sharp step in the isotherm.

At the point E, the snapshot in Fig. 3a shows that five domains (labelled as I–V) are formed inside the pore. Each domain contains an integer number of layers (commensurate packing) with an increment of one layer between the two adjacent domains, bifurcated via the sections termed as junction (incommensurate packing) [37].

As the pressure is decreased from point E to F, the menisci of both pore ends recede gradually into the pore, dominated by the one from the wider end. When the meniscus of the wider end approaches the junction between the domains IV and V (at Point G), where the adsorbate is less cohesive, a sharp evaporation is triggered due to the instant evaporation of molecules in domain IV, illustrated as the 1st step in the isotherm. Followed the sharp step is the gradual evaporation of the junction between domain III and IV. This evaporation process is repeated as the menisci are continued to recede, dominated by the meniscus at the wider end which proceeded through the domain III following by the domain II. This can be referred to the second and third steps in the isotherm (see Fig. 2). It should be noted that the commensurate packing in the domain I is retrograded with the reducing pressure. Consequently, the remaining mass evaporates simultaneously with domain II at point J.

From Fig. 3, the pore sizes corresponding to the junctions can be obtained, which are 6.14σ_ff, 7.12σ_ff, 8.07σ_ff and 9.03σ_ff, respectively. The interval of the pore size of junctions is approximately 0.96σ_ff and consistent with the results in Liu et al. [23]. The homogeneous slit pores with these pore sizes demonstrate incommensurate packing while those having pore sizes in between demonstrate commensurate packing [23].

3.2 Effects of temperature

The adsorption isotherms of CO₂ in the homogeneous wedge pore within a temperature range of 150–216.6 K are illustrated in Fig. 4. The following features are observed,

• (a) As the temperature increases, the hysteresis loop gradually transits from Type C (de Boer Classification) or Type H2(b) (in IUPAC) into Type A (or Type H1 in IUPAC) and then shrinks until it is completely disappeared at 216.6 K.

• (b) The distinct sharp steps formed in the desorption branch at 150 K are gradually smoothed out at higher temperatures (160 K in this case), indicating a critical temperature of this “stepwise” behaviour is between 155 and 160 K for the reference homogeneous wedge pore.

• (c) The stepwise desorption is originated from the alternation of commensurate and incommensurate packing along the pore axis direction. The higher thermal motion of particles at higher temperatures is adverse for packing, as further illustrated by the snapshots at various temperatures in Fig. 5.

• (d) The positions of the junctions (i.e., where incommensurate packing occurs) in a specific system are not affected by the temperature. However, with the increase of temperature, the adsorbate at the large open end become less structured and eventually propagate into the whole pore.

Fig. 4

Isotherms of CO₂ adsorption at various temperatures in the reference wedge pore of SH = 2 nm, L = 10 nm and α = 5° with a absolute pressure in log scale and b reduced pressure. Isotherms in b for 155 K, 160 K, 173 K, 194.7 K and 216.6 K have been shifted up by n × 25 kmol/m³, respectively

Fig. 5

Snapshots of saturated pressures at various temperatures in the reference wedge pore of SH = 2 nm, L = 10 nm and α = 5°

3.3 Effects of pore length

Figure 6 shows the isotherms at 150 K for wedge pores of lengths 10 and 15 nm with SH = 2 nm and α = 5°. Figure 7 illustrates the comparison of the respective snapshots just after the condensation and at pressure of 15 kPa. The following observations can be made.

• (a) The condensation pressures are found almost identical for both pore lengths and the fraction of the adsorptive capacity associated with condensation is decreased with pore length. However, the sections occupied by the condensed fluid are identical for both pore lengths (as shown in Fig. 7a).

• (b) After initial condensation, two extra steps are observed for the longer pore on its adsorption branch. These steps are correlated to the formation of the two domains VI and VII in Fig. 7b. These distinct steps are synchronized with the extra steps on desorption branch, which is in accordance with the result reported in Klomkliang et al. [37], where this phenomenon also occurs in a wedge pore with a closed narrow end for argon at 77 K [37]. The reason is due to that similar scenario as a closed end as the particles accumulating to a certain quantity at the narrow end in the open wedge pore.

Fig. 6

Isotherm for CO₂ at 150 K in the wedge pores of lengths 10 and 15 nm, SH = 2 nm and α = 5°

Fig. 7

Snapshots a just after condensation; b at 15 kPa for CO₂ at 150 K in wedge pore of lengths 10 and 15 nm, SH = 2 nm and α = 5°

3.4 Effects of angle

The effects of angle on the isotherms of wedge pores with a constant SH of 2 nm and the pore lengths of 10 and 15 nm, are illustrated in Fig. 8. When the angle is decreased from 5° to 1°, the adsorption and desorption branches shift to lower pressures due to the greater solid–fluid interaction exerted by the narrower average pore width. This enhanced solid–fluid interaction is also accounted for a higher saturation adsorption capacity. Moreover, the number of steps on desorption branch decreases along with a reduction in pore angle, indicating less domains are formed as shown in Fig. 9.

Fig. 8

Isotherm for CO₂ at 150 K in wedge pore of angles α = 1°, 2.5° and 5°, SH = 2 nm, a L = 10 nm; b L = 15 nm

Fig. 9

Snapshots at 10 kPa and 150 K in wedge pore of α = 5°, 2.5° and 1°, SH = 2 nm, L = 10 nm

Furthermore, the pore sizes corresponding to the junctions in these wedge pores are found to be consistent despite the variation of tilt angles. It is evident that the pore sizes of the junctions are specific and independent of the wedge angles. This feature could be potentially utilized to improve the characterization of porous materials. These observations are made in pores with smooth pore walls. The following section is to understand the effects of corrugated solid surface and the effects of non-uniformity of pore, both geometrically and energetically, along the pore axis on the adsorption behaviour and hysteresis.

3.5 Effects of corrugation

The effects of corrugation are examined by grafting small humps of 0.5 nm width along the pore axis onto the reference wedge pore at 150 K. The spacing between the humps and the homogeneous pore walls is kept as ∆ in graphite and the same affinity of pore was employed or otherwise stated. The configurations and properties of the humps are then elucidated for each case as follows.

3.5.1 Effects of the positions of humps

Two pairs of double-layers humps (i.e., amplitude equals 2∆) are grafted symmetrically on each side of the wall, with the center of the humps are aligned either with the junctions (y = 17.6σ_ff and 23σ_ff, i.e., J-II and J-III in Fig. 7b) or located within the domains (y = 19σ_ff and 25σ_ff, i.e., III and IV in Fig. 7b). The isotherms are presented in Fig. 10 with that of the reference homogeneous wedge pore for comparison purposes.

Fig. 10

Isotherms of adsorption in pores with two pairs of double-layers humps grafted on the pore walls at domains and junctions

In the reference homogeneous wedge pore, the evaporation of the domains IV and III are corresponding to the first and second steps (see Fig. 3), respectively, while the junctions J-II and J-III is accounted for the plateaus before reaching the second and third steps, respectively. By adding the humps at these positions, we can make the following observations:

• (a) The condensation occurs at a lower pressure when there are humps grafted to the pore walls, due to the enhanced solid–fluid interaction compared to the reference wedge pore.

• (b) In the corrugated pores, a new hysteresis is observed after the condensation, the one obtained with humps grafted at J-II and J-III is more pronounced.

• (c) When the humps are located within the domains III and IV, a same number of steps is observed in the major hysteresis as the reference wedge pore. However, the first step shifts to a higher pressure and the contrary was seen for the second and third steps. As learnt from the snapshots in Appendix 2, the first step is caused by the partial evaporation of the domain IV. The fraction between the two humps is retained and evaporated gradually as the plateau in the isotherm. The same mechanism is applicable for the second and third steps.

• (d) By changing the positions of the humps to the junctions J-II and J-III, the step numbers of the major hysteresis were reduced from three to two. The first step shifts to a lower pressure due to the enhanced junctions with the presence of humps. Subsequently, the second and third steps are merged into one and evaporated at the pressure of the third step as of the reference case. This is due to the packing of the domain III was reinforced by the presence of humps.

The results of adding one extra pair of humps are discussed in Appendix 3.

3.5.2 Effects of the affinity of the humps

Given the same affinity of the humps and the pore walls, the average pore size of the corrugated pore was smaller than the corresponding homogeneous wedge pore, hence stronger forces exerted to the adsorbate, as illustrated in the previous sections. Very often in practical applications, the impurities embedded in the solid have weaker affinity than carbon. For an extreme case, there is no interaction between the humps and the fluids, and this is realized by setting the well depth of the solids used to construct the humps as ε_ss/k = 0 K in this work. This humps therefore have no adsorptivity towards the fluids, and weaken the interaction between the corrugated pore and CO₂. Figure 11 presents the comparison of the adsorption isotherms between the strong humps (ε_ss/k = 28 K) and weak humps (ε_ss/k = 0 K), where two pairs of humps are grafted within the reference wedge pore in the domains III and IV. The snapshots of the points A–J as labelled in Fig. 11 are shown in Fig. 12 to facilitate the understanding of the underlying mechanism.

Fig. 11

Isotherms for CO₂ at 150 K in reference wedge pore having two double-layers humps (ε_ss/k = 0 K or 28 K) at the domains III and IV

Fig. 12

Snapshots of CO₂ adsorption at 150 K in the wedge pore containing two double-layers humps with weak affinity (ε_ss/k = 0 K) corresponding to the points A–J in Fig. 11. The dashed lines are labelled at the same positions as in Fig. 2, i.e., the positions of the junctions

The snapshots for the strong affinity humps can be referred to Fig. 13a in Appendix 2. The snapshots of the weak affinity humps with A–J labels are shown in Fig. 12 to facilitate the understanding of the underlying mechanism. Some key features are described as follows:

• (a) The condensation pressure shifts to a higher pressure as the total affinity of the pore walls is decreased due to the lower solid–fluid interactions.

• (b) With the presence of weak humps, multiple steps are formed in the adsorption branch. Interestingly, as illustrated in Fig. 12, the sharp condensation is corresponding to the formation of domains, while the development of the junctions is demonstrated as plateaus in the isotherm.

• (c) In the desorption branch, the domain V was not affected by the grafted weak humps. Therefore, the evaporation process from the saturated pore follows the comparable path as that of the reference homogeneous wedge pore. The sharp step of point H to I corresponds to the simultaneous evaporation of two domains III and IV, different from the sequential evaporation as in the reference wedge pore, due to the weakened packing within the two domains.

4 Conclusions

We investigated CO₂ adsorption and its stepwise behaviour under subcritical conditions in mesoporous wedge pores using the GCMC simulation. We found that the stepwise desorption behaviour in wedge pores can be a unique characteristic of any adsorbate using a single-site molecular model. For a given wedge pore, there exists a critical temperature for the occurrence of stepwise desorption. Low temperature facilitates the formation of ordered structures in the wedge pore and hence steps of desorption branch. As temperature increases, disordered structures are likely to occur at the wide end and then proceed at the narrow end, until propagated to the entire pore. For a given adsorbate, the pore sizes for junctions are fixed, specific and independent of temperature or pore tilt angle. The number of steps occurred during desorption is dependent on the number of alternating packing of junctions and domains inside the pore. Grafting humps that have strong affinity on the interior surface of wedge pore at different positions, i.e., at junctions or domains, not only can retain the stepwise desorption as more ordered structure is formed, but also facilitate the formation of steps in the adsorption branch. However, interference to the structured packing by the weak humps causes the diminish of the steps in the desorption branch. With more humps grafted on the pore walls, the wedge pore resembles the characteristics of ink-bottle pore and evaporate via cavitation-like pore blocking mechanisms.

Appendices

Appendix 1

1.1 VSE/VLE data for CO₂

We employed the Bin-Canonical Monte Carlo (Bin-CMC) scheme to determine the VSE and VLE data for CO₂ at various temperatures. The system for VSE simulation is initialized by placing a solid slab of 7 × 12 × 7 unit cells (i.e., 2352 CO₂ molecules) arranged in the fcc structure in the middle of an elongated simulation box with vacuum spaces on both sides of the slab. The main difference for VLE simulation is that the solid slab is replaced with a lattice having an initial density equals to the bulk liquid density at the boiling point of CO₂ (i.e., 3.55 × 10⁴ mol/m³). The simulation box is divided into 25 bins and the bin size is smaller in the interfacial and condensed phase regions and larger in the gas phase region. We used 6 × 10⁵ cycles, with 1000 displacement moves in each cycle, in both equilibration and sampling stages to ensure the accuracy of the outputted data. Details of the Bin-CMC scheme can be found in Fan et al. [38].

Appendix 2

2.1 Two layers two humps

See Fig. 13.

Fig. 13

Snapshots for CO₂ adsorption at 150 K in wedge pore having two humps located a in domains; b at junctions; SH = 2 nm, L = 10 nm and α = 5°

Appendix 3

3.1 Two layers three humps

To illustrate the effects of number of humps, an extra pair of humps is grafted to the pore walls based on the configurations presented in Fig. 7b, the centres of the humps are allocated at y = 12 σ_ff and 13 σ_ff, respectively, for the scenarios of located at junctions and within domains. The adsorption isotherms are shown in Fig. 14 and exhibit a stepwise behaviour in both adsorption and desorption branches, and formed multiple (fused) loops. Similar mechanisms can be seen from the experimental isotherms of noble gases in the nanoporous material [39].

Fig. 14

Isotherms of adsorption in pores with three pairs of double-layers humps grafted on the pore walls at different locations

With the increasing number of humps at domains and junctions, we can see from Fig. 15 that the wedge pore turns into a pore structure similar to an ink-bottle pore comprised of necks and cavities. The condensation occurs sequentially in the cavities, advancing from the small to the large end, and exhibited as the sharp steps in the adsorption branch. The necks between two adjacent domains filled gradually by pore filling and correspond to the plateaus in the isotherm. This adsorption process is identical as the case of weak humps that presented in Fig. 11. The evaporation mechanism is cavitation-like pore blocking [40], with two menisci recede into the pore interior, again the sharp steps in the desorption branch reflect the evaporation of the domains.

Fig. 15

Snapshots for CO₂ adsorption at 150 K in wedge pore having three humps located a in domains; b at junctions; SH = 2 nm, L = 10 nm and α = 5°

Appendix 4

4.1 Adsorption isosteric heat

As shown in Fig. 16a, the isosteric heat of the wedge pore with tilt angle of 2.5° is similar as that of the reference pore, i.e. α = 5°, except the peak shifts to higher loading. This is because larger tilt angle creates larger pore volume, with the same amount of adsorbate on the completion of the first adsorption layers, results in smaller pore density. For the case of corrugated wedge pore, the most interesting feature is for each step observed in the isotherm, the constant heat is found as seen in Fig. 16b.

Fig. 16

Isosteric heat curves for CO₂ adsorption at 150 K a in the reference wedge pore (α = 5°) of SH = 2 nm and L = 10 nm, b in the corrugated pore with two double-layers humps grafted at the domains III and IV (see isotherm in Fig. 11)