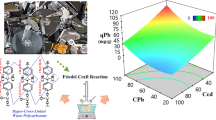
Abstract
Heavy metal water pollution is a global concern in recent years. Copper is a toxic metal at higher concentrations (> 20 μg /g) and needs to be removed using ion exchanger systems. This study investigates the removal efficiencies of copper by the non-metallic fraction (NMF) waste printed circuit boards (PCBs). The high maximum adsorption capacity of copper by the PCB-derived material after activation with KOH was 2.65 mmol/g, and the experimental isotherm was best correlated by the Temkin model. Finally, this study presents a novel dual site adsorption/ion exchange mechanism, wherein the potassium (from the activation) and calcium (present in the structure) served as ion exchange sites for the copper in the solution. Therefore, this recycling study, focusing on cyclic environmental management, converts a major waste material to an activated ion exchange resin (high capacity) for the removal of copper from wastewater solutions and successfully regenerates the resin for re-use while producing an acidic copper solution for recovery by electrolysius or chemical salt precipitation.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Water, without dispute, is one of the most vital resources for human life sustainability; daily human activities require water for drinking, food generation and many industrial activities. However, water pollution seems to pose one of the most critical global concerns. Increasing population and industrialization causes water scarcity issues, affecting approximately 80% of the world. Additionally, the reduction in clean water sources due to climate change is a further growing concern.
Heavy metal pollution is highly significant, with large amounts released from anthropogenic sources in mobile and toxic forms. It threatens both human and aquatic life due to its toxicity and carcinogenicity [1]. Furthermore, several review articles on heavy metal presence in the environment [2] have reported heavy metals, including cadmium, zinc, and copper, are related to toxic pollution in its dissolved form [3]. In the present study, the heavy metal of interest, copper, is used in pipes, wires, cookware, and in drinking water and swimming pools in the form of copper sulfate. Copper salts are also present in birth control pills and devices [4]. Additionally, copper is one of the most toxic heavy metals extensively present in industrial waters due to its versatile applications in industries including electroplating, etching, plastics, and metal finishing [1]. It is an essential element for human functioning, however, when its concentration is higher than 20 μg/g, it becomes toxic [5].
Several research groups have focussed on the removal of heavy metals from different sources of polluted water. Furthermore, there are plenty of review articles published to summarize all these studies [6]. Heavy metals are currently removed using electrochemical [7], electrocoagulation and precipitation [8], electrodeposition [9], ion exchange [10, 11], thermal and mechanical-chemical processes [12], membrane [6] and phytoremediation [13]. There are various wastewater treatments available,each has its advantages and disadvantages, especially in terms of capacity, efficiency, costs, feasibility, and environmental impact. For instance, the process of coagulation-flocculation is cheap and straightforward; however, it leads to incomplete heavy metal removal and the production of a massive amount of sludge. Similarly, inexpensive techniques such as precipitation are inefficient in removing heavy metal concentrations while producing toxic sludge.
Some studies have focused on adsorbents that remove heavy metals as they act as ion exchangers das Gracas et al., 2015; [11] in addition to synthetic ion exchangers [14]. Some examples of adsorbents and resins used for copper removal are biochars [15, 16], bone char [17,18,19], natural ion exchange materials, such as peat [20, 21], calcium alginate [22], activated bamboo [23], aminated MCM-41 [24], pyrolysed tyre char [25], iron nanocomposites [26], hydrogels (Ozay et al., 2020), CNT-dendrimers [27], magnetic adsorbents [28] and synthetic resins such as, imino-diacetate resin [29, 30] and Lewatit Monoplus [31].
Furthermore, a recent review by Wadhawan et al. [32] states that the adsorption process is gaining attention for the treatment of industrial wastewaters because of its simple design, cost-effectiveness, and low investment. Additionally, removal inefficiency and regeneration restrict their commercialization,researchers are working on increasing functionalization to enhance adsorption capacities and facile separation.
Various methods of copper removal are available, including cementation, membrane filtration, electrochemical, and photocatalytic techniques. They also discuss adsorption on modified natural material, biopolymers, industrial by-products, low-cost bio adsorbents, and nanomaterials. Although physicochemical methods are the best treatment method for copper removal, high operational costs remain a disadvantage. Also, adsorbents are low in initial costs and have simple designs but are usually limited to specific ions. The review concludes by stating the need for new testing of different bio-adsorbents for maximum efficiency.
Therefore, this study aims to find a cheap adsorbent/ion exchange material derived from using an e-waste derived material and propose a novel ion-exchange mechanism. The e-waste derived resin contains both calcium and potassium mobile ions, which act as ion exchange sites for copper. It is also possible to regenerate the metal loaded ion exchanger to recover and recycle the heavy metal and re-use the regenerated ion exchange material, thereby minimizing environmental impact.
2 Experimental methodology
2.1 Chemical and materials
The adsorbent was made from the non-metallic fraction (NMF) waste printed circuit boards (PCBs) received from Hong Kong. The separation of the non-metallic fraction and the metallic fraction (MF) was conducted by the recycling company using corona electrostatic separation [33, 34]. The non-metallic fraction (representing 70% w/w of the ground resin board) had about 0.1% of metal content, while the metallic fraction (representing 30% w/w of the ground fraction) had more than 96% w/w copper and is sold for commercial recovery. Analytical grade hydrate copper (II) nitrate salt (Cu (NO3)2·6 H2O) and deionized water (DI water) were used to prepare the simulated copper (II) ion bearing effluents. All salts were purchased from Sigma-Aldrich Corporation.
Additionally, NMF, the precursor, was continuously stirred with potassium hydroxide (KOH), the activating agent for impregnation, for 3 h at room temperature. The ratio of potassium hydroxide to the PCB NMF e-waste was in the ratio of 2:1 by mass. The slurry was then heated under a nitrogen atmosphere (purity 99.99%) up to to 250 °C at a rate of 5 °C min−1 for 3 h in an 18 L muffle furnace (AAF 11/18, Carbolite, UK). By keeping the nitrogen atmosphere constant, the furnace was cooled to room temperature. Also, to remove the unreactive activating agent, the resultant material was washed with hot water several times until the pH value is neutral. Finally, the material was stored in a desiccator after it was dried at 110 °C for 24 h for the later characterisation and water treatment experiments.
2.2 Characterization methods
2.2.1 Elemental analysis
Elemental composition was conducted using the CHNS elemental analyzer (Elementar Vario EL III, Varian, Germany), which provided the mass ratio of carbon, hydrogen, nitrogen, and sulfur in the material. Around 5 mg was carefully weighed and placed in a tin foil container, and the weights were recorded before sealing by compressing into a flat disc. The instrument then combusted the sample by cracking in a reductive atmosphere at 1423 K. The produced gases, a mixture of CO2, H2O, N2, and NOxs along with the steam, passed through adsorption columns and a thermal conductivity detection system (TCD). The constant helium flow was used as a reference to measure the conductivity of the combusted gases and subsequently quantifying the elements. A qualitative analysis of the elements was conducted using the X-ray fluorescence (XRF) technique (JSX-3201Z, Jeol).
2.2.2 Fourier transform spectroscopy (FTIR)
FTIR was used to identify the bond formations in the sample. The samples were first diluted with potassium bromide (KBr) at a weight ratio of 1:100 and then compressed into a flat disc. This study was carried out using Spectrum GX, Perkin Elmer FTIR spectrometer and recorded from 500 to 4000 cm−1.
2.2.3 N2 adsorption–desorption studies/ BET analysis
The surface area of the raw and activated adsorbent materials was conducted by Autosorb1-Quantachrome instrument using adsorption–desorption of nitrogen at 77 K. The sample underwent an outgassing process after keeping in the desiccator for 3 h at 150 °C to remove the moisture and impurities on the solid surface.
2.2.4 X-ray photoelectron spectrometry (XPS)
XPS is a surface-sensitive spectroscopic technique that quantifies the elemental composition, concentration, and chemical states in a sample. In this study, the X-ray spectra were acquired using the XPS-PHI5600 system, a monochromatic Al Kα as an energy source, 10 kV voltage, and a current of 15 mA. Water molecules were removed by drying and vacuum pumping the sample to avoid water adsorption influence in the results. Additionally, a low-resolution range spectrum was acquired by passing 70 eV pass energy, while 20 eV pass energy was used to obtain the high-resolution narrow range spectrum.
2.2.5 Scanning electron microscopy with energy dispersive x-ray spectroscopy (SEM–EDX)
Scanning Electron Microscopy (SEM/EDX) was used for the surface analysis of the samples, whereby high-resolution images were received. The study of the X-rays emitted from the sample also gives more quantitative elemental information. A scanning electron microscope, Jeol JSM-6700F, was used for the analysis after the samples were suspended in ethanol, coated with gold, and dropped on the carbon tape. The emitted X-rays also gave insight into the chemical compositions due to the atomic structure of the sample.
2.3 Experimental procedures
2.3.1 Methodology to perform isotherms
Adsorption studies were carried out in a temperature-controlled shaker at 25 ˚C, 120 rpm by mixing weighed adsorbents with adsorbate solutions with specified concentrations in plastic bottles. Inductively coupled plasma-atomic emission spectrophotometer (ICP-AES) (Optima 7300 DV, Perkin-Elmer) was used to measure the initial and final concentrations. The uptake capacities (Qe) were calculated using Eq. (1): -
Co and Ce are the initial and final concentrations (mmol/L) of the solution, respectively, V is the volume of the solution in liters, and m is the mass of the adsorbent in grams. For reference, the final pH values were also measured. All the experiments were done in triplicate, and the obtained results are within ± 5% error.
2.3.2 Equilibrium isotherm
Single-component adsorption of Cu2+ ions was carried out to evaluate the prepared activated material’s adsorption behavior and equilibrium capacity. Firstly, 50 mL of metal ion solution, from the range of 0 mmol/L to 3.35 mmol/L was added to 100 mL plastic bottles containing 50 mg of the adsorbent each. These bottles were then placed in a shaker at 120 rpm and 25 °C until the equilibrium statewas achieved. The solution pH was adjusted to an initial pH value of 5.0 resulting final pH values in the range 6.0 to 6.3 depending on the solution final concentration. Further, the equilibrium pH was measured, and the samples were filtered. Similar experiments were employed for the binary component system (calcium and potassium) to evaluate the behavior of the material.
3 Model theory
3.1 Equilibrium modelling
Empirical design procedures to predict the performance of the adsorption process are employed since the adsorption process proceeds via varied mechanisms. Therefore, the maximum capacity of adsorption was predicted under a set of conditions between the adsorbed sites and metal solution concentrations. These sorption curves were obtained by measuring the adsorption of metal ions onto the sorbents with fixed dosage, temperature, and pH. The following isotherm models, shown in Table 1, were used to fit the experimental data points and study the correlations of solid and fluid phase concentrations. Furthermore, a non-linear sum of the error squares (SSE) method was selected [35] to be used to evaluate the best fit model.
The differences between the experimental values and the calculated values were used to obtain the constants for each isotherm equation, using the solver function in the Microsoft Office Excel program for SSE as shown in Eq. (2):.
where qcal is theoretical sorption capacity calculated from each kinetic model, qexp is the experimental sorption amount. The equilibrium isotherm with the least SSE value was chosen as the best-fit isotherm model for this Cu ion exchange system. Similar calculations were conducted for the potassium and calcium desorption systems.
4 Results and discussion
4.1 Materials characterization
Although the starting material is from a different batch of ground printed circuit board (PCB), the raw unactivated material and the activated material from the PCB have been characterized in our previous studies [33, 36]. Consequently, the same methodologies have been used in the present studyand the values are different but similar. Therefore the characterization results are not presented and discussed in the paper but we have included them in our Supplementary Material.
-
Elemental Anlysis
-
Fourier transform spectroscopy (FTIR)
-
N2 adsorption–desorption studies/ BET analysis
-
X-Ray Photoelectron Spectrometry (XPS)
-
Scanning Electron Microscopy with Energy Dispersive X-ray Spectroscopy (SEM–EDX)
4.2 Experimental equilibrium results
Copper removal efficiency was studied at concentrations ranging from 0 mmol/L to 3.3 mmol/L. As seen in Fig. 1, the maximum experimental copper adsorption capacity (Qe) is very high at 2.65 mmol/g. This capacity is higher or comparable to most other research studies. Studies by Mahdi's research group on date seed removal of copper showed an increase in the adsorption from 0.421 mmol/g to 0.705 mmol/g after alkali treatment [37, 38].
Other biochar systems for copper removal include modified biochar [39], pyrolysed biochar (Park et al., 2016), agro-industrial waste [40] with copper uptake capacities of 0.28, 1.23 and 0.21 mmol/g respectively, and activation with potassium hydroxide helped. According to Yu et al. [41], nitrogen doping biochar increases copper adsorption capacities up to four times or 1.63 mmol Cu2+/g. Additionally, other novel adsorbents; ion exchange nanoparticles (Yurekli et al., 2019), activated carbon [42], sulphonated multi-walled carbon nanotubes (Ge et al., 2014), amino-functionalised silica [43] and alginate nanofibers [44] have lower adsorption capacities of 1.76, 1.4, 0.94, 0.53, and 1.37 mmol Cu/g, respectively. Also, adsorption by sewage sludge ash and aminated cellulose showed copper removal rates of 0.13 mmol/g [5] and 1.09 mmol/g [45], respectively. Therefore, our material provides a better or comparable copper removal efficiency.
4.3 Isotherm model analysis
A non-linear approach analyzed the different isotherm models mentioned in Table 1 – and compared them with the least square of the errors method. Microsoft Excel Solver was used to evaluate the model equations in the concentration range compared with the theoretical values. Furthermore, the sum of squared errors (SSE) for each model is used to evaluate which model was the ideal fit. Table 2 shows the estimated isotherm parameters and SSE values for the adsorption isotherm model equations and SSE values of copper on the activated material. All the models agree well, as shown in Fig. 2a and b, with the experimental results (adsorption of copper on the material), the Temkin model’s best fit model with the least sum of squares of error (0.18). Previous studies of copper removal using kernel activated carbon [46] and biochar [47, 48] preferred the Temkin model for fitting the adsorption as well.
The Langmuir and Freundlich isotherm models consider the adsorbate material to be homogenous and heterogeneous, respectively. Therefore, that justifies the differences between the SSE values (0.45 for Langmuir and 0.27 for Freundlich) to the experimental values. Furthermore, SIPS/Langmuir–Freundlich and Redlich-Peterson models are modified Langmuir models [49],our modeling results have a difference in SSE of approximately 0.20 with the Langmuir model. While Toth model displayed similar patterns, DR had the highest SSE of 0.56.
4.4 Mass balance analysis
The adsorption of Cu2+ on the activated material takes place via an ion-exchange mechanism. The hypothesis is that the raw material, NMF, is an ion exchange material with calcium (Ca2+) exchange sites bound in an aluminosilicate matrix, and, after treatment, it has acquired potassium (K+) exchange sites after activation with KOH, with available calcium sites due to the matrix bonds cleavage due to the alkali attack. The ICP-AES results confirm this statement. One copper (II) ion (Cu2+) can exchange with either one Ca2+ or two K+ ions in the adsorbent exchange material.
Figure 3 shows the adsorption of copper, along with the desorption isotherms of calcium and potassium. The maximum desorption capacity of calcium and potassium occurs at the highest concentration with 1.86 mmol/g and 0.80 mmol/g, respectively. The maximum adsorption of copper and desorption capacity of calcium and potassium occurs at 3.5 mmol KOH/L.
Theoretically, one divalent calcium or two monovalent potassium ions should replace one copper ion, as confirmed by Fig. 3, which shows the three metals' mole balance. The calcium and potassium desorption values added together reach values very close to the copper ion's capacity. Table 3 also shows a small difference between the adsorption capacities and the sum of potassium and calcium capacities (% error < 4%).
The mass balance equation can therefore be represented accurately by Eq. (3):-
4.5 Binary exchange model and analysis using the desorption isotherms
As discussed in Sect. 4.4, Fig. 3 shows the experimental results of copper adsorption on the adsorbate material with potassium and calcium exchange sites. The desorption modeling confirmed the proposed mechanism by comparing the isotherm models. Figure 4a, b and Table 4 shows the desorption modeling isotherms of calcium and potassium. They follow the same behavior as the copper adsorption models and experimental results – with maximum desorption capacities at the highest concentrations. When the copper adsorbed at the highest concentrations, the calcium and potassium concentrations increased in the solution, confirming the ion-exchange mechanism.
Therefore, there is a good correlation between the calcium and potassium desorption isotherms models and the copper models in both the experimental and theoretical results. As in the copper adsorption case, the Temkin type model was most applicable to the calcium and potassium desorption model with the minimum SSE of 0.06 and 0.02, respectively. With the proposed ion-exchange model in Fig. 5, the loaded metal (copper) can be recovered and recycled to reduce environmental impact. In terms of regeneration, copper can be leached out by dilute acid at pH 1.50 to 2.50, enabling the copper to be recovered by electrolysis or precipitated as a salt.
4.6 Comparison of models
This section compares the novel model methods applied in this study with the experimentally measured data values. The mass balance equation results from Table 3 and the overall best-fit isotherm models from Fig. 2 are compared with the novel model from Sect. 4.4 (Eq. 3 using the Temkin model equation from Table 1).
Based on Eq. (3) and the best fitting isotherm expressions for each of the three terms in Eq. (3), the following equation obtained for the removal of copper from water:-
Equation (5) reduces to Eq. (6), a composite model equation:-
Table 5 shows the validity of the composite Eq. (6) for copper removal since it correlates well with the experimental and calculated copper adsorption values (Temkin model); and the summation of the desorption values of calcium and potassium. The mean squared error (MSE) between the suggested models and the experimental adsorption capacities of copper by the adsorbent is ≤ 0.01. As seen in Table 3 and discussed before, the desorption model equation or the mass balance results showed little difference from the experimental values. Similarly, the desorption model's MSE values are 0.00, followed by the Temkin model and the composite equation with errors of 0.01 each. Since the composition equation summarizes the Temkin equations of calcium and potassium; similar error values to the Temkin values for copper are expected. Also, Fig. 6 shows the similarity in the behavior of the three models with the experimental values as well.
4.7 Regeneration
The objectives of an adsorbent exchange resin regeneration is twofold: (i) provide refreshed treated spent adsorbent material back to its original form for further service; (ii) recover the adsorbed metal or metal salt for recycle and reuse.
In this study hydrochloric acid was used to regenerate the copper loaded resin and the results are shown in Table 6. Three regeneration samples were performed at 3 min and 5 min and one at 10 min, with copper percentage recoveries of 82.14%, 82.50% and 82.65% respectively using an acid concentration of 0.1 M. When the acid concentration was increased to 0.2 M the percentage copper removal by regeneration was 91.70%, 93.4% and 93.5% at 3 min, 5 min and 10 min respectively. The parameters studied were the acid concentration and contact time. The contact time as shown does not have a significant effect on the recovery of the copper ions and the recovery efficiency is relatively constant after 5 min or more.
Although the regeneration contact time did not influence the copper recovery efficiency very much after 3, 5 and even 10 min, however, the acid concentration made a significant impact on the copper desorption. When the initial concentration of HCl was 0.3 M, the material started to dissolve and around 5% of the material was lost. Further increases in HCl concentration to 0.5 M and 1.0 M, resulted in 45% and 100% respectively of the material being dissolved in the acid solution. However, by controlling the initial acid concentration in the range of 0.1 M to 0.2 M, then it was possible to desorb more than 80% and 90% respectively of copper ions from the resin. The recovery efficiency increases around 10% when the initial concentration increases from 0.1 M to 0.2 M.
After the recovery of the copper ions, the material was backwashed with water several times and then filtered, followed by drying. After the drying process, the material was tested for the uptake ability for the second round, metal ions removal study.
The results of copper removal capacities by the fresh and regenerated adsorbent for three samples after initial adsorption and then after two rounds of regenerationin, namely, the first and second rounds are presented in Table 7. The results show that the removal capacity is decreasing at each regeneration.
The reason for the decreasing capacities during regeneration is twofold. The firstis due to some of the copper is strongly adsorbed onto the resin and does not desorb under the applied conditions. This effect can be seen and quantified from the results in Table 6. Under the conditions studied in Table 7 at 0.2 M acid concentration and 5 min contact time the copper remaining on the resin adsorbent is of the order of 6.5%. However, from the results in Table 7, the copper uptake is 84% and not 93.5%; the theoretical amount of site available based on the desorption only study. Consequently, there is a second reason for the lower copper uptake. In order to investigate the reason, a N2 adsorption–desorption analysis was used to investigate the change of the surface area after the regeneration process.
The surface area analysis shows that the surface area of the regenerated material is around 246 m2/g which is much larger that that of the original A-NMF around 218 m2/g. However, despite the increase of the surface area, the pore volume decreased from 0.80 cc/g to 0.58 cc/g. The decrease of the pore volume might be a reason that the regenerated material has lower adsorption capacity – active available adsorption sites being removed during the regeneration process, leaving the non-adsorbing sites at the surface. Another reason is that the functional adsorption sites are occupied by hydrogen ions during the acid regeneration process, and some of these hydrogen ions are not exchangeable.
5 Conclusion
The results obtained show the activated non-metallic fraction (A-NMF) of waste printed circuit boards as an excellent ion exchange adsorbent for copper removal, being comparable or better than many of the conventional ion exchange resins and exchange-adsorbents created from waste materials. The excellent copper adsorption capacity was 2.65 mmol/g and the best fit was the Temkin model with the least sum of squared error from the experimental data values. Additionally, the aluminosilicate structure in the NMF paves the way to a novel mechanism; when activated with alkaline KOH, the created potassium sites with the existing calcium sites serve as exchange sites for divalent copper ions in solutions. Finally, the mole balance of copper and potassium and the desorption model isotherms of calcium and potassium confirm the novel ion-exchange mechanism. Consequently, a new model equation is proposed, which is useful in assessing copper removal on binary site ion exchange materials.
Acid regeneration has proved to be successful by removing 80% of the adsorbed copper at each regeneration step but more studies are required in this area to optimize the regeneration phase and the eventual recovery of the copper for re-use.
References
Sarma, G.K., Sen Gupta, S., Bhattacharyya, K.G.: Nanomaterials as versatile adsorbents for heavy metal ions in water: a review. Environ. Sci. Pollut. Res. 26, 6245–6278 (2019). https://doi.org/10.1007/s11356-018-04093-y
Malik, L.A., Bashir, A., Qureashi, A., Pandith, A.H.: Detection and removal of heavy metal ions: a review. Environ. Chem. Lett. 17, 1495–1521 (2019). https://doi.org/10.1007/s10311-019-00891-z
Vardhan, K.H., Kumar, P.S., Panda, R.C.: A review on heavy metal pollution, toxicity and remedial measures: Current trends and future perspectives. J. Mol. Liq. 290, 111197 (2019). https://doi.org/10.1016/j.molliq.2019.111197
Azeh Engwa, G., Udoka Ferdinand, P., Nweke Nwalo, F., Unachukwu, N., M.: Mechanism and health effects of heavy metal toxicity in humans. Poisoning in the Modern World - New Tricks for an Old Dog (2019). https://doi.org/10.5772/intechopen.82511
Rehman, M., Liu, L., Wang, Q., Saleem, M.H., Bashir, S., Ullah, S., Peng, D.: Copper environmental toxicology, recent advances, and future outlook: a review. Environ. Sci. Pollut. Res. 26, 18003–18016 (2019). https://doi.org/10.1007/s11356-019-05073-6
Bilal, M., Shah, J.A., Ashfaq, T., Gardazi, S.M.H., Tahir, A.A., Pervez, A., Haroon, H., Mahmood, Q.: Waste biomass adsorbents for copper removal from industrial wastewater—A review. J. Hazard. Mater. 263, 322–333 (2013). https://doi.org/10.1016/j.jhazmat.2013.07.071
da Silva, M.S.B., de Melo, R.A.C., Lopes-Moriyama, A.L., Souza, C.P.: Electrochemical extraction of tin and copper from acid leachate of printed circuit boards using copper electrodes. J. Environ. Manage. 246, 410–417 (2019). https://doi.org/10.1016/j.jenvman.2019.06.009
Duarte-Nass, C., Rebolledo, K., Valenzuela, T., Kopp, M., Jeison, D., Rivas, M., Azócar, L., Torres-Aravena, Á., Ciudad, G.: Application of microbe-induced carbonate precipitation for copper removal from copper-enriched waters: Challenges to future industrial application. J. Environ. Manage. 256, 109938 (2020). https://doi.org/10.1016/j.jenvman.2019.109938
de Morais, C., Nepel, T., Landers, R., Vieira, G.A., M., Florêncio de Almeida Neto, A.: Metallic copper removal optimization from real wastewater using pulsed electrodeposition. J Hazardous Materials. 384, 121416 (2020). https://doi.org/10.1016/j.jhazmat.2019.121416
das Graças Nunes Matos, M., Gouveia Diniz, V., Moraes de Abreu, C.A., Knoechelmann, A., Lins da Silva, V., Santos de Lima, E.: Bioadsorption and ion exchange of Cr3+ and Pb2+ solutions with algae. Adsorption. 15, 535–535 (2009). https://doi.org/10.1007/s10450-009-9190-9
Bazargan, A., Shek, T.-H., Hui, C.-W., McKay, G.: Optimising batch adsorbers for the removal of zinc from effluents using a sodium diimidoacetate ion exchange resin. Adsorption 23, 477–489 (2017). https://doi.org/10.1007/s10450-016-9857-y
Ventura, E., Futuro, A., Pinho, S.C., Almeida, M.F., Dias, J.M.: Physical and thermal processing of Waste Printed Circuit Boards aiming for the recovery of gold and copper. J. Environ. Manage. 223, 297–305 (2018). https://doi.org/10.1016/j.jenvman.2018.06.019
Guo, X., Liu, M., Zhong, H., Li, P., Zhang, C., Wei, D., Zhao, T.: Potential of Myriophyllum aquaticum for phytoremediation of water contaminated with tetracycline antibiotics and copper. J. Environ. Manage. 270, 110867 (2020). https://doi.org/10.1016/j.jenvman.2020.110867
Wong, C.-W., Barford, J.P., Chen, G., McKay, G.: Kinetics and equilibrium studies for the removal of cadmium ions by ion exchange resin. J. Environ. Chem. Eng. 2, 698–707 (2014). https://doi.org/10.1016/j.jece.2013.11.010
Mochidzuki, K., Sato, N., Sakoda, A.: Production and Characterization of Carbonaceous Adsorbents from Biomass Wastes by Aqueous Phase Carbonization. Adsorption 11, 669–673 (2005). https://doi.org/10.1007/s10450-005-6004-6
Goh, C.L., Sethupathi, S., Bashir, M.J.K., Ahmed, W.: Adsorptive behaviour of palm oil mill sludge biochar pyrolyzed at low temperature for copper and cadmium removal. J. Environ. Manage. 237, 281–288 (2019). https://doi.org/10.1016/j.jenvman.2018.12.103
Cheung, C.W., Chan, C.K., Porter, J.F., McKay, G.: Combined Diffusion Model for the Sorption of Cadmium, Copper, and Zinc Ions onto Bone Char. Environ. Sci. Technol. 35, 1511–1522 (2001). https://doi.org/10.1021/es0012725
Cheung, C.W., Porter, J.F., McKay, G.: Removal of Cu(II) and Zn(II) Ions by Sorption onto Bone Char Using Batch Agitation. Langmuir 18, 650–656 (2002). https://doi.org/10.1021/la010706m
Shek, T.H., Ma, A., Lee, V.K.C., McKay, G.: Kinetics of zinc ions removal from effluents using ion exchange resin. Chem. Eng. J. 146(1), 63–70 (2009). https://doi.org/10.1016/j.cej.2008.05.019
Chen, B., Hui, C.W., McKay, G.: Film-Pore Diffusion Modeling for the Sorption of Metal Ions from Aqueous Effluents onto Peat. Water Res. 35, 3345–3356 (2001). https://doi.org/10.1016/s0043-1354(01)00049-5
Ho, Y.S., McKay, G.: Competitive Sorption of Copper and Nickel Ions from Aqueous Solution Using Peat. Adsorption 5, 409–417 (1999). https://doi.org/10.1023/a:1008921002014
da Silva, M.G.C., Canevesi, R.L.S., Welter, R.A., Vieira, M.G.A., da Silva, E.A.: Chemical equilibrium of ion exchange in the binary mixture Cu2+ and Ca2+ in calcium alginate. Adsorption 21, 445–458 (2015). https://doi.org/10.1007/s10450-015-9682-8
Wang, R.-Z., Huang, D.-L., Liu, Y.-G., Zhang, C., Lai, C., Wang, X., Zeng, G.-M., Zhang, Q., Gong, X.-M., Xu, P.: Synergistic removal of copper and tetracycline from aqueous solution by steam-activated bamboo-derived biochar. J. Hazard. Mater. 384, 121470 (2020). https://doi.org/10.1016/j.jhazmat.2019.121470
Lam, K.F., Chen, X., McKay, G., Yeung, K.L.: Anion Effect on Cu2+Adsorption on NH2-MCM-41. Ind. Eng. Chem. Res. 47, 9376–9383 (2008). https://doi.org/10.1021/ie701748b
Shahtalebi, A., Sarrafzadeh, M.H., McKay, G.: An adsorption diffusion model for removal of copper (II) from aqueous solution by pyrolytic tyre char. Desalin. Water Treat. 51, 5664–5673 (2013). https://doi.org/10.1080/19443994.2013.769659
Wu, Q., Wang, D., Chen, C., Peng, C., Cai, D., Wu, Z.: Fabrication of Fe3O4/ZIF-8 nanocomposite for simultaneous removal of copper and arsenic from water/soil/swine urine. J. Environ. Manage. 290, 112626 (2021). https://doi.org/10.1016/j.jenvman.2021.112626
Hayati, B., Maleki, A., Najafi, F., Daraei, H., Gharibi, F., McKay, G.: Super high removal capacities of heavy metals (Pb 2+ and Cu 2+ ) using CNT dendrimer. J. Hazard. Mater. 336, 146–157 (2017). https://doi.org/10.1016/j.jhazmat.2017.02.059
Feitoza, N.C., Gonc¸ alves, T.D., Mesquita, J.J., Menegucci, J., Santos, M.-K.M.S., Chaker, J.A., Cunha, R.B., Medeiros, A.M.M., Rubim, J.C., Sousa, M.H.: Fabrication of glycine-functionalized maghemite nanoparticles for magnetic removal of copper from wastewater. J. Hazard. Mater. 264, 153–160 (2014). https://doi.org/10.1016/j.jhazmat.2013.11.022
Ma, A., Hadi, P., Barford, J., Hui, C.-W., McKay, G.: Modified empty bed residence time model for copper removal. Ind. Eng. Chem. Res. 53, 13773–13781 (2014). https://doi.org/10.1021/ie501807c
Siu, P.C.C., Koong, L.F., Saleem, J., Barford, J., McKay, G.: Equilibrium and kinetics of copper ions removal from wastewater by ion exchange. Chin. J. Chem. Eng. 24, 94–100 (2016). https://doi.org/10.1016/j.cjche.2015.06.017
Wołowicz, A., Staszak, K., Hubicki, Z.: Static sorption of heavy metal ions on ion exchanger in the presence of sodium dodecylbenzenesulfonate. Adsorption 25, 393–404 (2019). https://doi.org/10.1007/s10450-019-00014-8
Wadhawan, S., Jain, A., Nayyar, J., Mehta, S.K.: Role of nanomaterials as adsorbents in heavy metal ion removal from waste water: A review. Journal of Water Process Engineering. 33, 101038 (2020). https://doi.org/10.1016/j.jwpe.2019.101038
Hadi, P., Ning, C., Ouyang, W., Xu, M., Lin, C.S.K., McKay, G.: Toward environmentally-benign utilization of nonmetallic fraction of waste printed circuit boards as modifier and precursor. Waste Manage. 35, 236–246 (2015). https://doi.org/10.1016/j.wasman.2014.09.020
Hadi, P., Xu, M., Lin, C.S.K., Hui, C.-W., McKay, G.: Waste printed circuit board recycling techniques and product utilization. J. Hazard. Mater. 283, 234–243 (2015). https://doi.org/10.1016/j.jhazmat.2014.09.032
Kalra, A., Hadi, P., Mackey, H.R., Al Ansari, T., McKay, G.: Sorption of heavy metal ions onto e-waste-derived ion-exchange material – selecting the optimum isotherm. Desalination Water Treatment 126, 196–207 (2018). https://doi.org/10.5004/dwt.2018.23038
Ning, C., Lin, C.S.K., Hui, D.C.W., McKay, G.: Waste Printed Circuit Board (PCB) Recycling Techniques. Top. Curr. Chem. (2017). https://doi.org/10.1007/s41061-017-0118-7
Mahdi, Z., El Hanandeh, A., Yu, Q.J.: Preparation, characterization and application of surface modified biochar from date seed for improved lead, copper, and nickel removal from aqueous solutions. J. Environ. Chem. Eng. 7, 103379 (2019). https://doi.org/10.1016/j.jece.2019.103379
Mahdi, Z., Yu, Q.J., El Hanandeh, A.: Investigation of the kinetics and mechanisms of nickel and copper ions adsorption from aqueous solutions by date seed derived biochar. J. Environ. Chem. Eng. 6, 1171–1181 (2018). https://doi.org/10.1016/j.jece.2018.01.021
Ding, Z., Hu, X., Wan, Y., Wang, S., Gao, B.: Removal of lead, copper, cadmium, zinc, and nickel from aqueous solutions by alkali-modified biochar: Batch and column tests. J. Ind. Eng. Chem. 33, 239–245 (2016). https://doi.org/10.1016/j.jiec.2015.10.007
Meseldzija, S., Petrovic, J., Onjia, A., Volkov-Husovic, T., Nesic, A., Vukelic, N.: Utilization of agro-industrial waste for removal of copper ions from aqueous solutions and mining-wastewater. J. Ind. Eng. Chem. 75, 246–252 (2019). https://doi.org/10.1016/j.jiec.2019.03.031
Yu, W., Lian, F., Cui, G., Liu, Z.: N-doping effectively enhances the adsorption capacity of biochar for heavy metal ions from aqueous solution. Chemosphere 193, 8–16 (2018). https://doi.org/10.1016/j.chemosphere.2017.10.134
Hotová, G., Slovák, V., Zelenka, T., Maršálek, R., Parchaňská, A.: The role of the oxygen functional groups in adsorption of copper (II) on carbon surface. Sci. Total Environ. 711, 135436 (2020). https://doi.org/10.1016/j.scitotenv.2019.135436
Quang, D.V., Kim, J.K., Sarawade, P.B., Tuan, D.H., Kim, H.T.: Preparation of amino-functionalized silica for copper removal from an aqueous solution. J. Ind. Eng. Chem. 18, 83–87 (2012). https://doi.org/10.1016/j.jiec.2011.11.089
Birajdar, M.S., Lee, J.: Hierarchically structured microgels of SPIONs, nanofibers, and alginate for copper ion removal. J. Ind. Eng. Chem. 77, 303–308 (2019). https://doi.org/10.1016/j.jiec.2019.04.052
Pereira, A.R., Soares, L.C., Teodoro, F.S., Elias, M.M.C., Ferreira, G.M.D., Savedra, R.M.L., Siqueira, M.F., Martineau-Corcos, C., da Silva, L.H.M., Prim, D., Gurgel, L.V.A.: Aminated cellulose as a versatile adsorbent for batch removal of As(V) and Cu(II) from mono- and multicomponent aqueous solutions. J. Colloid Interface Sci. 576, 158–175 (2020). https://doi.org/10.1016/j.jcis.2020.04.129
Tumin, N.D., Chuah, A.L., Zawani, Z., Rashid, S.A.: Adsorption of copper from aqueous solution by Elais Guineensis kernel activated carbon. J. Eng. Sci. Technol. 3(2), 180–189 (2008)
Amin, M.T., Alazba, A.A., Shafiq, M.: Application of the biochar derived from orange peel for effective biosorption of copper and cadmium in batch studies: isotherm models and kinetic studies. Arab. J. Geosci. (2019). https://doi.org/10.1007/s12517-018-4184-0
Mei, Y., Li, B., Fan, S.: Biochar from Rice Straw for Cu2+ Removal from Aqueous Solutions: Mechanism and contribution made by acid-soluble minerals. Water Air Soil Pollut. (2020). https://doi.org/10.1007/s11270-020-04791-9
Andelescu, A., Nistor, M.A., Muntean, S.G., Rădulescu-Grad, M.E.: Adsorption studies on copper, cadmium, and zinc ion removal from aqueous solution using magnetite/carbon nanocomposites. Sep. Sci. Technol. 53, 2352–2364 (2018). https://doi.org/10.1080/01496395.2018.1457696
Langmuir, I.: The Adsorption Of Gases On Plane Surfaces Of Glass, Mica And PlatinUM. J. Am. Chem. Soc. 40, 1361–1403 (1918). https://doi.org/10.1021/ja02242a004
Freundlich, H., Hatfield, H.S.: Colloid and capillary chemistry, pp. 110–114. Methuen and Co., Ltd., London (1926)
Dubinin, M.M.: The Potential Theory of Adsorption of Gases and Vapors for Adsorbents with Energetically Nonuniform Surfaces. Chem. Rev. 60, 235–241 (1960). https://doi.org/10.1021/cr60204a006
Sips, R.: On the Structure of a Catalyst Surface. J. Chem. Phys. 16, 490–495 (1948). https://doi.org/10.1063/1.1746922
Toth, J.: State equation of the solid-gas interface layers. Acta chim. hung. 69, 311–328 (1971)
Redlich, O., Peterson, D.L.: A Useful Adsorption Isotherm. J. Phys. Chem. 63, 1024–1024 (1959). https://doi.org/10.1021/j150576a611
Acknowledgements
The authors wish to thank Hamad Bin Khalifa University, Qatar Foundation, for supporting this research and express their gratitude to Qatar National Research Foundation for the provision of a research Award, Number: NPRP11S-0117-180328.
Funding
Open Access funding provided by the Qatar National Library.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Mariyam, S., Zuhara, S., Al-Ansari, T. et al. Novel high capacity model for copper binary ion exchange on e-waste derived adsorbent resin. Adsorption 28, 185–196 (2022). https://doi.org/10.1007/s10450-022-00360-0
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10450-022-00360-0