1 Introduction

While the adsorption of pure gases at cryogenic temperatures is a simple and convenient method for characterizing porous solids [1,2,3], the measurement and theoretical analysis of the adsorption isotherms of liquids [4,5,6,7] involves more effort because:

  1. 1.

    To date, commercial measuring devices for the adsorption of liquid mixtures are not available. Measuring reliable liquid adsorption isotherms requires experimental expertise, as both the pre-treatment of solids and liquids and the analytical method used to determine the composition of the bulk phase are crucial to the quality of liquid adsorption isotherms.

  2. 2.

    Liquid-phase adsorption, especially in the case of aqueous mixtures, is generally much more invasive than gas adsorption.

  3. 3.

    Since only mixture adsorption can be measured, the theoretical evaluation is quite complex. In addition to the adsorption behavior, the real mixing behavior of the liquid components also plays a role, as can be seen in similarities between separation diagrams and liquid–vapor diagrams [8].

Nevertheless, liquid adsorption is a fruitful field of research for at least the following reasons:

  1. 1.

    Knowledge of the preferential adsorption of one component and of separation diagrams is relevant for the design of separation and purification processes in industry and environmental technology, such as water treatment.

  2. 2.

    Binary or higher-component liquid adsorption provides information on the polarity of solid surfaces because the preferential adsorption of one component from a mixture strongly depends on the surface chemistry [8,9,10,11].

  3. 3.

    Liquid adsorption can be used as methodology to verify textural and energetic parameters of porous solids obtained from gas and vapor adsorption isotherms.

The present work is devoted to the precise measurement of the adsorption of water-containing mixtures by means of vibration densitometry, a good data fit to preserve the experimental information, the calculation of the separation efficiency of carbon materials, and the correlation of adsorption isotherms with immersion enthalpy data of mixtures, which are rarely measured because of the high experimental effort involved [12,13,14]. The model adsorbents are four carbon molecular sieves (CMS) with well-separated micro- and mesoporosity and more or less non-polar carbon surface. Their narrow micropore-size distribution can be flexibly adapted to the respective application by selecting suitable synthesis or pyrolysis conditions [15]. Furthermore, they exhibit high chemical and thermal stability, which makes them interesting for a wide range of applications [16,17,18].

The ethanol–water and propanol-water mixtures are completely miscible over the whole concentration range in the bulk phase and differ only minimally in the length of the alkyl chain of the alcoholic “oil component”, i.e. the possible influence of only one CH2 group on the liquid adsorption isotherms is to be investigated. Here, the limits of the sensitivity of the methodology are explored. Separation diagrams are calculated from the measured adsorption isotherms using the pore filling and saturation models [19,20,21]. The suitability of the models for determining reliable separation diagrams is critically evaluated. Since alcohol molecules are less polar than water molecules and are, so to speak, oil-like, the separation diagrams can be used to estimate the suitability of the various CMS samples for water treatment.

2 Theory

The preferential adsorption of one component i from a liquid mixture on a solid is described by the reduced adsorption excess \(\Gamma_{i}^{{\text{(n)}}}\) that is experimentally accessible by [20]:

$$ \Gamma_{i}^{(n)} = \frac{{n_{i}^{\sigma (n)} }}{{m_{A} }} = \frac{{n \cdot \left( {x_{i}^{0} - x_{i}^{l} } \right)}}{{m_{A} }}, $$
(1)

where \(n_{i}^{\sigma (n)}\) is the reduced excess amount of i, \(m_{{\text{A}}}\) the mass of the adsorbent, and n the total amount of substance of a binary liquid mixture. \(x_{i}^{0}\) and \(x_{i}^{{\text{l}}}\) are the mole fractions of i in the mixture before adsorption (index 0) and after reaching the adsorption equilibrium (index l).

To obtain a mathematical description \(\Gamma_{i}^{(n)} = f\left( {x_{i}^{l} } \right)\), the adsorption excess data, just like the mixture excess data, are often fitted by Redlich–Kister polynomials [22]. Since in the present case the Redlich–Kister polynomials tend to swing, we used the following functions that provide a better data fitting with smaller standard deviations:

  1. 1.

    The Kind function [23]

    with the four adjustable parameters a1, a2, b1, and b2,

    $$ \Gamma_{1}^{(n)} = b_{1} \left( {1 - x_{1}^{l} } \right)\left( {1 - \exp \left( { - a_{1} x_{1}^{l} } \right)} \right) - b_{2} x_{1}^{l} \left( {1 - \exp \left( { - a_{2} \left( {1 - x_{1}^{l} } \right)} \right)} \right) $$
    (2)
  2. 2.

    The Bi-Langmuir function [24]

    with the four parameters A, h1, K1, and K2,

    $$ \Gamma_{1}^{(n)} = A\left( {h_{1} \frac{{K_{1} x_{1}^{l} }}{{1 + \left( {K_{1} - 1} \right)x_{1}^{l} }} + (1 - h_{1} )\frac{{K_{2} x_{1}^{l} }}{{1 + \left( {K_{2} - 1} \right)x_{1}^{l} }} - x_{1}^{l} } \right) $$
    (3)
  3. 3.

    A Redlich–Kister polynomial with 3 parameters combined with an exponential term, which will be called RKE function:

    $$ \begin{aligned} \Gamma _{1}^{{(n)}} & = x_{1}^{l} \left( {1 - x_{1}^{l} } \right)\left( {\sum\limits_{{i = 1}}^{3} {\left( {A_{i} \left( {2x_{1}^{l} - 1} \right)^{{n - 1}} } \right)} } \right) \\ & \quad \cdot \exp \left( { - B\left( {2x_{1}^{l} - 1} \right)} \right) \\ \end{aligned} $$
    (4)

    with the four adjustable parameters A1, A2, A3, and B.

The obtained parameters for all measured isotherms are listed in Tables S7–S9 of the SI. On average, the smallest standard deviations are obtained with the Kind model.

As early as 1922, Ostwald and de Izaguirre [25] connected the experimentally accessible adsorption excess \(\Gamma_{i}^{{\text{(n)}}}\) with the absolute amounts \(\Gamma_{i}^{{\text{s}}} = {{n_{i}^{{\text{s}}} } \mathord{\left/ {\vphantom {{n_{i}^{{\text{s}}} } {m_{{\text{A}}} }}} \right. \kern-\nulldelimiterspace} {m_{{\text{A}}} }}\) of the components 1 and 2 of a binary liquid mixture in the sorption phase s:

$$ \Gamma_{1}^{(n)} = \Gamma_{1}^{s} x_{2}^{l} - \Gamma_{2}^{s} x_{1}^{l} ,\quad \Gamma_{2}^{(n)} = \Gamma_{2}^{s} x_{1}^{l} - \Gamma_{1}^{s} x_{2}^{l} . $$
(5)

Because a separate sorption phase s represents an idealization, Eq. (5) implies more or less justified model assumptions about the space requirements of s, such as the number of adsorbed layers on the surface, or the complete or incomplete filling of the pore system of porous adsorbents [5, 19, 20]. Assuming that the two adsorbed components 1 and 2 are both distributed on the surface, their relative loadings have to add up to 1:

$$ \frac{{\Gamma_{1}^{s} }}{{\Gamma_{1,\max }^{s} }} + \frac{{\Gamma_{2}^{s} }}{{\Gamma_{2,\max }^{s} }} = 1, $$
(6)

where \(\Gamma_{i,\max }^{{\text{s}}} = {{n_{i,\max }^{{\text{s}}} } \mathord{\left/ {\vphantom {{n_{i,\max }^{{\text{s}}} } {m_{{\text{A}}} }}} \right. \kern-\nulldelimiterspace} {m_{{\text{A}}} }}\) is the maximum loading of the pure substance i in s. Transforming Eq. (6) leads to:

$$ \Gamma_{1}^{s} = \Gamma_{1,\max }^{s} - \frac{{\Gamma_{1,\max }^{s} }}{{\Gamma_{2,\max }^{s} }}\Gamma_{2}^{s} = \Gamma_{1,\max }^{s} - \beta {\kern 1pt} \Gamma_{2}^{s} , $$
(7)

where β is the ratio of the maximum loadings \(\Gamma_{i,\max }^{{\text{s}}}\).

Combining Eqs. (5) and (7) leads to [20]:

$$ \Gamma_{1}^{s} = \frac{{\Gamma_{1,\max }^{s} x_{1}^{l} + \beta {\kern 1pt} \Gamma_{1}^{(n)} }}{{x_{1}^{l} + \beta x_{2}^{l} }};\quad \quad \Gamma_{2}^{s} = \frac{{\Gamma_{1,\max }^{s} x_{2}^{l} - \Gamma_{1}^{(n)} }}{{x_{1}^{l} + \beta x_{2}^{l} }}; $$
(8)
$$ x_{1}^{s} = \frac{{\Gamma_{1,\max }^{s} x_{1}^{l} + \beta {\kern 1pt} \Gamma_{1}^{(n)} }}{{\Gamma_{1,\max }^{s} + \left( {\beta - 1} \right)\Gamma_{1}^{(n)} }};\quad x_{2}^{s} = \frac{{\Gamma_{1,\max }^{s} x_{2}^{l} - \Gamma_{1}^{(n)} }}{{\Gamma_{1,\max }^{s} + \left( {\beta - 1} \right)\Gamma_{1}^{(n)} }}. $$
(9)

Equation (9) can be used to calculate the mole fractions \(x_{i}^{{\text{s}}}\) of the components 1 and 2 in the sorption phase s and to construct adsorption-equilibrium diagrams \(x_{i}^{{\text{s}}} = \;f\left( {x_{i}^{{\text{l}}} } \right)\), which are also called separation diagrams. For this purpose, however, \(\Gamma_{i,\max }^{{\text{s}}}\) has to be estimated under appropriate model assumptions. In the literature several ways are proposed, such as the monolayer model, the saturation model, and the pore filling model [19].

In the saturation model, \(\Gamma_{i,\max }^{{\text{s}}}\) is approximated by using saturation loadings \(\Gamma_{{i,{\text{sat}}}}^{{\text{s}}}\) obtained from the adsorption isotherms of pure vapors at p/p0 ≈ 1. In this case, the volume \(V^{{\text{s}}}\) of the sorption phase s changes with the composition of the adsorbed phase.

In the pore-filling model, \(\Gamma_{i,\max }^{{\text{s}}}\) is approximated by \(\Gamma_{{i,{\text{pf}}}}^{{\text{s}}} = {{V_{{\text{G}}} } \mathord{\left/ {\vphantom {{V_{{\text{G}}} } {V_{{\text{m}}} }}} \right. \kern-\nulldelimiterspace} {V_{{\text{m}}} }}\) (index pf for pore filling) calculated from the Gurvich total pore volumes VG of the adsorbents obtained from nitrogen isotherms at 77.3 K, and the molar volumes Vm of the pure liquids i at 298.15 K, i.e. at the measurement temperature of liquid adsorption. Since \(\Gamma_{{i,{\text{pf}}}}^{{\text{s}}}\) is the amount of substance that fits into the pore system of the adsorbent with the mass \(m_{{\text{A}}}\), here the volume \(V^{{\text{s}}}\) of the sorption phase s is independent of its composition. This implies that the pore-filling model contains an additional idealizing assumption.

Not only adsorption excesses, but also immersion enthalpies depend on the concentration of liquid mixtures. Experimental mass-specific immersion enthalpies \(H_{12}\) of a mixture with the components 1 and 2 can be fitted by a Langmuir-like equation:

$$ H_{12} \approx H_{L} = A + B \cdot \frac{{K \cdot x_{1}^{l} }}{{1 + K \cdot x_{1}^{l} }}, $$
(10)

where \(H_{{\text{L}}}\) is the fitted immersion enthalpy of the mixture, and A, B, and K represent adjustable parameters. While B and K are mathematical fitting parameters, the axis intercept A with the ordinate specifies the mass-specific immersion enthalpy \(H_{2}^{*}\) of the pure liquid 2. The mole fractions \(x_{i}^{{\text{l}}}\) in adsorption equilibrium are obtained from the adsorption isotherms fitted by appropriate functions.

Assuming that \(H_{12}\) of a mixture and \(H_{i}^{*}\) of a pure substance are generated exclusively in the sorption phase s, the molar immersion enthalpy \(H_{{i,{\text{m}}}}^{*}\) can be estimated from the maximum loadings \(\Gamma_{i,\max }^{{\text{s}}}\) obtained from the saturation model or the pore-filling model, respectively:

$$ H_{i,m}^{*} \approx \frac{{H_{i}^{ * } }}{{\Gamma_{i,\max }^{s} }}. $$
(11)

For a given \(x_{i}^{{\text{l}}}\), the immersion enthalpy \(H_{12}\) of the mixture can then be approximated from the absolute surface amounts \(\Gamma_{i}^{{\text{s}}}\) calculated in Eq. (8):

$$ H_{12} \approx \sum\limits_{i} {\Gamma_{i}^{s} \cdot H_{i,m}^{*} } . $$
(12)

Even if Eqs. (11) and (12) contain the idealizing assumption that the heat effects due to the non-ideality of the alcohol–water mixtures can be neglected compared to those of the interaction with the adsorbent, they can be used to evaluate the consistency of adsorption and immersion data in a first approximation.

3 Materials and methods

3.1 Adsorbents and chemicals

Four carbon molecular sieves from the Carbon Adsorbent Sampler Kit (CMS / SGCP II) from Supelco were investigated. The supplier’s information (Sigma Aldrich) is given in Table 1.

Table 1 Supplier information on the carbon molecular sieves (CMS) [26]
Full size table

The materials were comprehensively characterized by nitrogen and argon adsorption isotherms in our formerly work [12]. The nitrogen total pore volumes VG at p/p0 ≈ 0.98 and the specific BET surface areas determined according to the IUPAC recommendations for microporous materials [3] (cf. Table S1 in the Supporting Information (SI)) are listed in Table 2.

Table 2 Gurvich total pore volumes VG and BET surface areas ABET of CMS determined by gas adsorption [12]
Full size table

In Table 3, the properties of the adsorptives are listed. For liquid adsorption experiments, ultrapure water of type 1 [27] purified in a Milli-Q academic device was used. Furthermore, the water samples were degassed by means of ultrasound.

Table 3 Adsorptive properties at 298.15 K
Full size table

3.2 Measurement of densities ρ and refractive indices nD for calibration curves

The densities of the aqueous-alcoholic mixtures were determined at 298.15 K and atmospheric pressure by means of the vibrational densitometer DMA 58 (Anton Paar) with an uncertainty of 0.00001 g/cm3. For this purpose, liquid samples of about 1.5 ml were prepared on the analytical balance (Sartorius LA 120S). Additionally, the refractive indices of ethanol–water were measured by means of the refractometer DR 6300 (Krüss Optronic GmbH) with an uncertainty of 0.00001. The measured data are listed in Tables S2–4 of the SI.

3.3 Measurement of liquid-adsorption excesses \(\Gamma_{i}^{{\text{(n)}}}\)

Prior to the liquid-adsorption batch experiments, the adsorbent samples were stepwise heated up to 453.15 K, degassed under vacuum for about 16 h and after that loaded with nitrogen. The binary liquid mixtures were prepared gravimetrically by using the Sartorius LA120S analytical balance. For each batch, about 1.8 g of mixture were prepared in 4 ml screw-cap glasses, and about 0.3 g of the adsorbent were added under nitrogen atmosphere. After contact of adsorbent and adsorptive, the mass of the adsorbent was determined gravimetrically by difference weighing and the screw-cap glasses were shaken with a Thermomixer comfort (Eppendorf) at 300 rpm for at least 16 h at 298.15 K. The desorbing nitrogen was allowed to escape by briefly loosening of the screw-caps. Preliminary experiments showed that the adsorption equilibrium was reached after 20 h at the latest. The density of the aqueous-alcoholic mixture after adsorption was again determined by the DMA 58 vibrational densitometer. The obtained \(\Gamma_{i}^{{\text{(n)}}}\) data are listed in Tables S5–6 of the SI.

3.4 Measurement of immersion enthalpies

Prior to the immersion experiments, the adsorbent samples of 10–20 mg were stepwise heated and degassed in a glass ampoule with a fragile tip on the degassing ports of the device NOVA 2000e (Quantachrome Instruments) for 16 h at 453.15 K. Thereafter, the glass ampoule was filled with nitrogen and weighed again to determine the mass of the dry adsorbent. A second degassing was carried out for 5 h at 453.15 K to remove the nitrogen. Subsequently, the glass ampoules were melted off in the evacuated state.

The immersion enthalpies were measured with the microcalorimeter µDSC7 evo (Setaram Instrumentation) at 298.15 K with the measurement setup described in the literature [12]. The glass ampoule (with the fragile tip pointing downwards) was inserted into a measuring cell, then about 0.34 g of the liquid was added. The reference cell was filled with about the same amount of liquid. After reaching a stable heat flow, the fragile tip of the glass ampule was broken using a plunger mechanism. Due to the vacuum in the glass ampoule, the liquid passed into the ampoule and immediately immersed the adsorbent. The heat flow was recorded and the immersion enthalpy \(H_{i}^{*}\) as well as H12 was calculated by integration. The measured data are listed in Tables S10–12 of the SI.

4 Results and discussion

4.1 Calibration curves for the concentration analysis

The change in concentration due to adsorption is often analyzed refractometrically. In the case of ethanol–water mixtures, however, only a limited mole fraction range is accessible by means of refractive indices nD [9, 28] as illustrated in Fig. 1. Due to the elongated maximum (marked in red) in the curve, one nD value cannot be clearly assigned to only one x2 value.

Fig. 1
figure 1

Ambiguous mole fractions x2 of ethanol(1) + water(2) in the nD curve at 298.15 K

Full size image

For this reason, we used density measurements for the concentration analysis. The measured density calibration curves of the two alcohol-water mixtures are shown in Fig. 2.

Fig. 2
figure 2

Density curves of ethanol(1) + water(2) and propanol(1) + water(2) at 298.15 K

Full size image

To fit the calibration curves, polynomials of fourth and sixth degrees were used (cf. Table S13 of the SI). The densities of the ethanol–water mixture show very good agreement with literature data [29]. Due to the different slopes of the ethanol–water and propanol-water curves, the accuracy of the calculated mole fractions x2 of water is slightly different. Assuming a deviation of 0.0001 g/cm3 in the density measurement (which corresponds to the tenfold of the smallest measurement resolution of the DMA 58 and is thus certainly above the actual error), the deviation of x2 of the ethanol–water mixture averages 0.00047 and of the propanol-water mixture 0.00053. Thus, density measurement should be a very suitable analytical method to determine the composition of the binary mixtures.

The validity of the density data was also checked by calculating the molar excess volumes:

$$ V^{E} = \frac{{x_{1} M_{1} + x_{2} M_{2} }}{\rho } - \frac{{x_{1} M_{1} }}{{\rho_{1} }} - \frac{{x_{2} M_{2} }}{{\rho_{2} }}, $$
(13)

where ρi and Mi are the densities and molar masses of the pure liquids. The VE curves in Fig. 3 show a smooth progression without any outliers, which confirms the high quality of the measured density data. Again, the data of the ethanol–water mixture agree well with the literature data [29]. The VE are listed Tables S2–S3 of SI.

Fig. 3
figure 3

Molar excess volumes VE of ethanol(1) + water(2) and propanol(1) + water(2) at 298.15 K

Full size image

4.2 Adsorption excess isotherms

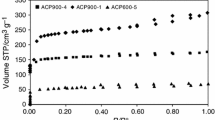
The measured adsorption excess isotherms of the two alcohol-water mixtures adsorbed on four CMS samples are shown in Figs. 4 and 5. On all carbon molecular sieves, the alcohol component is preferentially adsorbed from the mixture over the whole concentration range. This expected result reflects the strong dispersion forces between the relatively non-polar carbon surfaces and the alkyl groups of the alcohol molecules. The maximum excess amounts largely correspond to the BET surface areas of CMS materials listed in Table 2. All isotherms are similar to type III according to the classification of Schay and Nagy [30, 31].

Fig. 4
figure 4

Adsorption excesses \(\Gamma_{1}^{(n)}\) of ethanol in the system ethanol(1) + water(2)/CMS at 298.15 K. Symbols: experimental data points; solid line: Kind function; dotted line: Bi-Langmuir function, dashed line: RKE function

Full size image
Fig. 5
figure 5

Adsorption excesses \(\Gamma_{1}^{(n)}\) of propanol in the system propanol(1) + water(2)/CMS at 298.15 K. Symbols: experimental data points; solid line: Kind function; dotted line: Bi-Langmuir function, dashed line: RKE function

Full size image

Type III isotherms according to the classification of Schay and Nagy always mean that one component of the binary liquid mixture (in our case the alcoholic component) is strongly preferentially adsorbed compared to the other component (in our case water). In the excess isotherm, this becomes particularly visible in the range of low alcohol concentrations, since at equilibrium almost all alcohol molecules are located in the boundary layer, while the bulk phase in which the concentrations are measured is depleted of alcohol.

In the following, the excess isotherms in Figs. 4 and 5 are compared. Already at first glance, it becomes evident that the maximum \(\Gamma_{{1}}^{{\text{(n)}}}\) values of the ethanol and propanol isotherms are comparable within the limits of measurement accuracy. The stronger interaction of propanol with the rather non-polar carbon surfaces compared to ethanol only becomes clear if one takes into account that the space requirement of propanol molecules is larger than that of ethanol, i.e. comparable \(\Gamma_{1}^{{\text{(n)}}}\) values mean that propanol occupies a larger volume in the sorption phase than ethanol.

However, the stronger interaction of the carbon surfaces with the longer-chained “oil component” propanol is also directly reflected in the measured values. The excess isotherms show characteristic differences:

  1. (i)

    The maxima of the ethanol isotherms on all CMS materials lie at mole fractions \(x_{1}^{l} > 0.1\) (range 0.1–0.15), whereas those of the propanol isotherms on all CMS materials lie at \(x_{{1}}^{{\text{l}}} < 0.1\) (range 0.06–0.08). This means, the maxima of the propanol isotherms are shifted towards lower mole fractions.

  2. (ii)

    At higher ethanol concentrations, the ethanol isotherms show an almost linear course, while the course of the propanol isotherms is somewhat less linear. For the 1032 sample, even slightly negative excess amounts are found at \(x_{{1}}^{{\text{l}}} > 0.7\), which, however, is probably due to experimental scattering at very small \(\Gamma_{1}^{{\text{(n)}}}\) values.

The results demonstrate the high sensitivity of the method to the textural and energetic properties of the solids on the one hand and to the properties of the adsorptives on the other, with even one additional CH2 group leading to systematically modified isotherms.

4.3 Calculation of separation diagrams

In order to calculate the mole fractions \(x_{i}^{{\text{s}}}\) in the sorption phase, the maximum loadings \(\Gamma_{{i,{\text{sat}}}}^{{\text{s}}}\) for the saturation model and \(\Gamma_{{i,{\text{pf}}}}^{{\text{s}}}\) for the pore-filling model must be known (cf. Eq. (9)). While \(\Gamma_{{\text{i,sat}}}^{{\text{s}}}\) was taken from the adsorption data of pure vapors at 298.15 K at p/p0 ≈ 1 in the literature [12], \(\Gamma_{{i,{\text{pf}}}}^{{\text{s}}}\) was calculated from the total pore volumes VG obtained from N2 adsorption and the molar volumes Vm values, which are listed in Tables 2 and 3.

Table 4 shows that the \(\Gamma_{{i,{\text{pf}}}}^{{\text{s}}}\) values obtained from N2 adsorption are larger in any case than the \(\Gamma_{{i,{\text{sat}}}}^{{\text{s}}}\) values obtained from vapor adsorption. \(\Gamma_{{i,{\text{pf}}}}^{{\text{s}}} > \Gamma_{{i,{\text{sat}}}}^{{\text{s}}}\) can be explained by the fact that the pore systems of the nonpolar carbon adsorbents are more accessible to the nonpolar N2 molecules than to polar alcohol or even water molecules, for which the greatest differences between \(\Gamma_{{i,{\text{pf}}}}^{{\text{s}}}\) and \(\Gamma_{{i,{\text{sat}}}}^{{\text{s}}}\) are found. The very small \(\Gamma_{{{\text{water}},{\text{sat}}}}^{{\text{s}}}\) value of CMS 563 is unrealistic because its small micropores are hardly accessible to water vapor, i.e. the adsorption is kinetically hindered [12]. Only in case of the 1032 material with the lowest pH value and highest percentage of polar surface group (cf. Table 1), \(\Gamma_{{i,{\text{sat}}}}^{{\text{s}}}\) and \(\Gamma_{{i,{\text{pf}}}}^{{\text{s}}}\) agree quite well.

Table 4 Maximum loadings \(\Gamma_{{i,{\text{max}}}}^{{\text{s}}}\) determined from (i) vapor adsorption at 298.15 K [12] at p/p0 in brackets for the saturation model (sat), and (ii) N2 adsorption for the pore filling model (pf)
Full size table

In Figs. 6 and 7, the calculated separation diagrams \(x_{i}^{{\text{s}}} = \;f(x_{i}^{{\text{l}}} )\) are presented, except that for CMS 563 based on vapor adsorption because \(\Gamma_{{{\text{water}},{\text{sat}}}}^{{\text{s}}}\) does not fulfill the model assumptions. Comparing first the left and right sides in Figs. 6 and 7, it becomes obvious that the calculated separation diagrams strongly depend on the model assumptions and the maximal loadings \(\Gamma_{{i,{\text{max}}}}^{{\text{s}}}\) used in Eq. (9).

Fig. 6
figure 6

Separation diagrams for ethanol(1) + water(2)/CMS at 298.15 K; a saturation model, b pore-filling model. Symbols: experimental data. Solid line: calculation based on the Kind function for describing \(\Gamma_{1}^{(n)}\) (Eq. (2))

Full size image
Fig. 7
figure 7

Separation diagrams for propanol(1) + water(2)/CMS at 298.15 K; a saturation model, b pore-filling model. Symbols: experimental data. Solid line: calculation based on the Kind function for describing \(\Gamma_{1}^{(n)}\) (Eq. (2))

Full size image

In case of the pore-filling model on the right, the mole fractions \(x_{i}^{{\text{s}}}\) in the sorption phase s are in all cases only slightly larger than the bulk mole fractions \(x_{i}^{{\text{l}}}\). This clearly shows that the model assumption that the entire pore space would consist of adsorbed phase s is inappropriate for adsorbents with micro-, meso-, and macropores (cf. Table 1). Since in mesopores and macropores there is both adsorbed phase on the walls and bulk phase inside, the separation performance of the adsorbents is underestimated. The \(\Gamma_{{i,{\text{pf}}}}^{{\text{s}}}\) values are too high.

In case of the saturation model on the left, however, clear differences in the separation performance of the adsorbents become apparent. CMS 572, whose surface is weakly alkaline (pH value of 9.5), exhibits the best separation performance, followed by CMS 1034 (pH value of 10.5), and finally by CMS 1032 with an acidic surface (pH value of 3.0) suggesting the largest polarity of the internal surface. Although CMS 1034 causes the highest excess amounts \(\Gamma_{1}^{{\text{(n)}}}\) in Figs. 4 and 5 due to its largest BET surface area of \(S_{BET} \approx 1900{\text{ m}}^{2} {\text{/g}}\) (cf. Table 2), CMS1034 does not show the best separation performance because \(x_{i}^{{\text{s}}}\) strongly depends on the surface chemistry of the adsorbents. The low separation performance of CMS 1032 is also very plausible, as stronger surface polarity reduces the preferential adsorption of the alcohols from water:

Comparing the separation diagrams for ethanol und propanol obtained by the saturation model, it becomes evident that at low bulk mole fractions, \(x_{{{\text{propanol}}}}^{{\text{s}}}\) is always larger than \(x_{{{\text{ethanol}}}}^{{\text{s}}} ,\) i.e. propanol is stronger enriched in the sorption phase than ethanol. The results are plausible and show that a suitable combination of vapor, gas and liquid phase adsorption data by using realistic model assumptions can provide relevant information about.

  1. (i)

    the separation performance of adsorbents, and

  2. (ii)

    the separability of water and “oil components” in the mole fraction region relevant to water purification processes.

4.4 Mixture immersion enthalpies

In Figs. 8 and 9, the measured specific immersion enthalpies H12 of the alcoholic-aqueous mixtures on carbon molecular sieves are presented together with the immersion enthalpies \(H_{i}^{*} [{\text{J/g}}]\) of the pure liquids as the starting and end points of the graphs (cf. Tables S10–12 in the SI).

Fig. 8
figure 8

Immersion enthalpies of ethanol(1) + water(2)/CMS at 298.15 K. Symbols: experimental data. Solid line: Eq. (10). Dotted line: saturation model. Dashed line: pore-filling model

Full size image
Fig. 9
figure 9

Immersion enthalpies of propanol(1) + water(2)/CMS at 298.15 K. Symbols: experimental data. Solid line: Eq. (10). Dotted line: saturation model. Dashed line: pore-filling model

Full size image

The pure-substance immersion enthalpies \(H_{{{\text{water}}}}^{*}\) as starting points are in each case much smaller than \(H_{{{\text{propanol}}}}^{*}\) and \(H_{{{\text{ethanol}}}}^{*}\) as end points, which confirms the relatively nonpolar surfaces of the carbon molecular sieves. Smaller released heats suggest a lower bonding between the carbon surfaces and water, at least when the whole internal surface is accessible to water. The specific \(H_{i}^{*} [{\text{J/g}}]\) values of propanol and ethanol are comparable. However, the molar \(H_{{i,{\text{m}}}}^{*} [{\text{J/mol}}]\) values of propanol are higher than those of ethanol due to the higher space requirement of propanol at the solid surface.

It can be seen that in the initial mole fraction range of the alcohols, the released mixture enthalpies H12 increase very strongly with increasing alcohol concentration. The values of the pure alcohols are already reached at \(x_{{{\text{ethanol}}}} \approx 0.2\) or \(x_{{{\text{propanol}}}} \approx 0.1\), respectively. This tendency correlates with the maxima of the adsorption excess isotherms in Figs. 4 and 5, which are shifted toward smaller mole fractions in case of the propanol isotherms. Furthermore, the experimental results provide information about the composition of the first adsorbed layer. Since at \(x_{{{\text{ethanol}}}} > 0.2\) or \(x_{{{\text{propanol}}}} > 0.1\), respectively, the H12 values remain almost constant, it can be concluded that carbon surface is already completely covered with the alcohol.

The experimental \(H_{i}^{*}\) and H12 values were fitted by means of Eq. (10) with the parameters listed in Table S14 (cf. the solid lines in Figs. 8 and 9). Additionally, the H12 values were predicted using Eq. (12) from the molar pure-substance immersion enthalpies \(H_{{i,{\text{m}}}}^{*}\) and the absolute surface amounts \(\Gamma_{i}^{{\text{s}}}\) calculated by means of the saturation model or the pore filling model, respectively. The dotted and dashed lines in Figs. 8 and 9 show that the predicted H12 values indicate the correct trend, while their absolute values are too low (cf. Table S15). They do not capture the strong negative slope of the H12 curve in the low mole fraction region.

In this way, Figs. 8 and 9 suggest that:

  1. (i)

    Predictions of mixture enthalpies from pure-substance enthalpies are possible, provide qualitatively good results, and can be used to indicate the data trend.

  2. (ii)

    Experimental mixture immersion data remain essential, especially for geometrically inhomogeneous adsorbents with micro-, meso-, and macropores, where correct model assumptions about the sorption phase s are difficult.

  3. (iii)

    Immersion and adsorption data correlate significantly as can be seen in the \(\Gamma_{1}^{{\text{(n)}}}\) and H12 curves, although the theory presented still contains too many idealizing assumptions to cover the relationship between \(\Gamma_{1}^{{\text{(n)}}}\) and H12 completely.

5 Conclusions

The liquid-phase adsorption of ethanol–water and propanol–water mixtures on a series of carbon molecular sieves was comprehensively studied. It was shown that vibration densitometry proves to be suitable to analyze the adsorption of alcoholic–aqueous mixtures because it provides high accuracy and a larger accessible molar fraction range than refractometry. A strong preferential adsorption of the alcoholic component from water was found for all studied carbon molecular sieves.

Even if the chosen liquid mixtures differ only minimally in one CH2 group, the measured excess isotherms differ systematically, which demonstrates the high sensitivity of liquid-phase adsorption to the properties of the adsorptives. The basic difference in the isotherms is that the maximum adsorption-excess values of propanol occur always at a smaller mole fraction than those of ethanol, which is correlated with a complete coverage of the respective carbon surface as suggested by the measured mixture immersion enthalpies. Furthermore, it was shown that a suitable combination of vapor-, gas- and liquid-phase adsorption data can provide relevant information about the separation performance of adsorbents and the separability of water and “oil components”.

The predicted immersion enthalpies of mixtures based on pure-substance enthalpies and binary adsorption excess data were qualitatively correct. This is a convincing result in view of the idealizing model assumptions and the experimental errors of excess isotherms and immersion enthalpies.