Effect of pressure ratio on the separation performances of different DRPSA configurations under equilibrium conditions

Abstract

Dual reflux pressure swing adsorption is a peculiar application of pressure swing adsorption with relevant separation potential. In a proper range of operating parameters, high separation performances are achieved in many applications, including complete separation in the case of binary mixtures. In this work, a new representation of the design parameters suitable for complete separation based on the semi-analytical solution of the corresponding Equilibrium Theory model is proposed for the four basic process configurations. Namely, given feed position, feed composition, and adsorbent separation selectivity, the combinations of the remaining process parameters ensuring complete separation are identified in a 3D plot. Furthermore, the same model equations have been solved numerically to explore conditions of incomplete separation, where the semi-analytical solution is not available. In particular, the sensitivity of the separation performances of each configuration to the pressure ratio has been explored. More specifically, given the region of operating conditions suitable for complete separation, selected operating conditions outside this region have been explored aimed to recover/improve the separation quality. Even though the different configurations exhibit different behaviors, the general dependence of the product purity upon the pressure ratio is quite limited and only minor improvements can be obtained with a few exceptions.

1 Introduction

The dual reflux pressure swing adsorption (DRPSA) is a separation process based on selective adsorption of a gas mixture onto a solid adsorbent. The process involves the periodic variation of pressure, resembling the approach applied in the widely known Pressure Swing Adsorption (PSA) [14]. With respect to PSA, DRPSA involves two recycles and a lateral feed injection, thus overcoming the thermodynamic limitation of PSA [28, 37] and enabling complete separation of gas binary mixtures [8]. Twisting recycles and feed pressure, different DRPSA configurations are obtained [11], with different separation capability.

Many noticeable experimental [7, 13, 15, 18, 19, 24,25,26,27, 29, 31,32,33, 35, 36, 38] and modeling [1, 2, 4, 5, 11, 12, 17, 20,21,22,23, 30, 39] studies are available in the literature focused on DRPSA design. Among the different modeling approaches, a simplified but effective design tool is the semi-analytical solution based on the so-called Equilibrium Theory [8]. Even though attractive, especially to elucidate the role of the different design parameters, many assumptions are required: (i) instantaneous equilibrium between gas and solid phases, (ii) linear equilibrium isotherms, (iii) ideal gas behavior, (iv) ideal plug flow (no axial mixing), (v) isothermal operation, and (vi) negligible pressure drop (constant pressure along the column axis). As easily understood, several of these assumptions are not met in many real applications. Moreover, the semi-analytical solution is available only in the case of complete separation [1, 4, 5]. Therefore, despite the conceptual value of such a tool, its applicability to design optimal process conditions is limited.

Taking advantage of the semi-analytical solution mentioned above, a region of complete separation is identified in the operating parameter space. It is the so-called TOZ (Triangular Operating Zone) in the plane $C$ (dimensionless capacity ratio, which is roughly proportional to the productivity) vs. ${z}_{FE}$ (dimensionless feed position) at constant $G$(dimensionless recycle ratio of the light component recycle flowrate to the feed flowrate) [1]. Depending upon the characteristics of the mixture components and the process configuration under examination, such region can be quite impractical. As a matter of fact, when the same recycle ratio is applied and the required productivity is too large and/or the feed position is not optimal, the process is operated outside of the TOZ and incomplete separation is achieved. In a previous work we investigated how to recover the loss of purity in case of incomplete separation considering a specific process configuration (DRPSA with feed at High-pressure and pressurization with the heavy-component A, DRPHA) and tuning operating parameters such as the light recycle ratio, the feed step time, and the heavy product flowrate [23]. On the other hand, another key operating parameter of this process, the pressure ratio $\pi$, was not included in such analysis and it has been scarcely investigated in the literature.

In the frame of the Equilibrium Theory model, the aim of this work is twofold: (i) to perform a process sensitivity analysis with respect to $\pi$ and (ii) to apply such analysis to all process configurations. Since the semi-analytical solution of the Equilibrium Theory model is available only at complete separation, an effective numerical solution is applied to extend the analysis to incomplete separations. Therefore, the detailed model previously developed and validated for one of the possible DRPSA configurations [20] has been extended to other three common DRPSA configurations. The reliability of the numerical solution has been first checked by comparison with experimental data from the literature for the different process configurations. Then, the same reliability at equilibrium conditions has been checked by comparison with the semi-analytical solution at complete separation and considering negligible mass transport resistances and pressure drops. Finally, the effect of the variation of the pressure ratio has been examined at operating conditions not suitable for complete separation to verify the recovery potential for purity provided by such an operating parameter.

2 DRPSA basic configurations

DRPSA processes using two columns can operate in different configurations, according to the adsorption bed at which the feed stream is injected and how the pressure swing is performed. For instance, the feed stream can be fed into the high-pressure (H, at pressure ${P}_{H}$) or the low-pressure (L, at pressure ${P}_{L}$) bed and the pressure swing can be performed using the heavy component (A) or the light component (B). If the minimum number of steps (four) is performed for each cycle, then four DRPSA basic configurations can be designed:

• DRPHA, feed mixture is fed to the bed at ${P}_{H}$ and the A-rich stream switches the pressures;

• DRPHB, feed mixture is fed to the bed at ${P}_{H}$ and the B-rich stream switches the pressures;

• DRPLA, feed mixture is fed to the bed at ${P}_{L}$ and the A-rich stream switches the pressures;

• DRPLB, feed mixture is fed to the bed at ${P}_{L}$ and the B-rich stream switches the pressures.

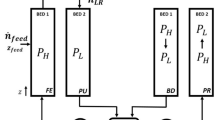
All these configurations are sketched in Fig. 1a, where the four columns operating the four steps of the process are shown. The process is operated in a cyclic way: in the figure, only half cycle is depicted, since the other half is made of the same four steps after interchanging the two columns. Each process cycle involves two adsorption beds that are both at constant pressure, one at ${P}_{H}$ and the other at ${P}_{L}$ . The bed which receives the lateral feed injection (at ${P}_{H}$ in DRPHA and DRPHB; at ${P}_{L}$ in DRPLB and DRPLA) performs the feed step (FE) while the other is purged (PU). The heavy product A is collected from the low-pressure bed and it is partly recovered as heavy product. The remaining stream rich in A is pressurized and recycled to the other bed. The same way, B is collected from the high-pressure bed and partly recycled to the low pressure one. Once these steps are completed, the pressure of the two beds is switched. This pressure variation is carried out by recycling a stream rich in one of the two components (A in DRPHA and DRPLA, B in DRPHB and DRPLB) to the low-pressure bed. This change in the operating pressure of the two beds is named pressurization (PR) for one bed and blowdown (BD) for the other. Obviously, like FE and PU, PR and BD steps occur simultaneously.

Fig. 1

a Scheme and b flow directions (coincident with $\mathrm{z}$ coordinate direction, from 0 to 1 as indicated in part (a)) and number of streams entering/leaving the two tanks ${\mathrm{\vartheta }}_{1}$ and ${\mathrm{\vartheta }}_{2}$ of each process configuration. FE feed/adsorption phase, PU purge/desorption phase, BD blowdown phase, PR pressurization phase

Two vessels delivering the product streams are used to buffer the flowrates and to reconcile the material balances during the various steps. For DRPHA and DRPLA the vessel ${\vartheta }_{1}$ receives only the stream from the high-pressure column and it delivers both the light product and the light recycle streams. The vessel ${\vartheta }_{2}$ receives the streams from both the low-pressure and the blowdown columns, while delivering three streams: the heavy product, the heavy recycle, and the one required by the pressurization step. For DRPHB and DRPLB the vessel ${\vartheta }_{1}$ receives the streams from both the high-pressure and the blowdown columns, while delivering three streams: the light product, the light recycle, and the one required by the pressurization step. The vessel ${\vartheta }_{2}$ receives only the stream from the low-pressure column and it delivers both the heavy product and the heavy recycle streams.

3 Model development

The different DRPSA configurations are described by the same governing equations, but the orientation of the flow coordinate changes according to the configuration considered, as reported in Fig. 1b. Taking the DRPHA as a reference configuration, the DRPLA has a reversed flow direction during FE and PU and the same direction during BD and PR. Moreover, the light product recycle enters the top of the column during FE, while for the DRPHA it enters during PU. The DRPHB has the same flow direction as the DRPHA for FE and PU, but the opposite for BD and PR; the light product recycle enters the top of the column during PU as for DRPHA. The DRPLB has all flow directions reversed with respect to DRPHA and the light recycle enters the top of the column during FE. The corresponding mathematical models can be derived from a mathematical model previously developed for the DRPHA configuration [20] by considering the different orientation of the flow in the four steps for the various configurations, different boundary conditions and different behavior of the two tanks used to connect the two columns.

Assumptions and constitutive equations of the previously developed model are thoroughly discussed elsewhere [20] and they are only briefly summarized in the following. In particular, the main assumptions are: ideal gas mixtures, isothermal conditions, mass transport between gas and solid phase described by the Linear Driving Force (LDF) model [9], pressure drops evaluated by the Blake-Kozeny equation [30], negligible axial dispersion [16]. Accordingly, the model equations are the following:

$$Overall ~material ~balance:~{\varepsilon }_{T}\frac{\partial P}{\partial t}+\frac{\partial (uP)}{\partial z}+{\rho }_{B}RT\sum_{i=1}^{N}\frac{\partial {q}_{i}}{\partial t}=0$$

(1)

$$Component~material~balance~in~gas~phase:~\varepsilon_{T}\frac{\partial \left(P{y}_{i}\right)}{\partial t}+\frac{\partial \left(uP{y}_{i}\right)}{\partial z}+RT{\rho }_{B}\frac{\partial {q}_{i}}{\partial t}=0, i=1\dots N$$

(2)

$$Component ~material ~balance ~in ~adsorbed ~phase: \frac{\partial {q}_{i}}{\partial t}={k}_{LDF,i}\left({q}_{i}^{*}-{q}_{i}\right), i=1\dots N$$

(3)

$$Adsorption~ isotherm: {q}_{ i}^{*}={H}_{i}P{y}_{i}, i=1\dots N$$

(4)

$$Pressure ~drop ~equation~ \frac{\partial P}{\partial z}=-\frac{u}{\frac{150}{4}\frac{1}{{r}_{p}^{2}}{\left(\frac{1-{\varepsilon }_{B}}{{\varepsilon }_{B}}\right)}^{2}\mu }$$

(5)

This system of non-linear Partial Differential Equations (PDEs) allows to compute the time and space evolution of the mole fraction of each species, of the amount adsorbed of each species, and of the pressure. Considering a binary mixture (that is, N = 2), Eqs. (1) to (5) represent a PDEs system of eight equations in eight unknowns.

Each configuration has its own system of streams entering and leaving the two tanks, resulting in a strong coupling between the two columns. The composition of the stream leaving each tank is evaluated assuming that the vessel volume is large enough to ensure constant composition of the leaving stream; this composition is thus assumed to be equal to the time-average mole fraction of the streams entering the tank (see Table S1 in the Supplementary Information for more details). Finally, the BCs for the four configurations account for the flow directions and the pressure values of each column in each step, as sketched in Fig. 1. The BCs actually used in the simulations are summarized in the Appendix A.

The model equations have been numerically solved using the Finite Volume Method [20] together with a combination of interpolation schemes [6, 10, 20, 34]. This approach resulted the best compromise between computational cost and accuracy, a key feature when multiple simulations have to be carried out, like in the case under examination. The code for each configuration has been written in Matlab® and the number of computational points along the column axis is selected according to the strategy proposed in [22]. The different orientation of the coordinate, $z$, is consistent with the orientation of the gas flow. As a single bed is simulated during the four phases, the profile obtained from the previous phase is reversed (if needed) to match the new coordinate of the current phase simulated. Another consequence of the use of a single bed approach is that the tanks require an initial condition at the beginning of the simulation. A poor choice of this initial condition can lead to long computational times or even divergence of the solving method. To overcome this issue a preliminary run with fewer computational points is usually carried out to obtain a first guess of the composition inside each tank. The discretized equations, together with the BCs for the four configurations, are detailed in Appendix A.

A key aspect in DRPSA simulation is to ensure that Cyclic Steady State (CSS) conditions are met. In fact, if CSS are not fully established, the estimated product purities may be affected by a relevant error, thus leading to incorrect prediction of the process performances. In our simulations, the achievement of CSS conditions has been checked mainly ensuring the closure of each component and overall material balances with a relative accuracy below 0.1%. Notably, largely different numbers of cycles (from 100 up to 1000) are required, with an average computational time equal to about 50 s per cycle. This large variability of the required number of cycles is due to the fact that very steep profiles may develop and travel along the bed depending upon the operating conditions. This profile shape is also the reason for the high accuracy required by the simulation in order to avoid numerical diffusion that could strongly affect the predicted product purities at CSS.

The proposed model is indeed suitable to predict the behavior of anyone of the four DRPSA configurations. This has been already shown by [20] in the DR-PHA case and with reference to the experimental data by [17]. In the same work, it was shown that isothermal behavior can be assumed being the influence on the results of temperature variations negligible. Therefore, the same comparison has been carried out here using literature experimental data [17] as summarized in Fig. 2 (the values of all model parameters and operating conditions are given in the Supplementary Information). Note that in the figure error bars have been added to highlight maximum and minimum values consistent with the reported experimental errors on the flowrate measurements. The simulated results show substantial agreement with the experimental ones for both the components. A bit larger discrepancy is evident in the trend of the heavy component purity; this is not surprising since the purity of the two product streams are related one to each other by the material balance over a cycle, which involves also the feed mole fraction. It can be easily seen that when the feed mole fraction of the heavy component is quite low (as in this case, being it equal to about 0.1), a small change in the composition of the light product stream requires a much larger change in the composition of the heavy product stream. Overall, the fair agreement with these experimental data provides a satisfactory validation of the reliability of the model predictions.

Fig. 2

Experimental validation for DRPLA (a), DRPLB (b) and DRPHB (c). Experimental data from May et al. [17], run number as in the original paper. G is the light recycle ratio, which is the main operating parameter changed from one run to another one

3.1 Equilibrium model: complete separation

When negligible transport resistances are assumed, instantaneous equilibrium between fluid and solid phases is established everywhere in the column. If in addition we consider negligible pressure drops and linear adsorption isotherm, the Eqs. (1) to (5) can be recast in the so-called Equilibrium Theory model, whose semi-analytical solution has been developed for binary mixtures in the case of complete separation [3,4,5]. Such solution provides the concentration profiles directly at CSS and enables the identification of the region of operating conditions suitable to guarantee complete separation. This region is called Triangular Operating Zone (TOZ) and it is conveniently represented in the plane $C$ (the dimensionless capacity ratio, which is proportional to the moles of feed processed per unit bed volume: $C=\frac{{\beta }_{A}G{t}_{FE}{\dot{n}}_{FE}RT}{{P}_{L}{V}_{bed}{\varepsilon }_{T}}$) vs. ${z}_{FE}$ (the dimensionless lateral feed location) at a given value of $G$ (the dimensionless ratio of the light recycle flowrate to the feed flowrate: $G={\dot{n}}_{LR}/{\dot{n}}_{FE}$), pressure ratio, $\pi ={P}_{H}/{P}_{L}$, feed composition in terms of heavy component mole fraction, ${y}_{FE}$, and solid sorbent selectivity, $\beta ={\beta }_{A}/{\beta }_{B}$. Once ${y}_{FE}$ (tat is, the mixture to be separated) and $\beta$ (that is, the solid sorbent) are given, $G$ is solely related to the value of $\pi$, and a function $G\left(\pi \right)$ can be obtained which guarantees complete separation if $C$ and ${z}_{FE}$ values are chosen inside the TOZ. According to the value of $\pi$, the TOZ changes shape depending upon the chosen DRPSA configuration. For each value of $\pi$, a maximum value of the capacity ratio, ${C}_{max}$, and the corresponding feed position, ${z}_{FE,opt}$, together with the maximum feed position, ${z}_{FE,max}$, can be computed as discussed elsewhere [3,4,5].

As an example, the TOZs are depicted in Fig. 3 at different values of $\pi$ for all the configurations, for assigned ${y}_{FE}$ and $\beta$. Note that each triangle is characterized by a specific $G$ value. The region of complete separation always shrinks at increasing $\pi$, thus limiting the values of ${z}_{FE}$ which can be chosen to obtain a complete separation of the mixture. This can represent an issue in practical cases, since the feed position cannot be changed without additional investment costs.

Fig. 3

TOZ for the DRPHA (a), DRPHB (b), DRPLA (c), and DRPLB (d) configurations at different values of $\uppi$ (${\mathrm{y}}_{\mathrm{FE}}=0.79$; $\upbeta =0.51$)

Another convenient representation of the same regions can be now proposed. Once the feed position is assigned, the leftover degrees of freedom for complete separation in DRPSA are $\pi$ and $C$ (as $G$ is set at given $\pi$) and the TOZ can be conveniently recast in a different space, where $\pi$, $G$, and $C$ are reported. This creates a bounded, vertical surface that represents all the possible values of $\pi$, $G$, and $C$ allowing for complete separation at assigned feed position (always at assigned feed composition and adsorbent selectivity). The upper boundary of this surface is given by the maximum possible values of $C$ in the TOZ at the given values of ${z}_{FE}$. Following the previous TOZ examples, and choosing the feed position of ${z}_{FE}=0.25$ (i.e., the feed position is at 1/4 of the column length), the TOZ can be recast in the new surface shown in Fig. 4. We can see that apart from DRPLB configuration this surface vanishes for some value of $\pi$ inside the investigated range, thus indicating that complete separation is no longer possible above this pressure ratio. The surface can exhibit a maximum, determined by the nontrivial changes of the TOZ shape at changing $\pi$. All other points in the space of the plot represent operating conditions where Equilibrium Theory predicts incomplete separation. This new plot in general allows to design a DRPSA process when the feed position is set, similarly to the TOZ where instead the recycle ratio is given. Moreover, it can help to understand the effect of changing the $\pi$ value when all the other parameter values are kept constant and equal to the values computed through the Equilibrium Theory at the original $\pi$ value, as discussed in the following.

Fig. 4

Recast TOZ for the DRPHA (a), DRPHB (b), DRPLA (c), and DRPLB (d) configurations (${\mathrm{y}}_{\mathrm{FE}}=0.79$, $\upbeta =0.51$, and ${\mathrm{z}}_{\mathrm{FE}}=0.25$)

3.2 Equilibrium model: incomplete separation

The semi-analytical approach discussed in the previous section allows predicting the operating conditions under the assumption of complete separation of the two components of the mixture. This can result in very strong requirements for either the capacity ratio (that is, the column size) or the lateral feed position. Seldom, the requirements of productivity constrain the capacity ratio to larger values with respect to those required by the TOZ, or the feed position available in practice guarantees complete separation only if very low values of the pressure ratio are adopted, making practically impossible to achieve complete separation. Nevertheless, the possibility of recovering the loss in purity given by non-optimal operating conditions by changing the value of π has not been investigated in the literature.

To explore operating conditions chosen outside the TOZ (equivalently, off the three-dimensional surface mentioned above), the mathematical model (Eqs. (1) to (5)) has been numerically solved as detailed above under the same local equilibrium assumptions. To approach equilibrium conditions, very large values of mass transport coefficients and particle size have been used, thus resulting in negligible mass transfer resistances and pressure drops.

To check the reliability of this numerical solution at equilibrium, the results have been compared to those obtained through the semi-analytical solution for complete separation conditions. This same comparison was previously carried out for DRPHA for operating conditions inside the TOZ [20]. The same validation procedure has been carried out in this work for the other three DRPSA configurations, that is, DRPHB, DRPLA, and DRPLB. Also in this case, the three developed models predict complete separation of the mixture when the operating conditions are set inside the TOZs shown in Fig. 3 at $\pi =2$.

4 Influence of the pressure ratio

Starting from the complete separation region predicted by the Equilibrium Theory model on the plane $C$ vs. ${z}_{FE}$ at a value of $\pi =2$, the TOZs of the four DRPSA configurations have been compared in Fig. 5 for the sake of clarity. We can see that shape and vertexes of the TOZ change significantly when changing the process configuration. The range of ${z}_{FE}$ available for a complete separation at the selected value of $\pi$ is the smallest for DRPHA, enlarges for DRPHB and DRPLA, and the whole domain of ${z}_{FE}$ can be exploited for a complete separation in DRPLB. The range of $C$ is instead the largest for DRPHB, while the other configurations exhibit smaller ranges.

Fig. 5

TOZ for the DRPSA configurations investigated at $\pi =2$, ${y}_{FE}=0.79$, and $\beta =0.51$

For each configuration, two operating points outside the TOZ have been considered, in the following referred to as Run1 and Run2. In particular, Run1 refers to an operating point on the $C$—${z}_{FE}$ plane below the vertex of the TOZ (that is, with $C<{C}_{max}$) but with ${z}_{FE}$ value outside the TOZ; this represents a situation where the column volume is adequate with respect to the feed amount, but the feed location is not suitable for the given value of π. On the other hand, Run2 is an operating point above the vertex of the TOZ (that is, with $C>{C}_{max}$) but ${z}_{FE}$ value in between ${0-z}_{FE,max}$; these conditions represent DRPSA processes where the feed location could be adequate but the column volume is too small for the feed amount, which happens when the desired productivity is too large. The coordinates of the runs for each investigated DRPSA configuration in the ${C-z}_{FE}$ plane are summarized in Table 1.

Table 1 Parameter values for the four DRPSA configuration

Let us now examine how purity changes in the two selected runs for each DRPSA configuration by changing only the value of $\pi$ while keeping the recycle ratio value equal to that predicted by the semi-analytical solution at $\pi =2$ for complete separation. Using the parameter values summarized in Table 1, several simulations were carried out for each process configuration at different values of the pressure ratio, by keeping the value of ${P}_{L}$ unchanged and equal to $1{0}^{5} Pa$.

The general behaviors found can be illustrated by considering for example the DRPHB configuration. While the recast TOZ is shown in Fig. 6a, Fig. 6b reports the purity of the light component stream according to the value of $\pi$. The purity of only one component was reported because it suffices to fully define the separation performance. In fact, since a single value of the heavy product flowrate is considered in all cases (the one corresponding to complete separation, ${\dot{n}}_{HP}={y}_{FE} {\dot{n}}_{FE}$), the purity of each component is equal to the corresponding recovery, and the purity of the heavy component, ${y}_{A,HP}$, can be easily computed from the purity of the light component, ${y}_{B,LP}$, through a material balance over a cycle [23] as:

Fig. 6

DRPHB simulation results for Run1: a parameters space with complete separation surface and investigated trajectory; b light component purity as a function of the pressure ratio. Filled symbols represent the point where the value of $G$ allowing complete separation inside the TOZ has been computed

$${y}_{A,HP}=\frac{{1-y}_{FE}}{{y}_{FE}}{y}_{B,LP}-\frac{1-2{y}_{FE}}{{y}_{FE}}$$

(6)

Note that, being ${y}_{FE}=0.79>0.5$, the purity of the heavy component is expected, and coherently found in the results, to be always larger than that of the light one.

From Fig. 6b we can see that purity is influenced by the pressure ratio value in a non-trivial way since increasing the $\pi$ value not always leads to better product purities, as expected in traditional PSA processes. In particular, reducing the value of $\pi$ with respect to the reference value of 2 (used in the Equilibrium Theory model to evaluate $G$), the purity at first increases and then sharply decreases, while increasing the value of $\pi$ above 2 the purity decreases. This behavior can be qualitatively understood taking advantage of the aforementioned recast form of the TOZ in the $\pi -G-C$ space shown in Fig. 6a together with a series of symbols forming a trajectory representing the investigated cases of incomplete separation in Run1. Note that such trajectory in the $\pi -G-C$ space is a straight line as only $\pi$ was varied; obviously, such a line never intersects the complete separation surface.

The purity changes according to $\pi$ can be explained considering the opposing effects of the incorrect choices of $G$ and $C$ with respect to the values that would be required by a specific $\pi$ value to get complete separation. Let us consider the distance of the analyzed trajectory with respect to the surface of complete separation: at $\pi <2$, much larger values of $G$ are required to achieve complete separation, since the values of $G$ required for complete separation sharply increase as $\pi$ decreases. This means that the recycled gas is not enough to complete the purge of the column, therefore compromising the purity of the product streams. On the other hand, at $\pi >2$ slightly lower values of $G$ are enough to achieve complete separation. In fact, the values of $G$ required for complete separation do not change significantly as $\pi$ increases and, therefore, they are not expected to impact significantly on the purity of the product streams. Focusing now on $C$, at $\pi <2$ larger values of $C$ are suitable to achieve complete separation, therefore making the trajectory quite close to the complete separation surface. On the contrary, at $\pi >2$ the values of $C$ allowing complete separation are farther from the trajectory, meaning that the trajectory always involves columns much smaller than needed, which is detrimental for good separations. To summarize, opposite effects on purity of the two parameters $C$ and $G$ changing along the investigated trajectory with the pressure ratio are expected. Their respective weight will impact how purity changes according to changes in $\pi$, thus possibly leading to a purity maximum as in Fig. 6b.

A different behavior in the investigated range of $\pi$ has been found for Run2, as shown in Fig. 7. In particular, Fig. 7b shows that purity is influenced by the pressure ratio value in a different way. In particular, purity decreases reducing the value of $\pi$ below the reference value of 2, while it increases at $\pi$ values above 2. This behavior also can be understood taking advantage of the recast form of the TOZ, as shown in Fig. 7a.

Fig. 7

DRPHB simulation results for Run2: a parameters space with complete separation surface and investigated trajectory; b light component purity as a function of the pressure ratio. Filled symbols represent the point where the value of $\mathrm{G}$ allowing complete separation inside the TOZ has been computed for each configuration

The qualitative effect of $G$ is quite similar to that discussed for Run1: at $\pi <2$ larger values of $G$ are required to achieve complete separation, while at $\pi >2$ slightly lower values of $G$ are enough to achieve complete separation. Regardless the values of $\pi$, larger or smaller than 2, the values of $C$ along the trajectory are not significantly farther or closer to the values of $C$ required to achieve complete separation, thus leading to a limited effect on purity inside the entire investigated range of $\pi$. Thus summarizing, the impact of $G$ prevails in this case, leading the purity to steadily increase with $\pi$ as depicted in Fig. 7b.

The relative importance of the two parameters $G$ and $C$ on the investigated trajectories depends both on the DRPSA configuration and the operating parameters in the ${C-z}_{FE}$ plane, as shown in Fig. 8. In all cases, too low values of $\pi$ worsen the separation, while the effect of larger values of $\pi$ depends on the DRPSA configurations: they lead to beneficial results only in DRPLA and DRPLB, while the light component purity exhibits a maximum in DRPHA and DRPHB. Notably, if a maximum in purity is obtained, it is found at a value of pressure ratio not far from the reference value $\pi =2$.

Fig. 8

Light component purity as a function of the pressure ratio for a Run1 and b Run2. Filled symbols represent the points where the value of $\mathrm{G}$ allowing complete separation inside the TOZ has been computed for each configuration

Some further insight can be deduced comparing the work per cycle required in the four configurations to obtain a given value of purity. Assuming ideal gas behavior, the specific work per $kmol$ of compressed gas is given by:

$$\tilde{W }=\left\{\begin{array}{ll}0& if \;{P}_{down}\le {P}_{up}\\ RT\frac{\gamma }{\gamma -1}\left({\left(\frac{{P}_{down}}{{P}_{up}}\right)}^{\left(\frac{\gamma -1}{\gamma }\right)}-1\right)& if\; {P}_{down}>{P}_{up}\end{array}\right.$$

(7)

where ${P}_{down}$ is the pressure downstream the compressor and ${P}_{up}$ that upstream. The overall work required in a given step (i.e., FE/PU or PR/BD) can be numerically computed as:

$${W}_{step}={\int }_{0}^{{t}_{step}}{\tilde{W }\dot{n}}_{step}dt$$

(8)

where ${t}_{step}$ is the step duration and ${\dot{n}}_{step}$ is the flowrate to be compressed in that step, that is, the heavy recycle flowrate during FE/PU and the flowrate from the column in BD to the column in PR during the PR/BD step. The specific cycle work is computed by summing up the work required for the four steps and dividing it by the number of fed moles:

$$W=\frac{{\int }_{0}^{{t}_{FE}}\tilde{W }{\dot{n}}_{HR}dt+{\int }_{0}^{{t}_{BD}}\tilde{W }{\dot{n}}_{BD}dt}{{\dot{n}}_{feed}{t}_{FE}}$$

(9)

The specific work required per cycle is shown for the investigated cases in Fig. 9 as a function of the light component purity.

Fig. 9

Light component purity as a function of the cycle work for a Run1 and b Run2. Filled symbols represent the values at $\pi =2$ where the value of $G$ allowing complete separation inside the TOZ has been computed for each configuration

As expected, the trends in Fig. 9 are quite similar to those in Fig. 8 since the compression work is roughly proportional to the pressure ratio. Looking at the filled markers in Fig. 9, the $\pi$ value for which the TOZs were derived ($\pi =2$) leads always to separation costs and separation performances close to the best ones (high purity and low work).

Notably, better performances (that is, higher purity and lower work) are obtained in specific cases reducing the pressure ratio with respect to the reference value. Unfortunately, this behavior can be hardly predicted without performing experiments and/or model simulations around the $\pi$ value at which the TOZ was derived. Therefore, it is generally worth investigating the effect of different $\pi$ values at least inside a narrow range (say, ± 20%) around the reference value, i.e. the one used to design the process conditions for complete separation through the semi-analytical solution of the Equilibrium Theory model.

5 Conclusions

In the frame of Equilibrium Theory modeling (negligible transport resistances and pressure drops, linear equilibrium isotherm), different DRPSA configurations have been explored with emphasis on the role of the parameter pressure ratio. A novel 3D representation of the complete separation region was first proposed, depicting the operating parameters more often adjusted in practice (namely, recycle ratio, capacity ratio, and pressure ratio) at given feed composition, adsorbent selectivity, and feed position. The recast representation is more effective than the previously proposed 2D TOZs, where the feed location was free but recycle and pressure ratios were set.

Selecting process conditions outside this region, incomplete separation is expected and the capability to recover the loss of purity tuning the pressure ratio was explored. Using a numerical solution of the Equilibrium Theory model applicable to all process configurations, a sensitivity analysis of the process performance at different $\pi$ values was performed. Namely, two different sets of operating parameter values have been investigated for each DRPSA configuration: feed injected too far from the optimal position (Run1) and column undersized with respect to the feed to be processed (Run2). The results of the analysis can be summarized as follows:

• whatever the process configuration is, the separation performance is invariably decreasing when $\pi$ is decreased enough. In some specific configuration, a limited decrease of $\pi$ can permit to enhance the separation performances;

• the increase of $\pi$ permits to enhance the separation performances only for specific configurations and at limited extents;

• the value of $\pi$ predicted by the Equilibrium Theory model for complete separation remains quite close to the optimal one also in cases where the separation is incomplete, both in terms of purity of the obtained streams and required work, thus confirming the general reliability of the design procedure previously proposed [1].

Appendix A

To introduce the BCs, it is necessary to briefly recall the discretized version of the model Eqs. (1)–(5) along with the peculiar modeling strategy adopted for the lateral feed injection in the four different configurations. The discretized model equations, obtained applying the FVM, are summarized below in dimensionless form, where $n=1\dots Np$ and $Np$ is the overall number of grid points in the spatial domain. The dimensionless variables have been obtained by dividing each dimensional variable by a suitable reference value, and they are indicated in the following with the corresponding symbol overlined.

$$Total ~mass ~balance~ \frac{\partial {\overline{P} }_{n}}{\partial \overline{t} }={c}_{1}\left({\overline{u} }_{n-\frac{1}{2}}{\overline{P} }_{n-\frac{1}{2}}-{\overline{u} }_{n+\frac{1}{2}}{\overline{P} }_{n+\frac{1}{2}}\right)-{c}_{2}\left(\frac{\partial {\overline{q} }_{A,n}}{\partial \overline{t} }+\frac{\partial {\overline{q} }_{B,n}}{\partial \overline{t} }\right)$$

(A1)

$$Component ~mass ~balance ~ \frac{\partial {y}_{A,n}}{\partial \overline{t} }=\frac{{c}_{1}}{{\overline{P} }_{n}}\left\{{\overline{u} }_{n-\frac{1}{2}}{\overline{P} }_{n-\frac{1}{2}}{y}_{A,n-\frac{1}{2}}-{\overline{u} }_{n+\frac{1}{2}}{\overline{P} }_{n+\frac{1}{2}}{y}_{A,n+\frac{1}{2}}\right\}-\frac{{c}_{2}}{{\overline{P} }_{n}} \frac{\partial {\overline{q} }_{A,n}}{\partial \overline{t} }-\frac{{y}_{A,n}}{{\overline{P} }_{n}}\frac{\partial {\overline{P} }_{n}}{\partial \overline{t} }$$

(A2)

$$\frac{\partial {y}_{B,n}}{\partial \overline{t} }=\frac{{c}_{1}}{{\overline{P} }_{n}}\left\{{\overline{u} }_{n-\frac{1}{2}}{\overline{P} }_{n-\frac{1}{2}}{y}_{B,n-\frac{1}{2}}-{\overline{u} }_{n+\frac{1}{2}}{\overline{P} }_{n+\frac{1}{2}}{y}_{B,n+\frac{1}{2}}\right\}-\frac{{c}_{2}}{{\overline{P} }_{n}} \frac{\partial {\overline{q} }_{B,n}}{\partial \overline{t} }-\frac{{y}_{B,n}}{{\overline{P} }_{n}}\frac{\partial {\overline{P} }_{n}}{\partial \overline{t} }$$

(A3)

$$Solid ~phase ~balance~ \frac{\partial {\overline{q} }_{A,n }}{\partial \overline{t} }={c}_{3} ({\overline{q} }_{A,n}^{*}-{\overline{q} }_{A,n})$$

(A4)

$$\hspace{1 cm} \frac{\partial {\overline{q} }_{B,n }}{\partial \overline{t} }={c}_{4} ({\overline{q} }_{B,n}^{*}-{\overline{q} }_{B,n})$$

(A5)

where ${\overline{q} }_{i}^{*}=f\left(P,{y}_{i}\right)$ is the dimensionless solid phase equilibrium concentration as evaluated by the equilibrium isotherm.

The pressure drops are described by the dimensionless and discretized form of the Blake-Kozeny equation:

$$Pressure ~drop ~equation~ {\overline{u} }_{n}={\overline{k} }_{bk}\left({\overline{P} }_{n-\frac{1}{2}}-{\overline{P} }_{n+\frac{1}{2}}\right)$$

(A6)

where ${\overline{k} }_{b\mathrm{k}}=\frac{{P}_{rif}{k}_{bk}}{{z}_{rif}\Delta \overline{z}{u }_{rif}}$

The ${c}_{i}$ parameters in Eqs. (A1–A5) are defined as:

$${c}_{1}=\frac{{u}_{rif}{t}_{rif}}{{z}_{rif}{\epsilon }_{T}\Delta \overline{z} }$$

(A7)

$${c}_{2}=\frac{{\rho }_{B}RT{q}_{rif}}{{\epsilon }_{T}{P}_{rif}}$$

(A8)

$${c}_{3}={k}_{LDF,\mathrm{A}}{t}_{rif}$$

(A9)

$${c}_{4}={k}_{LDF,\mathrm{B}}{t}_{rif}$$

(A10)

where the subscript rif means suitable reference values.

The boundary and initial conditions for each step of each configuration are summarized in the following similarly to those reported by [20] in the DRPHA case. Please, refer to Fig. 1 to identify flow orientation.

1.1 DRPHA

• BD step:

  $$ICs:t={\overline{t} }_{0,BD}\to P\left({\overline{t} }_{end,FE},z\right),{y}_{i}\left({\overline{t} }_{end,FE},z\right), {\overline{q} }_{i}({\overline{t} }_{end,FE},z)$$
  $${BCs:z=0\to \overline{u} }_\frac{1}{2}=0$$
  $$\hspace{1 cm} {y}_\frac{1}{2}={y}_{1}$$
  $${z=1\to \overline{P} }_{N+\frac{1}{2}}=P(t)/{P}_{rif}$$

  ${\overline{P} }_\frac{1}{2}$ and ${\overline{u} }_{N+\frac{1}{2}}$ are computed using ${\overline{u} }_\frac{1}{2}$ and ${\overline{P} }_{N+\frac{1}{2}}$ and through the Blake-Kozeny equation that links the velocity with the pressure gradient. Using the half-cell approximation, it results:

  $${\overline{P} }_\frac{1}{2}={\overline{P} }_{1}+\frac{{\overline{u} }_\frac{1}{2}}{2{\overline{k} }_{BK}}$$

  (A11)
  $${\overline{u} }_{N+\frac{1}{2}}=2{\overline{k} }_{BK}\left({\overline{P} }_{N}-{\overline{P} }_{N+\frac{1}{2}}\right)$$

  (A12)

  As last, ${y}_{N+\frac{1}{2}}$ is obtained through a first order upwind interpolation:

  $${y}_{N+\frac{1}{2}}={y}_{N}$$

  (A13)

  .

• PU Step:

  $$ICs:\overline{t }={\overline{t} }_{0,PU}\to \overline{P }\left({t}_{end,BD},z\right),{y}_{i}\left({\overline{t} }_{end,BD},z\right), {q}_{i}({\overline{t} }_{end,BD},z)$$
  $$BCs: z=0\to {\overline{u} }_\frac{1}{2}={u}_{LR}/{u}_{rif}$$
  $$\hspace{1 cm} {y}_\frac{1}{2}={y}_{i,L}$$
  $$z=1\to {\overline{P} }_{N+\frac{1}{2}}={P}_{L}/{P}_{rif}$$

  where ${u}_{LR}$ is obtained by setting the value of ${R}_{L}$. ${\mathrm{y}}_{i,L}$ is evaluated from the material balance in ${\vartheta }_{1}$:

  $${y}_{i,L}=\frac{{\int }_{{\overline{t} }_{0,FE}}^{{{\overline{t} }_{0,FE}+\overline{t} }_{FE}}{\overline{u} }_{N+\frac{1}{2},FE}\frac{{\overline{P} }_{H}}{RT}{y}_{i,N+\frac{1}{2},FE}d\overline{t}}{{\int }_{{\overline{t} }_{0,FE}}^{{{\overline{t} }_{0,FE}+\overline{t} }_{FE}}{\overline{u} }_{N+\frac{1}{2},FE}\frac{{\overline{P} }_{H}}{RT}d\overline{t} }$$

  (A14)

  Equations (A11–A13) are used for the computation of ${\overline{P} }_\frac{1}{2}, {y}_{i,N+\frac{1}{2}}$ and ${\overline{u} }_{N+\frac{1}{2}}$.

• PR Step:

  $$ICs:\overline{t }={\overline{t} }_{0,PR}\to \overline{P }\left({\overline{t} }_{end,PU},z\right),{y}_{i}\left({\overline{t} }_{end,PU},z\right), {q}_{i}({\overline{t} }_{end,PU},z)$$
  $${BCs:z=0\to \overline{P} }_\frac{1}{2}=P(t)/{P}_{rif}$$
  $$\hspace{1 cm} {y}_\frac{1}{2}={y}_{i,H}$$
  $$z=1\to {\overline{u} }_{N+\frac{1}{2}}=0$$

  ${y}_{i,H}$ is obtained from the material balance in ${\vartheta }_{2}$:

  $${y}_{i,H}=\frac{{\int }_{{\overline{t} }_{0,BD}}^{{{\overline{t} }_{0,BD}+\overline{t} }_{BD}}{\overline{u} }_{N+\frac{1}{2},BD}\frac{{\overline{P} }_{N+\frac{1}{2},BD}}{RT}{y}_{i,N+\frac{1}{2},BD}d\overline{t }+{\int }_{{\overline{t} }_{0,PU}}^{{{\overline{t} }_{0,PU}+\overline{t} }_{PU}}{\overline{u} }_{N+\frac{1}{2},PU}\frac{{\overline{P} }_{N+\frac{1}{2},PU}}{RT}{y}_{i,N+\frac{1}{2},PU}d\overline{t}}{{\int }_{{\overline{t} }_{0,BD}}^{{{\overline{t} }_{0, BD}+\overline{t} }_{BD}}{\overline{u} }_{N+\frac{1}{2},BD}\frac{{\overline{P} }_{N+\frac{1}{2},BD}}{RT}d\overline{t }++{\int }_{{\overline{t} }_{0,PU}}^{{{\overline{t} }_{0,PU}+\overline{t} }_{PU}}{\overline{u} }_{N+\frac{1}{2},PU}\frac{{\overline{P} }_{N+\frac{1}{2},PU}}{RT}d\overline{t} }$$

  (A15)

  Equations (A11–A13) are adapted and used to explicit ${\overline{P} }_{N+\frac{1}{2}},{\overline{u} }_\frac{1}{2}$ and ${y}_{i,N+\frac{1}{2}}$.

• FE Step

  $$ICs:\overline{t }={\overline{t} }_{0,FE}\to \overline{P }\left({\overline{t} }_{end,PR},z\right), {y}_{i}\left({\overline{t} }_{end,PR},z\right), {\overline{q} }_{i}({\overline{t} }_{end,PR},z)$$
  $$BCs:z=0\to {\overline{u} }_\frac{1}{2}={u}_{HR}/{u}_{rif}$$
  $$\hspace{1 cm} {y}_\frac{1}{2}={y}_{i,H}$$
  $$z=1\to {\overline{P} }_{N+\frac{1}{2}}={P}_{H}/{P}_{rif}$$

  The value of ${u}_{HR}$ is obtained by imposing the value of ${\dot{n}}_{HP}$ and fulfilling the molar balance in vessel ${\vartheta }_{2}$. ${y}_{i,H}$ has been computed in the previous step (Equation (A15)). Again, Equations (A11-A13) are adapted and used for ${\overline{P} }_\frac{1}{2},{\overline{u} }_{N+\frac{1}{2}}$ and ${y}_{i,N+\frac{1}{2}}$.

• Lateral feed injection

  The axial position is assumed coincident with the element wall separating ${n}_{feed}$ and ${n}_{feed}+1$ [20] and it splits the bed into bottom ($[0,{z}_{feed}^{-}]$) and top semi-column ($[{z}_{feed}^{+},1]$), as sketched in Fig. 

  Fig. 10

  

  Lateral feed modeling sketch

  10:

  The BCs for the two semi-columns are:

  $$z={z}_{feed}^{-}\to {\overline{P} }_{{n}_{feed}+\frac{1}{2}}={\overline{P} }_{{(n}_{feed}+1)-\frac{1}{2}}$$
  $$z={z}_{feed}^{+}\to {y}_{i.{(n}_{feed}+1)-\frac{1}{2}}=\frac{{{y}_{i,feed}\overline{u} }_{feed}{\overline{P} }_{feed}+{y}_{i,{n}_{feed}+\frac{1}{2}}{\overline{u} }_{{n}_{feed}+\frac{1}{2}}{\overline{P} }_{{n}_{feed}+\frac{1}{2}}}{{\overline{u} }_{{(n}_{feed}+1)-\frac{1}{2}} {\overline{P} }_{{(n}_{feed}+1)-\frac{1}{2}}}$$
  $$\hspace{1 cm} {\overline{u} }_{{(n}_{feed}+1)-\frac{1}{2}}=\frac{{\overline{u} }_{feed}{\overline{P} }_{feed}+{\overline{u} }_{{n}_{feed}+\frac{1}{2}}{\overline{P} }_{{n}_{feed}+\frac{1}{2}}}{{\overline{P} }_{{(n}_{feed}+1)-\frac{1}{2}}}$$

  ${\overline{P} }_{{(n}_{feed}+1)-\frac{1}{2}}, {\overline{u} }_{{n}_{feed}+\frac{1}{2}}$ and ${y}_{i,{n}_{feed}+\frac{1}{2}}$ are from Equations (A11–A13).

1.2 DRPHB

• BD step:

  $$ICs:\overline{t }={\overline{t} }_{0,BD}\to \overline{P }\left({\overline{t} }_{end,FE},z\right), {y}_{i}\left({\overline{t} }_{end,FE},z\right), {\overline{q} }_{i}({\overline{t} }_{end,FE},z)$$
  $$BCs:z=1\to {\overline{u} }_\frac{1}{2}=0$$
  $$\hspace{1 cm} {y}_\frac{1}{2}={y}_{1}$$
  $$z=1\to {\overline{P} }_{N+\frac{1}{2}}=P(t)/{P}_{rif}$$

  The values of ${\overline{P} }_\frac{1}{2}$, ${y}_{N+\frac{1}{2}}$ and ${\overline{u} }_{N+\frac{1}{2}}$ are obtained from Equation (A11–A13).

• PU Step:

  $$ICs:\overline{t }={\overline{t} }_{0,PU}{\to \overline{P }\left({t}_{end,BD},z\right), y}_{i}\left({\overline{t} }_{end,BD},z\right), {q}_{i}({\overline{t} }_{end,BD},z)$$
  $$BCs:z=0\to {\overline{u} }_\frac{1}{2}={u}_{LR}/{u}_{rif}$$
  $$\hspace{1 cm} {y}_\frac{1}{2}={y}_{i,L}$$
  $${z=1\to \overline{P} }_{N+\frac{1}{2}}={P}_{L}/{P}_{rif}$$

  ${\mathrm{y}}_{i,L}$ is computed by using the Eq. (A14).

  Equations (A11–A13) are used to explicit ${\overline{P} }_\frac{1}{2}, {y}_{i,N+\frac{1}{2}},$ and ${\overline{u} }_{N+\frac{1}{2}}$.

• PR Step:

  $$ICs:\overline{t }={\overline{t} }_{0,PR}\to \overline{P }\left({\overline{t} }_{end,PU},z\right), {y}_{i}\left({\overline{t} }_{end,PU},z\right), {q}_{i}({\overline{t} }_{end,PU},z)$$
  $$BCs: \mathrm{z}=0 \to {\overline{P} }_\frac{1}{2}=P(t)/{P}_{rif}$$
  $$\hspace{1 cm} {y}_\frac{1}{2}={y}_{i,L}$$
  $${\stackrel{-}{z=1\to u}}_{N+\frac{1}{2}}=0$$

  ${y}_{i,H}$, obtained through the Eq. (A14).

  Equations (A11-A13) are adapted and used to explicit ${\overline{P} }_{N+\frac{1}{2}},{\overline{u} }_\frac{1}{2}$ and ${y}_{i,N+\frac{1}{2}}$.

• FE Step

  $$ ICs:\overline{t }={\overline{t} }_{0,FE}\to \overline{P}\left({\overline{t} }_{end,PR},z\right),{y}_{i}\left({\overline{t} }_{end,PR},z\right), {\overline{q} }_{i}({\overline{t} }_{end,PR},z)$$
  $${BCs:\mathrm{z}=\to \overline{u} }_\frac{1}{2}={u}_{HR}/{u}_{rif}$$
  $${y}_\frac{1}{2}={y}_{i,H}$$
  $$z=1{\to \overline{P} }_{N+\frac{1}{2}}={P}_{H}/{P}_{rif}$$

  The lateral feed injection is modelled as in the DRPHA case and ${y}_{i,H}$ is computed through Equation (A15).

1.3 DRPLA

• BD step:

  $$ICs:\overline{t }={\overline{t} }_{0,BD}\to \overline{P }\left({\overline{t} }_{end,FE},z\right), {y}_{i}\left({\overline{t} }_{end,FE},z\right), {\overline{q} }_{i}({\overline{t} }_{end,FE},z)$$
  $${BCs:\mathrm{z}=0\to \overline{u} }_\frac{1}{2}=0$$
  $$\hspace{1 cm} {y}_\frac{1}{2}={y}_{1}$$
  $${\mathrm{z}=1\to \overline{P} }_{N+\frac{1}{2}}=P(t)/{P}_{rif}$$

  The values of ${\overline{P} }_\frac{1}{2}$, ${y}_{N+\frac{1}{2}}$ and ${\overline{u} }_{N+\frac{1}{2}}$ are obtained with Eqs. (A11–A13).

• PU Step:

  $$ICs:\overline{t }={\overline{t} }_{0,PU}\to \overline{P }\left({t}_{end,BD},z\right), {y}_{i}\left({\overline{t} }_{end,BD},z\right), {q}_{i}({\overline{t} }_{end,BD},z)$$
  $$BCs:z=0\to {\overline{u} }_\frac{1}{2}=\frac{{u}_{LR}}{{u}_{rif}}$$
  $$\hspace{1 cm} {y}_\frac{1}{2}={y}_{i,H}$$
  $${\mathrm{z}=1\to \overline{P} }_{N+\frac{1}{2}}={P}_{L}/{P}_{rif}$$

  ${\mathrm{y}}_{i,H}$ is computed by using Eq. (A15).

  Equations (A11–A13) are used to explicit ${\overline{P} }_\frac{1}{2}, {y}_{i,N+\frac{1}{2}},$ and ${\overline{u} }_{N+\frac{1}{2}}$.

• PR Step:

  $$ICs:\overline{t }={\overline{t} }_{0,PR}\to \overline{P }\left({\overline{t} }_{end,PU},z\right), {y}_{i}\left({\overline{t} }_{end,PU},z\right), {q}_{i}({\overline{t} }_{end,PU},z)$$
  $$BCs:\mathrm{z}=0\to {\overline{P} }_\frac{1}{2}=P(t)/{P}_{rif}$$
  $$\hspace{1 cm} {y}_\frac{1}{2}={y}_{i,H}$$
  $$\mathrm{z}=1\to {\overline{u} }_{N+\frac{1}{2}}=0$$

  ${y}_{i,H}$, obtained as in the previous PU step.

  Equations (A11–A13) are adapted and used to explicit ${\overline{P} }_{N+\frac{1}{2}},{\overline{u} }_\frac{1}{2}$ and ${y}_{i,N+\frac{1}{2}}$.

• FE Step

  $$ICs:\overline{t }={\overline{t} }_{0,FE}\to \overline{P }\left({\overline{t} }_{end,PR},z\right), , {y}_{i}\left({\overline{t} }_{end,PR},z\right), {\overline{q} }_{i}({\overline{t} }_{end,PR},z)$$
  $${BCs:\mathrm{z}=0\to \overline{u} }_\frac{1}{2}={u}_{HR}/{u}_{rif}$$
  $$\hspace{1 cm} {y}_\frac{1}{2}={y}_{i,L}$$
  $${{\mathrm{z }=1\to \overline{P}}}_{N+\frac{1}{2}}={P}_{H}/{P}_{rif}$$

  where ${y}_{i,L}$ is computed using Eq. (A14). Once again, the lateral feed injection is modeled as in the DRPHA case.

1.4 DRPLB

• BD step:

  $$ICs:\overline{t }={\overline{t} }_{0,BD}\to \overline{P }\left({\overline{t} }_{end,FE},z\right), {y}_{i}\left({\overline{t} }_{end,FE},z\right), {\overline{q} }_{i}({\overline{t} }_{end,FE},z)$$
  $${BCs:\mathrm{z}=0\to \overline{u} }_\frac{1}{2}=0$$
  $$\hspace{1 cm} {y}_\frac{1}{2}={y}_{1}$$
  $${\mathrm{z}=1\to \overline{P} }_{N+\frac{1}{2}}=P(t)/{P}_{rif}$$

  The values of ${\overline{P} }_\frac{1}{2}$, ${y}_{N+\frac{1}{2}}$ and ${\overline{u} }_{N+\frac{1}{2}}$ are obtained as in the previous cases.

• PU Step:

  $$ICs:\overline{t }={\overline{t} }_{0,PU}\to \overline{P }\left({t}_{end,BD},z\right), {y}_{i}\left({\overline{t} }_{end,BD},z\right), {q}_{i}({\overline{t} }_{end,BD},z)$$
  $${BCs: z=0\to \overline{u} }_\frac{1}{2}={u}_{LR}/{u}_{rif}$$
  $$\hspace{1 cm} {y}_\frac{1}{2}={y}_{i,H}$$
  $${\mathrm{z }=1\to \overline{P}}_{N+\frac{1}{2}}={P}_{L}/{P}_{rif}$$

  ${\mathrm{y}}_{i,H}$ is computed by using Eq. (A15).

  Equations (A11–A13) are used to explicit  ${\overline{P} }_\frac{1}{2}, {y}_{i,N+\frac{1}{2}},$ and ${\overline{u} }_{N+\frac{1}{2}}$.

• PR Step:

  $$ICs:\overline{t }={\overline{t} }_{0,PR}\to \overline{P}\left({\overline{t} }_{end,PU},z\right), {y}_{i}\left({\overline{t} }_{end,PU},z\right), {q}_{i}({\overline{t} }_{end,PU},z)$$
  $${BCs:\mathrm{z}=0\to \overline{P}}_\frac{1}{2}=P(t)/{P}_{rif}$$
  $$\hspace{1 cm} {y}_\frac{1}{2}={y}_{i,L}$$
  $${\mathrm{z}=1\to \overline{u} }_{N+\frac{1}{2}}=0$$

  with ${y}_{i,L}$ as in Equation (A14).

  ${\overline{P} }_{N+\frac{1}{2}},{\overline{u} }_\frac{1}{2}$ and ${y}_{i,N+\frac{1}{2}}$ are computed through Equations (A11- A13).

• FE Step:

  $$ICs:\overline{t }={\overline{t} }_{0,FE}\to \overline{P }\left({\overline{t} }_{end,PR},z\right), {y}_{i}\left({\overline{t} }_{end,PR},z\right), {\overline{q} }_{i}({\overline{t} }_{end,PR},z)$$
  $$BCs:\mathbf{z}=0\to {\overline{u} }_\frac{1}{2}={u}_{HR}/{u}_{rif}$$
  $$\hspace{1 cm} {y}_\frac{1}{2}={y}_{i,L}$$
  $${z=1\to \overline{P} }_{N+\frac{1}{2}}={P}_{H}/{P}_{rif}$$

  with ${y}_{i,L}$ as previously computed in the PR step.

The lateral feed injection is modeled as in the DRPHA case.