Accurate blank corrections for zero length column experiments

Abstract

In this study we present a new methodology for correcting experimental Zero Length Column data, to account for contributions to the measured signal arising from extra-column volumes and the detector. The methodology considers the experimental setup as a series of mixing volumes with diffusive pockets whose contributions to the overall measured signal can be accurately described by simple model functions. The composite effect of the individual contributions is subsequently described through the method of convolution. It is shown that the model parameters are closely related to the physical characteristics of the setup components and as such they remain valid over a range of process conditions. The methodology is firstly validated through fitting to experimental experiments without adsorbent present. The inverse procedure of deconvolution can in turn be applied to experimental data with adsorbent, to yield corrected data which can readily be modelled using standard tools for equilibrium and kinetic analysis. A number of case studies is finally presented exemplifying the effect of applying accurate blank corrections, demonstrating also the application to a nonlinear adsorption system.

1 Introduction

Adsorption is a widely used technology for separation, purification and drying, due to its simplicity, reliability and scalability. In industrial settings, the technology is run in a cyclical fashion, e.g. pressure swing adsorption (PSA), vacuum swing adsorption (VSA), temperature swing adsorption (TSA), etc. Key to running these processes efficiently is having a minute understanding of the process’ equilibrium and kinetic properties. Whereas equilibrium data can be obtained on either bulk or small sample quantities, kinetic data is often obtained on lab scale sample quantities. One method for obtaining such information is the Zero Length Column (ZLC) technique, which uses very small amounts of sample (typically less than 15 mg)(Brandani and Mangano 2020). Breakthrough experiments, which can be run on a range of sample sizes, are also routinely used for this purpose and kinetic properties may be extracted by fitting experimental data to simulations, where the kinetic properties are adjustable modelling parameters (Ruthven 1984; Wilkins et al. 2020).

Separation has become ever more important in recent years, in particular due to an effort to curtail global warming and limit emissions of greenhouse gases. For this reason, many groups are now pursuing the development of next generation adsorbents, such as MOFs, flexible zeolites, hierarchical silicas, etc. Naturally, these materials are initially synthesised on a small scale in the lab and so establishing their kinetic properties requires column experiments on a similarly small scale. Such small column experiments are liable to exhibiting non-negligible extra-column effects, which can lead to erroneous interpretation of data and thus inaccurate kinetic information. This effect from the extra-column-volume (ECV) has long been recognised in the field of liquid chromatography, in which non-square pulse inputs and detector effects need to be accounted for in the final analysis (Delley 1986; Kaltenbrunner et al. 1997; Gritti et al. 2006). A small number of studies also address this problem in step-response techniques (Wilkins et al. 2020). In the case of a linear response of the ECV, a point-by-point correction may be applied (Guntuka et al. 2008), whereby the gas phase concentration of a blank run at time t is subtracted from the uncorrected adsorbent run, performed under identical conditions, at the same time t. In order to avoid having to run blank experiments under identical conditions for each experiment with adsorbent, Rajendran et al. use a tanks-in-series model to account for ECV and subtract its contribution from the sample runs to leave a corrected signal (Rajendran et al. 2008). Joss and Mazzotti use a similar approach based on dispersed plug-flow and by adding a stagnant volume to their ECV model manage to account for mass transfer and heat effects to accurately describe extra-column contributions for a range of pressures and flow rates (Joss and Mazzotti 2012). As their model is partly empirical and does not attempt to capture the physics of their experimental setup, model parameters require adjusting for different process conditions. In this latter study, the ECV contributions are added to the simulated signal of the column to match experimental data, an approach also used by Friedrich et al., who add a detector model to their simulations. The detector model is based on Langmuir adsorption with LDF mass transfer limitation and is fit to experimental blank runs (Friedrich et al. 2015).

In this study, we take inspiration from several previous studies, but with the aim to describe the experimental setup based on its physical components. This has the advantage of requiring a minimum of modelling parameters and making the model valid over a large range of process conditions, i.e. without the need to modify parameters. The contributions of several components with different time constants to the experimental signal will yield a composite effect, which can mathematically be derived through the method of convolution, an approach also used in refs. (Delley 1986; Kaltenbrunner et al. 1997). The basis of this approach is the fact that each component will have a transfer function that converts the inlet concentration to an outlet response. Assuming linearity allows the solution of each model in the Laplace domain and the composite transfer function can then be obtained from the product of the individual terms, as all components are in series. This is a standard result from process dynamics and control (Stephanopoulos 1983). The model for the extra-column effects is parametrised by fitting experimental blank runs, i.e. column experiments with no adsorbent present. By applying the inverse procedure of deconvolution on signals from experimental runs with adsorbent, a corrected signal is obtained which corresponds to the dynamic response that the ZLC would have if a perfect step input could be achieved and the detector had an ideal response. The key assumption of the deconvolution procedure is linearity and this is typically the case for the dynamic response of all the components before the ZLC and the detector.

2 Experimental

2.1 Materials

Gases used in this study are helium (BOC, CP grade, 99.999% purity), carbon dioxide (BOC, 99.8% purity) and nitrogen (BOC, 99.998% purity). The adsorbents used in the case studies will be described in the corresponding section.

2.2 Equipment

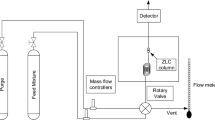
The experimental setups under consideration have been described in detail in refs. (Hu et al. 2015) and (Centineo and Brandani 2020). A simplified diagram of the experimental setup in ref.(Hu et al. 2015) is depicted in Fig. 1. The dosing mixture is prepared by mixing appropriate quantities of carrier gas (i.e. He or N₂) and the dosing component in four 1 L stainless steel canisters and leaving the mixture to equilibrate for at least 3 h. The flow rates of both the inert carrier and the dosing gas are controlled by mass flow controllers (MFC, Brooks Instrument). Thereafter the gases pass through solenoid valves (SV1 to SV4) towards the column and outlet with detector (MS; Dycor mass spectrometer, Ametek Process Instruments). A back pressure regulator (BPR, Brooks Instrument) at the outlet allows for operation at elevated pressures. The column is housed within a Carbolite oven, with a Eurotherm temperature controller. The solenoid valves are operated in an alternating fashion, such that either of the two gas streams are fed to the column and by activation allow a step change in the composition of the gas phase. A differential pressure gauge between the dosing and carrier lines allows for balancing the gas pressures, so that no pressure spikes occur upon switching the solenoid valves. All the components after the solenoid valves are connected by stainless steel pipes with outer diameter of 1/16″. The column and Tee-junction 2 have an outer diameter of 1/8″ and are thus connected to the piping through reducing unions. Although the experimental setup in ref.(Centineo and Brandani 2020) is modified for measuring vapour adsorption, the part which is relevant for our modelling purposes, i.e. the section situated between the solenoid valves and the detector, is essentially identical to that described in Fig. 1.

Fig. 1

Schematic diagram of the experimental setup

3 Theory

3.1 Simulation of blank experiments through the method of convolution

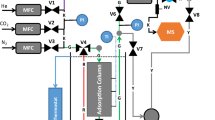
For our modelling purposes, we firstly consider the experimental setup as described in Fig. 1. Since the pressures between the dosing and carrier gas lines are balanced we assume that the concentrations at each solenoid valve are constant. We can therefore limit our section of interest to what is happening after solenoid valves SV1 and SV2. This section contains a number of mixing volumes and diffusive pockets, as described in detail in Fig. 2, where we use more accurate graphical representations of the actual setup components (Swagelok 2020). A particular area of interest is highlighted by the dashed box and concerns the Tee-junction between the solenoid valves. When the solenoid valves change position, a certain volume ceases to be in flow and thus becomes a diffusive pocket, shown in Fig. 3. More precisely, Tee-junction 1 is a mixing volume, whereas the combined volume of the solenoid valve and pipe connecting to this tee junction is a diffusive volume. The remaining reducing unions, ZLC and Tee-junction 2 are all considered as simple mixing volumes in flow. The following assumptions are additionally made:

• All gases are ideal

• The pressure drop in the system is negligible

• The system behaves isothermally

• Axial dispersion is negligible in pipes with convective flow

• Radial dispersion is negligible

Fig. 2

The experimental section of interest for our modelling purpose. The dashed box is shown in more detail in Fig. 3

Fig. 3

Diagram of diffusive volume (dashed box), composed of volume in the solenoid valve and the 1/16″ pipe. The total diffusive length is expected to be larger than the length of 1/16″ pipe, due to the ink-bottle configuration

For modelling purposes, the mixing volumes in flow in the experimental setup are treated as well-mixed cells, or CSTRs, for which the following mass balance applies:

$$V_{CSTR} \frac{dC}{{dt}} = F\left( {C_{in} - C} \right)$$

(1)

where $C$ is expressed in terms of a deviation function, i.e.

$$C = \frac{{c - c_{0} }}{{c_{\infty } - c_{0} }}$$

(2)

Converting to the Laplace domain yields:

$$s\tilde{C} - C\left( 0 \right) = \frac{F}{{V_{CSTR} }}\left( {\tilde{C}_{in} - \tilde{C}} \right)$$

(3)

And after re-arranging and considering that $C\left( 0 \right) = 0$, this yields:

$$\frac{{\tilde{C}}}{{\tilde{C}_{in} }} = \tilde{G}_{CSTR} \left( s \right) = \frac{{\lambda_{CSTR} }}{{s +\lambda_{CSTR} }}$$

(4)

with $\lambda_{CSTR} = \frac{F}{{V_{CSTR} }}$. Equation 4 is the so-called transfer function for a CSTR. The equivalent function in the time domain is:

$$G\left( t \right) =\lambda_{CSTR} e^{{ -\lambda_{CSTR} t}}$$

(5)

The mass balance for Tee-junction 1 is assumed to be that of a CSTR, with volume $V_{mix}$, connected to a diffusive pocket with slab geometry (i.e. one dimensional diffusion along length $L_{diff}$) and volume, $V_{diff}$:

$$V_{diff} \frac{{d\overline{Q}}}{dt} + V_{mix} \frac{dC}{{dt}} = F\left( {C_{in} - C} \right)$$

(6)

where $C$ is as previously defined and $\overline{Q}$ is the average dimensionless concentration in the slab, i.e.

$$\overline{Q} = \frac{{\overline{q} - \overline{q}_{0} }}{{\overline{q}_{\infty } - \overline{q}_{0} }}$$

(7)

The diffusion equation for a slab is

$$\frac{dQ}{{dt}} = D\frac{{\partial^{2} Q}}{{\partial x^{2} }}$$

(8)

and the average concentration is defined as

$$\frac{{d\overline{Q}}}{dt} = \frac{D}{{L_{diff} }}\left( {\frac{\partial Q}{{\partial x}}} \right)_{{x = L_{diff} }}$$

(9)

Solving these equations in the Laplace domains yields:

$$\tilde{G}_{{T1}} \left( s \right) = \frac{{\tilde{C}\left( s \right)}}{{\tilde{C}_{{in}} \left( s \right)}} = \frac{{L_{{T1}} \lambda _{{T1}} }}{{\sqrt {s\lambda_{{T1}} } \tanh \left( {\sqrt {\frac{s}{{\lambda _{{T1}} }}} } \right) + s\gamma _{{T1}} + L_{{T1}} \lambda _{{T1}} }}$$

(10)

where

$$\lambda_{T1} = \frac{D}{{L_{diff}^{2} }}$$

(11)

$$L_{T1} = \frac{F}{{V_{diff} }}\frac{1}{{\lambda_{T1} }}$$

(12)

$$\gamma_{T1} = \frac{{V_{mix} }}{{V_{diff} }}$$

(13)

Inverting Eq. (10) to the time domain, finally gives:

$$G\left( t \right) = \mathop \sum \limits_{{n = 1}}^{\infty } \frac{{ - 2L_{{T1}} \beta _{{slab,n }}^{2}{\lambda_{T1}} }}{{L_{{T1}} + \gamma _{{T1}} \beta _{{slab,n}}^{2} + \beta _{{slab,n}}^{2} + \left( {\gamma _{{T1}} \beta _{{slab,n}}^{2} - L_{{T1}} } \right)^{2} }} e^{{ - \beta _{{slab,n }}^{2}{\lambda_{T1} t} }}$$

(14)

where $\beta_{slab,n}$ are the roots of the following equation:

$$\beta_{slab,n} \tan \left( {\beta_{slab,n} } \right) + \gamma_{T1} \beta_{slab,n} - L_{T1} = 0$$

(15)

Transfer functions can be combined to obtain concentrations leaving various parts. In the Laplace domain they may simply be multiplied; for instance for Tee-junction 2:

$$\tilde{C}_{T2} \left( s \right) = \tilde{C}_{in} \left( s \right)\tilde{G}_{T1} \left( s \right)\tilde{G}_{RedUnion} \left( s \right)\tilde{G}_{ZLC} \left( s \right)\tilde{G}_{T2} \left( s \right)$$

(16)

By switching between a pure carrier and dosing gas, it can be assumed that the input concentration for Tee-junction 1 is a step function, i.e.

$$C_{in} \left( t \right) = \begin{array}{*{20}c} {0, t < 0} \\ {1, t \ge 0} \\ \end{array}$$

(17)

which in the Laplace domain becomes $\tilde{C}_{in} \left( s \right) = \frac{1}{s}$.

Alternatively, the effects on the concentration profile of the various parts in the time domain can be calculated using the convolution theorem. This states that for two functions, $C_{in} \left( t \right)$ and $G\left( t \right)$, acting in tandem, the resulting function,$F\left( t \right)$, is defined as:

$$F\left( t \right) = C_{in} \left( t \right) \times G\left( t \right) = \mathop \smallint \limits_{0}^{t} G\left( {t - u} \right)C_{in} \left( u \right)du = \mathop \smallint \limits_{0}^{t} G\left( u \right)C_{in} \left( {t - u} \right)du$$

(18)

As all the transfer functions in this study are exponential functions, it is straightforward to find analytical expressions to Eq. (18). Using the step function in Eq. (17) as the initial value for $C_{in}$ and using the resultant function $F\left( t \right)$ as the inlet function for the subsequent convolution integral, the cumulative effect of the various setup parts can be calculated as shown in Fig. 4. Here, an arbitrary sequence has been used, i.e. low volume tee, 1/16″–1/8″ reducing union, 1/8″ straight union, 1/8″ tee. It is important to note however that the convolution process can be performed in any order, as the procedure is symmetrical. This symmetry stems from the fact that the convolution integral is in essence a linear operator and is therefore, strictly speaking, only valid for linear systems. When viewed in a semi-log plot, the diffusive tail from Tee-junction 1 becomes more evident. The concentration profile in all these components is affected by flowrate; its effect can be seen in Fig. 5.

Fig. 4

Cumulative effect of the various setup components on the gas phase concentration profile

Fig. 5

Effect of flow rate on concentration profile at 1/8″ Tee-junction 2 (a) and at various components (dashed line at 2 cm³/min and solid line at 5 cm³/min) (b)

The modelling parameters can mostly be obtained by inspection of the dimensions of the various setup components, such as diameter and length of pipes and columns (as listed in Table 1) and through literature values of diffusivities for various species in the carrier gas, typically helium and nitrogen (Arora and Dunlop 1979; Ellis and Holsen 1969; Massman 1998; Paganelli and Kurata 1977; Schwertz and Brow 1951; Walker et al. 1960). The inner volume of the solenoid valves can be estimated by analysis of experiments using an empty column, a so-called blank run.

Table 1 Key dimensions for setup components

A number of blank runs for a typical mixture of 1% CO₂ in helium are shown in Fig. 6. It can be seen that the curves are essentially composed of two exponential decays: the initial decay corresponds to the part of the setup that comprises mixing volumes in flow, whereas the long-time tail is due to a diffusive process. When the curves are plotted versus $Flowrate \times time$, the area underneath the curves correspond to volume of the setup. The assumption of ideal plug flow through the 1/16″ pipes simply causes a delay in the detector response, which can easily be removed from the analysis. Consequently, the volume in flow and that of the diffusive pocket can be estimated by integrating the relevant parts of the curves. The results are shown in Table 2. It is evident that the total mixing volume is larger than the sum of the components in Table 1, but critically there is very little variation, as is also clear from Fig. 7, in which the initial part of the curves at different flow rates all overlap.

Fig. 6

Blank runs in a mixture of 1% CO₂ in helium, clearly showing two exponential decays. The initial decay corresponds to mixing volumes in flow, whereas the long-time tail corresponds to diffusive pockets within the setup

Table 2 Volumes as calculated from integration of blank runs at different flow rates

Fig. 7

Blank runs in a mixture of 1% CO₂ in helium; c/c₀ versus eluted volume (Flowrate × time). It is evident that the initial part of the curves overlap, as expected, since the mixing volumes of the setup do not change with changing the flowrate

The experimental blank runs can now be simulated using the expressions in Eqs. (5, 14 and 18) using appropriate parameters (which can be found in the supplementary material, Table S1), as shown in Fig. 8. Due to the fact that the total diffusive volume at the tee-junction (i.e. $V_{diff} = V_{valve} + V_{pipe}$) is large relative to $V_{pipe}$, in effect creating an ‘ink bottle’ type diffusive configuration (see Fig. 3), it was found that $L_{diff}$ in Eq. (11) is larger than the actual length of the connecting pipe. Due to some mixing in the valve itself, we are using the following approximation for $L_{diff}$, which works well for modelling purposes:

$$L_{diff} = \alpha \frac{{V_{diff} }}{{A_{pipe} }}$$

with $\alpha$ chosen such that:

$$\frac{{V_{diff} }}{{A_{pipe} }} \ge L_{diff} \ge L_{pipe}$$

whereas the simulated blanks in Fig. 8 show a decent fit at low flowrates, it is evident that significant deviation occurs at higher flowrates. The simulations do not capture the shape of the blanks at longer times and underestimate the total volume in flow. Therefore, a final optimisation of the simulated curves is obtained by including a response from the mass spectrometer, which is likely to cause some accumulation and have a kinetic limitation. This effect only becomes apparent at higher flow rates (F > 10 cm³/min). The mass spectrometer effect is similar to that of the low volume tee (Tee-junction 1), i.e. it can be modelled as a combination of a mixing volume with a diffusive side pocket. The inlet to the ionising volume of the mass spectrometer is through a fused silica capillary of approximately 1 m length, which continuously samples gas from the outlet of the ZLC at a flowrate of about 0.02 ± 0.01 cm³/min. The diffusive pocket is also more likely to be multidimensional; we are assuming a spherical geometry. The transfer function for this part is:

$$\tilde{G}\left( s \right) = \frac{{\tilde{C}\left( s \right)}}{{\tilde{C}_{{in}} \left( s \right)}} = \frac{{L_{{MS}} \lambda _{{MS}} }}{{\sqrt {\lambda _{{MS}} s} \coth \left( {\sqrt {\frac{s}{{\lambda _{{MS}} }}} } \right) - \lambda _{{MS}} + s\gamma _{{MS}} + L_{{MS}} \lambda _{{MS}} }}$$

(19)

where

$$\lambda_{MS} = \frac{1}{{\tau_{MS} }}$$

(20)

$$L_{MS} = \frac{1}{3}\frac{F}{{V_{diff} }}\frac{1}{{\lambda_{MS} }}$$

(21)

$$\gamma_{MS} = \frac{1}{3}\frac{{V_{mix,MS} }}{{V_{diff,MS} }}$$

(22)

Here it is recognised that $\tau_{MS}$ corresponds to the time constant of the mass spectrometer, which may not necessarily involve a diffusion process, but could instead be due to a capacitive effect of the Faraday cup. Inverting Eq. (19) to the time domain, finally gives:

$$G\left( t \right) = ~\mathop \sum \limits_{{n = 1}}^{\infty } \frac{{ - 2L_{{MS}} \beta _{{sphere,n}}^{2} \lambda_{MS} }}{{L_{{MS}} + \gamma _{{MS}} \beta _{{sphere,n}}^{2} + \beta _{{sphere,n}}^{2} + \left( {\gamma _{{MS}} \beta _{{sphere,n}}^{2} - L_{{MS}} + 1} \right)^{2} - 1}}e^{{ - ~ \beta _{{sphere,n}}^{2} \lambda_{MS} t }}$$

(23)

where $\beta_{sphere,n}$ are the roots of the following equation:

$$\beta_{sphere,n} \cot \left( {\beta_{sphere,n} } \right) - \gamma_{MS} { }\beta_{sphere,n}^{2} - 1 + L_{MS} = 0$$

(24)

Fig. 8

Experimental blank runs and simulated fits, using convolution theorem

Assuming that the flowrate into the mass spectrometer is constant, a single set of parameters, i.e. $L_{MS}$, $\lambda_{MS}$ and $\gamma_{MS}$ will be used for simulating this effect on the shape of the blank runs. The resulting fits when the detector is included in the convolution model are shown in Fig. 9. The modelling parameters are listed in Table 3.

Fig. 9

Experimental blank runs at 1% CO₂ in He and simulated fits using convolution theorem, now including kinetic limitations from the mass spectrometer

Table 3 Key parameters in the convolution model

3.2 Effect of changing process conditions

To validate the current model, it was applied on blank runs under a range of different process conditions. When using different concentrations of CO₂ or changing the dosing gas to N₂ in He, the only parameters expected to change are the value for the diffusivity in Tee-junction 1 (in the case of using N₂) and the mass spectrometer parameters. The various diffusive volumes and those in flow should remain unchanged. As can be seen from Figs. 10 and 11 and the modelling parameters in Table 3 this is indeed the case. Moreover, the diffusivities in tee-junction 1 for the models describing blanks in 1% N₂/He and 1% CO₂/He atmospheres scale by the square root of the molecular masses, as expected from a process described by molecular diffusion, i.e.:

$$\frac{{{\raise0.7ex\hbox{${D_{{CO_{2} - He}} }$} \!\mathord{\left/ {\vphantom {{D_{{CO_{2} - He}} } {L^{2} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${L^{2} }$}}}}{{{\raise0.7ex\hbox{${D_{{N_{2} - He}} }$} \!\mathord{\left/ {\vphantom {{D_{{N_{2} - He}} } {L^{2} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${L^{2} }$}}}} = \frac{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {\sqrt {Mw_{{CO_{2} }} } }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\sqrt {Mw_{{CO_{2} }} } }$}}}}{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {\sqrt {Mw_{{N_{2} }} } }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\sqrt {Mw_{{N_{2} }} } }$}}}} = \frac{{\sqrt {28.01} }}{{\sqrt {44.01} }} = 0.80$$

Fig. 10

Experimental blank runs at 1% N₂ in He and simulated fits using the convolution theorem

Fig. 11

Experimental blank runs at 10% CO₂ in He and simulated fits using the convolution theorem

Blanks were also run at elevated pressures and as Fig. 12 shows, the model can easily capture this effect by adjusting the diffusivity of CO₂ in helium. These experiments were performed prior to a major system upgrade and therefore the parameters describing the low volume Tee-junction 1 have different values. The model parameters at different pressures can be found in the supplementary material, Table S2.

Fig. 12

Blanks at p = 2.1 and p = 3.0 bar and model fits. The only model parameter which requires adjusting is the diffusivity of CO₂/He in tee-junction 1

3.3 Model transferability

The advantage of using the method of convolution is that it is based on the physical properties of the experimental setup, i.e. dimensions of parts, molecular diffusivities etc., and should therefore be transferable to describe results obtained on other setups with a similar configuration. Figure 13a shows a blank response in 1% CO₂/He on a different experimental setup in our lab, which comprises narrow bore 1/16″ pipes and a different mass spectrometer, for obvious reasons (although same make and model as previously). Due to the narrow bore pipes, the diffusive flux into Tee-junction 1 is reduced, as evidenced by a shallower long time slope of the diffusive tail. The model fits the data well, after adjustment of the relevant parameters, see Table 4. This particular setup is also routinely used for water vapour studies. Figure 13b shows the blank runs for a 2% H₂O/He mixture. It is evident that these blanks look significantly different from those run with typical gas mixtures. They exhibit less flow rate dependence and more accumulation (the overall blank volume of H₂O is roughly an order of magnitude larger than that of CO₂). The model cannot capture the behaviour of this blank in its entirety, but does fit the data accurately at short and long times, the latter being of particular importance for kinetic analysis. The discrepancy at intermediate times is probably due to water accumulating on the surface of pipes, which would introduce some axial dispersion. Such an effect could be introduced to the model if necessary. In order to fit the data, the model parameters reflect extra accumulation in the solenoid valves as well as in the mass spectrometer, as seen in Table 4. The fits resulting from not including this additional accumulation can be found in the supplementary material.

Fig. 13

Blank runs on a different setup with a similar configuration, but different components in 1% CO₂/He (a) and 2% H₂O/He atmospheres (b)

Table 4 Model parameters for a different experimental setup, comprising narrow bore 1/16″ pipes

3.4 Deconvolution of the experimental signal

Evidently, the presence of diffusive pockets within the setup can lead to erroneous interpretation when measuring kinetics or equilibrium behaviour of adsorbents. However, now that the system and the effects of its constituent parts on the concentration profile have been accurately modelled, these effects can be removed from any experimental signal by the process of deconvolution.

As an example, we are describing the process of deconvolution of the mass spectrometer effect (MS). For convenience we will call the concentration at the MS at time $t_{i}$, $F_{i} =$ $C_{MS} \left( {t_{i} } \right)$, whereas the concentration leaving Tee Junction 2, $C_{T2}$, is in this case the quantity of interest. And recognising that the transfer function is simply a summation of integrals, i.e. $\mathop \sum \limits_{n = 1}^{\infty } a_{n} e^{{ - b_{n} t}}$, we have for integral n at time $t_{i}$:

$$F_{i} = a_{n} e^{{ - b_{n} t_{i} }} \mathop \int \limits_{0}^{{t_{i} }} e^{{b_{n} u}} C_{T2} \left( u \right)du$$

(25)

It is similarly easy to derive that at time $t_{i + 1} = t_{i} + \Delta t$:

$$F_{i + 1} = a_{n} e^{{ - b_{n} t_{i + 1} }} \mathop \int \limits_{0}^{{t_{i + 1} }} e^{{b_{n} u}} C_{T2} \left( u \right)du$$

(26)

$$F_{i + 1} = a_{n} e^{{ - b_{n} \Delta t}} \left[ {\frac{{F_{i} }}{{a_{n} }} + \mathop \int \limits_{{t_{i} }}^{{t_{i + 1} }} e^{{b_{n} \left( {u - t_{i} } \right)}} C_{T2} \left( u \right)du} \right]$$

(27)

We can now approximate the concentration leaving Tee Junction 2 by a linear function, which should be accurate for small time steps, $\Delta t$, i.e.:

$$C_{T2} \left( u \right) = C_{T2} \left( {t_{i} } \right) + \frac{{C_{T2} \left( {t_{i + 1} } \right) - C_{T2} \left( {t_{i} } \right)}}{\Delta t} \left( {u - t_{i} } \right)$$

(28)

Then through integration by parts:

$$F_{i + 1} = a_{n} e^{ - b\Delta t} \left\{ {\frac{{F_{i} }}{{a_{n} }} + \left[ {\frac{1}{{b_{n} }}e^{{b_{n} \left( {u - t_{i} } \right)}} C_{T2} \left( u \right)} \right]_{{t_{i} }}^{{t_{i + 1} }} - \mathop \int \limits_{{t_{i} }}^{{t_{i + 1} }} \frac{1}{{b_{n} }}e^{{b_{n} \left( {u - t_{i} } \right)}} \frac{{dC_{T2} }}{du}du} \right\}$$

(29)

$$F_{i + 1} = a_{n} e^{{ - b_{n} \Delta t}} \left\{ {\frac{{F_{i} }}{{a_{n} }} + \frac{1}{{b_{n} }}\left[ {e^{{b_{n} \Delta t}} C_{T2} \left( {t_{i + 1} } \right) - C_{T2} \left( {t_{i} } \right)} \right] - \frac{{C_{T2} \left( {t_{i + 1} } \right) - C_{T2} \left( {t_{i} } \right)}}{{b_{n}^{2} \Delta t}}\left( {e^{{_{n}^{b} \Delta t}} - 1} \right)} \right\}$$

(30)

Extending this to N exponentials finally yields:

$$F_{i + 1} = \mathop \sum \limits_{n = 1}^{N} \left\{ {\left( {F_{i} } \right)_{n} e^{{ - b_{n} \Delta t}} + \frac{{a_{n} }}{{b_{n} }}\left[ {C_{T2} \left( {t_{i + 1} } \right) - C_{T2} \left( {t_{i} } \right)e^{{ - b_{n} \Delta t}} } \right] - \frac{{a_{n} \left( {C_{T2} \left( {t_{i + 1} } \right) - C_{T2} \left( {t_{i} } \right)} \right)}}{{b_{n}^{2} \Delta t}}\left( {1 - e^{{ - b_{n} \Delta t}} } \right)} \right\}$$

(31)

$F_{i + 1}$ and $F_{i}$ are known from the experimental signal, whereas $C_{T2} \left( {t = 0} \right) = 1$. $C_{T2} \left( {t = \Delta t} \right)$ can thus be calculated initially, and consecutive concentrations at Tee Junction 2 can be solved iteratively. This method of deconvolution can also be found in ref.(Brandani 1998).

Figure 14a shows how both the mass spectrometer effect and the effect of the low volume tee can be removed from a model blank curve using this methodology. Here, a different set of modelling parameters has been used, to more clearly show the effect of the two diffusive elements. The deconvolution process can be carried out consecutively, to remove both contributions. Figure 14b shows how after consecutively removing both diffusive contributions, the only remaining part are now the empty (no adsorbent) mixing volumes in flow, as evidenced by essentially a single exponential decay (i.e. a straight line in the semi-log plot). This contribution from elements in flow may also be removed as desired in a similar fashion, but this is less critical for kinetic analysis. When ZLC or breakthrough experiments are performed to rapidly assess an adsorbent’s capacity for adsorption, this gas volume in flow can easily be subtracted from the overall eluted volume. For experiments at low flow rates however, which can be used to measure equilibrium data (Brandani et al. 2003), it may be desirable to remove it, as the initial curvature of the desorption curve will lead to erroneous calculation of isotherm points (see supplementary material).

Fig. 14

Separate deconvolution of mass spectrometer and low volume tee contributions from model blank curve (a). Consecutive deconvolution of both mass spectrometer and low volume tee contributions from model blank curve in any order yields a simple exponential decay, corresponding to mixing volumes in flow (b)

As mentioned previously, the process of convolution and thus deconvolution is a symmetrical one, which means that the order in which various contributions to the overall signal are removed is inconsequential as long as each component is a linear system. When dealing with actual adsorbents however, some non-linearity may arise from the isotherms under consideration, which means that the ZLC itself is not a linear system. All the flow components remain linear, and signal linearity is an essential requirement for any detector. The effect of non-linearity will be discussed in a following section.

4 Deconvolution of actual experimental data—case studies

In order to apply the deconvolution procedure to actual experimental data without creating numerical issues, the raw data were first smoothened using polynomial fits. This can be done with predefined functions in most numerical software tools. For example in Mathcad the built in ‘regress’ function can be used to this end on a number of data segments, with a minimal polynomial order of 5. The final long-time approach to zero is always an exponential function, which can be identified easily. Naturally, this initial data treatment procedure results in curve smoothing, eliminating most of the noise, which is typical for un-corrected data.

4.1 Case study 1—CO2 adsorption on zeolite 13X, an adsorbent with large uptake

The first case study is of experimental adsorption data on zeolite 13X, measured in 10% CO₂/He atmosphere at 35 °C, at ambient pressure. The sample is a single bead with a diameter of 2.0 mm from UOP, Honeywell. Under the measurement conditions, this material has appreciable CO₂ uptake, i.e. in excess of 2 mol kg^–1 (Park et al. 2016). As shown in Fig. 15 the difference between the response of such a sample with a typical mass of ~ 6 mg and that of the blank run is substantial, and as such the response is not affected to a significant extent by extra-column effects. Consequently, carrying out the deconvolution procedure only leads to small changes in the desorption curve for the sample. Importantly too, the long-time asymptote remains unchanged. This part is often critical in determining diffusional time constants, especially in non-linear systems, and thus using the original normalised data would not lead to an erroneous interpretation (Hu et al. 2014). An additional system with large uptake, i.e. silica gel in water vapour, can be found in the supplementary material.

Fig. 15

ZLC desorption for zeolite 13X in 10% CO₂ in He) at 35 °C. Due to significant adsorption capacity under these conditions, the measured signal is far removed from the blank run without adsorbent. The deconvolution procedure therefore only has a small effect on the normalised signal

4.2 Case study 2—CO₂ adsorption on HISIV 3000, small uptake, fast kinetics

In the second case study we consider a sample with small uptake of adsorbate under the measurement conditions. HISIV 3000, a commercial silicalite from UOP, Honeywell (UOP 2020), is a high silicon molecular sieve material and due to its low aluminium content, interaction with polar molecules, such as CO₂ is low. The normalised desorption curves at different flow rates, as seen in Fig. 16, all show a long-time tail, which at first sight could be interpreted as being related to kinetics of CO₂ transport through the sample. Also, when plotted versus $Flowrate \times time$, a so called Ft plot, Fig. 16, it is clear that the curves are not overlapping, even at low flow rates, which would be indicative of flow rate dependency and thus kinetic limitations. However, when the curves are plotted together with the blank runs under the same conditions, it becomes evident that this long-time tail is caused by the experimental setup itself, Fig. 17. Performing the deconvolution procedure removes this contribution and leaves the actual gas phase concentration leaving the ZLC column, allowing for unambiguous determination of the sample’s actual kinetics. Now, when plotting the deconvoluted signals versus $Flowrate \times time$, it is clear that the desorption process is in fact independent of flow rate and thus controlled by equilibrium conditions, and therefore too fast to be determined under the measurement conditions.

Fig. 16

Uncorrected ZLC desorption data for HISIV 3000 in 10% CO₂ at 20 °C showing long-time tail (left). Uncorrected curves in the Ft plot are not overlapping, suggesting measurements are performed under kinetic control (right)

Fig. 17

Original and corrected signal with blank run at 5 cc/min, showing diffusive long-time tail is predominantly caused by extra column effects and is removed after deconvolution procedure (left). The Ft plot of deconvoluted curves are overlapping, indicating measurements are under equilibrium control (right)

4.3 Case study 3—water adsorption on SBA-15; effect of isotherm shape and different sample masses

Equilibrium and kinetic water adsorption measurements can be time consuming, especially when done gravimetrically or volumetrically. The ZLC method was shown to be a good alternative technique, which can be up to an order of magnitude faster, especially when small sample masses are used (Centineo and Brandani 2020). Figure 18a shows the desorption runs at a flowrate of 0.5 cm³ min^–1 for two different amounts of mesoporous SBA-15 at 35 °C, 0.5 mg and 1.5 mg, respectively (details for this adsorbent can be found in ref. (Centineo and Brandani 2020)). Under these conditions, water desorption is an equilibrium process and the data can thus be used to calculate the relevant isotherm. Upon inspection however, the run for 0.5 mg shows significant overlap with the blank run at low concentrations. When performing deconvolution on the original signals (Fig. 18b), it is clear that the long-time slope is affected, whereas the initial part of the desorption remains largely unchanged. Deconvolution does not affect the experimental signal for the larger sample of 1.5 mg, which is as expected since it is always far removed from the blank run. Figure 19 shows the calculated isotherms from both un-corrected and corrected desorption signals, as well as an isotherm measured by gravimetric means. Whereas the isotherm from the un-corrected 1.5 mg sample corresponds well with the gravimetric data, the Henry’s Law region of the un-corrected 0.5 mg sample shows some deviation. After correction, all isotherms match well. In this particular case, due to the adsorbent’s unusual isotherm, caused by hydrophobicity at low concentrations with subsequent capillary condensation, uptake alone is not sufficient in judging whether the correction procedure is necessary and visual comparison with the blank run is a better indicator.

Fig. 18

Desorption for SBA-15 in 5% H₂O / He atmosphere at 35 °C for two sample masses. The desorption data for 0.5 mg sample is close to the blank run at long times and so needs to be corrected

Fig. 19

Calculated isotherms from ZLC data. Using uncorrected data for the 0.5 mg sample leads to erroneous behaviour in the Henry’s Law region. Applying deconvolution yields the correct behaviour as found for by gravimetric means (Aquadyne) or a larger sample mass

4.4 Case study 4—effect of non-linearity on deconvolution procedure

As mentioned earlier, the convolution integral is a linear operator and as long as the various contributions to the overall system are linear in nature, the convolution integral yields the correct response, as measured at the outlet of the system, i.e. at the detector. This is evidently true for the blank runs, as these were shown to consist of linear processes such as CSTRs, and diffusing elements with linear isotherms. When considering actual measurements including a column packed with adsorbent, non-linearity may now arise from the adsorption system being studied. This will have the effect that the order in which the various contributions take place will actually matter. This is not seen in the previous example, as the deconvolution affects only the initial part of the isotherm which is linear. To illustrate the effect of nonlinearity, we consider another non-linear adsorption system, i.e. CO₂ on templated (Na,TEA)-ZSM-25. This system exhibits a stepped isotherm and constitutes a significant deviation from linearity at 20% CO₂ and 35 °C (as described in detail in Min et al. 2018; Verbraeken et al. 2020)). The ZLC desorption data for a measurement at low flow rate is shown in Fig. 20. The system’s response post-column is linear, so we may calculate the outlet concentration of the ZLC by removing the contributions of the detector and Tee-junction 2 alone through the deconvolution procedure. Similarly, the column’s inlet concentration can be calculated by applying the convolution integral to all the contributions occurring prior to the column, i.e. the step change in concertation and Tee-junction 1. Due to the low flow rate used during desorption, the gas phase concentration remains in equilibrium with the adsorbed phase concentration and in turn, each point on the ZLC curve would correspond to a point on the isotherm. The inlet and outlet concentration may thus be used to calculate the isotherm for this adsorption system through the mass balance, in accordance with:(Brandani et al. 2003)

$$q^{*} = \frac{{F_{in} c_{T} }}{{V_{s} }}\left\{ {\mathop \int \limits_{0}^{\infty } \frac{{y_{out} - y_{in} }}{{1 - y_{out} }}dt - \mathop \int \limits_{t}^{\infty } \frac{{y_{out} - y_{in} }}{{1 - y_{out} }}dt} \right\} - \frac{{V_{f} }}{{V_{s} }}c_{T} \left( {y_{out} - y_{in} } \right)$$

(32)

Fig. 20

Uncorrected desorption data for (Na,TEA)-ZSM-25 at 35 °C in 20% CO₂ / He. The low flow rate of 1 cc/min was used, at which the desorption is assumed to occur under equilibrium conditions

Here $q^{*}$ is the equilibrium amount adsorbed in mol m^–3, $F_{in}$ the inlet flowrate, $c_{T} = \frac{P}{RT}$, $V_{s}$ volume of the solid, $V_{f}$ the fluid volume, and $y_{out}$ and $y_{in}$ the mole fraction leaving the column, respectively. The resulting isotherm can be found in Fig. 21. Also shown in this figure is the isotherm calculated by simply removing all extra-column contributions through the deconvolution procedure, treating the system as a linear one. It can be seen that the difference between the two methods is in fact small even for a system which is highly non-linear, indicating that the full deconvolution procedure should be suitable for most adsorption systems. It is finally important to note that the long-time behaviour is always in the linear regime, due to the low concentrations involved. The effect of non-linearity and thus order of carrying out the deconvolution will therefore have an insignificant impact on this part of the experimental data. The long-time analysis on data which has received a full deconvolution procedure should thus lead to the correct kinetics/Henry’s law constants.

Fig. 21

Two different ways of calculating isotherms from equilibrium desorption data (a). A ‘straight’ deconvolution of all extra column components and subsequent integration of the area is indicated by the green curve and area. The red curve indicates the signal after deconvolution of the components post-column, whereas convolution of the components pre-column yield the inlet concentration shown by the blue line; subsequent integration is indicated by the red patterned area. The resulting isotherms are shown in b

In contrast, when these two methods for isotherm calculation are carried out for similar desorption data for HISIV 3000 in 10% CO₂ / He at 20 °C, it can be seen that the resulting two isotherms are practically identical, Fig. 22. This is to be expected, as this adsorption system is essentially linear for the concentration range studied. Isotherm data on silicalite from literature is also shown in Fig. 22, showing that the corrected data yields the correct isotherm (a binder content of 23 wt.% has been used (Brandani et al. 2016) to compare the isotherm measured on the pellets with the absolute isotherm in silicalite crystals (Golden and Sircar 1994)).

Fig. 22

Isotherms calculated by two methods for HISIV 3000 in CO₂ at 20 °C. Both isotherms are identical as this adsorption system is linear under the measurement conditions. Included are calculated isotherm data by Golden and Sircar (Golden and Sircar 1994), multiplied by 0.77 to account for 23 wt.% binder content

5 Conclusions

We have developed a correction procedure for adsorption column measurements, which accurately takes into account the extra-column effects due to the experimental setup configuration. The model is based on the physical components and layout of the setup and it is shown that their composite behaviour can be described by the method of convolution. The physical meaningfulness of the model is exemplified by the fact that the model is valid for a range of conditions (e.g. flow rates, pressures, gas compositions) and is transferable to other experimental setups. By carrying out the convolution procedure in reverse on actual experimental data with adsorbent present, the corrected signal is obtained which can be modelled using standard tools for analysing kinetics and equilibrium.

Carrying out this correction procedure is of particular importance for experiments involving samples with small uptake. This includes samples which inherently have small uptake of the dosing component, but is also applicable when experiments are run with small quantities of adsorbent, which may be required for kinetic studies. Since the correction procedure with the algorithm of Brandani (1998) is computationally very light, it would be advisable to perform it for any measurement for which the ratio of eluted volumes with and without adsorbent is smaller than 4 – 5. Under these conditions, the extra-column effect will start to affect the shape of the desorption curves, which may lead to erroneous interpretations. It has also been shown how the procedure can be applied to systems that exhibit non-linear isotherms.

In this study, we have exclusively shown how the procedure can be applied to ZLC experiments, but it should be noted that it is equally applicable to columns of larger dimensions. Indeed, the convolution model successfully fits blank experiments using our extended columns (described in refs. Georgieva et al. 2019; Lozinska et al. 2012)), without the need for additional terms.

As a final consideration, the deconvolution procedure can be applied to the experimental data to provide a corrected set of inlet and outlet concentrations for a ZLC experiment. These can then be used to extract physical parameters. For nonlinear systems, where this has to be done from a numerical solution of the model equations, it is also possible to add the parametrised models of the individual components, including the detector, to the numerical solution and regress the raw data directly, as similarly done in ref.(Friedrich et al. 2015). While the two approaches should be equivalent, the fact that the deconvolution process removes the noise from the signal makes it preferable.