Capillary bridge formation between hexagonally ordered carbon nanorods

Abstract

Capillary condensation within the pore space formed by a hexagonal arrangement of carbon nanorods is investigated using a thermodynamic model. Numerical solution of the corresponding non-linear differential equations predicts two characteristic equilibrium phase transitions corresponding to liquid-bridge formation between adjacent rods, and the subsequent filling of the entire pore space with liquid adsorbate at higher relative pressure, respectively. These separate transitions are predicted for a wide range of porosities, as demonstrated for two non-polar fluids, nitrogen and n-pentane, employing experimentally determined reference isotherms to model the fluid–solid interactions. The theoretical predictions are compared to experimental data for nitrogen and n-pentane adsorption in an ordered mesoporous CMK-3 type material, with the necessary structural parameters obtained from small-angle X-ray scattering. Although the experimental adsorption isotherms do not unambiguously show two separate transitions due to a high degree of structural disorder of the mesopore space, their general trends are consistent with the theoretical predictions for both adsorbates.

1 Introduction

Experimental and theoretical studies of gas adsorption in mesoporous materials have been performed for many decades (Haul et al.1982). The emergence of novel material synthesis routes enabled the fabrication of monodisperse and highly ordered cylindrical pore systems such as MCM-41 (Kresge et al. 1992) or SBA-15 (Zhao et al. 1998) silica materials, allowing for the quantitative validation of theories of adsorption and capillary condensation based on both, macroscopic thermodynamics (Broekhoff 1967) and atomistic descriptions (Ravikovitch et al. 1998). In the early 2000s, a new family of templated mesoporous carbon materials has been developed by using ordered mesoporous silicas as template (Ryoo et al. 2001; Jun et al. 2000). A representative member of this family is CMK-3 carbon derived from negative templating of SBA-15 silica, exhibiting hexagonally ordered carbon nanorods with an intermediate pore space resembling the original silica template. Therefore, the mesopores in CMK-3 are qualitatively different from the cylindrical pores in SBA-15 forming a continuous pore space with the shortest distance between adjacent nanorods. Some consequences of this special pore geometry have been evident already in the very early publications on CMK-3, with the shapes of the nitrogen adsorption isotherm being quite different from those of the original silica templates, and some of them show two step-like ascends at significantly different relative pressures (Jun et al. 2000; Joo et al. 2002). However, the physical origin of these features has not been addressed in detail so far, and gas adsorption in CMK-3 was frequently modeled as if the pores were cylindrical (Jun et al. 2000; Joo et al. 2002). Density functional theory (DFT) kernels developed for calculation of pore size distribution in CMK-3 materials were also based on the cylindrical pore model (Gor et al. 2012). While this model gave quite satisfactory predictions for the mean pore sizes, some of the data showed a “bimodal” size distribution in the mesopore regime, pointing also towards two separate condensation events. Generally, there is a clear discrepancy in the shape of a theoretical isotherm based on the cylindrical pore model with a sharp condensation point, and the much smoother adsorption isotherm measured experimentally on CMK-3 carbons.

To more accurately describe the adsorption isotherms on CMK-3 and alike materials, alternative models were developed, explicitly taking the rod-like geometry into account (Barrera et al. 2013; Jain et al. 2017; Yelpo et al. 2017). These alternative models were mainly based on molecular simulations using Grand Canonical Monte Carlo (GCMC). Barrera et al. (2013) followed the same principal idea as the DFT model by Gor et al. (2012) by representing the pore space of CMK-3 as a collection of cylindrical and slit pores. The interaction between the carbon nanorods and the nitrogen atoms was modeled by a Steele potential for micropores and an integrated, cylindrical Lennard–Jones potential for the mesopores. The resulting kernel was able to reproduce the results from Gor et al. (2012), thus justifying the applicability of the GCMC method. Yelpo et al. (2017) took this approach one step further and determined the carbon potential inside the pore space of CMK-3, creating a more realistic description for the GCMC simulation. Again, kernels were calculated and used to fit experimental data. Furthermore, a TEM image was analyzed and the pore size distribution obtained from TEM was compared to the pore size distribution obtained by their kernel. Jain et al. (2017) took a different route using an all-atom description of several CMK type systems. They represented the carbon rods by an assembly of individual carbon atoms and used a Lennard–Jones-type potential for the individual atoms to describe the interaction between the gas phase and the solid. Interconnections between the individual carbon rods were also introduced, to more accurately describe the CMK materials, which are seemingly necessary to get qualitatively sound results from the simulations. The adsorptive in this study was argon and the adsorption and desorption was modeled with GCMC for CMK-1, CMK-3 and CMK-5. The results from that study gave some insight into the role of imperfections in CMK materials, especially CMK-3.

Although the methods for modeling adsorption based on molecular simulations have become state of the art, there is still a drawback compared to macroscopic theories: generalization of the results for a different adsorbate would require setting up a new time-consuming simulation. In this sense, macroscopic approaches for modeling adsorption in mesoporous materials, such as theories developed by Derjaguin (1992) and Broekhoff and de Boer (1967) (DBdB theory), or by Saam and Cole (1975) are advantageous. While requiring only a few parameters and being not computationally intense, they reliably predict the adsorption isotherms for cylindrical pores not only for simple gases such as nitrogen or argon (Neimark and Ravikovitch 2001), but also for more complex molecules, such as water, methanol, toluene (Lépinay et al. 2015), pentane (Gor et al. 2013) or perfluoropentane (Hofmann et al. 2016).

Attempts to describe the adsorption and capillary condensation for geometries other than simple slit- or cylindrical pores were carried out by Philip (1977b) already in the 1970s for two parallel cylinders. This idea was further developed by Morishige and Nakahara (2008) into a comprehensive theoretical framework for the transition from a liquid film phase to a “bridged” phase, effectively spanning the void space between the two adjacent cylinders. Dobbs and Yeomans (1993) extended the approach of Philip by numerically minimizing the grand potential of different configurations of liquid in the open pore space between cylindrical rods located on a square lattice. However, that paper was published several years before the emergence of CMK-3, and to the best of our knowledge its predictions were never adapted to the hexagonal geometry and neither have they been compared to real experimental data.

Here we solve the problem of the hexagonal geometry of CMK-3 adapting the thermodynamic model from Ref. (Dobbs and Yeomans 1993). We calculate explicit solutions of the corresponding non-linear differential equations for two different adsorbates, namely nitrogen and n-pentane, by using appropriate reference isotherms to model the solid–fluid interaction (Gor and Neimark 2010, 2011). Equilibrium phase diagrams separating a “film phase” (liquid film on the carbon nanorods), a “bridged phase” (liquid bridges between adjacent nanorods) and a “filled” phase (entire liquid filled pore space) are obtained. Calculations with a simplified, analytical model of the “bridged phase” are performed to elucidate numerical results and provide comparison to traditional characterization approaches such as the Kelvin-Cohan (Neimark et al. 2003) equation. Predictions from the numerical results are compared with experimentally measured adsorption isotherms from CMK-3-like carbon materials (Koczwara et al. 2017) using nitrogen at 77 K and n-pentane at 290 K.

2 Theoretical model

For the thermodynamic description of adsorption in CMK-3-like materials we employ the first variation of the grand potential of three competing unique distributions of liquid-like phases in the open mesopore space (see Fig. 1).

• “Separated” phase: an adsorbed layer (liquid-like film) is present on each individual rod, but the films are not connected with each other.

• “Bridged” phase: a liquid bridge exists between neighboring rods, with a void space remaining between the three rods.

• “Filled” phase: The entire space between the carbon nanorods is filled with liquid.

Fig. 1

Sketch of the top-view pore-space geometry of the hexagonally arranged cylindrical carbon nanorods (grey) with radius r and distance D. Dark blue areas indicate the “separated” phase (liquid adsorbed film around each cylinder), while liquid bridges between the rods are labeled by light blue. The image at the bottom shows an enlarged detail including the two cylindrical coordinate systems used. For the “separated” phase the origin is set into the center of the rod (black system) and is denoted with the subscript 1, while for the “bridged phase” the origin is set into the center of the triangle (red) with the subscript 2 in the respective equations (Color figure online)

All derivations are based on the assumption that the aspect ratio between the diameter of the rods and their length is small, meaning that we can restrict the description to the plane perpendicular to the rod axis. Because of the radial symmetry of the rods we use cylindrical coordinates. To simplify calculations, we consider two different coordinate systems, with the “separated” phase having its origin in the center of the rods, while for the “bridged” phase the origin is located in the center of the unit cell set up by the three rods (see Fig. 1). To model fluid adsorption in this system, the grand potential per unit length of the rod $\Omega$ is treated as a functional $\Omega \left(l\right)$ of the liquid profile, where l is the radial coordinate. We assume uniform density of the liquid, meaning that $\Omega$ will depend on geometry only. This results in

$$ \Omega = \int_{{\theta _{a} }}^{{\theta _{b} }} {f\left( {\theta ,l,l_{\theta } } \right)d\theta } $$

(1)

with θ_a and θ_b being the limits of the angular interval, l being the distance of the vapor–liquid interface from the origin as a function of θ, and l_θ being the derivative of l with respect to θ.

2.1 Governing equations for the phases

Adapting the equation for the grand potential of the “separated” phase from (Dobbs and Yeomans 1993) to the hexagonal geometry, we have

$$ \Omega \left( {l_{1} } \right) = 6\int_{0}^{{\frac{\pi }{6}}} {d\theta _{1} \left( {\gamma \left( {l_{1}^{2} + l_{{\theta _{1} }}^{2} } \right)^{{\frac{1}{2}}} } \right)} + \Delta \tilde{\mu }\left( {6\int_{0}^{{\frac{\pi }{6}}} {d\theta _{1} \frac{1}{2}l_{1} \left( {\theta _{1} } \right)^{2} - \frac{\pi }{2}r^{2} } } \right) + 6\int_{0}^{{\frac{\pi }{6}}} {d\theta _{1} V\left( {l_{1} ,\theta _{1} } \right)}. $$

(2)

The subscript 1 denotes the “separated” phase with l₁ ≡ l(θ₁) and ${l}_{{\theta }_{1}}$≡ dl₁/dθ₁. The first part of the equation describes the contribution of the liquid–vapor interfacial energy γ, the second term describes the influence of the chemical potential $\Delta \tilde{\mu }$ of the liquid, and the last term describes the energy due to the solid–liquid film potential $V\left(l,\theta \right)$. The chemical potential per unit volume $\Delta \tilde{\mu }$ is:

$$ {\Delta }\tilde{\mu } = \frac{{R_{g} T}}{{v_{l} }}\ln \left( {\frac{p}{{p_{0} }}} \right) $$

(3)

where v_l is the molar volume of the liquid, R_g is the universal gas constant, T is the absolute temperature and $p/{p}_{0}$ is the relative pressure. The last term in Eq. 2 represents the integrated effect of the solid–fluid interactions, which can be related to Derjaguin’s disjoining pressure Π

$$ V\left( {l,\theta } \right) = \int\limits_{{l\left( \theta \right)}}^{{l_{{max}} }} {\Pi \left( {l,\theta } \right)l dl} $$

(4)

where l_max is the maximum value of the profile to be considered, which helps keeping the integration limited to a unit cell in ordered systems. The detailed discussion of Π(l) is given in Sect. 2.2.

Application of the Euler–Lagrange equation to Eq. 2 leads to a second order, non-linear, ordinary differential equation, which minimized the grand potential in any radially symmetric case:

$$ \gamma \frac{d}{{d\theta _{1} }}\left( {\frac{{l_{{\theta _{1} }} }}{{\left( {l_{1}^{2} + l_{{\theta _{1} }}^{2} } \right)^{{\frac{1}{2}}} }}} \right) - \gamma \frac{{l_{1} }}{{\left( {l_{1}^{2} + l_{{\theta _{1} }}^{2} } \right)^{{\frac{1}{2}}} }} + l_{1} \left( {\Delta \tilde{\mu } - \Pi \left( {\theta _{1} ,l_{1} } \right)} \right) = 0. $$

(5)

Noteworthy, for cylindrical pores Eq. 5 reduces to Derjaguin’s equation (Broekhoff 1967; Derjaguin 1992).

For the “bridged” phase we set the origin of the coordinate system in the center of the rod (Philip 1977b; Dobbs and Yeomans 1993; Gatica et al. 2002) as depicted in Fig. 1 with subscript 2 (l₂ ≡ l(θ₂)) and Eq. 2 becomes

$$ \Omega \left( {l_{2} } \right) = 6\int\limits_{0}^{{\frac{\pi }{3}}} {d\theta _{2} \left( {\gamma \left( {l_{2}^{2} + l_{{\theta _{2} }}^{2} } \right)^{{\frac{1}{2}}} } \right)} + \Delta \tilde{\mu }\left( {{\sqrt 3 }R^{2} - \frac{\pi }{2}r^{2} - 6\int\limits_{0}^{{\frac{\pi }{3}}} {d\theta _{2} \frac{1}{2}l_{2} \left( {\theta _{2} } \right)^{2} } } \right) + 6\int\limits_{0}^{{\frac{\pi }{3}}} {d\theta _{2} V\left( {l_{2} ,\theta _{2} } \right)}. $$

(6)

Here, R = D/2 is the half-distance between the centers of the adjacent rods and r is the radius of the rods (see Fig. 1), and we change the integration limit from $\frac{\pi }{6}$ to $\frac{\pi }{3}$ because of the change in origin from the center of a rod to the center of the interstitial void space.

Minimizing the functional we obtain again a second order, non-linear ordinary differential equation

$$ \gamma \frac{d}{{d\theta _{2} }}\left( {\frac{{l_{{\theta _{2} }} }}{{\left( {l_{2}^{2} + l_{{\theta _{2} }}^{2} } \right)^{{\frac{1}{2}}} }}} \right) - \gamma \frac{{l_{2} }}{{\left( {l_{2}^{2} + l_{{\theta _{2} }}^{2} } \right)^{{\frac{1}{2}}} }} - l_{2} \left( {\Delta \tilde{\mu } - \Pi \left( {\theta _{2} ,l_{2} } \right)} \right) = 0. $$

(7)

In the case of the completely filled pore space (“filled” phase) the sole contribution to the grand potential is the liquid inside the filled pore space

$$ {\Omega } = \Delta\tilde{\mu } \left( {\sqrt 3 R^{2} - \frac{\pi }{2}r^{2} } \right). $$

(8)

We note that the values of the grand potential obtained in this study are not absolute but are offset by a constant contribution (containing the surface energy of the solid). The discussion of these terms is given elsewhere (Gor and Neimark 2010). While these terms do not affect the transition points, they contribute to the solvation pressure in the pore and affect the thermodynamic properties of the fluid (Hill 1952).

To solve the differential equations Eqs. 5 and 7, two values of the film thickness or the slope at the boundaries of the unit cell have to be known. The boundary conditions for the “separated” phase, with the origin fixed at the center of the rod, are given by:

$$ \left. {l_{{\theta_{1} }} } \right|_{{\theta_{1} = 0}} = 0 \,and\,\left. {l_{{\theta_{1} }} } \right|_{{\theta_{1} = \frac{\pi }{6}}} = 0 $$

(9)

Similarly, for the “bridged” phase the conditions read:

$$ \left. {l_{{\theta_{2} }} } \right|_{{\theta_{2} = 0}} = 0 \, and \,\left. {l_{{\theta_{2} }} } \right|_{{\theta_{2} = \frac{\pi }{3}}} = 0 $$

(10)

Using these boundary conditions, the two-point Neumann boundary value problem was solved numerically, as outlined in Appendix A.

2.2 Determination of the solid–fluid interaction potential

The key term in the macroscopic theories of adsorption and capillary condensation is the term related to the solid–fluid interaction potential. Derjaguin used the concept of disjoining pressure Π(h) to represent it, where h is the film thickness, which can more generally be defined as the shortest distance between the substrate surface and the liquid–vapor interface. Disjoining pressure isotherms for adsorption of fluids on a flat surface are often modeled via the Frenkel-Halsey-Hill equation (Halsey 1948; Hill 1952):

$$ {\Pi }\left( h \right) = - \frac{{R_{g} T}}{{v_{l} }}\frac{k}{{\left( {\frac{h}{{h_{0} }}} \right)^{m} }} $$

(11)

where h₀ = 0.1 nm and k and m are the two free parameters of the model.

While the DBdB theory (Broekhoff 1967; Derjaguin 1992) typically neglects the curvature of the pores and uses Eq. 11 directly to represent the solid–fluid interactions in the cylindrical pore, we take here the curvature of the carbon nanorods into account. We use the integrated solid–fluid potential for an infinite rod derived for arbitrary inverse power-law potentials (Philip 1977a):

$$ {\Pi }\left( h \right) = - \frac{{\pi^{\frac{3}{2}} {\Gamma }\left( {\frac{ \epsilon - 1}{2}} \right)}}{{{\Gamma }\left( {\frac{ \epsilon }{2}} \right)}} \alpha r^{2} \left( {h + r} \right)^{1 - \epsilon} F_{2;1} \left( {\frac{ \epsilon - 1}{2};\frac{ \epsilon - 1}{2};2;\left( {\frac{r}{h + r}} \right)^{2} } \right) $$

(12)

where Π is the film potential, α is the interaction parameter, ε is the exponent of the inverse-power-law, $\Gamma$ denotes the Eulerian gamma function, and F_2;1 is the generalized hypergeometric function. The parameters α and ε are determined by fitting from reference isotherms, assuming infinite, planar substrates in any case. Consequently, one can think of this as an empirical function, with the units of α depending on the value of ε. These parameters can be readily related to the parameters of the Frenkel-Halsey-Hill equation (Eq. 11):

$$ m = \epsilon{-}3 $$

(13)

$$ R_{g} Tkh_{0}^{m} = \frac{2\pi \alpha }{{\left( { \epsilon - 3} \right)\left( { \epsilon - 2} \right)}} $$

(14)

Finally, we take into account that the adsorbing fluid interacts not with a single rod, but with the three rods of the unit cell and sum up the potentials at each single point of consideration, similar to the quadratic lattice considered in (Dobbs and Yeomans 1993).

3 Computational results

3.1 Reference isotherms and disjoining pressure

Theoretical predictions of adsorption isotherms require the knowledge of the disjoining pressure isotherm Π(h). In order to be able to compare our numerical results with experimental data, we used available experimental reference isotherms from nitrogen and n-pentane adsorption on carbon (Fig. 2). For nitrogen adsorption at 77 K we used the literature data of activated carbon annealed at high temperature (2000 °C) for 2.5 h (Silvestre-Albero et al. 2014). For n-pentane, no literature data were available. Therefore, we employed own data from n-pentane adsorption on a carbon xerogel thermally annealed at 1800 °C for 50 min. This sample contained a negligibly small amount of micropores, and mesopores of some tens of nanometers in size (Balzer 2018). Ideally, the reference isotherm should have been measured on a non-porous or at least a macroporous only sample, but no such sample was available to perform n-pentane adsorption measurements. The presence of large mesopores is probably the reason why the fit in Fig. 2b deviates from the data at relative pressures above 0.6. Nevertheless, the first layers are properly described by the Frenkel-Halsey-Hill (FHH) isotherm and should therefore approximate the interaction of the fluid molecules with the carbon substrate with sufficient accuracy. The interaction parameters derived from the fits of Eqs. 11, 13 and 14 to the corresponding reference isotherms are presented in Table 1.

Fig. 2

Plot of the film thickness h of the reference isotherms for nitrogen on annealed activated carbon [data from (Silvestre-Albero et al. 2014)] (a), and n-pentane on a carbon xerogel (b). The experimental reference isotherms are shown by (black) squares, the FHH-fits with solid (red) lines (Color figure online)

Table 1 Fitting parameters of the FHH isotherm (see Eq. 11) to the reference isotherms

We note the significance of the Cole-Saam approach (Saam and Cole 1975) for our work, which takes the curvature of the solid surface explicitly into account. In cylindrical mesopores, where capillary condensation usually happens at relatively low film thickness (only few monolayers of adsorbate), the effect of curvature is small. In our model, however, we need to consider the film potential at distances of several nanometers when solving the equations for the “bridged” phase. Figure 3 compares the disjoining pressure as a function of film thickness h for a flat surface and a single carbon cylinder with a radius of 3.7 nm. At low film thicknesses the overall difference between both potentials is small, but at distances above 1 nm, in case of the flat surface the overall potential is overestimated by 20 to 50 percent.

Fig. 3

Disjoining pressure calculated for a flat surface and for the surface of a cylinder with radius r = 3.7 nm for n-pentane on carbon (Balzer 2018). The inset shows the relative difference of the data for the flat surface in regard to the cylindrical potential as a function of the distance to the substrate

3.2 Calculated isotherms and phase diagrams

To predict adsorption isotherms for the geometry outlined in Fig. 1, the liquid–gas interface profiles for the “separated” and “bridged” phases were calculated by solving Eqs. 5 and 7, respectively. According to the available experimental data (see Sect. 4 and Appendix B), the rod radius r was varied between 3.3 and 4.4 nm in 0.05 nm steps, while the rod distance D was fixed at a value of 10.1 nm. Temperatures used in the simulations were 77.4 K and 290 K for nitrogen and n-pentane respectively, according to the temperatures at which the adsorption measurements were carried out. Experimental details are outlined in Appendix B. The differential equations were solved numerically by applying a finite difference scheme using a custom written code, outlined in some detail in Appendix A. Solutions were obtained for 20 equidistant relative pressure values ranging from 0.01 to 0.95 for both sets of interaction parameters.

From the interface profiles l(θ) the grand potentials were calculated using Eqs. 2 and 6 for the “separated” and “bridged” phases, respectively, and Eq. 8 was employed for the “filled” phase. The thermodynamically stable phase at a chosen pressure is now simply given by the lowest value of Ω, with the exact relative pressure values at which transitions between the phases occur obtained via interpolation and root finding. A selection of profiles of the “bridged” phase for $D/r =2.7$ are shown in Fig. 4a. With these profiles, the grand potential Ω of the “bridged” phase can be calculated (Eq. 6) and compared to the grand potentials of the “separated” and “filled” phases as shown in Fig. 4b. As can be seen in Fig. 4b, the “separated” phase is stable for low relative pressures, followed by the “bridged” phase and finally the “filled” phase. Figure 4c displays the corresponding nitrogen adsorption isotherm for a ratio D/r = 2.7, calculated from the “separated” and “bridged” profiles. The circles in Fig. 4c correspond to the film profiles for the “bridged” phase shown in Fig. 4a. With increasing relative pressure, the void space shrinks and changes its shape from rather triangular towards more circular, upon which the “bridged-to-filled” transition happens.

Fig. 4

a 2D interface profiles for the “bridged” phase. With increasing relative pressure, the overall size of the void space decreases, while the shape of the void space changes from more triangular towards more circular. The four relative pressures at which the profiles in (a) are shown are indicated by blue circles in panel (c). b The grand potential as a function of relative pressure for the three different phases (blue: “separated” phase; green: “bridged” phase; red: “filled” phase) for nitrogen on carbon and D/r = 2.7. c Corresponding adsorption isotherm (Color figure online)

From the isotherms determined for different D/r ratios we can extract phase diagrams, showing the stability range of the respective phases as a function of relative pressure and D/r ratio. This ratio can be related to the maximum inscribed radius ${r}_{u}^{*}$ between the three cylindrical rods

$$ r_{u}^{*} = \frac{\sqrt 3 }{3} D - r $$

(15)

or in a dimensionless representation

$$ r^{\prime}_{u} = \frac{{r_{u}^{*} }}{r} = \frac{\sqrt 3 }{3}\frac{D}{r} - 1 $$

(16)

linking the reduced sizes to the pore geometry considered in earlier work (Ryoo et al. 2001).

In Figs. 5a and 6a we show the resulting phase diagrams for nitrogen and n-pentane, respectively. For all calculations we used a fixed nanorod distance D = 10.1 nm, which is the mean value determined experimentally for the sample discussed (see Appendix B). Variation of D in the calculations was also considered, but its influence was found to be minor as compared to the impact of the nanorod radius r. The phase diagrams for the two fluids show a similar overall trend. Both adsorbates show a bridging transition at very low relative pressures for the smallest D/r ratio, which corresponds to a small distance of the rods of 1.3 nm only. With increasing D/r, the “separated” to “bridged” phase transition appears at increasingly larger relative pressures. While the “bridging” transition is strongly dependent on the nanorod radius, the “bridged” to “filled” transition appears at very similar relative pressures for all investigated radii (i.e. the corresponding phase boundary is almost vertical). The location of the phase boundaries are clearly different for the two investigated fluids, reflecting the different fluid–solid interactions. In particular, for a D/r ratio > 3.1 (corresponding to a mesoporosity > 62%), there is no more “bridged” phase for nitrogen, while for n-pentane there is still a quite broad stability range for the “bridged” phase.

Fig. 5

a Calculated phase diagram for nitrogen in CMK-3-like carbon at 77 K showing the “separated” phase (green), the “bridged” phase (white), and the “filled” phase (red). b Nitrogen (77 K) adsorption isotherm of hierarchically porous CMK-3-like carbon (black), and the derivative of the isotherm (grey). Vertical lines are drawn at the relative pressure of the two local maxima of the derivative indicating the pressure of the “separated-to-bridged” and the “bridged-to-filled” phase transitions in this sample. The grey vertical regions represent the uncertainty of the maximum derived from the experimental isotherm. The horizontal line in panel a indicates the ratio D/r of 2.6 measured with SAXS for the present sample, with the grey horizontal region representing the uncertainty of the experimentally determined D/r ratio (Color figure online)

Fig. 6

a Calculated phase diagram for n-pentane in CMK-3-like carbon at 290 K showing the “separated" phase (green), the “bridged” phase (white), and the”filled” phase (red). b n-pentane (290 K) adsorption isotherm in hierarchically porous CMK-3-like carbon (black), and the derivative of this curve (grey). Vertical lines are drawn at the relative pressure of two maxima of the derivative, indicating the pressure of the “separated-to-bridged” phase transition and the “bridged-to-filled” phase transition in this sample. The grey region represents the uncertainty of the maximum derived from the experimental isotherm. The horizontal line in a indicates the ratio D/r of 2.6 measured with SAXS for the present sample, with the grey horizontal region representing the uncertainty in the experimentally determined D/r ratio (Color figure online)

4 Comparison with experiment

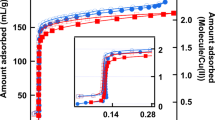
Despite of some experimental hints towards a double condensation transition already in the very early papers on CMK-3 carbons (Jun et al. 2000; Joo et al. 2002), and the corresponding appearance of a “bimodal” mesopore diameter distribution (Gor et al. 2012), the idea of a “film-to-bridged” phase transition without accompanying complete pore filling was not confirmed experimentally so far. The reason might be that the two steps in the adsorption isotherms are not, or at least not unambiguously, seen in many experimental data sets of CMK-3. For instance, in ref. (Gor et al. 2012), one sample showed only a very slight indication of a second step, while for the other sample this second step was clearly visible. This is probably a consequence of a quite large amount of disorder in the arrangement and a large surface roughness of the nanorods, which may smear out such transitions. Here we provide some experimental evidence that the experimentally observed double steps may indeed be related to the two transitions predicted by the thermodynamic model in the previous section. We have chosen a carbon sample with hierarchical porosity, synthesized via nanocasting into a hierarchical silica sample with SBA-15 type cylindrical mesopores. The resulting carbon sample exhibits a micro-/meso-/macroporous structure with the hexagonally ordered cylindrical carbon nanorods forming a CMK-3-like pore geometry (Koczwara et al. 2017). The structural parameters characterizing the mesopore space, D = 10.1 nm and r = 3.9 nm obtained from SAXS (see Appendix B), correspond to a mesoporosity of 46% and a ratio D/r = 2.6. Figures 5b and 6b show the experimentally determined adsorption isotherms of the sample for nitrogen at 77 K and n-pentane at 290 K, respectively (see Appendix B for experimental details). The isotherms show a rapid increase at very low pressures, which is attributed to the filling of micropores within the carbon nanorods. Besides this micropore filling, two shoulders with inflection points at p/p₀ ≈ 0.35 and p/p₀ ≈ 0.7 for nitrogen_, and at p/p₀ ≈ 0.20 and p/p₀ ≈ 0.6 for n-pentane are clearly recognized. This non-monotonic behavior becomes even clearer when considering the first derivative of the adsorption isotherm (grey curve in Figs. 5b and 6b). Thus, the hierarchical porous carbon material seemingly exhibits two distinct condensation events in adsorption for both nitrogen and n-pentane, but only a single one in desorption (shown in Appendix B). This is consistent with the study by Gor et al. (2012), where high resolution nitrogen adsorption isotherms recorded for CMK-3 samples showed two step-like features in adsorption, but only a single evaporation event for desorption. The data are also qualitatively in agreement with the very early papers on CMK-3 (Jun et al. 2000; Joo et al. 2002), but unfortunately all those data sets did not provide values for the nanorod radius nor their distance, which prevented to include them into our analysis. We mention that although the hierarchical sample investigated here exhibits also macropores, their size range (micrometers) is not compatible with a condensation event at p/p₀ ≈ 0.7 for nitrogen.

Vertical dashed lines in Figs. 5 and 6 denote the experimental transition pressures given by the maxima of the derivative, and grey intervals visualize the uncertainty range. It is seen that the second transition (“bridged-to-filled”) agrees with the calculated phase transition pressure for both fluids within the experimental error. In fact, this transition is not very sensitive to the D/r ratio, as the phase boundary is almost vertical in Figs. 5a and 6a. We note that this transition around p/p₀ ≈ 0.7 also agrees quite well with the second hump in the isotherm shown in Ref. (Gor et al. 2012). For the “separated-to-bridged” phase, the experimental transition lines cross the phase boundary at D/r ≈ 2.65 for nitrogen and at D/r ≈ 2.7 for n-pentane, respectively. The horizontal line drawn in Figs. 5a and 6a indicates the D/r value of 2.6 measured experimentally with small-angle X-ray scattering (SAXS). The agreement between calculated phase diagram and the experimental result for this given D/r ratio appears to be excellent within the experimental errors.

5 Discussion

The thermodynamic model of a bridging transition between two cylindrical rods was developed by Philip (1977b) and extended to a quadratic array of four cylindrical rods by Dobbs and Yeomans (1993). The latter work allowed predicting three different thermodynamic phases during physical adsorption of fluids in such a system, i.e., a “separated” phase (liquid-like adsorbed film on the cylinders), a “bridged” phase (liquid bridges between the cylinders), and a “filled phase”, where the entire space between the cylinders is filled with liquid. The transitions between these phases are first-order and should be observable in experiments by discontinuous, step-like events in the adsorption isotherms at specific relative vapor pressures. Unfortunately, the geometry of four cylinders on a square lattice proposed in (Dobbs and Yeomans 1993) is not realized experimentally for mesoporous materials, and also the hexagonal rod arrangement realized experimentally with CMK-3 came up only several years after Ref. (Dobbs and Yeomans 1993) was published. This is probably the reason why this elegant thermodynamic treatment of a complex, but still solvable pore space geometry has not found further attention so far. On a side note we mention that although such continuum approaches often exhibit deviations from microscopic simulations particularly at small pore sizes below 5 nm, general trends and at least qualitative agreement is still to be expected (Ravikovitch and Neimark 2000).

In the present work we have reformulated the theory of Dobbs and Yeomans for a hexagonal lattice, and we have calculated theoretical phase diagrams for the adsorption of nitrogen and n-pentane on CMK-3 carbon by deriving the fluid–solid interactions from respective reference isotherms. The relative pressures of the predicted phase transitions are qualitatively consistent with condensation events between two neighboring rods and in the space between three hexagonally arranged rods, respectively, employing the Kelvin-Cohan equation (Appendix C). The predictions of the model were then compared with experimental data from a CMK-3 type sample. Unfortunately, the experimental adsorption isotherms did not unambiguously show two step-like features related to the two transitions. Yet, the shape of the isotherms clearly reveals two “discontinuities” at relative pressures consistent with predictions from the model (Figs. 5 and 6). This agrees with earlier work from other authors on CMK-3 (Gor et al. 2012; Jun et al. 2000; Ryoo et al. 2001), where a second “shoulder” was clearly observed, although this feature was not discussed in these papers. Gor et al. (2012) used N₂ isotherms on CMK-3 to derive a pore size distribution from QSDFT, and observed a second class of mesopore sizes which would be consistent with a second condensation event. However, the experimentally observed step height of the transitions does not agree with the theoretical predictions. The experimentally observed second step of the “bridged-to-filled” transition (Fig. 5b) is much smaller than the one predicted (Fig. 4b). There are two possible reasons for this deviation: First, the mean-field theory used here predicts a more abrupt transition than a theory which would consider the density variation in the condensed phase, such as based on molecular simulations. Second, we may attribute this deviation also to the disorder in the system (see Fig. 7a). There is indeed strong evidence in literature that the nanorods exhibit a strongly corrugated surface with carbon cross-bridges between them (Solovyov et al. 2002). As sketched in Fig. 7b, such cross bridges might be local condensation points, and the geometry of the “bridged” phase might be realized only locally over a restricted volume (Fig. 7c). Due to the disorder of the carbon nanowires, specific locations in the sample may exhibit small interstitial spaces in-between three 2D-hexagonally ordered carbon nanowires, which fill already at lower pressures, thus the “separated-to-bridged” transition and the “bridged-to-filled” transition not being separately resolved, as sketched in Fig. 7d, I and II. This would naturally lead to larger filling fractions for the “separated-to-bridged” transition, with a broad transition-pressure regime, as observed experimentally. As a consequence, only a considerably smaller pore volume fraction than predicted by our model (Fig. 4c) would contribute to the “bridged-to-filled” transition. We note that the structural parameters ($D$ and $r$) from SAXS (see Fig. 8) are somewhat ambiguous, as they are related to the highly ordered part of the pore space. It has been shown already for SBA-15 silica (Jähnert et al. 2009; Findenegg et al. 2010) that there may be a considerable amount of “disordered porosity”, which we expect to be even higher for CMK-3 due to the additional synthesis step using SBA-15 as a template. We speculate that as long as the distance of mutual contact points between neighboring cylinders along the cylinder axis is clearly larger than the distance between the cylindrical rods, the geometry sketched in Fig. 1 would exist at least locally (see Fig. 7d, I), enabling in principle the proposed transitions. We are however fully aware of the fact that our experimental model system is much more complicated than the theoretical model. Consequently, the observed agreement between the calculated and the measured phase transition pressures is a strong indication, but no final proof for the existence of such capillary bridges between nanorods in CMK-3. A final proof would require the availability of samples with much higher structural order, which to our knowledge are not available so far.

Fig. 7

Sketch of a “realistic” 3D model of the carbon nanorods (a), their mean distance and radius corresponding to the values obtained from SAXS. b and c show sketches of vertical cuts for pressures below (b), and above (c) the “separated-to-bridged” transition, with the liquid adsorbate shown in opaque green. The liquid-like film covering the nanorods is omitted in c for better visualization, and only condensed regions in small “constrictions” are shown, which will act as nucleation sites for the “bridged” phase. In d, two top-view sketches at cuts through the positions I and II in c are shown, demonstrating the local existence of the “bridged” and the “filled” phases in different regions along the rod axis

Although kernels of isotherms from molecular simulations provide satisfactory fits to experimental data from CMK-3 carbons, none of them discusses the existence of liquid bridges spanning the shortest distance between neighboring nanorods (Yelpo et al. 2017; Barrera et al. 2013; Jain et al. 2017). The adsorption isotherms in these models are usually derived assuming the existence of a spinodal, which is not necessarily the case in highly conjugated pore spaces (Gommes and Roberts 2018). Our purely thermodynamic equilibrium approach was able to quite accurately predict the experimentally observed transition pressures. This implies that nucleation events in the void space between the nanorods must help overcoming the activation barrier right at the pressure of equilibrium, which consequently means that a spinodal transition is not present. Jain et al. (2017) performed simulations of argon adsorption on CMK-3 including interconnections between the individual nanorods. They could clearly show the influence of such irregularities on the general shape of the adsorption isotherm. The deliberately introduced interconnections basically shifted the relative pressure for condensation to significantly lower values, meaning that smaller structures within the void space could very well serve as nucleation sites. Hence, the presence of disorder and possible carbon interconnects in CMK-3 might be even the key to the formation of liquid bridges between neighboring rods by providing the nucleation sites for the “bridged” phase. The fact that no spinodal transition is needed to determine the relative pressures of condensation sheds light on the underlying physical processes and their relation to the actual structures present in the material.

6 Conclusion

In conclusion, we presented a comparison between computational and experimental results on the structural characterization of a monolithic CMK-3-like material using nitrogen and n-pentane adsorption and small angle X-ray scattering. Following an earlier theoretical approach (Dobbs and Yeomans 1993), three different phases of the fluid in the pore space (“separated”, “bridged” and “filled” phases) are proposed, and their grand potentials are minimized by the geometric arrangement of liquid inside the open pore space in the monolithic CMK-3-like material. The theoretical predictions for the adsorption isotherms of nitrogen and n-pentane on the carbon material for varying nanorod radii but constant nanorod distances were used to construct phase diagrams, linking the “separated-to-bridged” and “bridged-to-filled” phase transitions to experimental adsorption data and structural data from small angle X-ray scattering. For both, nitrogen and n-pentane adsorption, fair agreement between the theoretical predictions and experimental results is found, indicating that this model is able to qualitatively describe the physical processes governing adsorption in the open pore space of CMK-3 like materials. The resulting mean pore size is in good agreement with earlier work using state-of-the-art methods (Gor et al. 2012).

Appendices

Appendix A: Computational details

In Sect. 2, the Euler–Lagrange equations of the grand potential were developed, which yielded two second order, non-linear ordinary differential equations (ODE), Eqs. 5 and 7. Solving these ODEs with the appropriate boundary conditions (Eq. 9 for the separated phase and Eq. 10 for the “bridged” phase), results in profiles satisfying the Euler–Lagrange equation for the grand potential. Because the boundary conditions force the according solutions, they do not necessarily represent global, but at least local minima of the grand potential. Therefore, it is important to start with a physical reasonable “educated guess” for the resulting profile, which is rather simple for the separated phase, but more ambiguous for the “bridged” phase.

A custom written Python code (version 3.6) employing the Anaconda package (version 3.6.5) was used to numerically solve the ODEs. The two methods used to solve boundary value problems are the shooting and finite difference method (Kiusalaas 2013). Because the finite-difference method provides fast convergence and stability of results compared to the shooting method in two-point boundary value problems (Kiusalaas 2013), the former was applied in this paper. The main idea of this approach is to minimize a residual vector $R$ which is a numerical function of a discretized profile vector $L$. To construct a residual and profile vector $R$ and $L$, the differential equation needs to be discretized by constructing a mesh of $n$ nodes with a step width $\Delta \theta$, where the differentials in Eqs. 5 and 7 were defined by the central difference scheme. At the $ith$ node for $0<i<n$ of the mesh the first (${l}_{\theta ,i}={(l}_{i+1}-{l}_{i-i})/2\Delta \theta$) and second derivative (${l}_{\theta \theta }=({l}_{i-1}-2 {l}_{i}+{l}_{i+1})/\Delta {\theta }^{2}$) are uniquely determined. At the boundaries $i=0$ and $i=n$, the boundary conditions are clearly defined by Eqs. 9 and 10. As the first derivative needs to be zero at both boundaries, the nodal values must be identical to their neighbors (hence ${l}_{-1}={l}_{1}={l}_{0}$ and ${l}_{n-1}={l}_{n+1}={l}_{n}$ if the solution is symmetric to the left and right of the boundaries). With this approach, the differential equation is only dependent on the profile vector $L$ (and therefore on the discrete values ${l}_{i}$) and $\Delta \theta$. To numerically solve equations Eqs. 5 and 7, they need to be rewritten to the following form:

$$ l_{\theta \theta } = F\left( {\theta ,l,l_{\theta } } \right), $$

(17)

where $F$ and ${l}_{\theta \theta }$ can be rewritten in a discretized form with the definitions of ${l}_{\theta }$ and ${l}_{\theta \theta }$ provided above. With these definitions the residual vector $R$ of the differential equations can be defined as a function of the profile vectors components ${l}_{i}$ and the step width of the mesh $\Delta \theta$:

$$ R_{i} = l_{i - 1} - 2 l_{i} + l_{i + 1} - \Delta \theta^{2} F\left( {\theta_{i = 0} + i \Delta \theta ,l_{i} ,\frac{{l_{i + 1} - l_{i - 1} }}{{2 {\Delta }\theta }}} \right) $$

(18)

Suppling an initial solution to Eq. 18 results in a numerical value of the residual vectors entries which deviate from 0. Hence, if the entries of the residual vector $R$ are close or equal to 0, the differential equation defined by $F$ is solved by the profile vector $L$. A minimization algorithm, such as a least-squares algorithm, minimizes the residual by adjusting the supplied initial solution vector. If the differential equation being solved is linear, a singular minimization operation is sufficient. In the case of non-linear differential equations iterations have to be performed to find a solution. The ‘least-squares’ function of the Python-module ‘SciPy’ only needs a functional definition of the residual (Eq. 18) and an initial solution provided to solve a non-linear differential equation.

For an educated guess of the initial solution for the “bridged” phase, we employed a cosine function with a linear transform of the input variable θ to ensure that the derivative of the initial solution satisfies the boundary conditions (Eqs. 9 and 10), effectively compressing the cosine in an interval from 0 to π into the respective bounds. The values at $l(\theta =0)$ and $l(\theta =\pi /3)$ were chosen as follows: It can be assumed that the film thickness $h$ of the “bridged” solution at the largest angle π/3 is close to the thickness in the case of adsorption on a single cylinder. This value for $h(p/{p}_{0},\theta =\pi /3)$ can be easily obtained by solving Derjaguin’s equation for adsorption on a single cylinder. For $l(\theta =0)$, we assumed the bridge having a thickness of twice the value of the film thickness $h$ at the angle of π/3. For low relative pressures and consequently low fillings of the void space, the input argument of the compressed cosine was distorted with a power law $\propto \mathrm{c}\mathrm{o}\mathrm{s}({x}^{z})$, which results in a distorted shape of the cosine.

For the “separated” phase, convergence is easily achieved by choosing a flat profile within physically reasonable bounds. To obtain these bounds, it is of great advantage to solve the Derjaguin’s equation for a single cylinder for the relative pressure under consideration and use the corresponding film thickness $h(p/{p}_{0})$ as starting value.

Appendix B: Experimental details

2.1 B1: Synthesis of the carbon sample

The sample investigated was a monolithic carbon sample with hierarchical porosity. It consists of a macroporous network of struts (Fig. 8a), with each strut comprising a 2D hexagonal arrangement of carbon nanorods leaving a mesopore space between the rods resembling the geometry sketched in Fig. 1. The carbon monolith was synthesized via a nanocasting approach using silica monoliths with hierarchical porosity (Brandhuber et al. 2005; Putz et al. 2017) as template. The nanocasting procedure consisted of the infiltration of the cylindrical silica mesopores with a carbon precursor, its carbonization at 850 °C and finally the silica template removal by HF etching. As the material was synthesized for applications as supercapacitor electrodes, it was activated with carbon dioxide at 925 °C for 30 min to increase the microporosity within the carbon nanorods. The micropores are located within the carbon nanorods, being responsible for the steep increase of the adsorption isotherms at low pressures (Figs. 5b and 6b). They should however not influence the adsorption data from the mesopores at larger relative pressures A detailed description of the sample synthesis is given in Ref. (Koczwara et al. 2017).

2.2 B2: Determination of the D/r ratio using SAXS

The ordered mesopore structure of the sample was characterized by Small-angle X-ray scattering (SAXS) using a laboratory SAXS instrument (Nanostar, Bruker AXS, Karlsruhe). Figure 8b shows the SAXS pattern of the sample in a double logarithmic scale. Sharp Bragg reflections at positions q_hk confirm the 2D hexagonal order of the carbon nanorods, with ${q}_{hk}=\frac{4\pi \mathrm{s}\mathrm{i}\mathrm{n}({\theta }_{hk})}{\lambda }$, θ being half the scattering angle, λ the X-ray wavelength, and hk are the Miller Indices of the lattice. The diffuse scattering contributions below the Bragg peaks can mainly be attributed to scattering from the disordered micropores in the sample, which are however not relevant for the following. From the peak positions the lattice parameter (corresponding to the rod distance D) can be calculated by $D=\frac{4\pi }{\sqrt{3}{q}_{hk}}\sqrt{{h}^{2}+{k}^{2}+hk}$, giving a value D = (10.1 ± 0.1) nm for the present sample.

Fig. 8

a Scanning electron microsopy (SEM) image of the macroporous structure of the monolithic CMK-3 type carbon material. b Small-angle X-ray scattering profile of the material. Four distinct peaks with Miller indices (10), (11), (20), (30) are distinguishable

To estimate the radius of carbon nanorods from the SAXS data, the integrated SAXS intensities of the four observable Bragg reflections were analyzed by a double-shell cylindrical form factor model outlined in detail in Refs. (Zickler et al. 2006; Jähnert et al. 2009). As the sample is essentially the inverse replica of a silica sample with hexagonally arranged cylindrical mesopores, the SAXS model of a cylindrical nanorod with a rough (or microporous) corona can be applied. The fit delivers 3 parameters, i.e., an inner (R₁), an outer radius (R₀), and a relative density ρ_c of the corona, from which a “equivalent nanorod radius” r = $\sqrt{{R}_{1}^{2}+{\rho }_{c}\left({R}_{0}^{2}-{R}_{1}^{2}\right)}$ can be deduced (Jähnert et al. 2009). With the values ${R}_{1}=1.94 nm$, ${R}_{0}=4 nm$ and ${\rho }_{c}=0.9$ obtained from the fit, the equivalent nanorod radius determined for the present sample is r = (3.9 ± 0.4) nm, resulting in a ratio D/r = 2.6 ± 0.05. In the present geometry, the value ${\rho }_{c}=0.9$ is directly associated with the amount of carbon present in the corona, which means that the carbon nanowires are quite dense and well defined.

2.3 B3: Adsorption isotherms

Adsorption isotherms of the hierarchical carbon monolith were obtained for nitrogen at 77 K and n-pentane at 290 K, using a commercial volumetric adsorption instrument (ASAP2020, Micromeritics). Prior to the analysis, the sample was degassed at 300 °C within the sample holder for several hours. The adsorption isotherms are shown in Fig. 9. A slight hysteresis can be observed for both adsorbates in the region where the “bridged” phase is supposed to be stable.

In addition, a n-pentane reference isotherm was measured to obtain the interaction parameters for n-pentane with carbon, by using a sample of thermally annealed carbon xerogel. Details on the synthesis and further characterization of this sample can be found in Ref. (Balzer et al. 2011). The measurement was performed with an ASAP2020 (Micromeritics) at 273 K. Prior to the measurement the sample was degassed at 300 °C. Although this sample does not deliver an ideal reference isotherm of a purely non-porous material, the very low microporosity (0.01 cm³/g), and the large radius of the mesopores (Balzer 2018) provides a satisfactory estimate of the interaction parameters. We mention that the theoretical model was parameterized based on these n-pentane reference data measured at 273 K, while applied to the adsorption data measured on the CMK-3-type sample at 290 K. We believe that this approximation is acceptable, since the interaction parameter of alkanes only show a weak temperature dependence (Croucher and Hair 1977).

Fig. 9

In a and b the full adsorption isotherms of nitrogen and n-pentane respectively are shown. Closed symbols denote the adsorption, empty symbols the desorption branch of the isotherm

Appendix C: Comparison with the Kelvin-Cohan equation and with a simplified analytical model

First we compare the results reported in Figs. 5 and 6 with a simple analysis using the Kelvin-Cohan equation (Cohan 1938; Neimark et al. 2003). In their first paper on CMK-3 materials, Jun et al. (2000) used this approach to obtain the CMK-3 pore size based on earlier work on MCM-41 silica (Kruk et al. 1997), by interpreting this size as the diameter of the cylinder fitting between three hexagonally arranged rods.

$$ - \frac{{R_{g} T}}{{v_{l} }}ln\left( {\frac{p}{{p_{0} }}} \right) = \frac{{\gamma}}{{r_{u}^{*} - h}}. $$

(19)

In their work, the film thickness $h$ was adjusted with an additive factor 0.3 nm to correct for inaccuracies in the Harkins–Jura equation (Boer et al. 1966). Since the interaction between nitrogen/pentane and carbon was determined directly in the present work using reference isotherms, we employ here directly the values $h(p/{p}_{0})$ given in Fig. 2. The maximum inscribed radius ${r}_{u}^{*}$ between three cylindrical rods is calculated by Eq. 15 using $D$ and $r$ from SAXS (Appendix B2), which gives ${r}_{u}^{*}=1.93 nm$. Plugging this value into Eq. 19 in conjunction with Eq. 11, the pressure of capillary condensation is $p/{p}_{0}=0.68$, which is very close to the value of the proposed “bridged-to-filled” transition for nitrogen found in Fig. 5. For n-pentane, the pressure of capillary condensation predicted by Eq. 19 is $p/{p}_{0}=0.57$, which is again close to the value predicted theoretically and found experimentally in Fig. 6.

The gap between two neighboring carbon nanowires can be approximated by adsorption between two flat carbon surfaces with distance $2{r}_{gap}=D-2r$. Again, the classical Kelvin-Cohan equation can deliver approximate results (Restagno et al. 2002) for relative pressures of capillary condensation if the $D/r$- ratio is close to 2. The pressure of bridge formation is thus calculated to be $p/{p}_{0}=0.5$ for N₂ and $p/{p}_{0}=0.3$ for n-pentane. These values are somewhat larger than the ones in Figs. 5 and 6. We note that for the actual carbon, $D/r=2.6$, and the approximation of two flat carbon surfaces will only be a very rough approximation. Yet, this simple analysis proves that the classical Kelvin-Cohan equation (Eq. 19) gives comparable values for adsorption in the small gap between neighboring carbon nanowires, equivalent to a “separated-to-bridged” transition, and shows good agreement for capillary condensation in interstitial space between three hexagonally arranged nanowires, corresponding to a “bridged-to-filled” transition with the results from Figs. 5 and 6.

To shed more light on the model of adsorption introduced in Sect. 2, a simplified model allowing an analytical solution was adapted (Osborn and Yeomans 1995), which should still capture the essential physics. In this model, summarized in Fig. 

Fig. 10

Sketch of the simplified “bridged” phase model. The profile is shown as blue closed curve. The two radii $a$ and ${r}_{c}=r+h$ (red dashed circles), and the angle $\theta$ at which they meet, define the profile unambiguously (Color figure online)

10, the “bridged” profile is defined by two radii of curvature, one being ${r}_{c}=r+h$, and the other being $a={\gamma}/\Delta \tilde{\mu}$, the two being related by $cos\left(\theta \right)=\frac{D}{2\left({r}_{c}+a\right)}$. With $h$ calculated from Eq. 11 and $\Delta \tilde{\mu }$ from Eq. 3, the profile is uniquely determined by the relative pressure $p/{p}_{0}$. The grand potential of this approximated “bridged”-profile is explicitly given by (Osborn and Yeomans 1995):

$$ {\Omega }\left( {\frac{p}{{p_{0} }}} \right) = 6\gamma \left( {\left( {r + h} \right)\left( {\frac{\pi }{6} - \theta } \right) + \left( {\frac{\pi }{2} - \theta } \right)a} \right) + 6 {\Delta }\tilde{\mu }\left( {\frac{{\left( {2rh + h^{2} } \right)}}{2}\left( {\frac{\pi }{6} - \theta } \right) + \frac{{D^{2} }}{8}\tan \left( \theta \right) - \frac{{a^{2} }}{2}\left( {\frac{\pi }{2} - \theta } \right) - \frac{{r^{2} }}{2}\theta } \right), $$

(20)

where the first part describes the contribution from the liquid–vapor interface and the second part takes the change in the potential due to the liquid adsorbed into account. For the separated phase, the grand potential reads as:

$$ {\Omega }\left( {\frac{p}{{p_{0} }}} \right) = \gamma \left( {r + h} \right)\pi + 6{\Delta}{\mu} \left( {\left( {r + h} \right)^{2} - r^{2} } \right)\frac{\pi }{4} . $$

(21)

We note that in this model, the contribution of the disjoining pressure term taking the solid–liquid interaction into account is omitted (compare with Eq. 2). As a consequence, only vapors with very weak, short range interaction (ideally $m\sim 3$ in Eq. 11) with the substrate can be satisfactorily modelled. Consequently, only nitrogen adsorption ($m\sim 2.5)$ is considered in the following. A phase diagram similar to Fig. 5a was constructed for nitrogen using Eqs. 20 and 21 (Fig. 11). The overall shape of the phase diagram is close to Fig. 5a, with some deviations due to the fixed geometry of the bridge profile especially at higher relative pressures. In Fig. 11 we also included the predictions for capillary condensation using Eq. 19 in the gap between neighboring nanowires as a black dashed line and in the interstitial between three carbon nanowires as a blue dashed line. The results align well for the “bridged-to-filled” transition, yet they deviate significantly for the “separated-to-bridged” transition with increasing $D/r-$ ratio as expected.

Fig. 11

Calculated phase diagram for nitrogen in CMK-3-like carbon at 77.4 K showing the “separated” phase (green), the “bridged” phase (white), and the “filled” phase (red) using the simplified model (Eqs. 20, 21 and 8). The dashed lines correspond to pressures of capillary condensation for the “separated-to-bridged” (black) and “bridged-to-filled” (blue) transitions using the Kelvin-Cohan Equation (Eq. 19) (Color figure online)