1 Introduction

A phenomenon where surface chemistry has a dominant influence on the properties of bulk fluid is the process of capillary filling of silicon dioxide nanochannels. In this case the key parameter is pH which has a dominant influence on electric charge of channel walls and the properties of molecules in the solution (Eijkel and Berg 2010; Napoli et al. 2010).

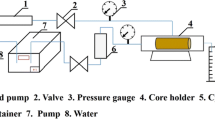
(Janssen et al. 2008) investigated the filling of silicon nanochannels with fluorescein solutions. They observed two zones in the fluid introducing into nanochannels. The front part of liquid was dark, and the back part exhibited fluorescence. The ratio of lengths of two zones was constant in time (Fig. 1a). The fluorescein molecule exhibits intense light emission when it is doubly deprotonated (for pH > 7), and it is inactive in protonated form (for pH < 4). It means that the pH in the dark zone is significantly lower than the pH in the bright zone. This increase in the concentration of hydrogen ions results from titration of solution by protons released from nanochannel walls (Fig. 2b).

Fig. 1
figure 1

a The capillary filling of silicon dioxide nanochannel. Two zones in liquid can be distinguished (dark and fluorescent one). Ratio LD/LFL is constant in time for given solution composition (ionic strength, buffer capacity). b The hydrogen ions released from nanochannel walls in the fluorescent zone move with filling solution to the dark zone where they decrease pH and quench fluorescein molecules by their protonation

Full size image
Fig. 2
figure 2

The structure of the 2-pK triple layer model (2-pK TLM). Three planes can be distinguished: the surface plane (0), the plane of adsorbed electrolyte ions (β), and the plane being onset of diffuse layer (d). ψ denotes electric potential and δ charge located in the individual planes. c 1 stands for inner-layer capacitance and c 2 is outer-layer capacitance

Full size image

The research on filling of silica nanochannels was continued by (Andersen et al. 2011) who analyzed the dependence of electrokinetic potential and the ratio of dark and fluorescent lengths on ionic strength for bare and 3-cyanopropydimethylchlorosilane coated silica nanochannels.

In this paper, we have developed the model describing surface deprotonation of silica nanochannels taking into account energetic heterogeneity of silanol groups. Next, we apply our model to describe experimental results published in literature so far. Finally, we give concise critical discussion of the modeling of coated silica nanochannels.

2 Theory

According to (Janssen et al. 2008) the balance of hydrogen ions in the investigated system can be calculated as follows.

The released number of protons in fluorescent zone is equal to:

$$ {\text{N}}_{{{\text{H}}^{ + } }}^{\text{released}} {\text{ = N}}_{\text{s}} {{\uptheta}}_{\text{dep}} {\text{L}}_{\text{FL}} 2 ( {\text{h}} + \text{{w}}) $$
(1)

The number of protons absorbed by the solution in the dark zone is equal to:

$$ N_{{H^{ + } }}^{absorbed} = N_{A} B_{S} L_{D} hw $$
(2)

The meaning of symbols in the above equations and in the Fig. 1 is following: \( N_{A} \)is the Avogadro’s number, h is the nanochannel height, w is the nanochannel width, Ns is the number of silanol groups per nm2, θdep is the fraction of deprotonated surface groups, LFL is the length of fluorescent zone, LD is the length of dark zone, pHB is the bulk pH of introduced solution, pHpzc is the pH at the point of zero charge of the silica surface, BS is the concentration of protons needed to change pH of solution from pHB to pHpzc.

We can experimentally determine the number of protons released per area of nanochannel wall \( {\text{N}}_{{{\text{H}}^{ + } }}^{ \exp } \) assuming that \( N_{{H^{ + } }}^{released} = N_{{H^{ + } }}^{absorbed} \) and applying w > > h (because in rectangular nanochannel, its width is usually expressed in micrometers and its height in nanometers):

$$ N_{{H^{ + } }}^{\exp } = N_{s} \theta_{dep} = N_{A} B_{S} h\frac{{L_{D} }}{{2L_{FL} }} $$
(3)

To analyze proton release in nanochannels we applied the 2-pK surface complexation model combined with the Triple Layer Model of interfacial region (2-pK TLM), which was depicted in Fig. 2 (Davis et al. 1978; Yates et al. 1974). The parameters of electric double layer in the 2-pK TLM are interconnected by the following expressions (Piasecki et al. 2001),

$$ {\text{c}}_{ 1} { = }\frac{{{{\updelta}}_{ 0} }}{{{{\uppsi}}_{ 0} - \psi_{{{\upbeta}}} }} $$
(4a)
$$ {\text{c}}_{ 2} { = }\frac{{ - {{\updelta}}_{\text{d}} }}{{{{\uppsi}}_{{{\upbeta}}} - \psi _{\text{d}} }} $$
(4b)
$$ {{\uppsi}}_{\text{d}} { = }\frac{{ 2 {\text{kT}}}}{{\left| {\text{z}} \right|{\text{e}}}}{ \ln }\left[ {\frac{{ - \delta_{\text{d}} }}{{\sqrt { 8 \varepsilon_{ 0} \varepsilon_{\text{r}} {\text{kTI}}} }}{ + }\sqrt {\frac{{{{\updelta}}_{\text{d}}^{ 2} }}{{ 8 \varepsilon_{ 0} \varepsilon_{\text{r}} {\text{kTI}}}}{ + 1}} } \right] $$
(4c)

The equation (4c) follows from Gouy-Chapman theory of diffuse layer in electrolyte solutions.

The formation of surface complexes visible on Fig. 2 one can describe by the following reactions and equilibrium constants:

$$ {\text{SiO}}^{ - } + {\text{H}}^{ + } \leftrightarrow {\text{SiOH}}^{ 0} , {\text{ K}}_{ 0} $$
(5a)
$$ {\text{SiO}}^{ - } + 2 {\text{H}}^{ + } \leftrightarrow {\text{SiOH}}_{2}^{ + } {\text{ , K}}_{ + } $$
(5b)
$$ {\text{SiO}}^{ - } + {\text{C}}^{ + } \leftrightarrow {\text{SiO}}^{ - } {\text{C}}^{ + } {\text{ , K}}_{\text{C}} $$
(5c)
$$ {\text{SiO}}^{ - } + 2 {\text{H}}^{ + } +{\text{A}}^{ - } \leftrightarrow {\text{SiOH}}_{2}^{ + } {\text{A}}^{ - } {\text{ , K}}_{\text{A}} $$
(5d)

where SO − denotes deprotonated silanol group at the oxide surface (empty adsorption site).

Additionally, in our model we have taken into account energetic heterogeneity of the silica surface. We have assumed that adsorption constants may have different values for different silanol groups. Assuming Gaussian-like distribution of adsorption energy (binding constants) and applying the the 2-pK TLM one arrives at the following expressions (heaving the form of Langmuir–Freundlich isotherms) for mean surface coverage by i-th adsorption complex (Rudzinski et al. 1999; Rudzinski and Everett 1992):

$$ {{\uptheta}}_{\text{it}}^{{}} { = }\frac{{\left[ {{\text{K}}_{\text{i}}^{{}} {\text{f}}_{\text{i}} } \right]^{{{\raise0.5ex\hbox{$\scriptstyle {\text{kT}}$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle {{\text{c}}_{\text{i}} }$}}}} }}{{ 1 { + }\sum\nolimits_{\text{i}} {\left[ {{\text{K}}_{\text{i}}^{{}} {\text{f}}_{\text{i}} } \right]^{{{\raise0.5ex\hbox{$\scriptstyle {\text{kT}}$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle {{\text{c}}_{\text{i}} }$}}}} } }}{\text{ i = 0, + ,A,C}} $$
(6)

where \( {\text{kT/c}}_{\text{i}} \) are the dimensionless heterogeneity parameters. To simplify the analysis, we assumed in our calculations that heterogeneity parameters of different complexes have the same value \( {\text{kT/c}}_{\text{het}} \).

Next, fi can be expressed as functions of pH and electrolyte ions concentrations aC and aA:

$$ {\text{f}}_{ 0}= {\text{exp}}\left\{ {{ - }\frac{{{\text{e}\psi}_{ 0} }}{\text{kT}}{ - 2} . 3 {\text{pH}}} \right\} $$
$$ {\text{f}}_{ + } = {\text{exp}}\left\{ {{ - }\frac{{ 2 {\text{e}\psi}_{ 0} }}{\text{kT}}{ - 4} . 6 {\text{pH}}} \right\} $$
(7)
$$ {\text{f}}_{\text{C}} = {\text{a}}_{\text{C}} { \exp }\left\{ {{ - }\frac{{{\text{e}\psi}_{ 0} }}{\text{kT}}{ + }\frac{{{\text{e}\delta}_{ 0} }}{{{\text{kTc}}_{ 1} }}} \right\} $$
$$ {\text{f}}_{\text{A}}={\text{a}}_{\text{A}} { \exp }\left\{ {{ - }\frac{{{\text{e}\psi}_{ 0} }}{\text{kT}}{ - }\frac{{{\text{e}\delta}_{ 0} }}{{{\text{kTc}}_{ 1} }}{ - 4} . 6 {\text{pH}}} \right\} $$

The surface charge and diffuse layer charge can be expressed using surface coverages defined in eq (6),

$$ {{\updelta}}_{ 0}={\text{eN}}_{\text{s}} ( {{\uptheta}}_{+\text{t}} {+\theta}_{\text{At}}-\theta_{\text{Ct}} - \theta_{-\text{t}} ) $$
(8a)
$$ {{\updelta}}_{\text{d}} = {\text{eN}}_{\text{s}} ({{\uptheta}}_{-\text{t}} {\,-\,\theta }_{+\text{t}} ) $$
(8b)

The total fraction of deprotonated surface groups can be calculated theoretically using the following equation,

$$ {\text{N}}_{{{\text{H}}^{ + } }}^{\text{theory}} = {\text{N}}_{\text{s}} {{\uptheta}}_{\text{dep}} = {\text{N}}_{\text{s}} ( {{\uptheta}}_{-\text{t}} +\theta_{\text{Ct}} {\,-\,\theta}_ + {\text{t}} {-\theta }_{\text{At}} ) $$
(9)

The last value can be compared with experimentally determined number of protons released per area of nanochannel wall \( {\text{N}}_{{{\text{H}}^{ + } }}^{ \exp } \), defined in eq (3).

To calculate the value of \( {\text{N}}_{{{\text{H}}^{ + } }}^{\text{theory}} \), first we have combined three equations (4a-c) into one

$$ {{\uppsi}}_{ 0} { - }\frac{{{{\updelta}}_{ 0} }}{{{\text{c}}_{ 1} }}{ + }\frac{{{{\updelta}}_{\text{d}} }}{{{\text{c}}_{ 2} }}{ - }\frac{{ 2 {\text{kT}}}}{{\left| {\text{z}} \right|{\text{e}}}}{ \ln }\left[ {\frac{{{ - \delta}_{\text{d}} }}{{\sqrt { 8 {\varepsilon }_{ 0} {\varepsilon}_{\text{r}} {\text{kTI}}} }}{ + }\sqrt {\frac{{{{\updelta}}_{\text{d}}^{ 2} }}{{ 8 {\varepsilon}_{ 0} {\varepsilon}_{\text{r}} {\text{kTI}}}}{ + 1}} } \right]{ = 0} $$
(10)

Next we have applied eqs (8b, 6, 7) to express diffuse layer charge δd as a function of δ0 and ψ0. Finally, we have gotten two nonlinear equations (8a) and (10) with two unknowns δ0 and ψ0. This system of equations can be solved numerically using mathematical software like Mathematica. Having determined the values of surface charge and potential for given pH and ionic strength we can easily calculate \( {\text{N}}_{{{\text{H}}^{ + } }}^{\text{theory}} \) from eq (9) or ψd from eq (4c).

3 Results and Discussion

In experiments performed by (Janssen et al. 2008) nanochannels were 40–50 nm deep and 20 μm wide. They used two types of filling solutions: unbuffered KCl solution (mean pH = 7.2) and KCl solution buffered with TRIS (mean pH = 8.5). The both solutions contained fluorescein as pH-sensitive fluorescent dye. In Fig. 3, we have depicted the number of protons released per area of nanochannel wall \( {\text{N}}_{{{\text{H}}^{ + } }}^{ \exp } \) as a function of ionic strength.

Fig. 3
figure 3

The influence of energetic surface heterogeneity on the number of proton released to bulk per nm2 in silica nanochannel. Experimental data were measured for two different pH (i.e. pHB in fluorescent zone) and for various electrolyte concentration in filling solutions. The lines were plotted assuming various degrees of surface heterogeneity (kT/c het  = 1.0, homogenous surface, solid line; kT/c het  = 0.8, dashed line, kT/c het  = 0.6, finely dashed line). The data were taken from (Janssen et al. 2008)

Full size image

Similar experiments were continued by (Andersen et al. 2011). However, these authors introduced some important modifications. First they determined electrokinetic potential in nanochannels using electro-osmotic current monitoring data, and second they modified nanochannel walls by coating silica surface with 3-cyanopropyldimethylchlorosilane. These authors used the solution of KH 2 PO 4 as a filling buffer. In their experiments, nanochannel depth was in the range of 115–195 nm and their width changed in the range of 5–40 μm. Buffer pH was equal to 7.2 (mean value). In Fig. 4, we presented results obtained by Andersen et al. There are data for bare silica surface and coated by cyanosilane.

Fig. 4
figure 4

The number of proton released to bulk per nm2 of wall (a) and electrokinetic potential (b) determined for bare (circles, red) and coated (squares, blue) silica nanochannels. Red line denotes the values calculated by using the parameters collected in the Table 1. For each ionic strength several measurements were done. The huge dispersion of data is visible for I = 0.8. The data were taken from (Andersen et al. 2011) (Color figure online)

Full size image

Our aim was to fit the data for bare silica nanochannel obtained in two different laboratories using our model assuming surface energetic heterogeneity and only one parameter set. Because there is some controversy concerning charging mechanism of coated silica nanochannels we have not analyzed the data for modified nanochannels. This issue is discussed later in this paper.

We have fitted the data for bare nanochannels applying the parameters collected in Table 1. The starting values of these parameters were taken from Sverjensky’s paper (Sverjensky, 2005) for amorphous silica. This is quite recent, and the most reliable collection of parameters for the 2-pK TLM determined for different oxides and various electrolytes. However, these parameters can be treated as starting values, and their precise adjustment can be done.

Table 1 The parameter values used in the calculations
Full size table

Figure 3 shows how energetic surface heterogeneity affects on the number of proton released to bulk solution. The higher degree of surface heterogeneity means that the surface is more deprotonated. We have found that the optimal value for heterogeneity parameter was \( {\text{kT/c}}_{\text{het}} { = 0} . 8 \).

To fit ζ-potential data we had to increase outer Stern layer capacitance c 2 from standard value 0.2 to 1.2. In our calculations we assumed that electric potential in d-plane ψd corresponded to measured electrokinetic ζ-potential. The value of c2 has very little impact on the degree of surface deprotonation, but significantly changes calculated ζ-potential. Another way to fit ζ-potential data is introducing the separation distance between outer Helmholtz plane (d-plane in Fig. 2) and slipping plane, where electrokinetic potential is measured (Kallay et al. 2012; Lutzenkirchen et al. 2008). This procedure requires an additional parameter (slip plane distance).

The crucial parameter in our modeling was the equilibrium constant for electrolyte cation adsorption KC. We had to decrease its value from the initial one taking from Sverjensky’s paper. The equilibrium constant for anion adsorption KA was insignificant in the modeling, because the investigated pH values were much higher than PZC of silica and anion adsorption was completely negligible.

Janssen et al. (2008) and Andersen et al. (2011) did also theoretical modeling of their own experimental data. The first group used the 2-pK Basic Stern Model neglecting electrolyte cation adsorption. The second group applied the 2-pK TLM including cation adsorption. The obtained results were satisfactory. In our opinion the modeling results for cyanosilane coated silica nanochannels are questionable.

According to Andersen et al. cyanosilane replaced about 25 % silanol groups on the surface. Nevertheless coated silica exhibited much higher deprotonation than bare silica. Additionally, coated surface should have higher PZC value. Silanol groups should have different acidity (consequence of energetic heterogeneity), and the most acidic group should first react with cyanosilane molecules. This should increase PZC value of silica, and decrease the level of deprotonation. To fit the number of protons released to bulk solution Andersen et al. had to assume very high value for inner Stern layer capacitance c 1 (13-15 \( {\text{F/m}}^{ 2} \)) which was about 20 times higher than the value used for bare silica surface.

In the simplest way capacitance c 1 can be defined by the following equation,

$$ {\text{c}}_{ 1} { = }\frac{{{\varepsilon}_{\text{IL}} }}{\text{d}} $$
(11)

where ɛIL is dielectric constant of the interfacial layer, and d is the distance between the silica surface and adsorbed electrolyte ions. It is not likely that any of these quantities could increase or decrease 20 times after surface coating.

One can try to explain this contradiction using the results from (Kallay et al. 2012; Lutzenkirchen et al. 2008). They found that for hydrophobic surfaces, there is an additional mechanism which increases the surface deprotonation. The silica surface which is coated by short hydrocarbon chains may enhance the autolysis of interfacial water molecules. As a result of this process, hydroxyl groups stay on the surface, and hydrogen ions are released to solution.

Andersen and co-workers assumed the following surface reaction with equilibrium constants \( {\text{pK}}_{ + }^{\text{A}} \) and \( pK_{ - }^{A} \),

$$ {\text{SiOH}}_{ 2}^{ + } \leftrightarrow {\text{SiOH}}^{ 0} {\text{ + H}}^{ + } {\text{ , pK}}_{ + }^{\text{A}} $$
(12a)
$$ {\text{SiOH}} \leftrightarrow {\text{SiO}}^{ - } {\text{ + H}}^{ + } {\text{ , pK}}_{ - }^{\text{A}} $$
(12b)

In their calculations, they assumed that \( {\text{pK}}_{ + }^{\text{A}} \) is the key fitting parameter. The value of pK A- was kept constant.

For pH > 7 the concentration of SiOH +2 groups on the silica surface should be very small, and in practice only the reaction (12b) regulates the degree of surface deprotonation. Remembering that \( {\text{PZC = }}\tfrac{ 1}{ 2} ( {\text{pK}}_{ + }^{\text{A}} {\text{ + pK}}_{ - }^{\text{A}} ) \) it is clear that the real key parameter was the PZC of the silica surface in the modeling described above. It is surprising that for fused silica, which covered the nanochannels, PZC value was not determined experimentally (it was assumed to be PZC = 2.8). It could be done, for example, by applying ISFET device or single crystal electrode technique (Kallay et al. 2007).

4 Conclusions

Surface complexation models like the 2-pK Triple Layer Model were successfully applied to describe the equilibria at oxide/electrolyte interface in silica nanochannels. However, for silica nanochannels coated by 3-cyanopropydimethylchlorosilane probably additional charging mechanism occurs. According to Kallay et al. the interfacial water on hydrophobic surfaces preferentially accumulates OH − ions, which increases hydrogen ions release to solution. This mechanism is not incorporated into surface complexation models. So, we have decided not to analyze the data for coated silica nanochannels.

Additionally, it has been shown that parameters values obtained by Andersen et al. who tried to fit the data for coated nanochannels were in conflict with the model assumptions.

For the bare silica nanochannels we have developed the 2-pK TLM assuming the surface energetic heterogeneity. Simply put, we assumed that different silanol groups should have various deprotonation constants. We have simultaneously analyzed the data obtained by Janssen et al. and by Andersen et al. We have used the parameter values predicted by Sverjensky for silica. We have found that more heterogeneous nanochannel walls were more charged. This means that the degree of surface energetic heterogeneity may influence on the transport of ionic solutes through nanochannels.