Abstract
This work deals with a construction of an implicit solvent model which can be used in molecular dynamics simulations of systems comprising colloid nanoparticles and carbon nanotubes. Such systems, due to finite sizes of both components, cannot be accurately approximated by a smaller slab geometry and thus represent a particularly difficult case in terms of computer simulations. Adsorption of large colloid nanoparticles on the surfaces of carbon nanotubes were studied and we determined the adsorption energy profiles of the nanoparticles on the carbon nanotubes surfaces. We also determined the adsorption isotherms which help to understand a preferred location of the nanoparticles on the nanotubes surfaces.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
This work deals with adsorption of colloid nanoparticles, NPs, on surfaces of carbon nanotubes, CNTs. Such composite materials have recently been extensively studied due to their numerous applications in the fields of drug delivery (Panczyk et al. 2011a, b; Shi et al. 2010; Yang et al. 2011; Zhan et al. 2011), gas sensing and biosensing (Charlier et al. 2009; Leghrib et al. 2011; Son et al. 2005), magnetic force microscopy, data storage etc. (Belesi et al. 2011; Guo et al. 2011; Korneva et al. 2005; Saha and Kundu 2010; Schaffel et al. 2009; Tsoufis et al. 2008). A non-covalent binding of nanoparticles to the carbon nanotube surfaces is particularly interesting because it offers the possibility of attaching metallic, inorganic or organic nanoparticles without affecting the electronic structure of the nanotubes (Dyke and Tour 2004; Moghaddam et al. 2004).
The adsorption process was studied using molecular dynamics as well as grand canonical Monte Carlo simulations. The systems under consideration, due to finite nanometer sizes of CNTs and NPs cannot be accurately approximated by a smaller slab geometry and thus represent a particularly difficult case in terms of computer simulations. Nanoparticle sizes of a few tens of nanometers lead to billions of solvent molecules in a simulation box and require very long cut-off distances. Therefore, we applied the recently proposed implicit solvent model, ISM, based on the Hamaker theory of dispersion interactions (Panczyk et al. 2012a). The validity of the ISM was verified by comparing the results obtained from the exact model, involving full description of all atoms (AA) including solvent molecules, with the results obtained from the proposed ISM. As the agreement between these two approaches was good we concluded that the proposed ISM reproduces key properties of the original model involving incomparably less computational resources. Particularly, the work of adhesion and average configuration of the nanoparticle-nanotube systems were very well reproduced when the Hamaker constants for interactions across solvent were suitably determined. Very good agreement was found for the dynamics of motion of a probe nanotube towards the nanoparticle without any extra assumptions (Panczyk et al. 2012a). Therefore, the proposed implicit solvent model can successfully be applied to studies of large systems which are not tractable using the exact AA approach.
By utilizing the above methodology we determined the adsorption energy profiles of large colloid nanoparticles on the surfaces of single- and multi-walled carbon nanotubes. The main component of adsorption energy is the dispersion interaction energy between the NPs and CNTs. So, this is a key factor which controls properties of the nanoparticle-nanotube hybrid materials. It was found, that depending on the range of dispersion interactions the adsorption of NPs on CNTs might be reversible or irreversible. This is determined solely by the NPs building material and the solvent Hamaker constant (Panczyk et al. 2012b). Irreversible adsorption occurs in the case of metallic NPs while NPs revealing the Hamaker constants representative to oxides adsorb reversibly at ambient temperatures. The adsorption isotherms, determined for the latter cases, show that the NPs locate preferentially on the single-walled CNTs sidewalls at low concentrations. In the case of multi-walled CNTs the NPs occupy either tips or sidewalls even at low NPs concentrations. Thus, this work shows some key results concerning the mechanism of colloid nanoparticles adsorption on carbon nanotubes.
2 Methods
2.1 Theoretical considerations
According to the Hamaker theory the energy of interaction of an atom with large spherical particle U cs is an integral of pairwise Lennard–Jones interactions taken over the volume of the particle,
where V is the volume, ρ is the number density of the nanoparticle and U LJ (r) is the Lennard–Jones pairwise potential at a distance r between the atom and some point within the nanoparticle. For spherical nanoparticle Eq. (1) can be integrated analytically giving the following convenient formula:
where a is the radius of the nanoparticle, \(\varepsilon\) and σ are the usual Lennard–Jones parameters and R is the center-center distance between the atom and the nanoparticle. By using the definition of the Hamaker constant (Everaers and Ejtehadi 2003),
we can express the prefactor in Eq. (2) as a function of the Hamaker constant for a colloid-single atom interactions, \(A_{cs}=\sqrt{A_{cc} A_{ss}} = \sqrt{A_{cc} 144 \varepsilon}\). The factor \(144\varepsilon\) is a formal Hamaker constant for single atom interactions A ss , and it is the result of assuming that the number density of single atom is 1 per volume occupied by a sphere of radius σ/2, that is \(A_{ss} = 4 \pi^2 \varepsilon (\rho_s \sigma^3)^2, \) ρ s = 6/ (πσ 3).
The Lifshitz theory of van der Waals interactions allows for determination of the interaction energy between various media (Israelachvili 1985–2004). For example, the Hamaker constant for the interactions between media 1 and 2 across medium 3, A 132, stands:
where A ii are the Hamaker constants for a given medium across vacuum.
Equation (4) is valid for the case of macroscopic continuum objects, however, if we go towards microscopic pairwise-additive evaluation of the energy by applying Eq. (2), the calculation of the net Hamaker constant need careful analysis. We can consider at least four concepts which lead to different results.
First, we can assume that the mixing rule (4) still holds. Then, the net Hamaker constant for the interaction between the single atom s and the entire colloid nanoparticle c across solvent (water) w reads:
where \(144\varepsilon = A_{ss}.\) It conceptually means that the single atom removes from the system one solvent molecule. We can thus consider the opposite approach in which we assume that that single atom does not remove any solvent molecules because it can fit within the intermolecular space available in the solvent network. Then, the suitable mixing rule simplifies to:
and means that the net energy comes from direct interactions of the atom with the nanoparticle minus the energy of the replacement of the nanoparticle volume by the solvent. Further, we can consider an intermediate case, namely we can assume that the atom removes some number of solvent molecules which is related to the ratio of volumes occupied by the atom and the solvent molecule. We can thus define a correction factor v which means how many solvent molecules are removed by a single atom. The mixing rule transforms then to:
In case of charged nanoparticles, e.g. silica in water, the polar solvent molecules might create an electrostatically bound thin adsorbed layer which further affects the dispersion interactions. Closer analysis of this phenomenon leads to the conclusion that A cws is somewhat enhanced when compared to the uncharged case and the following combining rule should hold (Panczyk et al. 2012a):
where
2.2 Computational details
The molecular dynamics simulations were performed using the large-scale atomic/molecular massively parallel simulator (LAMMPS) code (Plimpton 1995). In the case of the AA model the simulation box consisted of one nanoparticle (d NP = 12 Å) located and fixed at the center of the box, one (6,0) carbon nanotube consisted of 72 carbon atoms and 12 terminal hydrogens, 3,279 water molecules and a small number of sodium and chloride ions since we are particularly interested in the accuracy of the ISM at conditions close to physiological ionic strength 0.145 mol L−1. The size of the CNT is relatively small; however, this is mainly due to high energies of CNT interactions with solvent. Larger CNT would lead to a very large component to the work of adhesion, as will be shown in the next section, and it would worsen the accuracy of its estimation.
We used the TIP3P water model with the parameters optimised for Ewald summation of long range electrostatic interactions (Price and Brooks 2004). Other non-bonded interaction parameters are taken from the OPLS-AA force field (Jorgensen et al. 1996). The intramolecular interactions within the carbon nanotube were described using the Adaptive Intermolecular Reactive Empirical Bond Order (AIREBO) potential developed by Brenner et al. (2002); Stuart et al. (2000) Interaction of the NP with water, Na+, Cl− and the carbon nanotube (actually carbons comprising the CNT as the interaction with the terminal hydrogens is omitted) was computed using Eq. (2).
The grand canonical Monte Carlo, GCMC, simulations were performed according to standard Metropolis sampling scheme. The insertion probability was proportional to the available surface area on the tips and sidewalls, respectively, and to the usual energy factor coming from the adsorption energy, dispersion interactions between NPs and electrostatic interactions. The electrostatic interactions between charged NPs were treated according to the Yukawa potential (Zhan et al. 2011; Panczyk et al. 2011a) and assuming ionic strength of solution 0.145 mol L−1 and NPs concentration 2 × 10−4 mol L −1. At the assumed conditions the Debye length κ = 0.125 Å −1 and effective charge of every single NP is −125e. The deletion and displacement probabilities were computed according to the standard rules associated with the grand canonical MC scheme.
Because we compare the interaction energies in the all-atom explicit solvent model and in the ISM (without explicit water molecules) we call those energies as "work of adhesion" or "adsorption energy". The former is used while considering the all-atom model whereas the latter stands for the results obtained within the ISM. Both energies are directly comparable since in the ISM the work of adhesion is equivalent to the adsorption energy.
3 Results and discussion
3.1 Applicability of the ISM
Let us consider how the proposed ISM recovers the work of adhesion of NPs on the CNT surfaces. Table 1 defines two systems considered here; namely metallic cobalt nanoparticles interacting with a single-walled carbon nanotube across electrolyte solution, and silica NP in these same conditions.
Table 2 shows the values of the work of adhesion determined according to the various approaches to the calculation of the net Hamaker constant defined in Eqs. (5–8). Looking at values obtained for the Hamaker constants calculated according to Eq. (5) we notice that in any case the works of adhesion are strongly underestimated. Application of Eq. (5) means that every carbon atom in the CNT formally replaces one water molecule which is actually not true. Therefore, we can conclude that the mixing rule (5), though valid for continuum systems is not applicable in the atomistic approach when the total interaction energy is a sum of individual contributions from all atoms creating a given object.
The next approach, which assumes that a carbon atom does not replace any water molecule, i.e. based on Eq. (6) leads to very good prediction of the work of adhesion for cobalt nanoparticles. Thus, the assumption that a single atom does not remove any solvent atoms seems to work correctly but we must be aware that such assumption is not general. In the particular case of the carbon nanotube analysed in this study we found that 72 carbon atoms replaces only 16 water molecules. Thus, the ratio v = 16/72 = 0.22 is not a big number and if we compare the Hamaker constants calculated according to Eqs. (6) and (7), A (2) cws = 13.6 × 10−20 J, A (2) cws = 11.4 × 10−20 J, respectively, we can see that the difference between them is not big. Therefore, as discussed in the recent work (Panczyk et al. 2012a), the approach based on Eq. (7) is more reliable. We can, thus, propose a simple recipe for tuning the ISM model, so that it correctly predicts an equilibrium behavior in a system composed of a NP and another molecule immersed in a solvent. Namely, we need to determine how many solvent molecules are replaced by the volume occupied by that molecule and incorporate to the mixing rule (7) a correction factor, v, being a ratio of the number of atoms in the molecule to the number of solvent molecules replaced by the molecule. The correction factor v can, thus, be determined from a simple geometric analysis of the considered system.
However, Eq. (7) does not work for the charged SiO2 system. This is obviously indirect effect of electrostatic interactions and thus cannot be directly handled by e.g. Yukawa or just Coulomb interactions within the ISM. Note that electrostatic interactions affect the interaction energy between the uncharged nanotube and the charged NP. Due to charge dipole interactions the water molecules tend to firmly stick to the NP surface and create a kind of monomolecular shell. As a result, a charged silica NP behaves like a core-shell nanoparticle with the core being the NP material and the shell being a thin water layer. Thus, it is possible to formally handle this effect in terms of theory of dispersive interactions though it has purely electrostatic origin. Eq. (8) assumes that the effective NP diameter is larger due to additional water shell dragged with the NP. Thus, by utilizing simple geometric analysis it is possible to derive Eq. (9) which mimics that effect by rescaling the value of the Hamaker constant \(A_{cc} \rightarrow A^*_{cc}. \) As a result we find a very good agreement in the work of adhesion for the SiO2 system as well.
The radial distribution functions for both case studies confirm that the ISM correctly predicts geometry of the NP-CNT systems. These are shown in Figs. 1 and 2. Clearly, for uncharged NPs the Eq. (7) gives the best description while for the charged NPs a very well coincidence of rdf’s is obtained for Eq. (8). Thus, we can conclude that the work of adhesion and average configuration of the NP-CNT systems are very well reproduced when the Hamaker constants for interactions across solvent are suitably determined.
3.2 Adsorption energy of NPs on CNTs surfaces
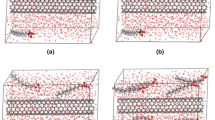
Carbon nanotubes are not energetically uniform, therefore a preferred location of colloid NPs on the CNT surfaces will be governed by the adsorption energy profile. Therefore, further calculations were focused on determination of the mean energy of dispersion interactions in various spatial arrangements of the CNT and NP thus giving a notion about energy of various adsorption sites on the CNT surface. The calculations were performed using the ISM at constant temperature 300 K, constant volume, and constant number of atoms (from 7,702 to 83,008 depending on the number of layers within the multi-walled CNTs, i.e. from 1 to 7). Two NPs were placed symmetrically at selected positions (Fig. 3) and their motion was constrained by hard reflecting walls in order to keep their predefined positions within the range ±0.5 Å. The studied positions are denoted here as a shift vector from the reference 0R position which corresponds to the NP center located at sidewall and over the terminal nanotube ring. Accordingly, the positions 0.5R and 1.5R stand for the NP center shifted toward the CNT middle by the distances 0.5 and 1.5 NP radius, respectively. The e-tip and c-tip positions were used for determination of the adsorption energy at the CNT edges. In the case of the e-tip position the NP center was located at the very edge of the CNT tip while the c-tip stand for location of the NP at the CNT tip center. In every case interaction between both NPs was zeroed, thus, such arrangement of the simulation box allowed to probe various adsorption sites on the CNT surface as a function of the NP position.
Creation of a protective shell on the surface of metallic nanoparticles is necessary in order to improve their stability in solution and avoid degradation. Among various possible approaches application of oxides as shell materials is particularly interesting because electrostatic stabilization of the nanoparticles in aqueous media can be simultaneously utilized (Lu et al. 2007). Therefore, we assumed in further calculations that metallic NPs are covered by 10 Å thick silica layer. It has recently been found that such a thickness of the oxide layer totally dominates the net interaction energy and the whole NP exhibits the same dispersion interaction energy as it would be composed exclusively of the oxide material (Panczyk et al. 2012b).
Figure 4 shows the adsorption energy profile for 60 Å in diameter metallic NP covered by 10 Å thick silica layer. The number of carbon nanotube layers range from 1 to 7 showing how the multi-walled architecture of the CNT affects the interaction energy. The CNT internal structure was described by applying the AIREBO potential, thus the CNTs are flexible and might undergo deformations due to interaction with the NPs.
Adsorption energy of the NPs on the CNT surfaces considered in water solution. The results are for 60 Å in diameter metallic NPs covered by 10 Å thick silica layers, thus the total diameters are of the NPs are 80 Å. The CNT is either single-walled(n = 1) or multi-walled with the number of layers from 3 to 7. The innermost CNT has chiral index (50,0) that is, its diameter is 39 Å. The outermost CNT has chiral index (119,0) thus its diameter is 72 Å. The CNT lengths are 160 Å. The calculations were performed at temperature 300 K using the AIREBO potential for description of flexible CNT structures
It is clearly seen in Fig. 4 that transition of the NP from full sidewall position (1.5R) towards the CNT tip is accompanied by significant edge barriers. This is understandable because at these e-tip positions the NPs loose significant portion of pair interactions due to purely geometric reasons. Therefore, location of NPs at these edge positions at thermodynamic equilibrium is unfavourable and the NPs will either move to full sidewall positions or to c-tip positions. Very interesting observation is the relation between the energy at full sidewall and c-tip position. In the case of single-walled CNTs (n = 1) the sidewall position is more energetically favorable, however the multi-walled CNTs reveal a stronger binding at c-tip positions. The more layers in CNT the higher energy of dispersion interactions, but this trend seems to quickly saturate. In any case the difference between the sidewall and c-tip position is not big, in this particular case of silica covered NP it is not more than 20 kJ mol−1. This is probably not enough to get preferred occupation of tips at low NPs concentrations. In this case entropic factors will prevail the energetic ones as the number of adsorption sites at sidewalls is normally much larger than at tips. Finally, the adsorption of silica covered NPs on the CNTs should be reversible due to moderate values of energy found in Fig. 4.
The determination of the adsorption energy of the nanometer sized NPs and flexible carbon nanotubes, which were described by the AIREBO potential, are computationally very expensive since the number of carbon atoms reaches 83,000 for the largest system corresponding to 7-walled CNT. It is therefore interesting to study whether the flexible model is really necessary to assume or we can safely rely on a simpler rigid CNT model. Comparison of the results obtained using the flexible and rigid models for silica covered metallic NPs is shown in Fig. 5.
We can thus state that both models give similar results. Simply, the energy of dispersion interactions is not enough to affect the CNTs structure and it remains intact within the flexible model. Therefore, because the rigid model gives the same results the application of the AIREBO potential is obviously a computational overkill. Figure 5, however, gives insight not only in the computational problems but obviously it leads to a more general physical conclusion. Namely, if we consider interaction of CNTs with NPs and the system is tuned in such a way that the range of dispersion interactions energy is not high, say less than ca. 100 kJ mol−1, then the CNTs behave like stiff cylinders. No deformation of CNTs structure occurs even in the case of single-walled CNTs.
3.3 Adsorption isotherms
The determined adsorption energy profiles as a function of the NP position were used for calculation of the adsorption isotherms of NPs on the CNT surfaces. To that purpose the grand canonical Monte Carlo method was applied. The total energy change due to creation, displacement or removal of NPs was also depended on the colloid–colloid dispersion interaction energy and electrostatic interaction energy according to the Yukawa potential.
Study of the adsorption isotherms is very useful if we aim at analysis of a preferred location of NPs on the CNTs surfaces. The determined, from the molecular dynamics simulations, adsorption energy profiles do not provide definite answer to that question because they do not account for entropy changes. However, having determined the full energetic picture of the system we can easily perform GCMC simulations which provide strict relationship between the chemical potential of the NPs and occupation of various sites on the CNT surface.
The results of GCMC simulations for the silica covered metallic NPs are shown in Fig. 6. In this case the NPs are negatively charged, as mentioned in the Sect. 2. The chemical potential of the NPs can be viewed as a logarithm of the NPs concentration, at least in the low concentration limit. So, the results in Fig. 6 show the shapes of the adsorption isotherms which can be compared with experimental results.
As seen in Fig. 6 the single-walled CNTs are covered by NPs mainly on sidewalls, occupation of tips is zero at low NPs concentrations and it slowly grows with the increasing concentration of the NPs. This is due to the electrostatic repulsion because the adsorption energy on sidewalls and tips is similar provided that NPs locate on the tip center. However, due to electrostatic repulsion the positions of NPs at tips are strongly affected by the presence of other NPs at sidewalls; this leads to displacements of the NPs from the tip center and, in turn, it leads to strong reduction of the adsorption energy and facile desorption from the tips.
In the case of multi-walled CNTs we observe significant occupation of tips at very low concentrations. However, the tips are not filled first; there is simultaneous adsorption on the sidewalls and tips though the energy on the tips is greater than that on the sidewalls. This is obviously the mentioned entropy effect; the number of available adsorption sites on the sidewalls is larger than on the tips. Nevertheless, keeping a low NPs concentration may facilitate an addition reaction occurring between chemically functionalized tips and the NPs. This is important conclusion because covalently bonded NPs to the CNT tips through organic linkers create a kind of a nanocontainer. Controlling the position of NPs by using e.g. an external magnetic field was found as very promising approach for creation of safe and easy to apply in vivo drug delivery nanovehicles (Panczyk et al. 2011a, b).
4 Summary and conclusions
In this work we provided a simple method of carrying the molecular dynamics simulations of large systems composed of carbon nanotubes and colloid nanoparticles. Suitably determined Hamaker constants for interaction between colloid NPs and atoms comprising the CNT allows for creation of the implicit solvent model which correctly describes either the works of adhesion or topography of the CNT-NPs systems. By utilizing this approach we were able to determine the adsorption energy profiles of the NPs on the CNTs surfaces for the systems sizes impossible to study within the explicit solvent approach. We found that adsorption energy on the tips is higher than on the sidewalls for multi-walled CNTs; the single-walled CNTs exhibit the opposite relationship. By applying grand canonical Monte Carlo simulations we determined the adsorption isotherms of the NPs on the CNTs surfaces. We found that occupation of tips is less likely than sidewalls for the single-walled CNTs. For the multi-walled CNTs both regions of the CNTs are filled simultaneously though the adsorption energy on the tips is higher. This is due to entropy factors which promote location of the NPs on the sidewalls because of much larger geometric area associated with the sidewalls.
References
Belesi, M., Panagiotopoulos, I., Pal, S., Hariharan, S., Tsitrouli, D., Papavassiliou, G., Niarchos, D., Boukos, N., Fardis, M., Tzitzios, V.: Decoration of carbon nanotubes with CoO and Co nanoparticles. J. Nanomater. 2011, 320516 (2011)
Brenner, D.W., Shenderova, O.A., Harrison, J.A., Stuart, S.J., Ni, B., Sinnott, S.B.: A second-generation reactive empirical bond order (REBO) potential energy expression for hydrocarbons. J. Phys. Condens. Matter 14, 783–802 (2002)
Charlier, J.-C., Arnaud, L., Avilov, I.V., Delgado, M., Demoisson, F., Espinosa, E.H., Ewels, C.P., Felten, A.: Carbon nanotubes randomly decorated with gold clusters: from nano2hybrid atomic structures to gas sensing prototypes. Nanotechnology 20, 375501 (2009)
Dyke, C.A., Tour, J.M.: Overcoming the insolubility of carbon nanotubes through high degrees of sidewall functionalization. Chem. Eur. J. 10, 812–817 (2004)
Everaers, R., Ejtehadi, M.R.: Interaction potentials for soft and hard ellipsoids. Phys. Rev. E 67, 041710 (2003)
Guo, S., Pan, X., Yu, L., Bao, X.: Dispersion of metal nanoparticles on carbon nanotubes with few surface oxygen functional groups. Mater. Lett. 65, 1522–1524 (2011)
Israelachvili, J.N.: Intermolecular and surface forces, Academic Press, London (1985–2004)
Jorgensen, W.L., Maxwell, D.S., Tirado-Rives, J.: Development and testing of the OPLS all-atom force field on conformational energetics and properties of organic liquids. J. Am. Chem. Soc. 118, 11225 (1996)
Korneva, G., Ye, H., Gogotsi, Y., Halverson, D., Friedman, G., Bradley, J.-C., Kornev, K.G.: Carbon nanotubes loaded with magnetic particles. Nano Lett. 5, 879–884 (2005)
Leghrib, R., Dufour, T., Demoisson, F., Claessens, N., Reniers, F., Llobet, E.: Gas sensing properties of multiwall carbon nanotubes decorated with rhodium nanoparticles. Sens. Actuators B 160, 974–980 (2011)
Lu, A.-H., Salabas, E.L., Schuth, F.: Magnetic nanoparticles: synthesis, protection, functionalization, and application. Angew. Chem. Int. Ed. 46, 1222–1244 (2007)
Moghaddam, M.J., Taylor, S., Gao, M., Huang, S.M., Dai, L.M., McCall, M.J.: Highly efficient binding of DNA on the sidewalls and tips of carbon nanotubes using photochemistry. Nano Lett. 4, 89–93 (2004)
Panczyk, T., Camp, P.J., Pastorin, G., Warzocha, T.P.: Computational study of some aspects of chemical optimization of a functional magnetically triggered nanocontainer. J. Phys. Chem. C 115, 19074–19083 (2011)
Panczyk, T., Warzocha, T.P., Camp, P.J.: Enhancing the control of a magnetically capped molecular nanocontainer: Monte Carlo studies. J. Phys. Chem. C 115, 7928–7938 (2011)
Panczyk, T., Szabelski, P., Drach, M.: Implicit solvent model for effective molecular dynamics simulations of systems composed of colloid nanoparticles and carbon nanotubes. J. Colloid Interface Sci. 383, 55–62 (2012)
Panczyk, T., Rudzinski, W., Jagusiak, A.: Adsorption of colloid nanoparticles on carbon nanotubes studied by means of molecular dynamics simulations. Colloids Surf. A 409, 149–158 (2012)
Plimpton, S.: Fast parallel algorithms for short-range molecular dynamics. J. Comp. Phys. 117, 1–19 (1995). http://lammps.sandia.gov. Accessed 28 May 2012
Price, D.J., Brooks, C.L.: A modified TIP3P water potential for simulation with Ewald summation. J. Chem. Phys. 121, 10096 (2004)
Saha, M.S., Kundu, A.: Functionalizing carbon nanotubes for proton exchange membrane fuel cells electrode. J. Power Sources 195, 6255–6261 (2010)
Schaffel, F., Taschner, C., Rummeli, M.H., Neu, V., Wolff, U., Queitsch, U., Pohl, D., Kaltofen, R., Leonhardt, A., Rellinghaus, B., Buchner, B., Schultz, L.: Carbon nanotubes terminated with hard magnetic FePt nanomagnets. Appl. Phys. Lett. 94, 193107 (2009)
Shi, J., Votruba, A.R., Farokhzad, O.C., Langer, R.: Nanotechnology in drug delivery and tissue engineering: from discovery to applications. Nano Lett. 10, 3223–3230 (2010)
Son, S.J., Reichel, J., He, B., Schuchman, M., Lee, S.B.: Magnetic nanotubes for magnetic-field-assisted bioseparation, biointeraction, and drug delivery. J. Am. Chem. Soc. 127, 7316–7317 (2005)
Stuart, S.J., Tutein, A.B., Harrison, J.A.: A reactive potential for hydrocarbons with intermolecular interactions. J. Chem. Phys. 112, 6472–6486 (2000)
Tsoufis, T., Tomou, A., Gournis, D., Douvalis, A.P., Panagiotopoulos, I., Kooi, B., Georgakilas, V., Arfaoui, I., Bakas, T.: Novel nanohybrids derived from the attachment of FePt nanoparticles on carbon nanotubes. J. Nanosci. Nanotechnol. 8, 5942–5951 (2008)
Yang, F., Jin, C., Yang, D., Jiang, Y., Li, J., Di, Y., Hu, J., Wang, C., Ni, Q., Fu, D.: Magnetic functionalised carbon nanotubes as drug vehicles for cancer lymph node metastasis treatment. Eur. J. Cancer 47, 1873–1882 (2011)
Zhan, Y., Zhao, R., Lei, Y., Meng, F., Zhong, J., Liu, X.: Preparation, characterization and electromagnetic properties of carbon nanotubes/Fe3O4 inorganic hybrid material. Appl. Surf. Sci. 257, 4524–4528 (2011)
Acknowledgments
This work was supported by the Polish National Science Centre (NCN) Grant No. N204 205240.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
About this article
Cite this article
Panczyk, T., Rudzinski, W. Effects of surface heterogeneity of carbon nanotubes in adsorption of colloid nanoparticles studied by means of computer simulations. Adsorption 19, 611–618 (2013). https://doi.org/10.1007/s10450-013-9484-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10450-013-9484-9