Abstract
We describe a general approach for constructing a broad class of operators approximating high-dimensional curves based on geometric Hermite data. The geometric Hermite data consists of point samples and their associated tangent vectors of unit length. Extending the classical Hermite interpolation of functions, this geometric Hermite problem has become popular in recent years and has ignited a series of solutions in the 2D plane and 3D space. Here, we present a method for approximating curves, which is valid in any dimension. A basic building block of our approach is a Hermite average — a notion introduced in this paper. We provide an example of such an average and show, via an illustrative interpolating subdivision scheme, how the limits of the subdivision scheme inherit geometric properties of the average. Finally, we prove the convergence of this subdivision scheme, whose limit interpolates the geometric Hermite data and approximates the sampled curve. We conclude the paper with various numerical examples that elucidate the advantages of our approach.
Similar content being viewed by others
References
de Boor, C., Höllig, K., Sabin, M.: High accuracy geometric Hermite interpolation. Comput. Aided Geomet. Des. 4(4), 269–278 (1987)
Meek, D.S., Walton, D.J.: Geometric Hermite interpolation with Tschirnhausen cubics. J. Comput. Appl. Math. 81(2), 299–309 (1997)
Xu, L., Shi, J.: Geometric Hermite interpolation for space curves. Comput. Aided Geom Des. 18(9), 817–829 (2001)
Coburn, J., Crisco, J.J.: Interpolating three-dimensional kinematic data using Quaternion Splines and Hermite curves. J. Biomech. Eng. 127(2), 311–317 (2004)
Tremblay, Y., Shaffer, S.A., Fowler, S.L., Kuhn, C.E., McDonald, B.I., Weise, M.J., Bost, C.-A., Weimerskirch, H., Crocker, D.E., Goebel, M.E.: Interpolation of animal tracking data in a fluid environment. J. Exp. Biol. 209(1), 128–140 (2006)
Vargas, A., Hagstrom, T., Chan, J., Warburton, T.: Leapfrog time-stepping for Hermite methods. J. Sci. Comput. 80(1), 289–314 (2019)
Beudaert, X., Pechard, P.-Y., Tournier, C.: 5-axis tool path smoothing based on drive constraints. Int. J. Mach. Tools Manuf. 51(12), 958–965 (2011)
Merrien, J.-L.: A family of Hermite interpolants by bisection algorithms. Numer. Algorithm. 2(2), 187–200 (1992)
Dubuc, S., Merrien, J.-L.: Hermite subdivision schemes and taylor polynomials. Construct. Approx. 29(2), 219–245 (2009)
Dyn, N., Levin, D.: Analysis of Hermite-type subdivision schemes. Series in Approximations and Decompositions. 6, 117–124 (1995)
Han, B., Yu, T., Xue, Y.: Noninterpolatory Hermite subdivision schemes. Math. Comput. 74(251), 1345–1367 (2005)
Jeong, B., Yoon, J.: Construction of Hermite subdivision schemes reproducing polynomials. J. Math. Anal. Appl. 451(1), 565–582 (2017)
Merrien, J.-L., Sauer, T.: From Hermite to stationary subdivision schemes in one and several variables. Adv. Comput. Math. 36(4), 547–579 (2012)
Aihua, M., Jie, L., Jun, C., Guiqing, L.: A new fast normal-based interpolating subdivision scheme by cubic bézier curves. Vis. Comput. 32(9), 1085–1095 (2016)
Lipovetsky, E., Dyn, N.: A weighted binary average of point-normal pairs with application to subdivision schemes. Comput. Aided Geom. Des. 48, 36–48 (2016)
Reif, U., Weinmann, A.: Clothoid fitting and geometric Hermite subdivision. Adv. Comput. Math. 47(4), 1–22 (2021)
Chalmovianskỳ, P., Jüttler, B.: A non-linear circle-preserving subdivision scheme. Adv. Comput. Math. 27(4), 375–400 (2007)
Romani, L.: A circle-preserving C2 Hermite interpolatory subdivision scheme with tension control. Comput. Aided Geom. Des. 27(1), 36–47 (2010)
Conti, C., Romani, L., Unser, M.: Ellipse-preserving Hermite interpolation and subdivision. J. Math. Anal. Appl. 426(1), 211–227 (2015)
Costantini, P., Manni, C.: On constrained nonlinear Hermite subdivision. Constr. Approx. 28(3), 291–331 (2008)
Manni, C., Mazure, M.-L.: Shape constraints and optimal bases for C\(^{1}\) Hermite interpolatory subdivision schemes. SIAM J. Numer. Anal. 48(4), 1254–1280 (2010)
Moosmüller, C.: C\(^{1}\) analysis of Hermite subdivision schemes on manifolds. SIAM J. Numer. Anal. 54(5), 3003–3031 (2016)
Moosmüller, C.: Hermite subdivision on manifolds via parallel transport. Adv. Comput. Math. 43(5), 1059–1074 (2017)
Dyn, N., Goldman, R.: Convergence and smoothness of nonlinear Lane-Riesenfeld algorithms in the functional setting. Found. Comput. Math. 11(1), 79–94 (2011)
Dyn, N., Sharon, N.: Manifold-valued subdivision schemes based on geodesic inductive averaging. J. Comput. Appl. Math. 311, 54–67 (2017)
Schaefer, S., Vouga, E., Goldman, R.: Nonlinear subdivision through nonlinear averaging. Comput. Aided Geom. Des. 25(3), 162–180 (2008)
Lipovetsky, E.: Subdivision of point-normal pairs with application to smoothing feasible robot path. Vis. Comput. 1–14 (2021)
Kels, S., Dyn, N.: Subdivision schemes of sets and the approximation of set-valued functions in the symmetric difference metric. Found. Comput. Math. 13(5), 835–865 (2013)
Lane, J.M., Riesenfeld, R.F.: A theoretical development for the computer generation and display of piecewise polynomial surfaces. IEEE Transactions on Pattern Analysis and Machine Intelligence. 2(1), 35–46 (1980)
Floater, M.S., Surazhsky, T.: Parameterization for curve interpolation. In: Studies in Computational Mathematics. 12, pp. 39–54. Elsevier, (2006)
Itai, U., Sharon, N.: Subdivision schemes for positive definite matrices. Found. Comput. Math. 13(3), 347–369 (2013)
Dyn, N., Sharon, N.: A global approach to the refinement of manifold data. Math. Comput. 86(303), 375–395 (2017)
Dokken, T., Daehlen, M., Lyche, T., Mørken, K.: Good approximation of circles by curvature-continuous bézier curves. Comput. Aided Geom. Des. 7(1–4), 33–41 (1990)
Dyn, N., Hormann, K.: Geometric conditions for tangent continuity of interpolatory planar subdivision curves. Comput. Aided Geom. Des. 29(6), 332–347 (2012)
Yang, X.: Normal based subdivision scheme for curve design. Comput. Aided Geomet. Des. 23(3), 243–260 (2006)
Prautzsch, H., Boehm, W., Paluszny, M.: Bézier and B-spline Techniques. 6, Springer, (2002)
Lin, H., Bao, H.: Regular Bézier curve: Some geometric conditions and a necessary and sufficient condition. In: Ninth International Conference on Computer Aided Design and Computer Graphics (CAD-CG’05), p. 6 (2005). IEEE
Funding
N. Sharon is partially supported by BSF grant number 2018230. H. Ben-Zion Vardi and N. Sharon are partially supported by the NSF-BSF award 2019752.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare no competing interests.
Additional information
Communicated by: Tomas Sauer
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A. Validation of Lemma 3.4
In this section we discuss the claim in Lemma 3.4. First, by the symmetry of the Bézier average (see Definition 2.2), it is sufficient to investigate only \(\sigma \begin{pmatrix}\begin{pmatrix} p_{0} \\ v_{0} \\ \end{pmatrix},\begin{pmatrix} p_{\frac{1}{2}} \\ v_{\frac{1}{2}} \\ \end{pmatrix} \end{pmatrix}.{ Westartbyprovidinganexplicitformof}\sigma \begin{pmatrix}\begin{pmatrix} p_{0} \\ v_{0} \\ \end{pmatrix},\begin{pmatrix} p_{\frac{1}{2}} \\ v_{\frac{1}{2}} \\ \end{pmatrix} \end{pmatrix}{} { intermsofelementaryfunctionsof}\theta _0,\theta _1{ and}\theta\). Then, we present numerical indications for the correctness of the claim by evaluating appropriate functions. Finally, we outline the required steps to make the above numerical study into a formal proof.
1.1 A.1 Expressing \(\sigma\) as a function of \(\theta _0,\theta _1\) and \(\theta\)
Let
Then,
Some algebraic manipulations lead to the following expressions for \(\tilde{\theta }_{0,0}{} { and}\tilde{\theta }_{0,1}{}\):
Thus, \(\sigma \begin{pmatrix}\begin{pmatrix} p_{0} \\ v_{0} \\ \end{pmatrix},\begin{pmatrix} p_{\frac{1}{2}} \\ v_{\frac{1}{2}} \\ \end{pmatrix} \end{pmatrix}{} { isafunctionof}\theta _0,\theta _1{ and}\theta\). Recall that by its definition, see (2.5), the quantity \(\sigma \begin{pmatrix}\begin{pmatrix} p_{0} \\ v_{0} \\ \end{pmatrix},\begin{pmatrix} p_{1} \\ v_{1} \\ \end{pmatrix} \end{pmatrix}{} { isalsoafunctionof}\theta _0 { and}\theta _1\).
To prove the inequality of Lemma 3.4 we consider two auxiliary functions, the quotient and the difference:
In particular, we have to show that for all optional choices of \(\theta _0,\theta _1,\theta ,\,{ weobtainthat}Q\) of (A5) is not greater than \(0.9{ orequivalentlythat}D\) of (A6) is non-negative.
By the assumption of Lemma 3.4, \(\sqrt{\theta _0^2+\theta _1^2}\le \frac{3\pi }{4}.{ Also},\,{ since}\theta _0,\theta _1{ and}\theta { aretheangulardistancesbetweenthreevectors},\,{ wehavebythetriangleinequalitythat}|\theta _{1} - \theta _{0}|\le \theta \le \theta _{0} + \theta _{1}.{ Therefore},\,{ wedefinethesetofallrelevantvaluesof}\theta _0,\theta _1{ and}\theta\) to be
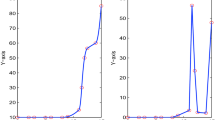
As a first illustration, we present a 4D visualization of \(Q{ and}D{ over}\Omega\) in Fig. 9. The values of the functions appear in color and indicate that indeed \(Q{ islessthan}0.9{ and}D\) is non-negative when considering the domain \(\Omega\).
1.2 A.2 Ensuring non-negativity of the difference function
Here, we provide a more comprehensive numerical method for ensuring the non-negativity of \(D(\theta _0,\theta _1,\theta ){ over}\Omega .{ Thebasicideaistocompute}D{ overagridofpointscovering}\Omega\), which is dense enough to guarantee non-negativity at all the points of \(\Omega ,\,{ if}D\) is non-negative at the points of the grid.
In more detail, since the function \(D(\theta _0,\theta _1,\theta ){ vanishesattheorigin},\,{ wefirstdetermineaneighborhoodoftheoriginwheretheminimumof}D{ iszero}.{ Thenwesamplethefunction}D{ ontherestof}\Omega { usingstepswithalengthbasedonaboundoftheanalyticformofthegradient},\,{ derivedfromtheexplicitformof}D.{ Takingintoaccountalsothefiniteprecisionofthemachineweuse},\,{ suchaprocedureprovesthat}D{ ispositiveover}\Omega\).
We recall two basic results of classical analysis. The first result is concerned with possible locations of points where a minimum value of a function is achieved.
Result
The minimum of \(f{ in}\Omega { isobtainedontheboundariesof}\Omega (\partial \Omega ),\,{ orinthesetofcriticalpointsof}f{ intheinteriorof}\Omega ,\,{ i}.{ e}.,\,\{ x\in \Omega \setminus \partial \Omega : \nabla f(x)=0 \}{}\).
The second result implies how to sample \(\Omega\) outside the neighborhood of the origin.
Result
Assume a gradient bound \(\Vert {\nabla f} \Vert _\infty \le M{ over}\Omega { andalocalfunctionbound}\min _B(f)=m,\,B \subseteq \Omega .{ Then},\,{ if}d(x,B )\le d^*{ forany}x\in \Omega\), we have
In particular, if \(d^*=\frac{m-\varepsilon }{M}{} { then}f(x)\ge \varepsilon { forany}x\in B\).
The strategy of our proof consists of the following three main stages:
-
1.
Split \(\Omega { intotwodomains},\,\Omega = \Omega _1\bigcup \Omega _2.{ Inparticular},\,{ findaradius}r>0{ ofanopenballcenteredintheorigin}B_r(0){ suchthatin}\Omega _1=B_r(0)\bigcap \Omega { theminimumof}D\) is at the origin.
-
2.
Find M such that \(\Vert {\nabla D}\Vert _\infty \le M{ in}\Omega ({ enoughin}\Omega _2\)).
-
3.
Construct a grid \(G{ over}\Omega _2 = \Omega \setminus \Omega _1\) such that
$$\begin{aligned} d(x,G) \le \frac{f(g^{*}) - \varepsilon }{M}, \quad g^*= \arg \min _{g \in G} d(x,g), \quad x \in \Omega _2. \end{aligned}$$Here \(\varepsilon { isaboundontheroundofferror},\,{ relatedtothemachinedoubleprecision}(2^{-52}\approx 2.2\times 10^{-16}{}\)).
The last step above guarantees, in view of Result 1, the non-negativity of \(D{ over}\Omega _2.{ Asto}\Omega _1\), we show that the gradient is non-vanishing and deduce by Result 1 that the non-negativity of \(D{ dependsonthevaluesof}D{ ontheboundariesof}\Omega _1\), which take the form
Here \(P_i, i=1,2,3{ arethreeplanesin}\mathbb {R}^3{ and}C=\partial B_r(0).{ Thenextlemmapresentsvaluesof}r{ and}M\) allowing for the application of our strategy of proof.
Lemma 5.1
i If \(x\in B_{0.1}(0){ and}x\ne 0{ then}\nabla D(x)\ne 0\). ii \(\Vert {\nabla D}\Vert _\infty \le 6.3\times 10^4\).
The proof of Lemma 5.1 is highly technical, and so we omit it. Nevertheless, it is important to note that the values \(r=0.1{ and}M= 6.3\times 10^4{ arenotoptimal}.{ Specifically},\,{ numericaltestsimplythattheactualbound}M{ ismuchlower},\,{ andweconjecturethat}M{ canbedecreaseddownto}10.{ Thisissueisfundamentalashigher}M{ meansamuchdensergrid}G\) in step 3 above.
To illustrate the last point above, we ran a test with \(M=10,\,{ whichyieldedanexhaustivesearchwithinlessthan}0.1{ ofasecond}.{ Inthiscase},\,{ thegrid}G{ consistedof}3,747,179{ pointsscatteredover}\Omega _2\), and the exhaustive search ended up with success; that is, non-negativity was validated. To compare, the same test for \(M=100{ took}68{ secondsandrequiredasearchover}3,469,028,128\) points. The tests were executed on a standard desktop (Windows-based, runs on Intel i7-9700 CPU with 32G of RAM), and the Matlab script is available at https://github.com/nirsharon/Hermite_Interpolation. We extended the above test scenario up to \(M=1000\) on a designated server. Like the preceding ones, this test also yields a success, meaning the non-negativity was retained. However, we have not reached with our tests the value of \(M\), as computed analytically in Lemma 5.1. Nevertheless, the current test reassures with high confidence that the non-negativity, in this case, is indeed obtained.
Appendix B. Proofs of the Bézier average properties
Proof of Lemma 2.7
One can verify that
Assume by contradiction that \(\frac{d}{dt}b\left( \frac{1}{2}\right) =0\), and observe that in view of (2.10), \(\left\| p_{1} - p_{0} - \frac{1}{2}\alpha \left( v_{0} + v_{1}\right) \right\| ^{2}{}\) is equal to
Since \(p_1\ne p_0{ weget} 1 +\frac{1 + \cos \left( \theta \right) }{18\cos ^{4}\left( \frac{\theta _{0} + \theta _{1}}{4}\right) } -\frac{\cos \left( \theta _{0}\right) + \cos \left( \theta _{1}\right) }{3\cos ^{2}\left( \frac{\theta _{0} + \theta _{1}}{4}\right) } = 0\). Thus,
However,
The last inequality holds, since by (2.4) we have \(|{\theta _{0}-\theta _{1}}|\in |[0,\pi ]|\), and therefore \(|{2\cos \left( \frac{\theta _0-\theta _{1}}{2}\right) -\frac{3}{2} }\le \frac{3}{2},\,{ withequalityonlywhen}|{\theta _0-\theta _{1} }|=\pi .{ Howeverinthiscase}|{\cos \left( \frac{\theta _0+\theta _1}{2}\right) }|=0.{ Thelastdisplayedinequalitycontradictsourassumptionthat}\frac{d}{dt}b\left( \frac{1}{2}\right) =0,\,{ andtherefore},\,{ weobtainthat} v_{\frac{1}{2}}\ne 0. \square\)
Proof of Proposition 2.8
By the definition of \(X\), it remains to show that properties (1)–(3) in Definition 2.2 hold for the Bézier average. For identity on the limit diagonal, observe that from (2.18) (which is proved next independently) we get:
For symmetry, note that each couple of Hermite data \(\left( \begin{pmatrix} p_{0} \\ v_{0} \\ \end{pmatrix},\begin{pmatrix} p_{1} \\ v_{1} \\ \end{pmatrix}\right) { and}\left( \begin{pmatrix} p_{1} \\ - v_{1} \\ \end{pmatrix},\begin{pmatrix} p_{0} \\ - v_{0} \\ \end{pmatrix}\right)\) defines the same control points in reverse order and therefore defines the same Bézier curve corresponding to a reversed parametrization. End points interpolation is easily verified by (2.11) and (2.12). \(\square\)
Proof of Lemma 2.9
Equation (2.17) is easy to verify by Definition 2.5 and specifically by looking at (2.10), (2.11) and (2.12).
To observe that (2.16) holds, we exploit the fact that Bézier curves are invariant under affine transformations. Let \(\Phi { beanisometryover}\mathbb {R}^{n}.{ Inparticular},\,\Phi { isanaffinetransformation}.{ Itisthereforesufficienttoshowthatthecontrolpointsassociatedwith}B_\omega \left( \tilde{\Phi }\begin{pmatrix} p_0\\ v_0\\ \end{pmatrix},\tilde{\Phi }\begin{pmatrix} p_1\\ v_1\\ \end{pmatrix}\right) { aregivenbyapplying}\Phi\) to
The control points associated with \(B_\omega\) are:
where \(\tilde{\alpha }=\alpha \left( \Phi (p_0),\Phi (p_1),\Phi (v_0)-\Phi (0),\Phi (v_1)-\Phi (0)\right)\).
It is clear that the first and last control points are obtained by applying \(\Phi\) to the original points. As for the second and third control points, since \(\Phi\) is an isometry, \(\tilde{\alpha }=\alpha\) and since \(\Phi\) is an affine transformation it is of the form \(\Phi (x)=Rx+t\) with R an orthogonal matrix, and \(t\in \mathbb {R}^{n}\). Therefore, \(t=\Phi (0)\) and
This completes the proof of (2.16). \(\square\)
Proof of Lemma 2.10
Let \(p_0,p_1 \in \mathbb {R}^{n}\) s.t. \(p_0\ne p_1\), and let \(v_{0}=v_1=u\). Then, we have that \(\alpha \left( p_0,p_1, u,u\right) =\frac{1}{3}\Vert p_{1} - p_{0}\Vert\). By Definition 2.5
and by simple calculations based on (2.11) and on (2.12), we arrive at the claim of the lemma.
Proof of Lemma 2.11
By lemma 2.9, it is sufficient to show that for data sampled from the unit circle in \(\mathbb {R}^{2}\), the Bézier average with \(\omega =\frac{1}{2}\) the midpoint of the circular arc determined by the data, and its ntangent.
Assume \(\left( \begin{pmatrix} p_0\\ v_0\\ \end{pmatrix}\begin{pmatrix} p_1\\ v_1\\ \end{pmatrix}\right) \in \mathbb {R}^{2}\times S^{1}\) are sampled from a unit circle. We further assume w.l.o.g that \(p_0=\begin{pmatrix}1\\ 0\\ \end{pmatrix}, v_0=\begin{pmatrix}0\\ 1\\ \end{pmatrix}\) and denote \(p_1=\begin{pmatrix}\cos (\varphi )\\ \sin (\varphi )\end{pmatrix}, v_1=\begin{pmatrix}-\sin (\varphi )\\ \cos (\varphi )\end{pmatrix}\) where \(0<\varphi <2\pi\). Basic geometrical reasoning shows that \(\theta _0=\theta _1=\frac{\varphi }{2}\), and that if \(p_1\) lies on the upper semicircle, namely if \(\varphi \le \pi\), then \(\varphi =\theta\), while otherwise, \(\varphi =2\pi -\theta\). Using known trigonometric identities we obtain,
which is the parameter used in [33]. Therefore, by Theorem 1 in [33], the point of the Bézier average with weight \(\frac{1}{2}\) of \(\begin{pmatrix}p_0\\ v_0\\ \end{pmatrix}\) and \(\begin{pmatrix}p_1\\ v_1\\ \end{pmatrix}\) is the midpoint of the circular arc defined by the two points and their ntangents.
To verify that the average tangent is tangent to the unit circle at \(p_{\frac{1}{2}}\), note that the tangent to the unit circle at \(p_{\frac{1}{2}}\) is in the direction of \(p_1-p_0\). Observe as well that \(v_0+v_1\) linearly depends on \(p_1-p_0\). In fact, it implies that:
and that \(\Vert {v_0+v_1}\Vert =\sqrt{2+2\cos (\theta )}=2\cos \left( \frac{\theta }{2}\right)\). See Fig. 10 for a graphical demonstration.
The sum of two directed tangent vectors to the unit circle linearly depends on the vector of difference between the two points of tangency. The yellow vector is the other tangent moved to form the sum of the two tangents which appears in red. The three sub-figures demonstrate the three possibilities mentioned in (B2)
The above means that
Considering the numerator of \(v_{\frac{1}{2}}\) given by (2.15), and applying (B1) and (B3), we get
Since both \(\left( \frac{1}{3}+\frac{1}{3\cos ^{2}\left( \frac{\theta }{4}\right) }\right) ,\left( 1+\frac{\sqrt{2+2\cos (\theta )}}{6\sin ^{2}\left( \frac{\theta }{4}\right) }\right) >0\), we get that \(v_{\frac{1}{2}}\) is in the direction of \(p_1-p_0\) and thus is the tangent to the circle at \(p_{\frac{1}{2}}\). \(\square\)
Proof of Lemma 3.1
We prove that \(\left( \begin{pmatrix} p_0\\ v_0\\ \end{pmatrix},\begin{pmatrix} p_{\frac{1}{2}}\\ v_{\frac{1}{2}} \end{pmatrix}\right)\) and \(\left( \begin{pmatrix} p_{\frac{1}{2}}\\ v_{\frac{1}{2}}\\ \end{pmatrix},\begin{pmatrix} p_1\\ v_1\\ \end{pmatrix}\right)\) satisfy conditions (2.8), namely,
i \(p_{\frac{1}{2}}\ne p_j, \quad j=0,1\). ii Let \(u_0=u\left( \begin{pmatrix} p_0\\ v_0\\ \end{pmatrix},\begin{pmatrix} p_{\frac{1}{2}}\\ v_{\frac{1}{2}}\\ \end{pmatrix}\right)\) and \(u_1=u\left( \begin{pmatrix} p_{\frac{1}{2}}\\ v_{\frac{1}{2}}\\ \end{pmatrix},\begin{pmatrix} p_1\\ v_1\\ \end{pmatrix}\right)\). Then \(v_j=v_\frac{1}{2}=u_j\) or \(v_j,v_\frac{1}{2},u_j\) are not pair-wise linearly dependent for \(j=0,1\).
First we prove (i). By algebraic manipulations we obtain that \(\Vert {p_\frac{1}{2}-p_{0}}\Vert\) is equal to
Then, we argue that
and hence \(\Vert {p_\frac{1}{2}-p_{0}}\Vert >0\). In other words, \(p_\frac{1}{2}\ne p_0\).
To show that (A4) holds, we observe that
Let
Then, \(0\le t < \frac{\pi }{2}\), and \(-\frac{\pi }{2}< s < \frac{\pi }{2}\). We define,
and obtain
To derive the critical points of h, we observe that \(\frac{\partial h}{\partial t}=0\) iff \(\sin (s)=\frac{\sin (2t)}{3\sin ^2(t)-\cos ^2(t)}\) and similarly \(\frac{\partial h}{\partial s} = 0\) iff \(\sin (s)=2\cos ^2(t)\sin (2t)\). In other words,
However, the only solution of the latter system of equations over \(\left[ 0,\frac{\pi }{2}\right) \times \left( -\frac{\pi }{2},\frac{\pi }{2}\right)\) is (0, 0). Thus, we conclude that the minimum value of h is obtained on the boundary of \(\left[ 0,\frac{\pi }{2}\right) \times \left( -\frac{\pi }{2},\frac{\pi }{2}\right)\) or in (0, 0), which is also on the boundary (see Result 1). We further explore all candidates of extremal points on the boundary of \(\left[ 0,\frac{\pi }{2}\right) \times \left( -\frac{\pi }{2},\frac{\pi }{2}\right)\).
We consider the restriction of h to the boundaries, which are functions of one variable, and get that
Now, \(h_{t,r}(t)=0\) iff \(t=\frac{\pi }{4}\),namely at the point \((\frac{\pi }{4},\frac{\pi }{2})\), while \(h_{s,r}(s)=0\) iff \(s=0\), namely at the point \((\frac{\pi }{2},0)\). Thus the above two equalities to 0 are not satisfied simultaneously. Finally, by the continuity of h and since \(h(t\pm \epsilon _0,s\pm \epsilon _1)\ne h(t,s)\) for small enough \(\epsilon _0\) and \(\epsilon _1\), we get that \(h(t,s)>0\) for any \((t,s)\in \left[ 0,\frac{\pi }{2}\right) \times \left( -\frac{\pi }{2},\frac{\pi }{2}\right)\) and conclude that \(p_{\frac{1}{2}}\ne p_0\). By symmetric reasoning we can show that also \(p_\frac{1}{2}\ne p_1\).
For the second claim, assume \(v_j,v_\frac{1}{2},u_j\) are pair-wise linearly dependent. That is, \(v_j=\pm u_j\) and \(v_\frac{1}{2}=\pm u_j\) for some \(j\in \{0,1\}\). For simplicity we assume \(j=0\). We follow De Casteljau’s algorithm for obtaining \(p_\frac{1}{2}\) and \(v_\frac{1}{2}\). As in (2.9), consider the initial control points of the associated Bézier curve and denote:
The following points are obtained by De Casteljau’s algorithm:
Then, \(p_\frac{1}{2}=q_0^3\) and \(v_\frac{1}{2}=\frac{q_1^2-q_0^2}{\Vert {q_1^2-q_0^2}\Vert }\). For further information about De Casteljau’s algorithm, we refer the reader to [36]. Since \(v_0=\pm u_0\), the points \(q_0^0,q_1^0\) and \(q_0^3\) lie on the same line. We denote this line by l. Since \(v_{\frac{1}{2}}=\pm u_0\), we have that \(q_0^2\) and \(q_1^2\) also lie on l. \(q_0^1\) is the average of \(q_0^0,q_1^0\) and hence it also lies on l. Now, since \(q_0^2,q_0^1\) and \(q_1^1\) lie on the same line, it follows that \(q_1^1\) is on l. Similarly, \(q_2^0\) is on l. Now \(q_2^1\) is on l since it lies on the line passing through \(q_1^2\) and \(q_1^1\) and finally we get that \(q_3^0\) is on l. Thus \(v_0,v_1,u\) are pair-wise linearly dependent and hence, by our assumption, \(v_0=v_1=u\). It is shown in Lemma 2.10 that in this case \(v_0=v_\frac{1}{2}=u_0\) as required. \(\square\)
Proof of Lemma 3.3
For the first part,
Since \(\theta _{0} + \theta _{1}\le \pi\) we have that \(\cos ^{2}\left( \frac{\theta _{0} + \theta _{1}}{4}\right) \ge \frac{1}{2}\) and \(d\left( p_{\frac{1}{2}},p_{0}\right) \le d\left( p_{0},p_{1}\right)\). In the same way we obtain \(d\left( p_{\frac{1}{2}},p_{1}\right) \le d\left( p_{0},p_{1}\right)\). For the second claim of the lemma, simply set \(\mu = \frac{1}{2} +\frac{1}{4\cos ^{2}\left( \frac{\gamma }{4}\right) }\) for any \(\gamma\) satisfying \(\theta _{0} + \theta _{1}\le \gamma <\pi\). \(\square\)
Appendix C. The set X of the Bézier Average
The set \(X\subset \left( \mathbb {R}^n\times S^{n-1}\right) ^2\) consists of all pairs where the Bézier average is a Hermite average by Definition 2.2 Namely, for any pair in X, the Bézier average fulfills the conditions (2.8) and produces averaged vectors in \(S^{n-1}\) for any weight in [0, 1]. This section further investigates the properties of elements in X to receive some perception of the size and significance of X.
Let \(x = \left( \begin{pmatrix} p_0\\ v_0\\ \end{pmatrix},\begin{pmatrix} p_1\\ v_1\\ \end{pmatrix}\right) \in \left( \mathbb {R}^n\times S^{n-1}\right) ^2\) be a pair that meets the conditions (2.8). Then, following the notation of Section 2, \(x\in X\) iff b(t) of (2.11) is regular over [0, 1]. Nevertheless, recall that the regularity of b(t) depends on the parameters \(\theta _0,\theta _1\) and \(\theta\) of x. In particular, to obtain regularity, the linear independence of \(v_0,v_1,u\) is sufficient; therefore, if \(p_0,p_0+v_0,p_1,p_1+v_1\) do not lie on the same plane, then we conclude that \(x\in X\). Thus, it remains to characterize the case where \(p_0,p_0+v_0,p_1,p_1+v_1\) are in a two-dimensional space.
Consider the vectors of difference between each two consecutive control points,
By Theorem 2 in [37], if the angles between each pair of those vectors are acute, then b(t) is regular. That is, if
Then, \(x\in X\). The inner products in (C1) are
Namely, if \(\theta <\frac{\pi }{2}\) and \(3\cos ^2\left( \frac{\theta _0+\theta _1}{4}\right) \cos (\theta _j)-1-\cos (\theta )>0\) for any \(j=0,1\), then \(x\in X\).
In the plane we have the following relationship between \(\theta _0,\theta _1\) and \(\theta\):
In Fig. 11 we plot the domains of positivity of (C2) for \(\theta =\theta _0+\theta _1\) and for \(\theta =|{\theta _{0}-\theta _{1}}|\). Note that the first case is equivalent in sense of the positivity of (C2) to the case where \(\theta =2\pi -\left( \theta _0+\theta _1\right)\) and therefore the latter is omitted. We consider the intersection of the domains in question, for both \(j=0,1\), together with \(\theta <\frac{\pi }{2}\). We conclude that even in the case where the control points \(p_0,p_0+v_0,p_1,p_1+v_1\) lie on a plane (a rare event in high dimensions) the domain where \(x\in X\) is not minor.
Intersections as sufficient conditions for a pair to be in X when control points lie on a plane. The graphs show the two fundamental cases of relations between the parameters. In each graph, we see the possible domain of the parameters \(\theta _0\) (horizontal axis) and \(\theta _1\) (vertical axis), where the blue and red subdomains indicate \(\langle v_j,p_1-p_0-\alpha (v_0+v_1)\rangle >0\) for \(j=0\) and \(j=1\), respectively. The black domain is when \(\theta <\frac{\pi }{2}\). The intersections are when all conditions are met
The conditions on \(\theta _0,\theta _1\) defined by the intersections, as presented in Fig. 11, are sufficient to determine that \(x\in X\). Nevertheless, these conditions are not necessary. To complete the picture, we briefly show a necessary conditions for a pair x to be in \(\left( \mathbb {R}^n\times S^{n-1}\right) ^2\setminus X\).
Recall that we consider only the case when the control points are planer. Therefore, we assume, w.l.o.g, that \(p_0=\begin{pmatrix} 0\\ 0\\ \end{pmatrix}, p_1=\begin{pmatrix} 1\\ 0\\ \end{pmatrix}, v_0=\begin{pmatrix} \cos {x}\\ \sin {x}\\ \end{pmatrix}, v_1=\begin{pmatrix} \cos {y}\\ \sin {y}\\ \end{pmatrix}\) for some arbitrary \(x,y \in \left[ -\pi ,\pi \right]\). In this case, \(\theta _0=|{x}|\) and \(\theta _{1}=|{y}|\). Assigning the above to (2.12) yields:
Therefore, \(\frac{d}{dt}b\left( t\right) =0\) iff
The equations in (C4) are quadratic in t but transcendental in x,y and their absolute value sum and so we conclude that \(x \notin X\) iff the system (C4) has a solution in \(t \in [0,1]\).
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Hofit, BZ.V., Nira, D. & Nir, S. Geometric Hermite interpolation in \(\mathbb {R}^{n}\) by refinements. Adv Comput Math 49, 38 (2023). https://doi.org/10.1007/s10444-023-10037-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10444-023-10037-z