Free and Forced Vibration Analysis of Carbon/Glass Hybrid Composite Laminated Plates Under Arbitrary Boundary Conditions

Abstract

This paper presents the theoretical investigations on the free and forced vibration behaviours of carbon/glass hybrid composite laminated plates with arbitrary boundary conditions. The unknown allowable displacement functions of the physical middle surface are expressed in terms of standard cosine Fourier series and sinusoidal auxiliary functions to ensure the continuity of the displacement functions and their derivatives at the structural boundaries. Arbitrary boundary conditions are achieved through the introduction of an artificial spring technique. The first shear deformation theory and Lagrange equations are utilized to derive the energy expression, and the eigenvalue equations associated with free and forced vibration are obtained by Rayleigh-Ritz variational operations. Subsequently, these equations are then solved to determine the natural frequency, mode of vibration, and the steady-state displacement response under forced excitation. The new results are compared with those from references and finite element methods to verify the convergence, accuracy and efficiency of the analytical method. The effects of hybrid ratios, stacking sequences, lamination schemes, fibre orientation, boundary conditions and excitation force on the free and forced vibration behaviours of the carbon/glass hybrid composite laminated plates are analyzed in detail.

1 Introduction

Advanced fibre-reinforced composite materials are widely employed in large structures in aerospace, wind power, and marine fields (see Fig. 1a) due to their excellent properties such as high strength-to-weight and stiffness-to-weight ratios, good corrosion and fatigue resistance [1, 2]. In contrast to the aerospace industry, the marine industry currently prefers the use of glass fibre-reinforced plastics (GFRP) over carbon fibre-reinforced plastics (CFRP) due to high manufacturing costs, and these composite materials have been utilized in the construction of both complete ship hulls [3, 4] and constituent parts [5,6,7,8,9,10,11]. However, as the dimensions of marine structures (such as ships and offshore wind turbines) have been steadily increasing over time (see Fig. 1b), conventional pure glass fibre-reinforced composites lead to the problem of insufficient stiffness and large deformation [12]. For instance, as the size of the GFRP hull girder increases, it becomes more susceptible to deformation under wave loads, which can significantly impact both hydrodynamic performance and structural safety, as depicted in Fig. 2. Although CFRP can effectively improve the structural stiffness of large composite vessels, the high price of CFRP limit its large dimensional application in these marine structures. As a compromise solution (see Fig. 2), carbon/glass hybrid composite laminated plates (as structural units used in hull construction) can make up for the shortcomings of different fibres and achieve improved performance of large composite vessels, such as balanced deformation (stiffness) and reduced cost [13,14,15,16,17]. In addition, hybrid composite materials offer further advantages for composite ship-hull structures under extreme conditions, such as sagging, hogging, and slamming. For instance, in cases involving the delamination propagation of laminates under compressive loads, the presence of rough fracture surfaces between hybrid composite materials can enhance the resistance to damage propagation [18]. Moreover, the hybrid effects significantly enhance the ultimate strength of bonded and bolted FRP-steel joints [19, 20], as well as the critical buckling load of laminated panels and stiffened plates [21, 22]. Through well-designed approaches, hybrid composite materials can maximize the utilization of positive hybrid effects to enhance the fundamental vibration frequency of laminated plates [23]. Therefore, hybrid composite reinforcement holds great importance in ship engineering. It is important to study the natural frequencies (free vibration) and vibration suppression characteristics (forced vibration) of the marine carbon/glass hybrid laminate under the excitation sources of waves, propellers, the main engine of the ship, among others.

Fig. 1

Large composite structures drawn to scale [24]

Fig. 2

Prospects for hybrid FRP composites in a hull girder with large dimensions

In recent years, many researchers have investigated the flexural [25,26,27], tensile [28,29,30], shear [31], and impact [32,33,34,35,36] characteristics of hybrid composite structures. In addition, the dynamic responses of hybrid composite structures have also received increasing attention [37, 38]. For example, as shown in Fig. 2, composite hulls are exposed to various types of vibrations and shocks and they require high vibration resistance and avoid structural resonance to prevent structural safety and reliability in such environments. Therefore, it is necessary to study the free-forced vibration characteristics of carbon glass hybrid plates.

In recent years, a large number of models for predicting dynamic responses of hybrid composite structures have been proposed. Roy et al. [39] proposed a modified higher-order zigzag theory for the free vibration response behaviour of laminated composite hybrid and GFRP shells. Li et al. [23] investigated the free vibration characteristics of carbon/glass hybrid composite plates through first-order and higher-order deformation theories. The free vibration characteristics of the laminated Glass-Carbon-Kevlar hybrid composite curved panels have been studied based on the experimental and finite element methods by Sahu et al. [40]. Song [41] analyzed the dynamic characteristics of three-dimensional hybrid composite beams based on numerical methods.

The influences of stacking sequences on the vibration responses of hybrid composites have also been investigated by Kumar et al. [42]. The effects of hybrid layups and hybrid ratios on the damping properties of hybrid composites were investigated by Nega et al. [43]. Bulut et al. [44] researched the effect of fibre hybridization on the dynamic characteristics of the Kevlar/glass/epoxy resin composite laminates experimentally and numerically. Barai and Durvasula [45] investigated the dynamic and buckling responses of the hybrid laminated composite curved panels on simply supported boundary conditions based on first-order shear deformation theory and Reissner’s shallow shell theory. Bhudolia et al. [46] studied the effect of vibration-damping characteristics of the electrically nonconductive composites experimentally and numerically. Tiwari et al. [47] presented a modified higher-order shear deformation theory and an experimental method to analyze the free vibration responses of hybrid composite panels.

The vibration and damping characteristics study of hybrid composite laminates were determined experimentally by Bulut et al. [48]. Assarar et al. [49] utilized experimental and numerical methods to analyze the damping properties of hybrid composite beams. Lee and Kim [50] reported a theoretical model for the nonlinear vibration of laminated hybrid composite plates based on the Lagrangian equation. Pingulkara et al. [51] analyzed the vibration, tensile, flexural, and shear characteristics of interlaminar hybrid composite laminates using experimental, numerical and analytical methods. The vibration and damping responses of hybrid composite reinforced fabrics were investigated experimentally by Bulut et al. [52]. Using the variational energy method, Chen et al. [53] developed an analytical method for studying the effect of temperature and moisture on the vibration and stability of the hybrid composite plates. Ebrahimi and Dabbagh [54] developed a refined trigonometric shear deformation theory to estimate the thermo-mechanical vibration behaviour of the multi-scale hybrid composite beams.

Zhu et al. [55] predicted the dynamic characteristics of hybrid composites based on experimental methods. A higher-order beam theory was employed by Prasad et al. [56] to evaluate the free vibration and bending responses of hybrid composite beams and the analytical results were compared with experimental, finite element and literature ones. A thermo-hygro-elastic finite element model based on the first-order shear deformation theory was developed by Kallannavar et al. [57] for the free vibration responses of hybrid laminates and sandwich plates.

A review of the literature shows that the existing researches on hybrid composite structures are limited to free, clamped or simply supported boundary conditions. However, complex boundary conditions exist in a wide range of practical engineering applications, and the modification of the solution process for complex boundary conditions leads to a reduction in computation efficiency [58]. To solve this problem, there are several publications concerning the vibration of plates and shells with general elastic boundaries with the help of artificial spring technology [59,60,61,62,63].

Shao et al. [64] proposed a refined higher-order shear deformation theory to investigate the vibration behaviours of composite laminated beams under general boundary conditions. Li et al. [65] analyzed the vibration of truncated conical shells based on the first-order shear deformation theory and differential quadrature method. Rostami and Salami [66] investigated the large amplitude free vibration responses of the sandwich beams using a higher-order sandwich panel theory. Sun et al. [67] obtained the vibration characteristics of rotating cylindrical shells by using the Rayleigh–Ritz method. Based on the first-order shear deformation theory and the spectral-Tchebychev technique, Guo et al. [68] employed the artificial spring technique to predict the free vibration behaviour of laminated stepped and stiffened cylindrical shells under arbitrary boundary conditions. Li et al. [69] presented a dynamic model for predicting the large amplitude vibration of the thin-wall rotating laminated shells under arbitrary boundary conditions. Li et al. [70] studied the free vibration of conical-conical shells under elastic boundary conditions. Jin et al. [71] proposed a unified method for the vibration analysis of moderately thick laminated cylindrical shells based on the first-order shear deformation theory.

According to the above-mentioned references, the existing works have focused on the free-vibration behaviours of hybrid composite structures with classical boundary conditions. Due to the hull deformation under working conditions, the structural boundaries of local laminates are no longer the conventional classical boundary conditions. To the best knowledge of the authors, however, few works have been reported on the analytical modelling and dynamic analysis of the hybrid laminated plates with arbitrary boundary conditions. Therefore, in the framework of the first-order shear deformation theory, the improved Fourier series method in conjugation with the Rayleigh–Ritz method is employed for the analytical formulation. The applied method is systematically verified by comparing the obtained results with reference data and finite element ones. The parametric studies are carried out in detail and new results of the free and forced vibration characteristics of hybrid laminated plates are also given in this work.

Abbreviations
C, S, E, F	Clamped, Simply support, Elastic, Free boundary conditions
x, y, z	Coordinates axes
a, b, h	Length, width and thickness of the plate, (m)
H, L	High and low modulus fibre-reinforced polymer lamina
Ku, Kv, Kw, Kx, Ky	Spring stiffness coefficients
E1H, E2H, E1L, E2L	Elastic modules of high and low modulus fibre in the 1-direction and 2-direction, (GPa)
µ12	Poisson’s ratio
G12, G13, G23	In-plane and out-plane shear modules, (GPa)
ρ	Density, (kg/m3)
w	Natural frequency (rad/s)
ξ	Hybrid ratio
M, N	Truncation numbers
θ	Fiber angles
X	Transformed displacement response (dB)

2 Theoretical Formulations

In this section, the governing differential equations and solution methods for interlayer hybrid composite laminated plates with arbitrary boundary conditions based on the first-order shear deformation theory, the improved Fourier series method and the Rayleigh-Ritz method are presented. This is followed by the convergence study and the accuracy verification of the applied method. Finally, the parametric studies of the free and forced vibration characteristics of the hybrid composite laminated plates are given in detail.

2.1 Mathematical Model of Interlayer Hybrid Composite Laminated Plates

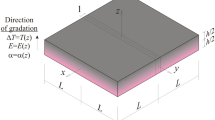
The geometry parameters and the coordinate system of carbon/glass hybrid composite laminated plates are given, as shown in Fig. 3. The hybrid laminated plate with length a, width b and constant thickness h is located in the rectangular Cartesian coordinate system (x-y-z). The mid-plane of the hybrid laminated plate is considered the reference plane.

Fig. 3

A theoretical model of a hybrid laminated plate under arbitrary boundary conditions

For the hybrid laminated plate in Fig. 3, the displacement components u, v and w can be written based on the first-order shear deformation theory as the following formula:

$$\left\{ {\begin{array}{*{20}{c}} {u(x,y,z,t)} \\ {v(x,y,z,t)} \\ {w(x,y,z,t)} \end{array}} \right\}=\left[ {\begin{array}{*{20}{c}} 1&0&0&z&0 \\ 0&1&0&0&z \\ 0&0&1&0&0 \end{array}} \right]\left\{ {\begin{array}{*{20}{c}} {{u_0}(x,y,t)} \\ {{v_0}(x,y,t)} \\ {{w_0}(x,y,t)} \\ {{\varphi _x}(x,y,t)} \\ {{\varphi _y}(x,y,t)} \end{array}} \right\}$$

(1)

where u₀, v₀ are the in-plane displacement of the middle surface of the plate, w₀ is the transverse displacement, and φ_x, φ_y designate the transverse normal about the y and x directions, respectively. Moreover, t is the time variable. The strain relations in accordance with displacements are expressed as follows:

$$\begin{array}{l}\varepsilon_x=\varepsilon_x^0+z\varepsilon_x^b,\;\varepsilon_y=\varepsilon_y^0+z\varepsilon_y^b\\\gamma_{xy}=\gamma_{xy}^0+z\gamma_{xy}^b,\;\gamma_{xz}=\gamma_{xz}^0,\;\gamma_{yz}=\gamma_{yz}^0\end{array}$$

(2)

where

$$\begin{array}{l}\varepsilon_x^0=u_{0,x},\;\varepsilon_x^b=\varphi_{x,x},\;\gamma_{xy}^0=v_{0,x}+u_{0,y}\\\varepsilon_y^0=v_{0,y},\;\varepsilon_y^b=\varphi_{y,y},\;\gamma_{xy}^b=\varphi_{y,x}+\varphi_{x,y}\\\gamma_{xz}^0=w_{0,x}+\varphi_x,\gamma_{yz}^0=w_{0,y}+\varphi_y\end{array}\\$$

(3)

Herein, ‘“x” and “y” represent partial derivatives with respect to x and y, respectively. The stress-strain relations in the arbitrary point of the hybrid laminated plate are given based on Hooke’s law:

$$\left\{ {\begin{array}{*{20}{c}} {{\sigma _x}} \\ {{\sigma _y}} \\ {{\sigma _{xy}}} \end{array}} \right\}=\left[ {\begin{array}{*{20}{c}} {\bar {Q}_{{11}}^{k}}&{\bar {Q}_{{12}}^{k}}&{\bar {Q}_{{16}}^{k}} \\ {\bar {Q}_{{12}}^{k}}&{\bar {Q}_{{22}}^{k}}&{\bar {Q}_{{26}}^{k}} \\ {\bar {Q}_{{16}}^{k}}&{\bar {Q}_{{26}}^{k}}&{\bar {Q}_{{66}}^{k}} \end{array}} \right]\left\{ {\begin{array}{*{20}{c}} {{\varepsilon _x}} \\ {{\varepsilon _y}} \\ {{\gamma _{xy}}} \end{array}} \right\},\left\{ {\begin{array}{*{20}{c}} {{\sigma _{xz}}} \\ {{\sigma _{yz}}} \end{array}} \right\}=\left[ {\begin{array}{*{20}{c}} {\bar {Q}_{{55}}^{k}}&{\bar {Q}_{{45}}^{k}} \\ {\bar {Q}_{{45}}^{k}}&{\bar {Q}_{{44}}^{k}} \end{array}} \right]\left\{ {\begin{array}{*{20}{c}} {{\gamma _{xz}}} \\ {{\gamma _{yz}}} \end{array}} \right\}$$

(4)

where $\left\{ {{\sigma _x},{\sigma _y},{\sigma _{xy}},{\sigma _{xz}},{\sigma _{yz}}} \right\}$ and $\left\{ {{\varepsilon _x},{\varepsilon _y},{\gamma _{xy}},{\gamma _{xz}},{\gamma _{yz}}} \right\}$ are stress and strain vectors, and $\bar {Q}_{{i,j}}^{k}$ indicate the transformed lamina stiffness coefficients of the kth layer.

The following force and moment resultants for the hybrid laminated plates are obtained by integrating Eq. (4) through the thickness of the plates:

$$\left\{ {\begin{array}{*{20}{c}} {{N_x}} \\ {{N_y}} \\ {{N_{xy}}} \\ {{M_x}} \\ {{M_y}} \\ {{M_{xy}}} \\ {{N_{yz}}} \\ {{N_{xz}}} \end{array}} \right\}{\text{=}}\left[ {\begin{array}{*{20}{c}} {{A_{11}}}&{{A_{12}}}&{{A_{16}}}&{{B_{11}}}&{{B_{12}}}&{{B_{16}}}&0&0 \\ {{A_{12}}}&{{A_{22}}}&{{A_{26}}}&{{B_{12}}}&{{B_{22}}}&{{B_{26}}}&0&0 \\ {{A_{16}}}&{{A_{26}}}&{{A_{66}}}&{{B_{16}}}&{{B_{26}}}&{{B_{66}}}&0&0 \\ {{B_{11}}}&{{B_{12}}}&{{B_{16}}}&{{D_{11}}}&{{D_{12}}}&{{D_{16}}}&0&0 \\ {{B_{12}}}&{{B_{22}}}&{{B_{26}}}&{{D_{12}}}&{{D_{22}}}&{{D_{26}}}&0&0 \\ {{B_{16}}}&{{B_{26}}}&{{B_{66}}}&{{D_{16}}}&{{D_{26}}}&{{D_{66}}}&0&0 \\ 0&0&0&0&0&0&{\kappa {A_{44}}}&{\kappa {A_{45}}} \\ 0&0&0&0&0&0&{\kappa {A_{45}}}&{\kappa {A_{55}}} \end{array}} \right]\left\{ {\begin{array}{*{20}{c}} {\varepsilon _{x}^{0}} \\ {\varepsilon _{y}^{0}} \\ {\gamma _{{xy}}^{0}} \\ {\varepsilon _{x}^{b}} \\ {\varepsilon _{y}^{b}} \\ {\gamma _{{xy}}^{b}} \\ {\gamma _{{yz}}^{0}} \\ {\gamma _{{xz}}^{0}} \end{array}} \right\}$$

(5)

where N_x, N_y and N_xy are the total in-plane force resultants, M_x, M_y and M_xy are the total bending moment resultants, Q_yz and Q_xz are the transverse shear force resultants. In addition, the shear correction coefficient $\kappa$ in this study is taken as 5/6. A_ij, B_ij and D_ij are the extensional, bending-extensional coupling and bending stiffness respectively, which can be obtained by:

$$({A_{ij}},{B_{ij}},{D_{ij}})=\int_{-h/2}^{h/2} {{{\bar {Q}}_{ij}}(1,z,{z^2})dz} =\sum\limits_{{k=1}}^{N} {\int_{z_k}^{z_k+1} {\bar {Q}_{{ij}}^{k}(1,z,{z^2})} } (i,j=1,2,4,5,6)$$

(6)

The strain energy U_s of the hybrid laminated plates can be defined as:

$$U_s=\frac12\int_{0}^{a}\int_{0}^{b}\begin{Bmatrix}\begin{array}{l}N_x\varepsilon_x^0+M_x\varepsilon_x^b+N_y\varepsilon_y^0+M_y\varepsilon_y^b\\+N_{xy}\gamma_{xy}^0+M_{xy}\gamma_{xy}^b+N_{xz}\gamma_{xz}^0+N_{yz}\gamma_{yz}^0\end{array}\end{Bmatrix}dxdy$$

(7)

Substituting Eq. (5) into Eq. (7), the integral form of the strain energy can be obtained as follows:

$$U_s=\frac12\int_{0}^{a}\int_{0}^{b}\begin{Bmatrix}\begin{array}{l}A_{11}{(u_{0,x})^2}+2A_{12}u_{0,x}v_{0,y}+2A_{16}(u_{0,y}+v_{0,x})u_{0,x}+A_{22}{(v_{0,y})^2}\\+2A_{26}(u_{0,y}+v_{0,x})v_{0,y}+A_{66}{(u_{0,y}+v_{0,x})^2}+\kappa A_{44}{(w_{0,y}+\varphi_y)^2}\\+\kappa A_{55}{(w_{0,x}+\varphi_x)^2}+2\kappa A_{45}(w_{0,x}+\varphi_x)(w_{0,y}+\varphi_y)+2B_{11}u_{0,x}\varphi_{x,x}\\+2B_{12}(u_{0,x}\varphi_{y,y}+v_{0,y}\varphi_{x,x})+2B_{22}v_{0,y}\varphi_{y,y}+2B_{66}(v_{0,x}+u_{0,y})(\varphi_{x,y}+\varphi_{y,x})\\+2(B_{16}u_{0,x}+B_{26}v_{0,y})(\varphi_{x,y}+\varphi_{y,x})+2(B_{16}\varphi_{x,x}+B_{26}\varphi_{y,y})(v_{0,x}+u_{0,y})\\+D_{11}{(\varphi_{x,x})^2}+2D_{12}\varphi_{x,x}\varphi_{y,y}+2D_{16}(\varphi_{x,y}+\varphi_{y,x})\varphi_{x,x}\\+D_{22}{(\varphi_{y,y})^2}+2D_{26}(\varphi_{x,y}+\varphi_{y,x})\varphi_{y,y}+D_{66}{(\varphi_{x,y}+\varphi_{y,x})^2}\end{array}\end{Bmatrix}dxdy$$

(8)

In this paper, the artificial spring technology [72, 73] is used to conduct the vibration analysis of the hybrid laminates under different boundary conditions. Therefore, the boundary spring potential energy U_sp needs to be determined by

$$\begin{aligned}U_{sp}&=\frac12\int_{-h/2}^{h/2}\int_0^b\begin{Bmatrix}\lbrack k_{x0}^uu_0^2+k_{x0}^vv_0^2+k_{x0}^ww_0^2+K_{x0}^x\varphi_x^2+K_{x0}^y\varphi_y^2\rbrack_{x=0}\\\lbrack k_{xa}^uu_0^2+k_{xa}^vv_0^2+k_{xa}^ww_0^2+K_{xa}^x\varphi_x^2+K_{xa}^y\varphi_y^2\rbrack_{x=a}\end{Bmatrix}dydz\\&+\frac12\int_{-h/2}^{h/2}\int_0^a\begin{Bmatrix}\lbrack k_{y0}^uu_0^2+k_{y0}^vv_0^2+k_{y0}^ww_0^2+K_{y0}^x\varphi_x^2+K_{y0}^y\varphi_y^2\rbrack_{y=0}\\\lbrack k_{yb}^uu_0^2+k_{yb}^vv_0^2+k_{yb}^ww_0^2+K_{yb}^x\varphi_x^2+K_{yb}^y\varphi_y^2\rbrack_{y=b}\end{Bmatrix}dxdz\end{aligned}$$

(9)

Moreover, the kinetic energy T of the hybrid laminated rectangular plate can be expressed as:

$$\begin{array}{l}T=\frac12\iiint_V{\rho(z)\lbrack{(u_{,t})}^2+{(v_{,t})}^2+{(w_{,t})}^2\rbrack}dV\\=\frac12\int_0^a\int_0^b{I_0\lbrack{(u_{0,t})}^2+{(v_{0,t})}^2+{(w_{0,t})}^2\rbrack+2I_1(u_{0,t}\varphi_{x,t}+v_{0,t}\varphi_{y,t})+I_2\lbrack{(\varphi_{x,t})}^2+{(\varphi_{y,t})}^2\rbrack}dxdy\end{array}\\$$

(10)

where the mass inertias (I₀, I₁, I₂) are defined as:

$${I_0}=\sum\limits_{{k=1}}^{N} {\int_{{{Z_k}}}^{{{Z_{k+1}}}} {{\rho _k}(z)dz}},\quad {I_1}=\sum\limits_{{k=1}}^{N} {\int_{{{Z_k}}}^{{{Z_{k+1}}}} {{\rho _k}(z)zdz}},\quad {I_2}=\sum\limits_{{k=1}}^{N} {\int_{{{Z_k}}}^{{{Z_{k+1}}}} {{\rho _k}(z){z^2}dz}}$$

(11)

2.2 Admissible Functions of Displacements and the Solution Procedure

As mentioned above, the strain energy, the spring potential energy and the kinetic energy of the hybrid laminated plate can be expressed in terms of the displacement components u₀, v₀, w₀, φ_x, φ_y. To use the Rayleigh-Ritz method to construct the dynamic analysis, it is crucial to select the appropriate displacement admissible functions. However, the traditional Fourier series such as the orthogonal polynomials are only available for classical boundary conditions (for instance, free, simply supported and clamped supported boundary). In addition, most conventional displacement admissible functions have poor convergence due to discontinuities at the boundary. Therefore, the modified Fourier series are applied to overcome these shortcomings and to express the admissible displacements of the hybrid laminated plate. The displacements and rotations components of the middle surface can be described as a periodic function:

$$\begin{array}{l}u_0(x,y,t)=U(x,y)\psi_ve^{iwt}\\v_0(x,y,t)=V(x,y)\psi_ue^{iwt}\\w_0(x,y,t)=W(x,y)\psi_we^{iwt}\\\varphi_x(x,y,t)=X(x,y)\psi_xe^{iwt}\\\varphi_y(x,y,t)=Y(x,y)\psi_ye^{iwt}\end{array}$$

(12)

where U, V, W, X, Y represent the displacement distribution functions of the middle surface. It is noted that they have the same function expressions, as shown in Eq. (13). Once these function expressions are determined, the following task is to obtain the two-dimensional Fourier series coefficients ${\psi _u},{\psi _v},{\psi _w},{\psi _x},{\psi _y}$ (see Eq. (14)).

$$\begin{aligned}&U\left(x,\;y\right)=V\left(x,\;y\right)=W\left(x,\;y\right)=X\left(x,\;y\right)=Y\left(x,y\right)\\&=\begin{Bmatrix}\sin\left(\lambda_{-2}x\right)\sin\left(\lambda_{-2}y\right),\sin\left(\lambda_{-2}x\right)\sin\left(\lambda_{-1}y\right),\sin\left(\lambda_{-2}x\right)\cos\left(\lambda_0y\right),\sin\left(\lambda_{-2}x\right)\cos\left(\lambda_{-1}y\right),...,\\\sin\left(\lambda_{-2}x\right)\cos\left(\lambda_ny\right),...,\sin\left(\lambda_{-2}x\right)\cos\left(\lambda_Ny\right),\sin\left(\lambda_{-1}x\right)\sin\left(\lambda_{-2}y\right),\sin\left(\lambda_{-1}x\right)\cos\left(\lambda_{-1}y\right),\\\begin{array}{l}\sin\left(\lambda_{-1}x\right)\cos\left(\lambda_0y\right),...,\sin\left(\lambda_{-1}x\right)\cos\left(\lambda_ny\right),...,\sin\left(\lambda_{-1}x\right)\cos\left(\lambda_Ny\right),\cos\left(\lambda_0x\right)\sin\left(\lambda_{-2}y\right),\\\cos\left(\lambda_0x\right)\sin\left(\lambda_{-1}y\right),\cos\left(\lambda_0x\right)\cos\left(\lambda_0y\right),\cos\left(\lambda_0x\right)\cos\left(\lambda_1y\right),...,\cos\left(\lambda_0x\right)\cos\left(\lambda_ny\right),...,\\\begin{array}{l}\cos\left(\lambda_0x\right)\cos\left(\lambda_Ny\right),...,\cos\left(\lambda_mx\right)\sin\left(\lambda_{-2}y\right),\cos\left(\lambda_mx\right)\sin\left(\lambda_{-1}y\right),\cos\left(\lambda_mx\right)\cos\left(\lambda_0y\right),\end{array}\\\begin{array}{l}\cos\left(\lambda_mx\right)\cos\left(\lambda_ny\right),...,\cos\left(\lambda_mx\right)\cos\left(\lambda_Ny\right),...\cos\left(\lambda_Mx\right)\sin\left(\lambda_{-2}y\right),\cos\left(\lambda_Mx\right)\sin\left(\lambda_{-1}y\right),\\\cos\left(\lambda_Mx\right)\cos\left(\lambda_0y\right),\cos\left(\lambda_Mx\right)\cos\left(\lambda_1y\right),...,\cos\left(\lambda_Mx\right)\cos\left(\lambda_ny\right),...,\cos\left(\lambda_Mx\right)\cos\left(\lambda_Ny\right)\end{array}\end{array}\end{Bmatrix}\end{aligned}$$

(13)

$$\psi_{u=}\begin{Bmatrix}\begin{array}{l}A_{-2,-2},...,\;A_{-2,n},...,\;A_{-2,N},\;A_{-1,-2},...,\;A_{-1,n},...,\;A_{-1,N},...,\\A_{m,-2},...,\;A_{m,n},...,\;A_{m,N},\;A_{M,-2},...,\;A_{M,n},...,\;A_{M,N}\end{array}\end{Bmatrix}^T\\$$

(14a)

$$\psi_{v=}\begin{Bmatrix}\begin{array}{l}B_{-2,-2},...,\;B_{-2,n},...,\;B_{-2,N},\;B_{-1,-2},...,\;B_{-1,n},...,\;B_{-1,N},...,\\B_{m,-2},...,\;B_{m,n},...,\;B_{m,N},\;B_{M,-2},...,\;B_{M,n},...,\;B_{M,N}\end{array}\end{Bmatrix}^T\\$$

(14b)

$$\psi_{w=}\begin{Bmatrix}\begin{array}{l}C_{-2,-2},...,\;C_{-2,n},...,\;C_{-2,N},\;C_{-1,-2},...,\;C_{-1,n},...,\;C_{-1,N},...,\\C_{m,-2},...,\;C_{m,n},...,\;C_{m,N},\;C_{M,-2},...,\;C_{M,n},...,\;C_{M,N}\end{array}\end{Bmatrix}^T\\$$

(14c)

$$\psi_{x=}\begin{Bmatrix}\begin{array}{l}D_{-2,-2},...,\;D_{-2,n},...,\;D_{-2,N},\;D_{-1,-2},...,\;D_{-1,n},...,\;D_{-1,N},...,\\D_{m,-2},...,\;D_{m,n},...,\;D_{m,N},\;D_{M,-2},...,\;D_{M,n},...,\;D_{M,N}\end{array}\end{Bmatrix}^T\\$$

(14d)

$$\psi_{y=}\begin{Bmatrix}\begin{array}{l}E_{-2,-2},...,\;E_{-2,n},...,\;E_{-2,N},\;E_{-1,-2},...,\;E_{-1,n},...,\;E_{-1,N},...,\\E_{m,-2},...,\;E_{m,n},...,\;E_{m,N},\;E_{M,-2},...,\;E_{M,n},...,\;E_{M,N}\end{array}\end{Bmatrix}^T\\$$

(14e)

Based on the above energy expression, the Lagrange equation L can be written as below:

$$L={U_s}+{U_{sp}} - T$$

(15)

Then, according to the Rayleigh-Ritz method, the partial derivation of Lagrange equations against each unknown Fourier coefficient should be zero:

$$\frac{{\partial L}}{{\partial {\psi _u}}}=\frac{{\partial L}}{{\partial {\psi _v}}}=\frac{{\partial L}}{{\partial {\psi _w}}}=\frac{{\partial L}}{{\partial {\psi _x}}}=\frac{{\partial L}}{{\partial {\psi _y}}}=0$$

(16)

By substituting Eqs. (8), (9), (10) and (15) into Eq. (16), the equation of motion in terms of forced vibration can be obtained as

$$\left\{ {\left[ {\begin{array}{*{20}{c}} {{K_{uu}}}&{{K_{uv}}}&0&{{K_{ux}}}&{{K_{uy}}} \\ {{K_{vu}}}&{{K_{vv}}}&0&{{K_{vx}}}&{{K_{vy}}} \\ 0&0&{{K_{ww}}}&{{K_{wx}}}&{{K_{wy}}} \\ {{K_{xu}}}&{{K_{xv}}}&{{K_{xw}}}&{{K_{xx}}}&{{K_{xy}}} \\ {{K_{yu}}}&{{K_{yv}}}&{{K_{yw}}}&{{K_{yx}}}&{{K_{yy}}} \end{array}} \right] - {w^2}\left[ {\begin{array}{*{20}{c}} {{T_{uu}}}&0&0&{{T_{ux}}}&0 \\ 0&{{T_{vv}}}&0&0&{{T_{vy}}} \\ 0&0&{{T_{ww}}}&0&0 \\ {{T_{xu}}}&0&0&{{T_{xx}}}&0 \\ 0&{{T_{yv}}}&0&0&{{T_{yy}}} \end{array}} \right]} \right\}P=F$$

(17)

where K_ij and M_ij are the stiffness and mass matrices of the hybrid laminated plates. P represents the unknown Fourier coefficient vector and can be expressed as $P={[{\psi _u},{\psi _v},{\psi _w},{\psi _x},{\psi _y}]^T}$. F is the external force vector and w represents the corresponding excitation frequencies.

For free vibration analysis of hybrid laminated plates, by making the external force vector zero, the governing eigenvalue equation can be obtained in a matrix form:

$$\left\{ {\left[ {\begin{array}{*{20}{c}} {{K_{uu}}}&{{K_{uv}}}&0&{{K_{ux}}}&{{K_{uy}}} \\ {{K_{vu}}}&{{K_{vv}}}&0&{{K_{vx}}}&{{K_{vy}}} \\ 0&0&{{K_{ww}}}&{{K_{wx}}}&{{K_{wy}}} \\ {{K_{xu}}}&{{K_{xv}}}&{{K_{xw}}}&{{K_{xx}}}&{{K_{xy}}} \\ {{K_{yu}}}&{{K_{yv}}}&{{K_{yw}}}&{{K_{yx}}}&{{K_{yy}}} \end{array}} \right] - {w^2}\left[ {\begin{array}{*{20}{c}} {{T_{uu}}}&0&0&{{T_{ux}}}&0 \\ 0&{{T_{vv}}}&0&0&{{T_{vy}}} \\ 0&0&{{T_{ww}}}&0&0 \\ {{T_{xu}}}&0&0&{{T_{xx}}}&0 \\ 0&{{T_{yv}}}&0&0&{{T_{yy}}} \end{array}} \right]} \right\}P=0$$

(18)

After solving the above eigenvalue equation, the natural frequencies and the eigenvectors can be obtained. Finally, the modal shapes of the hybrid laminated plate can be obtained by substituting the unknown Fourier coefficient vector P into Eq. (12).

3 Numerical Results and Discussions

In this section, the dynamic behaviours of the hybrid composite laminated plates with arbitrary boundary conditions are studied in detail. To simplify the expression, the acronyms are used to express the boundary conditions along four edges and the stacking sequences of the hybrid composite laminated plates. For instance, CSEF denotes the Clamped (C), Simply support (S), Elastic (E) and Free (F) boundary conditions at x = 0, y = 0, x = a and y = b respectively. In addition, HLLH denotes the four-layer hybrid composite laminated plates with high modulus (H) fibre-reinforced polymer lamina on external layers and low modulus (L) fibre-reinforced polymer lamina on internal layers. In addition, based on the artificial spring technique [72, 73], the above arbitrary boundary conditions can be achieved by assigning the spring stiffness coefficients (K_u, K_v, K_w, K_x, K_y) with different values, as shown in Table 1.

Table 1 The spring stiffness for arbitrary boundary conditions

Moreover, unless otherwise specified, the default material properties of the hybrid composite laminated plates are given as follows. For the high modulus fibre reinforced polymer lamina: $E_1^H=150\mathrm{GPa}$, $E_2^H=10\mathrm{GPa}$, $\mu_{12}^H=0.25$, $G_{12}^H=G_{13}^H=6\mathrm{Gpa}$, $G_{23}^H=5\mathrm{GPa}$ and $\rho_H=1500\mathrm{kg}/\mathrm m^3$. For the low modulus fibre reinforced polymer lamina: $E_1^L=50\mathrm{GPa}$, $E_2^L=12\mathrm{GPa}$, $\mu_{12}^L=0.3$, $G_{12}^L=G_{13}^L=5\mathrm{GPa}$, $G_{23}^L=4\mathrm{GPa}$ and $\rho_L=2000\mathrm{kg}/\mathrm m^3$. Assuming that the total thickness of the hybrid laminated plate is h, the total thicknesses of the high and low modulus fibre-reinforced polymer lamina are h₁ and h₂, respectively, and the hybrid ratio is defined as ξ = h₁/h₂. For convenience, in this study, the following non-dimensional frequencies are used by the formula: $\overline w=wa^2/h\sqrt{\rho_L/E_2^L}$.

3.1 Convergence Analysis

First, the convergence analysis of the truncation numbers (M and N) is conducted before the free and forced vibration characteristics of the hybrid composite laminated plates with arbitrary boundary conditions and geometric parameters are studied. The HLLH hybrid laminated plates with a = b = 1, h = 0.005 and the lamination scheme [0/90/0/90] under SSSS boundary condition is taken into consideration. The first eight non-dimensional frequencies with different truncation numbers are given in Table 2, the results show that the value of truncation numbers (from 2 × 2 to 20 × 20) does not affect the first four non-dimensional frequencies. In addition, there is a rapid decrease of the fifth to eighth non-dimensional frequencies as the number of truncations increases from 2 to 4, followed by a steady fall after M = N = 6, and eventually, the non-dimensional frequencies remain almost constant after M = N = 12. Therefore, by considering the computational cost and the accuracy, the truncation numbers are set as M = N = 12 in this study.

Table 2 The convergence analysis of the first eight non-dimensional frequencies for the HHLL hybrid laminated plates with lamination scheme [0/90/0/90] and SSSS boundary condition

3.2 Free Vibration Analysis of Hybrid Laminated Plates

Firstly, to verify the correctness and accuracy of the applied method, the natural frequencies of the non-hybrid laminates are calculated and the obtained results are compared with those from literature. The first sixth non-dimensional frequencies for the non-hybrid laminated plates with different lamination schemes and different aspect ratios under CCCC boundary conditions are given in Table 3. The geometric parameters and the material properties: h/a = 0.01, E₁ = 250GPa, E₂ = 10GPa, G₁₂ = G₁₃ = 5GPa, G₂₃ = 2GPa, µ = 0.25, ρ = 1300 kg/m³. It should be noted that the dimensionless form of the frequencies in this case is $\overline w=wa^2/h\sqrt{\rho/E_2}$. It can be seen from Table 3 that the calculation results of the method are very close to the results from Refs. [72, 74], the good agreement shows the accuracy of the model.

Table 3 Comparison of the first six non-dimensional frequencies for the non-hybrid laminated plates with different lamination schemes and different aspect ratios under CCCC boundary conditions (h/a = 0.01, E₁ = 250GPa, E₂ = 10GPa, G₁₂ = G₁₃ = 5GPa, G₂₃ = 2GPa, µ = 0.25, ρ = 1300 kg/m³)

To further verify the accuracy of the model for the free vibration responses of the hybrid laminates, the first sixth natural frequencies of the square hybrid laminates with different boundary conditions and different thickness ratios are given in Table 4 and the obtained results are compared with those from the finite element method. The mode shapes of the square hybrid laminates for certain frequencies are also given in Fig. 4. In these cases, the default material parameters are used. As can be seen from Table 4; Fig. 4, the present natural frequencies and mode shapes are in good agreement with the FEM ones in all cases, and this further verifies the model’s accuracy. The comparison results show the effectiveness of the present approach for the hybrid laminated plates.

Table 4 Comparison of the first six non-dimensional frequencies for the square HLLH hybrid laminated plates with different thickness ratios and different boundary conditions (a = b = 1)

Fig. 4

Comparison of mode shapes of CGGC hybrid laminates (h/a  = 0.01, a = b , [0,90,90,0])

After the verification of the model accuracy, the analysis of the free vibration responses of the hybrid laminated plates with arbitrary boundary conditions is carried out. The first six non-dimensional natural frequencies of the hybrid laminate plates with different stacking sequences (L6, HLLLLH, LLHHLL, H3L3, L3H3, HLHLHL, H6) under different boundary conditions (CCCC, SSSS, CFCF, CFFF, E₁E₂E₁E₂, CE₃CE₃) are given in Fig. 5, and the geometric parameters and materials of the hybrid laminates are as follows: a = b = 1, h/a = 0.01, the lamination scheme are [0]₆, and the default material is used. It can be seen from Fig. 5 that the boundary conditions have a large effect on the natural frequencies of the hybrid laminated plates. For example, the natural frequency of the hybrid laminates under elastic boundary condition CE₃CE₃ is intermediate between those under CCCC and CFCF boundary conditions. The reason is that, according to Table 1, the boundary stiffness coefficients of the boundary condition E₃ (K_u=K_v=K_w=K_x=K_y=10⁸) are between those of C (10¹⁴) and F (0), and the boundary stiffness is positively related to the natural frequency. In addition, for all boundary conditions, the non-hybrid laminated plates H6 (high stiffness) and L6 (low stiffness) have the maximum and minimum natural frequencies, respectively. The reason behind this is that structural stiffness has a positive correlation with natural frequency. For the hybrid plates (HLLLLH, LLHHLL, H3L3, L3H3, HLHLHL), they can be classified as hybrid ratio ξ = 0.5 (HLLLLH, LLHHLL) and ξ = 1 (H3L3, L3H3, HLHLHL). For ξ = 0.5, it can be seen that the natural frequency of HLLLLH is much higher than that of LLHHLL, which indicates that the high modulus fibre-reinforced polymer lamina distributed on the outer side of the plates can significantly enhance the structural stiffness and natural frequency, while the high modulus lamina distributed on the inner side has a negative effect on the performance enhancement of the hybrid laminates. This phenomenon can be explained by the stiffness coefficients in Eq. (6). In addition, for ξ = 1 (H3L3, L3H3, HLHLHL), it can be seen that the natural frequencies of H3L3 and L3H3 are the same because they can be regarded as the same plate. The natural frequencies of HLHLHL are larger than those of H3L3 and L3H3, and this indicates that the stacking sequences also have a large effect on the natural frequencies of the hybrid laminated plates. In addition, by comparing HLLLLH and HLHLHL, it can be observed that the arrangement of high-stiffness fibres in the outer layer has a more significant impact on increasing the frequency compared to the increase in the hybrid ratio.

Fig. 5

The first six non-dimensional natural frequencies of the hybrid laminate plate with different stacking sequences and different boundary conditions

Next, the effects of different lamination schemes ([0,θ,0,θ], [θ,0,θ,0], [θ,θ,0,0], [θ,-θ,θ,-θ]) and different fibre orientation on the first four non-dimensional natural frequencies of HLHL hybrid laminates (a = b = 1, h = 0.1) under SSSS boundary condition are also investigated. The fibre orientations are varied between 0° and 180° with an interval of 5°. As can be seen from Fig. 6, for all cases, the obtained curves are symmetric about θ = 90°. By comparing the non-dimensional natural frequencies of the HLHL hybrid plates with [θ,0,θ,0] and [0,θ,0,θ], it can be seen that the first three natural frequencies, the high modulus fibre orientation has a larger effect on the natural frequencies than the low modulus fibre orientation does. For the hybrid plates with [θ,-θ,θ,-θ], the non-dimensional natural frequencies show trigonometric-like fluctuations with the fibre orientations. For the hybrid plates with [θ,θ,0,0], the result shows that the fibre orientations from 60° to 120° have a negligible effect on the first four natural frequencies. In addition, by comparing [θ,0,θ,0] with [0,θ,0,θ], it shows that carbon fiber orientation has a larger effect on fundamental frequency than glass fibre orientation.

Fig. 6

The first four non-dimensional natural frequencies of the hybrid laminate plates with different lamination schemes and different fiber orientations

3.3 Forced Vibration Analysis of Hybrid Laminated Plates

To study the forced vibration characteristics of the hybrid laminated plates, the model validation is carried out before the deep investigation of the structural parameters on the forced vibration characteristics of the hybrid laminated plates. It should be noted that only the steady-state response is discussed in detail in this paper. Figure 7 gives the transformed displacement response X (Unit: dB) of HLLH hybrid laminated plates under SSSS boundary conditions. The transformed displacement response X can be obtained based on the formula: $X=20 \times \log (\left| x \right| \times {10^{12}})$, where the displacement response x (Unit: m) has been obtained according to Eqs. (12) and (17). In this case, the geometric parameters of HLLH hybrid laminated plates are assumed as: a = b = 1, h = 0.01, and the lamination scheme is [0/90/90/0]. The external force F = 1 N along the negative direction of the z-axis is applied at (0.25, 0.25, 0). The coordinates of the measurement points are (0.75, 0.5, 0) and (0.25, 0.25, 0), respectively. Figure 7 gives the comparison of the predicted displacements based on the present method and the finite element method. The obtained results are in good agreement with the FEM ones, which confirms the accuracy of the analytical model in analyzing the forced vibration characteristics of the hybrid laminated plates.

Fig. 7

The comparison results of displacement response of the hybrid laminate plates: a The excitation point (0.25, 0.25, 0) and the measurement point (0.75, 0.5, 0); b The excitation point (0.25, 0.25, 0) and the measurement point (0.25, 0.5, 0)

The influence of structural parameters on the forced vibration characteristics is carried out after further verification of the model’s accuracy. The effects of different stacking sequences (HLLH, HHLL, LHHL) and arbitrary boundary conditions (CCCC, SSSS, E₁E₂E₁E₂, CE₃CE₃) on the steady-state response of the hybrid laminated plate with the same hybrid ratio are investigated, as shown in Fig. 8. The properties of the hybrid plate are as follows: (a = b = 1, h = 0.01, F = 1 N, and the lamination schemes is [0]₄). The coordinates of the excitation point and the measurement point are (0.25, 0.25, 0) and (0.75, 0.5, 0), respectively. It can be seen from Fig. 8 that, under the same boundary conditions, for the hybrid laminates with high modulus fibre-reinforced polymer lamina on external layers, the resonant frequency corresponding to the peak of displacement response moves toward the high-frequency direction. This is because the resonant frequency of the hybrid plate increases with the plate stiffness. However, the different stacking sequences have a negligible effect on the peak values. In addition, different boundary conditions significantly affect the resonant frequency, the peak values and the curve trends.

Fig. 8

The variations of the displacement response of the hybrid laminate plates with different stacking sequences and different boundary conditions

To study the forced vibration response of the hybrid laminated plates under arbitrary boundary conditions, the steady-state displacement responses of the hybrid laminated plates with different stacking sequences (HHLLHH, LHHHHL, HHHLLL, HLHLHL) under arbitrary boundary conditions (E₃E₃E₃E₃, E₄E₄E₄E₄, E₅E₅E₅E₅) are given in Fig. 9. The properties of the hybrid plate are as follows: (a = b = 1, h = 0.01, F = 1 N, and the lamination schemes is [0]₆). The coordinates of the excitation point and the measurement point are (0.5, 0.5, 0) and (0.6, 0.8, 0), respectively. Figure 9 shows that the boundary conditions significantly affect the steady-state displacement response curves. More specifically, the hybrid laminated plates with small boundary stiffness coefficients (for instance, E₅E₅E₅E₅ in this case) have a fewer number of resonant frequencies and larger peaks. For the same hybrid ratio of HHHLLL and HLHLHL, the steady-state displacement response curves are almost the same, while there is a huge difference between the response curves of the HHLLHH hybrid plates and those of LLHHLL. This indicates that the hybrid ratio has a more obvious effect on the steady-state response, compared with the stacking sequences.

Fig. 9

The variations of the displacement response of the hybrid laminate plates with different stacking sequences and different boundary conditions

The effect of different magnitudes of external force on the forced vibration response is also investigated. The HLLH hybrid plates under the CSE₁E₂ boundary condition are considered. The geometric parameters are a = b = 1, h = 0.1, and the stacking sequence is [90/0/0/90]. The coordinates of the excitation point and the measurement point in Fig. 10a are (0.25, 0.25, 0) and (0.75, 0.5, 0), respectively. The coordinates of the excitation point and the measurement point in Fig. 10b are (0.25, 0.25, 0) and (0.75, 0.5, 0), respectively. The magnitudes of excitation force are set to 1N, 10N and 100N. It can be seen from Fig. 10 that regardless of the position of the excitation point and the measurement point, the peak values increase with the magnitudes of the excitation force, and the excitation force has no effect on the curve trend.

Fig. 10

The variations of the displacement response of the hybrid laminate plates with different magnitudes of external force: a The excitation point (0.25, 0.25, 0) and the measurement point (0.75, 0.5, 0); b The excitation point (0.5, 0.5, 0) and the measurement point (0.6, 0.8, 0)

The effect of different thicknesses on the forced vibration response is investigated in this part. The steady-state responses of the HLLLLH hybrid plates under CE₃CE₃ boundary condition are given in Fig. 11. The geometric parameters are a = b = 1, h = 0.01, 0.05, 0.1, and the lamination scheme is [0/90/0/90/0/90]. The coordinates of the excitation point and the measurement point are the same as in the last example. It can be easily found that, with the increase of thickness, the peak values of displacement response decrease and the resonant frequency moves toward the high-frequency direction.

Fig. 11

The variations of the displacement response of the hybrid laminate plates with different thicknesses: a The excitation point (0.25, 0.25, 0) and the measurement point (0.75, 0.5, 0); b The excitation point (0.5, 0.5, 0) and the measurement point (0.6, 0.8, 0)

4 Conclusions

This study investigates the free and forced vibration characteristics of carbon/glass hybrid laminated plates based on the first-order shear deformation theory, the artificial spring technique and the Rayleigh-Ritz method. The accuracy of the analytical model is validated through comparisons with published results and FEM solutions. On this basis, a comprehensive parametric study is conducted to analyze the influences of geometric parameters, hybrid ratios, stacking sequences, lamination schemes and boundary conditions on both the free vibration and the steady-state displacement responses of the hybrid laminated plates. The key findings are given as follows:

• 1. The accuracy of the applied method is ascertained by comparing the obtained results with reference data and finite element results. The excellent agreement shows the high precision for both free and forced vibration analysis of interlayer hybrid composite laminated plates.

• 2. The increase of boundary stiffness coefficients, hybrid ratios and the number of carbon fiber reinforced lamina distributed on the outer side lead to the increase of natural frequency and the movement of displacement response peak toward the high-frequency direction. In addition, the arrangement of carbon fibres in the outer layer has a more significant impact on increasing the frequency compared to the increase in the hybrid ratio.

• 3. The carbon fibre orientation has a larger effect on fundamental frequency than the glass fibre orientation.

• 4. The peak values of displacement response curves increase with the increase of excitation force, and the excitation force does not affect the curve trend.

• 5. As the thickness ratios of hybrid laminated plates increase, the peak values of displacement response curves decrease and the resonant frequency moves toward the high-frequency direction. Increasing the thickness ratio can improve the vibration suppression effect within the frequency range of 600 Hz.