1 Introduction

Carbon fibre reinforced polymers (CFRP) have found many applications as structural parts in the aerospace industry due to their superior mechanical properties and wear resistance compared to traditional metals. CFRPs are used when high structural strength and stiffness are required; however, they show some criticalities. Out-of-plane loading scenarios such as low velocity impact can result in barely visible impact damage (BVID) which can cause severe material degradation and are hard to detect during the inspection. Extensive research has been performed on the mechanical response of composite structures subjected to low velocity impacts [1,2,3,4,5,6]. The damage caused by low velocity impact may lead to premature buckling of composite structure and has a detrimental effect on its flexural properties and compressive strength [7].

Meanwhile, the presence of open holes in a composite laminate changes the behaviour in terms of mechanical response and failure. The complex stress concentration in the vicinity of the open hole edge depends on the material orientation, mechanical constants, and the stacking sequence of the laminate, which makes it different from isotropic materials. This stress concentration results in a decrease in the mechanical strength and stiffness, and the vicinity of the open hole edge is considered as a location with a high probability of interlaminar and intralaminar damage initiation. Accordingly, the presence of open holes in composite structures should be avoided. However, a composite structure with open holes is desired for reasons such as assembly requirements, wiring, and maintenance access [8].

The tensile and compressive behaviour of composite with holes has been studied in numerous contexts including experimental [9,10,11], numerical [12,13,14,15] and analytical [10, 16] studies; however, the behaviour of composite structures with open holes subjected to low velocity impact has drawn less attention, despite the severity of the damage that is promoted by low velocity impact. Regarding the influence of the open holes on the damage in initiation composite laminates with open holes, Green et al. [17] performed an experimental and numerical study on notched laminates subjected to impact, considering the effect of the diameter of the hole, the thickness of the laminate, and ply. Matrix damage initiation was directly attributed to the presence of holes that caused the initiation of multiple matrix cracks at the impact location towards the hole edge in the lower laminae. Luo [18] observed identical parallel matrix crack paths between the impact point and the hole edge and the damage in the vicinity of the hole was delamination correlated with the matrix damage. In a comparison between laminates with or without a hole, an increase in matrix crack density was observed for the laminate with a hole. Roy et al. [19] investigated the delamination propagation in composite specimens with two open holes subjected to transverse impact. The results showed that delamination initiates at the inner side of the free edges of the holes and propagates with time toward one another to form a big delamination area.

Amaro et al. [20] studied the delamination in composite with one and two open holes. The presence of holes did not have a meaningful influence on the mechanical response of the laminates; however, the absorbed energy and delamination were increased in laminates with holes. The presence of holes also changed the shape of the delamination which was also verified numerically using finite element simulation with a mixed-mode cohesive damage model. Santos et al. [21] carried out an experimental and numerical study on the influence of the presence of inclined holes, i.e., non-vertical holes, on low velocity impact damage in CFRP composite. The results from laminates with vertical and inclined holes were compared with the results of the control sample. An asymmetric delamination shape was observed with a higher damage density in the vicinity of the hole, which was more pronounced for the laminate with an inclined hole. A cohesive zone based finite element model was developed, which used vertical cohesive elements to account for the matrix damage. Santos et al. [8] experimentally investigated the effect of an open hole to impact point distance on the fatigue behaviour of glass fibre/epoxy laminates. The fatigue life was increased with the increase of the hole distance from the impact point.

It can be concluded from the literature that the presence of open holes has a significant influence on the damage accumulation of composite laminates [17,18,19,20]. Nevertheless, the extent of this influence, especially the accumulation of intralaminar damage, remains unclear. Therefore, in the present study, a Continuum Damage Mechanics (CDM) approach is employed for the numerical simulation of CFRP laminates with open holes subjected to low velocity impact. The failure mode concept model of Cuntze [22, 23] is implemented in a user-defined user material model (VUMAT) to account for the progressive intralaminar damage with five failure modes for fibre failure in compression and tension, matrix failure in compression and tension, and shear failure. The failure mode concept model of Cuntze showed high accuracy in reproducing failure under several conditions in the World-Wide Failure Exercises (WWFE) [24, 25] and predicted the matrix failure without the need to search for the fracture angle which makes it more efficient compared to similar criteria such as Puck action plane strength model [26]. In addition, a cohesive zone model is implemented to simulate the damage at the interfaces. A total of eight FE models are developed with one and two open holes of different diameters and different distances from the centre of the hole to the impact location. This paper first presents the validation of the numerical model in ABAQUS/Explicit with different failure models to account for the progressive failure of composite laminates with an open hole. Then the influence of the number of holes and the distance between the centre of the hole to the centre of the plate in the mechanical response and damage accumulation is discussed. This paper presents a detailed description of the initiation and propagation of different failure models of the composite laminate with open holes in comparison with the pristine specimens in order to identify the influencing parameters related to the presence of the open holes in the structure.

2 Material Model

During recent years, different failure criteria such as Chang Chang, Hashin, Puck, and Cuntze have been expressively used for the simulation of composites subjected to impacts. It has been shown that while all these criteria are accurate in the prediction of the mechanical response of the composite laminate subjected to low velocity impact, i.e., the force–time, force–displacement, and energy-time curves, there are some dissimilarities in the damage pattern and the prediction of damage area by different failure criteria [27, 28]. As mentioned in the introduction, Puck and Cuntze have received more attention due to their accuracy. In this work, the progressive damage model for the composite laminae uses the failure model of Cuntze for two reasons: i) the accuracy of this model in the prediction of the matrix damage which predicts the damage similar to the Puck failure criterion [27, 29], and ii) the ease of the computational implementation compared to the failure criterion of Puck. The Cuntze failure model is easier to implement since, unlike the Puck action plane strength model, there is no need for the definition of a search algorithm for the fracture angle search which leads to a faster and more robust VUMAT [30].

2.1 Failure Mode Concept Model of Cuntze

The failure mode concept of Cuntze [22, 23] is established on distinguishing between five different failure topologies or failure modes according to the state of stress that is applied to the composite material. The failure modes are related to fibre and inter-fibre failure which are distinguished by FF and IFF abbreviations, see Eq. (1). Equations FF1 and FF2 are defined for tensile fibre breakage and compression fibre breakage, respectively. IFF1, IFF2, and IFF3 dominate the inter-fibre failure and correspond to the tensile matrix failure, compressive matrix failure, and matrix shear failure, respectively. The definition of a separate equation for shear failure mode is a unique feature of this failure model.

$$FF1 : {Eff}^{\parallel \sigma }={\sigma }_{1}^{*}/{S}_{FF1}={\sigma }_{eq}^{\parallel \sigma }/{R}_{\parallel }^{t}$$
$$FF2 : {Eff}^{\parallel \tau }={\sigma }_{1}^{*}/{S}_{FF2}={\sigma }_{eq}^{\parallel \tau }/{R}_{\parallel }^{c}$$
$$IFF1 : {Eff}^{\perp \sigma }=\left[({\sigma }_{2}+{\sigma }_{3})+\sqrt{{({\sigma }_{2}-{\sigma }_{3})}^{2}+4{\tau }_{23}^{2}}\right]/(2{\cdot S}_{IFF1})={\sigma }_{eq}^{\perp \sigma }/{R}_{\perp }^{t}$$
$$IFF2 : {Eff}^{\perp \tau }=\left[{b}_{\perp \perp }.\sqrt{{\left({\sigma }_{2}-{\sigma }_{3}\right)}^{2}+4{\tau }_{23}^{2}}+\left({b}_{\perp \perp }-1\right).\left({\sigma }_{2}+{\sigma }_{3}\right)\right]/{S}_{IFF2}={\sigma }_{eq}^{\perp \tau }/{R}_{\perp }^{c}$$
$$IFF3 : {Eff}^{\perp \parallel }={\left\{\left[\sqrt{{b}_{\perp \parallel }^{2}.{I}_{23-5}^{2}+4{R}_{\perp \parallel }^{2}.{({\tau }_{31}^{2}+{\tau }_{21}^{2})}^{2}}+{b}_{\perp \parallel }.{I}_{23-5}\right]/(2{\cdot S}_{IFF3}^{3})\right\}}^{0.5}={\sigma }_{eq}^{\perp \parallel }/{R}_{\perp \parallel }$$
(1)

In the above equation \({S}_{FF1}\), \({S}_{FF2}\) are the tensile and compressive material strength in the fibre direction. \({S}_{IFF1}\), \({S}_{IFF2}\) and \({S}_{IFF3}\) stand for matrix tensile failure, matrix compression failure and in-plane shear failure. In IFF3, \({I}_{23-5}=2{\sigma }_{2}{\tau }_{21}^{2}+2{\sigma }_{3}{\tau }_{31}^{2}+4{\tau }_{23}{\tau }_{31}{\tau }_{21}\). In addition, the indices \(\parallel\) and \(\perp\) represent the fibre parallel and transverse material directions, respectively. To perform structural analysis using the failure model of Cuntze, five elasticity parameters, five strength parameters, and two friction parameters should be defined. Internal friction parameters of \({b}_{\perp \perp }\) and \({b}_{\perp \parallel }\) are used to characterise the physical phenomena within the material based on the Mohr–Coulomb theory. Interaction of different failure modes are considered in a probabilistic manner by the following equation by the failure model of Cuntze:

$${Eff}^{m}=\sum_{1}^{5}{Eff}^{mode}={\left({\sigma }_{eq}^{\parallel \sigma }/{R}_{\parallel }^{t}\right)}^{m}+{\left({\sigma }_{eq}^{\parallel \tau }/{R}_{\parallel }^{c}\right)}^{m}+{\left({\sigma }_{eq}^{\perp \sigma }/{R}_{\perp }^{t}\right)}^{m}+{\left({\sigma }_{eq}^{\perp \tau }/{R}_{\perp }^{c}\right)}^{m}+{\left({\sigma }_{eq}^{\perp \parallel }/{R}_{\perp \parallel }\right)}^{m}$$
(2)

In the equation stated above, m is the interaction exponent which is normally 2.5 < m < 3, which is used to estimate the global material effort. Since in this work a progressive failure model is considered for each failure mode, a mixed-mode damage parameter is defined for fibre and matrix damage instead of Eq. (2), see Sect. 2.2.

2.2 Constitutive Behaviour

Carbon fibre reinforced polymer composites show a non-linear irreversible behaviour when subjected to in-plane shear loads, which leads to a completely different elastic material behaviour compared to the linear material response which resulted from loads in longitudinal and transverse directions. Therefore, a non-linear shear stress–strain relationship was considered according to Eq. (3) [31].

$${\tau }_{12}={c}_{1}{\gamma }_{12}^{3}+sign\left({\gamma }_{12}\right).{c}_{2}{\gamma }_{12}^{2}+{c}_{3}{\gamma }_{12}$$
(3)

The non-linear material behaviour is responsible for the permanent indentation at the location of the impact that occurs during a low velocity impact event. The third-degree polynomial of Eq. (3) has been proposed in [32] and has been proven to be accurate in the prediction of the non-linear behaviour of CFRP. Coefficients \({c}_{1}\), \({c}_{2}\) and \({c}_{3}\) of Eq. (3) were acquired by fitting the equation to the experimental shear stress–strain curve. In order to measure the irreversible portion of the shear strain, the shear strain is split into elastic and plastic strain.

$${\gamma }_{12}={\gamma }_{12}^{e}+{\gamma }_{12}^{p}$$
(4)

The plastic strain, \({\gamma }_{12}^{p}\), is calculated according to Eq. (5).

$${\gamma }_{12}^{p}={\gamma }_{12}-\frac{{\tau }_{12}}{{G}_{12}^{0}}$$
(5)

It should be mentioned that while Eq. (3) constitutes the shear loading, the shear unloading follows a linear law, for more information on the material model and the shear cyclic behaviour see [27].

The post damage response of the composite material is governed by the degraded stiffness matrix of Eq. (6). The Continuum Damage Mechanics (CDM) approach is used here by selectively degrading the stiffness parameters of the material. The damage variables for fibre, matrix and shear damage are used to degrade the corresponding stiffness parameters of Eq. (6) [31].

$$\begin{aligned}dC&= \left[\begin{array}{cccccc}{d}_{f}{E}_{1}\left(1-{d}_{m}{v}_{23}{v}_{32}\right)/\Delta & {d}_{f}{E}_{1}\left({d}_{m}{v}_{21}-{d}_{m}{v}_{31}{v}_{23}\right)/\Delta & {d}_{f}{E}_{1}\left({v}_{31}-{d}_{m}{v}_{21}{v}_{32}\right)/\Delta & 0& 0& 0\\ & {d}_{m}{E}_{2}\left(1-{d}_{f}{v}_{13}{v}_{31}\right)/\Delta & {d}_{m}{E}_{2}\left({v}_{32}-{d}_{f}{v}_{12}{v}_{31}\right)/\Delta & 0& 0& 0\\ & & {E}_{3}\left(1-{d}_{m}{d}_{f}{v}_{12}{v}_{21}\right)/ \Delta & 0& 0& 0\\ & symmetric& & {{d}_{ms}G}_{12}& 0& 0\\ & & & & {d}_{ms}{G}_{13}& 0\\ & & & & & {d}_{ms}{G}_{23}\end{array}\right] \\ \Delta &=(1-{d}_{f}{d}_{m}{v}_{12}{v}_{21}-{d}_{m}{v}_{23}{v}_{32}-{d}_{f}{v}_{31}{v}_{13}-2{ d}_{f}{d}_{m}{v}_{21}{v}_{32}{v}_{13})\end{aligned}$$
(6)

In Eq. (6), \({d}_{f}\), \({d}_{m}\) and \({d}_{ms}\) are the damage variables for fibre, matrix, and matrix-shear. These damage variables are related to the failure modes of the Cuntze failure criterion according to Eq. (7).

$$\begin{aligned}{d}_{f}&=\left(1-{d}_{FF1}\right)\left(1-{d}_{FF2}\right) \\ {d}_{m}&=\left(1-{d}_{IFF1}\right)\left(1-{smc\cdot d}_{IFF2}\right) \\ {d}_{ms}&=\left(1-{d}_{IFF1}\right)\left(1-{smc\cdot d}_{IFF2}\right)\left(1-smc\cdot {d}_{IFF3}\right)\end{aligned}$$
(7)

In which \(smc\) is equal to 0.6 and is used to avoid a numerical instability problem and element distortion, similar values have been used in [33,34,35] as loss control factors. The problem of element distortion was more relevant in compression and shear failure modes to avoid element distortion and numerical instability. Therefore, the loss control factor was not considered for the tensile failure mode to better represent composite failure. The failure mode damage variables \({d}_{FF1}\), \({d}_{FF2}\), \({d}_{IFF1}\), \({d}_{IFF2}\) and \({d}_{IFF3}\) correspond to the failure modes of Cuntze according to Table 1, and are equal to zero when there is no damage. A larger than zero damage variable means that the corresponding failure mode is met and a damage value equal to one is the complete failure of the element. The failure mode damage variables are calculated according to Eq. (8).

Table 1 Ultimate strain and current strain formulation for the strain-softening law
Full size table
$${d}_{i}=\frac{{\varepsilon }_{i,u}}{{\varepsilon }_{i,u}-{\varepsilon }_{i,on}}\left(1-\frac{{\varepsilon }_{i,on}}{{\varepsilon }_{i}}\right)$$
(8)

In which, the subindex \(i\) represents FF1, FF2, IFF1, IFF2, and IFF3 for different failure modes; \({\varepsilon }_{i}\) is the equivalent strain for each failure mode according to Table 1, and \({\varepsilon }_{i,u}\) stands for the ultimate failure strain which is calculated by the fracture energy for each one of the failure modes, i.e., \({G}_{i}\), and the characteristic length element, i.e., \(l\), to avoid the mesh sensitivity problem. In addition, \({\varepsilon }_{i,on}\) is the onset strain for the failure mode which is calculated as the value of the equivalent strain at the moment that the failure modes are met. The characteristic length element is calculated as the cube root of the element volume.

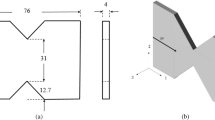
Table 2 shows the mechanical properties of the CFRP composite. The parameters, \({E}_{1}\), \({E}_{2}\), \({\nu }_{12}\),\({{R}_{\parallel }}^{t}\), \({{R}_{\perp }}^{t}\), \({R}_{\perp \parallel }\), \({c}_{1}\), \({c}_{2}\) and \({c}_{3}\) were measured by performing tensile tests on composite specimens in different material directions. Figure 1a to c shows the experimental results of the tensile test in fibre, transverse, and in-plane shear direction, respectively. The fibre and transverse properties were measured according to the ASTM D3039 standard [36], while in-plane shear properties were calculated according to the ASTM D3518 standard [37]. The remaining material properties were taken from the literature for the same CFRP composites. Since the fracture toughness values were not available for the CFRP material of this study, the values for similar CFRP material was taken from Ref. [31]. The effect of strain rate has been neglected in this paper due to the relatively low levels of the strain rate in composite materials subjected to low velocity impacts [38].

Table 2 Material properties of CFRP
Full size table
Fig. 1
figure 1

Experimental stress–strain curves. (a): Tensile fibre direction, (b): Tensile transverse direction, and (c): In-plane shear direction

Full size image

2.3 Damage Model for the Interface

The interface damage was simulated by considering a bilinear traction–separation curve for the prediction of the interface damage initiation and the mixed-mode fracture energy law of Benzeggagh and Kenane (B-K) [44] for the damage evolution at the ply interface. The bilinear traction–separation curve uses a quadratic stress failure criterion according to Eq. (9).

$$\frac{{\langle {t}_{n}\rangle }^{2}}{{N}^{2}}+\frac{{t}_{s}^{2}}{{S}^{2}}+\frac{{t}_{t}^{2}}{{S}^{2}}=1$$
(9)

In the above equation <  > is the Macaulay bracket which returns zero for negative input values which result in damage only for the tensile normal traction and not for the tensile compressive traction. \({t}_{s}\) and \({t}_{t}\) are shear tractions and \({t}_{n}\) is the normal traction, while N and S indicate the interface strength in normal and shear directions, respectively. The (B-K) damage evolution follows the following relationship

$${G}_{n}^{C}+\left({G}_{s}^{C}-{G}_{n}^{C}\right){\left\{\frac{{{G}}_{{s}}}{{{{G}}}_{{{T}}}}\right\}}^{{{\eta}}}={{{G}}}^{C}$$
(10)

where \({G}_{n}^{C}\) and \({G}_{s}^{C}\) are the critical normal fracture energy, critical shear fracture energy, respectively. \({G}_{S}={G}_{s}+{G}_{t}\) and \(G_T=G_n+G_s\) are the dissipated energies and \(\eta\) is the (B-K) material constant. The properties of the interface damage model are summarised in Table 2. Here, the cohesive interface elements, which were completely failed, were considered in the measurement of the delaminated area.

3 Finite Element Simulation

The numerical models of low velocity impact were developed in Abaqus/Explicit. The numerical models consisted of a control specimen with no holes, four finite element (FE) models with a single hole with different distances to the impact zone, and a model with two open holes. A summary of the FE models is presented in Table 3. In the FE models used in this paper, the composite laminate was impacted by a rigid hemispherical impactor of 1.325 kg mass and 8 mm radius. The 24-layer laminates of 150 × 100 mm2 size with a stacking sequence of [45/0/-45/90]3 s were subjected to a 12 J impact at the centre for each laminate of Table 3. The impactor was dropped and hit the laminate with the velocity of 4.25 m/s. The thickness was considered constant for all the models and was equal to 4.8 mm.

Table 3 Summary of FE models
Full size table

The 3D FE models are shown in Fig. 2, in which only the composite laminate is different for each case of Table 3. Reduced integration 8-noded linear brick elements (C3D8R) were used to discretise the solid composite plies. A region of fine mesh with the element size of 1 mm × 1 mm was defined at the impactor/laminate contact zone while a course mesh area was defined for the region outside this contact area. The 1 mm × 1 mm mesh area was chosen based on the mesh sensitivity analysis performed in [29]. The laminates were plates between two rigid rectangular clamps and a penalty based contact with the friction coefficient of 0.9 was defined between the laminate and the camps to reproduce the experimental boundary conditions, to avoid out-of-plane movement, and to reduce the slip at the boundary [27, 45,46,47]. The interface of the composite plies was simulated by implementing zero thickness cohesive elements (COH3D8) at the interface of each two plies which resulted in 23 layers of cohesive interface elements.

Fig. 2
figure 2

Fully clamped low velocity impact model which shows the stacking sequence of laminates and different laminate geometry according to Table 3

Full size image

In order to study the effect of open holes on the low velocity impact response of the composite laminate, eight different laminates with the same geometry and a different configuration of open holes were considered. For details on the number of open holes and their positions in each laminate and their identification code see Table 3. In Table 3, different configurations are coded according to the following notations: the first character is a representer of the number of holes in the configuration, S for laminates with a single hole and D for laminates with two holes. The second and third characters show the diameter of the hole and the distance of the centre of the open hole to the impact origin, respectively. The first model of Table 3 is the pristine laminate without holes, i.e., the control specimen (CS). The results of the low velocity impact on CS laminate were used for validation of the FE approach. Four models were developed to investigate the effect of a single open hole and its distance from the impact origin on the mechanical response and damage in the composite laminate. The diameter of open holes was studied by developing three models in which the diameter of the hole was set equal to 3, 5, and 7 mm. Open holes to impact origin distances of 5, 10, 15, and 20 mm were simulated here. Also, a model with two holes was developed to study the influence of the different number of holes around the impact zone on the impact response of the composite laminates subjected to a low velocity impact.

4 Results and Discussion

In this section, the influence of the open holes on the mechanical response and progressive intralaminar and interlaminar damage is discussed based on the numerical results. First, the numerical model is validated by comparison with the numerical results with the corresponding experimental data on the control specimen. Then the results are divided into two parts, first, the effect of the distance of the open holes from the plate centre, i.e., the impact origin, and then the effect of the interaction of multiple open holes on the impact response is investigated. The global response of the plates and the interlaminar and intralaminar damage is the focus of the discussion.

4.1 Validation of the Numerical Model

The initial part of the result section is focused on the validation of the numerical model by comparing the FE prediction of the mechanical response and the damage of the CFRP specimen with the experimental low velocity impact test results [5, 6]. A hemispherical impactor with a diameter of 16 mm and a total mass of 1.325 kg was used for the drop weight low velocity impact test on CFRP specimens based on ASTM D7136 [48]. A fully clamped specimen of 150 × 100 mm2 was subjected to a 12 J low velocity impact in the centre and the impactor was trapped after the initial impact to prevent subsequent unwanted impacts. The specimen with a total thickness of 4.8 mm and a stacking sequence of [45°, 0°, -45°, 90°]3s was manufactured using unidirectional pre-preg laminae CYCOM® 977–2-34%-24 K IMS-196-T1.

The validity of the numerical model in predicting the mechanical response of composite laminate subjected to low velocity impact is demonstrated by a comparison of the force–time, force–displacement, and energy-time curves. Figure 3 shows the numerical and experimental comparison of the 12 J impact response. The numerical model can effectively predict the mechanical response of the laminate subjected to low velocity impact. The absorbed energy of 4.92 J was observed in the experimental test which was predicted equal to 4.56 J by the numerical one with an error of -7.3%. The comparison of experimental and numerical force–time curves of Fig. 3a also shows that the model is capable of giving a good prediction of the peak impact force and the impact time duration. The force–displacement curve from the numerical model and the experiment is shown in Fig. 3b. The numerical maximum displacement is in good agreement with the experimental result and is predicted with an error equal to 3.6%.

Fig. 3
figure 3

Experimental and numerical comparison of the impact response. (a): Force–time and energy-time curves, (b): force–displacement curve, and (c): delamination area

Full size image

The numerically predicted delamination area is shown in Fig. 3c which estimates the experimentally observed delamination area with an error of 3.9%. The solid red line of Fig. 3c represents the region of the projected delamination area and was recorded by a non-destructive ultrasonic test. The peanut shape delamination pattern at different interfaces propagates at 0°, + 45°, − 45° and 90° direction and is controlled by the fibre orientation of the layer below each interface. Therefore, the peanut shape delamination rotates through the thickness of the laminate and shapes a rotating fan pattern [4].

In order to investigate the capability of the numerical model in predicting the response of composite laminates with open holes, the experimental data of [20] were used. In [20] unidirectional glass/epoxy composite laminates with a stacking sequence of stacking sequence [452, 902, − 452, 02]s was tested. The control specimen, the specimen with one hole, and specimen with two holes were considered which had the size of 100 × 100 × 2.1 mm3. The specimens were clamped using rigid fixtures with a circular impact area of 70 mm diameter. The impactor of 10 mm diameter with a total mass of 3.4 kg impacted the plates with an impact energy of 6 J. The open holes had a diameter of 4 mm and were located at a 10 mm distance from the impact point. The mechanical properties of unidirectional glass/epoxy composite for these simulations were taken from [49]. The comparison between experimental and numerical impact responses is shown in Fig. 4 for laminates with and without the hole. The numerical model is capable of accurately predicting the impact response in the models with and without holes. The absorbed energy by the laminate is predicted with a discrepancy of -19.1%, -18.2%, and 14.1% for the pristine laminate, laminate with one hole, and laminate with two holes, respectively. In addition, the total delamination area was predicted within the error margin of 10% in different models.

Fig. 4
figure 4

Comparison of the experimental [20] and numerical results. Force–time and energy-time curves: (a): Control specimen, (b): Laminate with one open hole, (c): Laminate with two open holes. Force–displacement curves: (d): Control specimen, (e): Laminate with one open hole, (f): Laminate with two open holes

Full size image

4.2 Effect of the Distance of Open Holes and the Impact Origin

In order to study the effect of a low velocity impact on the mechanical response and damage behaviour of a composite laminate with open holes, different numerical models were developed with a variety of impact origin to the centre of hole distances. In each model, the impactor hits the plate at the centre and the open hole was defined in different models according to Table 3. Figures 5 and 6 show the energy-time and force–time curves for models with a single open hole with varying distances from the impact point. The presence of open holes resulted in higher energy absorption in the laminates compared to the control specimen. This effect was more profound in S-D5-L5 which showed energy absorption equal to 4.87 J which means an 8.2% increase compared to the CS. From Fig. 5 it can be observed that for open hole positions which are far away from the impact origin, for instance, S-D5-L20, the presence of the open hole had a less profound effect on the mechanical response compared to the impacts on the laminates with the open hole in the vicinity of impact origin. In all laminates with single open holes, the impactor rebounded, showing that the impact energy was too small to cause perforation. The values of the peak force, maximum deformation, and absorbed energy of the laminates with single open holes are presented in Table 4. The increase in the maximum deformation of the laminates while the peak impact force is decreased shows lower stiffness of the laminates with the open hole when compared to the CS which is consistent with the experimental findings of [20]. More fluctuations are visible in Figs. 6 and 7 for models with holes compared to the CS. The fluctuations increased with the decrease of the open hole distance to the impact point which is in good agreement with the results for patch repaired laminates [50]. In addition, the zoom region of Fig. 6 shows that the first drop of the force–time curve happens sooner in models with open holes this faster drop can be attributed to the initiation of delamination in models with holes at lower impact forces. The changes in the impact response showed due to the presence of a single hole was observed to be small which can be attributed to the material type and the highly stacked lay up in the simulated laminate or the low impact energy of the impactor which did not cause any fibre damage inside the specimens.

Fig. 5
figure 5

Comparison of energy-time curves of laminates with a single hole at different positions with the control specimen

Full size image
Fig. 6
figure 6

Comparison of force–time curves of laminates with a single hole at different positions with the control specimen

Full size image
Table 4 Peak force, maximum displacement, and absorbed energy of laminates with a single open hole
Full size table
Fig. 7
figure 7

Comparison of force–displacement curves of laminates with a single hole at different positions with the control specimen

Full size image

Figure 8a shows the comparison between the total projected delamination area of models with a single hole and the control specimen. Delamination is one of the main energy absorption sources of composite laminates when subjected to low velocity impact and this barely visible impact damage cannot be detected without proper inspections. In most cases, a bigger delamination area in the composite panel means higher energy absorption from the impact event. In Fig. 8a, the red cross mark shows the origin of the impact, the white circle shows the open hole position and the black region is the projected delamination area. For composite laminates with open holes, it can be observed that the presence of the hole has a significant influence on the total projected delamination area. For instance, in S-D5-L15, the total projected delamination area was increased by 20% due to the presence of the open hole.

Fig. 8
figure 8

Total projected delamination area, (a): For models with different single hole positions, (b): For models with open holes of different diameters, (c): For models with different numbers of holes

Full size image

In all of the models, the presence of the open hole led to a bigger projected delamination area, except for the S-D5-L5 in which the open hole is close to the origin of the impact. This is consistent with the experimental findings of [8] in which a smaller projected delaminated area compared to the control sample was reported for laminates with holes close to the impact origin. It can be said that the presence of an open hole leads to a more in-plane spread of damage as can be seen for S-D5-L10, S-D5-L15, and S-D5-L20 in Fig. 8a; while in the case of laminate with an open hole at 5 mm with respect to the impact origin, a reduction of the in-plane spread of the delamination can be observed which resulted in a more concentrated and in-depth propagation of the damage. This means that although the projected delamination area is smaller, more elements are failed in the local damage area compared to the other single hole models. This is consistent with the lower impact peak force, higher peak displacement, and lower impact bending stiffness that was observed for S-D5-L5 compared to the other models.

In thin composite laminates subjected to a low velocity impact, the matrix damage initiates at the back surface due to the dominance of bending stresses [29, 30] while the damage in laminated composites with open holes can also initiate at the edge of the open hole [8, 17] due to stress concentration caused by the open hole. Figure 9 shows the matrix damage area for two typical plies with the orientation of -45° and 45° located at the backside of the laminate. In this figure, the red area shows the matrix damage, and the white circles indicate the open hole location. It can be observed that the presence of the hole leads to damage initiation at two distinct locations near the edge of the hole and the impact origin. As for delamination, the presence of the hole mitigates the damage spread in the S-D5-L5 laminate; while for the S-D5-L10 and S-D5-L15, the open hole led to a stretch in the damaged area which resulted from the unification of the two impact initiation zones. The initiation and spread of damage at the edge of the open hole depend on the distance to the impact origin and the impact energy since it can be seen that for the S-D5-L20 model no damage was detected on the edge of the hole in the -45° and for the 45° the two impact damage regions were not merged.

Fig. 9
figure 9

Matrix damage in two typical plies with different hole positions. (a): A ply with -45° fibre orientation, (b): a ply with 45° fibre orientation

Full size image

Figure 10 shows the absorbed comparison of the energy, the sum of damage for the delamination area of all the laminate interfaces, and the sum of the matrix damaged area for all the plies of the laminates with a single hole with the corresponding values of the control specimen. This figure clearly shows that the projected delamination area is not a reliable indication of the damage inside the specimen since a bigger projected deamination area was observed for S-D5-L15, while the aggregation of both delamination area and matrix damage is in all the layers of the laminate is bigger for the S-D5-L5 which resulted in higher absorbed energy by internal damage in S-D5-L5, see Fig. 8a.

Fig. 10
figure 10

Summation of delamination, matrix damage from all of the plies in comparison with the absorbed energy of each model with a single hole

Full size image

4.3 Effect of the Size of the Open Hole

In order to investigate the influence of the open hole size, three models with different open hole diameters of 3, 5, and 7 mm, i.e., S-D3-L10, S-D5-L10, and S-D7-L10 were compared in this section. Figure 11 shows the comparison between the force–time curves of the control specimen with laminates with different hole sizes. Similar force–time responses in terms of peak force and impact time duration were observed from the open hole laminates of this section which showed that the size of the open hole has a less significant effect on the response compared to the open hole to impact origin distance. In addition, no clear trend could be observed from the energy-time curves of Fig. 12 for the energy absorption capacity of laminates with holes of different diameters. As discussed in the previous section, the presence of the open holes led to more interlaminar and intralaminar damage compared to the control specimen which was also observed from the low velocity impact results of this section.

Fig. 11
figure 11

Comparison of force–time curves of laminates with open holes of different diameters

Full size image
Fig. 12
figure 12

Comparison of energy-time curves of laminates with open holes of different diameters

Full size image

Figure 8b shows the comparison of the projected delamination area in which the change in the size of the open hole led to a significant change in the projected delamination area. A more stretched delaminated area was observed for the S-D3-L10 model. The delaminated area becomes smaller with the increase of the hole diameter. That being so, the aggregated delaminated area and matrix damage area were approximately the same for the single hole laminates of this section which indicates that changing the diameter of the open hole does not change the total damage area in the laminated composite. These results seem inconsistent with the concept of stress concentration in infinite plates with open holes subjected to in-plane loads in which smaller holes should lead to more intense zones of stress [51]. In order to shed light on this inconsistency, the stress distribution, σ22, for two typical plies of the laminate with orientations of 45° and 0° is shown in Fig. 13 at the impact time of 0.25 ms which is at the beginning of the impact event before initiation of matrix damage in the mentioned plies. This figure shows that the existence of the open hole leads to a significant change in the stress distribution resulting from the impact event. Zones of high stress can be observed at the vicinity of the edge of the open hole which causes the initiation and propagation of the damage to occur not only at the impact origin but at the vicinity of the edge hole. Interestingly, the presence of the open hole of different sizes resulted in a changed stress distribution compared to the control specimen with a higher value of the peak stress, while the diameter of the hole did not have a meaningful effect on the peak stress. This shows that the stress concentration of the open hole in a low velocity impact may be independent of the diameter of the hole similar to the isotropic bending problem that has been discussed in [51]. The mentioned finding was limited to the results of L = 10 mm and to open hole diameters investigated in this section and needs a more in-depth experimental and numerical verification for different hole diameters and locations.

Fig. 13
figure 13

Stress distribution of two typical plies with fibre orientation of 45° and 0° at the impact time of 0.25 ms

Full size image

4.4 Effect of the Multiple Open Holes

In this section, the effect of the number of open holes on the impact response of the CFRP laminate is discussed. Therefore, the low velocity impact response of CS was compared with the results of a single open hole laminate i.e., S-D5-L10, and a laminate with two open holes, i.e., D-D5-L10, see Table 3. Figures 14 and 15 show the comparison of the force–time and force–displacement curves. It can be seen that the models with open holes show a lower impact stiffness compared to the CS which is intensified with increasing the number of open holes from one to two. The same intensified trend can be observed for the peak force, impact peak displacement and impact time duration when the impact response of S-D5-L10 is compared to D-D5-L10. In addition, it can be seen Fig. 16 that the laminate with two open holes absorbed more energy compared to the two other laminates which can be attributed to the severity of internal damage in this case. For the laminate with a single hole the absorbed energy was increased by 6.7% compared to the CS, while for the laminate with two open holes the increase was 15.8%. The observation that the delamination initiation happened at a lower impact force for the D-D5-L10 model compared to the two other laminates is also of interest. The delamination initiated at an impact force of 2.18 kN for the CS, 1.73 kN for the S-D5-L10, and 1.34 kN for the D-D5-L10 laminate which can be a sign of stress concentration due to the presence of the open hole which led to damage initiation at lower impact forces.

Fig. 14
figure 14

Comparison of force–time curves of laminates with different numbers of holes and the control specimen

Full size image
Fig. 15
figure 15

Comparison of force–displacement curves of laminates with different numbers of holes and the control specimen

Full size image
Fig. 16
figure 16

Comparison of energy-time curves of laminates with different numbers of holes and the control specimen

Full size image

The comparison of the projected delamination area for the CS, S-D5-L10, and D-D5-L10 laminates is shown in Fig. 8c, while the interface-by-interface delamination of selected interfaces through the thickness of the models is compared in Fig. 17. It can be seen that both S-D5-L10 and D-D5-L10 models predicted a bigger projected delamination area compared to the CS. Although the projected delamination area of S-D5-L10 and D-D5-L10 was approximately identical, the absorption energy of D-D5-L10 was significantly higher than the S-D5-L10 potentially indicating more severe through-thickness damage within the delaminated area. The phenomenon is a specific characteristic of the laminates with open holes or patch repaired laminates, since for most composite materials subjected to low velocity impact a more spread projected damage area means more energy absorption [8]. This is well illustrated in Fig. 17 in which the significant increase in the damaged area for the S-D5-L10 and D-D5-L10 compared to the CS is limited to the interfaces in which a small damage area was reported for CS, for instance, see interfaces C1, C12, and C14 of Fig. 17. It was also noted that the open holes alter the delamination shape and orientation in almost every interface of the laminate and in most interfaces, regions of intensified delamination around the edge of the holes were observed, interfaces C22 for instance.

Fig. 17
figure 17

Interface by interface delamination area for CS, S-D5-L10, and D-D5-L10 at selected interfaces

Full size image

In order to make a balance between the delamination and matrix damaged area and the absorbed energy, the sum of damage in all the interfaces and layers was compared with the absorbed energy in Fig. 18. It was observed that the more severe damage of D-D5-L10, that resulted from the presence of two open holes in the vicinity of impact origin, did not spread along the in-plane direction, meaning that the projected delamination area was the same, while 8.7% more of total delamination area and 21.9% more of total matrix damage area was observed in D-D5-L10 compared to S-D5-L10 laminate. This severity of damage resulted in a higher peak displacement, lower impact stiffness which is consistent with the higher energy absorption of the laminate with two open holes. It is worth mentioning that the results of this paper were presented for the laminates subjected to a low velocity impact of 12 J. Further analysis and parametric studies are required to describe the effect of open holes in different energy ranges.

Fig. 18
figure 18

Summation of delamination, matrix damage from all of the 24 plies in comparison with the absorbed energy of with different numbers of holes and CS

Full size image

5 Conclusions

In the present work, a numerical study was performed of CFRP laminated composites with one and two open holes of different diameters in the vicinity of the impact origin to investigate the influence of the open holes on the impact response of laminated composites. A total of eight FE models were developed in which the distance of the centre of the open hole to the impact origin and the number of open holes were different. The models were validated by comparing the impact response of the control specimen without holes with the experimental data of force–time, force–displacement, energy-time, and delamination area. The conclusions of this paper can be useful in practice and real engineering applications, but it should be mentioned that the conclusions are limited to the to the low velocity impact of 12 J simulated in this paper and further investigations may be required for more general conclusions in different energy ranges. With the presence of open holes smaller damaged areas can be expected which may affect the maintenance of the composite structures. But it should be considered that due to the presence of the open holes the damage spread mechanism in the composite laminate is changed and has to be taken into account for the design or maintenance of structures. The main conclusions are the following:

  • Laminates with open holes show lower impact peak force, and higher energy absorption compared to the control specimen. The distance at which a single hole in a structure is located in relation to the impact origin influences the impact response of the laminate and for a 12 J impact, open holes at distances of less than 20 mm have a significant influence on the impact performance of the laminate.

  • The open holes change the shape and size of the damage caused by low velocity impact. If an open hole is close to the impact origin it can stop the in-plane spread of damage which results in a smaller projected damage area compared to the control specimen. In addition, the presence of holes leads to regions of damage initiation in the vicinity of the edge of the open hole which differs from the damage initiation location at the impact origin for the control specimen.

  • The presence of holes increases the severity of impact damage by increasing the sum of the delamination area and matrix damage inside the laminate while the projected delamination area may not change due to the presence of the open holes, therefore the projected damaged area is not a reliable source for impact analysis. The presence of open increases the severity of the damage in the local impact zone.

  • Increasing the number of holes intensifies the influence of presence of open holes and results in the initiation of damage at lower impact forces compared to the control specimen.