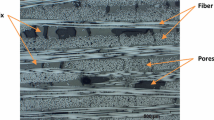
Abstract
In this reported research activity, a quantitatively 3D characterization at microscale of a CFRP reference composite with controlled porosity was performed by micro X-ray CT (µXCT); the results were compared with the destructive acid digestion analyses, following the procedure reported in the standard test method (ASTM D 3171 15) used to determine the composites’ porosity in General Aviation (GA). The μXCT analyses revealed a pore content of 4.37%v and identified the components, respectively, in 66%w of carbon fibres and 34%w of matrix; all obtained results demonstrated a high correspondence to the theoretical values of porosity (5.0%v) and components (67%w of carbon fibre and 33%w of polymer matrix). Instead, a not complete correspondence of the measures obtained by acid digestion was reported: 4.36%v of porosity, but 57%w of carbon fibre and 43%w of matrix. Therefore, the conformity of the μXCT results to the theoretical values demonstrated the feasibility and distinctiveness of the proposed NDT method for a rapid and reliable inspection of CRFP components used in GA in substitution of the standard DT and time-consuming digestion procedure. The proposed NDT inspection technique permitted not only the individuation and visualization in the reconstruction of the 3D analysed material of different components (e.g. pores, carbon fibres and polymer matrix) but also the 3D evaluation of the material composition with the identification and quantification of each constituent element.
Graphical abstract
E. Dilonardo*, M. Nacucchi, F. De Pascalis, M. Zarrelli, and C. Giannini
Inspection of Carbon Fibre Reinforced Polymers: 3D identification and quantification of components by X-ray CT

Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The use of carbon fibre-reinforced polymer (CFRP) composites to reduce the structural weight and to improve the fuel efficiency in aeronautical field is increasing every year, specifically for manufacturing components as flaps, ailerons, landing-gear doors, and other artefacts [1], up to the extreme example of the Boeing 787 fuselage. This increase can be ascribed to their high specific properties, such as low density and corrosion resistance, that make these composites competitive respect to the commonly used monolithic metals [2].
The properties of each component are important since they affect the performance of the overall composite whose it is made up, as, for example, the quality of the fibre-polymer matrix interphase; specifically, the porosity or the presence of voids, particularly at the interface, has a negative effect on the overall performance of the composite [3]. Therefore, the knowledge of the porosity value of the composite is important to calculate and predict its mechanical properties [4,5,6]; indeed, porosity in CFRPs can negatively affect the material strength: the interlaminar shear strength of the composites can be reduced by about 7% per porosity of 1%vol [7]. Nowadays, the most published researches have correlated the average through-thickness void volume fraction to the composite mechanical properties, demonstrating that the individual void features and their distribution affect the failure analysis [8]. For this reason, to evaluate the effect of the porosity defects on the material strength is important to determine non-destructively the pores’ volume distribution in a component. Moreover, also the appropriate selection of the matrix material, fibre length and orientation, and, particularly, the fibre content has a great influence on the composite’s mechanical characteristics [9]. In a CFRP composite, fibres are the primary load-carrying component in a composite; in general, their typical volume content is about 60 vol.%, since its positively result on the composites mechanical properties [10, 11].
The product quality and the optimization of CFRP properties can be ensured by the quantification of the volume of fibres and pores in the composite. The conventional techniques used to characterize the CFRP composites rely to DIN EN 2564 and ASTM D 3171 standard test methods [12, 13], based on physical or chemical experiments, such as matrix burn-off and acid digestion. Specifically, such techniques, used alone or in combination with others, include those listed below.
(a) Archimedes test to calculate the sample density, releasing on the accurate knowledge of fibre and matrix density and their weight fraction; indeed, the pore volume fraction is obtained by the theoretical composite density with no pores present [14]. This method could give as result a negative pores fraction, which is theoretically not possible [15].
(b) Matrix burn-off, based on an oven to degrade and remove the matrix from the fibres, permitting the measurement of the fibre weight. The determination of the sample density by the Archimedes test, together with the accurate knowledge of the constituent density, is necessary to calculate the composite pore volume fraction.
(c) Matrix digestion, based on an exposure to a highly oxidizing acid (commonly concentrated sulfuric acid) to completely dissolve the matrix leaving only the chemically resistant carbon fibres.
The use of concentrated acids and high operating temperature, and the production of toxic fume is dangerous for the health and the environment [16]; moreover, the procedure is time-consuming, has a low sample yield, and must be constantly controlled.
All of these three listed methods are not visual, and give only information on the total components, including the porosity, but not the pores size and distribution [13].
(d) 2D imaging by optical and/or electron microscopy (e.g. Scanning Electron Microscopy) [17], based on visual and destructive analysis method, permitting to evaluate the pores size, shape and distribution [18]. Although, it is largely used in industry thanks to the easiness of a visual characterization, inherent section-bias errors are associated to sample cross-sectional 2D analyses. Moreover, 2D imaging methods can give important visual information, but limited by the information on 2D, that is not representative of the whole sample [19, 20].
(e) Ultrasonic imaging based on the ultrasonic attenuation levels to predict the pores content [18], with direction-dependent wave speeds and strong ply/resin boundary reflections [21]. This technique shows beam-skewing effects due to sample anisotropy that causes several problems like inaccurate sizing and faulty location of the defects with respect to quantitative non-destructive evaluation [22]. The complexity of ultrasonic inspection not only arises from the nature of anisotropy but there are other problems due to complex geometries [23]. Moreover, the ultrasonic wavelengths, used for the quality control, are too large to provide sufficient resolution to determine void size and shape, and may not detect micro voids at all [24]. Finally, this NDT method has the distinct disadvantages of being intrinsically slow and requiring a coupling agent in most situations [25]. Ultrasonic imaging is commonly used for quality control by detecting delamination and large spots. In general, it is applied to detect general attenuation, which is in turn correlated to the void content, thus providing an estimate of local void concentrations across the entire part surface [26, 27]. The ultrasonic inspection has some disadvantages, such as the inspection speed, a limited lateral and axial spatial resolution, and the requirement of a coupling agent, which may contaminate the sample [28−30], or of a coupling with another NDT method as thermography [31].
The all reported conventional composites inspection analyses have limits in accuracy and reliability, including also problems in the extraction of information from their data [13, 26−32].
Nowadays, among various NDT methods, X-ray CT is increasingly used to evaluate and reconstruct three-dimensional (3D) internal structures and to inspect the structural characteristics of composites [31, 33−35]. Recently, the use of X-ray micro-CT has increased in various application fields (e.g. medical, geological, biological, material, and food sciences), allowing not only qualitative but also quantitative non-destructive inspection of composite materials [32]. Radiographical slices permit to obtain unique insights, providing information across the length scales, from the whole sample to the individual components (e.g. pores, fibres, etc.) [33, 34, 36, 37]. The X-ray CT technology is based on the computational reconstruction of the radiographs (projections) acquired at various angles of illumination; the image contrast relies on differences in the attenuation of X-rays paths through the object under investigation [35]. This permits to mathematically reconstruct a cross-sectional image by the attenuation measurements at different angles on the detector. Moreover, since the thickness of each 2D slice is known, a 3D model can be virtually created by stacking the 2D images [32].
The image conversion in the binary format, created from the grayscale histogram, permits to individuate and to separate each identified phase from the others [38]. However, some challenges and limitations in utilizing X-ray CT still have not been overcome such as the time-consuming scan duration, which affects the analysis cost, and the limitation on type of materials and on size of specimens [39].
In the previous manuscript, the versatility of NDT X-ray CT in the inspection strategy to evaluate various types of CFRP-based structures, not only monolithic but also sandwich configurations which otherwise could not have been analysed by the standard DT acid digestion method, was demonstrated [40].
In this study, a monolithic CFRP-based panel with controlled porosity (about 5 vol.%) has been used as composite reference to compare the two techniques, the NDT X-ray micro-CT and the acid digestion method reported in the standard procedure ASTM D3171 DT, both used in the structural inspection of materials for GA. The porosity and composition analyses acquired by μXCT have revealed values comparable with both methods, the theoretical and the standard DT ones, demonstrating, at the same time, its accuracy and versatility based on a 3D visual reconstruction and inspection.
Finally, the conformity of the obtained μXCT results respect to the theoretical values has demonstrated the possible application of this NDT technique as a fast screening analyses of GA components, in substitution of the standard DT and time-consuming digestion procedure.
2 Materials and Methods
2.1 CFRP-based Panel
A reference panel made up by T700 twill prepreg epoxy resin/carbon fibres (2 × 2 twill 12 k T700S pre-impregnated epoxy carbon fibre as supplied by Torayca) [41], consisting of [(0°/90°)6]S layers, was built in high-pressure autoclave; details about the processing conditions and procedure can be find in Ref. [42].
The description of the CFRP-based panel is reported in Table 1.
Three samples with approximately the same dimensions were cut in parallelepiped form from the same panel. Firstly, they were analysed by NDT X-ray CT. To have a good resolution of 5 µm, the analysed volume had to be lower, for each sample, therefore three different regions with the same volume were selected for a statistical evaluation, and the post-analysis data treatments were repeated 5 times for a good measure reproducibility.
Subsequently, the entire three samples were digested by the DT acid treatment.
2.2 Acid Digestion
Three samples, with the same dimensions and minimum weight of 1 g, were obtained from the same CFRP-based panel. After the panel cutting, the samples were conditioned, following the D procedure reported in the ASTM D5229 standard test method, at a temperature of 25 °C ± 5 °C and relative humidity of 65% [43].
Following the A procedure of ASTM D3171 standard test method, the polymeric matrix was dissolved in an acid nitric solution [13]. The residue, consisting only of the reinforced carbon fibres, was, subsequently, filtered, cleaned, dried, and weighted to calculate the weight percentage of fibres in the sample. Therefore, knowing the composite and fibres densities, that were obtained following the ASTM D792 standard procedure and/or extrapolating by dimensional measurements [43], the weight percentages allowed to obtain the volumetric percentages; moreover, information on the voids (porosity) content was extracted.
In Table 2, the measured weight, before (Mi) and after the acid digestion (Mf), and volume values of three tested samples, Reference 1 (Ref. 1) and Reference 2 (Ref. 2), and Reference 3 (Ref. 3), with the use of a hydrostatic balance, on the basis of the indications reported in ASTM D792 standard procedure, are reported.
The extrapolated densities values of the composite components, fibres and resin, and of the entire material are listed in Table 3.
After the acid digestion, the resin matrix was removed, the residual content was the carbon fibres that were cleaned and weighted to calculate the parameters of interest by the following equations, reported in ASTM D792 standard procedure [44].
The content of reinforced carbon fibres (WF), expressed in weight percentage, is calculated as reported in Eq. 1:
where Mi and Mf are the sample weights before and after the acid digestion, respectively.
The volume fraction of the carbon fibres (VF), expressed in volume percentage, is obtained by the following equation:
where ρC is the composite density, ρF is the fibre density.
In the same manner, the polymer matrix weight and volume fractions, WM and VM, both expressed in percentages, are calculated, as reported in Eqs. (3) and (4):
where ρM is the polymer matrix density.
These data permit to calculate the percentage volumetric quantity of pores (porosity) in the composite by Eq. 5:
The extrapolated components content, referred in weight and volume percentages, and the porosity values of three tested samples, originated from the same panel, are reported in Table 4.
2.3 Optical Microscopy
A preliminary screen of the composite lay-up structure and thickness was carried out by optical microscopy. The optical images were acquired by an optical Nikon microscope (AZ100 Multizoom), equipped with a Digital Camera Nikon DS-Fil.
2.4 X-ray CT
The 3D structure of the composite was evaluated by a high resolution X-ray micro-CT system, GE Phoenix Nanatom S, equipped with a nano-focus X-ray tube and a 12 bit Hamamatsu flat panel detector (2300 × 2300 pixels and pixel pitch, P, of 50 μm). The experimental conditions used for -ray CT analyses, optimized after a preliminary evaluation of the best set-up regarding the tomographic system parameters, are reported in Table 5.
By measuring the X-ray attenuation on the detector plate while rotating the specimen, the regional density in specific 3D locations, or voxels, of the part was reconstructed; to each voxel (3D pixel) a grayscale unit was assigned, representing its relative density.
The 2D radiographs in each scan were then reconstructed into 3D absorption contrast images by a filtered-back projection algorithm. The generation of virtual sections and the 3D object reconstruction were obtained by processing the total acquired X-ray CT data thanks to GE Datos|× 2 software. Qualitative analyses of the images, including segmentation, porosity calculation, etc. were carried out on software Avizo 8 Fire Edition of Visualization Science Group. The X-ray micro-CT datasets were cropped to a prismatic region of interest (ROI) to exclude voxels associated with outside air (background). Then, a gaussian filter in AVIZO was applied on the X-ray images to smooth out noise.
To evaluate the reproducibility of the analysis process, five different samples taken from the same panel were checked, replicating the computing (e.g. porosity, fibre content, etc.) for three times for each analysed sample [40].
The segmentation/separation of the carbon fibres from the polymer matrix has been repeated 5 times for each X-ray CT dataset, selecting the threshold boundary values in a small range of values, in the manner which each value deviated a little from the others.
3 Results and Discussion
A preliminary evaluation of composite structure was achieved by conventional optical microscopy. In Fig. 1 the optical microscopy images of composite’s top view and section, each at two different magnifications, are reported.
Fig. 1A shows the plain disposition of the carbon fibres on the first ply on the top. The carbon fibres are enclosed in a polymeric matrix, which has the function of keeping them together and, therefore, of compacting the material. Carbon fibres form a "twill" type knitted structure: each fibre passes alternately under and over each warp fibre. The structure is symmetrical; although the distribution of the carbon fibres is homogeneous, on the surface, discontinuity and defects of micrometric dimension are evident.
Figure 1B shows the optical microscopy images of the material section at two different magnifications. From these images the 12 plies that build-up the monolithic panel are distinguishable; each ply has a thickness of about 0.23 mm, and the total thickness is about 2.8 mm. The acquired images reveal that the plies sequence, reported in the experimental section, is respected although some of them are dislocated; moreover, entrapped air in the plies sequence is evident: voids (dark areas) are shown mainly in the interplay regions of the cross section.
To evaluate in 3D non-destructive manner the material composition, identifying and quantifying the different components (e.g. pores, carbon fibres and polymer matrix), five different samples of the composite, from the same panel, were analysed by X-ray CT at a resolution of 5 μm (the used experimental conditions are reported in the experimental section). The choice of the selected resolution has been motivated because of the preliminary X ray CT set up, necessary to find the best analysis conditions with the optimum acquisition time-resolution ratio, and on the preliminary material evaluation by optical microscopy that revealed the presence of detectable sub-millimetre pores in the section of the composite panel.
The extraction of quantitative information from X-ray CT images requires appropriate image processing (e.g. filtering) and further segmentation.
The post analysis data treatment was based on these following steps: (i) the use of Gaussian filter to de-noise the acquired grayscale images by reducing noise and artefacts without worsening the edge and the details visibility in the images; (ii) the image segmentation by defining threshold intensity values associated to the different components of the composite; (iii) the labelling of all identified components.
The quantification of each identified component in the analysed sample volume was computed as volume percentage and defined as the ratio between the total volume of the specific component (pores, fibres, matrix) and the total composite volume multiply by 100, as reported in Eq. (6):
The most important process’ phase for the component calculation is the choice of the threshold for the image binarization that permits to separate the selected component, e.g. pores, from the rest of the composite (e.g. polymeric matrix and carbon fibres): specifically, pixels with a grey-scale intensity in a range of selected threshold values are indicated as voids/pores and settled as background, therefore equal to zero (black); all those with higher intensity are considered solid material, therefore equal to one (white) [38]. Therefore, the same procedure was repeated to individuate each component, the polymeric matrix and the carbon fibres, in the composite, changing only the threshold value range specific for the component.
The threshold boundary, where a phase ends and the other begins, has been determined by taking the average intensity level of each phase similar to the grayscale image histogram technique. Once each phase has been defined and segmented, each component has been individually inspected and separated. Practically, the threshold value was selected evaluating the grayscale intensity histogram of the total dataset. Figure 2 depicts the grayscale histogram of the composite.
In general, the segmentation can be easily performed by determining threshold values based on the contrast (i.e., absorption) of the reconstructed 3D volume data since each component has a different X-ray mass attenuation coefficient [45]. However, the case of, segmentation of carbon fibres and polymeric matrix has been much more challenging, since these two components have a similar density-contrast.
As in other reported histograms related to CFRPs data set [45], also in this case, the grayscale histogram has a bimodal trend; therefore, the phase separation between the voids (pores inside the composite and the background) and the carbon fibres reinforced polymeric matrix is well defined: the threshold value was selected by a visual analysis in an area around the abscissa of the relative minimum between the two peaks of the distribution. The same simple procedure could not be used to separate carbon fibres and polymeric matrix; indeed, the histogram reveals a unique and widened peak at higher intensity. To resolve this peak and to permit a phase separation of these two components a visual evaluation of each slice, including the line probe analysis, as reported in Fig. 3, was necessary; finally, defined the threshold value to distinguish these two phases, the histogram was then segmented into different phases according to grey level intensities characterising the internal microstructure.
The “line-probe” command, in the Avizo software, was used to evaluate the point-to-point variation of grayscale values along a selected dimension in the acquired slice of the analysed sample, as showed for the two slices in the XZ and XY planes, reported in Fig. 3.
Since the line probe reveals the correspondence between the grayscale intensity and the material composition, the correspondence between the cursor point position on the sample slice and the grayscale value in the histogram plot has permitted to associate the threshold values to each sample component: the minimum intensity values are placed in correspondence to the background (the extreme A and B points in Fig. 3) and the pores (voids) inside the sample, included within the 29 threshold value (in a scale from 0 to 255). Not a sharp distinction exists by X-ray CT between the polymeric matrix and the reinforced carbon fibres since both are carbon-based materials; thus, a visual segmentation of the polymeric matrix and reinforced carbon fibres has been necessary, evaluating a point-to-point variation of the grayscale intensity, along the selected line, in each reconstructed sample slices (more than 300 slices for each dimension). Two lines were drawn in Fig. 3 to separate the material phases: one at 29 and another at 32, so that all voxels with greyscale values less than 29 were classified as pores, those with values higher than 32 as the fibres, and the rest as matrix.
To determine the accuracy of the components’ segmentation, which controls the final data, various tests have been done choosing different threshold value in a selected range, deviating from each other of a small quantity; it was evaluated that the final calculated data differ from each other of a not significant entity.
In Fig. 4 the grayscale histogram reports the phase separation on the bases of the threshold values above reported [45]. Despite individual carbon fibres appeared in the µCT slices, as shown in Fig. 3, the segmentation method had not allowed to separate each individual fibre, since they were lumped together.
In Figs. 5 the tomographic slices in XY and XZ planes, before and after segmentation process to label pores, matrix, and carbon fibres, are reported.
The segmentation was followed by the component identification and labelling processes; for each component, the volume was calculated. In Fig. 6 all individuated components are labelled by different colours: pores are black, carbon fibres are green, and matrix is blue, respectively.
In the volume evaluation of each component, to avoid the pixel noise contribution, volumes lower than 8.0 10–6 mm3 were excluded (volumes underestimation). The correctness of adopted procedure was confirmed by overestimation (evaluation of all detected volumes) since the variation of the total component content calculated affected just the third significant digit (relative variation less than 2%) [40].
To evaluate the measurement accuracy of the µXCT respect to the standard procedure based on the acid digestion, the total content of pores, CFs and matrix was calculated and compared to the reference data.
In Fig. 7A the volume percentage of the various components obtained by µXCT and acid digestion are reported; in the figure inset the porosity values obtained by the two different methods are compared with the theoretical one.
The two compared methods reveal the same pores content, and, therefore, the same porosity, comparable with the theoretical value (about 5 vol.%); instead, for the other two labelled components, CFs and polymeric matrix, the contents, expressed in vol. %, are not comparable.
To have reference data also for the total CFs and matrix content, the weight percentages obtained by two methods were compared respect to the tabulated ones in the material datasheet [34], as reported in Fig. 7B. The weight percentages of the two components obtained by µXCT, 66 w.% of CFs and 34 w.% of matrix, are comparable with the tabulated ones, 67 w.% and 33 w.% respectively.
The values obtained by the standard acid digestion method, 57 w.% of CFs and 43 w.% of matrix, differ from the reference ones. The not complete correspondence of these measured values with the theoretical ones probably depends on the low accuracy of this technique that requires an accurate knowledge of the total analysed sample volume, and of the components densities. Indeed, the acid digestion is a destructive technique with a high measurement uncertain to uncontrollable random variations in the measurement processes (e.g. sample volume determination).
4 Conclusions
Considering the required sample preparation and the total analysis processes, the characterization information available, the total cost and the overall accuracy and reliability, it can be concluded that µXCT is more accurate and reliable technique to characterize composite materials, such as CFRPs, respect to the standard acid digestion procedure. The standard destructive technique requires an accurate knowledge of the sample volume and of its components, this being an inherent disadvantage, limiting its application; indeed, small variations in the determination of the sample volume can lead to great variations in the results, compared to the reference data. In this context, µXCT permits not only to quantify the material components and to evaluate the composite porosity, without any material destroy, but also, at the same time, gives an interactive 3D exploration and visual analysis of the material components, by the complete 3D volume rendering of the analysed material. Therefore, the NDT μXCT seems to have all the qualities to substitute the standard DT and time-consuming acid digestion procedure, permitting, indeed, a more accurate and faster screening of GA components.
Finally, the proposed procedure based on μXCT analysis represents a promising NDT inspection technique, that can provide 3D information across a very wide range of composite materials in a great variety of application fields, not only industrial metrology and manufacturing, but also, more generally, materials science, biomedical and life sciences, food science, palaeontology, and earth sciences.
Data Availability
The data that support the findings of this study are available from the corresponding authors on reasonable request.
References
Schwartz, M.M.: Composite Materials Vol.1: Properties, Nondestructive Testing, and Repair, Prentice-Hall Inc., New Jersey, USA (1997)
Faulstich de Paiva, J.M., Mayer, S., Rezende, M.C.: Comparison of tensile strength of different carbon fabric reinforced epoxy composites. Mater. Res. 9, 83–90 (2006)
Wilbers, A., Biguri, A., Schillings, J., Loos, J.: Application of iterative reconstruction algorithms to mitigate CT-artefacts when measuring fibre reinforced polymer materials. Polymer 177, 120–130 (2019)
Leali Costa, M., Frascino, S., de Almeida, M., Cerqueira Rezende, M.: The influence of porosity on the interlaminar shear strength of carbon/epoxy and carbon/bismaleimide fabric laminates. Compos. Sci. Technol. 89, 89–97 (2013)
Khosravani, M.R.: Influences of Defects on the Performance of Adhesively Bonded Sandwich Joints. Key Eng. Mater. 789, 45–50 (2018)
Abdellah, M.Y.: Comparative study on prediction of fracture toughness of CFRP laminates from size effect law of open hole specimen using cohesive zone model. Eng. Fract. Mech. 191, 277–285 (2018)
Birt, E., Smith, R.: A review of NDE methods for porosity measurement in fibre-reinforced polymer composites. Insight-Non-Destructive Testing and Condition Monitoring 46, 681–686 (2004)
Gagauz, I., Kawashita, L.F., Hallett, S.R.: Effect of voids on interlaminar behaviour of carbon/epoxy composites. ECCM 2016 – Proceeding 17th Eur Conf Compos Mater 26–30 (2016)
Mohsin, M.A.A., Iannucci, L., Greenhalgh, E.S.: Fibrevolume-fraction measurement of carbon fibre reinforced thermoplastic composites using thermogravimetric analysis. Heliyon 5, e01132 (2019)
Rasheed, H.A.: Strengthening Design of Reinforced Concrete with FRP, CRC Press (2014)
Grund, D., Orlishausen, M., Taha, I.: Determination of fibre volume fraction of carbon fibre-reinforced polymer using thermogravimetric methods. Polym. Testing 75, 358–366 (2019)
European Committee for Standardization: Determination of the Fibre-, Resin- and Void Contents, DIN EN 2564
ASTM International: Standard Test Methods for Constituent Content of Composite Materials, ASTM D3171
American Society for Testing of Materials (ASTM): Standard test methods for void content of reinforced plastics, Designation D 2734 – 09
Kellyand, A., Zweben, C.: Comprehensive Composite Materials - Test Methods, Nondestructive Evaluation, and Smart Materials, Elsevier Science Ltd. 5, (2000)
American Society for Testing of Materials (ASTM): Standard test methods for constituent content of composite materials. Designation D 3171–09
Waterbury, M.C., Drzal, L.T.: Determination of fibre volume fractions by optical numeric volume fraction analysis. J. Reinf. Plast. Compos. 8, 627–636 (1989)
Liu, L., Zhang, B., Wang, D., Wu, Z.: Effects of Cure Cycles on Void Content and Mechanical Properties on Composite Laminates. Compos. Struct. 73, 303–309 (2006)
Lundstreom, T.S., Gebart, B.R.: Influence from process parameters on void formation in RTM. Polym. Compos. 15, 25–33 (1994)
Hamidi, Y., Aktas, L., Altan, M.: Effect of packing on void morphology in resin transfer molded E-Glass/epoxy composites. Polym. Compos. 26, 614–627 (2005)
Caminero, M.A., García-Moreno, I., Rodríguez, G.P., Chacón, J.M.: Internal damage evaluation of composite structures using phased array ultrasonic technique: Impact damage assessment in CFRP and 3D printed reinforced composite. Compos. B Eng. 165, 131–142 (2019)
Ibrahim, M.E., Smith, R.A., Wang, C.H.: Ultrasonic detection and sizing of compressed cracks in glass and carbon-fibre reinforced plastic composites. NDT E Int. 92, 111–121 (2017)
Barry, T.J., Kesharaju, M., Nagarajah, C.R., Palanisamy, S.: Defect characterisation in laminar composite structures using ultrasonic techniques and artificial neural networks. J. Compos. Mater. 50, 861–871 (2016)
George, A., Brandley, M., Dart, R., Fullwood, D.T.: Void modelling in resin infusion. J. Adv. Mater. 1, 79–93 (2015)
Duan, Y., Zhang, H., Maldague, X.P.V., Ibarra-Castanedo, C., Servais, P., Genest, M., Sfarra, S., Meng, J.: Reliability assessment of pulsed thermography and ultrasonic testing for impact damage of CFRP panels. NDT and E Int. 102, 77–83 (2019)
Almeida, S., Neto, Z.: Effect of void content on the strength of composite laminates. Compos. Struct. 28, 138–148 (1994)
Liu, L., Zhang, B., Wang, D., Wu, Z.: Effects of cure cycles on void content and mechanical properties of composite laminates. Compos. Struct. 73, 303–309 (2006)
Gholizadeh, S.: A review of non-destructive testing methods of composite materials. Procedia Structural Integrity 1, 050–057 (2016)
Kersemans, M., Verboven, E., Segers, J., Hedayatrasa, S., Van Paepegem, W.: Non-Destructive Testing of Composites by Ultrasound. Local Defect Resonance and Thermography, Proceedings 2, 554–563 (2018)
Wang, J., Zhang, J., Chang, T., Cui, H.-L.: A Comparative Study of Non-destructive Evaluation of Glass Fibre Reinforced Polymer Composites Using Terahertz. X-ray, and Ultrasound Imaging, International Journal of Precision Engineering and Manufacturing 20, 963–972 (2019)
Burrows, S.E., Rashed, A., Almond, D.P.: Combined laser spot imaging thermography and ultrasonic measurements for crack detection. Nondestructive Testing and Evaluation 22, 217–227 (2007)
Garcea, S.C., Wang, Y., Withers, P.J.: X-ray computed tomography of polymer composites. Compos. Sci. Technol. 156, 305–319 (2018)
Sisodia, S.M., Garcea, S.C., George, A.R., Fullwood, D.T., Spearing, S.M., Gamstedt, E.K.: High-resolution computed tomography in resin infused woven carbon fibre composites with voids. Compos. Sci. Technol. 131, 12–21 (2016)
Chowdhury, N.T., Tao, C., Pearce, G.M., Walsh, S.D.C., Latham, S.J., Middleton, J.P., Beeching, L.: Design of an uncontaminated textile CFRP specimen optimised for both mechanical testing and X-ray microtomography. Compos. A 123, 208–221 (2019)
Tretiak, I., Smith, R.A.: A parametric study of segmentation thresholds for X-ray CT porosity characterisation in composite materials. Compos. A 123, 10–24 (2019)
Stock, S.R.: X-ray microtomography of materials. Int. Mater. Rev. 44, 141–164 (1999)
Stock, S.R.: Recent advances in X-ray microtomography applied to materials. Int. Mater. Rev. 53(3), 129–181 (2008)
Landis, E.N., Keane, D.T.: X-ray microtomography. Mater. Charact. 61, 1305–1316 (2010)
Khosravani, M.R., Reinick, T.: On the Use of X-ray Computed Tomography in Assessment of 3D-Printed Components. J. Nondestr. Eval. 39, 75 (2020)
Dilonardo, E., Nacucchi, M., De Pascalis, F., Zarrelli, M.: Giannini C, High resolution X-ray computed tomography: A versatile non-destructive tool to characterize CFRP-based aircraft composite elements. Compos Sci Technol 192, 108093 (2020)
Toray Composites America, Torayca Prepreg Data Sheet
Lionetto, F., Buccoliero, G., Pappadà, S., Maffezzoli, A.: Resin pressure evolution during autoclave curing of epoxy matrix composites. Polym. Eng. Sci. 57, 631–637 (2017)
American Society for Testing of Materials (ASTM): Standard Test Method for Moisture Absorption Properties and Equilibrium Conditioning of Polymer Matrix Composite Materials, Designation D5229
American Society for Testing of Materials (ASTM): Standard Test Methods for Density and Specific Gravity (Relative Density) of Plastics by Displacement, Designation D792
Hamid, S., Reza Sanei, Fertig R.S.: Uncorrelated volume element for stochastic modeling of microstructures based on local fibre volume fraction variation. Compos Sci Technol 117, 191–198 (2015)
Acknowledgements
The authors thank the Regional Apulian Call “Support for Regional Technological Cluster for Innovation” for financial support, specifically COGEA-Composite Certification in General Aviation (OES4AM4). Finally, the authors thank Dr Marco Pugliese of CNR-Nanotec for the porosity determination by acid digestion and Ing. Giuseppe Buccliero of CETMA-Materials and Structures Engineering Department for the preparation of the reference CFRP panel.
Funding
Open access funding provided by Politecnico di Bari within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Highlights
• Comparison of the non-destructive X ray CT vs destructive acid digestion to inspect the structure of aircraft CFRP-based components.
• Interactive 3D exploration and quantitative analysis of CFRP composites by µXCT.
• Multiple images processing technique for components quantification, individuation and visualization in 3D reconstruction.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Dilonardo, E., Nacucchi, M., De Pascalis, F. et al. Inspection of Carbon Fibre Reinforced Polymers: 3D identification and quantification of components by X-ray CT. Appl Compos Mater 29, 497–513 (2022). https://doi.org/10.1007/s10443-021-09976-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10443-021-09976-x