1 Introduction

Reinforced materials have become of high interest over the last decades due to the improved weight-specific material properties. Those heterogeneous materials usually consist of two components, the matrix material and reinforcing particles or fibers, respectively. One example here are short fiber-reinforced composites (SFRC), where thermoplastic matrix materials are combined with fibers of 100μm to 300μm length. Due to the finite length of the reinforcing elements, these materials are capable of serial production processes like injection molding. However, the manufacturing with injection molding results in a probabilistic microstructure of the component and hence leads to a spatial fluctuation of the material properties.

Since these fluctuations on the mesoscale influence the structural response on the component level, the representation of the varying material properties for numerical simulations of the component is of particular interest. For an adequate verification of proposed modeling approaches on the mesoscale experimental investigations are essential. One testing technique, that is frequently used for small-scale testing is nanoindentation [1]. By nanoindentation, the material properties are analyzed in the \(\mu\)N to mN domain using indentation loads in the range of nm to \(\mu\)m. This allows one to not only characterize the material on the mesoscale but also to derive a spatial distribution of the near-surface material properties [2]. With quasi-static indentation tests test elastic as well as plastic material properties can be derived. The elastic material response is obtained by measuring the Young’s modulus, whereas the plastic behavior is characterized by the hardness. Due to this multivariate use, indentation tests are used in a wide range of applications for the analysis of heterogeneous material properties. This includes the characterization of MEMS-devices [3, 4], biomedical material like brain tissue [5, 6], dental restorative composites [7, 8], as well as nanocomposites [1, 9, 10]. For fiber-reinforced polymers so far only the interphase between the two constituents are analyzed experimentally by nanoindentation for example in [11,12,13]. A comprehensive review of nanoindentation applications for polymer composites is provided in [14].

The studies presented in the literature provide promising results on the analysis of the microstructural properties of reinforced heterogeneous materials. But so far, in contrast to the macroscopic analysis as shown in [15, 16], there is only little investigation on the combination of this experimental approach with the characterization of SFRC on the mesoscale and corresponding numerical simulations. Therefore, in this work first, the spatial distribution of the linear-elastic quasi-static material properties for a thermoplastic matrix filled with glass fibers on the mesoscale is experimentally obtained by indentation tests. In contrast to the work presented in [11,12,13] not the interface properties and the characteristics of the constituents are measured individually, but a region comparable to a statistic volume element is considered. The size of this area defined by the projected area of the indentation tip at maximum load varies between \(2500 \mu \mathrm {m}^2\) and \(7000 \mu \mathrm {m}^2\) and hence, includes not only a single phase of the heterogeneous material but the constituents as well as the interphase. Due to this, the experimentally obtained results are not only affected by the projected area but also by the surrounding material. This study aims to determine the size of the effective cross-section, analyzed by indentation tests on the mesoscale.

The structure of the presented work is as follows. First, the fundamentals of the multiscale approach are introduced in Sect. 2. Next, Sect. 3 gives a brief overview of the theoretical framework for the material characterization by indentation tests as well as the experimental setup and procedure of this study. This is followed by the presentation of the experimental results in Sect. 4. These results are discussed in detail in Sect. 5. This includes the numerical simulations as well as the determination of the effective cross-section size. Finally, Sect. 6 gives a summary and a conclusion of the presented work.

Fig. 1
figure 1

Multiscale approach [17]

Full size image

2 Multiscale Approach

Usually, materials are assumed to be homogeneous when observed at the component level. However, the microstructure of materials is mostly heterogeneous. This leads to the conclusion, that the material properties of a volume element, taken from a component, depend on the volume’s edge length d. In case that the material properties of the volume element are independent of its origin, one speaks of a representative volume element (RVE). A well-known definition of the RVE size is given in [18]. For an RVE the effective material properties are independent of the used load case. This is equivalent to the fact, that an RVE consists of a statistically sufficient number of inhomogeneities to be representative of the microstructure. Therefore, the material properties of this volume can be replaced by a homogeneous representation. It is obvious that the scale d must be much larger than the size l of an inhomogeneity and much smaller than the component scale L. This approach is known as the separation of scales, which is also formulated as [19,20,21]

$$\begin{aligned} l \ll d \ll L. \end{aligned}$$
(1)

The dimension l is assigned to the microscale, L to the macroscale, and the edge length d of the RVE to the mesoscale. The concept is also shown in Fig. 1.

Fig. 2
figure 2

Scheme load cycle indentation test, [22, 23]

Full size image

3 Indentation Tests

3.1 Theory

For the experimental determination of the linear-elastic quasi-static material properties by indentation tests the slope of the force-displacement curve of the unloading process is evaluated in order to derive the indentation modulus, see Fig. 2. Hence, the indentation modulus, which is also referred to as the reduced modulus, is expressed by [24, 25]

$$\begin{aligned} E_r = \frac{{\text {d}} P}{{\text {d}} h} = \frac{1}{\beta } \frac{\sqrt{\pi }}{2}\frac{S}{\sqrt{A_p(h_c)}}, \end{aligned}$$
(2)

where S is the stiffness of the contact, \(A_p\) the projected area of the indentation tip for a contact depth \(h_c\), and \(\beta\) an empirical correction factor of the indenter uniaxial symmetry when using pyramidal indenter [26, 27].

The indentation or reduced modulus is not equal to the Young’s modulus of the specimen’s material, because the measurement is affected by the material of the indentation tip. Therefore, a correction of the obtained indentation modulus is necessary. Regarding the Poisson’s ration \(\nu _i\) and the Young’s modulus \(E_i\) of the indentation tip the Young’s modulus of the specimen \(E_s\) is obtained by evaluating

$$\begin{aligned} E_s = \frac{1-\nu _s^2}{\frac{1}{E_r} - \frac{1-\nu _i^2}{E_i}} \end{aligned}$$
(3)

It is obvious that for the determination of the Young’s modulus the Poisson’s ratio \(\nu _s\) of the analyzed material must be known or needs to be approximated first. The tip material is usually diamond or sapphire. The presented framework was developed for homogeneous material. However, in context of determining the apparent material properties of a heterogeneous material, it seems appropriate to use these formulas since the apparent material properties are a homogeneous representation of a heterogeneous material on the mesoscale.

The definition of the indentation modulus in Eq. (2) shows that the result of an indentation test is influenced significantly by the geometry of the indentation tip. There is a variety of shapes available for material characterization by indentation tests. This includes pyramids, flat punch, and conospherical indentation tips. Most common is a three-sided triangular based pyramid, the Berkovich tip [28], which is also used in this study. The pyramidal shape is characterized by a nominal angle of \(65.3^\circ\) between the face and the normal to the base at apex as well as an angle of \(76.9^\circ\) between edge and normal. The radius of the tip is less than \(0.1 \mu \mathrm {m}\) [29]. Corresponding to the geometry the projected area of a perfectly sharp Berkovich tip is given by [30]

$$\begin{aligned} A_p = \pi h_c^2 \tan ^2 \varphi = 24.5 h_c^2, \end{aligned}$$
(4)

where \(\varphi\) is the effective semi-angle of \(70.32^\circ\) [31].

Since imperfections influence the true projected area of a Berkovich tip significantly, instead of using Eq. (4) a calibration function is mostly used to approximate the projected area. This function is expressed as [24]

$$A_p(h_c) =24.56 h_c^2 + C_1 h_c^1 + C_2 h_c^{1/2} + C_3 h_c^{1/4} + \dots + C_8 h_c^{1/128}.$$
(5)

Finally, the empirical correlation factor \(\beta\) needs to be determined. It is shown in [24, 25], that the value of \(\beta\) usually varies between 1.02 and 1.08. This results in a deviation of up to 3% regarding the indentation modulus. Due to this the value for \(\beta\) is set to one in this study as done in [32].

The used Berkovich tip is made of diamond with a Young’s modulus of 1143 GPa and a Poisson ratio of 0.0691 [33].

Fig. 3
figure 3

Arrangement of the measurement points for the indentation tests at 500mN and 1500mN

Full size image

3.2 Experimental Procedure

For the characterization of the material properties of SFRC on the mesoscale cuboids with an edge length of 20mm x 5mm x 3mm are used. The specimens are cut out of a quadratic plate of 300mm x 300mm x 3mm produced by injection molding. The used material is a polybutylenterephthalat (PBT) filled with glass fibers. The fiber mass fraction is specified with 30% (PBT GF 30) and the material properties of the two components are given in Table 1.

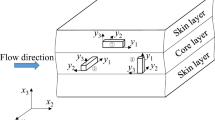
Table 1 Material properties of the fiber and matrix material
Full size table

Due to the manufacturing process, the reinforcement of the matrix by the fibers is directional for the component, so that the material properties are non-isotropic and, hence, depending on the direction. Because of that, different orientations of the specimens with respect to the main melt flow direction of the initial plate are analyzed. They are cut out perpendicular to and in the direction of the main melt flow direction. This allows one to derive the linear-elastic quasi-isotropic material properties in the three main directions namely with the main flow direction, perpendicular to it, and in the thickness direction. Figure 4 gives an overview of the used specimens. There is also a coordinate system introduced, that is used throughout this study.

Fig. 4
figure 4

Specimens for experimental investigation and numerical validation

Full size image

For the characterization of the material properties for PBT GF 30 the indentation or reduced modulus is measured at several points to obtain the spatial distribution as well as the statistical characteristics. The measurement points are arranged in a grid with a vertical and horizontal distance of \({250}\mu \mathrm {m}\) between each point, see Fig. 3. Since the experimental procedure is validated by numerical simulations based on a two-dimensional micrograph with a size of 3.37mm x 3mm the number of measurement points is selected in such a way that an identical area is covered. To minimize boundary effects a distance of \({250}\mu \mathrm {m}\) to each specimen boundary is kept. In accordance with the distance of the measurement points to the edges and between each other the measurement points are arranged in a grid of 13 x 11 points, see Fig. 3. Hence, in total 143 measurements per grid are performed.

At each of these points first, the indentation modulus is determined for a maximum load of 500mN and 1500mN, respectively. The used range for the approximation of the indentation modulus is set to 98% and 40% of the maximum load. As discussed in Sect. 3.1, the indentation area function \(A_p(h_c)\) of the used Berkovich tip is calibrated before obtaining the indentation modulus with respect to Eq. (2).

4 Results

Based on the experimentally obtained indentation modulus mean values and the corresponding standard deviations for the analysis of the material properties in each direction are derived. The results are summarized in Table 2. In addition, the minimal and maximal value of each measurement series is provided. Figure 5 gives an overview of the spatial distribution of the indentation modulus for each analysis.

Table 2 Results of the experimentally obtained indentation modulus
Full size table
Fig. 5
figure 5

Spatial distribution of the indentation modulus for each load case and direction

Full size image

5 Discussion

Below first the experimentally obtained results are discussed in detail in Sect. 5.1. This is followed by a numerical analysis based on the microstructure of the specimen in Sect. 5.2. The discussion is concluded by a comparison of the results obtained by experimental investigation and numerical analysis in Sect. 5.3.

5.1 Experimental Results

The main aspects can be derived from the results provided in Table 2 in combination with the microstructural properties of the cross-section given in Table 3. First, the measured values indicate that, compared to a tensile test specimen on the component level, there is only a small degree of anisotropy due to the reinforcing fibers on the mesoscale. The main reason here is the considerably small aspect ratio of the detected fibers. Based on a mean fiber length of \({46.6}\mu \mathrm {m}\) and a mean diameter of \({9.6}\mu \mathrm {m}\) the aspect ratio is 4.85, whereas a three-dimensional characterization on the component level results in an aspect ratio of up to 25 [34]. Furthermore, the obtained mean value of the Young’s modulus for each direction appears to be independent of the maximal indentation force used. This meets the results presented in [29]. Finally, the standard deviation and the range of the obtained indentation modulus decrease with an increasing indentation force. Since the indentation force correlates with the indentation depth and hence, the projected area, the characterized cross-section is larger for a higher indentation force. In combination with the decreasing standard deviation and range, this allows one to assign the conducted experiments to the mesoscale in context of the multi-scale approach [19, 21].

Table 3 Microstructural characteristics of the specimen taken from [35]
Full size table

Components manufactured by an injection molding process show a layered structure in thickness direction due to different melt flow velocities and shear forces [36]. As shown in Fig. 6, usually the cross-section is characterized by three or five individual layers, namely skin, shell, and core layers [37,38,39,40,41]. Each of these layers shows a different main fiber orientation. For the core layer, located in the middle of the cross-section, the fiber is orientated mainly perpendicular to the main melt flow direction, whereas the adjacent shell layers show a fiber orientation, that coincides with the main melt flow direction. The skin layers at the upper and lower surface are only used within the five-layer characterization. In these thin layers, the fibers are usually randomly orientated. Since the material properties are highly influenced by the fiber orientation as shown in [42] the layers have different material properties.

Fig. 6
figure 6

Fiber orientation scheme consisting of five different layers due to injection molding process, compare [41]

Full size image

This variation of the material properties and hence, the layered structure of the cross-section can be clearly observed in the experimental results of the indentation test in the z-direction. In the center of the cross-section, the obtained Young’s modulus is significantly higher in comparison to the remaining cross-section. This also meets the results of the microstructural analysis of the cross-section presented in [35]. However, this characteristic of the cross-section is not detected by the results shown in Fig. 5 for the indentation test in the x-direction. At first, this contradicts the results of the measurement in the z-direction as well as the findings regarding the cross-section layout due to an injection molding process as described in [37,38,39,40,41] and the results of the cross-section analysis in [35]. This is resolved by analyzing the obtained values more in detail. Therefore, the mean value is calculated for each layer. The information about the corresponding coordinates is derived from the results of the indentation tests in the z-direction. The values measured at \(y \le {1.25}\mathrm{mm}\) and \({1.75}\mathrm{mm} \le y \le {2.75}\mathrm{mm}\) are assigned to the shell layers, whereas the experimentally obtained values at \(y = {1.25}\mathrm{mm}\) are assigned to the core layer. The results are provided in Table 4. Furthermore, the corresponding fiber mass fraction \(\varphi\) taken from the microstructural analysis in [35] is given.

Table 4 Mean values of the indentation modulus
Full size table

First of all, again the mean values of the measurement results at 500mN and 1500mN match very well for each layer, which meets the results presented in [29]. The results also indicate a layered structure of the cross-section not only based on the experiments conducted perpendicular to the main melt flow (z-direction) but also in the main flow direction (x-direction). However, the difference between the shell and core layers is less prominent in the melt flow direction (x-direction) and hence, cannot be observed in Fig. 5. There are two main reasons for the more pronounced difference of the mean indentation modulus between the shell and core layers perpendicular to the main flow direction (z-direction). First, the fiber mass fraction is not identical for the shell and core layers as shown in Tables 3 and 4. Due to the higher fiber mass fraction of the core layer in combination with a \({0}^\circ\) fiber orientation the difference to the shell layer with a lower fiber mass fraction and a fiber orientation of \({90}^\circ\) is more significant in contrast to an interchanged combination. Second is the orientation within the core and shell layers. The shell layers show an overall orientation characteristic in melt flow direction whereas the fibers in the core layer are mostly orientated perpendicular to the melt front. However, the orientation characteristics are not identical when transforming one by \({90}^\circ\) [35]. Because of the different fiber mass fraction and slightly different fiber orientation in these layers, the mean value for the shell layer in a fiber direction of \({0}^\circ\) and the corresponding value of the core layer differ significantly.

5.2 Numerical Simulation

It is expected that the experimentally obtained values for the indentation modulus are not only affected by the projected area \(A_p\) but also its surroundings. Therefore, the effective cross-section of the indentation test is analyzed by numerical simulations. The term effective cross-section is interpreted as the area that is characterized by the indentation test. In other words, the surface of the material around the indentation center, which influences the results of the indentation test, defines the effective area. The numerical simulations are based on a two-dimensional micrograph of the used material. Since the micrograph represents the x-y-plane the numerical validation is exemplarily done for these two directions.

The validation process consists of two steps. First, the overall properties on the mesoscale are derived by obtaining the Young’s modulus for the complete micrograph with a size of 3.37mm x 3mm in both, the x- and y-directions by numerical simulations of tensile tests. For the determination of the Young’s modulus, the following boundary conditions are applied. For the analysis in the x-direction a horizontal load of 100MPa is applied to the right edge, whereas for the analysis in y-direction a vertical load of 100MPa is applied to the upper edge of the numerical model, which represents the micrograph. In both cases, the horizontal displacement is fixed at the left edge and the vertical displacement is fixed at the lower edge, see Fig. 7. The generation of the numerical model is described in detail in [35] and will, therefore, only discussed briefly here. To be able to analyze the overall material properties of the micrograph by numerical simulation the obtained image is transferred to an array that holds a zero or one for each pixel of the image, indicating whether the pixel represents matrix or fiber material. Based on these additional arrays are constructed holding the material properties of linear-elastic material, the Young’s modulus, Poisson’s ratio, and the density for each coordinate. The numerical model itself is a rectangle of the same size as the micrograph discretized by a mapped mesh. To model the microstructure of the SFRC the arrays are used to pass the material properties directly to the integration points.

Fig. 7
figure 7

Numerical models used for the determination of the Young’s modulus by tensile tests

Full size image
Table 5 Summary indentation characteristics
Full size table

Second is the analysis of the effective cross-section. This is done by extracting squares with different edge lengths at different locations from the original micrograph. These squares are referred to as windows and the window size gives the edge length of the corresponding square. In this case, the same grid of measurement points is applied to the micrograph as used for the experimental analysis in Sect. 3. This leads to a grid of 12 x 11 measurement points. Each measurement point is interpreted as the center of indentation by the Berkovich tip and with respect to the numerical analysis as the center of an extracted window. Based on the experimentally obtained contact depth, which depends on the maximum load, the corresponding projected area \(A_p\) is approximated by evaluating Eq. (4). A square with an edge length of \(l_e = \sqrt{A_p}\) gives the smallest value of the effective cross-section and therefore, is used as an initial window size for the numerical analysis. The results, provided in Table 5, indicate that the projected area is only influenced by the maximum load and not by the direction of the indentation test, which allows one to use the same window sizes for the analysis in both directions. Based on this the smallest window size analyzed by numerical simulation has an edge length of 50μm. With an overall size of 3.37mm x 3mm and a minimum distance of \({250}\mu \mathrm {m}\) to the micrograph boundaries the maximum window size, that can be extracted, has an edge length of \({500}\mu \mathrm {m}\). With these boundaries window sizes with an edge length of \({50}\mu \mathrm {m}\) to \({500}\mu \mathrm {m}\) in \({50}\mu \mathrm {m}\) steps are investigated. At each point of the grid and for each window size a square with the corresponding edge length is extracted. The microstructure and hence, the corresponding material properties are again represented by arrays, as done in [35]. The information of the material properties, stored in these arrays, are passed to the integration points of the numerical model of a square with identical edge length. For the analysis of the effective cross-section, the Young’s modulus in x- and y-direction are determined by applying the same two load cases as done before. Furthermore, it is considered that the indentation modulus in the y-direction is only measured at the surface of the specimen. Therefore, with respect to the micrograph, the Young’s modulus in the y-direction is only derived at the measurement points located at the upper and lower row of the grid. For more details, see Fig. 4. In contrast to this, the Young’s modulus in the x-direction is obtained for all extracted cross-sections.

Fig. 8
figure 8

Results of the numerical simulation in \(x-\) and \(y-\)direction and comparison with experimental results

Full size image

The results of the numerical simulations are depicted in the first row of Fig. 8. The diagrams show the results of both performed investigations. This includes the Young’s modulus of the complete cross-section as well as the mean value for each window size and the corresponding minimum and maximum. Furthermore, the standard deviation is indicated by error bars. On the left-hand side, the results for the analysis in the melt flow direction (x-direction) are shown. The diagrams in the right column give the results for the analysis in the thickness direction (y-direction). For the numerical simulation in the x-direction the range, as well as the standard deviation of the obtained Young’s modulus decrease continuously with an increasing window size and the maximum and minimum, converge to the mean value. Furthermore, the mean values are constant within the standard deviation over all window sizes and meet the Young’s modulus of the whole micrograph. Based on this observation the numerical simulation can also be clearly assigned to the mesoscale with respect to the multi-scale modeling approach. The results for the analysis in thickness direction indicate a similar trend. However, the minimum and maximum don’t show a monotonously increasing and decreasing behavior, respectively. The main reason is the low number of analyzed cross-sections in comparison to the analysis in the melt flow direction. Instead of 132 only 24 cross-sections are used due to the extraction limited to the near-surface area.

A detailed summary of the results is provided in Appendix 1.

5.3 Comparison

For the comparison of the numerically obtained values and the measurement results, the Young’s modulus needs to be derived from the indentation modulus. As discussed in Sect. 3.1 for this the Poisson’s ratio of the specimen material needs to be approximated first. Based on the microstructural properties of the material provided in Table 3 and the material model by Halpin-Tsai [43, 44] the Young’s modulus and the Poisson’s ratio are predicted. The framework of the material model by Halpin-Tsai is given in Appendix 2. For the Young’s modulus, a value of 6.21GPa is obtained. The Poisson’s ratio is approximated at 0.379 which is used to derive the Young’s modulus of the specimen from the indentation modulus in the x-direction. Due to the oriented material properties, this Poisson’s ratio cannot be used for the remaining two testing directions, which is also indicated by the mismatch of the mean indentation modulus in each direction. The results are provided in Table 6. Comparing the calculated Young’s modulus in Table 6 with the analytical value shows a good agreement. Therefore, the use of the predicted Poisson’s ratio of 0.379 appears to be suitable for the determination of the specimen’s Young’s modulus. Furthermore, the local variation of the Poisson’s ratio due to the changing fiber volume fraction has only a small impact on the resulting Young’s modulus. For a fiber volume fraction range of 0% up to 44%, which is equal to a maximum fiber mass fraction of 60%, the Poisson’s ratio lays between 0.326 and 0.42. Calculating the Young’s modulus using these values leads to an upper and lower bound of 6.61GPa and 6.15GPa. With respect to the resulting value of 6.33GPa given in Table 6, this equals an error of 4% which is covered by the standard deviation.

Table 6 Results of the experimentally obtained Young’s modulus in x-direction
Full size table

The comparison between the experimentally obtained values and the results of the numerical analysis are done individually for each load case and each load direction. First, in the second row of Fig. 8 is the comparison of the indentation test at 500mN in the main flow direction (x-direction) on the left-hand side and in the thickness direction (y-direction) on the right-hand side. In addition to the diagrams in the first row, the experimentally obtained mean values, as well as the minimal and maximal measured value for the Young’s modulus, are added (for the analysis in y-direction the indentation modulus is used). Furthermore, the standard deviation is indicated. To be able to compare the standard deviation of the experimental results with the standard deviation of the numerical analysis the error bars of the experimental results are added to the numerically obtained mean values. Therefore, at each window size, two error bars are depicted at the numerical mean value. One represents the standard deviation resulting from the numerical analysis (black) and a second corresponding to the experimental investigation (red). The Young’s modulus derived from experimentally obtained indentation modulus, the Young’s modulus characterizing the complete microstructure represented by a two-dimensional micrograph, and the mean value regarding the effective cross-section size analysis show only small deviations for the investigation in the x-direction. This holds for both indentation forces. In contrast to this in the y-direction the experimental results are higher than the values obtained by numerical simulation. The main reason here is the use of the indentation modulus instead of the Young’s modulus. In addition to this, the center point of the extracted window has a distance of \({250}\mu \mathrm {m}\) to the surface of the micrograph. Hence, the ratio of the shell and skin layers in the extracted window may differ from the effective cross-section of the indentation test and may also lead to a slight deviation between the results.

In the next step, the size of the effective cross-section is determined by the window size where the standard deviations show the best match. For the experimental investigation in melt flow direction at 500mN this is the case for a window size of \({250}\mu \mathrm {m}\). In contrast to this at a load of 1500mN the corresponding window size is \({400}\mu \mathrm {m}\), as depicted in the third row of Fig. 8. This meets the expectation because with an increasing maximum load the indentation depth increases and hence, the effective area should do so as well. Comparing these values with the edge length \(l_e\) of the projected area given in Table 5 leads in both cases to a factor of 5 between the window size and the edge length, which corresponds to a factor of 25 between the projected area and the effective cross-section. The same correlation is found for the results in the thickness direction.

Another approach for the determination of the effective cross-section is the comparison of the maximal and minimal obtained values of both investigations. In this case, the window size, where the numerical obtained values coincide with the experimental measuring results, gives the effective cross-section. However, the test results of the investigation in x-direction reveal that this procedure indicates not a specific value but a range for the effective cross-section. Furthermore, the values obtained based on the minimum and maximum do not necessarily coincide. For the test at 500mN, for example, the maximal value of the numerical analysis and the experimental investigation indicates an effective cross-section of approximately \({200}\mu \mathrm {m}\) to \({250}\mu \mathrm {m}\), which meets the conclusion based on the standard deviation. This is also indicated by the minimal value. In contrast to this, the test with a maximal indentation force of 1500mN reveals a discrepancy between the effective cross-section based on the minimal and maximal value. For the maximal value, an effective cross-section edge length of \({300}\mu \mathrm {m}\) to \({350}\mu \mathrm {m}\) is derived whereas the minimal value indicates an edge length of \({500}\mu \mathrm {m}\). One reason for this is the sensitivity of the minimum and maximum on the number of samples, as discussed before. This can also be observed for the analysis in the thickness direction. Due to the limited number of extracted windows, the comparison of the minimal and maximal values is not suitable to derive the effective cross-section size.

In summary, the effective cross-section is determined sufficiently based on the comparison of the standard deviation obtained by numerical simulation and experimental investigation. A prediction of the effective cross-section based on the minimal and maximal obtained values appears to be not suitable.

6 Conclusion

The presented work consists of two parts. First is the experimental characterization of a SFRC made of PBT filled with glass fibers and a fiber mass fraction of 30% with special regard to the determination of the Young’s modulus. The experimentally obtained results are validated by analytical treatment and numerical simulations in a second step to determine the effective cross-section size.

The material characterization of SFRC by indentation tests along the three major axis that is along and perpendicular to the main flow direction of the injection molding process as well as in thickness direction reveals the layered structure of the cross-section due to different melt flow velocities during manufacturing. Furthermore, the deviation of the obtained means for the Young’s modulus for the two different indentation loads stays within the standard deviation. This meets the observations described in [29]. In contrast to this, the results for the different analyzed orientations differ, which is assigned to the oriented material properties of reinforced material. However, the anisotropy is not very profound due to the small aspect ratio of the reinforcing fibers.

The numerical simulations for the determination of the Young’s modulus are based on the microstructural characteristics of the used material. They confirm the results of the indentation tests. Furthermore, the numerically obtained results for different window sizes clearly indicate that the presented approach is assigned to the mesoscale because the minimal and maximal value derived by the numerical simulation converges to the mean value for increasing window size and the standard deviation also shows a decreasing development with increasing window size.

Comparing the experimentally obtained standard deviation with the standard deviation of the numerical simulations for different window sizes reveals, that the ratio between the indentation area and the effective cross-section of the indentation test is independent of the maximum indentation load. In this study, experiments are conducted with a maximum load of 500mN and 1500mN. In both cases, the standard deviation of the numerical simulation meets the experimentally obtained value for window sizes 25 times larger than the indentation area.

It is concluded that indentation tests are a suitable procedure to determine the material properties of SFRC on the mesoscale. This does not only involve the overall material properties but also the spatial distribution. The obtained values characterize the material for an effective cross-section that is 25 times larger than the projected area of the used Berkovich tip for a given indentation depth. Furthermore, the procedure is adaptable to other fiber volume fractions. In this case, the ratio between the effective cross-section and the projected area might be different due to the differing reinforcement level and the change in the microstructural properties.