Abstract
The perforation resistance of fibre metal laminates (FMLs) made of an S-glass fibre reinforced poly-ether-ketone-ketone (GF/PEKK) composite and an aluminium alloy (2024-T3) is investigated. Initial attention is focused on assessing the effect of the processing temperature on the tensile strength of the aluminium alloy. Here, it has shown that the processing cycle results in a reduction of approximately 35% in both the tensile strength and yield strength of the aluminium alloy. A comparison of the quasi-static and dynamic perforation responses of the FMLs highlighted the rate-sensitivity of these laminates, with the perforation energy increasing as the loading rate varies from quasi-static to impact. After testing, the FML specimens were sectioned to highlight the prevailing failure modes. An examination of the cross-sections indicated that the impact energy of the projectile is absorbed through plastic deformation and tearing of the metal layers, delamination between the composite plies and metal layers as well as fibre fracture. Finite element models (FEM), using ABAQUS/Explicit, have been developed to predict the behaviour of the FMLs subjected to dynamic loading. The outputs of the FE models were then validated against the measured experimental force–displacement traces and the observed failure modes. The results of the FE models were in a good agreement with the experimental data, in terms of the initial stiffness, maximum force and maximum displacement, as well as the perforation mechanisms.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In recent decades, the demand for high-performance lightweight materials in the aircraft industry has led to the development of new types of composites and hybrids, such as fibre metal laminates (FMLs). FMLs are layered structures, in which a number of thin sheets of a metal alloy and plies of composite material (prepregs) are stacked together and cured [1]. FMLs have been used as structural materials in a number of applications as a result of their high fatigue resistance, excellent corrosion resistance, impact resistance, damage tolerance and low density [2,3,4,5]. Previous work has shown that the rate of fatigue crack growth is lower in FMLs than in a plain aluminium alloy, due to crack bridging by the reinforcing fibres [4].
FMLs have attracted significant attention for use in aerospace industry in designing primary aircraft structures, such as the upper fuselage of the Airbus A380, due to their outstanding fatigue properties [4, 6]. FMLs also exhibit attractive properties under impact loading [7]. The quasi-static and dynamic response of ARALL (aramid fibre reinforced aluminium), CARALL (carbon fibre reinforced aluminium laminates) and GLARE (glass fibre reinforced aluminium) laminates has been investigated in detail by Vlot [8], where it was shown that FMLs exhibit smaller post-impact damage zones than fibre-reinforced composites.
Extensive work has been undertaken to investigate the impact properties of FMLs based on aluminium alloys and glass fibre reinforced epoxies [8,9,10,11,12,13,14,15]. The impact behaviour of FMLs based on an aluminium alloy type 2024-O under low velocity impact loading was investigated by Fan et al. [16]. The authors observed that FMLs exhibits superior properties to the plain composite that was used to manufacture the FMLs. Zhou et al. [7] conducted split Hopkinson bar tests, quasi-static perforation tests and low velocity impact tests on a range of epoxy-based laminates to investigate their rate-sensitivity. The authors observed that FMLs exhibited a low rate-sensitivity. They also showed that the failure processes observed in the specimens following quasi-static loading, i.e. plastic deformation, fibre fracture and delamination, were similar to those tested at impact loading rates.
Compared with thermoplastic based-FMLs, longer processing cycles, lower interlaminar fracture toughness properties and repair are some of the key limitations associated with the first generation of thermosetting based-FMLs (i.e. epoxy-based composites)[17]. More recently, FMLs based on thermoplastic composites have been developed and tested to overcome some of the limitations associated with epoxy-based FMLs [17,18,19,20]. High-performance thermoplastic (TP) composites, reinforced with glass fibres (GF), carbon fibres (CF) and natural fibres (NF) have found increasing use in aerospace, marine and automotive industries, owing to their lightweight, recyclability, weldability, unlimited shelf life and superior impact properties [21,22,23,24,25,26,27]. The wider use of traditional thermoplastic matrices has been limited, due to their low stiffness, poor thermal stability at high temperature and low glass transition temperature (Tg) [28].
FMLs based on high-temperature composites, such as PEEK and PEKK, represent attractive options for use in potentially aggressive loading environments [29]. PEEK has been widely investigated in recent decades [30,31,32,33], due to its high-temperature capability and excellent resistance to oxidation and chemicals. Recently, PEKK has attracted interest from the aerospace industry, since it is more than 60% cheaper than PEEK and offers a higher glass transition temperature (Tg) than PEEK, i.e. 165 °C compared to 145 °C [25]. Furthermore, the manufacturing temperature for PEKK is less than that required for PEEK, which can lead to shorter processing cycles and lower manufacturing costs [34]. To the author’s knowledge, the impact response of fibre metal laminates based on PEKK and an aluminium alloy has not thus far been examined.
In order to understand the response and perforation failure mechanisms of the new FMLs under impact loadings, a large number of experimental tests are required to cover as many scenarios as possible, such as target dimensions, stacking sequences, constituent materials, impact velocity and boundary conditions. Therefore, the optimization process will be costly and time consuming. However, this issue can be mitigated by developing computer models using the finite element analysis which is a quick and inexpensive process. Here, for the validation purpose, only a limited number of experiments is needed. Once the FE models are verified against the corresponding experimental data, further parametric studies can be undertaken using the validated computer models, to identify the response of the new FMLs under various loading conditions [35].
The aim of this investigation is to therefore study the impact response of fibre metal laminates (FMLs) based on S-glass/ PEKK composite and aluminium sheets (2024-T3). Initially, the effect of the temperature excursion of the processing cycle on the tensile strength of the aluminium alloy is investigated. A number of fibre metal laminates based on an aluminium alloy and glass fibre/PEKK composites are then manufactured and subjected to quasi-static testing and impact loading. Finite element analyses are then developed to predict the perforation impact of these FMLs and subsequently validated using the obtained experimental data.
2 Experimental Procedure
2.1 Materials
The aluminium-based FMLs used in this study were manufactured by bonding glass fibre/PEKK prepreg layers to 0.5 mm thick 2024-T3 aluminium alloy sheets. The aluminium alloy was supplied by Aircraft Materials Ltd (U.K). The GF/PEKK prepregs were based on PEKK as a matrix material and woven S-glass fibre as the reinforcing phase. Here, the PEKK powder was deposited evenly on the glass fibre woven to make the prepregs. Then, a number of prepreg plies were stacked with aluminium sheets to make the designed fibre metal laminates. The manufacturing procedure for producing the GF/PEKK prepregs is described in Ref. [36]. The stacking configurations considered ranged from a 2/1 lay-up to a 5/4 laminate. Table 1 summarises the stacking configurations of the FMLs investigated in this study.
A PEKK film with a thickness of 50 µm (ARKEMA, France) was inserted between the aluminium alloy and the GF/PEKK prepregs to ensure good bonding between the constituent materials [37, 38]. The FMLs were manufactured by stacking an appropriate number of metal layers and composite plies in a picture frame mould with dimensions of 100 × 100 mm and heating the stack using a Meyer hydraulic hot press, as shown in Fig. 1.
Tensile tests were conducted on the aluminium alloy to determine its tensile properties. The specimens were prepared according to ASTM E8/E8M-16a [39], as shown in Fig. 2. An extensometer, with a 50 mm gauge length (GL), was employed to measure the displacement of the test specimens. The tensile tests were conducted using a screw-driven Instron 3369 universal testing machine at a constant crosshead displacement rate of 0.5 mm/minute.
2.2 Surface Pre-Treatment of Aluminium Alloy
The aluminium sheets were pre-treated using a sand-blasting technique to enhance the surface properties, as well as to increase the resin-metal adhesion properties. Here, glass beads with an average diameter of 200–300 µm were used. A pen type hand held blaster was used for the sandblasting procedure with an air pressure of 65 psi. During the sandblasting process, the nozzle was maintained perpendicular to the specimen surface. A distance of approximately 30 mm was maintained between the nozzle and the work-piece and the duration of the sandblasting treatment was 15 s for all specimens.
2.3 Quasi-Static and Dynamic Tests
The FML plates investigated in this study were subjected to perforation tests at quasi-static and impact rates of loading. The panels were clamped in a square mould with inner dimensions of 72 mm × 72 mm. Quasi-static tests were undertaken on an Instron 3369 universal testing machine with a maximum loading capacity of 50 kN at a crosshead displacement rate of 1 mm/min.
Low velocity impact testing was performed using a drop-weight tower. Here, a mass of steel was attached to a carriage with a hemispherical steel indenter (10 mm diameter) to impact the targets, as shown in Fig. 3. Four stacking configurations of FML were considered, these being 2/1, 3/2, 4/3 and 5/4. Here the composite layers are based on four plies of GF/PEKK prepreg. The stacking arrangements, carriage masses and impact velocities are detailed in Table 2. After testing, the samples were sectioned and ground using various grades of silicon carbide paper before polishing. An optical microscope, fitted with a camera (Infinity 2, Lumenera Corporation) was used to elucidate the failure mechanism in the damaged FMLs.
3 Finite Element Modelling
The response of the FMLs under impact loading was predicted using finite element (FE) models. The composite layers were modelled using an orthotropic elastic material with 2D Hashin’s failure criteria. The damage initiation criteria can be determined by using the components of the effective longitudinal \((\tilde{\sigma}_{11})\), transvers \((\tilde{\sigma}_{22})\) and shear \((\tilde {\sigma}_{12})\) stresses within the plane of the composites, which are expressed as [40]:
Fibre tension
Fibre compression
Matrix tension
Matrix compression
where XT, XC are the tensile and compressive strengths in the longitudinal direction, \({Y}_{T}\), \({Y}_{C}\) denote the tensile and compressive strengths in the transverse direction, \({S}_{T}\), \({S}_{L}\) are the longitudinal and transverse shear strengths, α is a coefficient for shear contribution to the fibre tension failure initiation criterion. The damage variables, corresponding to a specific failure mode, are given by the following expression [40]:
where \({\delta }_{eq}^{0}\) is the initial equivalent displacement at which the initiation criterion for a particular failure mode is met and \({\delta }_{eq }^{f}\) refers to the displacement at which the material is damaged. Both parameters are estimated based on the element size and the damage initiation and ultimate failure strains of the GF/PEKK laminates.
The material and damage properties of the GF/PEKK composites are shown in Table 3 and Table 4. A procedure of element removal was used to delete the failed composites elements. An isotropic elasto-plastic model, with associated damage criteria, was used to simulate the aluminium sheets. The elastic properties of the aluminium alloy are given in Table 5. The plastic behaviour of the aluminium sheets was modelled by assuming isotropic hardening. The relationship between the plastic strain and the flow stress, obtained experimentally from the uniaxial tests, is given in Table 6.
Damage initiation in the aluminium layers was modelled using ductile and shear damage models, which are available in ABAQUS.
The failure strain, obtained from the experimental stress–strain curves, was taken as the fracture strain at the onset of damage. The damage properties for the aluminium alloys were taken from Hooputra et al. [41]. When damage initiates in the aluminium sheets, an effective plastic displacement was adopted to model subsequent damage evolution. The interface layers in the FMLs were modelled using cohesive elements, based on a nominal stress and energy conjunction, defined in terms of traction–separation. The material properties of the cohesive layer are given in Table 7.
For modelling purposes, a square plate with dimensions of 72 mm × 72 mm was considered. To simulate the boundary conditions, the edges of the plate were fully-fixed. Due to the symmetry of the specimen geometry and loading, only one half of the target was considered in order to reduce the CPU time and associated cost. An initial velocity was applied to the impactor in the vertical direction (normal to the target) as the only degree of freedom, as shown in Fig. 4.
The GF/PEKK prepregs were meshed using eight-noded continuum shell elements (SC8R) along with Hashin-2D criteria. Eight-noded solid brick elements (C3D8R), with reduced integration and hourglass control, were used to model the aluminium sheets. The element size of 1 mm × 1 mm was used in the central square impact region of the target. The interfaces between the aluminium layers and the prepregs were modelled using eight-noded 3D cohesive elements (COH3D8). A general contact interaction was used to define interaction between the layers, while the interaction between the projectile surface and the node-set at the centre of each layer was defined as surface-to-surface contact (contact pair). The friction coefficient between the projectile and the target was taken as 0.1, as there is limited friction between the smooth projectile and the target. The configurations, projectile masses, velocities and energies for the models were the same as those used in the impact tests, as reported earlier in Table 2.
4 Results and Discussion
4.1 Experimental Results
Initially, the effect of the processing cycle adopted during the manufacturing process on the stress–strain response of the aluminium alloy (2024-T3) was investigated. Here, aluminium sheets were heated in a press to the temperature used to consolidate the thermoplastic prepregs, i.e. 330 °C. The sheets were maintained at this temperature for 30 min before cooling down slowly. The tensile strength of the aluminium specimens following this thermal cycle is shown in Fig. 5. Clearly, the modulus of elasticity of the samples is not affected by the temperature cycle. However, the tensile strength and yield strength values show a significant reduction after heating. For example, the tensile strength of the annealed aluminium alloy was approximately 34% lower than the as-received value. The aluminium alloy investigated here belongs to the 2xxx series that is heat-treated by precipitation hardening, during which the material strength increases with time at a constant temperature (aging temperature) after rapidly cooling from the solution heat-treatment temperature. Thus, the observed reduction in strength is due to over-aging, which leads to a significant coarsening of the precipitate within the alloy. This in turn lowers the yield strength (and therefore the tensile strength). The resulting stress–strain values following the heating cycle were then taken as the material properties in the finite element models.
Figure 6 shows the load–displacement curves for the FMLs subjected to quasi-static perforation testing. From the figure, the load–displacement traces exhibit three stages. Initially, the specimens exhibit a high stiffness during the initial linear elastic loading phase. However this initial stiffness is decreasing for lower thickness laminates due to unproportional decrease of the laminate thickness i.e. from 5/4 to 4/3 as 22% reduction in thickness, from 4/3 to 3/2 as 29% reduction, but from 3/2 to 2/1 as 40% reduction. In the second stage, the load increases monotonically with displacement as the indenter continues to impinge on the target. Once a tensile crack initiates on the rear surface, and the indenter begins to perforate the target, the force drops gradually during the third stage of the test, due to the initiation of debonding (delamination) as well splitting of the composite layer and the aluminium alloy. Clearly, the stiffness of the FML plates increases as the thickness is increased. Here, the thickest FML panel, i.e. the 5/4 stacking configuration, exhibits the highest peak force, which is more than four times that offered by the thinnest plate (the 2/1FML). Interestingly, the FMLs exhibit similar values of the maximum displacement at damage initiation.
The effect of strain-rate on the perforation resistance of the aluminium-based FMLs was investigated and the traces of load–displacement under impact testing are presented in Fig. 7. From the figure, it is clear that the specimens deformed in a similar fashion to those tested quasi-statically. It is interesting to note that the FMLs tested under dynamic loading conditions exhibit an oscillatory response, due to ringing effects in the load-cell.
The area under the load–displacement trace was used to determine the energy absorbed by the FMLs during the perforation process. In order to investigate the influence of strain-rate on the perforation resistance of the FMLs, the values of absorbed energy for samples tested quasi-statically and dynamically are plotted against sample thickness in Fig. 8. Clearly, for both loading conditions, the perforation energy increases as the number of layers (i.e. thickness) of the FMLs increases. It can also be noted that the impact-loaded plates offer a higher level of energy absorption, with average values being 20% higher than those recorded following quasi-static testing.
4.2 Numerical Modelling of the Impact-Loaded FMLs
FE models were developed to predict the response of the four stacking configurations of aluminium-based FML under impact loading. The predictions offered by the FE models were then compared with the corresponding experimental data in terms of the load–displacement traces, energy absorption and failure modes. Figure 9 shows comparisons of the predicted and measured load–displacement traces for the FMLs following low velocity impact loading. It is interesting to note that the trends in the simulated and experimental traces are similar, with the impact force increasing with displacement to a peak value, before dropping rapidly as the projectile begins to perforate the target.
The FE models capture the peak loads for the various target thicknesses with reasonable success. The predicted values of peak force for the 2/1, 3/2, 4/3 and 5/4 FMLs are 0.3, 5.6, 9.5 and 1.1% higher than those obtained experimentally. Interestingly, the values of the predicted initial stiffness of the FMLs are slightly higher than those obtained experimentally. This is due to the assumption of perfect contact between the target and the projectile in the FE model.
The predicted values of absorbed energy were again determined from areas under the load–displacement traces, and these values are compared with the corresponding experimental data in Fig. 10. Again, the results indicate that the simulated and experimental values of energy absorption are in good agreement. The predicted values of perforation energy for the 2/1, 3/2, 4/3 and 5/4 FMLs exhibit discrepancies of 5.9, 3.4, 5.5 and 4.3%, relative to the corresponding experimental values.
The predicted failure modes observed on the rear surfaces of the 2/1 and 4/3 FMLs are compared with the corresponding experimental failure modes in Fig. 11. It can be seen that the deformation modes and the failure mechanisms are successfully predicted by the FE models. Interestingly, the simulations also predicted the cross-shaped fracture pattern in the central region of the target that was observed experimentally.
Figure 12 compares the experimental and numerical cross-sections of the impacted FMLs. The observed failure mechanisms include fracture of the composite plies, local plastic deformation and fracture of the aluminium alloy. A closer examination of the figure suggests that the panels exhibit a significant amount of delamination, along with some petalling of the rear surface of the aluminium alloy. Again, the failure modes observed following impact testing are predicted by the model.
For 2/1 FMLs, there is more membrane type deformation mode due to the relatively thin laminates (Fig. 12a). Both the front and back face of aluminium layers have tension dominant failure with cross cracks, and the deformation mode and damage of the composite layer between them are controlled by the aluminium layers. There is clear a delamination between the composite layer and the back face aluminium layer in the perforation area, which is also captured by the finite element simulation due to the failure of the cohesive layer. The deformation mode and failure around the perforation opening for 3/2 FMLs (Fig. 12b) are similar to those of 2/1 FMLs, accompanied by tension cracks and delamination between the metal and composite layers. With increasing the constituent layers of FMLs to 4/3 (Fig. 12c) and 5/4 (Fig. 12d), the perforation failure is more localised in comparison to 2/1 and 3/2 FMLs. This is likely attributed to increasingly less membrane effects on the deformation and failure modes, due to increased number of metal and composite layers (i.e. thickness). The crack is still initiated from the back face aluminium layer due to tension and propagated to the front metal layer, accompanied with a local crush around the perforation hole. All composite layers have a tension dominant failure with delamination (failure of cohesive layers) in the simulation, which can be clearly seen in Figs. 12c, d.
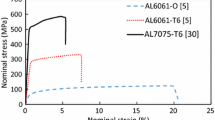
Apart from glass fibre thermoset based fibre metal laminates, there are also extensive studies on impact response of carbon fibre reinforced aluminium laminates (CARALLs) [43,44,45,46,47]. As carbon fibres are stiffer and stronger than glass fibres, CARALLs subjected to projectile impact have higher stiffness and strength in comparison to glass fibre based FML counterparts in general. However, the thermoplastic (PEKK) based FMLs presented in the current study show more ductile impact response, with the relatively high permanent deflection of 13 mm but lower peak load of 3200 N versus about 10 mm and 5000 N in Ref. [47] for a 2/1 stacking sequence. The impact perforation energies of the thermoplastic (PEKK) composite based FMLs investigated were also compared with those of thermoset (Epoxy) composite based for FMLs [16]. For both the laminated systems, a hemispherical projectile with a diameter of 10 mm was used to perforate targets with the similar planer dimensions and boundary conditions to those considered here. It should be noted that the sample thickness of GF/PEKK based FMLs is slightly greater than those of GF/Epoxy based FMLs. To facilitate comparisons, the perforation resistances of both sets of plate are compared in terms of specific energy absorption by normalising the perforation energy of each system by its areal density, as shown in Fig. 13. From the figure, it can be seen that the values of specific energy absorption for the GF/PEKK based FMLs are significantly higher than those for the GF/Epoxy based FMLs, for the various stacking sequences investigated. This evidence indicates that using a thermoplastic resin (PEKK) as a matrix material increases the absorbed energy due to the improved ductility of this composite in comparison to the epoxy resin. Although the Al (2024-T3) sheets, used for making the FMLs, exhibit a reduction in tensile strength after heating cycle, the perforation resistance of these FMLs is still promising in comparison to the more common epoxy based FMLs.
5 Conclusions
The effect of strain-rate on the perforation resistance of aluminium-based FMLs with various stacking configurations has been investigated. Finite element models have also been developed to predict the perforation behaviour of the FMLs following low velocity impact loading. Based on the research outputs the following conclusions can be drawn.
-
The perforation energy increases with the loading rate from quasi-static to dynamic loading, which highlights the strain rate-sensitivity of these laminates.
-
The failure takes in the form of a cross-shaped fracture on the rear face of the target and a circular hole on the front face.
-
For the range of stacking sequences studied, the perforation resistances of the aluminium-based FMLs were successfully predicted using the FE models.
-
The predicted peak forces, maximum displacements, absorbed energy values and failure modes were in good agreement with the corresponding experimental measurements.
-
The results show that the specific energy absorption values of the GF/PEKK-based FMLs are higher than those of GF/Epoxy-based FMLs, highlighting the high ductility of the FMLs based on PEKK resin.
References
Vlot, A.: “Low-velocity impact loading on fibre reinforced aluminium laminates (ARALL and GLARE) and other aircraft sheet materials.” Delft University of Technology, 1993.
Morinière, F.D., Alderliesten, R.C., Benedictus, R.: Modelling of impact damage and dynamics in fibre-metal laminates - A review. Int. J. Impact. Eng. 67, 27–38 (2014)
Cortés, P., Cantwell, W.J.: Fracture properties of a fiber-metal laminates based on magnesium alloy. J. Mater. Sci. 39, 1081–1083 (2004)
Vogelesang, L.B., Vlot, A.: Development of fibre metal laminates for advanced aerospace structures. J. Mater. Process. Technol. 103, 1–5 (2000)
Sharma, A.P., Khan, S.H., Parameswaran, V.: Experimental and numerical investigation on the uni-axial tensile response and failure of fiber metal laminates. Compos. Part B Eng. 125, 259–274 (2017)
Cortes, P., Cantwell, W.J.: The tensile and fatigue properties of carbon fiber-reinforced PEEK-Titanium fiber-metal laminates. J. Reinf. Plast. Compos. 23, 1615–1623 (2004)
Zhou, J., Guan, Z.W., Cantwell, W.J.: The influence of strain-rate on the perforation resistance of fiber metal laminates. Compos. Struct. 125, 247–255 (2015)
Vlot, A.: Impact loading on fibre metal laminates. Int. J. Impact Eng. 18, 291–307 (1996)
Rajkumar, G.R., Krishna, M., Murthy, H.N.N., Sharma, S.C., Mahesh, K.R.V.: Experimental investigation of low-velocity repeated impacts on glass fiber metal composites. J. Mater. Eng. Perform. 21, 1485–1490 (2012)
Li, X., Zhang, X., Zhang, H., Yang, J., Nia, A.B., Chai, G.B.: Mechanical behaviors of Ti/CFRP/Ti laminates with different surface treatments of titanium sheets. Compos. Struct. 163, 21–31 (2017)
Bernhardt, S., Ramulu, M., Kobayashi, A. S.: “Low-velocity impact response characterization of a hybrid titanium composite laminate,” J. Eng. Mater. Technol., vol. 129, p. 220, 2007.
Rajkumar, G. R., Krishna, M., Narasimha Murthy, H. N., Sharma, S. C., Vishnu Mahesh, K. R.: “Investigation of repeated low velocity impact behaviour of GFRP/aluminium and CFRP/aluminium laminates,” Int. J. Soft Comput. Eng, vol. 1, pp. 50–58, 2012.
Morinière, F.D., Alderliesten, R.C., Tooski, M.Y., Benedictus, R.: Damage evolution in GLARE fibre-metal laminate under repeated low-velocity impact tests. Cent. Eur. J. Eng. 2, 603–611 (2012)
Caprino, G., Spataro, G., Del Luongo, S.: Low-velocity impact behaviour of fibreglass-aluminium laminates. Compos. Part A Appl. Sci. Manuf. 35, 605–616 (2004)
Wu, G., Yang, J.M., Hahn, H.T.: The impact properties and damage tolerance and of bi-directionally reinforced fiber metal laminates. J. Mater. Sci. 42, 948–957 (2007)
Fan, J., Cantwell, W., Guan, Z.: The low-velocity impact response of fiber-metal laminates. J. Reinf. Plast. Compos. 30, 26–35 (2011)
Abdullah, M. R., Prawoto, Y., Cantwell, W. J.: “Interfacial fracture of the fibre-metal laminates based on fibre reinforced thermoplastics,” Mater. Des., vol. 66, no. PB, pp. 446–452, 2015.
Simeoli, G., Acierno, D., Meola, C., Sorrentino, L., Iannace, S., Russo, P.: The role of interface strength on the low velocity impact behaviour of PP/glass fibre laminates. Compos. Part B Eng. 62, 88–96 (2014)
Alcock, B., Cabrera, N.O., Barkoula, N.M., Reynolds, C.T., Govaert, L.E., Peijs, T.: The effect of temperature and strain rate on the mechanical properties of highly oriented polypropylene tapes and all-polypropylene composites. Compos. Sci. Technol. 67, 2061–2070 (2007)
Bartus, S.D., Vaidya, U.K.: Performance of long fiber reinforced thermoplastics subjected to transverse intermediate velocity blunt object impact. Compos. Struct. 67, 263–277 (2005)
Parlevliet, P. P., Weimer, C.: “Thermoplastic high performance composites : environmental requirements on future helicopter airframes,” ICCM-18. 21 - 26 Aug 2011, . Jeju Int. Conv. Center, Jeju Island, South Korea.
Lukaszewicz, D.H.J.A., Ward, C., Potter, K.D.: The engineering aspects of automated prepreg layup: History, present and future. Compos. Part B Eng. 43, 997–1009 (2012)
Stewart, R.: “Thermoplastic composites - Recyclable and fast to process,” Reinf. Plast., 2011.
Gilliot, A.: “From carbon fibre to carbon-fibre-reinforced thermoplastics,” JEC Composites Magazine, pp. 60–62, Mar-2012.
Salek, M.H.: Effect of processing parameters on the mechanical properties of carbon/PEKK thermoplastic composite materials. Concordia University, Canada, Master diss. (2005)
Choi, B., Diestel, O., Offermann, P.: “Commingled CF / PEEK hybrid yarns for use in textile reinforced high performance rotors,” 12th Int. Conf. Compos. Mater. (ICCM), Paris, pp. 796–806, 1999.
Taylor, N.S., Jones, S.B., Weld, M.: The feasibility of welding thermoplastic composite materials. Constr. Build. Mater. 3, 213–219 (1989)
Herrod-Taylor, A. J.: “The crystallisation of poly (aryl ether etherketone) (PEEK) and its carbon fibre composites,” MSc thesis, Univ. Birmingham, UK, 2011.
Barkoula, N.M., Alcock, B., Cabrera, N.O., Peijs, T.: Fatigue properties of highly oriented polypropylene tapes and all-polypropylene composites. Polym. Polym. Compos. 16, 101–113 (2008)
Wang, H., Vu-Khanh, T.: Damage extension in carbon fiber/PEEK crossply laminates under low veIocity impact. Compos. Mater. 28, 684–707 (1994)
Vieille, B., Casado, V.M., Bouvet, C.: About the impact behavior of woven-ply carbon fiber-reinforced thermoplastic- and thermosetting-composites: A comparative study. Compos. Struct. 101, 9–21 (2013)
Ghasemi Nejhad, M. N., Parvizi-Majidi, A.: “Impact behaviour and damage tolerance of woven carbon fibre-reinforced thermoplastic composites,” Composites, vol. 21, pp. 155–168, 1990.
Davim, J.P., Cardoso, R.: Effect of the reinforcement (carbon or glass fibres) on friction and wear behaviour of the PEEK against steel surface at long dry sliding. Wear 266, 795–799 (2009)
Cortes, L.Q., Causse, N., Dantras, E., Lonjon, A., Lacabanne, C.: Morphology and dynamical mechanical properties of poly ether ketone ketone (PEKK) with meta phenyl links. J. Appl. Polym. Sci. 133, 1–10 (2016)
Guan, Z. W., Cantwell, W. J., Abdullah, R.: “Numerical modeling of the impact response of fiber–metal laminates,” Polym. Compos., pp. 603–609, 2009.
Nassir, N., Birch, R.S., Cantwell, W.J., Wang, Q.Y., Liu, L.Q., Guan, Z.W.: The perforation resistance of glass fibre reinforced PEKK composites. Polym. Test. 72, 423–431 (2018)
Reyes V.G., Cantwell, W. J.: “The high velocity impact response of composite and FML-reinforced sandwich structures,” Compos. Sci. Technol., vol. 64, no. 1, pp. 35–54, 2004.
Mckown, S., Cantwell, W.J., Jones, N.: Investigation of Scaling Effects in Fiber-Metal Laminates. J. Compos. Mater. 42(9), 865–888 (2008)
ASTM E8/E8M − 16a, “Standard test methods for tension testing of metallic materials,” (2016)
Dassault Systèmes Simulia, “Abaqus CAE User’s Manual,” Abaqus 6.12, 2012.
Hooputra, H., Gese, H., Dell, H., Werner, H.: A comprehensive failure model for crashworthiness simulation of aluminium extrusions. Int. J. Crashworthiness 9, 449–463 (2004)
Tan, W., Falzon, B.G.: Modelling the nonlinear behaviour and fracture process of AS4/PEKK thermoplastic composite under shear loading. Compos. Sci. Technol. 126, 60–77 (2016)
Bienias, J., Jakubczak, P., Surowska, B., Dragan, K.: Low-energy impact behaviour and damage characterization of carbon fibre reinforced polymer and aluminum hybrid laminates. Arch. Civ. Mech. Eng. 4, 925–932 (2015)
Dhaliwal, G.S., Newaz, G.M.: Modeling Low Velocity Impact Response of Carbon Fiber Reinforced Aluminum Laminates (CARALL). J dynamic behavior mater. 2, 181–193 (2016)
Song, S.H., Byun, Y.S., Ku, T.W., Song, W.J., Kim, J., Kang, B.S.: Experimental and Numerical Investigation on Impact Performance of Carbon Reinforced Aluminum Laminates. J. Mater. Sci. Technol. 26, 327–332 (2010)
Bienias, J., Jakubczak, P., Dadej, K.: “ Low-velocity impact resistance of aluminium glass laminates – experimental and numerical investigation. Compos. Struct. 152, 339–348 (2016)
Jakubczak, P., Bienias, J., Dadej, K.: Experimental and numerical investigation into the impact resistance of aluminium carbon laminates. Compos. Struct. 244, 112319 (2020)
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Nassir, N.A., Birch, R.S., Cantwell, W.J. et al. The Perforation Resistance of Aluminum-Based Thermoplastic FMLs. Appl Compos Mater 28, 587–605 (2021). https://doi.org/10.1007/s10443-021-09873-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10443-021-09873-3