1 Introduction

Carbon fibre reinforced polymers (CFRP) are widely applied in aerospace. Compared with metallic structures, they have the advantage of a high strength at low weight [1]. However, CFRP are less stable under thermal loading [2]. An example for thermal impact are hot engine gases impinging on the outer shell of an aircraft, which causes an uneven heat distribution and consequently no equally distributed thermal damage inside the CFRP [3,4,5]. Many studies show that one-sided thermal loading influences the mechanical performance significantly. With increasing exposure time and temperature, mechanical properties like compressive and tensile strength decrease [6,7,8,9,10]. Also, interlaminar shear strength (ILSS) decreases with increasing thermal loading due to its sensitivity towards structural damage like, e.g., delaminations [8, 11,12,13]. For understanding this decrease, a closer look is necessary on the single degradation phenomena such as structural damage (e.g., delaminations) or the chemical decomposition of the polymer matrix (matrix degradation) and their distribution inside the CFRP [6, 9].

Thermally induced structural damage inside the CFRP like, e.g., delaminations can be analyzed with different non-destructive testing methods like, e.g., microfocused computed X-ray tomography (µCT) or ultrasonic testing [6, 13,14,15,16]. Especially µCT enables the detection of small delaminations due to its resolution in the micrometer-scale compared with other non-destructive testing (NDT) methods. However, µCT has sophisticated technical requirements, which make it difficult to realize a portable device setup and to investigate large structures compared with other NDT-techniques [15].

For analyzing matrix degradation as a consequence of thermal loading, infrared spectroscopy (ATR-FTIR) is a convenient tool [11-13, 17-20]. Especially hand-held ATR-FTIR-spectrometers provide the advantage of measurements directly at an, e.g., thermally damaged aircraft [21, 22]. Measuring along a ground incline plane provides a depth-resolved insight into the CFRP and therefore a view on the distribution of thermally induced matrix degradation within the CFRP [23].

Furthermore, IR spectral data can be used to predict properties of CFRP by means of multivariate data analysis. Regression methods like, e.g., principal component regression, partial least square regression (PLS), or artificial neural networks are suitable to predict residual strength as well as storage time and temperature of CFRP after isothermal treatment [24,25,26,27,28]. Wolfrum et al. developed a PLS-model for the prediction of ILSS based on surface spectra for CFRP after one-sided thermal laoding at 50 kW/m2 [11]. Beside that, classification methods are also used. Werner et al. used linear discriminant analysis (LDA) to distinguish CFRP based on different resin types [29].

The goal of this work is to get a deeper insight into the correlation of delaminations, matrix degradation, and residual strength with a special attention to the influence of delaminations on the residual ILSS. Furthermore, a model shall be introduced to predict the presence of thermally induced delaminations in the micrometer-scale by using IR-spectroscopy in combination with LDA as a classification tool of chemometric analysis. In general, IR spectroscopy shall be assessed considering the precision of quantified thermal damage and its limits for application under non-isothermal loading conditions.

2 Experimental

2.1 Material and Thermal Treatment

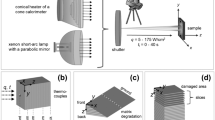
All investigations are performed with the commercial CFRP material HexPly® 8552/IM7 by Hexcel Corporation [30]. The HexTow® IM7 fibers are pre-impregnated with the epoxy based HexPly® 8552, which addtionally contains about 6% of the thermoplastic polyethersulfone (PES) [23]. The 0.125-µm-thick prepregs are laid up unidirectionally to 4 or 8 mm thick laminates with a stacking sequence of [0]32 or [0] 64, respectively. The bulk material is cut into samples with a size of 100 × 100 mm2. These samples are positioned with a distance of 25 mm to the conical heater of a cone calorimeter by Fire Testing Technology Ltd. and irradiated at different heat fluxes (15, 30, and 50 kW/m2) for varying time intervals (see Table 1). The maximum irradiation time is defined as the time, where delaminations penetrate through the whole CFRP or a kind of equilibrium delamination depth is achieved (see Sect. 3.2, valid for 15 and 30 kW/m2). If the CFRP ignite before achieving this, the maximum irradiation time corresponds to the ignition time (valid for 50 kW/m2). The temperature inside the CFRP is measured in additional samples equipped with type K thermocouples laminated on the irradiated side, the back side, and in various depth of the CFRP, respectively. For 4 mm thick CFRP samples, the laminated thermocouples are placed after the 1st, 2nd, 3rd, 4th, 5th, 9th, 13th, 17th, 21st, 25th, and 29th ply; for samples with 8-mm thickness, they are placed after the 1st, 3rd, 5th, 7th, 9th, 12th, 15th, 19th, 28th, 37th, 46th, and 55th ply. Temperature data is recorded with a data logger USB TC-08 from pico Technologies (Fig. 1).

Table 1 Overview of the tested CFRP samples with given heat flux, sample thickness, and irradiation time. Additionally, the non-delaminated depth znd and the corresponding delamination temperature at znd are given (*znd is equal to the sample thickness, i.e., the temperature corresponds to the front side temperature and therefore given in brackets)
Full size table
Fig. 1
figure 1

μCT-cross sections of 4 mm thick CFRP samples after irradiation at 50 kW/m² for various time intervals. The non-delaminated thickness znd is indicated. Dotted arrows mark the irradiated surface.

Full size image

Furthermore, CFRP samples with a size of 8 mm x 8 mm x 8 mm are stored isothermally for 1 h at 250 °C, 270 °C, 275 °C, 280 °C, and 300 °C for analyzing structural damage with µCT.

2.2 Testing Methods

Microattenuated total reflection Fourier transform infrared spectroscopy (ATR-FTIR) allows the detection of matrix degradation. The spectra are recorded with a Bruker Tensor 27 spectrometer using a Harrick ATR cell with a silicon crystal (diameter = 100 µm). Depth-resolved data are generated by measuring in small steps along a ground incline plane with an angle of 3° resulting in a depth-resolution of 0.2 mm [23].

Microfocused computed X-ray tomography (µCT) is a non-destructive testing method to detect structural damage (e.g., delaminations or matrix cracking) induced by thermal treatment. For this study, a V-TOME XL 300 system by GE Sensing & Inspection Technologies with a 300-kV microfocus X-ray source is used. For gaining a resolution of 7.1 µm, a sample size of 8 mm x 8 mm x z mm is chosen. For measuring distances between two points in a cross section image, an uncertainty of about 6 voxels (= 42.6 µm) can be expected.

Testing the apparent interlaminar shear strength (ILSS) is performed on a Zwick/Roell Z020 (load cell capacity: 20 kN) for 4 mm thick samples and on a Zwick/Roell Zmart.Pro (load cell capacity: 250 kN) for 8 mm thick samples following DIN EN 2563 [33]. Samples are prepared with a size of 40 mm x 20 mm x 4 mm and 80 mm × 40 mm x 8 mm, respectively. The distance between the supports is scaled up to 20 mm for the 4 mm thick samples and to 40 mm for the 8 mm thick samples. Also, the radii of loading nose and supports are increased to 5 mm or 10 mm, respectively [11].

The apparent interlaminar shear strength τ is calculated according to Eq. (1), where PR is the test force, b is the sample width, and z is the sample thickness [33].

$$\tau = \frac{3 \cdot {P}_{R}}{4 \cdot b \cdot z}$$
(1)

Finally, beside shear failure, also compressive failure under the loading nose can occur and affect the real ILSS and can lead to higher values [31, 32]. As the influence of the compressive failure is assumed to be within the range of measurement tolerance especially for thicker CFRP samples, it is not considered in the following.

2.3 Chemometrics

Chemometric analyses are done with the software The Unscrambler® X 10.2 by Camo Software. Linear discriminant analysis (LDA) is performed as a supervised classification tool using spectral data to assign samples regarding specific properties to different groups. To minimize the influence of the spectroscopy measurement in the model, the spectral data have to be preprocessed [34]. Therefore, two different strategies with and without principal component analysis (PCA) are applied. For perfoming the LDA without PCA, the spectral data are limited to the wave number range between 1800 and 1250 cm−1 and treated with Standard Normal Variate (SNV) Transformation. For the LDA with PCA, spectral data in a range between 1800 and 900 cm−1 are chosen. Before performing the PCA, the 1st derivative after Savitzky Golay (2nd polynomial order, 13 points) and SNV transformation are applied on the data. The PCA is performed by calculating 7 principle components. The scores of the PCA are used as variables for the LDA.

All spectral data are divided into two data sets: a training data set, which contains 90% of the total data and a test data set containing the remaining 10% of the data. The models are developed by using the training data set. The prediction accuracy is subsequently calculated by doing cross validation with the training data set and by doing the prediction with the spectra in the test data set (not considered at modelling) and verifying if the spectra are assigned to the right group.

3 Results and Discussion

3.1 Influence of Thermal Loading on Matrix Degradation

ATR-FTIR-spectroscopy proved itself as an appropriate non-destructive testing method for the detection of matrix degradation in CFRP after thermal loading [11-19]. Figure 2a shows an IR spectrum of 8552/IM7 CFRP without thermal loading. Characteristic bands for the epoxy resin (EP) can be found at 1510 cm−1 and 1610 cm−1, which occur due to C–C stretching vibrations of the aromatic ring structure. The bands at 1486 cm−1 and 1586 cm−1 are assigned to polyethersulfone (PES), which is the thermoplastic component in 8552 [23]. Furthermore, overlapping bands between 1630 and 1760 cm−1 are characteristic for C=O stretching vibrations (νC=O) of oxidation products (e.g., ketone, aldehyde, or amide structures [35]), which emerge at thermal treatment in an oxidative atmosphere [17-18]. In addition to the spectra of untreated CFRP, Fig. 2 shows spectra of CFRP irradiated at 50 kW/m2 for 60 and 80 s. It is shown that the band intensity at 1510 cm−1 decreases with increasing irradiation time due to a degradation of the aromatic ring structure in the epoxy resin. Conversely, the band intensity at 1486 cm−1 remains constant due to the higher thermal stability of PES compared with the epoxy resin [19]. Therefore, calculating the intensity ratio of the bands at 1510 cm−1 and 1486 cm−1 is used as a parameter characterizing thermally induced matrix degradation. The bands at 1586 cm−1 and 1610 cm−1 show a comparable behaviour with the bands at 1510 cm−1 and 1486 cm−1 but due to their worse separation and their overlap with the bands characteristic for νC=O (1630 to 1760 cm−1), the calculation of the intensity ratio using those two bands is not recommended.

Fig. 2
figure 2

ATR-FTIR-spectra taken at the surface of 8552/IM7 CFRP samples without thermal loading a and after an irradiation at 50 kW/m for 60 s b and 80 s c

Full size image

Additionally, the intensity of the overlapping bands between 1630 and 1760 cm−1 increases with increasing irradiation time due to thermo-oxidative reactions.

Figure 3 shows the intensity ratio of the bands at 1510 cm−1 and 1486 cm−1 as a function of the sample depth for different heat fluxes and irradiation times. For all heat fluxes, matrix degradation rises with increasing irradiation time and is more pronounced close to the irradiated surface (depth = 0 mm). It is shown that for a given matrix degradation, the irradiation at lower heat fluxes needs a longer time than for higher heat fluxes. For a given matrix degradation of about 0.53, the CFRP has to be irradiated for 1800s at 15 kW/m2, for 120 s at 30 kW/m2, and for about 80 s at 50 kW/m2, respectively. It can be observed that for a low heat flux, the intensity ratio of the bands at 1510 cm−1 and 1486 cm−1 increases nearly linear from the irradiated surface through the CFRP to the back side. However, for samples treated at high heat fluxes and long irradiation time (80 s at 50 kW/m2 and 180 s at 30 kW/m2), matrix degradation is steeper close to the irradiated surface and consequently non-linear. Also, it is noticeable that data points on the irradiated surface (0 mm) or at the back side (4 mm) are either higher or lower. An explanation for the higher intensity ratio is that spectra taken at the surface or back side of the CFRP are more intensive than those taken inside because of a resin enrichment caused by the manufacturing process. If there are no fibres at the measuring point (e.g., CFRP surface or back side), which absorb IR radiation (the higher the wavenumber the higher the absorbance), the intensity ratio of the bands at 1510 cm−1 and 1486 cm−1 calculated for thermally unloaded CFRP is about 0.06 higher than calculated for spectra taken at measuring points with fibres (e.g., inside the CFRP). This effect can be distinct for irradiated CFRP.

Fig. 3
figure 3

Intensity ratio of the bands at 1510 cm and 1486 cm over the sample depth of 4 mm thick CFRP (0 mm = irradiated surface) irradiated at different heat fluxes (left: 50 kW/m , middle: 30 kW/m , right: 15 kW/m ) and varying irradiation time

Full size image

On the other side, matrix degradation is very pronounced at the irradiated surface (0 mm) and back side (4 mm) for medium and strong thermal damage. This is explained by the presence of oxygen which causes a more pronounced matrix degradation than in a non-oxidative atmosphere. TGA measurements of Eibl show the beginning decomposition of the 8552 epoxy resin at about 260 °C at oxidative atmosphere, while the degradation starts at about 340 °C in nitrogen [36]. Due to the low diffusion of oxygen into the CFRP, thermo-oxidative matrix degradation only occurs close to the irradiated surface (penetration depth: ~ 100 µm); i.e., this is only relevant for the matrix degradation on the irradiated surface and the back side [37,38,39]. For the back side, however, oxygen is present but matrix degradation is less pronounced due to a lower temperature than on the irradiated surface.

CFRP with a thickness of 8 mm show a comparable behaviour to 4 mm thick CFRP (data not depicted). Matrix degradation also rises with increasing irradiation time and is more pronounced close to the irradiated surface especially after thermal loading at a high heat flux and long irradiation time. But in contrast to the thin (4 mm) samples, the irradiation time has to be about twice as long until pronounced gradients of matrix degradation occur close to the irradiated surface. Also, the strong matrix degradation close to the irradiated surface penetrates about twice as deep inside the CFRP for 8 mm thick samples than for 4 mm thick samples.

3.2 Influence of Thermal Loading on the Development of Delaminations

The presence of thermally induced structural damage in CFRP can be observed by means of µCT. Figure 1 shows CFRP samples irradiated at 50 kW/m2 after different irradiation times. Visible cracks are formed close to the irradiated surface beginning at an irradiation time of 65 s and migrate deeper inside the CFRP with increasing irradiation time. Due to the predominantly horizontal orientation of the cracks (see Fig. 1), the structural damage is assumed to be dominated by delaminations according to Mouritz et al. [3]. However, µCT does not provide a resolution high enough to distinguish the visual separation of matrix and fibres, which is why matrix cracking cannot be excluded.

The distance between the back side and the deepest delamination in a cross section is denoted as the non-delaminated thickness znd (see Table 1). Figure 4 shows znd plotted against the irradiation time for 4 mm (left) and 8 mm (right)thick samples. It is shown that for higher heat fluxes and thinner samples, delaminations develop faster.

Fig. 4
figure 4

Thickness of the non-delaminated CFRP (znd) plotted against the irradiation time t for CFRP with a thickness of 4 mm (left) and 8 mm (right) irradiated at different heat fluxes (error bars within the symbols)

Full size image

Regarding Table 1, delaminations occur beyond a temperature of 270 °C. Complementary investigations with CFRP stored isothermally for 1 h at temperatures between 250 and 300 °C and a subsequent analysis with µCT confirmed that delaminated areas may occur beyond a critical temperature of 270 °C (see Fig. 5) [40]. Therefore, delaminations only start to develop after thermally induced matrix degradation (see Sect. 3.3). However, high stress occurs at the fibre-matrix-interface at high temperatures caused by different coefficients of thermal expansions of fibre and matrix. This stress in combination with cracked or weakened bonds in the polymer matrix can facilitate the development of delaminations.

Fig. 5
figure 5

µCT-cross sections of CFRP after storing isothermally at different temperatures for one hour. Delaminations are marked with arrow

Full size image

In case of medium and high heat fluxes (30 and 50 kW/m2), delaminations are formed deeper inside the CFRP with increasing irradiation time until they penetrate through the entire CFRP [3]. For a low heat flux (15 kW/m2), however, the depth where the deepest delaminations develop is limited. At the irradiation times of 900 and 1800s for 4 mm thick samples and of 1800 and 2700 s for 8 mm thick samples, delaminations do not completely penetrate the CFRP but remain at a constant znd. Normalizing these non-delaminated depths to the sample thickness (znd/ztotal), delaminations penetrate 77% ± 4% into the CFRP. Having a look on the locally occurring temperature at this points of deepest delaminations for all samples (see Table 1), the mentioned samples at 15 kW/m2 show a temperature between 270 and 290 °C, which corresponds to the temperature necessary to form delaminations (see above). In deeper areas of the CFRP, this temperature cannot be reached, and therefore, no delaminations arise. For all other samples, the deepest delaminations develop at a temperature higher than 300 °C; i.e., within the conducted experiments, the development of delaminations seems to be favoured at temperatures beyond ~ 300 °C. Vetter et al. shows a more pronounced matrix degradation beyond 300 °C [13]. Considering this stronger matrix degradation, an accelerated development of delaminations beyond 300 °C is plausible.

3.3 Correlation of Matrix Degradation and Delamination Depth

Considering the development of delaminations after matrix degradation (see Sect. 3.2), Vetter et al. defined a threshold value for matrix degradation measured by infrared spectroscopy (I1510 cm−1/I1486 cm−1 = 0.79) for the development of delaminations for 4 mm thick 8552/IM7 CFRP samples after thermal treatment at 50 kW/m2 [13]. Below this threshold value, delaminations arise. Figure 6 shows a comparable correlation of the intensity ratio of the IR bands at 1510 cm−1 and 1486 cm−1 calculated for spectra taken at the depth of the deepest delamination with the normalized non-delaminated sample thickness (znd/ztotal) for 4 and 8 mm thick CFRP after irradiating with varying heat fluxes. At a ratio znd/ztotal = 1, which corresponds to the irradiated surface, delaminations cannot be observed and, consequently, I1510 cm−1/I1486 cm−1 is higher than the threshold. When delaminations are formed inside the CFRP (znd/ztotal < 1), the corresponding intensity ratios of the IR bands decreases to 0.74 ± 0.05, which fits to the threshold given in Vetter et al. [13]. It is shown that delaminations occur at a certain degree of matrix degradation independent of sample thickness or heat flux, which allows to use the observed threshold universally for 8552/IM7 CFRP.

Fig. 6
figure 6

Intensity ratio of the bands 1510 cm−1 and 1486 cm−1 calculated from IR spectra measured at the depth of the deepest occurring delamination plotted against the normalized non-delaminated thickness znd of CFRP panels with a thickness of 4 and 8 mm irradiated at 15, 30, and 50 kW/m2 and different irradiation times

Full size image

3.4 Prediction of the Presence of Delaminations By Means of Multivariate Data Analysis

Linear discriminant analysis (LDA) is a multivariate data analysis tool, which allows the supervised classification of data by using a linear transformation to minimize the distance between data points inside one group and maximize the distance between different groups [44,45,46].

Based on the preceding findings of the threshold value of matrix degradation determined with ATR-FTIR-spectroscopy necessary to be lower than 0.74 for the formation of delaminations, it is possible to develop a LDA model based on spectral data for the prediction of the presence or absence of delaminations at the measuring point of the spectra. Therefore, IR spectra taken in different depths of thermally damaged CFRP have to be organized into two groups: one group contains spectra taken in depths, where delaminations occur, the other group is without delaminations. The information of the presence or absence of delaminations in the corresponding depth is determined by means of µCT.

A training data set contains spectra taken at different depth of thermal damaged CFRP for varied parameters (e.g., different sample thicknesses and heat fluxes) and is used for calculating the model. For getting an idea about external influences, models are established with different parameter settings. The easiest one is using CFRP of one thickness irradiated at one heat flux (8 mm, 50 kW/m2). Regarding the single influences of either heat flux or sample thickness, only one of these parameters is varied; i.e., models are established for 8 mm CFRP irradiated at 15, 30, and 50 kW/m2 or 4 and 8 mm thick CFRP are irradiated at 50 kW/m2. At least, the whole data set (4 and 8 mm, 15, 30, and 50 kW/m2) is used for calculating a LDA model. Table 2 lists the accuracy determined via cross validation for LDA models developed with a training data set. For 8 mm thick CFRP damaged at 50 kW/m2, an accuracy of 99.8% is achieved, i.e., 99.8% of the spectra are assigned to the right group. Varying the heat flux or sample thickness causes a slight decrease in the prediction accuracy to 98.3% or 98.6%, respectively. For the whole data set, i.e., 4 and 8 mm thick CFRP irradiated at 15, 30, and 50 kW/m2, the accuracy drops down to 97.1%. A test data set allows the determination of the prediction quality with data not considered in the LDA model and gives therefore a more realistic assessment of the quality. Using a test data set, a prediction accuracy of 97.9% for 8 mm thick CFRP irradiated at 50 kW/m2 is achieved. With increasing parameter complexity, the prediction accuracy decreases to 93.7% for varying heat flux to 95.3% for varying sample thickness and to 95.2% for the entire data set (see Table 2).

Table 2 Results for LDA models developed with IR spectra of CFRP after different thermal treatment (varying heat flux and irradiation time) to predict the presence or absence of delaminations. For robustness testing, spectra belonging to the bold printed parameters are used in the training data set, the underlined ones in the test data set
Full size table

3.4.1 Improvement of the Model Robustness by Using Principal Component Analysis

For checking the robustness of LDA models regarding unknown influence parameters, LDA is performed with spectra recorded for CFRP with varying parameters (e.g., heat flux or sample thickness; see Table 2, bold parameters) and subsequently tested with spectra attributed to CFRP which are not considered in the LDA model (see Table 2, underlined parameters). Therefore, a model is created with a training data set containing spectra of 4 and 8 mm thick CFRP irradiated at 15 and 50 kW/m2 and a test data set representing the same thicknesses but irradiated at 30 kW/m2. A second model is created for all heat fluxes (15, 30 and 50 kW/m2) but the training data set contains only spectra of 8 mm thick CFRP, while the test data set contains spectra of 4 mm thick CFRP. Table 2 shows the results for this models: both show an accuracy of about 98% after cross-validation. As expected, the accuracy of the prediction decreases conspicuously when determining it with the test data set due to no consideration at modelling. For varying heat flux, the accuracy of the prediction decreases down to 76%. Thereby, the prediction is mainly false positive; i.e., delaminations are predicted although there are none at the point of the taken spectra. For the varying sample thickness, the prediction accuracy decreases only down to 86.9% and the amount of false positive and false negative results are approximately the same.

By using principal component analysis (PCA) as additional preprocessing step, the robustness of LDA models regarding not considered parameters can be raised partially. Predicting the presence of delaminations of 4 mm thick CFRP irradiated at all heat fluxes by using a LDA model established for 8 mm thick CFRP irradiated at 15, 30, and 50 kW/m2 shows an accuracy of 84.9%, which is comparable with the prediction accuracy of the same model without PCA pretreatment. However, the prediction accuracy of the test data set containing spectra from 4 and 8 mm thick CFRP irradiated at 30 kW/m2 predicted with the LDA-model developed with the training data set containing spectra taken at thin and thick CFRP but only thermally treated at 15 and 50 kW/m2 is 92.7% with PCA pretreatment instead of 76% without PCA-pretreatment. This means that the robustness of LDA models can be increased significantly by applying PCA especially for models with not considered heat flux.

PCA as a suitable preprocessing step can be explained due to two main reasons: at first, the data reduction in consequence of the PCA allows to consider more wavenumbers, i.e., more variables, per spectra. Without this data reduction, LDA can only be performed with a number of variables lower than samples per class, which limits the number of variables for the models without PCA pretreatment to a wavenumber range between 1250 and 1800 cm−1, whereas for the prediction with PCA-pretreatment, a wider wavenumber range (e.g., 900 to 1800 cm−1) can be considered.

Secondly, the data after PCA are already slightly separated with regard to thermal loading. The score plot in Fig. 7 shows the scores loading on the principal components (PC) one and two, which explain most of the variance. The data points in the score plot are assigned to groups explaining the absence or presence of delaminations (grey dotted boxes). The plot shows two groups with an overlapping area (grey area). The separation of the points depending on the delaminations is possible because the wavenumber ranges 1510 cm−1 and 1530 cm−1 (EP) and 1470 cm−1 and 1490 cm−1 (PES) load in opposite directions on PC 1, i.e., 1510 to 1530 cm−1 loads positive on PC 1 and 1470 to 1490 cm−1 loads negative on PC 1 (loading plot not depicted). As discussed in Sect. 3.1, the intensity ratio of the bands at 1510 cm−1 and 1486 cm−1 is calculated as parameter characteristic for thermal loading. This bands lie within the above-named ranges; i.e., the data points in the PCA are separated regarding thermal loading. Section 3.2 additionally shows that delaminations also occur with increasing thermal loading. Due to that, a first separation of the spectral data with respect to delaminations in the PCA can be expected.

Fig. 7
figure 7

Score plot of a PCA done with spectra measured in different depths of 4- and 8-mm-thick CFRP after irradiation at 15, 30, and 50 kW/m2 for different time intervals

Full size image

In summary, LDA is a helpful tool to predict the presence or absence of delaminations. If the sample parameters are known, the usage of a LDA model without PCA pretreatment is recommended. If the sample parameters, e.g., the heat flux, are unknown, a pretreatment with PCA is proposed due to a higher robustness towards unknown influence parameters.

3.5 Importance of the Prediction of the Presence of Delaminations in Thermal Damaged CFRP

3.5.1 Influence of Thermal Loading on the Apparent Interlaminar Shear Strength

Residual apparent interlaminar shear strength testing (ILSS) is an appropriate method to characterize one-sided thermal loading of CFRP with regard to the formation of structural damage like, e.g., delaminations [11, 13, 41,42,43]. Figure 8 against the irradiation time for 4 mm (left) and 8 mm (right) thick CFRP after irradiation at different heat fluxes. It is shown that ILSS decreases faster for thin CFRP than for thick ones comparable with the curve progression of znd plotted against the irradiation time (see Fig. 4). In addition, ILSS decreases slower for low heat fluxes. For example, a 4 mm thick CFRP shows an ILSS of about 80 N/mm2 after irradiating either at 50 kW/m2 for 65 s or at 15 kW/m2 for 600 s. An explanation therefore is the earlier exceedance of the critical temperature of 270 °C at higher heat fluxes, which is necessary for the formation of delaminations (see Sect. 3.2). Interesting is that the ILSS curve for CFRP irradiated at 15 kW/m2 slightly flattens at high irradiation times. Considering the same flattening for the development of delaminations (see Sect. 3.2; Fig. 4), the presence of delaminations as dominant reason for the loss of ILSS can be assumed.

3.5.2 Influence of Delaminations on the Residual Strength

In Sect. 3.5.1, the decrease of ILSS accompanied by increasing delamination depth and an impact of delaminations on ILSS is already mentioned. Therefore, the influence of the formation of delaminations on the residual ILSS should be considered in more detail. Figure 9a shows ILSS plotted against the normalized non-delaminated thickness of the CFRP analysed with µCT. With increasing depth of delaminations inside the CFRP, decreasing ILSS is recognized. In general, stress is calculated as force per area (see Eq. (1). Assuming, that in case of bending, delaminated CFRP can only carry stress in a non-damaged area, the load bearing area is minimized with increasing migration of delaminations into the bulk material of the CFRP. Due to a constant sample width, a simple approach is the calculation of the residual ILSS τ by multiplying the ILSS of non-damaged CFRP τunloaded with the normalized non-delaminated thickness znd/ztotal (see Eq. (2) and dotted line in Fig. 9a).

$$\tau = {\tau }_{\mathrm{unloaded}}\cdot\frac{{z}_{\mathrm{nd}}}{{z}_{\mathrm{total}}}$$
(2)

If delaminations migrate less than the half of the sample thickness into the CFRP, the assumption of the decrease of ILSS depending on occurring delaminations seems to be right; i.e., the data points follow the calculated line. For CFRP with a delamination depth deeper than 50% of the total thickness, ILSS decreases not proportional to the non-delaminated thickness anymore. This means that load is not transmitted anymore only into non-delaminated areas but into non-delaminated and delaminated areas of the CFRP. For CFRP with delaminations penetrating deeper than 50% of the sample thickness, there is already a strong thermal damage inside. This entails more pronounced degradation phenomena like the exposure of whole fibre bundles, strong matrix degradation, and even maybe char formation, which can lead to an increase in the surface roughness between the plies. Due to resulting roughness-induced mechanical interlocking, a higher shear load is required to cause shear failure (Fig. 8).

Fig. 8
figure 8

Interlaminar shear strength (ILSS) τ plotted against the irradiation time t for CFRP with a thickness of 4 mm (left) and 8 mm (right), irradiated at different heat fluxes

Full size image

Based on the results in Fig. 9a, the following simple approach can be introduced: If the load is only transmitted into non-delaminated areas of CFRP, then the replacement of z in Eq. (1) with znd should lead to the same ILSS value τ as for thermally unloaded CFRP (see Eq. (3)). This calculated ILSS value is introduced as τcalc.

Fig. 9
figure 9

ILSS vs. the normalized non-delaminated thickness znd/ztotal of 4 and 8 mm thick CFRP irradiated at 15, 30, and 50 kW/m2 (a ILSS τ calculated with the sample thickness; b ILSS τcalc calculated with the non-delaminated thickness)

Full size image
$${\tau }_{\mathrm{calc}}= \frac{3 \cdot{P}_{R}}{4 \cdot b \cdot{z}_{\mathrm{nd}}}$$
(3)

Figure 9b shows the calculated ILSS τcalc plotted against the normalized non-delaminated thickness for znd/ztotal > 0.5. The mean of the calculated ILSS is 103 ± 5 N/mm2. For comparison, the ILSS of CFRP without thermal loading is 101 ± 3 N/mm2. Having nearly no difference between the calculated ILSS and the ILSS of CFRP without thermal loading allows the assumption, that only delaminations are responsible for the loss of strength and load is carried by the non-delaminated CFRP. Both Fig. 9a and b show that a prediction of the ILSS is possible by means of the non-delaminated thickness determined via µCT for samples with a delamination depth < 50%.

3.5.3 Consequences for the Prediction of One-Sided Thermal Damage By Means of IR Spectroscopy

The preceding chapters discuss the correlation of matrix degradation analyzed by means of ATR-FTIR-spectroscopy and resulting in a LDA model for the prediction of the presence or absence of delaminations as well as the influence of thermally induced delaminations on the residual strength. In the following, these findings are summarized with regard to the prediction of residual strength by means of IR spectroscopy.

Therefore, ILSS is plotted against the intensity ratio of the bands at 1510 cm−1 and 1486 cm−1 calculated for spectra recorded on the irradiated surface (see Fig. 10a) and in the middle of 4 and 8 mm thick CFRP samples (see Fig. 10b), i.e., at a sample depth of 2 mm and 4 mm, respectively. With increasing matrix degradation, a loss of strength can be registered. Due to stronger matrix degradation close to the irradiated surface compared with the middle of the CFRP (see Fig. 3), there is a lower intensity ratio of the bands at 1510 cm−1 and 1486 cm−1 for the same ILSS in Fig. 10a than in Fig. 10b. For example, for an ILSS of 33 N/mm2, an intensity ratio at the irradiated surface of 0.33 is found, whereas the intensity ratio in the middle of the CFRP amounts 0.56. This results in a less steep slope for the correlation of ILSS with matrix degradation at the irradiated surface (see Fig. 10a) than with matrix degradation in the middle of the sample (see Fig. 10b). Regarding this different slopes for both correlations, it is shown that for a meaningful correlation of ILSS and matrix degradation, the knowledge of depth of the taken spectra is indispensable. This should also be considered with regard to the prediction of residual ILSS by means of IR spectroscopy.

Fig. 10
figure 10

Interlaminar shear strength τ plotted against the intensity ratio of the bands at 1510 cm−1 and 1486 cm−1 from spectra recorded a at the irradiated surface and b in the middle of 4 and 8 mm thick CFRP panels after irradiation at different heat fluxes and times

Full size image

The data points in Fig. 10 are assigned to three different groups corresponding to a defined range of delamination depth: (1) CFRP without delaminations and (2) CFRP with a non-delaminated depth higher and (3) lower than 50% of the total thickness. Additionally, a dotted line marks the threshold value of matrix degradation for the development of delaminations (see Sect. 3.3). It is shown that this line separates data points with and without delaminations for spectra taken at the irradiated surface (see Fig. 10a). When spectra are taken in the middle of the CFRP, data points with a delamination depth higher and lower than 50% are separated (see Fig. 10b). Therefore, for the correlation of ILSS with the intensity ratio calculated for spectra taken at the irradiated surface, a significant decrease of ILSS occurs at first below the threshold value. For the analogue correlation for spectra recorded in the middle of the CFRP, a decrease of ILSS occurs already before passing the threshold value, because delaminations already occur inside the upper 50% of the CFRP. This confirms that the knowledge of the depth of the taken spectrum is mandatory for the prediction of residual ILSS by means of IR spectroscopy.

Furthermore, it is shown that especially on the irradiated surface, the data points scatter with decreasing ILSS and increasing matrix degradation. This can be explained by the presence of delaminations; i.e., if there are no delaminations inside the CFRP, the scattering is low and vice versa. This means by implication that the prediction of the residual strength by means of the intensity ratio of the IR bands at 1510 cm−1 and 1486 cm−1 < 0.74 is not reliable for CFRP with a lot of thermally induced delaminations. Inside the CFRP, a reliable prediction with IR spectroscopy is also difficult because of the steep slope caused by a less pronounced matrix degradation compared with the surface, which leads to a loss of sensitivity.

Performing LDA with an IR spectrum of the irradiated surface enables the prediction of the absence or presence of delaminations inside the CFRP. If no delaminations are predicted inside the CFRP, no significant loss of residual strength is expected. If delaminations are predicted on the surface, a loss of strength can be expected, but without an assertion about the amount of strength loss because there is no information about the depth of delaminations, which is mandatory for the prediction of residual strength (see Sect. 3.5.2).

However, it is possible to remove the damaged CFRP ply by ply in form of, e.g., grinding or milling and predicting the presence of delaminations via LDA by taking a spectrum after each removed ply. With the thickness of one ply, the depth of the taken spectrum can be determined and used for the prediction of the residual strength. If removing the plies until no presence of delaminations can be predicted anymore, all the damaged CFRP is already removed. Furthermore, the delamination depth can be calculated with an error of one ply. By knowing the delamination depth, the residual strength can be determined according to Eq. (3) in Sect. 3.5.2. This proceeding is recommended for CFRP which is penetrated with delaminations maximum to the middle of the CFRP because of more sensitive spectral information towards thermal loading in this area (see steep gradient of matrix degradation close to the irradiated surface in Fig. 3). Also, the calculation of ILSS taking delaminated structures into account is limited for znd > 0.5 (see Fig. 9).

4 Conclusions

This study focuses on chemical, structural, and mechanical properties of CFRP samples with different thicknesses irradiated at one side with different heat fluxes and varying irradiation time. Therefore, ATR-FTIR-spectroscopy along a ground incline plane for observing matrix degradation through the CFRP, µCT for measuring the depth of delaminations penetrating the CFRP, and ILSS measurements for determining the residual strength after one-sided thermal loading are applied.

It is shown that delaminations at rapid heat-up do not occur below a temperature of 270 °C [40]. Furthermore, correlating the matrix degradation (IR) with the non-delaminated thickness of CFRP (µCT) shows that there is a threshold value (I1510 cm−1/I1486 cm−1 = 0.74 ± 0.05) for matrix degradation, below which delaminations develop [13]. Following this threshold value, LDA-models can be established, which allow to predict the presence or absence of delaminations at the point of a taken spectrum. Additionally, applying PCA as data pretreatment increases the robustness of the models and allows a good prediction of the presence of thermally induced delaminations also in CFRP damaged at unknown parameters (e.g., heat flux).

Therefore, ATR-FTIR-spectroscopy can be considered as a powerful NDT-method to detect thermally induced delaminations indirectly. Compared with other NDT-techniques like, e.g., ultrasonic testing or shearography, which detect delaminations in the millimetre-scale, ATR-FTIR-spectroscopy allows to detect delaminations already in the micrometer-scale due to the training data based on µCT measurements with a resolution of 7 µm. On the other side, the indirect determination of delaminations by means of IR spectroscopy does not allow to define the exact locality of delaminations.

However, a strategy is proposed to predict residual strength of unidirectional CFRP by means of IR spectroscopy and LDA and the suggestion of a possible application of this method in form of using it during repair processes: If no delaminations are predicted via LDA, no significant loss of strength is expected. If the presence of delaminations is predicted, the maximum depth of delaminations can be determined by removing ply by ply. Knowing the delamination depth, an assessment of the residual ILSS is possible.

The detailed insight into the chemical, structural, and mechanical behaviour of one-sided thermally damaged CFRP points up the difficulties of the prediction of residual strength with IR spectroscopy. It is shown that without depth information, a precise prediction is not possible. A solution to improve the accuracy of a prediction could be the combination of data from different depths, which is the topic of ongoing research.