1 Introduction

The use of composite materials reinforced by natural fibers is growing strongly in many industrial fields, particularly in the automotive sector [1,2,3], but also in the civil construction area and in the naval field. Thanks to recyclability and renewability, but also to low weight and low costs, biocomposites allow not only to comply with increasingly stringent environmental protection regulations, but also to reduce costs of production (lower cost) and operating costs (lower weight) of machines and structures [4,5,6,7,8,9,10,11].

Between the various natural fiber proposed in literature for the manufacture of biocomposites, sisal fiber is one of the most interesting, not only for its good mechanical properties, but also for various important characteristics as low damageability, low skin irritability, high commercial disposal, low weight and very low cost [12,13,14,15,16,17,18]. It has been considered for the manufacture of both long and short fiber biocomposites. The random short fiber configuration is however very attractive for its characteristic low manufacturing cost, especially for large series productions in various industrial fields.

Although many research works reported in literature have aimed at improving the mechanical properties of the natural fibers (included sisal) and, above all, at enhancing the fiber-matrix adhesion by proper chemical/mechanical treatments [19, 20], to date the objective of increasing the tensile strength of the random short fiber biocomposites, has not been reached. Consequently, the improvement of the mechanical performance of these materials is still an important goal for the scientific community and for the industry, to spread their use not only in non-structural applications, but also in structural and semi-structural applications (panels, bins, etc.).

For various pairs of matrix-natural fibres, as the green epoxy-sisal considered in the present study, the way followed by most researchers to date, consisting in improving the fiber-matrix interface strength, is not adequate because the low transversal tensile strength of such biocomposites is not due to the low fiber matrix-adhesion but, it is due to the low internal transversal strength of the fiber, related to its intimate anisotropic fibrous structure that cannot be easily enhanced by surface treatments.

In order to overcome such a drawback, by this work the authors proposes the proper introduction of low fractions Carbon Nanotubes (CNTs) to activate advantageous matrix-fiber bridging effects, that can led to appreciable increments of the biocomposite transversal tensile strength; obviously further contribution is expected from the contemporary toughened matrix determined by the introduction of the CNTs.

In general, the experimental evidence has shown that biocomposites reinforced by natural fibers present damage mechanisms [21,22,23,24,25,26] quite similar to those observed in traditional composites reinforced by synthetic fibers [27], as fibre-matrix debonding, delaminations, inter fibre fractures and fibre fractures [e.g. 27]. In more detail, when fiber-reinforced polymers are tested with axial and/or multiaxial tensile loading, the damage mechanisms happen in a particular order [e.g. 28]: in a first phase cracks in the matrix between the reinforcing fibres in off-axis layer form and growth; the second phase is characterized by a saturation of transverse cracks in the matrix, transversal tensile failure and longitudinal inter fibre fractures. Degradation progresses slowly before phase three begins and fiber-reinforced polymer rapidly collapses due to the growth of delamination and/or fiber fractures.

Therefore, since the scientific literature [29,30,31,32,33,34,35,36,37,38,39,40] shows that the incorporation of single-walled and multi-walled carbon nanotubes in traditional fiber-reinforced polymers (FRPs) can significantly increase their static strength and the fatigue life, it seems reasonable to theorise that the dispersion of CNTs in the matrices could lead to significant improvements in the mechanical performance of biocomposites, especially under fatigue loading. This is a very important goal, considering that the improving of the fatigue performance of FRPs is currently an important research objective for both scientific community and industry.

Although most of the literature focused the dispersion of CNTs on high performance CFRP, several works have been devoted also to GFRP, whose behaviour and properties are closer to those of the natural fiber biocomposites.

As an example, Zhu et al. [29] investigated the CNTs potential for increasing the interlaminar fracture toughness of a glass fiber/epoxy composite. Adding CNTs enhanced resin interlayer at the fracture interface and resulted in a 52–95% improvement in mode I fracture toughness and 74–109% improvement in mode II fracture toughness, compared to the original material. Based on the increased toughness of the composites, it appears that the placement of dense concentrations of CNTs in between the glass fibers is the best method of inhibiting delamination propagation.

Loos et al. [32] analysed the effects of carbon nanotube inclusion on cyclic fatigue behavior and the tensile properties of polyurethane (PU) composites containing 0.3 wt.% MWCNTs. Tension-tension cyclic fatigue tests were carried out at various load levels (30–50 MPa) to establish the relationship between stress and the number of cycles to failure (S–N curves). The tensile energy to break PU composites was enhanced up to 38%. In addition, the incorporation of CNTs increased the fatigue life of PU in the high-stress amplitude, low-cycle regime by up to 248%. Micrographs show highly dispersed CNTs and indicate the key mechanisms for enhancement in fatigue life such as CNT crack-bridging and pull-out.

Grimmer et al. [34, 35] proved that the addition of 1% by weight of CNTs to the polymer matrix of glass fiber-epoxy composite laminates improved their high-cycle fatigue strength by 60–250%, depending on the loading condition. Inspection of the composite specimens tested in fatigue showed CNTs that were either pulled out of the resin matrix or fractured, suggesting energy-absorbing mechanisms that may be responsible for the increase in the fatigue life observed.

Finally, it is important to note how one of the mechanisms at the origin of the reinforcing action of the CNTs in all the FRPs, has been described by Levitt and Perutz [36], and is the formation of hydrogen bonds between the p orbital system of the CNTs and the hydroxyl functions of the fibers.

In order to analyse if the dispersion of low fraction CNTs leads to appreciable fiber-matrix bridging effects, other than a significant matrix toughening, as well as to detect the evolution of the damaging processes and the main parameters that govern both the static and fatigue strength of biocomposites reinforced by sisal fibers, systematic experimental static and fatigue test have been performed on high quality random short sisal fiber biocomposites obtained by an optimized compression molding process; also, the relative results have been accurately analysed in order to determine a reliable model to predict the mechanical performance of such biocomposites on both low cycles and high cycles fatigue fields.

2 Experimental

2.1 Materials

The random short sisal fiber biocomposites considered in the present work, have been obtained by using a green epoxy matrix produced by the American Entropy Resin Inc. (CA) USA, named SUPERSAP CNR, with IHN-type hardener [37]. As widely described in previous works [21,22,23,24,25,26], it is an eco-compatible matrix with good mechanical properties, comparable to those of common epoxy resins used for the manufacture of composites reinforced with synthetic fibers.

Multi-wall carbon nanotubes (MWCNT) having an average diameter between 30 and 50 nm, have been finely dispersed within the matrix, before adding the hardener, by using a proper mixer and a FLOUREON sonicator. The batch of structural sisal fibers used in the present work, have been opportunely extracted from mature leaves of agave sisalana. As explained in detail in [21,22,23,24,25,26] the selection process consists in choosing only the perimeter fibers from the middle third of mature leaves (4–5 years), discarding the less resistant central fibers (non-structural fibers). Once selected, the fibers were cut with an optimal length of 5 ± 2 mm.

2.2 Processing

Preliminary studies carried out on polymeric matrix (PLA, epoxy resin) biocomposites reinforced by similar agave fibers, have shown [21, 22] that for these biocomposites good mechanical strength can be obtained by means of an optimized compression molding process coupled with a thermomechanical cure process. In accordance with these indications, the manufacture of the biocomposites was performed by mixing short fibers and green epoxy resin, in a special removable rectangular mold having dimensions 140 × 340x10 mm (Fig. 1); the high compaction pressure was applied by using a 100-ton hydraulic press (Fig. 1). The cure process was integrated by a suitable thermal cycle [21,22,23,24], obtained by heating the mold with appropriate electrical resistances and monitoring the temperature using proper thermoresistances.

Fig. 1
figure 1

Mould, counter-mould and hydraulic press used for biocomposites manufacture

Full size image

In order to compare the performances of biocomposites with nanotubes, with that of the same bio-composites without nanotubes, as well as to detect the optimal concentration of nanotubes, three different random short-fiber biocomposites have been considered, all having the same fiber volume fraction of 35%, but different volume concentration of dispersed nanotubes. Taking into account the results of literature related to the usual concentrations of nanotubes, in addition to the biocomposite without nanotubes, called CNT0%, a biocomposite with 1% of nanotubes, called CNT1%, and a biocomposite with 2% of nanotubes, called CNT2%, have been considered:

  • • CNT0%: biocomposite without nanotubes;

  • • CNT1%: biocomposite with 1% of nanotubes;

  • • CNT2%: biocomposite with 2% of nanotubes.

The accurate dispersion of the carbon nanotubes in the epoxy resin was obtained in advance (before mixing it with the hardener) by using a suitable FLOUREON sonicator. Figure 2 shows the short fibers impregnated with green epoxy resin premixed with the nanotubes and then mixed with the hardner, inside the mould, before the compression molding process.

Fig. 2
figure 2

Mixture of sisal fibers and green epoxy with nanotubes inside the mould

Full size image

In detail, the initial impregnation of the fibers took place in excess of resin and the desired volumetric percentage of fibers, equal to 35%, was obtained by adjusting properly the final thickness of the panel under pressure. Figure 3a illustrates the initial phase of the compression process after the mould is closed, while Fig. 3b represents the final phase characterized by the leakage of the excess resin.

Fig. 3
figure 3

(a) Initial phase and (b) final phase of the compression moulding process (note the excess resin leakage)

Full size image

Figure 4 shows, as an example, a CNT0% (Fig. 4a), CNT1% (Fig. 4b) and CNT2% (Fig. 4c) biocomposite panel extracted from the mould, before the necessary specimens are cut for static and fatigue tensile tests.

Fig. 4
figure 4

Panels of (a) CNT0%, (b) CNT1% and (c) CNT2% biocomposites obtained by the optimized compression moulding process

Full size image

2.3 Material Testing

In accordance with the ASTM D 3039/D 3039 M-00 standard [38], the mechanical behavior of the different biocomposites under static loading have been determined by tensile tests on rectangular specimens of 25 × 220 × 3 mm size. These rectangular specimens have been equipped with special aluminum tabs (25 × 60 mm) and instrumented with an MTS type knife extensometer (see Fig. 5). The tests have been carried out by using an MTS 810 type servo-hydraulic machine, with a traverse speed of 1 mm/min. Five distinct samples have been tested for each type of analyzed biocomposite.

Fig. 5
figure 5

Biocomposite specimens (a) without nanotubes and (b) with carbon nanotubes, under tensile test

Full size image

Similar specimens and the same servo-hydraulic test machine have been used to the successive fatigue analysis performed to assess the actual effects of the CNTs on the fatigue performance of the biocomposites analyzed; in particular, a fatigue load ratio R = 0.01 (traction-traction fatigue) and a loading frequency of 5 Hz, which ensures the absence of significant dissipative effects related to mechanical hysteresis, have been considered. The fatigue tests have been performed under constant amplitude loading by monitoring both the current residual strain and the current Young’s modulus defined by the ratio of the maximum strain to the maximum applied load, in accordance with the ASTM D 3479/D 3479 M-19 standard. In more detail, for each biocomposite the fatigue tests have been carried out by considering four distinct load levels equal to 80%, 70%, 60% and 50% of the corresponding static failure load, by using samples consisting of five specimens for each load level. As an example, Fig. 5 shows a specimen without nanotubes (Fig. 5a) and of one with nanotubes (Fig. 5b), during tensile test.

3 Results and Discussion

3.1 Static Tensile Tests

The following Fig. 6 shows the tensile curves relating to the biocomposite specimens type CNT0% (Fig. 6a), CNT1% (Fig. 6b), and CNT2% (Fig. 6c).

Fig. 6
figure 6

Static tensile curves related to the biocomposite specimens (a) without nanotubes CNT0%, (b) with 1% of nanotubes CNT1%, (c) with 2% nanotubes CNT2%

Full size image

From these figures it is possible to observe how all the analyzed biocomposites exhibit a linear elastic behavior up to about 50% of the static failure load, followed by a subsequent stretch with decreasing stiffness that shows a progressive and irreversible damage of the material until final failure that occurs with a significant drop-down of the load up to final load values of the order of 10% of the maximum load supported. Also, unlike it was expected by considering the possible matrix toughening described in literature, there are no significant differences in term of failure strain, although it is evident how the introduction of CNTs leads to an improvement of both the tensile stiffness and the tensile strength (ultimate load) most probably related to the expected fiber-matrix bridging effects. However, the energy to failure increases appreciably by the introduction of 1% of CNTs, whereas neglecting effects are observed for the biocomposite with 2% of CNTs.

With reference to the particular damage mechanisms, the experimental evidence has shown that the failure of the specimens (Fig. 7) occurs through a mixed process that begins with a first phase (I) characterized by local failures essentially linked to the splitting and/or debonding of the fibers orthogonal to the loading direction, followed by a second phase (II) characterized by progressive transversal matrix microcracking and then by a subsequent third phase (III), characterized by the final rupture of the longitudinal fibers present near the damaged section, mixed to secondary fiber pull-out.

Fig. 7
figure 7

Specimens damaged at the end of the tensile test: (a) CNT0%, (b) CNT1% and (c) CNT2%

Full size image

In more detail, passing from the biocomposite CNT0% to the biocomposites with CNT1% the amount of the damaging corresponding to the first two phase decreases whereas the pull-out amount increase; both phenomena justify the increasing of the energy to failure of about 20%. No significant effects in term of damage evolution is instead observed by the direct analysis of the CNT2% specimens.

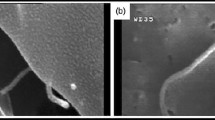
In order to characterise the dispersion and the microstructure of the nanocomposites, as well as to better analyse the various damage mechanisms involved, a Scanning Electron Microscopy (SEM) was used to investigate the fracture surfaces of the various biocomposites studied (see Fig. 7). In detail, Fig. 8 shows four different zooms of the fracture surface of a specimen with 1% of CNTs subjected to static tensile load.

Fig. 8
figure 8

Typical SEM micrographs of the fracture surfaces of the biocomposite specimens containing 1% of CNTs, subjected to static tensile loading

Full size image

It is seen clearly the random distribution of the fibers after the local complete matrix damage (Fig. 8a), as well as the debonding phenomena (fibers with free lateral surfaces) and limited secondary pull-out phenomena (free end fibers, see Fig. 8b), fiber damage that involves evident partial/incipient sub-fibers separation (fiber splitting, Fig. 8c and 8d), limited by the increase in matrix toughness and the inter-fiber bridging effects produced by the CNTs.

In more details, a high zoom of the same fracture surface, shown in the following Fig. 9, allows to observe the presence of the CNTs in the inter-fiber zones, that can lead to significant fiber-matrix “bridging” effects, as well as significant bridging effects versus matrix microcracking.

Fig. 9
figure 9

High zoom SEM micrography of the fracture surfaces of a specimen containing 1% of CNTs, subjected to static tensile loading

Full size image

From the following Fig. 10, that refers to the biocomposite without CNTs, it is possible to observe the widespread “transversal failures” that starts in the zone where the fibers are not aligned with the load (see Fig. 10a), mixed to longitudinal fracture of the fibers aligned to the loading direction (Fig. 10b, c).

Fig. 10
figure 10

Typical SEM micrographs of the fracture surfaces of a biocomposite specimen without CNTs, subjected to static tensile loading

Full size image

Such damage involves locally more appreciable fiber splitting (Fig. 10d) clearly highlighted also by the streaks on the lateral fiber surfaces (Fig. 10b). It is confirmed that in any case a sufficient fiber-matrix adhesion does not lead to significant pull-out phenomena: the length of the free fiber segments (i.e. of the actual critical length) observed by the SEM micrographs is in fact always much lower, in general lower than 3 ÷ 4 times the fiber diameter (see Fig. 10b).

Table 1 shows the results of the static tensile tests for all three types of biocomposites analyzed, in terms of average values and standard deviation of the ultimate tensile stress σu and tensile Young's modulus E.

Table 1 Results of static tensile tests related to the analyzed biocomposites with and without CNTs
Full size table

From Table 1 it is possible to observe that the highest mechanical characteristics are exhibited by the CNT1% biocomposite. In particular, passing from the biocomposite without nanotubes (CNT0%) to the toughened biocomposite with 1% of nanotubes (CNT1%), the static tensile strength passes from about 45 MPa to about 58 MPa (increment of about 30%), while the toughening with 2% of nanotubes gives rise to a more modest increase, from 45 to 47 MPa (increment of about only 6%).

The same qualitative/quantitative trend was observed by analyzing the values ​​of the elastic modulus. In detail, the addition of 1% of nanotubes to the matrix has resulted in an increase of the Young’s modulus still from about 5 GPa to about 6.5 GPa (increment of about 28%). As the percentage of nanotubes increases furtherly (2%), a more limited increase in the stiffness of the biocomposite is observed, by about 13%, although it is higher than the advantage observed in terms of tensile strength (6%), which is very limited.

The accurate visual observation of the progressive damage during the tests shows, as expected, that the matrix toughening due to the nanotubes, gives rise to a reduction of the phenomena of debonding between matrix and transverse fibers (phase I), as well as of the microcracking of the matrix (phase II), probably due also to the bridging of the nanotubes.

Unfortunately, the increase in the concentration of nanotubes from 1 to 2% does not, contrary to expectations, led to a further improvement in static performance. This could be attributed to the agglomeration effects of bundled nanotubes that occur as their concentration increases [39]. Therefore, further studies are recommended in order to avoid such agglomeration effects and, consequently, to further increase the positive toughening effects produced by the introduction of CNTs.

3.2 Fatigue Tensile Tests

As it is well known in the literature focused on composite materials, the introduction of fibers or any other stiff elements into a generic polymer matrix, induces in general an appreciable improvement of the fatigue performance, also when such introduction does not lead to any improvements of the static performance, or lead in some cases to a slight reduction of the static strength due to stress concentration effects. Such fatigue performance enhancements are essentially due to the increment of the material stiffness that, for a fixed applied load level, leads to beneficial strain decrements that corresponds to a significant increment of the fatigue life and/or of the fatigue strength, especially for high cycles fatigue (i.e. low fatigue load lower than the elastic limit of the material). Consequently, a significant fatigue performance increment is expected from the introduction of the CNTs which, as it has been observed from the above reported tensile test, leads to appreciable increments in material stiffness, especially in the case of CNT1% which leads also to a tensile Young’s modulus increment of about 30%.

In order to detect the evolution of the main material parameters during the fatigue loading, the following Fig. 11 shows the residual strain, i.e. the strain of the unloaded specimen (Fig. 11a) and the tensile Young’s modulus (Fig. 11b) vs. N/NR, being N the current fatigue cycles and NR the cycles corresponding to the final fatigue failure. These figures refer to the fatigue loading case with σmax = 0.8σu, but similar trends have been observed also for the other three cases σmax = (0.5, 0.6, 0.7) σu examined. As it is well known, both the residual strain and the Young’s modulus variations are two important indices of the progressive fatigue damage to which the material is subjected.

Fig. 11
figure 11

Evolution of the (a) residual strain and of the (b) Young’s modulus of the three biocomposites examined, subjected to tensile fatigue loading equal to 0.8σu

Full size image

The examination of residual strains depicted in Fig. 11a shows that, like most composites reinforced by synthetic fibers [40], for all the biocomposites examined it is possible to distinguish three successive zone: a first zone, included in the range 0 < N/NR <0.2 (in practice the first 10 ÷ 30 fatigue cycles), characterized by a relatively quick increasing of the residual strains (up to values between about 0.2% for CNT1%, to 0.5% for CNT0%), due to the formation of transverse matrix cracks in the most stressed areas, including debonding and/or fiber splitting; it follows a second zone included in the range 0.2 < N/NR < 0.8 (in practice the most fatigue life, from about 10 ÷ 30 cycles to about 1.5 × 105 ÷ 1.5 × 106 cycles), characterized by slow increasing of the matrix microcracking until its saturation. The third zone, that begin from 1.5 × 105 ÷ 1.5 × 106 cycles, includes the final phase characterized by an exponential damage process that involves the progressive fracture of the fibers aligned with the applied load, and limited secondary pull-out phenomena. Such damage mechanisms are qualitatively identical to that above observed for the static tensile case, also with accurate SEM micrographs (see Fig. 8–10), although under fatigue loading they do not occur one after another, but have a very different grow rate, especially those involved in the second phase; for these reason the micrograph of the fracture surfaces of the specimens subject to fatigue loading, are not reported.

All the observations above reported for the residual strains, are completely confirmed by the evolution of the Young’s modulus depicted in Fig. 11b, although the variations in the extreme zones (start and end zones) appears relatively more modest with respect to the residual strains. However, also in term of Young’s modulus the best effects are detected for the CNT1%.

In accordance with the composite literature [41,42,43], for most composite materials reinforced by synthetic fibers a reliable parameter to assess the current health under fatigue loading, is the damage parameters D defined by the relative variation of the Young’s modulus: (Eq. 1)

$$D(N)=\frac{{E}_{o}-E(N)}{{E}_{o}}$$
(1)

Such a parameter has been assessed in [44] to be able to represent the progressive internal damaging of biocomposites reinforced by flax fiber. The following Fig. 12 shows the evolution of such a parameter for the examined biocomposites by considering the two extreme cases of σmax = 0.5σu (Fig. 12a) and σmax = 0.8σu (Fig. 12b).

Fig. 12
figure 12

Evolution of damage parameter D vs. fatigue cycles, for (a) σmax = 0.5σu and (b) σmax = 0.8σu

Full size image

From Fig. 12 it is seen how the introduction of 1% of CNTs influences significantly the evolution of the fatigue damage that, after a limited initial phase in which it growth rapidly, it increases linearly up to the final fatigue fracture that is characterized by its exponential increasing. However, unlike biocomposite without CNTs, for any σmax /σu ratio the damage parameter of the toughened biocomposite CNT1% is limited to value of about 10% for about all the fatigue life, whereas the biocomposite CNT0% exhibits a higher progressive increments toward values that tends to the conventional fatigue limit of 30%.

The following Fig. 13 summarizes the results of the fatigue tests for all the specimens analyzed, through the representation of the relative semi-logarithm Wohler curves.

Fig. 13
figure 13

Results of the fatigue tests: Wohler curves (a) σmax vs. Log[NR] and (b) σmax / σu vs. Log[NR]

Full size image

From Fig. 13a it is possible to observe how, like traditional composites reinforced by synthetic fibers, also the fatigue curves of the analyzed biocomposites reinforced by sisal fiber, can be represented by a semi-logarithmic model called modified Wohler law [45]:

$${\sigma }_{max}=a+b Log(N)$$
(2)

where a and b are two constants that, in the common hypothesis that the material exhibits a fatigue limit σF at 106 cycles, theoretically would take the value of static tensile strength σu and (σF - σu)/6 respectively. Since in general Eq. 2 does not describes the fatigue behavior at low cycle fatigue (N < 103), as it is also the case of the examined biocomposites, i.e. it fits well the experimental data for high fatigue cycles, but does not converge to the static strength (see Fig. 13a that also shows the static strength on the ordinate axis), the two constants a and b are accurately determined by considering the experimental results corresponding to N > 103 fatigue cycles; the values determined in such a manner for the three biocomposites considered have been reported in Table 2 and can be used to describe accurately the fatigue behavior of the examined biocomposite for high cycles fatigue.

Table 2 Static strength, fatigue limit and fatigue ratios of the analyzed biocomposites
Full size table

In order to evidence in more detail the possible difference on the fatigue behavior of the three biocomposites examined, in Fig. 13b the Wohler curves are represented by considering the non-dimensional fatigue load ratio σmax/σu data along with the corresponding fitting straight line given by the following equation:

$$\frac{{\sigma }_{max}}{{\sigma }_{u}}=\stackrel{-}{a}+\stackrel{-}{b} Log(N)$$
(3)

From Fig. 13b it is seen clearly how in practice the high cycles fatigue behavior of the two toughened biocomposites CNT1% and CNT2% are represented by the same fitting curve, being the relative deviation less than the observed data scattering, whereas the non-toughened biocomposite CNT0% is represented by a very different Wohler curve. This result permits to evidence that the two biocomposites with CNTs exhibit in practice the same fatigue behavior, but different static strength; in other word, the biocomposite CNT2% exhibits absolute fatigue performance lower than CNT1%, only because it has lower static strength. Consequently, to improve its fatigue performance it is necessary to enhance its static strength by studying the causes (agglomeration effects of bundled nanotubes etc.) that determine such a lower value. Therefore, it is possible to state that 1% and 2% of CNTs have similar effects on the fatigue behavior but very different effects on the static strength.

In [46] Vasconcellos et al. have proved that the model proposed in [47] by D’Amore et al. for synthetic fiber composites:

$${N}_{R}={\left[1+\frac{1}{\alpha \left(1-R\right)}\left(\frac{{\sigma }_{u}}{{\sigma }_{max}}-1\right)\right]}^{1/\beta }$$
(4)

can be used also for the complete (low cycles and high cycles) fatigue life prediction of biocomposites reinforced by hemp fibers; in Eq. 4\(\alpha\) and \(\beta\) are the two constant that describe the complete fatigue behavior, whereas R is always the well-known fatigue load ratio given by σmax/σmin. In order to asses if such an interesting model can be used also for the prediction of the fatigue response of the examined biocomposites, Eq. 4 have been used to fit the experimental data and the comparison is depicted in the following Fig. 14.

Fig. 14
figure 14

Results of the fatigue tests: D’Amore et al. model [47] (a) σmax vs. Log[NR] and (b) σmax / σu vs. Log[NR]

Full size image

From Fig. 14a it is seen how the D’Amore et al. model [47] represented by Eq. 4 provides a very good approximation of the actual fatigue behavior for all the examined biocomposites, from the static loading case (NR = 1) to the fatigue limit at NR = 106 cycles. Also this model confirm that the two toughened biocomposite have in practice the same fatigue behavior that can be represented by a unique non-dimensional curve, as it is shown in Fig. 14b (the two curves fitting the experimental data, in fact, overlap each other).

Finally, for the three different biocomposites analyzed, Table 2 shows the static strength values (σu), the fatigue strength limit value (σF) at 106 cycles, the relative characteristic fatigue ratio (σF /σu), as well as the two constants a and b that appear into Eq. 2 and the two constants \(\alpha\) and \(\beta\) of Eq. 4. In order to allow a comparison of the fatigue performance of the biocomposites with that of the simple matrix, Table 2 also contains the static and fatigue strength of the matrix alone, given by the provider.

From the analysis of Fig. 13a (or 14a), as well as of Table 2, it is observed how the dispersion of 1% of nanotubes gives rise to a significant improvement in the fatigue performance of the analyzed biocomposite, quantitatively much superior to the effect observed in static loading conditions. In particular, in terms of fatigue strength, a nearly constant increase of about + 52% is observed throughout the “high cycles fatigue” range (103–106 fatigue cycles). Unfortunately, as for the static case above analyzed, the toughening with 2% of nanotubes does not lead to further fatigue performance improvements, but corresponds instead to markedly more limited effects, around about 20%, so that, as for static tensile strength, the fraction of 1% can be considered as the optimal one. Instead, referring only to the fatigue strength of the matrix alone, it is possible to state that the simple reinforcing with agave fibers permits in practice a redouble of the fatigue strength (from 11.5 MPa of the matrix to 19.9 MPa of the CNT0%, see Table 2), while the further introduction of 1% of CNT allows to further double this increase, up to a fatigue strength of 30.3 MPa (about + 200% respect to the matrix one); in other word, the effects of the CNTs are comparable to that of the reinforcing fibers.

As it has been confirmed by the evolution of the fatigue damage represented by the D parameter (see Fig. 12a and b), the effects of the nanotubes (see also Fig. 9) significantly slows down the speed of microcracking, (i.e. the damage growth rate in the second phase) that is the most important damage mechanism in the fatigue of composites, so that the most relevant improvements observed are in terms of fatigue life duration. In detail, Fig. 13a shown how passing from the biocomposite without nanotubes to that with 1% of nanotubes, the fatigue life increases of at least 3 orders of magnitude. For example, for a 30 MPa fatigue load, the fatigue life goes from about 103 cycles for the biocomposite without CNTs, to about 106 cycles for the biocomposite with 1% CNTs (see Fig. 13a). Effects that are always relatively more modest, but still very significant and greater than an order of magnitude (about + 150%), are observed for the biocomposite toughened with 2% of nanotubes; for example for the same load of 30 MPa the fatigue life goes from about 103 to about 1.5×104 cycles (see Fig. 13a).

Also, from Table 2 it is possible to observe how the fatigue ratio (which is an index of the fatigue response of the material) improves significantly with the CNTS dispersion, going from 0.45 for the bio-composite without nanotubes, to a mean value of 0.51 ÷ 0.52 (about + 15%) for the biocomposites toughened with CNTs. This is a respectable value, certainly well above those of plastic materials (ranging generally from 0.15 to 0.30), comparable with those of good technical metal and GFRP (ranging from 0.4 to 0.6).

4 Conclusions

A systematic experimental analysis of eco-friendly biocomposites properly manufactured by a green epoxy matrix reinforced with random short sisal fibers and toughened by introducing variable low fraction multi-walled carbon nanotubes (MWCNT) by a proper automated mixer and a successive sonicator, allowed to highlight how this practice makes it possible to improve significantly the mechanical performance of such biocomposites, both in terms of mechanical strength and stiffness. In particular, it was found:

  • Biocomposites with 1% of CNTs, exhibit an improvement of the tensile stiffness and the static tensile strength of about 30%. Biocomposites with 2% of CNTs show instead more limited improvement of 13% stiffness and only 6% strength.

  • Toughening with 1% of nanotubes gives rise to an appreciable decreasing (more than a halving) of the fatigue damage under tensile loading, as experimentally well evidenced by the evolution of the residual strain and of the well-known damage parameter D related to the current Young’s modulus, with a consequent increasing in fatigue strength by over 50%. Also, in this case, further increases in the CNTs fiber volume fraction are not advantageous either in terms of fatigue strength or in terms of fatigue life.

  • Thanks to the appreciable decrease of the damage growth rate, the fatigue duration is the parameter that is affected by the most increments: lifetime improves by at least 3 orders of magnitude with the introduction of 1% of CNTs. For example, in the presence of a simple tensile fatigue load of 30 MPa, toughening passes the fatigue life from 103 to 106 cycles. The introduction of 2% of CNTs leads instead to a lower lifetime increment, of about + 150%.

  • Regarding to the fatigue strength of the matrix alone, it is possible to state that the introduction of the optimal low fraction of CNTs (1%) allows to obtain an improvement of the fatigue properties comparable with that given by the sisal fiber reinforcement.

  • In terms of fatigue ratio, the experimental evidence has shown that it goes from the value of 0.45 for the non-toughened biocomposite, to values of about 0.51 ÷ 0.52 (about + 15%) for the biocomposites incorporating CNTs.

  • The high cycles fatigue behavior of all the analyzed biocomposites reinforced by sisal fibers (with and without CNTs) is well modeled by the so called semi-logarithm modified Wohler law, whereas their complete fatigue behavior (low and high cycles fatigue) can be advantageously represented by using the model of D’Amore et al. that allows also to include the fatigue ratio R.

As it has been observed by the analysis of the damage processes, also by using SEM micrographs, these remarkable effects, in static conditions and, above all, in the presence of fatigue loads, can be attributed to the significant slowing down of the propagation speed of the microcracking of the matrix due to the potential beneficial fiber-matrix bridging effects operated by the CNTs.

Such enhancement of mechanical properties increases the possibility of using these biocomposites in semi-structural and structural applications, especially in the automotive and naval sectors, characterized by the recurring presence of fatigue loading, due respectively to random ground roughness and random wave height.

Further studies carried out with other nanotubes fractions included in the range 0–2% are necessary in order to identify accurately the concentration that optimizes the improvement effects observed with the present study. Also the implementation of an improved mixing processes, which permit to avoid the suspected agglomeration effects of bundled nanotubes and, consequently, to increase the optimal volume fraction of CNTs beyond the value of 1%, should be performed in the future.

Obviously, additional studies are necessary too to detect the expected potential positive effects of the CNTs introduction on the other mechanical performances of biocomposites, as impact strength and fracture strength under different modes (I, II and mixed modes) of crack growth, as well as versus particular debonding phenomena that occur in presence of significant environmental effects (humidity, ultraviolet rays, corrosion etc.).