1 Introduction

The effect of impact, and the consequence of the associated damage mechanisms, is a key consideration in the use of composite material and has been widely researched [1,2,3,4]. There is a wealth of knowledge regarding the use of composite materials in the aerospace [5] and sports sectors, where the material has seen successful implementation and growth. However, it is now not uncommon to find the material in more diverse applications, including offshore oil and gas and renewable energy. As confidence in the material grows in these new arenas, it is expected that the use of composites will continue to increase [6] and soon the material will be used increasingly in safety critical applications. Therefore, it is important that issues such as long-term performance, continued structural integrity and serviceability are considered. To that end, the aim of this paper is to investigate how design factors influence low-velocity impact (impact speeds of less than 10 m/s [1, 7]) on materials commonly seen in the composite piping industry.

Low-velocity impact damage is usually characterised by matrix cracking and delamination [2, 8, 9] through the thickness of the impacted laminate. Some research suggests that low-velocity impact response can be equivalent to a quasi-static three-point bend loading [10, 11]. Damage caused by low-velocity impacts is usually experienced on the mesoscale and microscale and does not necessary lead to catastrophic failure [12].

Delamination is considered as the critical failure mode under low-velocity impact by many authors. This has probably stemmed from the aerospace sector, where research has shown that delaminations can reduce the compression resistance of a composite by as much as 60%. It is widely agreed that delaminations are peanut shaped and in the orientation of the lower ply [3, 13,14,15,16] and occur at interfaces with varying fibre orientations; this has been attributed to the difference in bending stiffness between ply’s of different orientation [16].

In previous research [3, 15, 17,18,19], it has been suggested that the initiation of delamination can be related to a critical load, commonly referred to as the delamination threshold load (DTL). It is thought that delaminations will not occur within the laminate if the peak load remains less than the DTL. It is widely reported that the delamination threshold can be detected by examining the load history of an impact, with the first significant drop in load coinciding with the onset of delamination. This initial drop in load, sometimes referred to as the critical load (Pcr ), represents the DTL [18, 20].

Impact induced matrix cracking (intralaminar cracking) followed by delamination are also the main damage modes observed in composite pipes and they become critical as they provide the leak path through the pipe wall for the transported media [21,22,23]. Matrix cracks can be caused by tensile, compressive and shear stresses within the laminate, this complex nature makes the prediction and detection for the onset of matrix cracking relatively difficult [3].

Several models exist to predict the DTL during drop-weight impact. Models have included material strength based criteria [3], as well as fracture mechanics concepts [20, 24]. One aspect that remains constant throughout the reviewed models is that DTL varies with the laminate thickness to the 3/2 power.

This paper presents the results of drop weight impact testing on five different curved laminates. The laminates had a radius of curvature ranging from 75 mm to 125 mm and wall thicknesses varying from 2.5 mm to 6.6 mm. A comparison in the impact response and damage observed is made across the varying radii and wall thicknesses. The effect of curvature on current DTL models is also investigated, and comment made on the applicability of current models for the impact prediction of curved laminates and complete cylindrical glass-reinforced epoxy (GRE) pipe sections.

2 Materials

Five commercially manufactured, filament wound pipes made of ±55° E-glass fibre reinforcement impregnated with an aromatic amine (MDA) cured epoxy resin were used. This combination of material constituents is commonly seen in the construction of GRE pipes due to its corrosion resistance, thermal, physical, and mechanical properties. Fibres angles of ±55° is selected for thin-wall pipes subjected to internal pressure as it is the optimum winding angle for the 2:1 hoop to axial stress ratio [25]. The mechanical properties of the tested pipes are presented in Table 1.

Table 1 Average mechanical properties of ± 55 laminates
Full size table

The five pipe designs used in this study had wall thicknesses ranging from circa 2 mm to 6 mm across three common piping diameters: 150 mm 200 mm and 250 mm. The pipes were cut into several single skinned curved sections, Table 2, to allow a number of repeat tests to be conducted. Testing single skinned laminates, whilst not fully representative of an impact on a complete cylindrical pipe section, will allow the investigation of how laminate thickness, radius of curvature, and the combination of the two affect impact behaviour. Testing single skinned laminates will reduce time and cost, especially if results obtained for the curved section can characterise a pipe’s response.

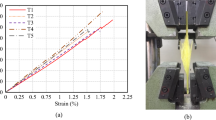
Table 2 Geometric parameters of the five laminates tested
Full size table

There are no recognised international standards for impacting GRE pipes or curved laminates. For this reason this testing was based on the requirements laid out in ASTM D7136 [26], which specifies sample design, support design and method for the drop weight impact testing of flat panels. Following the principles outlined in ASTM D7136 the pipes were sectioned to produce samples 150 mm in length and a chord length of 100 mm. Figure 1a shows a test specimen taken from a 150 mm diameter pipe with a reinforced wall thickness of 2.5 mm secured to the support, details of which are discussed later.

Fig. 1
figure 1

a A curved test specimen created from a sectioned pipe installed on impact support. b 150 mm × 75 mm window over which the impact event occurred

Full size image

All the pipes tested had the same wall design, consisting of three distinct regions. The internal region, which is directly in contact with the pipe’s transported fluid, had a nominal thickness of 0.5 mm and was resin rich with an embedded C-glass fleece to provide resistance to any chemically aggressive media transported through the pipe. The centre of the pipe’s wall construction was the reinforced region that contained multiple layers of E-glass reinforcement. The reinforcement provides the tailorable strength and stiffness to the pipe, and therefore, the thickness of the reinforced layer determines the pipe’s pressure rating. The thickness of the reinforced region, labelled as the effective thickness, is presented in Table 2. The outer region, a resin rich top coat, had a nominal thickness of 0.3 mm, and provides protection to the reinforcement from the external environment. As the resin rich outer region and the internal C-glass fleece region are believed to provide little, if any, enhancement to mechanical properties of the laminate, for the remainder of this study the effective, or reinforced, laminate thickness is taken as the wall thickness.

3 Testing Methods

3.1 Impact Testing

Drop weight impact testing was conducted on a Rosand impact tester V.5, referred to as the drop tower. The drop tower dropped a set mass at set speeds, or energies, precisely onto test specimens located at the base of the tower. The projectile, Fig. 2, had a steel 50 mm diameter hemispherical nose and a total mass of 5.94 kg.

Fig. 2
figure 2

Projectile used during all impact events reported in this study. The test fixture is made up from the guided carriage keeping the projectile on target, a load link, interconnects, and the 50 mm hemispherical projectile head

Full size image

The projectile was dropped from varying heights to generate four impact energies, 5 J, 10 J, 20 J, and 30 J, with a velocity varying from approximately 1.3 m/s to 2.6 m/s. This energy range was selected as it broadly conforms to industry definition of a low velocity impact, and they are all energies plausible in an operational environment, i.e. an accidentally dropped tool. A guide rail system guaranteed that the impact occurred at a central location of each laminate, which was secured in a bespoke laminate support, Fig. 1b. The laminate support was based on ASTM D7136 and consisted of an aluminium former machined to match the internal diameter of the tested specimen. A recess, shown in Fig. 1b, of 125 mm × 75 mm was machined out of the central location; over which the impact event would take place. Four M6 bolts and washers were used to secure the laminate to the support to reduce any movement during the impact.

A pneumatic anti-rebound device caught the projectile after the initial impact to ensure that multiple impacts did not occur during a single test. A light gate measured the impact velocity and triggered the impact testing software (Impacqt) to collect data from a calibrated dynamic load link at a frequency of 320 kHz for a duration of 0.1 s. The data recorded from the load link and the impact velocity were analysed in ‘Impacqt’, via a series of integrations, to produce the projectile velocity, displacement, and energy. All data has been run through a Butterworth notch filter removing frequencies ranging from 1.3 kHz to 1.7 kHz to eliminate noise effect. These were selected by calculating the frequency of the noise in the form of a recurring ringing, which was present, and consistent, on the majority of the impact tests. Applying this filter to tests where ringing did not occur had a negligible effect on the key impact features, with the load histories remaining largely unaffected. This type of noise filtering is common practice across research and industry.

In total 42 impact tests across the five pipe designs are presented, each of the five designs underwent three repeats of the four tested impact energies.

3.2 Non-destructive Testing and Damage Analysis

The damage observed, and reported, in this research consisted of surface damage on the impacted face, delaminations throughout the material thickness detected visually, and any splitting of the face opposite the impact location. Indentation, or plastic deformation during impact is discussed, and theoretical values provided but was not measured. Comment has not been made on the extent or presence of matrix, or intra-laminar, cracking during impact.

The laminates, even at the greatest wall thickness tested, created a translucent structure. This allowed the determination of damage area non-destructively by using a light source and a calibrated digital calliper. Figure 3 shows a laminate with a radius of 200 mm and an effective wall thickness of 4.1 mm following a 20 J impact. Figure 3a shows the impacted surface, Fig. 3b the opposite surface, and Fig. 3c the impacted surface with a light source placed behind the damaged region. Fig. 3 is largely representative of all the damage presented in this study, in less otherwise stated. A small number of samples produced damage patterns less rectangular with and hourglass shape, thinning in the axial direction of the laminate. This thinning leads to a slight over measurement in the damage area recorded.

Fig. 3
figure 3

100 mm radius laminate with an effective wall thickness of 4.1 mm following an impact of 20 J. a impacted surface showing radial cracking, b opposite surface, and (c) impacted surface with a light source used to highlight the damaged area. The point of impact is highlighted by a light spot in the middle of the associated damaged region

Full size image

4 Results

4.1 Wall Thickness Effect

Table 3 presents the results of the impact testing completed on the laminates with a radius of 100 mm and effective wall thicknesses of 2.5 mm, 4.1 mm, and 6.6 mm. Consistent repeatability in the testing was observed, with only a small deviation across all results. Figure 4 presents the load history (Fig. 4a), energy history (Fig. 4b), and load-displacement plot (Fig. 4c) of a 20 J impact on each of the thicknesses. The solid arrow in Fig. 4b is showing the elastic energy absorbed during the impact, while the dashed arrow corresponds to the energy absorbed in the form of permanent damage. The arrow in Fig. 4c highlights the indentation, or plastic deformation, of the 2.5 mm laminate during impact. It can be seen in Fig. 4a, the load histories, as the effective wall thickness increased, the bending stiffness of the plate also increased. This change in stiffness lead to decreased contact times and increased peak loads. A short plateau early in the loading stage, at an impact time of circa 0.2 ms, can be observed in each of the laminates. This plateau is usually associated with the crushing of the top resin rich layer. Following the plateau, a linear loading stage can be observed where only minor matrix cracking is occurring, seen as deviations in the loading, before reaching the first significant drop in load. As discussed earlier, the first significant drop in load is identified as the DTL and for the cases shown corresponded to the peak load. The energy absorbed, in the form of damage (as defined in section 3.2), during impact stayed largely consistent across the three laminate thicknesses at impact energies up to 10 J. At impact energies of 20 J and above the 2.5 mm laminate (R/t ~ 40) absorbed less energy in the form of damage, approximately 60% of the impact energy during impact, compared to the 75% absorbed by the 4.1 mm and the 6.6 mm thick laminates. The 2.5 mm laminate had far greater deflections during impact, allowing more energy to be stored elastically, as shown in Fig. 4b. However, these larger central deflections lead to higher strains in the laminate facilitating a change in damage area. The change in stiffness between the laminates is also evident studying the energy histories presented in Fig. 4b. It can be seen that the peak load occurred later in the event as laminate thickness decreases. Additionally, the rate of change in energy is greater during impact as laminate thickness increases.

Table 3 Impact testing results of laminates with a radius of 100 mm and an effective wall thickness of 2.5 mm, 4.1 mm, and 6.6 mm. Standard deviation of the three repeats presented in brackets
Full size table
Fig. 4
figure 4

a Load history, b energy history, and c load-displacement plots of 2.5 mm, 4.1 mm and 6.6 mm laminates with a 100 mm radius of curvature, subjected to 20 J impact. The dashed arrow in b shows the energy absorbed during the impact as damage and plastic deformation and the solid arrow the energy absorbed elastically. The arrow in (c) shows the indentation of the 2.5 mm laminate

Full size image

Figure 4c shows the load-displacement plots, highlighting the difference in lateral displacement during impact across the three laminate thicknesses. The indentation, or plastic deformation, remained consistent at the impact energies tested.

Figure 5a shows a load history of a 6.6 mm laminate (R/t ~ 15) during a 30 J impact and Fig. 5b shows a load history of a 6.6 mm laminate during a 5 J impact. The contact time, DTL, and peak load are identified in the figure. Figure 5a shows a significant drop in contact load, at a load of approximately 15 kN, and delaminations were present in the laminate following the impact. This drop in load is evident due to the change in material stiffness following the onset of delamination. The 5 J impact, Fig. 5b did not lead to any visible damage in the laminate and did not exhibit a significant drop in load in the load history of the impact. The fluctuations in the load can be explained by crushing of the resin rich zone, any movement of the sample during impact, and minor damage not detectable by the techniques implemented during this study.

Fig. 5
figure 5

a Load history of a 30 J impact and (b) Load history of a 5 J impact on a 6.6 mm thick laminate with a curvature radius of 100 mm. The blue arrow indicates contact time, the black arrow indicates peak contact load, and the red arrow indicates the point of damage initiation (DTL)

Full size image

The damage pattern stayed consistent, with the exception of damage area, across the tested energies. Small radial scaring/minor cracking in the resin rich surface could be seen emanating from the impact point at energies in excess of 5 J. The impact point could be identified as a discoloured spot at the centre of the delaminations. No Major cracking was observed on the impacted surface, no sign of splitting on the opposite surface was observed following impact on the 6.6 mm and 4.1 mm laminates. Following impacts of energies of 20 J and greater, internal splitting could be observed on a number of the 2.5 mm laminates. This splitting was not consistent due to the nature of the internal resin rich layer of the internal surface of the laminate.

Figure 6 shows the damage area from the impacted surface of the 2.5 mm laminate (Fig. 6a), 4.1 mm laminate (Fig. 6b), and the 6.6 mm laminate (Fig. 6b). As can be seen in Fig. 6, the delaminations were largely rectangular shaped, with a varying contrast shadow when a light source is introduced behind the region of damage. The change in contrast can provide information on the damage pattern through the thickness of the laminate. As can be seen in Fig. 6a at least two regions of damage can be observed, a lighter region between the two solid markers and a darker region between the dashed markers. The darker region indicates that a greater number of delaminations are present through the thickness of the material obstructing the path of the light behind. This can be seen to a lesser extent examining the 4.1 mm laminate and cannot be observed during examination of the 6.6 mm laminate utilising the techniques used during this study.

Fig. 6
figure 6

Impact damage following a 20 J impact on a (a) 2.5 mm laminate, (b) a 4.1 mm laminate, and (c) a 6.6 mm laminate. The arrows in (a) highlighting the different regions of damage through the laminate thickness, the darker region between the dashed arrows indicating a greater number of delaminations through thickness compared to the larger lighter region between the solid arrows

Full size image

A dimensional survey looked at ten impacts across a number of laminate thicknesses, radii, and impact energies. The laminates were sectioned through the point of impact in the hoop direction exposing the through thickness damage in the axial direction (Fig. 7a) and a calibrated traveling microscope was used to measure the uppermost and lowermost delamination. The mirroring half of the impact damage was sectioned through the point of impact in the axial direction (Fig. 7b) exposing half of the impact damage in the hoop direction. Once again, the uppermost and lowermost delaminations were measured, and the measured values doubled as the damage was assumed to be symmetrical. It was found that the average reduction in delamination area between the lowermost and uppermost delamination was 44% and 46% in the hoop and axial direction, respectively. These reductions in delamination area were similar across all tested laminates. All damage observed in this research, with the exception of the 30 J impact on the 2.5 mm laminate, which lead to displacements that surpassed the limitations of the support structure, exhibited the ‘pine tree’ damage pattern as seen in Fig. 7. This pine tree pattern is responsible for the varying contrast of the damage area discussed above.

Fig. 7
figure 7

Damage volume showing ‘pine tree’ damage pattern following a 30 J impact of a laminate with a 6.6 mm effective wall thickness (a) axial direction and (b) in the hoop direction. Red dye penetrant was used to highlight the damage pattern

Full size image

As seen in Fig. 8a, damage area, generally decreased as laminate thickness increased. It was seen that the 2.5 mm thick laminate exhibited damage at lower impact energies than the 4.1 mm and the 6.6 mm laminates. Not only was the delamination threshold lower, the 2.5 mm laminate had a, generally, larger damage area at all tested energies. This increase in damage area can be attributed to the additional strain during impact, as the thinner laminates reduced stiffness lead to a considerable increase in lateral displacement. The energy absorbed during an impact is generally (minus minimal losses to sound, heat, friction) dissipated during the displacement of the material and in the initiation and propagation of damage. However, the change in laminate thickness did not largely influence the absorbed energy, despite a reduction in displacement and damage area.

Fig. 8
figure 8

a damage area during impact and (b) damage volume during impact observed during the impact testing of laminates with 100 mm radius

Full size image

The damage volume of each impact was calculated, assuming the impact damage was truncated pyramid in shape, and is presented in Fig. 8b. The damage volume was found to be largely consistent for all three laminates. As the laminate thickness increases, the number of layers of reinforcement increases, leading to more interfaces available for delamination. This led to an increased number of delaminations of a smaller size. This is shown most prominently in the 6.6 mm laminate, where the damage area only increased slightly with impact energy, a far larger increase in damage volume can be seen as impact energy increased.

Figure 9a shows the central deflection at the delamination threshold, Fig. 9b the absorbed energy at the delamination threshold, and Fig. 9c the DTL of the three laminates at an impact energy of 20 J. It was found that the displacement at delamination onset of the 4.1 mm laminate and the 6.6 mm thick laminate were consistent (with an average displacement of 2.0 mm at failure) and about half of that seen during the testing of the 2.5 mm laminate (an average displacement of 4.2 mm at failure). Despite similar displacements at failure, the 6.6 mm laminate required significantly more energy (approximately 80% more) to achieve this displacement. The DTL increased with laminate thickness and showed only a small scatter amongst the results, providing confidence that the first significant drop in load seen in the load history is the DTL and consistent for a given laminate.

Fig. 9
figure 9

a Central deflection at delamination threshold, b Absorbed energy at delamination threshold, and (c) DTL of laminates with a radius of 100 mm at an impact energy of 20 J

Full size image

4.2 Curvature Effect

Table 4 shows the results of drop weight impact testing on circa 2.5 mm thick laminates with radii of 75 mm, 100 mm, and 125 mm. The 75 mm radius laminate had greater damage absorbed energy and lower lateral deflection at all tested impact events in comparison to the 100 mm and 125 mm laminates, which stayed largely consistent. The smaller radii also showed larger contact loads at impact energies up to 10 J before all three radii showing consistent loads at energies of 20 J and over. All three radii had comparable contact times during impact. The 100 mm radius and the 125 mm radius laminates had broadly comparable results for all analysed impact parameters.

Table 4 Impact testing results of laminates with a wall thickness of circa 2.5 mm and a radius of 75 mm, 100 mm, and 125 mm. Standard deviation of the three repeats presented in brackets
Full size table

As seen in Fig. 10, at an impact energy of 5 J, damage was initiated on all three tests conducted on a laminate with a 75 mm radius. This was not seen on the laminates with a larger radii, only two of the three impacts showed damage on the 100 mm radius laminate at this energy and the 125 mm radius laminate did not show any damage. At an impact energy of 10 J, all three impacts on the laminates with a radius of 75 mm and 100 mm exhibited damage, only two of the three impacts on the 125 mm laminate caused visible damage. Impact energies of 20 J and 30 J lead to visible damage during every test. The fact that under a number of loading conditions only two of the three laminates tested showed damage following the event highlights small variances in the laminate’s construction. For instance, during a 5 J impact the 4.1 mm laminate experienced an average contact load of 6.1 kN and had a DTL range from 6.1 kN to 7.3kN, it is, therefore, possible that at this energy not all of the samples would meet the required threshold load.

Fig. 10
figure 10

Damage area following drop weight impact loading of 2.5 mm thick laminates with varying radius

Full size image

Despite the 75 mm laminate being more susceptible to damage at lower energies, it showed smaller damage areas at the higher energies tested. The increased displacement during impact of the larger radius laminates being responsible for the increased damage areas. Due to the laminates being a consistent thickness the damage volume was not calculated.

Figure 11 presents the load history (Fig. 11a), energy history (Fig. 11b), and force-displacement plot (Fig. 11c) of a 20 J impact on each of the tested radii. It can be seen in Fig. 11 that the 100 mm radius and the 125 mm radius laminates behaved very similarly. This relationship can also be seen in the results presented in Table 4. The loading rates between the two radii are the broadly the same, with the load histories and force-displacement plots following similar shapes and patterns. The only real variations observed between the two radii are the contact time, peak contact load and the indentation following impact. As laminate radius increased a larger proportion of the impact energy was absorbed elastically, the same trend was observed to a lesser extent during the laminate thickness testing presented earlier, with the thinner laminates showing an increase in elastic energy absorption due to reduced stiffness. All three radii had similar indentation following impact.

Fig. 11
figure 11

a Load history, b energy history, and (c) force-displacement plots of three 20 J impacts on laminates of varying radius and a wall thickness of circa 2.5 mm

Full size image

The 75 mm laminate had a different response, with the laminate appearing stiffer under impact loading. The 75 mm radii laminate had higher contact loads at lower energies, smaller lateral displacements, shorter contact times, and stored less elastic energy during impact; similar behaviour to as seen when wall thickness was increased earlier in the study.

Figure 12a shows the central deflection at the delamination threshold and Fig. 12b the absorbed energy at the delamination threshold during a 20 J impact. Linear relationships can be seen for both the displacement and absorbed energy at the onset of delamination, with the smaller radii laminates failing at less energy, and at smaller displacements, than the larger radii laminates. For these 2.5 mm thick curved laminate radii appeared to have little effect (5–10%) on the DTL, Fig. 12c, with an average value of approximately 4 kN for the tested radii.

Fig. 12
figure 12

Impact parameters of circa 2.5 mm thick laminates with varying radii. a Central deflection at delamination threshold, b absorbed energy at delamination threshold, and (c) DTL versus radius

Full size image

5 Discussion

The aim of this study was to investigate the design factors that affect the impact behaviour of GRE pipes and how these design parameters influence the critical loads seen on a laminate during impact loading. It is clear from this study that laminate thickness and, to a lesser extent, radius, do play a role in the material response during an impact. The drop weight impact testing conducted in this study demonstrated good repeatability, with only acceptable scatter seen during the repeated tests for all measured impact characteristics and the damage initiated.

As discussed in the introduction, a number of models exist for the prediction of the DTL in flat plates. All the models reviewed assume that DTL increases with thickness to the power of 3/2. Figure 13 shows the DTL of the 2.5 mm, 4.1 mm, and the 6.6 mm laminates with a radii of 100 mm at an impact energy of 20 J. The DTL of an impacted full pipe section (effective wall thickness 3.1 mm and an internal radius of 250 mm) from a previous study [23], is shown as red triangle markers in Fig. 13. The green square markers show laminates of the same geometric specification used throughout this study sectioned from the pipe. These have been included for comparison and is discussed further below.

Fig. 13
figure 13

DTL of 2.5 mm, 4.1 m, and 6.6 mm laminates with a radius of 100 mm at an impact energy of 20 J. The red triangle markers show the DTL of an impacted full pipe section with an effective wall thickness of 3.1 mm. The solid trendline plotted is \( DTL=0.53{t}^{\frac{3}{2}} \) and the dashed trendline is \( DTL=0.78{t}^{\frac{3}{2}} \)

Full size image

Equation (1) is a model developed for quasi-isotropic laminates, based on a fracture mechanics approach [20], where Ef is flexural modulus, v the Poisson’s ratio, and GIIc the mode II fracture toughness of the laminate. Equation (1) simplifies to Eq. (2) where C becomes a laminate constant.

$$ {DTL}^2=\frac{8{\pi}^2{E}_f{t}^3{G}_{IIc}}{9\left(1-{v}^2\right)} $$
(1)
$$ DTL=C{t}^{\frac{3}{2}} $$
(2)

Using the laminate properties in the hoop direction as reported by the manufacturer, Table 1, and the measured [27] mode II fracture toughness, ~900 J/m2, the material constant C is found equal to 0.53 kN/mm3/2, which is shown as the solid line in Fig. 12.

It can be seen from looking at the plotted line, \( DTL=0.53{t}^{\frac{3}{2}} \), that this leads to a conservative prediction for DTL, approximately 40% lower than the measured value. It became clear from the empirical testing that the radius of the laminate plays a role in the stiffness, a slightly thinner 2.4 mm laminate with a radius of 75 mm (R/t ~ 30) showed smaller lateral displacement during impact compared to the 2.5 mm laminate with a radius of curvature of 100 mm (R/t ~ 40). Consequently, despite the material elastic modulus being largely consistent, the effective flexural modulus of the smaller radius laminate was found to be higher. This stiffness enhancement due to the curvature effect is not considered in the simplified beam analysis [23]. Therefore, the anisotropy of the material and the radius of curvature of the laminate are likely to be responsible for the conservative prediction.

The dashed line in Figure 13 for the \( DTL=0.78{t}^{\frac{3}{2}} \) is drawn by data fitting; in order to achieve a C value of 0.78 kN/mm3/2 the flexural modulus of the material would need to increase approximately by 120% to 45 GPa, assuming the same fracture toughness and Poisson’s ratio values. If it is assumed the flexural modulus and the Poisson’s ratio of the material stay constant, the fracture toughness would need to increase by 120% to 1980 J/m2. However, it is not believed that the material properties used during this analysis would have such a large error and these increased values would be considerably higher than expected. An increase in both flexural modulus and fracture toughness of 50% would achieve a C value of 0.79 kN/mm3/2 matching the experimentally obtained results.

The triangle markers on Figure 13, are impacts on full cylindrical pipe sections produced by the same manufacturer, with the same materials, and following the same manufacturing procedure. The full pipe samples presented have a designed wall thickness of 3.1 mm and an internal diameter of 250 mm. 500 mm lengths of the pipe were supported in a V-block and impacted with the same projectile as the laminates presented in this study. The projectile struck a central location on the pipes which had no internal pressurisation, and enclosed ends to limit excessive movement during impact. The square markers are laminates sectioned from the pipe to the same geometrical specification as the other laminates presented in this study, i.e. cord length of 100 mm and a sample length of 150 mm. Looking at the square markers it can be seen that the radii of the laminate appears to have had little effect on the DTL as the DTL of the 125 mm radii laminate largely follows the \( DTL=0.78{t}^{\frac{3}{2}} \) line despite a larger degree of scatter than that seen during the testing of the 100 mm radii laminates. It can be seen that the DTL was found to be slightly higher during an impact on a complete pipe an average of 6.1 kN compared to the 5.1kN seen in the testing of the curved laminates of the same wall thickness and radius. Despite the vastly differing boundary conditions impact testing on curved laminates was found to be a good indication of the behaviour of full pipe impact testing, producing similar DTLs and displacements (with only a 6% difference seen in displacement between the laminate and full pipe section). Looking at the scatter in the DTL results of the curved laminate, it is probable that if more tests were conducted, the impact of full pipe samples would lead to similar, albeit possibly slightly conservative, DTLs as the curved laminates.

Laminate radius was found to have a non-significant influence on DTL, Figure 12c, during impact testing on the 2.5 mm laminates studied. This was despite the curvature of the laminate altering the other impact response parameters. However, comparing the radius/thickness ratios (R/t) of all five laminates tested in this study, a number of trends can be identified, Figure 14. Figure 14a shows that displacement increased linearly with R/t. A linear relationship was not identified between the percentage of energy absorbed elastically or the DTL and R/t. Figure 14b had a steady elastic absorption rate of (circa 23%) at R/t ratios of 15 and 24, before increasing to circa 41% at R/t ratios of 40 and 50. The DTL (Figure 14c) decreased rapidly at the higher R/t ratios before levelling off at R/t ratios greater than 30, approaching flat plate behaviour.

Fig. 14
figure 14

a Lateral displacement against radius/thickness ratio (R/t), b % of energy absorbed elastically during impact against R/t, and (c) DTL against R/t during an impact of 20 J

Full size image

6 Conclusions

This study completed drop weight impact testing on a range of curved laminates seen in the oil and gas sector. Currently there are no recognised international standards for impacting GRE pipes or curved laminates, but the test method described in this study provides a reliable way of testing and characterising such composite configurations. It was found that at impact energies of up to 30 J no change in damage mechanism and pattern could be observed during the testing of laminates of varying wall thickness or curvature. The damage pattern stayed consistent, with the exception of damage area, across the tested energies and was dominated by internal matrix cracking and multiple delaminations. However, no damage was recorded following a 5 J impact on the 2.5 mm thick laminates with a radius of curvature of 100 mm (R/t = 40) and 125 mm (R/t = 50), all energy was absorbed elastically, while the one with a 75 mm radius of curvature (R/t = 15) developed an over 80 mm2 damage area.

The delamination threshold load was found to vary with laminate thickness to the power of 3/2 in line with the research conducted on flat laminates. Curvature was found to have little effect on DTL for 2.5 mm thin laminates (constant thickness) but with varying radii of 75 mm, 100 mm, and 125 mm, showing a DTL value of approximately 4 kN for a 20 J impact event.

A simplified beam theory and a fracture model for the prediction of DTL was found to under predict the DTL of the laminates examined by about 40% (depending on R/t ratio). This is mainly due to the curvature of the laminate that can enhance bending stiffness by more than 2 times. An increase in the laminate’s flexural modulus of approximately 24.5 GPa (a factor of 2) is required to bring the model’s predictions in line with the DTL values measured experimentally, see Fig.12. Lessons could be learned from masonry arches that have been used for a few thousand years, due to their ability to span larger distances (higher flexural stiffness) than masonry post and beam constructions.

The behaviour of curved plates was found to be largely representative of impact testing on a complete cylindrical pipe section, broadly producing a similar DTL value. This could reduce effort and cost in testing and characterisation of glass epoxy pipes, but further work will be needed to confirm.