Model of Calcium Dynamics Regulating $IP_{3}$, ATP and Insulin Production in a Pancreatic $\beta$-Cell

Abstract

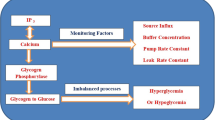
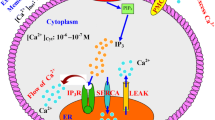
The calcium signals regulate the production and secretion of many signaling molecules like inositol trisphosphate ($IP_{3}$) and adenosine triphosphate (ATP) in various cells including pancreatic $\beta$-cells. The calcium signaling mechanisms regulating $IP_{3}$, ATP and insulin responsible for various functions of $\beta$-cells are still not well understood. Any disturbance in these mechanisms can alter the functions of $\beta$-cells leading to diabetes and metabolic disorders. Therefore, a mathematical model is proposed by incorporating the reaction-diffusion equation for calcium dynamics and a system of first-order differential equations for $IP_{3}$, ATP-production and insulin secretion with initial and boundary conditions. The model incorporates the temporal dependence of $IP_{3}$-production and degradation, ATP production and insulin secretion on calcium dynamics in a $\beta$-cell. The piecewise linear finite element method has been used for the spatial dimension and the Crank-Nicolson scheme for the temporal dimension to obtain numerical results. The effect of changes in source influxes and buffers on calcium dynamics and production of $IP_{3}$, ATP and insulin levels in a $\beta$-cell has been analyzed. It is concluded that the dysfunction of source influx and buffers can cause significant variations in calcium levels and dysregulation of $IP_{3}$, ATP and insulin production, which can lead to various metabolic disorders, diabetes, obesity, etc. The proposed model provides crucial information about the changes in mechanisms of calcium dynamics causing proportionate disturbances in $IP_3$, ATP and insulin levels in pancreatic cells, which can be helpful for devising protocols for diagnosis and treatment of various metabolic diseases.

Appendix A

The piecewise linear finite element scheme is employed to solve equations (25), (11), (12) and (13). The Euler-Lagrange equation has been used to find out the variational form of equation (25) which is given as follows:

$$\begin{aligned} A^{(e)}=\frac{1}{2}\int _{x_i}^{x_j}[(w^{(e)'})^2+a(w^{(e)})^2-2bw^{(e)}+\frac{1}{D_{Ca}}\frac{\partial (w^{(e)})^2}{\partial t}]dx-\mu ^{e}\left( \frac{\sigma _{Ca}}{D_{Ca}}w^{(e)}_{x=0}\right) . \end{aligned}$$

(A1)

Here, $'w'$ denotes the $[Ca^{2+}]$ and e=1, 2.... 40. The $\mu ^{e}$ defined as:

$$\begin{aligned} {\left\{ \begin{array}{ll} 1, &{} when \quad e=1 \\ 0, &{} otherwise \end{array}\right. } \end{aligned}$$

The cell is discretized into 40 elements. Since the thickness of elements is relatively small, therefore, $w^{(e)}$ can be interpolated by a linear function as given below:

$$\begin{aligned} w^{(e)}=c_1+c_2 x, \end{aligned}$$

(A2)

The equation (A2) is expressed as:

$$\begin{aligned} w^{(e)}=P^TC^{(e)}, \end{aligned}$$

(A3)

where    $P^T=\begin{bmatrix} 1&\quad x \end{bmatrix}$,       $C^{(e)}=\begin{bmatrix} c_1\\ c_2 \end{bmatrix}$.

Substituting the nodal values for each element in equation (A2),

$$\begin{aligned}{} & {} w^{(e)}(x_i)=c_1+ c_2 x_i=w_i, \end{aligned}$$

(A4)

$$\begin{aligned}{} & {} \quad w^{(e)}(x_j)=c_1+ c_2 x_j=w_j, \end{aligned}$$

(A5)

$$\begin{aligned}{} & {} \quad \bar{w}^{(e)}=P^{(e)}C^{(e)}, \end{aligned}$$

(A6)

where       $\bar{w}^{(e)}=\begin{bmatrix} w_i\\ w_j \end{bmatrix}$,      $P^{(e)}=\begin{bmatrix} 1&{} \quad x_i\\ 1&{} \quad x_j \end{bmatrix}$,

$$\begin{aligned} C^{(e)}=(P^{(e)})^{-1}\bar{w}^{(e)}, \end{aligned}$$

$$\begin{aligned} C^{(e)}=R^{(e)}\bar{w}^{(e)}, \end{aligned}$$

(A7)

where

$$\begin{aligned} R^{(e)}= (P^{(e)})^{-1}=\frac{1}{x_j-x_i}\begin{bmatrix} x_j&{} \quad -x_i\\ -1&{} \quad 1 \end{bmatrix}, \end{aligned}$$

From equation (A3) and (A7) we obtain,

$$\begin{aligned} w^{(e)}=P^T R^{(e)}\bar{w}^{(e)}, \end{aligned}$$

(A8)

and

$$\begin{aligned} w^{(e)'}=P_{x}^T R^{(e)}\bar{w}^{(e)}, \end{aligned}$$

(A9)

Substituting equation (A8) and (A9) in equation (A1), integrations are evaluated to obtain $A^{(e)}$ for each element,

$$\begin{aligned}{} & {} A^{(e)}=\frac{1}{2}\int _{x_i}^{x_j}[(P_{x}^T R^{(e)}\bar{w}^{(e)})^2+a(P^T R^{(e)}\bar{w}^{(e)})^2-2b P^T R^{(e)}\bar{w}^{(e)}\nonumber \\{} & {} +\frac{1}{D_{Ca}}\frac{\partial (P^T R^{(e)}\bar{w}^{(e)})^2}{\partial t}]dx-\mu ^{e}\left( \frac{\sigma _{Ca}}{D_{Ca}}P^T R^{(e)}\bar{w}^{(e)}_{x=0}\right) , \end{aligned}$$

(A10)

$$\begin{aligned}{} & {} \frac{\partial A^{(e)}}{\partial \bar{w}^{(e)}}=\int _{x_i}^{x_j}[(P_{x}^T R^{(e)}\bar{w}^{(e)}P_{x}^T R^{(e)})+a(P^T R^{(e)}\bar{w}^{(e)}P^T R^{(e)}) -b P^T R^{(e)}]dx\nonumber \\{} & {} \quad -\mu ^{e}\left( \frac{\sigma _{Ca}}{D_{Ca}}P^T R^{(e)}_{x=0}\right) , \end{aligned}$$

(A11)

$$\begin{aligned}{} & {} \frac{\partial A^{(e)}}{\partial \bar{w}^{(e)}}=\int _{x_i}^{x_j}[(R^{(e)^T}P_{x}P_{x}^T R^{(e)}\bar{w}^{(e)})+a(R^{(e)^T}PP^T R^{(e)}\bar{w}^{(e)})-b R^{(e)^T}P\nonumber \\{} & {} \quad +\frac{1}{D_{Ca}}\frac{\partial }{\partial t}(R^{(e)^T}PP^T R^{(e)}\bar{w}^{(e)})]dx-\mu ^{e}\left( \frac{\sigma _{Ca}}{D_{Ca}}R^{(e)^T}P_{x=0}\right) . \end{aligned}$$

(A12)

Then the equation (A12) can be extremize as given below:

$$\begin{aligned} \frac{\partial A^{(e)}}{\partial \bar{w}^{(e)}}= \sum _{i=1}^{5} \frac{\partial A_i^{(e)}}{\partial \bar{w}^{(e)}} = 0, \end{aligned}$$

(A13)

where

$$\begin{aligned}{} & {} \frac{\partial A_1^{(e)}}{\partial \bar{w}^{(e)}}=\int _{x_i}^{x_j}(R^{(e)^T}P_{x}P_{x}^T R^{(e)}\bar{w}^{(e)})dx,\\{} & {} \frac{\partial A_2^{(e)}}{\partial \bar{w}^{(e)}}=a\int _{x_i}^{x_j}(R^{(e)^T}PP^T R^{(e)}\bar{w}^{(e)})dx,\\{} & {} \frac{\partial A_3^{(e)}}{\partial \bar{w}^{(e)}}=-b \int _{x_i}^{x_j}(R^{(e)^T}P)dx,\\{} & {} \frac{\partial A_4^{(e)}}{\partial \bar{w}^{(e)}}= \frac{1}{D_{Ca}}\frac{\partial }{\partial t}\int _{x_i}^{x_j}(R^{(e)^T}PP^T R^{(e)}\bar{w}^{(e)})dx,\\{} & {} \frac{\partial A_5^{(e)}}{\partial \bar{w}^{(e)}}= -\mu ^{e}\left( \frac{\sigma _{Ca}}{D_{Ca}}R^{(e)^T}P_{x=0}\right) . \end{aligned}$$

From equation (A13) we get a system of first order linear differential equations expressed as:

$$\begin{aligned}{}[ \bar{A}]_{41\times 41}\left[ \frac{d\bar{w}^{(e)}}{dt}\right] _{41\times 1} +[\bar{B}]_{41\times 41} \left[ \bar{w}^{(e)}\right] _{41\times 1}=[\bar{C}]_{41\times 1}. \end{aligned}$$

(A14)

Here $\bar{w}^{(e)}$=$\left[ w_{1},w_{2},w_{3},\ldots ,w_{41}\right]$. $\bar{A}$ and $\bar{B}$ represents the system matrices and $\bar{C}$ represents a system vector. Temporal system given in equation (A14) is solved using Crank Nicolson scheme and simulated on MATLAB to obtain the numerical results.