Abstract
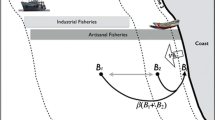
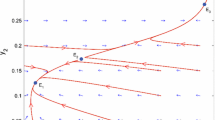
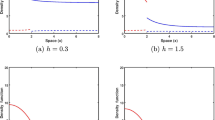
We consider a fishery model with two sites: (1) a marine protected area (MPA) where fishing is prohibited and (2) an area where the fish population is harvested. We assume that fish can migrate from MPA to fishing area at a very fast time scale and fish spatial organisation can change from small to large clusters of school at a fast time scale. The growth of the fish population and the catch are assumed to occur at a slow time scale. The complete model is a system of five ordinary differential equations with three time scales. We take advantage of the time scales using aggregation of variables methods to derive a reduced model governing the total fish density and fishing effort at the slow time scale. We analyze this aggregated model and show that under some conditions, there exists an equilibrium corresponding to a sustainable fishery. Our results suggest that in small pelagic fisheries the yield is maximum for a fish population distributed among both small and large clusters of school.




Similar content being viewed by others
References
Arreguín-Sánchez F (1996) Catchability: a key parameter for fish stock assessment. Rev Fish Biol Fish 6:221–242
Auger P, Bravo de la Parra R, Poggiale JC, Sanchez E, Nguyen Huu T (2008a) Aggregation of variables and applications to population dynamics. In: Magal P, Ruan S (eds) Structured population models in biology and epidemiology. Lecture Notes in Mathematics, 1936, Mathematical Biosciences Subseries. Springer, Berlin, pp 209–263
Auger P, Bravo De La Parra R, Poggiale JC, Sanchez E, Sanz L (2008b) Aggregation methods in dynamical systems variables and applications in population and community dynamics. Phys Life Rev 5:79–105
Auger P, Poggiale J-C, Sanchez E (2012) A review on spatial aggregation methods involving several time scales. Ecol Complex 10:12–25 P.
Bazykin AD (1998) Nonlinear dynamics of interacting populations. World Scientific series on nonlinear science. World Scientific, Singapore
Brehmer P, Do TC, Laugier T, Galgani F, Laloë F, Darnaude AM, Fiandrino A, Caballero PI, Mouillot D (2011) Field investigations and multi-indicators for management and conservation of shallow water lagoons: practices and perspectives. Aquat Conserv Mar Freshw Ecosyst 21(7):728–742
Brehmer P, Georgakarakos S, Josse E, Trygonis V, Dalen J (2008) Adaptation of fisheries sonar for monitoring large pelagic fish school: dependence of schooling behaviour on fish finding efficiency. Aquat Living Resour 20:377–384
Brehmer P, Gerlotto F, Laurent C, Cotel P, Achury A, Samb B (2007) Schooling behaviour of small pelagic fish: phenotypic expression of independent stimuli. Mar Ecol Prog Ser 334:263–272
Brehmer P, Lafont T, Georgakarakos S, Josse E, Gerlotto F, Collet C (2006) Omnidirectional multibeam sonar monitoring: applications in fisheries science. Fish Fish 7(3):165–179
Brochier T, Echevin V, Tam J, Chaigneau A, Goubanova K, Bertrand A (2013) Climate change scenarios experiments predict a future reduction in small pelagic fish recruitment in the humboldt current system. Glob Change Biol 19:1841–1853
Brochier T, Ecoutin JM, de Morais LT, Kaplan DM, Lae R (2013) A multi-agent ecosystem model for studying changes in a tropical estuarine fish assemblage within a marine protected area. Aquat Living Resour 26:147–158
Clark CW (1990) Mathematical bioeconomics: the optimal management of renewable resources, 2nd edn. Wiley, New York
Dao DK, Auger P, Nguyen-Huu T (2008) Predator density dependent prey dispersal in a patchy environment with a refuge for the prey. S Afr J Sci 104(5–6):180–184
de Lara M, Doyen L (2008) Sustainable management of renewable resources: mathematical models and methods. Springer, Berlin
Fréon P, Werner F, Chavez FP (2009) Conjectures on future climate effects on marine ecosystems dominated by small pelagic fish. Climate change and small pelagic fish. Cambridge University Press, Cambridge, pp 312–343
Fulton EA, Link JS, Kaplan IC, Savina-Rolland M, Johnson P, Ainsworth C, Horne P, Gorton R, Gamble RJ, Smith ADM, Smith DC (2011) Lessons in modelling and management of marine ecosystems: the atlantis experience. Fish Fish 12:171–188
Gonzalez EO, Ramos RJ (2003) Dynamic consequences of prey refuges in a simple model system: more prey, fewer predators and enhanced stability. Ecol Model 166(1–2):135–146
Iwasa Y, Andreasen V, Levin SA (1987) Aggregation in model ecosystems. I. Perfect aggregation. Ecol Model 37:287–302
Iwasa Y, Levin SA, Andreasen V (1989) Aggregation in model ecosystems. II. Approximate aggregation. IMA J Math Appl Med Biol 6:1–23
Krivan V (2011) On the gause predator–prey model with a refuge: a fresh look at the history. J Theor Biol 274(1):67–73
Leah EK (2005) Mathematical models in biology. SIAMs classics in applied mathematics, vol 46. Random House, New York
MacLennan DN, Simmonds EJ (2005) Fisheries acoustics: theory and practice, 2nd edn. Blackwell, London
Maury O (2010) An overview of apecosm, a spatialized mass balanced “apex predators ecosystem model” to study physiologically structured tuna population dynamics in their ecosystem. Progr Oceanogr 84:113–117
Mchich R, Charouki N, Auger P, Raissi N, Ettahihi O (2006) Optimal spatial distribution of the fishing effort in a multi fishing zone model. Ecol Model 197(3/4):274–280
Nguyen ND, Nguyen-Huu T, Auger P (2012) Effects of refuges and density dependent dispersal on interspecific competition dynamics. Int J Bifurc Chaos 22(2):1–10
Petitgas P, Levenez JJ (1996) Spatial organization of pelagic fish: echogram structure, spatio-temporal condition, and biomass in senegalese waters. ICES J Mar Sci 53:147–153
Pinsky ML, Jensen OP, Ricard D, Palumbi SR (2011) Unexpected patterns of fisheries collapse in the worlds oceans. Proc Natl Acad Sci USA 108:8317–8322
Schaefer MB (1957) Some considerations of population dynamics and economics in relation to the management of the commercial marine fisheries. J Fish Res Board Can 14:669–681
Smith VL (1968) Economics of production from natural resources. Am Econ Rev 58(3):409–431
Smith VL (1969) On models of commercial fishing. J Polit Econ 77(2):181–198
Tacon AGJ (2004) Use of fish meal and fish oil in aquaculture: a global perspective. Aquat Resour Cult Dev 1:3–14
Yemane D, Shin Y-J, Field JG (2009) Exploring the effect of marine protected areas on the dynamics of fish communities in the southern Benguela: an individual-based modelling approach. ICES J Mar Sci 66:378–387
Acknowledgments
Nguyen Trong Hieu was supported by the Grand NAFOSTED, N0 101.02-2011.21. This work have been supported by the tripartite AWA Project (BMBF and MESR-MAEE-IRD) “Ecosystem Approach to the management of fisheries and the marine environment in West African waters”. We thank the anonymous referees for their valuable comments.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Hieu, N.T., Brochier, T., Tri, NH. et al. Effect of Small Versus Large Clusters of Fish School on the Yield of a Purse-Seine Small Pelagic Fishery Including a Marine Protected Area. Acta Biotheor 62, 339–353 (2014). https://doi.org/10.1007/s10441-014-9220-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10441-014-9220-1