Global Stability of Enzymatic Chains of Full Reversible Michaelis-Menten Reactions

Abstract

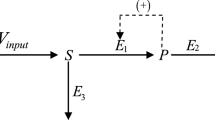
We consider a chain of metabolic reactions catalyzed by enzymes, of reversible Michaelis-Menten type with full dynamics, i.e. not reduced with any quasi-steady state approximations. We study the corresponding dynamical system and show its global stability if the equilibrium exists. If the system is open, the equilibrium may not exist. The main tool is monotone systems theory. Finally we study the implications of these results for the study of coupled genetic-metabolic systems.

Appendices

Appendix 1: A Monotone Systems

Monotone systems form an important class of dynamical systems, and are particularly well adapted to mathematical models in biology (Sontag 2004), because they are defined by conditions related to the signs of Jacobian matrix. The reader may consult the references (Smith 1995) for a review or an exhaustive presentation of the theory of monotone systems.

In summary, if the system is cooperative, then the flow preserves the partial order of trajectories in ℜⁿ (the flow is monotone). Cooperativity is easy to check by looking at the signs of the elements of the Jacobian matrix, that should verify $\displaystyle\frac{\partial f_i}{\partial x_j}(t,x) \geq 0\,\,{\forall i\neq j}$. These systems have a strong tendency to converge to the set of their equilibria (Smith 1995). Here we only need a simple proposition, easily deduced from Proposition 2.1 p. 34 of (Smith 1995). The monotone system is defined on a convex set X.

Proposition 4

Let us suppose that only one equilibrium x ^* exists in X; if moreover it exists two points x ⁺, x ⁻ in X such that f(x ⁺) ≤ 0 and f(x ⁻) ≥ 0, with x ⁻ < x ^* < x ⁺, then the hyperrectangle built by the two points x ⁻, x ⁺ is invariant, and every solution in this rectangle converges toward the equilibrium point.

Appendix 2: Matrices and Compartmental Systems

We introduce the notion of irreducibility of a matrix: we give one of the possible definition, which will be used in theorem 3.

Definition 1

(Irreducible Matrix) A matrix is irreducible if its graph is strongly connected (there is a directed path from any compartment to any other compartment).

Let us now give a few reminders about compartmental systems [see (Jacquez and Simon 1993)]. This kind of models describes the dynamics of interconnected n-compartments.

Definition 2

(Compartmental Matrix) Matrix J is a compartmental (n × n) matrix if it satisfies the following three properties (Jacquez and Simon 1993):

$$\displaystyle J_{ii} \leq 0 \quad for\,all\quad i,$$

(18)

$$\displaystyle J_{ij} \geq 0 \quad for\,all \quad i\quad \ne j,$$

(19)

$$\displaystyle -J_{jj} \geq \sum_{i\ne j} J_{ij}\quad for\,all \quad j$$

(20)

There are also some theorems on the stability of linear and nonlinear compartmental systems (see Jacquez and Simon 1993).

We recall some definitions and properties concerning output, see (Jacquez and Simon 1993, p. 47) and (Bastin and Guffens 2006).

Definition 3 (Fully outflow connected network)

A compartment x _i is outflow (output) connected if there is a path $x_i \rightarrow x_j \rightarrow...\rightarrow x_l$ from x _i until a compartment x _l with an outflow to the exterior of the system. The network is fully outflow connected if all compartments are outflow connected.

The following proposition is in (Jacquez and Simon 1993, p. 52).

Proposition 5 (Invertibility of a compartmental matrix)

A compartmental matrix is regular if and only if the associated network is fully outflow connected.

Intuitively, it means that the system has no traps where the flows accumulate [see (Jacquez and Simon 1993)]. We recall that in this case the matrix has eigenvalues with negative real parts (Jacquez and Simon 1993, p. 51), and the associated linear system is asymptotically stable.