Reduction of Supercritical Multiregional Stochastic Models with Fast Migration

Abstract

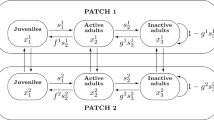
In this work we study the behavior of a time discrete multiregional stochastic model for a population structured in age classes and spread out in different spatial patches between which individuals can migrate. The dynamics of the population is controlled both by reproduction-survival and by migration. These processes take place at different time scales in the sense of the latter being much faster than the former. We incorporate the effect of demographic stochasticity into the population, which results in both dynamics being modelled by multitype Bienaymé–Galton–Watson branching processes. We present a multitype global model that incorporates the effect of both processes and, making use of the existence of different time scales for demography and migration, build a reduced model in which the variables correspond to the total population in each age class. We extend previous results that relate the behavior of the original and the reduced model showing that, given a large enough separation of time scales between demography and migration, we can obtain information about the behavior of the multitype global model through the study of the simpler reduced model. We concentrate on the case where the two systems are supercritical and therefore the expected number of individuals grows to infinity, and show that we can approximate the asymptotic structure of the population vector and the asymptotic population size of the original system through the study of the reduced model.

Appendix

Proof of Proposition 3

In the proof of the result, and in order to highlight the dependence of the variables of the original system on k, we will denote these variables by X _n,k . The limit (9) is a direct consequence of Proposition 2, r _k being the right Perron eigenvector of matrix MP ^k normalized so that $\left\Vert {{\mathbf{r}}}_{k}\right\Vert =1$ and W _k being such that with probability one

$$ W_{k}=\lim_{n\rightarrow \infty }{\frac{\left\Vert {{\mathbf{X}}} _{n,k}\right\Vert }{\lambda_{k}^{n}}} $$

(1) and (2) follow directly from Proposition 3 in Sanz et al. (2003), where it is shown that for large enough k the dominant eigenvalue of matrix MP ^k has the form λ _k  = λ + o(γ^k) and its normalized right Perron eigenvector verifies

$$ {{\mathbf{r}}}_{k}:={\frac{{{\mathbf{MVr}}} +{{\mathbf{o}}}(\gamma^{k})}{\left\Vert {{\mathbf{MVr}}}+{{\mathbf{o}}}(\gamma^{k})\right\Vert }}={\frac{{{\mathbf{MVr}}}} {\left\Vert {{\mathbf{MVr}}}\right\Vert }}+{{\mathbf{o}}}(\gamma^{k}) $$

Regarding (3), by applying Proposition 2 to the auxiliary system and the aggregated system, we can define the following limits with probability 1

$$ {{\mathbf{Q}}}_{k}:=\lim_{n\rightarrow \infty }{\frac{{{\mathbf{X}}} _{n,k}}{\lambda_{k}^{n}}};\quad {{\mathbf{Q}}}^{\prime }:=\lim_{n\rightarrow \infty }{\frac{{{\mathbf{X}}} _{n}^{\prime }}{\lambda^{n}}};\quad W^{\prime }:=\lim_{n\rightarrow \infty } {\frac{\left\Vert {{\mathbf{X}}} _{n}^{\prime }\right\Vert }{\lambda^{n}}};\quad \bar{W }:=\lim_{n\rightarrow \infty }{\frac{\left\Vert {{\mathbf{Y}}} _{n}\right\Vert }{ \lambda^{n}}} $$

(12)

It is straightforward to check that $\left\Vert {\mathbf {Y}}_{n}\right\Vert =\left\Vert {{\mathbf{X}}}_{n}^{\prime }\right\Vert ,$ so we have $\bar{W}=W^{\prime }$ and therefore in order to prove that W _k converges when $k\rightarrow \infty$ to $\bar{W}$ in distribution, all we need to prove is that W _k converges when $k\rightarrow \infty$ to W′ in distribution. Since $W_{k}=\left\Vert {{\mathbf{Q}}}_{k}\right\Vert$ and $W^{\prime }=\left\Vert {{\mathbf{Q}}}^{\prime }\right\Vert$ and the norm is a continuous mapping, Theorem 29.2 in Billingsley (1986) guarantees that it suffices to show that Q _k converges when $k\rightarrow \infty$ to Q′ in distribution. The proof of this fact is carried out in Lemma 4, which in turn hinges on Lemmas 1, 2 and 3. Then, from the definition of convergence in distribution, we have that for all x ≥ 0 such that ${\mathbb{P}}(\bar{W}=x)=0$ then

$$ \lim_{k\rightarrow \infty }{\mathbb{P}}(W_{k}\leq x)={\mathbb{P}}(\bar{W}\leq x) $$

(13)

All we still need to do to prove the result is to show that (13) holds for all x ≥ 0 (without including the restriction ${\mathbb{P}}(\bar{W}=x)=0$). In order to do so we use the fact that under the hypotheses of Proposition 2, if the process Z _n has finite second order moments of offspring production then the distribution of the random variable W conditioned to Z ₀ = e ⁱ is absolutely continuous except at the origin, where it has a jump of magnitude $\lim_{n\rightarrow \infty }{\mathbb{P}}({{\mathbf{Z}}}_{n}=0\mid {{\mathbf{Z}}}_{0}=e^{i})$ (Mode 1971). In our case both the original and the aggregated system have finite second order moments of offspring production (their p.g.f.’s are finite sums) and so $\bar{W}$ has an absolutely continuous distribution in (0,∞), so for all x > 0, ${\mathbb{P}}(\bar{W}=x)=0$ and (13) holds. Moreover, with the notation used in Proposition 1 we have ${\mathbb{P}}(\bar{W}=0\mid {{\mathbf{Y}}}_{0}={{\mathbf{e}}}^{i})=\bar{q}({{\mathbf{e}}}^{i})$ and ${\mathbb{P}}(W_{k}=0\mid {{\mathbf{X}}}_{0,k}={{\mathbf{e}}}^{ij})=q_{k}({{\mathbf{e}}}^{ij}).$ Since $\lim_{k\rightarrow \infty }q_{k}({{\mathbf{e}}}^{ij})=\bar{q}({\mathbf {e}}^{i})$ (Proposition 1), then (13) also holds for x = 0.

Now we proceed to state and prove Lemmas 1, 2 and 3. For notational convenience, let us define

$$ {{\mathbf{Q}}}_{n,k}:={\frac{{{\mathbf{X}}} _{n,k}}{\lambda_{k}^{n}}};\quad {{\mathbf{Q}}} _{n}^{\prime }:={\frac{{{\mathbf{X}}} _{n}^{\prime }}{\lambda^{n}}} $$

□

Lemma 1

Let us assume hypothesis H1 holds. Then there exists a positive integer k ₀ such that when $n\rightarrow \infty , {\bf Q}_{n,k}$ converges in L ²(Ω) (and therefore in distribution) to Q _k uniformly for k ≥ k ₀.

Proof

We already know that for large enough k, with probability one ${{\mathbf{Q}}}_{n,k}\underset{n\rightarrow \infty }{\rightarrow }{\mathbf {Q}}_{k}.$ Now we will show that Q _n,k is a Cauchy sequence in L ²(Ω) uniformly for large enough k and therefore the convergence in L ²(Ω) is uniform.□

Let Z _n be a supercritical MGWBP with growth rate μ, matrix of expected values A and let H _n  := E[Z _n Z ^T _n ]. Let $\left\vert \mu_{s}\right\vert$ be the modulus of the subdominant eigenvalue of A. Since A is a primitive matrix and therefore μ is a simple and strictly dominant eigenvalue of A, then

$$ {\frac{{{\mathbf{A}}}^{p}}{\mu^{p}}}={{\mathbf{B}}}+{{\mathbf{o}}}(\gamma^{p}) $$

(14)

for a certain matrix B, where γ is any real number verifying $\gamma >\left\vert \mu _{s}\right\vert /\mu.$ Let γ meet this condition plus the restriction γ < 1. Following the proof of Lemma 5 in Sanz et al. (2003) we have

$$ {\frac{{{\mathbf{H}}} _{n}}{\mu^{2n}}}={{\mathbf{C}}}+{{\mathbf{o}}}(\gamma^{n}) $$

(15)

for a certain symmetric matrix C. Moreover (expression (9.4) in Harris, 1963) we have that

$$ {{\mathbf{A}}}^{p}{{\mathbf{C}}}={{\mathbf{C}}}\left( {{\mathbf{A}}}^{T}\right) ^{p}=\mu^{p} {{\mathbf{C}}} $$

(16)

for any positive integer p.

Let p be a positive integer. Then

$$ \begin{aligned} {\varvec{\Sigma}} _{n,p} :&=E\left[ \left( {\frac{{{\mathbf{Z}}}_{n+p}}{\mu^{n+p}}} -{\frac{{{\mathbf{Z}}} _{n}}{\mu ^{n}}}\right) \left( {\frac{{{\mathbf{Z}}}_{n+p}}{\mu^{n+p}}}-{\frac{{\mathbf {Z}}_{n}}{\mu^{n}}}\right)^{T}\right]\\ &={\frac{{\mathbf {H}}_{n+p}}{\mu^{2n+2p}}}+{\frac{{{\mathbf{H}}} _{n}}{\mu^{2n}}}- {\frac {E\left[ {{\mathbf{Z}}} _{n+p}{\mathbf {Z}}_{n}^{T}\right] }{\mu^{2n+p}}}-{\frac{ E\left[ {{\mathbf{Z}}} _{n}{\mathbf {Z}}_{n+p}^{T}\right] }{\mu^{2n+p}}} \end{aligned} $$

(17)

Now

$$ \begin{aligned} {\frac{E\left[ {{\mathbf{Z}}}_{n+p}{\bf Z}_{n}^{T}\right] }{\mu ^{2n+p}}} &= {\frac{1} {\mu^{2n+p}}}E\left[ E[{\mathbf {Z}}_{n+p}\mid {{\mathbf{Z}}}_{n}]{{\mathbf{Z}}} _{n}^{T}\right] \\ &= {\frac{1} {\mu^{2n+p}}}E\left[ {{\mathbf{A}}}^{p}{{\mathbf{Z}}}_{n}{{\mathbf{Z}}} _{n}^{T}\right] ={\frac{{{\mathbf{A}}}^{p}}{\mu^{2n+p}}}E\left[ {\mathbf {Z}}_{n} {{\mathbf{Z}}}_{n}^{T}\right] ={\frac{{{\mathbf{A}}}^{p}}{\mu ^{p}}}{\frac{{{\mathbf{H}}} _{n}}{\mu^{2n}}} \end{aligned} $$

Similarly

$$ {\frac{E\left[ {{\mathbf{Z}}}_{n}{{\mathbf{Z}}}_{n+p}^{T}\right] }{\mu ^{2n+p}}}={\frac{ {{\mathbf{H}}} _{n}}{\mu^{2n}}} {\frac{{\left( {\mathbf{A}}^{T}\right)^{p}}}{{\mu^{p}}}} $$

Let $\left\Vert \ast \right\Vert$ be any matrix norm. From (17),

$$ \begin{aligned} \left\Vert{\varvec{\Sigma}}_{n,p}\right\Vert &=\\ &=\left\Vert \left({{\mathbf{C}}}+{{\mathbf{o}}}(\gamma^{n+p})\right) +\left({{\mathbf{C}}}+{{\mathbf{o}}}(\gamma^{n})\right)-{\frac{{\mathbf{A}}^{p}}{\mu^{p}}}\left({{\mathbf{C}}}+ {{\mathbf{o}}}(\gamma^{n})\right)-\left({{\mathbf{C}}}+{{\mathbf{o}}}(\gamma^{n})\right) {\frac{\left({{\mathbf{A}}^{T}}\right)^{p}}{\mu^{p}}} \right\Vert\\ &=\left\Vert{{\mathbf{C}}}+{{\mathbf{o}}}(\gamma^{n+p})+{{\mathbf{C}}}+ {{\mathbf{o}}}(\gamma^{n})-{{\mathbf{C}}}-{\frac{{{\mathbf{A}}}^p}{\mu^{p}}} {{\mathbf{o}}}(\gamma^{n})-{{\mathbf{C}}}-{{\mathbf{o}}}(\gamma^{n}){\frac{\left( {{\mathbf{A}}}^T\right)^{p}}{\mu^{p}}}\right\Vert\\ &=\left\Vert{{\mathbf{o}}}(\gamma^{n+p})+{{\mathbf{o}}}(\gamma^{n})-{\frac{ {{\mathbf{A}}}^p}{\mu^{p}}}{{\mathbf{o}}}(\gamma^{n})-{{\mathbf{o}}}(\gamma^{n}) {\frac{\left({{\mathbf{A}}}^T\right)^{p}}{\mu^{p}}}\right\Vert\\ &\leq{{\mathbf{o}}}(\gamma^{n+p})+{{\mathbf{o}}}(\gamma^{n})\left[1+\left\Vert {\frac{{{\mathbf{A}}}^p}{\mu^{p}}}\right\Vert+\left\Vert {\frac{\left({{\mathbf{A}}}^T\right)^{p}}{\mu^{p}}}\right\Vert \right] \end{aligned} $$

(18)

where we have used (15) and (16).

We will particularize this expression to the case of the original system, which is supercritical, non-singular and positively regular for k greater than a certain k ₁. We know λ _k and λ are the dominant eigenvalues of matrices MP ^k and ${\mathbf{M}}\bar{\mathbf{P}},$ respectively. Let $\left\vert \lambda_{s,k}\right\vert$ and $\left\vert \lambda_{s}\right\vert$ be the modulus of the subdominant eigenvalues of these matrices, and let α and β be real numbers such that $\left\vert\lambda_{s}\right\vert < \alpha < \beta <\lambda.$ Since ${{\mathbf{MP}}}^{k}={\mathbf{M}}\bar{\mathbf{P}}+{\mathbf{o}}(\gamma^{k})$ (Proposition 3 in Sanz et al. 2003) and using the continuous dependence of the eigenvalues of a matrix on its entries, the eigenvalues of MP ^k tend when $k\rightarrow \infty$ to the eigenvalues of ${\mathbf{M}}\bar{\mathbf{P}},$ and therefore we have that for k greater than a certain k ₂,

$$ {\frac{\left\vert\lambda_{s,k}\right\vert}{\lambda_{k}}}\leq {\frac{\alpha}{\beta}}<1 $$

Let γ be such that ${\frac{\alpha}{\beta}}<\gamma <1.$ Now using (14) we can write that for all k ≥ k ₀ := max{k ₁, k ₂}

$$ \begin{aligned} \left({\frac{{\mathbf{M}}\bar{\mathbf{P}}}{\lambda}}\right)^{p}&={\bf B}+{\bf o }(\gamma^{p})\\ \left({\frac{{\mathbf{MP}}^{k}}{\lambda_{k}}}\right)^{p}&={{\mathbf{B}}}_{k}+ {{\mathbf{o}}}(\gamma^{p}) \end{aligned} $$

for certain matrices B _k and B. Since $\lim_{k\rightarrow \infty }{\bf MP}^{k}={\mathbf{M}}\bar{\mathbf{P}}$ and $\lim_{k\rightarrow \infty }\lambda_{k}=\lambda$ then it follows that $\lim_{k\rightarrow \infty }{\bf B}_{k}={\bf B}$ and therefore, if $\left\Vert \ast \right\Vert$ is any matrix norm, there exists η such that

$$ \left\Vert\left({\frac{{{\mathbf{MP}}}^k}{\lambda_{k}}}\right) ^{p}\right\Vert \leq \eta $$

for all p and all k ≥ k ₁. Now we have from (18) that for all k ≥ k ₀

$$ \begin{aligned} &\left\Vert E\left[\left({{\mathbf{Q}}}_{n+p,k}-{{\mathbf{Q}}}_{n,k}\right) \left( {{\mathbf{Q}}}_{n+p,k}-{{\mathbf{Q}}}_{n,k}\right)^{T}\right] \right\Vert\\ &\quad\leq o(\gamma^{n+p})+o(\gamma^{n})\left[1+\left\Vert \left({\frac{{\mathbf{MP}}^{k}}{\lambda_{k}}}\right)^{p} \right\Vert+\left\Vert\left({\frac{({\mathbf{MP}}^{k})^{T}} {\lambda_{k}}}\right)^{p}\right\Vert\right]\\ &\quad\leq o(\gamma^{n+p})+o(\gamma^{n})\left[ 1+2\eta \right] \end{aligned} $$

Since the right hand member is independent of k and tends to zero when $n,p\rightarrow \infty$ we have that Q _n,k is a Cauchy sequence in L ²(Ω) uniformly for k ≥ k ₀ and therefore the result follows (in fact it is easy to prove that there is convergence with probability one, but this fact is not needed for our purpose).

Lemma 2

Let us assume hypothesis H1 holds. Then for each n = 1, 2,…, X _n,k converges to X ^′ _n in distribution when $k\rightarrow \infty.$

Proof

Let n be fixed. We need to show that for all ${\bf x}\in {\mathbb{R}}^{d}$ such that ${\mathbb{P}}({\bf X}_{n}^{\prime }={\bf x})=0$ we have $\lim_{k\rightarrow \infty }{\mathbb{P}}({{\mathbf{X}}}_{n,k}\leq{{\mathbf{x}}})={\mathbb{P}} ({{\mathbf{X}}}_{n}^{\prime }\leq{{\mathbf{x}}}).$ Now, since X _n only takes values in ${\mathbb{N}}^{d}$ we have that for all x

$$ {\mathbb{P}}({{\mathbf{X}}}_{n,k}\leq{{\mathbf{x}}})=\underset{{{\mathbf{z}}}\in {\mathbb{N}}^{d},\ [{{\mathbf{z}}}]\leq{{\mathbf{x}}}}{\sum}{\mathbb{P}}({{\mathbf{X}}}_{n,k}={{\mathbf{z}}}), $$

where $[\ast]$ denotes integer part, and since the sum is finite we have

$$ \lim_{k\rightarrow \infty}{\mathbb{P}}({{\mathbf{X}}}_{n,k}\leq{{\mathbf{x}}})=\underset{{{\mathbf{z}}} \in {\mathbb{N}}^{d},\ [{{\mathbf{z}}}]\leq{{\mathbf{x}}}}{\sum } \lim_{k\rightarrow \infty }{\mathbb{P}}({{\mathbf{X}}}_{n,k}={{\mathbf{z}}})=\underset{{{\mathbf{z}}}\in {\mathbb{N}}^{d},\ [{{\mathbf{z}}}]\leq{{\mathbf{x}}}}{\sum }{\mathbb{P}}({{\mathbf{X}}}_{n}^{\prime }={{\mathbf{z}}})={\mathbb{P}}({{\mathbf{X}}}_{n}^{\prime}\leq{{\mathbf{x}}}) $$

where we have used that for all ${{\mathbf{z}}}\in {\mathbb{N}}^{d}, \lim_{n\rightarrow \infty }{\mathbb{P}}({{\mathbf{X}}}_{n,k}={{\mathbf{z}}})={\mathbb{P}}({{\mathbf{X}}}_{n}^{\prime} ={{\mathbf{z}}})$ (Sanz et al. 2003).□

Lemma 3

Let us assume hypothesis H1 holds. Then for each n = 1, 2,…, Q _n,k converges to ${Q}^{\prime}_n$ in distribution when $k\rightarrow \infty.$

Proof

By the properties of convergence in distribution, it suffices to show that there exists a set D dense in ${\mathbb{R}}^{d}$ and such that for all x ∈ D we have $\lim_{k\rightarrow \infty }{\mathbb{P}}({{\mathbf{Q}}}_{n,k}\,\leqslant\,{{\mathbf{x}}})={\mathbb{P}} ({{\mathbf{Q}}}_{n}^{\prime}\,\leqslant\,{{\mathbf{x}}}),$ i.e., such that $\lim_{k\rightarrow \infty }{\mathbb{P}}({{\mathbf{X}}}_{n,k}\,\leqslant\,{{\mathbf{x}}} \lambda_{k}^{n})={\mathbb{P}}({{\mathbf{X}}}_{n}^{\prime}\, \leqslant\,{{\mathbf{x}}}\lambda^{n}).$

Let us define the sets

$$ \begin{aligned} M_{k}=&\left\{{{\mathbf{x}}}:{\mathbb{P}}({{\mathbf{X}}}_{n,k}={{\mathbf{x}}} \lambda_{k}^{n})\neq 0\right\} \hbox{ and their union \ }M=\underset{k}{ \cup }M_{k}\\ \overline{M} =&\left\{{{\mathbf{x}}}:{\mathbb{P}}({{\mathbf{X}}}_{n}^{\prime }={{\mathbf{x}}}\lambda^{n})\neq 0\right\}\\ \widetilde{M} =&M\cup \overline{M} \end{aligned} $$

Since any distribution function can have at most a denumerable number of discontinuities and the union that defines M is denumerable, the set $\widetilde{M}$ is denumerable and therefore its complementary $D:={\mathbb{R}}^{d}-\widetilde{M}$ is dense in ${\mathbb{R}}^{d}.$

Let ${{\mathbf{x}}}\in {\mathbb{R}}^{d}-\widetilde{M}.$ We know (Lemma 2) that X _n converges to ${\mathbf{X}}^{\prime}_n$ in distribution when $k\rightarrow \infty$ and therefore

$$ {\mathbb{P}}({{\mathbf{X}}}_{n,k}\,\leqslant\,{{\mathbf{x}}}\lambda_{k}^{n})= {\mathbb{P}}({{\mathbf{X}}}_{n}^{\prime}\,\leqslant\,{{\mathbf{x}}} \lambda_{k}^{n})+a_{k}\quad\hbox{where}\quad \lim_{k\rightarrow \infty}a_{k}=0 $$

(19)

Since ${{\mathbf{x}}}\in {\mathbb{R}}^{d}-\widetilde{M},$ ${\mathbb{P}}({{\mathbf{X}}}_{n}^{\prime }={{\mathbf{x}}}\lambda^{n})=0$ and therefore the distribution function of ${\mathbf{X}}^{\prime}_n$ is continuous at the point xλⁿ. Now, since $\lim_{k\rightarrow \infty }\lambda_{k}=\lambda$ (Sanz et al. 2003, Proposition 3) then $\lim_{k\rightarrow \infty }{\bf x}\lambda_{k}^{n}={\bf x}\lambda^{n},$ and taking the limit in (19) we obtain

$$ \lim_{k\rightarrow \infty }{\mathbb{P}}({{\mathbf{X}}}_{n,k}\,\leqslant\, {{\mathbf{x}}}\lambda_{k}^{n})={\mathbb{P}}({{\mathbf{X}}}_{n}^{\prime}\,\leqslant\, {{\mathbf{x}}}\lambda^{n}) $$

as we wanted to show.□

Lemma 4

Let us assume hypothesis H1 holds. Then Q _k converges to Q′ in distribution when $k\rightarrow \infty.$

Proof

Using (12) and the fact that convergence with probability one implies convergence in distribution, we have that for all ${{\mathbf{x}}}\in {\mathbb{R}}^{d}-N_{1},$

$$ \forall{{\mathbf{x}}}\in{\mathbb{R}}^{d}-N_{1},\quad \lim_{n\rightarrow\infty}{\mathbb{P}}({{\mathbf{Q}}}_{n}^{\prime}\,\leqslant \,{{\mathbf{x}}})={\mathbb{P}}({{\mathbf{Q}}}^{\prime }\leq{{\mathbf{x}}}) $$

(20)

where N ₁ is a denumerable set.□

Moreover, from the convergence in distribution guaranteed by Lemmas 1 and 3 we know that

$$ \forall{{\mathbf{x}}}\in{\mathbb{R}}^{d}-N_{2},\quad \lim_{n\rightarrow \infty}\sup_{k\geq k_{0}}\left\vert {\mathbb{P}}({{\mathbf{Q}}}_{n,k}\,\leqslant\,{{\mathbf{x}}})-{\mathbb{P}} ({{\mathbf{Q}}}_{k}\leq{{\mathbf{x}}})\right\vert=0 $$

(21)

$$ \forall{{\mathbf{x}}}\in {\mathbb{R}}^{d}-N_{3},\quad \lim_{k\rightarrow \infty}{\mathbb{P}}({{\mathbf{Q}}}_{n,k}\,\leqslant\,{{\mathbf{x}}})= {\mathbb{P}}({{\mathbf{Q}}}_{n}^{\prime}\leq{{\mathbf{x}}}) $$

(22)

where again N ₂ and N ₃ are denumerable sets.

Since the set $D:={\mathbb{R}}^{d}-\left( N_{1}\cup N_{2}\cup N_{3}\right)$ is dense in ${\mathbb{R}}^{d},$ it suffices to show that for all $x\in D,\ \lim_{k\rightarrow \infty}{\mathbb{P}}({{\mathbf{Q}}}_{k}\,\leqslant\,{{\mathbf{x}}}) ={\mathbb{P}}({{\mathbf{Q}}}^{\prime}\leq{{\mathbf{x}}}).$ Now

$$ \begin{aligned} \left\vert {\mathbb{P}}({{\mathbf{Q}}}_{k}\,\leqslant\,{{\mathbf{x}}})-{\mathbb{P}} ({{\mathbf{Q}}}^{\prime}\leq{{\mathbf{x}}})\right\vert &\leq \sup_{k\geq k_{0}}\left\vert {\mathbb{P}}({{\mathbf{Q}}}_{n,k}\,\leqslant\,{{\mathbf{x}}})- {\mathbb{P}} ({{\mathbf{Q}}}_{k}\leq{{\mathbf{x}}})\right\vert\\ &\quad+\left\vert {\mathbb{P}}({{\mathbf{Q}}}_{n,k}\,\leqslant\, {{\mathbf{x}}})-{\mathbb{P}} ({{\mathbf{Q}}}_{n}^{\prime} \leq{{\mathbf{x}}})\right\vert +\left\vert {\mathbb{P}} ({{\mathbf{Q}}}_{n}^{\prime}\,\leqslant\,{{\mathbf{x}}}) -{\mathbb{P}} ({{\mathbf{Q}}}^{\prime}\leq{{\mathbf{x}}}) \right\vert \end{aligned} $$

Taking the limit as $n\rightarrow \infty$ and making use of (20) and (21), and then passing to the limit when $k\rightarrow \infty$ and using (22), we have the desired result.