Hysteresis Dynamics, Bursting Oscillations and Evolution to Chaotic Regimes

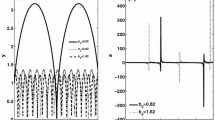
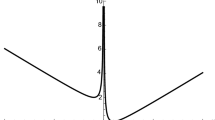
Abstract

This article describes new aspects of hysteresis dynamics which have been uncovered through computer experiments. There are several motivations to be interested in fast-slow dynamics. For instance, many physiological or biological systems display different time scales. The bursting oscillations which can be observed in neurons, β-cells of the pancreas and population dynamics are essentially studied via bifurcation theory and analysis of fast-slow systems (Keener and Sneyd, 1998; Rinzel, 1987). Hysteresis is a possible mechanism to generate bursting oscillations. A first part of this article presents the computer techniques (the dotted-phase portrait, the bifurcation of the fast dynamics and the wave form) we have used to represent several patterns specific to hysteresis dynamics. This framework yields a natural generalization to the notion of bursting oscillations where, for instance, the active phase is chaotic and alternates with a quiescent phase. In a second part of the article, we emphasize the evolution to chaos which is often associated with bursting oscillations on the specific example of the Hindmarsh–Rose system. This evolution to chaos has already been studied with classical tools of dynamical systems but we give here numerical evidence on hysteresis dynamics and on some aspects of the wave form. The analytical proofs will be given elsewhere.