Forces of Infection Allowing for Backward Bifurcation in an Epidemic Model with Vaccination and Treatment

Abstract

We consider an epidemic model for the dynamics of a vaccine-preventable disease, which incorporates the treatment and an imperfect vaccine given to susceptible individuals. We show that in spite of the simple structure of the model, a backward bifurcation may always occur if the treatment rate is above a threshold value. This occurs regardless of the specific form of the force of infection, which is only required to be infinitesimal of the same order of the size of the infectious compartment I, as I→0. This includes many commonly used functionals, as the linear, the monotone saturating Michaelis-Menten and the non-monotone force of infection used to represent the ‘psychological effect’.

Appendix

Here we recall the result obtained in [10]. Consider a general system of ODEs with a parameter ϕ:

$$ \dot{x}=f(x,\phi); \quad f: R^{n} \times R \rightarrow R^{n}, \quad f \in C^{2}\bigl(R^{n} \times R\bigr). $$

(8)

Without loss of generality, we assume that x=0 is an equilibrium for (8).

Theorem 2

Assume:

• (A1) A=D _x f(0,0) is the linearization matrix of system (8) around the equilibrium x=0 with ϕ evaluated at 0. Zero is a simple eigenvalue of A and all other eigenvalues of A have negative real parts;

• (A2) Matrix A has a (nonnegative) right eigenvector w and a left eigenvector v corresponding to the zero eigenvalue.

  Let f _k denotes the k-th component of f and,

  

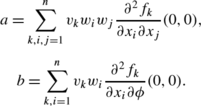
Then the local dynamics of system (8) around x=0 are totally determined by a and b.

• (i) a>0, b>0. When ϕ<0, with |ϕ|≪1, x=0 is locally asymptotically stable and there exists a positive unstable equilibrium; when 0<ϕ≪1, x=0 is unstable and there exists a negative and locally asymptotically stable equilibrium;

• (ii) a<0, b<0. When ϕ<0, with |ϕ|≪1, x=0 is unstable; when 0<ϕ≪1, x=0 is locally asymptotically stable and there exists a positive unstable equilibrium;

• (iii) a>0, b<0. When ϕ<0, with |ϕ|≪1, x=0 is unstable and there exists a locally asymptotically stable negative equilibrium; when 0<ϕ≪1, x=0 is stable and a positive unstable equilibrium appears;

• (iv) a<0, b>0. When ϕ changes from negative to positive, x=0 changes its stability from stable to unstable, and a negative unstable equilibrium becomes positive and locally asymptotically stable.

Proof

(see [10]) # □

Remark 1

Taking into account of Remark 1 in [10], we observe that if the equilibrium of interest in Theorem A.1 is a non negative equilibrium x ₀, then the requirement that w is non negative is not necessary. When some components in w are negative, one can still apply the theorem provided that w(j)>0 whenever x ₀(j)=0; instead, if x ₀(j)>0, then w(j) need not to be positive. Here w(j) and x ₀(j) denote the j-th component of w and x ₀ respectively.