Introduction

Computational finite element (FE) models of the knee joint are able to offer a quantitative estimation about risks for the onset and development of knee osteoarthritis (OA) based on mechanical signals experienced by tissues.18,19,40 They can also be used to assess the feasibility of different rehabilitation and surgical protocols. These models are typically based on subject-specific knee joint geometries with varying types of loading conditions. Physiologically relevant loadings have also been implemented, such as gait.1,4 Recently developed knee models with a cartilage degeneration algorithm were even able to predict mechanical changes of articular cartilage during the development of OA in a time-dependent manner.28,32

The main reason why the aforementioned models have not been utilized in clinical purposes is related to time needed to generate the models. Especially manual segmentation to generate knee geometries is time-consuming. There has been evolution in segmentation methods toward automatization.2,24,27,37 However, these methods are typically critically dependent on the image quality, and manual work is still needed after the initial segmentation. For instance, automated segmentation methods may cause easily inaccuracies (roughness) in contacting surfaces. This leads to difficulties in generation of proper FE meshes and causes also convergence problems.

Generation of proper FE meshes for tissues and contact interactions may be even more time-consuming challenge compared with the time required for segmentation. Especially models that include several tissues in contact with each other, complex loading conditions, and large tissue deformations are critically dependent on the mesh quality. Currently, there is one approach available to generate automatic FE meshes for soft tissues in the knee joint.33 However, even in this highly promising approach the mesh is geometry-specific and always different which could again cause challenges in complex contacts and simulations.

To save time in generation of model geometries and proper FE meshes, a template-based FE modeling may offer a solution. In template approaches, an existing template (geometry of a certain tissue, i.e., atlas) is deformed to match certain anatomical landmarks/dimensions determined either manually or automatically from clinical images.9,16 Interestingly, current literature does not include any attempts to apply template modeling to evaluate knee joint cartilage mechanics and subject-specific onset and progression of knee OA. Easy implementation of feasible loading conditions and meniscal load transfer are also desired features if rapid model generation and simulation are of interest.6,7,12,13,–14

Without considering knee injuries, two main risk factors for OA are overweight and aging.38,44 Currently, there are no computational studies available where these parameters would have been considered simultaneously for the prediction of subject-specific onset and development of OA. In computational FE models, the weight of a subject can be simply considered by the boundary conditions. However, there have been no attempts to consider aging. Though, the mechanisms behind OA due to aging can be very complex,29,38 it could be considered in the model simply by changing tissue material properties with age according to experimental evidence.20

In the current study, the main aim is to introduce a workflow for template-based modeling of the knee joint and show its potential to predict the development of knee OA. In addition to rapid generation of knee geometries and FE meshes, the template model includes automatic implementation of tissue material properties and boundary conditions. It also utilizes the previously developed cartilage degeneration algorithm to predict the development of OA26,31 and considers aging. Model predictions are compared against experimentally observed radiographic Kellgren–Lawrence follow-up data and subject-specific FE models.

Methods

Subject Information

Data used in the preparation of this article were obtained from the Osteoarthritis Initiative (OAI) database, which is available for public access at http://oai.epi-ucsf.org/. Specific datasets used are AllClinical00, AllClinical06, 0.C.2 0.E.1, 6.C.1, 6.E.1, kxr_sq_bu00 and kxr_sq_bu06. The same experimental data used previously was applied here.26 Baseline and 4-year follow-up MRIs and radiographic KL grades were collected from 21 subjects (8 males and 13 females). Ages and weights of subjects were obtained from the baseline visit. Subjects were divided into three groups based on the baseline weight and the experimentally observed 4-year follow up KL grade (KL0 (BMI = 23.1 ± 1.6 kg/m2), KL2 (BMI = 33.0 ± 2.2 kg/m2) and KL3 (BMI = 33.7 ± 3.7 kg/m2), 7 subjects in each group). At the baseline, KL grade was zero (indicating no signs of OA) in each group, whereas at 4-year follow-up, KL grades for KL0, KL2 and KL3 groups were 0 (intact), 2 (doubtful OA) and 3 (severe OA), respectively. The subjects were selected in order to show that in addition to mechanical overloading (overweight subjects in KL2 and KL3 groups), other factors, such as subject-specific knee joint geometries, can have a contribution in the initiation and development of cartilage degeneration. Specific exclusion criteria are seen from a previous study where the same subjects were used.26 Ethical approval and informed consent for collecting all subject information was provided by the OAI. The present project has been reviewed by a local data protection officer, and the local approval to conduct the study was granted by the University of Eastern Finland Committee on Research Ethics.

Patient-Specific Approach

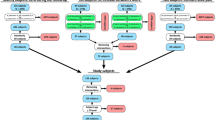
Since the patient-specific approach with manual phases in the model generation is not new, here it is described only briefly. Knee joint geometries and FE meshes of cartilages and menisci were utilized directly from our previous study.26 Then, each knee joint was exposed to physiologically relevant loading,8,23 mimicking simplified walking (Fig. 1). The flexion angle and joint reaction force (scaled by subject weight in bodyweight) were implemented in the model as a function of stance. In order to produce smooth contact between medial and lateral tibiofemoral compartments, the varus-valgus rotation was set free, while other degrees of freedoms were fixed (Fig. 1, Patient-specific approach—top row).

Figure 1
figure 1

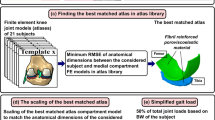
Workflows for the patient-specific (top) and template (bottom) approaches. In the patient-specific approach, the model geometry (whole knee joint) is generated via manual segmentation and then the simplified gait load assumed to occur during the stance phase of the gait is applied. Next, boundary conditions and forces from the whole knee joint simulation are used as an input in the compartment model. In the compartment model, the effect of meniscus is considered by subtracting forces through the meniscus from the total joint loads in the compartment (see variation of forces through menisci from Fig. 4). Finally, cartilage degeneration in the compartment model is simulated with the degeneration algorithm [Eq. (10)]. In the template approaches, anatomical dimensions (AD) are first measured from all subjects (N = 21) based on the MRI data (see details from Fig. 2). Then, the matching template model for the subject of interest is found based either on the minimum RMSE of ADs between the subject of interest and templates (multiple templates) or the minimum RMSE of ADs between each subject and all templates (one, best-matching template is chosen). Next, the optimal template model is scaled to match AD’s for the subject of interest. Finally, the scaled template model is simulated together with the simplified gait loading (50% of the total joint loads assumed to occur in the medial compartment) and the degeneration algorithm [Eq. (10)]. The effect of meniscus is considered identically with the manual approach.

Full size image

In order to have accurate predictions within a reasonable time, compartment models with finer meshes were generated. The compartment models were run by the outputs from the whole knee joint models (Fig. 1). In the compartments models, the load transfer of meniscus was subtracted from the total reaction forces through the compartment. This simplification may affect the simulation results, especially during complex loading conditions. However, as demonstrated in a previous study,28 this assumption was shown to have a negligible effect on the simulated stress, contact pressure and pore pressure levels at the tibiofemoral contact. See detailed description of these different model generation phases from a previous study.26 Implementation of the materials and the degeneration algorithm have been described below.

Template Approach

First, morphological dimensions (anterior–posterior, AP and medial–lateral, ML) of distal femur and tibiofemoral joint space width (JSW, sum of total cartilage thicknesses from femoral and tibial cartilage) were measured from each knee joint based on the MRI data (Fig. 1, Template approach and Fig. 2). The ML dimension was determined for clinical transepicondylar axis. The AP dimensions were determined for the lines producing the maximum anterior–posterior distance for the ellipse-like shaped medial and lateral condyles. Cartilage thicknesses (JSWs) were obtained from both medial and lateral compartments, measured at the central locations of tibiofemoral contact regions. Each dimension was determined from sagittal images. To study the influence of different joint shapes based on anatomical dimensions,21 two different template approaches were tested:

Figure 2
figure 2

Determining anatomical dimensions. Number 1 is the maximum anterior–posterior length of lateral femoral condyle, number 2 is the maximum anterior–posterior length of medial femoral condyle, number 3 is the medial tibiofemoral cartilage thickness, number 4 is the lateral tibiofemoral cartilage thickness, and number 5 is the maximum medial–lateral distance of distal femur (clinical transepicondylar axis). All measurements were measured based on the sagittal view.

Full size image
  1. (1)

    Multiple templates (Best corresponding individual template) Morphological dimensions and cartilage thicknesses were first normalized with respect to the ML dimensions in each template, similarly as in earlier studies.21,35 The most suitable template from 21 geometries (meshes) was selected based on the smallest root mean square error (RMSE) in the normalized morphological dimensions between the current subject under investigation and templates. While calculating the RMSE, the template for the current subject was omitted from the template library. Finally, the chosen template model geometry was scaled to match exactly with the morphological dimensions of the current subject.

  2. (2)

    One template (Best from 21 templates) Based on the normalized morphological dimensions, the sum of the RMSE was calculated between each subject and all other subjects. Then, those normalized subject dimensions that produced the smallest sum of RMSE was considered to represent average morphological joint dimensions and geometry. Finally, the model geometry from that one single template was scaled to match with morphological dimensions of each subject.

In both template methods, the scaling was based on the cartesian coordinate system. Each template was positioned so that AP, ML and tibiofemoral cartilage thickness directions corresponded to cartesian axes (x, y, z). The scaling was considered by multiplying the nodal values of the best template with percentage differences in ML, AP and cartilage thickness directions (x, y, z) between the subject of interest and the best template (Fig. 3).

Figure 3
figure 3

Scaling of the template. Nodal values in the best matching template model are multiplied with percentage differences in the measured ML, AP and cartilage thickness directions (dx, dy, dz) between the subject of interest and the best template.

Full size image

In this template approach, in order to speed up the model generation and simulation process, the whole knee joint was not simulated. Instead, only the medial compartment was considered in further simulations. The flexion angle and varus-valgus rotation were obtained from the best matching template (Fig. 1, subject-specific approach—loading in the medial compartment), whereas the joint reaction force was considered with 50% of the total knee joint forces during gait loading based on the bodyweight of the subject of interest.22 The effect of meniscal support was considered similarly as in the patient-specific approach. This produced a good match in joint reaction forces through the medial compartment between patient-specific and template approaches. Implementation of the materials and the degeneration algorithm have been described below.

Material Models and Cartilage Degeneration Algorithm

The following phases in the model generation and simulation were done similarly in the patient-specific and template approaches. Based on previous studies, cartilage and meniscus were considered as fibril reinforced poroviscoelastic (FRPVE) and transverse isotropic elastic materials, respectively.39,41,42,45 See the material properties from Table 1. Though meniscus is a poroelastic material, it could be assumed that only negligible fluid flow would occur during fast loading conditions. Thus, the effect of fluid in meniscus was omitted.

Table 1 Material parameters of the FPRVE material model for the femoral and tibial cartilages and the transverse isotropic elastic material for the meniscus.
Full size table

Osteoarthritic changes have been reported to be more frequently in the medial than lateral compartment.5,43 Also these patients developed OA in the medial compartment.26 For these reasons, only cartilage degeneration in the medial compartment was simulated. Based on the previous experimental studies,17,30,34,36 cartilage degeneration may be initiated and progressed due to excessive and cumulatively accumulated tissue tensile stresses experienced primarily by the collagen fibril network. In our previous studies,26,31 this was considered iteratively by degenerating the collagen fibril network as follows:

$$D_{el,i} = 1,\quad \quad \quad {\text{if}}\;(i = 1),$$
(1)
$$D_{el,i} = D_{el,i - 1} - \left( {D_{el,i - 1} \sqrt[{1.5}]{{\mathop \sum \limits_{t = 1}^{TOT} D_{el,t} \times INC_{t} }}} \right),\quad \quad \quad {\text{if}}\;(i > 1),$$
(2)

where, \(D_{el,i}\) is the current degeneration level (1 = no degeneration; 0 = total degeneration) inside a specific element (el) after certain iteration (i), INCt is the duration of each time increment, TOT is the total number of required time points (t) during each iterative loading step, and \(D_{el,t}\) is the fibril degeneration factor. The degeneration equations [Eqs. (1) and (2)] were applied during the stance phase of the gait with the fibril degeneration factor (\(D_{el,t}\)), which was calculated for each element (el) at each time point (t) using as follows:

$$D_{el,t} = \left( {\frac{{\left( {S_{el,t} - T_{{\sigma_{\text{f}} }} } \right)/T_{{\sigma_{\text{f}} }} }}{100}} \right) ,\quad \quad \quad {\text{if}}\;(S_{el,t} > T_{{\sigma_{\text{f}} }} ),$$
(3)
$$D_{el,t} = 0,\quad \quad \quad {\text{if}}\;(S_{el,t} \le T_{{\sigma_{\text{f}} }} ),$$
(4)

where \(S_{el,t}\) is the tensile stress for each element at each time point during the stance phase of the gait and \(T_{{\sigma_{\text{f}} }}\) is the threshold value for cartilage damage. In this previous study, the iterative process reduced the collagen network stiffness as a function of time, simulating changes in OA.26,31 In the present, this approach was modified (see below).

Aging

The link between aging and increased probability for the cartilage degeneration was considered by the experimentally observed relation between age and tensile failure limit for cartilage tissue.20 Thus, the following equations are proposed to link age and the threshold for the initiation and development of cartilage degeneration:

$$T_{{\sigma_{\text{f}} }} = 30 \;{\text{MPa}},\quad \quad \quad {\text{if}}\;({\text{Age}} < 30),$$
(5)
$$T_{{\sigma_{\text{f}} }} = 30 \;{\text{MPa}} - \left( {\left( {{\text{Age}} - 30} \right)\left( {20/15} \right)} \right),\quad \quad \quad {\text{if}}\; ( 3 0\le {\text{Age}} \le 4 5 ) ,$$
(6)
$$T_{{\sigma_{\text{f}} }} = 10\;{\text{MPa}} - \left( {\left( {{\text{Age}} - 45} \right)\left( {3/20} \right)} \right) \quad \quad \quad {\text{if}}\; ( 4 5< {\text{Age}} \le 6 5 ) ,$$
(7)
$$T_{{\sigma_{\text{f}} }} = 7\;{\text{MPa}} - \left( {\left( {{\text{Age}} - 65} \right)\left( {2/100} \right)} \right) \quad \quad \quad {\text{if}}\; ( 6 5< {\text{Age}} \le 7 5 ) ,$$
(8)
$$T_{{\sigma_{\text{f}} }} = 6.8 \,{\text{MPa}},\quad \quad \quad {\text{if}}\;({\text{Age}} < 75),$$
(9)

These thresholds were then used with Eqs. (1)–(4) to simulate cartilage degeneration. To provide degeneration evaluations within reasonable times, which is again important for clinical purposes, iterative interphases from Eq. (2) were removed and final predictions were based only on the tissue tensile stresses after one simulation. Only degenerated volumes were analyzed, i.e., information about elements where \(D_{el,i}\) was reduced was sufficient. This was an acceptable simplification, because time in Eq. (2) is arbitrary and the predicted degeneration volume was shown to be only slowly progressive (over 70% of total volumetric degeneration (\(D_{el,i} < 1\)) occurred after the first iteration in subjects with substantial volumetric degeneration after 100 iterations).26 Based on this assumption, iterations (i) were replaced with aging (Age). Thus, Eqs. (1) and (2) were merged into the following formation:

$$D_{{el,{\text{Age}}}} = 1 - \left( {\sqrt[{1.5}]{{\mathop \sum \limits_{t = 1}^{\text{TOT}} D_{el,t} \times INC_{t} }}} \right)$$
(10)

where \(D_{{el,{\text{Age}}}}\) is indicating element-wise cartilage degeneration and Age refers to the subject age.

Meniscus

First, by the subject-specific approach, the forces through the medial and lateral menisci of the whole knee joint models were simulated for each subject. Based on these simulations, input data for the models with subject-specific and average meniscus support were produced and they could be used as an input in further analysis of the compartment modes in patient-specific and template approaches. The average meniscus support was calculated separately as a fraction of total forces through tibiofemoral contact for the medial and lateral menisci. In computational consideration of meniscus, subtraction of load transfer of meniscus from the total reaction forces through the compartment was justified in a previous study.28 That study demonstrated identical cartilage responses between knee joint models with menisci and those with menisci considered as described above.

Simulations

All FE simulations were performed with Abaqus FE package (v6.13-3, Dassault Systèmes, Providence, RI, USA) using UMAT subroutine to implement FRPVE material properties for cartilage tissues. Before comparing patient-specific and template approaches, volumetric degeneration predictions based on the Eqs. (1), (2) and (10) were compared with each other, because that parameter has been shown to correlate well with the predicted level of OA.26 For this comparison, a test subject was selected based on the preliminary simulations where severe cartilage degeneration was expected. It was noticed that volumetric degenerations matched between the Eqs. (1), (2) and (10). Then, patient-specific and template approaches were introduced for each subject and predictions for the development of knee OA were simulated with the Eq. (10) for the following approaches:

  1. (1)

    Subject-specific approach 1—subject-specific geometry with subject-specific meniscus support

  2. (2)

    Subject-specific approach 2—subject-specific geometry with average meniscus support

  3. (3)

    Multiple templates 1—the best template with subject-specific meniscus support

  4. (4)

    Multiple templates 2—the best template with average meniscus support

  5. (5)

    One template 1—average template with subject-specific meniscus support

  6. (6)

    One template 2—average template with average meniscus support

In each simulation, cartilage degeneration [Eq. (10)] was based on the maximum principal (tensile) tissue stresses during physiologically relevant loading conditions, mimicking the stance phase of the gait.8,23 Finally, degenerated volumes were determined for each subject and those were compared between different cases (see above).

Statistical Analysis

Statistical differences between KL grade groups and predicted degeneration volumes were analyzed with the Kruskal–Wallis H test. Predictive accuracy of the algorithm was tested using receiving operating characteristics (ROC) and area under curve (AUC).25 The level of significance was set to p < 0.05. Statistical analysis was performed using SPSS software (SPSS 23.0, SPSS Inc., Chicago, IL, USA).

Results

In the subject-specific approach, time from the model generation till the final prediction for one subject was at minimum of 1 week. This time was reduced to ~ 2 min in the template approach.

In the analysis of the whole knee joint models, it was noticed that the meniscus support force was highly subject-specific at both the medial and lateral compartments (Fig. 4). The ranges of maximum and average support in the medial compartment were 0–35 and 6–25% of the total knee joint forces, respectively (Fig. 4, left). The corresponding values at the lateral compartment were 0–37 and 5–11%, respectively (Fig. 4, right).

Figure 4
figure 4

Forces through the lateral (left) and medial (right) meniscus as a function of stance phase of the gait cycle.

Full size image

In each patient-specific and template-based model (1–6), KL2 and KL3 groups produced higher degenerated volumes compared to KL0 group (Fig. 5). In the subject-specific approach with both subject-specific and average meniscus forces, statistically significant differences were found between KL0 and KL2 groups and between KL0 vs. KL3 groups, but no differences were found between KL2 and KL3 groups (Fig. 5, left). In the multiple template approach with subject-specific meniscus support, statistically significant differences were not found between any groups. When the effect of meniscus support was changed to average, statistically significant differences were found between KL0 and KL3 groups (Fig. 5, middle). In the one template approach with subject-specific meniscus support, statistically significant differences were found only between KL0 and KL3 groups. Interestingly, when the effect of meniscus support was changed to average, statistically significant differences were found between all groups (Fig. 5, right).

Figure 5
figure 5

Predicted degenerated volumes in patient-specific (left), multiple template (middle) and one template (right) approaches for each KL group. Patient-specific and template approaches were utilized with both subject-specific and average meniscal support. Crosslines (–) represent median values. Statistical significances between different KL groups were evaluated by using Kruskal–Wallis H test, *p < 0.05 and **p < 0.01.

Full size image

In terms of statistical differences between different KL groups, the receiving operating characteristic (ROC)-curves and area under the curves (AUC) produced identical results compared to what were obtained from Kruskal–Wallis H test (Figs. 5 vs. 6). Based on the ROC analysis, KL0 and KL3 groups were separated perfectly from each other (AUC = 1, p < 0.01) in the models with subject-specific geometries and one template with average meniscus support (Fig. 6, top-right and bottom-right). In these models, statistical differences between KL0 and KL2 groups was also observed (AUC > 0.8, p < 0.05). Interestingly, statistically significant differences between KL2 and KL3 groups were seen only in the template approach with one template (AUC = 0.878, p < 0.05).

Figure 6
figure 6

Receiving operating characteristics (ROC)-curves and area under curve (AUC)-values for the volume of degenerated elements in each approach. *p < 0.05 and **p < 0.01.

Full size image

Discussion

In the current study, the ability of a template based modeling approach to predict development of knee osteoarthritis during physiologically relevant loading conditions (simplified gait load) was tested. The model results were compared against patient-specific models and experimental follow-up radiographic KL grades of 21 subjects. Both subject-specific and template- or population-based models (excluding the multiple template approach with subject-specific meniscus consideration) were statistically able to separate healthy subjects from those whom KL grades were increased from 0 to 3, especially when the average consideration of forces through the meniscus (meniscus support) was considered. Surprisingly, the approach with one template (average geometry) and the average meniscus support was statistically able to separate all KL grade groups from each other.

We initially suspected that the subject-specific approach would provide best predictions to classify studied subjects into correct KL grade groups. However, in terms of statistical significance, the simplest method with one template showed the most promising results. The reason for this may be related to differences in implemented loads. In the subject-specific approaches, free varus/valgus rotation can lead to cases where either one of the compartments is more loaded than the other, while the template approach considered 50% of the total joint loads throughout the loading. Here, in the subject-specific approach, there were two subjects in the KL3 group, where the peak forces through the medial compartment were considerably lower than those in the KL2 group. This may explain why the statistical difference was not found between the KL2 and KL3 groups, though the mean forces through the medial compartment during the entire stance phase remained similar between these groups.

Due to similar BMIs of the subjects in KL2 and KL3 grade groups, and the same material and boundary conditions, the only major difference between these subjects was the knee geometry. Therefore, different volumetric degenerations obtained for these groups suggest that geometrical variation plays an important role to predict the onset and development of knee OA. This same result was obtained for all studied approaches (patient- and population-specific), though some differences in the statistical analysis were seen, suggesting that the used anatomical dimensions in the template approach may be sufficient when predicting OA. This is a very promising result, since the main bottleneck in the simulations of large number of subjects is time required in segmentation, meshing, implementing boundary conditions and material, and model simulation. In the subject-specific approach, this entire process from the model generation till prediction took at minimum of 1 week per subject. Sometimes it can take weeks or months to get results. The template approach was able to decrease this time to ~ 2 min. Furthermore, the working reliability in the template approach was excellent because the used FE mesh was tested thoroughly beforehand. Nonetheless, it is still too early to say which one of the presented methods is the best due to the subject number. More simulations are needed with more subjects.

Interestingly, by considering the average meniscus support with the subject-specific cartilage geometries, model predictions did not change from the statistical point of view. Instead, in multiple template and one template approaches, consideration of the average meniscus support helped to separate all KL grade groups from each other. True validation of the meniscal support is obviously impossible to conduct in vivo, and for instance pretensions of the meniscal attachments affect the distribution of knee joint loads.14 Furthermore, small errors (error of one pixel in MRI) in meniscus segmentation may lead to overestimated or underestimated tissue thicknesses, which may substantially influence the meniscus support. Nonetheless, eliminating the possible influence of these uncertainties, and using only one meniscus supporting force (in bodyweight) in each model, produced promising results and could provide a simple solution to consider meniscus.

Meniscal support forces varied a lot between subjects. Current literature knows very few experimental studies related to meniscal support during physiological loading conditions. In 2014, a group of researchers was able to attach 5 knee joints from cadavers into a modified knee joint stimulator and to measure forces through meniscus under loadings suspected to occur during normal walking.13 In that study, forces through the lateral meniscus were constantly ~ 50% of the total forces recorded in the lateral compartment, whereas forces through the medial meniscus were between ~ 25 and ~ 50% of the total forces recorded in the medial compartment. In the current study, only in some subjects such high meniscal support was achieved, whereas the average forces through the lateral and medial meniscus varied between ~ 10–25 and ~ 15–45% of the total forces, respectively. Recently, forces through the meniscus during gait were evaluated for two subjects using multibody simulation with different consideration of zero-load length for meniscal attachments.14 In that study, one of the results was that the medial meniscus transfers more loads compared to the lateral meniscus during the stance phase of gait, and the amount of load transmission may be influenced by the subject geometry. This result is consistent with the results of the current study.

In earlier studies,3,22 it has been shown that the subject-specific joint loading is important to consider when investigating force distributions between the lateral and medial compartments and forces in the patellofemoral contact. For instance, forces through the medial compartment may vary from 55 to 88% and from 44 to 84% of the total joint forces during the first and second peak forces of gait, respectively.22 This subject-specific variation in the force distributions may be explained mainly by the geometrical differences and hip-knee-ankle (HKA) angle.22 In the current study, in the subject-specific approach, free varus/valgus rotation produced ~ 50%/50% force distribution between medial and lateral compartments and only small variations in this force balance through entire loading. Though, as discussed above, it should be noted that even small variation in this force balance may slightly influence the predicted degeneration volume. This distribution matches adequately with the selected experimental measurements.22 This was also the motivation to use exactly 50% of the total reaction force in the medial compartment of the template approach. Even though subject-specific gait data was unavailable and thus could not be implemented, surprisingly good predictions for the development of knee OA were obtained.

In addition to mechanical overloading and aging, it has been shown that the risk for the onset and development of knee OA is also strongly correlated for instance with knee alignment, gender, occupational hazard (long-term kneeling/squatting), inflammation due to joint injuries or overload, and genetic factors.10,11 These factors were not considered in the current study. To consider the above-mentioned parameters, (i) they should be known, (ii) subject number should be increased considerably, and/or (iii) they should be studied first in controlled in vitro and/or animal model experiments.

The choice to use the relatively complex material model for cartilage is justified by its ability to distinguish between different tissue constituents (collagen, proteoglycan, fluid) and to model local and constituent-specific tissue degradation.26,31,32 Simplification of the material model would not enable this. However, especially as we compare the modeling results against KL grades, simpler modeling approaches might produce the same conclusions. In order to make clear conclusions about the needed level of model sophistication to provide adequate results, different modeling approaches should to be compared in the future.

The presented results suggest that a population-, template-based knee joint models may be applicable to predict OA and classify subjects into correct groups. In the future, the presented workflow should be tested against larger subject groups. This could provide a fast clinical tool for prediction of osteoarthritis and simulation of interventions.