Introduction

The reversible aggregation of human red blood cells (RBCs) continues to be of interest in the field of hemorheology because RBC aggregation is a major determinant of the in vitro rheological properties of blood and the in vivo flow dynamics and flow resistance of blood.2 An abnormally high level of RBC aggregation has been observed in many disease states, such as diabetes, thrombosis, myocardial infarction, vascular diseases, and hematological pathology.9 There is now general agreement regarding the correlations between elevated levels of fibrinogen or other large plasma proteins and enhanced RBC aggregation and platelet aggregation.22,32 RBC aggregation can also be induced by large macromolecules such as high molecular weight dextrans and other polymers.6

RBC aggregation can be assessed using different techniques, including erythrocyte sedimentation rate (ESR), zeta sedimentation rate, low-shear viscometry, image analysis in a flow chamber, ultrasound back-scattering,10–12,39 and photometry.14,25 Recording the intensity of transmitted or back-scattered light under shearing conditions has been widely used to assess different aspects of RBC aggregation. Several commercially available instruments of optical aggregometry in a photometric shearing system have been developed using the principles developed by Schmid-Schönbein et al.24 In optical aggregometry, the cells should be completely disaggregated, by applying a high shear rate (i.e., 500–600 s−1), where they are suddenly exposed to zero-flow conditions or slowed to a shear rate of 3–5 s−1, prior to testing. Light scattering signals, with respect to time, provide information about the cell aggregation characteristics. Even though these methods define meaningful parameters representing RBC aggregation, these measurements are quite different from the actual flow environment.37 The conventional aggregation parameters in terms of an arbitrary unit “M” and “M1” with Myrenne aggregometer and the laser-assisted optical rotational cell analyzer (LORCA) may not directly relate to the in vivo hemorheological characteristics.18

Therefore, creating a new principle and method to measure RBC aggregation mimicking actual in vivo flow is of great interest. In our recent study, we found that RBC aggregation of flowing blood within a microchannel caused changes in the variance of optical Doppler frequency spectrum using spectral domain Doppler optical coherence tomography (SD-D-OCT),33 and this requires further interpretation of the proposed index, i.e., the standard deviation (SD) of Doppler frequency spectrum as an aggregation parameter as well as the measurement principles.

Since the proposed SD of Doppler frequency spectrum as an aggregation parameter may be dependent on shear rate, hematocrit, aggregation level, and geometrical conditions, the present study investigates the effects of these conditions on the SD value of the normal and aggregated blood. In addition, this study evaluates the instrument precision and sensitivity. Our purpose is to validate a SD of the velocity power spectrum as a new aggregation index for qualitative measurement of RBC aggregation.

Theory

OCT or Doppler OCT is able to achieve high imaging speed, high velocity sensitivity, and high spatial resolution simultaneously.8,15 It has demonstrated considerable potential as a method for static and dynamic imaging of various kinds of tissue and blood. The refractive index mismatching between RBC cytoplasm and blood plasma is the major source of light scattering in blood.17,26,28 The scattering properties of blood are also dependent on RBC volume, shape, and orientation, aggregation and disaggregation capability and hematocrit (HCT). The OCT depth-reflectivity profile has been used to study blood optical clearing that reduces blood scattering by biocompatible agent-induced refractive index matching between RBCs and plasma in order to enhance the capability of light penetration depth, aggregation, sedimentation, and HCT by our and other groups.7,16,17,29,34–36 In our previous work, we demonstrated that the slope of the OCT depth-reflectivity profile decreased with the level of RBC aggregation.35,36 This is so because RBC aggregation leads to a decrease in scattering of RBCs.21 Unfortunately, the relationship between the slope and the aggregation of RBCs could not be directly used because the slope is also HCT-dependent.40

We have demonstrated Doppler variance tomography using the variance of the Doppler frequency spectrum to more efficiently map the flows in highly scattering biological tissues by Doppler OCT (D-OCT).31,40 In addition to the local velocity information, phase-resolved D-OCT systems give the variance of the Doppler frequency spectrum,31,40 which is given by

$$ \sigma^{2} = {\frac{2}{{T^{2} }}}\left\{ {1 - {\frac{{\left| {\frac{1}{N}\sum\nolimits_{j = 1}^{N} {\left[ {f_{jT} (z) \cdot f_{(j + 1)T}^{*} (z)} \right]} } \right|}}{{\frac{1}{N}\sum\nolimits_{j = 1}^{N} {\left[ {f_{jT} (z) \cdot f_{jT}^{*} (z)} \right]} }}}} \right\}, $$
(1)

where N is the number of A-lines used for averaging; T is the time interval between two exposures, and f(z) is a complex signal from an inverse Fourier transform of the interference pattern. The corresponding Doppler shift can be estimated by comparing the phasors of f(z) between two complex signals during two exposures at a same location. The phase change is recorded by the product of f jT (z) and f* (j+1)T (z), where * denotes the conjugate operation. The value of σ2 depends on the flow velocity distribution. Variations of flow velocity broaden the Doppler frequency spectrum and result in a larger σ2. Thus, the Doppler variance obtained by phase-resolved D-OCT systems can be an indicator of flow variations.

Individual particles within concentrated suspensions exhibit significant random movements when the suspension is subjected to shear flow. These movements are dependent on the local shear rate of the suspension and on particle size.4 Previous studies have shown variation in the instantaneous velocity of individual RBCs and the effect of aggregation on the dispersion of RBCs flowing in venules.5,27 RBC aggregation in the flow stream decreases the variability in instantaneous cellular velocity.5 This effect is most likely the result of an increased particle size. The magnitude of particle movements is decreased when the particle diameter increases.13,23 Therefore, decreased variance/SD in the Doppler frequency spectrum with RBC aggregation is expected.

Materials and Methods

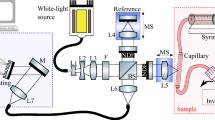
A schematic of the spectral-domain D-OCT system is shown in Fig. 1. A super-luminescent diode (SLD) with a spectrum centered at 1310 nm, and a full width at half maximum bandwidth of 95 nm and a total delivered power of 8 mW was used. Back-reflected light from the reference and sample arms was guided into a spectrometer and dispersed over a 1 × 1024 InGaAs detector array at 7.7 kHz (corresponding to 1/T). The total wavelength range spreading on the detector array was 130 nm, corresponding to a spectral resolution of 0.13 nm and an imaging depth of 3.6 mm in air. The resulting axial resolution was about 8 μm and the lateral resolution of the system was about 13.8 μm.1,36

FIGURE 1
figure 1

Schematic of a fiber-based spectral-domain OCT system used in the experiments (FL, focusing lens; DG, diffraction grating; CM, collimator; LSC, line-scan camera)

Full size image

The interference signal was inversely Fourier transformed after reducing the DC component. In the phase-resolved D-OCT, the phase change of the interference fringe between sequential A-line scans was used to calculate the Doppler frequency shift.40 The SD of phase shift between two consecutive exposures (=σT) was calculated from the cross correlation using Eq. (1).31

Various HCT levels from 30% to 55% were obtained by mixing extracted RBCs with porcine plasma using ethylenediaminetetraacetic acid (EDTA) as an anticoagulant (Animal Technologies, Inc., Tyler, TX). Different suspensions of normal RBCs, artificially aggregated with dextran, were prepared. RBCs were resuspended in plasma with dextran 500 (Dx500, average molecular mass 500 kDa; Sigma-Aldrich Co., St. Louis, MO, USA). A plasma dextran concentration of 0.5–2% [in weight/volume (w/v)] was used to induce the RBC aggregation. In another set of experiments, the RBCs were resuspended in PBS for the control samples and in 400 mg/dL fibrinogen (F4129, Sigma-Aldrich Co., St. Louis, MO, USA) PBS solution for the aggregating samples at a HCT of 40%. For in vivo situation, fibrinogen or other large plasma proteins enhance RBC aggregation rather than dextran. The experiments are to further demonstrate that the variance can reflect the erythrocyte aggregation mimicking the in vivo situation. All OCT measurements were performed just after RBC suspensions were prepared and pumped through a round glass capillary tube with a 300-μm inner diameter (VitroCom Inc., Mountain Lakes, NJ) at a Doppler angle of 5°. The two ends of the glass tube were connected with two around 50 cm-long plastic tubes to develop a lamina flow. A programmable syringe pump (Harvard Apparatus, Holliston, MA) was used to make the blood flow with an approximately constant speed at a rate of 1.1, 2.3, and 3.4 mm/s, corresponding to a pseudo shear rate of 20, 40, and 60 s−1. The shear rate simulates the real values within major human retinal venular vessels. OCT “M-scans” (a single A-line repeatedly acquired in time without transverse scanning) were performed. A total of 512 OCT A-lines were acquired in a M-mode scan with the probe beam targeting at the center of the tube. It takes about 66 ms for the acquisition. Averaging is used to improve the measurement sensitivity. All final results of SD values for both normal and aggregated blood were means of five separate measurements on aliquots of a sample. Each measurement consisted of triplicate data acquired from the same aliquot. A paired t test statistical analysis was applied for the differences in SD between the control group (without dextran) and the treated group (with dextran). For all tests, a level of 0.05 was chosen as a significant level.

Instrument precision for SD parameter was assessed by calculating the coefficient of variation (CV) of 12 measurements on aliquots of normal porcine blood samples with fixed HCT at 40% at the flow rate of 15 μL/min within the 300 μm microchannel; each measurement consisted of triplicate determinations followed by introducing a new aliquot. To determine the sensitivity of the aggregation parameter, two groups of blood samples, i.e., the normal blood group and the blood with 2% Dx500, with fixed HCT at 40% were measured. The “standardized difference” between these two groups for SD parameter was calculated by dividing the difference between the two groups by the mean of the two standard deviations for that parameter. Note that a higher standardized difference for a parameter indicates that the parameter has a higher power to detect a difference in aggregation.

Results and Discussion

Standard Deviation Measurement for RBC Aggregation Characterization

Figure 2 shows the OCT structural images (Figs. 2a and 2b) and the Doppler variance images that give the variation of the blood velocity distribution for the blood without dextran (Fig. 2c) and the aggregated blood with 0.5% Dx500 (Fig. 2d) at HCT of 40% flowing through a 300-μm glass tube at a shear rate of 60 s−1. The different OCT signals between the control blood (Fig. 2a) and the aggregated blood (Fig. 2b) are visualized in the blood with 0.5% Dx500. The presence of different velocity variations between the control and the aggregated within the glass tube was observed (Figs. 2(c) and 2d). Note that, although the measured profile of the Doppler velocity fits closely to a parabolic shape, the SD data are not perfectly symmetrical about the r = 0 axis. The results might be because Doppler velocity is a direct measurement of the phase difference between adjacent A-lines, while the (complex) SD measurement is a function of both the phase and amplitude of adjacent A-lines (according to Eq. 1). The SD will hold a parabolic distribution if the amplitude is uniform across all cross-sectional A-lines. However, the amplitude is normally not a uniform distribution given the existence of speckle noise and velocity-related motion artifacts (sensitivity reduction) of the flow.

FIGURE 2
figure 2

Structural OCT images (top) and Doppler variance images (bottom) of the blood at HCT = 40%. (a, c) Normal. (b, d) The blood with 0.5% dextran 500

Full size image

The quantitative values of the SD along the depth calculated according to (1) for the control and the treated blood were determined and are plotted in Fig. 3 for HCT of 40% (Fig. 3a) and HCT of 55% (Fig. 3b) at a shear rate of 60 s−1. For the nonaggregated blood at HCTs of 40% or 55%, the upper lines of the SD profiles in Figs. 3a and 3b show that the velocity fluctuations vary with radial position in the glass tube. A higher SD is found near the center of the tube where the shear rate is minimal for the flow. The decrease in the SD in the center of the tube could be the result of a decrease in the variability in instantaneous cellular velocity due to changes in the size of scatterers associated with RBC aggregation. When aggregates migrate to the center of the tube, particle size will be greater in the center of the tube than near the tube wall.4

FIGURE 3
figure 3

Standard deviation vs. depth profiles for normal and dextran-treated blood at HCT: (a) 40% and (b) 55%

Full size image

The centerline SD values were calculated for each of the RBCs flowing at a shear rate of 60 s−1 and are shown in Fig. 4. The mean values of 74.6 ± 2.8 for the control group at a HCT of 40% is significantly (p < 0.01) higher than the values for the aggregated blood induced by dextran from 0.5% to 2%. The addition of dextran decreases the SD by around 40%, indicating the velocity variation in the aggregated blood is reduced. This finding is consistent with the in vivo work5 that the magnitude of the velocity variations in dextran-treated blood is less than that in the nonaggregating blood. It is most likely that RBCs residing in aggregates could be both shielded from interactions with surrounding cells and also hindered in their movements or the magnitude of particle movements is decreased when the particle diameter increases.

FIGURE 4
figure 4

Difference in mean centerline SD for the blood (HCT 40%) at various concentrations of dextran. Values for dextran-treated blood are significantly (p < 0.01) smaller than those for normal blood

Full size image

It is known that dextran-induced aggregation is higher at higher concentrations up to an optimum concentration.20 We noted that there is no significant difference the SD values between the samples with dextran at concentrations of 0.5–2%. Because dextran 500 used in our experiment, which has a very high molecular weight, is a strong aggregation inducer producing large aggregates after the concentration over 0.5%,5,19 it seems that the variance cannot distinguish the size difference between the samples with dextran at concentrations of 0.5–2% after the aggregates exceeding a certain size, i.e., the SD value rapidly drops down to around 45°. Further improvement of the signal-to-noise ratio of the SD-D-OCT system may be helpful to address the issue. Nevertheless, dextran is only used to demonstrate the method and dextran 500 at 0.6% is widely used to induce RBC aggregation in the range for healthy humans.5,19 Studies on mimicking the in vivo situation with fibrinogen at the measured concentrations and blood samples from patients that the actual aggregation is assessed are under way to develop a quantitative method rather than the current qualitative method.

Figure 5 shows the Doppler variance images that give the variation of the blood velocity distribution for the control (Fig. 5a) and the aggregating blood with fibrinogen (Fig. 5b) at a HCT of 40% flowing through a 300-μm glass tube at a shear rate of 40 s−1. The quantitative values of SD along the depth calculated for the control and the aggregating blood are plotted in Fig. 5c. The presence of different velocity variations between the two groups was evident. The centerline SD for each of the RBCs flowing at shear rates of 40 and 60 s−1 is shown in Fig. 6. Fibrinogen at 400 mg/dL results in a significant decrease in the SD by 26.7% (p < 0.01) at 40 s−1 and 39.8% (p < 0.01) at 60 s−1, respectively.

FIGURE 5
figure 5

Doppler variance images of the normal (a) and the aggregating blood with fibrinogen (b) at HCT of 40%, (c) quantitative values of SD along the depth for the normal and the aggregating blood

Full size image
FIGURE 6
figure 6

Centerline SD values of the normal blood and the blood with fibrinogen at shear rates of 40 and 60 s−1

Full size image

Effect of Shear Rate on SD Measurements

Figure 7 shows the centerline SD of 40% blood under three shear rates of 20, 40, and 60 s−1 for the normal (nonaggregating) and 2% Dx500-treated (aggregating) blood. As expected, the SD value increases with increasing shear rate for both groups. When dextran is added to the flowing blood, RBC aggregation causes a significant decrease in the SD values at 40 and 60 s−1.

FIGURE 7
figure 7

Centerline SD values of the blood (HCT 40%) under three shear rates of 20, 40, and 60 s−1 for the normal blood and 2% Dx500-treated blood. The value for 20 s−1 with 2% dextran is not shown in the figure because it drops down to noise level and so meaningless

Full size image

Hematocrit Dependence

Figure 8 shows the centerline SD of control blood with HCTs from 30% to 55% at shear rates of 40 and 60 s−1. The SD value tends to decrease with increasing HCT, but that is not significantly affected at the both shear rates. In other words, the SD value is nonsignificant dependence on hematocrits in the range of 30–55%. The relationship between the SD value and HCT is quite unlike that between scattering and HCT. We and other groups have reported very large changes in attenuation with HCT.16,36

FIGURE 8
figure 8

Centerline SD values of the control blood at HCTs from 30% to 55% at shear rates of 40 and 60 s−1

Full size image

Instrument Precision and Sensitivity

The mean, standard deviation, and the coefficient of variation (CV) for 12 repeated measurements on aliquots of the same control blood sample are 74.6%, 2.8%, and 3.8%, indicating the SD measured by the SD-D-OCT system is highly repeatable. The percentage difference and standardized difference between the two groups (n = 12 for each group) of the control and the aggregating blood with 2% Dx500 are 60.4% and 8.16. The standardized difference is much larger than that of commercial available optical aggregometers (Table 1).3 The large percentage difference and standardized difference between the two groups implies the SD value is highly sensitive to aggregation difference.

TABLE 1 Comparison of instrument precision and sensitivity between Doppler variance method and light transmission method4
Full size table

The data presented in this work point to the possibility of optical Doppler variance determination of the RBC aggregation. In all our experiments, RBC aggregation induced by dextran or at the presence of fibrinogen caused a practically 30–40% decrease in the SD of Doppler frequency spectrum. The normal blood has a SD value larger than 70 and the aggregated blood has a SD value smaller than 50 at a pseudo shear rate of 60 s−1. The shear rates between 40–60 s−1 mimicking the venular vessels where RBC aggregation often exists were found to be optional operating flow velocities for sensitivity, especially higher signal-to-noise ratio at 60 s−1.

One may speculate why the dimension of the round microchannel with an inner diameter of 300 μm was used. Typical RBC aggregometers have similar dimensions for their present channel gap. For instance, the LORCA has a 300 μm gap in concentric annulus. Myrenne aggregometer has an approximately 70 μm gap in a cone-plate geometry, which may limit the formation of normal 3D aggregates.

We have found a new qualitative measure of red blood cell aggregation, directly measured through a SD of the velocity power spectrum. The new qualitative index function can provide information matching the in vivo microvascular blood flow with shear rates of 40–60 s−1 and is of nonsignificant hematocrit dependence. However, for practical use, a quantitative model relating the SD to the aggregate size is needed. A wide range of aggregation schemes are possible for RBCs (e.g., diffusion limited aggregation or rouleaux patterns) and understanding their impact on velocity fluctuations is very challenging. Furthermore, as known, the Doppler frequency shift depends on the Doppler angle between the probe and flow directions and would vary during in vivo measurements. However, it was demonstrated that variance imaging is less sensitive to the Doppler angle during in vitro and in vivo measurements in our previous results.30,38 Nevertheless, we currently aim to develop an optical-microfluidic rheometry with a fixed Doppler angle for in vitro routine medical test. Although the variance of Doppler frequency spectrum is less sensitive to the Doppler angle, the studies on the possible effects on in vivo measurements are under way. Except for the possible effects of the Doppler angle, the phase instability caused by bulk-motion artifacts and optical heterogeneity are also the limitations for in vivo use. A technique to be established using the new index to quantitate RBC aggregation either for in vitro or in vivo measurements requires further studies.

Conclusions

We proposed SD-D-OCT technique to qualitatively measure RBC aggregation with high sensitivity and reproducibility. The SD of Doppler frequency spectrum of RBCs in flowing blood was validated as a new RBC aggregation index, which was independent of blood hematocrit. Clear evidence of correlation between the SD value of Doppler frequency spectrum and RBC aggregation induced by dextran and fibrinogen which is similar to in vivo blood flow was demonstrated.