Introduction

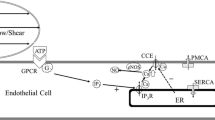
Blood flow-mediated mechanotransduction in vascular endothelial cells (ECs) is essential for normal vascular function,15,26 and abnormalities in EC flow signaling play a role in the development of atherosclerosis.2,18,27 A prominent early response to flow in ECs is mobilization of intracellular calcium,1,12,13,17,31 an important second messenger that regulates downstream signaling. It remains unknown, however, how the flow-induced calcium response is triggered. A key question in this regard, and one that has been the subject of long-standing controversy, is whether intracellular calcium changes are induced by a direct effect of the flow force on the EC surface (shear stress effect), by an indirect effect whereby calcium is mobilized due to flow-induced alterations in cell-surface concentration of agonists such as the adenine nucleotides ATP and ADP (shear rate effect), or by a combination of these processes.12,13,17,31 An important additional consideration is that flow induces ATP release in ECs.6,16,33

Mathematical models were previously developed to assess the effect of flow on adenine nucleotide concentration at the EC surface. The earliest models focused exclusively on ATP and on the simple case of flow between two infinitely wide parallel plates.19,20 Because ADP is virtually as potent as ATP in mobilizing EC intracellular calcium,22,24 subsequent modeling included ADP.30 Experimental data demonstrating that flow elicits ATP release in ECs16 and the unsteady nature of blood flow in large arteries motivated incorporation of these effects into the modeling.14 Most recently, the models have been extended to more complex flow fields including regions of flow separation and recirculation as well as arterial branchings.8,9

Despite previous modeling efforts, it remains unclear if flow-induced changes in intracellular calcium are mediated entirely by shear stress or if changes in ATP/ADP concentration contribute significantly. One reason for the uncertainty is the incomplete information on the dependence of flow-induced ATP release, which is a critical parameter for determining cell-surface nucleotide concentration,8,14 on shear stress. Another limitation in previous models is that they have all treated the endothelium as a flat (non-wavy) surface. The undulating nature of the endothelium has previously been shown to greatly impact the shear stress distribution on the cell surface3,4,28; however, the ramifications of these subcellular shear stress variations for adenine nucleotide concentration at the EC surface remain unexplored. In the present work, we performed computational simulations to probe the impact of cell waviness on ATP/ADP concentration at the EC surface. The results demonstrate that: (1) in the absence of flow-induced ATP release, EC waviness has a negligible effect on total nucleotide (ATP + ADP) concentration at the EC surface; (2) in the presence of robust flow-induced ATP release, EC waviness significantly alters the ATP + ADP concentration at the EC surface; and (3) the absence of ATP in the perfusion media amplifies the effect of cell waviness on nucleotide concentration at the cell surface.

Computational Methods

Computational Geometry

Similar to previous models,19,20,30 the simulations assume fully developed steady flow in a parallel plate flow chamber with ECs fully covering the bottom chamber surface. Unlike previous studies, however, the EC surface is considered to be wavy (Fig. 1). The model assumes a flow chamber height, H, of 200 μm, a typical value used in EC experiments and a chamber length, L, of 1500 μm. h denotes EC height, while λ and ω denote cell length in the streamwise and spanwise directions respectively. Based on atomic force microscopy (AFM) imaging of live cultured bovine aortic endothelial cells (BAECs),3 we consider the range 0 ≤ h/λ ≤ 0.15. The wavy EC surface is assumed to be sinusoidal with undulations in both the streamwise and spanwise directions as follows:

Figure 1
figure 1

Geometric model used in the numerical simulations illustrating the wavy EC surface along the bottom surface of a parallel plate flow chamber as well as the computational mesh used in the simulations. Note that the depicted mesh shows only a portion of the entire computational domain

Full size image
$$ y = h \cdot \sin^{2} \left( {\pi x/\lambda } \right) \cdot \sin^{2} \left( {\pi z/\omega } \right). $$
(1)

Baseline parameter values for the simulations are provided in Table 1.

Table 1 Geometric parameters used in the simulations
Full size table

A structured mesh is used (shown for the EC surface in Fig. 1), and the grid distribution has been verified to yield mesh-independent solutions for both flow and concentration. More specifically, for the most challenging computational case, increasing mesh density by 20% relative to that shown in Fig. 1 (which reduces the minimum mesh size in the y-direction to less than half of that in Fig. 1) leads to peak wall shear stress and total nucleotide concentration values that are within 1% of those shown in “Results.” The finer mesh distribution in the vicinity of the walls allows resolution of the large velocity and concentration gradients in those regions.

Governing Equations and Numerical Methods

The simulations involve solving the continuity and linear momentum equations for the flow field and the convection-diffusion equation for nucleotide concentration. Previous modeling has shown that for typical flow chamber dimensions and a physiological frequency of 1 Hz, flow unsteadiness has very little impact on the mean (time-average) nucleotide concentration at the EC surface14; therefore, all present simulations assume steady flow. The governing equations are:

$$ {\text{Continuity:}}\quad \quad {\frac{{\partial u_{i} }}{{\partial x_{i} }}} = 0 $$
(2)
$$ {\text{Momentum:}}\quad \quad \rho {\frac{{\partial \left( {u_{i} u_{j} } \right)}}{{\partial x_{j} }}} = - {\frac{\partial p}{{\partial x_{i} }}} + \mu {\frac{\partial }{{\partial x_{j} }}}\left( {{\frac{{\partial u_{i} }}{{\partial x_{j} }}}} \right) $$
(3)
$$ {\text{Convection}}{\text{-}}{\text{Diffusion:}}\quad\quad u_{i} {\frac{\partial c}{{\partial x_{i} }}} = D{\frac{\partial }{{\partial x_{i} }}}\left( {{\frac{\partial c}{{\partial x_{i} }}}} \right), $$
(4)

where ρ is the fluid density, u i is the fluid velocity in the i direction, μ is the dynamic viscosity of the fluid, c is the nucleotide concentration, and D is the nucleotide diffusion coefficient in the fluid. The working fluid is assumed to be cell culture medium with ρ = 1000 kg m−3 and μ = 7.77 × 10−4 kg m−1 s−1. Equation (4) applies for both ATP and ADP, except that the value of D is different for the two nucleotides.

A no-slip (zero velocity) boundary condition is applied at the top wall of the flow chamber and at the EC surface (bottom wall). At the flow inlet (x/λ = 0), a parabolic fully developed velocity profile is imposed with the mean inlet velocity (u o) adjusted to yield wall shear stress levels at the inlet (τ o) in the physiologically relevant range of 0.5–8 Pa (5–80 dyne cm−2). Fully developed flow (zero velocity gradient in the axial direction) is specified at the flow outlet (x/λ = 50). A periodic boundary is assumed along the lateral sides of the computational domain, implying that the domain repeats infinitely in the spanwise direction.

For nucleotide concentration, boundary conditions are needed for both ATP and ADP. At the flow inlet, most simulations are performed with a constant ATP concentration c o = 0.1 μM, a value that approximates normal ATP levels in the bloodstream.5 Limited simulations are also performed with a zero ATP concentration at the inlet. ADP concentration at the flow inlet is assumed to be zero in all simulations. At the flow outlet, a zero diffusion flux (D∂c/∂x = 0) is assumed for both ATP and ADP. At the top wall, a zero mass flux is imposed for both ATP and ADP. At the bottom surface of the chamber where the ECs are present, ATP and ADP hydrolysis follows irreversible Michaelis-Menten kinetics. For ATP, the net mass flux is given as:

$$ D_{\text{ATP}} \left. {{\frac{{\partial c_{\text{ATP}} }}{\partial n}}} \right|_{w} = {\frac{{V_{{\max ,{\text{ATP}}}} \cdot c_{\text{ATP}} }}{{K_{{{\rm m},{\text{ATP}}}} + c_{\text{ATP}} }}} - S_{\text{ATP}} \left( {\tau_{\text{w}} } \right), $$
(5)

where n is the unit vector normal to the EC surface, D ATP is the ATP diffusion coefficient in cell culture medium, V max,ATP is the maximum enzyme reaction velocity for ATP hydrolysis, K m,ATP is the Michaelis constant for the enzyme, and S ATP is the source term for flow-induced ATP release. Similar to our previous studies,8,14 S ATP is assumed to be a sigmoidally increasing function of wall shear stress (τw) as follows:

$$ S_{\text{ATP}} \left( {\tau_{\text{w}} } \right) = S_{\max } \left[ {1 - \exp \left( { - {\frac{{\tau_{\text{w}} }}{{\tau_{\text{ref}} }}}} \right)} \right]^{3} , $$
(6)

where τref is a reference shear stress that regulates the rate at which maximum ATP release is reached and S max is the maximum value of ATP release rate. Because the actual dependence of flow-induced ATP release on the applied shear stress remains to be established, we also consider a second model of more abrupt ATP release where S ATP is a step function of wall shear stress occurring at τw = 1 Pa (10 dyne cm−2) as follows:

$$ S_{\text{ATP}} \left( {\tau_{\text{w}} } \right) = \left\{ {\begin{array}{ll} 0 & {\tau_{\text{w}} < 1.0}\; {\text{Pa}} \\ {S_{\max } } & {\tau_{\text{w}} \ge 1.0} \; {\text{Pa}} \\ \end{array} } \right.. $$
(7)

Similar to our previous work,8 τref = 0.4 Pa and S max = 10−9 mol m−2 s−1. The τref value is based on the experimental measurements of Bodin and Burnstock6 and assumes that a shear stress of 2.5 Pa elicits more than 99% of S max. The value of S max = 10−9 mol m−2 s−1 is considered conservative as discussed by John and Barakat14 and is in agreement with experimental observations.33 The two profiles of ATP release (Eqs. 6 and 7) are illustrated schematically in Fig. 2.

Figure 2
figure 2

Normalized shear stress-induced ATP release rate as a function of wall shear stress for “sigmoidal” and “step” ATP release

Full size image

In the case of ADP, the net ADP mass flux at the bottom surface of the chamber is given by:

$$ D_{\text{ADP}} \left. {{\frac{{\partial c_{\text{ADP}} }}{\partial n}}} \right|_{w} = {\frac{{V_{{\max ,{\text{ADP}}}} \cdot c_{\text{ADP}} }}{{K_{{{\rm m},{\text{ADP}}}} + c_{\text{ADP}} }}} - {\frac{{V_{{\max ,{\text{ATP}}}} \cdot c_{\text{ATP}} }}{{K_{{{\rm m},{\text{ATP}}}} + c_{\text{ATP}} }}}, $$
(8)

where the ADP-subscripted variables are the ADP equivalents of those defined above for ATP. Baseline model parameter values for both ATP and ADP are the same as those used in previous work8,14 and are provided in Table 2.

Table 2 Parameter values for adenine nucleotides used in the simulations
Full size table

The finite volume commercial package FLUENT (version 6.3.26, Fluent Inc., Lebanon, NH) was used to solve the governing equations. The equations were discretized and solved using the SIMPLE algorithm. Surface fluxes were evaluated using a third-order MUSCL. For all simulations, the computational domain consisted of 1,200,000 allocated rectangular elements. All simulations were performed on a 3.4 GHz Pentium IV processor with 4 GB of memory.

Results

Effect of Cell Waviness on Shear Stress Distribution at the EC Surface

Figure 3 depicts contour plots of normalized wall shear stress on the EC surface (τw/τo) for different degrees of cell waviness (0 ≤ h/λ ≤ 0.15). The normalization shear stress τo is defined as the wall shear stress at the inlet of the flow chamber (x/λ = 0 where h/λ = 0). Although Fig. 3 is for τo = 1.0 Pa, the results are virtually identical over a wide range of τo (0.5 ≤ τo ≤ 8 Pa)—the absolute magnitude of τw naturally increases with increasing τo for all values of h/λ; however, the behavior of the normalized wall shear stress (τw/τo) is virtually independent of τo. In the absence of cell waviness (h/λ = 0; Fig. 3a), the wall shear stress is everywhere τo as expected. Consistent with previous studies,4 the shear stress on the EC surface in the presence of waviness (h/λ > 0; Figs. 3b–3d) is significantly larger than τo in the central portion of the cell and significantly smaller than τo toward the cell periphery. The magnitude of these subcellular variations in shear stress increases with increasing cell waviness.

Figure 3
figure 3

Contours of the normalized wall shear stress (τw/τo) on the EC surface for different degrees of cell waviness. (a) h/λ = 0; (b) h/λ = 0.05; (c) h/λ = 0.1; (d) h/λ = 0.15

Full size image

As apparent from Fig. 3, the magnitude of the peak shear stress on the EC surface increases with increasing cell waviness. Figure 4a demonstrates that this increase is linear for the range of waviness studied (0 ≤ h/λ ≤ 0.15). The peak wall shear stress for the most undulating surface (h/λ = 0.15) is 127% larger than that for a flat surface. The average shear stress on the cell surface, however, is only weakly dependent on waviness and in fact decreases slightly with increasing waviness (Fig. 4b); the average wall shear stress for h/λ = 0.15 is 7% smaller than that for a flat surface. Because the EC surface area obtained by surface integration of Eq. (1) along a single EC surface is virtually the same for all values of h/λ studied (a difference of less than 4% for 0 ≤ h/λ ≤ 0.15), the results of Fig. 4b indicate that the total shear force exerted on a single EC remains virtually constant or even decreases slightly with increasing EC waviness.

Figure 4
figure 4

Effect of EC waviness on the ratio of (a) peak wall shear stress on the wavy EC surface to that on a flat surface and (b) cell-average wall shear stress on the wavy EC surface to that on a flat surface. τo = 1.0 Pa

Full size image

Effect of Cell Waviness on ATP + ADP Concentration at the EC Surface

Nucleotide concentration at the EC surface is determined by a balance among the rates of convective/diffusive transport to and from the EC surface, flow-induced ATP release, and nucleotide hydrolysis at the EC surface by the three ectonucleotidases that catalyze the reaction sequence ATP → ADP → AMP → adenosine.23 As in previous studies,8,14,30 we focus in the present study on the ATP + ADP concentration since both ATP and ADP (but not AMP or adenosine) induce significant mobilization of intracellular calcium in endothelium.22,24

Figure 5 depicts contour plots of normalized ATP + ADP concentration (c ATP+ADP/c o) on the EC surface for τo = 1.0 Pa and for different degrees of cell waviness. We consider a group of cells positioned near the flow outlet (45 ≤ x/λ ≤ 50) and the three cases of no flow-induced ATP release, sigmoidal release, and step release (see Fig. 2). In the absence of ATP release (Fig. 5a), the concentration values are not significantly different for the different h/λ values and cell waviness leads to very small subcellular variations in ATP + ADP concentration. In the presence of flow-induced ATP release (Figs. 5b and 5c), on the other hand, the ATP + ADP concentration globally decreases as the EC surface becomes more wavy (i.e. h/λ increases), reflecting the effect of decreased average wall shear stress (cf. Fig. 4b) which leads to decreased ATP release plus increased fluid residence time and hence to increased nucleotide hydrolysis. Increased cell waviness is also accompanied by a significant increase in the amplitude of subcellular variations in concentration as a result of the larger subcellular variations in wall shear stress (cf. Fig. 3).

Figure 5
figure 5

Contours of the normalized ATP + ADP concentration (c ATP+ADP/c o) on the EC surface for τo = 1.0 Pa and for different degrees of cell waviness (0 ≤ h/λ ≤ 0.15). (a) No flow-induced ATP release; (b) sigmoidal release; (c) step release

Full size image

Although the subcellular variations in normalized ATP + ADP concentration, even at their largest level (h/λ = 0.15 and step release in Fig. 5), are significantly smaller than those of wall shear stress (compare to Fig. 3), the effect of cell waviness on nucleotide concentration at the EC surface is significant. Figure 6 depicts the ratio of average c ATP+ADP at the EC surface for a wavy cell to that of a flat cell (h/λ = 0) as a function of h/λ for τo = 1.0 Pa and for the cases of no flow-induced ATP release, sigmoidal release, and step release. Because nucleotide concentration depends on the axial position within the flow chamber due to the development of the concentration boundary layer, the results are shown separately for a cell whose center is positioned toward the inlet of the flow chamber (x/λ = 9.5; Fig. 6a) and one whose center is toward the outlet (x/λ = 39.5; Fig. 6b). In the absence of flow-induced ATP release, the cell-average ATP + ADP concentration on a wavy EC surface exhibits negligible deviation from that of a flat EC irrespective of where the EC of interest is located. In the presence of flow-induced ATP release, however, the cell-average ATP + ADP concentration decreases with increasing waviness. This decrease is more pronounced for step release than for sigmoidal release and has a larger magnitude further downstream as the concentration boundary layer eventually becomes fully developed.

Figure 6
figure 6

Effect of EC waviness on the ratio of cell-average ATP + ADP concentration for a wavy EC surface to that for a flat EC surface for the different ATP release profiles and τo = 1.0 Pa. (a) Cell positioned toward the flow inlet (centered at x/λ = 9.5). (b) Cell positioned towards the flow outlet (centered at x/λ = 39.5)

Full size image

The results thus far were for a nominal wall shear stress τo = 1.0 Pa, which corresponds to the step in the ATP step release model (cf. Fig. 2). It is important to establish if the impact of cell waviness on ATP + ADP concentration also occurs at other shear stress levels. Figure 7 depicts the ratio of cell-average ATP + ADP concentration for a wavy EC (h/λ = 0.15) to that for a flat cell (h/λ = 0) as a function of the applied nominal shear stress for the case of step ATP release and at the two axial positions defined previously in Fig. 6. The results demonstrate that at both positions, the effect of cell waviness is pronounced for τo in the range 1.0–2.0 Pa but is significantly smaller at lower or higher shear stresses. In light of the finding that flow-induced ATP release is required for cell waviness to have a significant effect on the ATP + ADP concentration at the EC surface (cf. Fig. 5), the behavior in Fig. 7 is attributable to the fact that at the low end of the shear stress spectrum, the wall shear stresses are too low to induce significant ATP release whereas at the high end of the shear stress spectrum, the release is “saturated” such that there is no significant difference in ATP release between the wavy and flat surfaces.

Figure 7
figure 7

Effect of the nominal wall shear stress τo on the ratio of cell-average ATP + ADP concentration for a wavy EC surface to that for a flat EC surface. Step ATP release is assumed and h/λ = 0.15. (a) Cell positioned toward the flow inlet (centered at x/λ = 9.5). (b) Cell positioned toward the flow outlet (centered at x/λ = 39.5)

Full size image

Effect of EC Waviness on ATP + ADP Concentration for ATP-Free Perfusion

There has been a long-standing controversy about whether or not the presence of ATP in the perfusion medium plays an important role in flow-induced intracellular calcium mobilization in ECs.12,13,17,31 John and Barakat14 demonstrated that if flow-induced ATP release is accounted for and if this release is sufficiently robust, then different shear stress levels may lead to significantly different nucleotide concentrations at the EC surface even in the absence of ATP in the perfusion medium. To investigate the effect of EC waviness on nucleotide concentration in the absence of ATP in the perfusion medium, we performed a limited number of simulations for both sigmoidal and step ATP release at τo = 1.0 Pa and with c o = 0. As illustrated in Fig. 8, the reduction in ATP + ADP concentration induced by cell waviness is amplified in the absence of ATP in the perfusion medium for both sigmoidal and step ATP release (compare with Fig. 6). Therefore, EC waviness appears to have a more pronounced effect on adenine nucleotide concentration at the EC surface when the perfusion medium contains no ATP.

Figure 8
figure 8

Effect of EC waviness on the ratio of cell-average ATP + ADP concentration for a wavy EC surface to that for a flat EC surface for ATP-free perfusion at τo = 1.0 Pa. Shown are the results for a cell toward the flow outlet (centered at x/λ = 39.5). (a) Step ATP release; (b) sigmoidal ATP release

Full size image

Discussion

The adenine nucleotides ATP and ADP are involved in regulating nitric oxide release and intracellular calcium mobilization in ECs7,24; therefore, establishing how flow modulates ATP/ADP concentration at the EC surface is important for understanding flow-mediated mechanotransduction. Previous studies had presented mathematical models for ATP/ADP concentration under steady and pulsatile flow within parallel plate flow chambers as well as geometries that elicit flow disturbance such as backward facing steps8,11,14,19,20,25,30 and aortic branchings.9 All previous reports, however, neglected the waviness of the EC surface. EC surface topography has previously been shown to have a profound effect on the subcellular wall shear stress distribution.4,28 To our knowledge, the present study is the first to investigate the effect of EC waviness on nucleotide concentration at the cell surface.

Similar to findings in other studies,4,28 our results demonstrate significant subcellular variations in wall shear stress with peak levels corresponding to the location of maximal cell height. Interestingly, however, we found that the cell-average shear stress is only weakly dependent on cell waviness and is in fact smaller for a very wavy surface than for a flat surface for the sinusoidal EC surface topography considered. The implications of these findings for flow-mediated mechanotransduction in ECs depend on how cells sense shear stress when stimulated by flow. If ECs respond to the peak shear stress level or to subcellular spatial gradients of wall shear stress, then cell waviness plays a critical role. If, on the other hand, ECs respond to the average shear stress or the total applied shear force, then cell waviness would be expected to contribute only minimally.

Our simulations have demonstrated that in the absence of flow-induced ATP release, the wavy nature of the EC surface has virtually no impact on the ATP + ADP concentration at the EC surface. Once flow-induced ATP release is accounted for, however, the undulating EC surface significantly affects the ATP + ADP concentration. More specifically, the average ATP + ADP surface concentration over a single EC decreases significantly as cell waviness increases, and this decrease is more pronounced for a more developed concentration boundary layer than within the entrance region. We had previously demonstrated that the ATP + ADP concentration at the EC surface within flow recirculation zones is significantly lower than that outside these zones.8 Because ECs are cuboidal within flow recirculation regions and elongated outside these regions18,21 and because elongated ECs are less wavy than cuboidal cells,3 the present findings suggest that cell waviness may amplify the effect of flow recirculation to result in even lower ATP + ADP concentration at the EC surface. In light of the involvement of adenine nucleotides in the release of nitric oxide and the mobilization of intracellular calcium in ECs and the importance of these responses for normal EC signaling, lower ATP + ADP concentrations within flow recirculation zones might lead to impaired signaling and hence may contribute to endothelial dysfunction within flow recirculation zones. The validity of this conjecture needs to be experimentally verified.

The effect of cell waviness on ATP + ADP concentration at the EC surface was determined to be most pronounced at a nominal wall shear stress τo = 1.0 Pa. This finding is not surprising as this level corresponds to the “critical” shear stress at which the step increase in flow-induced ATP release is assumed to occur and hence is the level around which ATP release is most sensitive to changes in shear stress. It is noteworthy, however, that the effect of waviness on nucleotide concentration is not confined to the critical nominal shear stress but also occurs at other shear stress levels, although the effect vanishes as the nominal shear stress levels become very small or excessively large. Naturally, selecting a different critical shear stress for the occurrence of the step increase in ATP release would lead to a shift in the results; however, the fundamental behavior will not be altered. These results underscore the need for carefully controlled experimental measurements of the detailed dependence of ATP release on the applied shear stress in ECs.

Whether or not flow-induced mobilization of intracellular calcium in ECs requires the presence of ATP in the perfusion medium has been a matter of long-standing controversy. Some studies12,17 have suggested that the calcium response only occurs in the presence of ATP in the perfusion media while others13,31 have observed the response even for ATP-fee perfusion. Consistent with our previous studies,8,14 the present simulations have shown that when flow-induced ATP release is accounted for, significant concentrations of ATP + ADP are attainable within flow chambers even in the absence of ATP in the perfusion medium. The present simulations have also demonstrated that the effects of EC waviness on ATP + ADP concentration on the EC surface that are observed for ATP-containing medium are amplified in the absence of ATP in the perfusion medium.

In the present study, we investigated the effect of different levels of cell waviness (0 ≤ h/λ ≤ 0.15) on the ATP/ADP concentration at the cell surface. The primary motivation for considering different levels of waviness is the fact that experiments on cultured BAECs have demonstrated a reduction in cell height in response to flow. It should be noted, however, that a detailed reading of the literature suggests that the effect of shear stress on EC waviness remains incompletely characterized. Barbee et al.3 reported a significant reduction in BAEC height following exposure to a shear stress of 1.2 Pa (12 dyne cm−2) for 24 h. Stamatas and McIntire32 reported that BAECs exposed to either venous (1.3 dyne cm−2) or arterial (13 dyne cm−2) levels of shear stress undergo a rapid height reduction of ~1 μm after 3 min of flow and suggested that this reduced-height configuration is maintained thereafter. Conversely, Sato et al.29 reported no significant height reduction in BAECs exposed to a shear stress of 20 dyne cm−2 for 24 h. Reasons for the differences among the various studies remain to be determined. Furthermore, how these in vitro observations compare to the situation in vivo remains to be determined.

In light of the data suggesting an effect of shear stress on endothelial cell waviness3,32 and our current findings that cell waviness modulates ATP/ADP concentration at the cell surface, it might appear reasonable for future simulations to investigate the coupling between flow-induced changes in waviness and ATP/ADP concentration at the cell surface. Such simulations would account for the fluid-structure interaction which determines the effect of shear stress on cell waviness and then dynamically couple the results to adenine nucleotide concentration at the cell surface. Our present simulations, however, suggest that such an approach is not necessary. The flow-modulated changes in nucleotide concentration reported here occur much more rapidly than flow-induced changes in cell waviness. More specifically, the nucleotide changes attain their steady-state values within ~10 s of flow onset, whereas changes in cell waviness require at least a few minutes32 or possibly longer. Given this discrepancy in time constants, it is reasonable to assume, as done in the present paper, that ATP/ADP changes for a given set of flow conditions occur in the presence of a constant degree of cell waviness (i.e. a constant h/λ value).

Many of the predictions of the present simulations await experimental verification. The rapidly evolving technology of microscale fluidic systems in combination with submicron-scale sensors promises to provide the necessary tools for making measurements of subcellular wall shear stress levels and adenine nucleotide concentrations. The resulting information will undoubtedly enhance our understanding of the fundamental mechanisms governing flow-mediated cellular mechanotransduction.