Digital Auscultation Analysis for Heart Murmur Detection

Abstract

This work presents a comparison of different approaches for the detection of murmurs from phonocardiographic signals. Taking into account the variability of the phonocardiographic signals induced by valve disorders, three families of features were analyzed: (a) time-varying & time–frequency features; (b) perceptual; and (c) fractal features. With the aim of improving the performance of the system, the accuracy of the system was tested using several combinations of the aforementioned families of parameters. In the second stage, the main components extracted from each family were combined together with the goal of improving the accuracy of the system. The contribution of each family of features extracted was evaluated by means of a simple k-nearest neighbors classifier, showing that fractal features provide the best accuracy (97.17%), followed by time-varying & time–frequency (95.28%), and perceptual features (88.7%). However, an accuracy around 94% can be reached just by using the two main features of the fractal family; therefore, considering the difficulties related to the automatic intrabeat segmentation needed for spectral and perceptual features, this scheme becomes an interesting alternative. The conclusion is that fractal type features were the most robust family of parameters (in the sense of accuracy vs. computational load) for the automatic detection of murmurs. This work was carried out using a database that contains 164 phonocardiographic recordings (81 normal and 83 records with murmurs). The database was segmented to extract 360 representative individual beats (180 per class).

Introduction

Cardiac mechanical activity is appraised by auscultation and processing of heart sound recordings (known as phonocardiographic signals—PCG), which is an inexpensive and noninvasive procedure. The importance of classic auscultation has decreased due to its inherent restrictions: the performance of human ear with its physical limitations, the subjectivity of the examiner, difficult skills that take years to acquire and refine, etc. Anyway, the PCG has preserved its importance in pediatric cardiology, cardiology, and internal diseases,34 evaluating congenital cardiac defects,33 and primary home health care, where an intelligent stethoscope with decision support abilities would be valuable.2,33

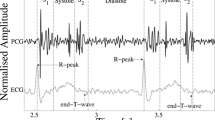
Mostly, heart sounds consist of two regularly repeated thuds, known as S1 and S2, each appearing one after the other, for every heart beat. The time interval between S1 and S2 is the systole, while the S2 and next S1 gap corresponds to the diastole. S1 implies the closing of the tricuspid and mitral valves immediately preceding the systole, while S2 corresponds to the closing of the aortic and pulmonary valves at the end of systole. The normal blood flow inside the heart is mainly laminar and therefore silent; but when the blood flow becomes turbulent it causes vibration of surrounding tissue and hence the blood flow is noisy and perceivable, originating the murmur, which according to the instant they appear are sorted into systolic (Fig. 1a) or diastolic (Fig. 1b). Murmurs are some of the basic signs of pathological changes to be identified, but they overlap with the cardiac beat and can not be easily separated by the human ear.

Figure 1

One period of PCG signals showing evidence of murmurs: (a) Systolic murmur and (b) Diastolic murmur

The automatic detection of murmurs strongly depends on the appropriate features (data representation), which mostly are related to timing, morphology, and spectral properties of heart sounds.35 Although cardiac murmurs are nonstationary signals and exhibit sudden frequency changes and transients,10 it is common to assume linearity of the feature sets extracted from heart sounds (time and spectral features, frequency representation with time resolution, and parametric modeling25,36). To capture nonstationary transients and fast changes of PCG, the time–frequency features are widely used in heart sound analysis.31 Different approaches have been proposed to deal with that nonstationary nature. In Jeharon et al.,16 an expert system was trained with spectrograms and energy features using clinic knowledge for an effective rule codification. Anyhow, the main restriction is how to choose the relevant features that adequately represent cardiac dynamics. In Javed et al.,15 the features extracted from individual systolic and diastolic intervals using the spectrogram were classified depending on their position within the cardiac cycle using the Wigner–Ville distribution (WVD) obtaining accuracy around 86.4%. In Debbal and Bereksi-Reguig,8 several spectral techniques were used to process the heart sounds, among them: Fourier transform, short-time Fourier transform, WVD, and continuous wavelet transform, the last one being the most successful, although the wavelet decomposition of PCG tends to produce a wrong time location of the spectral components.11 In Leung et al.,22 using time–frequency features, a sensitivity of 97.3% and a specificity of 94.4% was reported for systolic murmur detection using a neural network based classifier.

On the other hand, the human heart produces low-frequency sounds (20–1000 Hz), and therefore in former studies,2,17 the PCG has been characterized by means of perceptual analysis, using well-known techniques from speech processing such as Mel-Frequency Cepstral Coefficients (MFCC).37

To provide a robust representation of sounds in an automatic heart disease diagnosis system, a Mel-scaled wavelet transform was developed in Wang et al. 37 It combines the advantages of linear perceptual scale by Mel-mapping with the suitability of analyzing nonstationary signals by means of wavelet transform. In Johnson et al.,17 the MFCC representation is proposed in combination with Principal Component Analysis (PCA) to interpret the acoustic information, showing a fair performance (specificity 72.4%, and sensitivity 63.4%). In Telatar and Erogul,34 Waveform Similarity Overlap-Add and Multi-resolution Time Scale Modification algorithms were used for the diagnosis of cardiac disorders, yet results are not suitable due to high nonconsistent nature of murmurs.

The aforementioned features indirectly take into account the variability of the PCG induced by the murmurs, rather than to characterize the dynamic behavior of the acoustic recordings. Since heart sounds contain nonlinear and non-Gaussian information, the dynamic behavior is not revealed directly in the spectral components.9 In this sense, features inspired in higher-order statistics, chaos theory, and fractal complexity have been proposed to describe such behavior of the PCG signal,2 taking into account that many diseases are described by less complex dynamics than those observed under healthy conditions (e.g., in ECG signals), although in PCG signals the opposite takes place, because a more intense murmur originates from a more complex flow.14 The complexity is referred specifically to a multiscale, fractal type of variability in structure or function. For complex processes, fractal long-range correlations produce a kind of memory effect, so the value of some variables (e.g., heart beat at a particular instant) is related not just to the immediately preceding values, but to fluctuations in the remote past. In this sense, certain pathologies are marked by a breakdown of this long-range organization property, producing an uncorrelated randomness similar to white noise. Cardiac interbeat intervals in PCG signals normally fluctuate in a complex, apparently in an erratic manner, even in individuals at rest.12 This highly irregular behavior confronts with a conventional analysis that requires stationary datasets, and fractal analysis is a good candidate for studying this type of time series where fluctuations on multiple time scales take place.

In Wang et al.,38 a detailed analysis was carried out using spectral and energy features together (MFCC, Short-Time Fourier Transform (STFT), and instantaneous energy) for murmurs detection, using a Hidden Markov Models-based classifier, obtaining a sensitivity of 95.2% and specificity of 95.3%.

To find the feature subset that minimizes the classification error, a feature extraction stage should be used. In Ahlstrom et al.,2 a feature extraction procedure was proposed for systolic heart murmurs classification using 207 features, such as Shannon energy, wavelet transform, fractal dimensions, and recurrence quantification analysis. After dimensionality reduction using the Stepwise Floating Forward Selection (SFFS) method, a multidomain subset consisting of 14 features was calculated. Using a neural network-based classifier, the selected multidomain subset gave 86% of detection accuracy for mitral insufficiency, aortic stenosis, and physiological murmurs.

The main goals of the present paper are: (a) the extraction of time-varying, time–frequency, perceptual, and fractal-type features taking into account directly the variability of the PCG induced by the murmurs originated by valve pathologies; (b) the comparison and evaluation of the best feature set suitable for the classification of heart murmurs. To achieve these goals this paper proposes to characterize directly the dynamical behavior of the cardiac sound signal, specifically, fractal-type features for heart murmur detection. The main purpose is to generate a feature set that represents correctly the dynamics of the PCG signal, to detect pathologies, and then increasing the accuracy of the algorithms. Consequently, we used a simple k-nn classifier, since the aim is to emphasize the characterization and representation rather than the classification stage.

The paper is organized as follows: the section “Background” presents the background about time-varying and time–frequency analysis, the perceptual study, and the complexity based on fractal features. Section “Experimental Outline” refers to the experimental framework, describing the database and methodology used. In section “Experimental Results”, the results obtained are presented in comparison with different feature sets. Finally, in the last section the conclusions are exposed.

Background

Throughout this work, three families of parameters have been considered to parameterize the PCG beats: (a) time-varying & time–frequency; (b) perceptual; and (c) fractal features. A brief review of these families is given next.

Time-Varying and Time–Frequency Analysis (TV&TF)

Based on the expansion and inner product concepts, a direct way of describing a signal in time and frequency domains consists on its comparison to elementary functions that are compacted in the time frequency plane. In this scope, the STFT, grounded on classical Fourier Transform (FT), introduces a time localization by using a sliding window function φ(t) going along with the signal x(t). Since the location of the sliding window adds a time dimension, time-varying frequency analysis is accomplished as follows:

$$ X_\varphi (b,f) = \left\langle {x,\varphi } \right\rangle = \int\limits_{ - \infty }^{ + \infty } {x(t)\varphi _{a,b} (t,f)dt,} \quad \forall \varphi _{a,b} (t,f) \in \mathbb{R} $$

(1)

The windowing function must be symmetrical, $\varphi _a (t) = \varphi _a ( - t),$ and normalized, so that $||\varphi _{a,b} (t)|| = 1,$ and the time–frequency atom is defined in:

$$ \varphi _{a,b} (t,f) = e^{ - 2\pi jft} \varphi _a (t - b) $$

(2)

giving a relationship between the signal, x(t), and a sort of functions with the energy compacted in narrow strips of the time–frequency plane. The spectral density of x(t), on the time–frequency plane, can be calculated by means of the spectrogram:

$$ \left| {X_\varphi (t,f)} \right|^2 = \left| {\int\limits_{ - \infty }^{ + \infty } {x(t)\varphi _{a,b} (t,f)dt} } \right|^2 $$

(3)

In the STFT the window length remains constant. Therefore, the extraction of information with fast changes in time (i.e., high-frequency values), must be accomplished with short and well-timed localized intervals, but not in the whole interval of definition of the PCG signal. And vice versa, low-frequency components involve large time intervals of analysis.

The problem enumerated before can be partially solved by means of the WVD:

$$ X_G (t,f) = \int\limits_{ - \infty }^{ + \infty } {x(t - \tau /2)x^ * (t + \tau /2)e^{ - 2\pi jf\tau } d\tau } $$

(4)

where * implies complex conjugation. The WVD minimizes the inherent averaging over time and frequency of the STFT, but at the expense of the introduction of cross products.

An alternative to the WVD and STFT is the Gabor transform (GT¹), a signal decomposition method that uses frequency-modulated Gaussian functions. Because Gaussian functions are optimally concentrated in the joint time–frequency plane, the comparisons reflect a signal’s behavior in local time and frequency. GT has been found to be a good alternative for the STFT-based spectrogram and WVD. However, regardless of windowing functions, and given a value of window width, the spatial resolution remains constant and it is bounded by the time window aperture.

Another way to characterize the signal is the wavelet transform (WT). This transformation is grounded in the basis functions, constructed from shifted and scaled versions of a given mother function $\varphi (t) \in L^2 (\mathbb{R}),$ keep the energy concentrated on short intervals of time–frequency plane. The WT spectral density, equivalent to (1) is performed making time–frequency atoms (2) as follows (5):

$$ \varphi _{a,b} (t) = \frac{1} {{\sqrt a }}\varphi \left( {\frac{{t - b}} {a}} \right),\quad a \in {\mathbb{R}}^ + ,\;\;b \in {\mathbb{R}} $$

(5)

So, WT of a function x(t) is defined like:

$$ WT\{ x(t)\} = \int\limits_{ - \infty }^\infty {\frac{1} {{\sqrt a }}x(t)\varphi^{\ast}\left( {\frac{{t - b}} {a}} \right)dt} . $$

(6)

Since WT can be expressed by means of TF as:

$$ WT\{ x(t)\} = a^{1/2} \int\limits_{ - \infty }^\infty {X(s)\Upphi ^ * (as)e^{jbs} ds} $$

(7)

then, it can be deduced that the WT is a smoothed version of the Fourier spectrum. Bottom line, the spectral band wide of the WT can be changed, and hence, the time resolution is adjusted to information speed; this property being the most significant advantage of WT in time-varying spectral analysis.

From the spectrogram (3), and taking into account a unit value norm $||\varphi _{a,b} (t)|| = 1,$ the total energy contained in a signal can be considered as a feature, which is defined as its integrated square magnitude

$$ E = \int\limits_{ - \infty }^\infty {\left| {x(t)} \right|^2 dt} = \left\| x \right\|_2^2 $$

(8)

Besides total energy amount, another signal characteristic to be analyzed is the distinctive pattern of changes in (8) extended along the time: this is the instantaneous energy, E(t), required to distinguish the temporal behavior of the heart sound amplitude, which is time varying.16 Several techniques have been proposed to estimate energy contour for a band-limited discrete signal x[n], obtained from the continuous version x(t) by sampling, but Shannon approach is the most usual. For a given number of samples N it is calculated as2:

$$ \hat E_{\text{S}} [k] = - \frac{1} {N}\sum\limits_{n = 1}^N {x^2 [n]} \log \left( {x^2 [n]} \right) $$

(9)

However, Teager’s filter has shown several advantages for extracting the signal energy based on mechanical and physical considerations.32 This quadratic time–frequency operator is approximated by:

$$ \hat E_{\text{T}} [n] = x^2 [n] - x[n + 1]x[n - 1] $$

(10)

Perceptual Analysis

The human heart produces sounds with low-frequency components (20–1000 Hz), a large dynamic range, and changing content. On the other hand, psychophysical studies have shown that human perception of the frequency content of audio sounds does not follow a linear scale but also a Mel-warped frequency, which spaces linearly for low-frequency contents and logarithmically at high frequencies to capture important characteristics from audible sounds.24 This fact makes the conventional frequency-domain algorithms unable to reveal the spectral and temporal acoustic information of heart sounds. In this sense, the MFCC parameters, which are grounded on the perceptual analysis of sound, were used before to extract features from PCG signals providing a good performance in typical heart sound.38 Thus, to simplify the PCG spectrum without any significant loss of data, a set of triangular band-pass filters were used, which are nonuniform in the original spectrum and uniformly distributed at the Mel-warped spectrum. Each filter is multiplied by the spectrum so that only a single value of magnitude is returned per filter.

A Mel-scaled filter bank is used to calculate the Mel-warped spectrum, which is followed by a discrete cosine transform to extract the Mel-scaled features.37 So the MFCC coefficients are a family of parameters that are estimated as1:

$$ c[p] = \sum\limits_{m = 0}^{M - 1} {X_F [m]\cos (\pi p(m - 0.5)/M),} \quad 0 \le p < M $$

(11)

where $X_F [m] = \ln (\sum\nolimits_{i = 0}^{N - 1} {\left| {X[i]} \right|^2 H_m [i]} ),$ 0 < m ≤ M and X[n] is the FT of an input random sequence x[n]. A filter bank with M filters ($m = 1, \ldots ,M$), m being a triangular filter with central frequency f[m], is given by:

$$ H_m [i] = \left\{ {\begin{array}{*{20}c} {0,} &\quad {i < f[m - 1]} \\ {\frac{{2(i - f[m - 1])}} {{(f[m + 1] - f[m - 1])(f[m] - f[m - 1])}},} &\quad {f[m - 1] \le i \le f[m]} \\ {\left( {\frac{{2(f[m + 1] - i)}} {{(f[m + 1] - f[m])}}} \right),} & \quad{f[m] \le i \le f[m + 1]} \\ {0,} &\quad {i > f[m + 1]} \\ \end{array} } \right. $$

(12)

To complement the feature vector formed by the MFCC parameters, in Beyar et al.,4 another method is suggested to characterize the perceived perturbations of the PCG signal by measuring the variations of the fundamental frequency along the time. The variability of the fundamental frequency is defined as the jitter, which can be used experimentally to clarify some of the cardiac electromechanical mechanisms. Jitter designates small and random, perturbations of the cycle lengths, i.e., the amount of variation in the fundamental frequency among segments of the signal. These segments are extracted windowing the signal uniformly. The jitter is estimated as follows1,13:

$$ Jitter = \frac{{L\sum\nolimits_{i = 2}^{N - 1} {{{(f_0 [i - 1] + f_0 [i] + f_0 [i + 1])} \mathord{\left/ {\vphantom {{(f_0 [i - 1] + f_0 [i] + f_0 [i + 1])} 3}} \right. \kern-\nulldelimiterspace} 3}} }} {{(L - 1)\sum\nolimits_{i = 1}^N {f_0 [i]} }} $$

(13)

where L is the total number windows in each segment of the beat and f ₀[i] is the fundamental frequency in the ith window. The estimation of f ₀[i] is performed by means of the FT in the segment under analysis, and then, the first moment of the spectral decomposition is computed.5

Fractal Analysis

In this work, the correlation dimension, the Largest Lyapunov Exponent, and the Hurst exponent have been considered as in Ahlstrom et al. 2 A brief description of these features is given next.

Correlation Dimension (D ₂)

Nonlinear dynamics can be quantified by reconstruction of an attractor containing the intrinsic variability of system. With this purpose the factor D ₂ is defined as a measure of the dimensionality of the space occupied by a set of random points, and gives a quantity of the nature of attractor trajectory. Commonly, attractor value of D ₂ is unknown. Then, for any time series $\{ x[n]:n = 1, \ldots ,N\} ,$ starting at continuous instant t ₀ and consisting of N points in an d-dimensional space, the following vector space is determined:

$$ {\vec{\mathbf s}}[n] = \{ x[n],x[n + \tau ],x[n + 2\tau ], \ldots ,x[n + \tau (d - 1)]\} $$

(14)

where x[n] = x(t ₀ + nT _S) and T _S is the sampling period. In the phase space, an attractor can be reconstructed from sequence (14), with an embedding dimension d and delay τ, according to Takens’ theorem.19 Different approaches have been proposed to estimate the embedding dimension d (in this study Cao’s method was implemented6). Specifically and related to PCG signals, D ₂ value of the attractor is calculated as follows19:

$$ D_2 = \mathop {\lim }\limits_{r \to 0} \frac{{\log \,C(r)}} {{\log (r)}} $$

(15)

where C(r) is the correlation integral:

$$ C(r) = \frac{2} {{N(N - 1)}}\sum\limits_{i = 1}^N {\left[ {\sum\limits_{j = 1}^N {\Theta \left( {r - \left| {{\vec{\mathbf s}}_i [n] - {\vec{\mathbf s}}_j [n]} \right|} \right)} } \right]} $$

(16)

where ${\vec{\mathbf s}}_i [n]$ and ${\vec{\mathbf s}}_j [n]$ are the points of the trajectory in the phase space, and r is the radial distance to each reference point ${\vec{\mathbf s}}_i [n].$ Notation Θ stands for Heaviside function.

Largest Lyapunov Exponent—LLE (λ ₁)

For a dynamical system, sensitivity to initial conditions is quantified by the Lyapunov exponents. For example, consider two trajectories with nearby initial conditions on an attracting manifold. When the attractor is chaotic, the trajectories diverge, on average, at an exponential rate characterized by the LLE.28 Small deviations of both trajectories, ${\vec{\mathbf s}}_x [n]$ and ${\vec{\mathbf s}}_y [n],$ can be given by:

$$ u[n + 1] = {\mathbf{J}}\{ {\vec{\mathbf s}}_x [n]\} {\text{ }}u[n] $$

(17)

where ${\mathbf{J}}\{ {\vec{\mathbf s}}_x [n]\}$ is the Jacobian matrix, evaluated for a reference point of ${\vec{\mathbf s}}_x [n].$ If n ₀ is the initial sample and u[n ₀ + Δn] is the distance between the ${\vec{\mathbf s}}_x [n]$ and ${\vec{\mathbf s}}_y [n]$ trajectories after Δn sampling periods, then:

$$ \begin{aligned}{} u[n_0 + \Updelta n] & = {\mathbf{J}}\{ n_0 + \Updelta n\} u[n_0 ], \\ {\mathbf{J}}\{ n_0 + \Updelta n\} & = {\mathbf{J}}\{ {\vec{\mathbf s}}_x [n_0 + \Updelta n - 1]\} {\mathbf{J}}\{ {\vec{\mathbf s}}_x [n_0 + \Updelta n - 2]\} \cdots {\mathbf{J}}\{ {\vec{\mathbf s}}_x [n_0 ]\} \\ \end{aligned} $$

(18)

Thus, the matrix J{n ₀ + Δn} is compounded by the product of the Jacobian matrices, evaluated in the states constituting the ${\vec{\mathbf s}}_x [n]$ trajectory. To measure the exponential separation of the trajectories, it is assumed that in the future distant ($\Updelta n \gg 0$), the norm of the u[Δn] vector behaves like19:

$$ \left| {u[n_0 + \Updelta n]} \right| = \left| {u[n_0 ]} \right|e^{(\lambda \Updelta n)} ;\quad \forall \lambda \in {\mathbb{R}},\;\;u[n_0 ] \ll 1,\;\;\Updelta n \gg 1 $$

(19)

Hurst Exponent (H)

This parameter determines whether any time series can be represented as Brownian motion. If H exists, its value ranges from 0 to 1, showing a nonlinear behavior of the time series.7 Particularly, H = 0 means Brownian motion, 0 < H < 0.5 means that high-frequency terms are contained in the time series, so the previous tendencies tend to be reversed in the future. Lastly, 0.5 < H < 1 means a soft dynamic of the time series (previous tendencies persist in the future). The calculation of the Hurst exponent of ${\vec{\mathbf s}}[n]$ is obtained by the following empirical regression as the slope of the ratio,

$$ R/\sigma = (\tau /2)^H $$

(20)

where R is the span variation (difference between maximum value and minimum value in the ${\vec{\mathbf s}}[n]$ series), σ is the standard deviation, and τ is the delay used in the reconstruction of the attractor.

Experimental Outline

Database

The database used in this study is made up of 148 de-identified adult subjects, who gave their informed consent, and underwent a medical examination with the approval of the ethical committee. An electronic stethoscope (WelchAllyn ^® Meditron model) was used to acquire the heart sounds simultaneously with a standard 3-lead ECG (the DII derivation was used as a time reference because the QRS complex is clearly defined). Both signals were digitized at 44.1 kHz with 16 bits per sample. Tailored software was developed for recording, monitoring, and editing the heart sounds and ECG signals. Besides, eight recordings corresponding to the four traditional focuses of auscultation (mitral, tricuspid, aortic, and pulmonary areas) were taken for each patient in the phase of postexpiratory and postinspiratory apnea. Each recording lasts approximately 8 s and was obtained with the patient standing in dorsal decubitus position. The recording time could not be extended more because patients suffering cardiac problems are not capable of maintaining both postinspiratory and postexpiratory apnea for a longer period. A diagnosis was carried out for the eight recordings of each patient and the severity of the valve lesion was evaluated by cardiologists according to clinical routine. A set of 50 patients were labeled as normal, while 98 were labeled as exhibiting cardiac murmurs, caused by valve disorders (aortic stenosis, mitral regurgitation, etc). Furthermore, for training and validation of the algorithms, PCG signals labeled as normal and those labeled as murmur were separated, keeping in mind that not necessarily all of the eight recordings of each patient with murmurs were labeled as murmur, because it does not generally appear in all focuses at once. This is why it is necessary to perform the diagnosis in each beat rather than in the whole set of PCG signals acquired from each patient. Then, 360 individual beats were extracted, 180 for each class. The individual beats were picked out as the best from each cardiac sound signal, after a visual and audible inspection by a cardiologists; this was done to select beats without artifacts and other types of noise that can impair the performance of the algorithms. It is important to remark that all focuses and phases (postinspiratory and postexpiratory) were treated equally during the tests done in this study.

Preprocessing and Segmentation

Due to the presence of perturbations or artifacts, a noise reduction of the PCG is carried out by means of denoising procedures, using threshold selection rules.23 Specifically, denoising is implemented using different mother functions of the WT, including Haar, Daubechies, Symlets, and Coiflets, for different levels of decomposition (ranging from 1 to 10), and using each one of the threshold selection rules given in Messer et al.23 for rescaling. Afterwards, a group of three experienced cardiologists judged perceptually the quality of the noise reduction algorithm and preprocessing filtering by comparing with original recordings. The tests carried out as described previously concluded that the best mother wavelet for denoising procedure is Coiflet 4 up to 8th level of decomposition and soft threshold. The time–frequency response of the denoising procedure applied to a signal with murmur is shown in Fig. 2. Moreover, the signals were resampled to 3 kHz before feature estimation.

Figure 2

Time–frequency response of a pathologic unfiltered and filtered PCG signal

Beat Segmentation

The automatic beat segmentation of PCG recordings demands a considerable effort due to the dependency between the beat structure and the recording focus. As it was quoted above, a murmur can show up into any of the PCG signals taken from auscultation areas. Usually, S1 is more intense than S2 in the mitral and tricuspid focuses, while S2 is more intense than S1 in the aortic and pulmonary areas. Nevertheless, this is not a rule because the opposite can also occur. As a result, this morphological beat variability leads to a serious restriction for automated division into segments of the PCG signal. Therefore, the segmentation algorithm developed is based on the DII lead of the ECG recording, which was used to locate the occurrence of the S1 sounds since the beginning of the first cardiac sound co-occurs with the origin of the respective QRS complex. The detection of R peak in the ECG signal is carried out according to the procedure presented in Sahambi et al.,30 which is based on the WT since the maximum modules and the zero crossing values of this transform correspond to abrupt changes of the signal.

Intrabeat Segmentation

After beat segmentation, the following stage is the division into the four events present in the PCG signal: S1, systole, S2, and diastole. Due to the interbeat variability of the S1 and S2 duration, the reference markers in the ECG trace are insufficient to perform effective intrabeat segmentation, although they can be used to initialize any searching procedure. Thus, the proposed algorithm for intrabeat segmentation is derived from the estimation of the energy envelope (envelogram27) of the PCG recording. Through empirical observation (Fig. 3a), it was found that the smoothed and low-energy silent events (systole and diastole) have a different energy threshold compared to the heart sounds (S1 and S2). So the initial and ending instants of S1 segment are assumed to be the first and second values over a fixed energy threshold (the threshold is chosen at 0.1 level of the maximum normalized value). Similarly, the third and fourth crossing values stand for initial and ending instants of S2 segment. Nevertheless, because of the presence of a murmur, pathological PCG recordings not necessarily follow the previous rule, so additional restrictions about the length of the event intervals are imposed. Specifically, the length values must be determined within empirical limits, calculated from all PCG recordings. The average relative time can be determined, for each segment of a beat, by the following expressions:

$$ T_{{\text{S1}}} = \frac{{T_1 }} {T};\quad T_{{\text{S2}}} = \frac{{T_2 }} {T};\quad T_{\text{S}} = \frac{{T_3 }} {T};\quad T_{\text{D}} = \frac{{T_4 }} {T} $$

(21)

where T is the duration of a whole beat, T ₁ is the duration of S1, T ₂ is the duration of S2, T ₃ is the duration of the systole, and T ₄ is the duration of the diastole. These temporary relationships are taken into account at the end of the segmentation algorithm, so that if the results obtained in the segmentation of a new beat are outside of these ranges, the points of segmentation are located based on the relationships obtained for T _S1, T _S2, T _S, and T _D. Figure 3b shows the estimate of each event length for all the recordings stored in the database.

Figure 3

(a) PCG envelogram and (b) Boxplots of the interval lengths

Feature Extraction

After the preprocessing and segmentation of the PCG signal, several features were extracted for the intrabeat events and some others for each complete beat: five of the TV&TF features were extracted during systole and diastole, whereas the rest of the features belonging to this family were extracted for the whole beat; the fractal features were extracted for each complete beat; and the perceptual features were extracted for every intrabeat segment. A final feature vector is built up for each beat concatenating all the features extracted. Table 1 summarizes the entire feature set estimated on each beat of the PCG signal.

Table 1 Description of the feature set extracted for each beat segmented from the PCG signal

The details of the feature extraction are given next.

TV&TF Features

The time–frequency spectral analysis is carried out using four different approaches (Fig. 4): STFT, GT, WVD, and WT transforms. For the first two transforms, the window length has been chosen as 64-points in the time domain, and 100-points in frequency domain. For the WT, it was found that the murmurs become more evident adding 1 and 2 decomposition levels (Fig. 5).

Figure 4

(a) Mean spectrograms using STFT and (b) Mean spectrograms using Gabor transform

Figure 5

Sum of the level 1 and 2 details of the normal and pathologic PCG signal after a level 5 WT decomposition

As a result, each spectrogram is a two-dimensional array that can be considered as an image matrix, A, and therefore, PCA can be used to carry out a conventional eigenspace representation.2 This type of representation encodes efficiently the contiguous time–frequency relations that characterize the dynamics depicted by spectrograms. That is, PCA thrives on the inherent correlations among the matrix entries that represent the variations in the event of interest at specific time–frequency locations. After carrying out eigenspace representation analysis, a total of 20 main components of the matrix A were used to characterize the spectrograms.

On the other hand, the presence of a murmur can be clearly evidenced estimating the instantaneous energy of heart sounds within systole and diastole intervals, but constraining the spectral analysis up to 500 Hz of bandwidth. In this work, a method for fast and simple estimation of instantaneous energy using the Teager energy quadratic operator (10) is proposed. The energy estimation, using Teager algorithm,18 is accomplished by a multiresolution representation of the heart sound,21 using the WT with a Daubechies mother function. This approach facilitates the discrimination between S1, S2, and more complex murmurs.

Finally, the subset of the feature vector that characterizes each beat using the time–frequency spectral features and energy features consists of the following features:

• The overall area of the energy under each beat event, as proposed in Sharif et al.32 Since the energy in systole and diastole is often far less than the energy evaluated over a PCG beat, consequently is better to evaluate the energy values separating systole and diastole. In fact, at present work, it is suggested to evaluate the maximum value between the energy in the systole (Ê _S) and diastole (Ê _D) intervals, i.e., $\max \{ \sum\nolimits_n {\hat E_{\text{S}} [n]} ,\sum\nolimits_n {\hat E_{\text{D}} [n]} \} ,$ where n is the time index.

• Based on the STFT, WT, and GT,20 the overall spectral volume confined under the surface of each transform in the systole and diastole intervals and the maximum value between these two values are computed: $\max \{ \sum\nolimits_{n_\omega } {\sum\nolimits_n {TFD_{\text{S}} [n_\omega ,n]} } ,\sum\nolimits_{n_\omega } {\sum\nolimits_n {TFD_{\text{D}} [n_\omega ,n]} } \} ,$ where TFD _S and TFD _D are the time–frequency representations of systole and diastole, respectively, and n and n _ω are the time and frequency indexes, respectively. Because the relevance of the features can be related to the scattering of its values, the estimation of the GT is proposed adapting the time aperture depending on the statistical variance of the input random signal, and consequently the interval of estimation outcomes inversely proportional to the standard deviation of signal.

• The eigenspace representation analysis is achieved for STFT, GT, WVD, and WT. A total of 20 main components were used as features for each representation.2

Perceptual Features

The estimation of the perceptual features requires the intrabeat segments to be divided into frames of 5 ms, with an overlapping of 30%. The window length was selected under the assumption that the lowest frequency component considered is 20 Hz. The upper frequency considered is 1500 Hz, since some of the murmurs are characterized by high-frequency components. For the estimation of the MFCC parameters, each PCG beat is filtered using 14 triangular filters (M = 14). In view of the fact that the heart murmurs have spectral components very concentrated in the band around 600 Hz (698 Mels), the information from the filter centered in this frequency is the most relevant in this study.37 The final subset of the MFCC that characterizes each intrabeat segment using the perceptual features is calculated averaging in time the parameters extracted for each window.

The averaged MFCCs coefficients were complemented with the jitter estimated for each intrabeat segment. The computation of the jitter is based on a former estimation of the fundamental frequency. The fundamental frequency is calculated for each intrabeat segment (S1, systole, S2, and diastole). As a result, a sequence of fundamental frequency values for each event segment is obtained. From this sequence the jitter is calculated.

Besides, to complement the discriminative capabilities of the MFCC, representation for the systole and diastole segments (where the presence of a murmur is supposed to show the strongest evidence) is suggested to evaluate the absolute difference of their respective estimated coefficients.

Therefore, the subset of the feature vector that characterizes each beat using the perceptual features consists of the following features:

• 14 MFCC mean values for each intrabeat segment.

• Relative 4th MFCC: This feature is determined as the maximum value between the 4th MFCC coefficient in the systolic and diastolic segment. The reason to use the 4th coefficient lays on the fact that according to the Sequential Forward Floating Selection Algorithm (SFFS) method with a cost function based on k-nearest neighbors (k-nn),3 the most relevant information of the MFCCs stands on the 4th coefficient. Furthermore, the motivation to compute the relative MFCC is that murmurs can appear in systole and/or diastole, and then is a good way to identify it independently from its location in the PCG signal.

• Jitter: Fundamental frequency variations across windows containing at least one period of the minor spectral component with significant energy from PCG beat.

Fractal Features

The fractal features are based on nonlinear dynamics and have the ability to quantify the nonlinear behavior of the PCG signal. The use of fractal features is motivated since the dynamics of the system (including the nonstationary behavior) are embedded intrinsically into the attractor, and the measure of complexity in the reconstructed trajectory is able to characterize the dynamics.

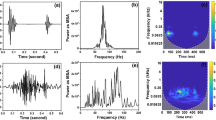
On dependence on the range of value D ₂ distinct heart diseases can be identified.7 The calculation of D ₂ is achieved following the method proposed in Rosenstein et al.,28 requiring a previous estimation of the correlation sum, C(r) (16). The function ln{C(r)} vs. ln(r) is evaluated for every PCG beat, estimating its scaling region by the derivation, d{ln[C(r)]}/d{ln(r)}, as well as the respective evolution of D ₂ vs. d, d being the embedding dimension. The scaling region is determined taking into account that in any linear region of the function ln{C(r)}, either slope or derivative dependences tend to be similar. In this case, the estimation of the derivative function is done by calculating the slopes of neighboring points and finding τ = 1 as a proper delay value.

The input arguments of the algorithm used to calculate the scaling region are the values of ln{C(r)} and ln(r), and the output arguments are two values corresponding to the maximum and minimum indexes of the scaling region contained in the vector of values of the axis ln(r). The first step is the estimation of the function d{ln[C(r)]}/d{ln(r)}, through computing the slopes in neighbor points. Next, the similarity of the magnitudes obtained after the differentiation of ln{C(r)} is analyzed, using the standard deviation of each analyzed segment, because the segment with the least deviation is the most similar in magnitude. Finally, the indexes that produce the least dispersion segment in the vectors ln{C(r)} and ln(r) are selected.

Figures 6 and 7 show the same procedure applied to one cardiac cycle. The value of τ obtained with the auto mutual information function is equal to 15; this value does not define a clear scaling region (Fig. 6). On the other hand, if the estimation is performed using τ = 1, a plateau appears in the function d{ln[C(r)]}/d{ln(r)} vs. ln(r) (Fig. 7).

Figure 6

Computing of D ₂ for a normal subject and τ = 15: (a) Correlation sum; (b) Scaling region; and (c) Correlation dimension

Figure 7

Computing of D ₂ for a normal subject and τ = 1: (a) Correlation sum; (b) Scaling region; and (c) Correlation dimension

The LLE (λ ₁) can be estimated as the average rate of the separation from the nearest neighbors28 by the expression:

$$ \lambda _1 (\Updelta n) = \frac{1} {{\Updelta n\Updelta T}}\frac{1} {{(N - \Updelta n)}}\sum\limits_{i = 1}^{N - \Updelta n} {\ln \frac{{u_i (\Updelta n)}} {{u_i (n_0 )}}} $$

(22)

where ΔT is the sampling period of the time series, u _i (Δn) is the distance between the ith pair from nearest neighbors after Δn discreet steps in time, and N is the number of reconstructed points in accordance to (14). To improve the convergence (with regards to Δn), an alternate form of is given in (23):

$$ \lambda _1 (\Updelta n,K) = \frac{1} {{K\Updelta T}}\frac{1} {{(N - K)}}\sum\limits_{i = 1}^{N - K} {\ln \frac{{u_i (\Updelta n + K)}} {{u_i (n_0 + \Updelta n)}}} $$

(23)

where K is a constant, and λ ₁ is extracted localizing the plateau of λ ₁(Δn, K) with respect to Δn. In addition, it is important to remark that the plateau of λ ₁ is determined automatically according to the algorithm proposed in Rosenstein et al. 28

The value of H is defined as the slope that is obtained when calculating the average of the R(N)/σ(N) relationship given by (20), for different scales in the data length of the analyzed time series. The algorithm for estimating the Hurst exponent, designed in this work, does not overlap data regions, basically because overlapping regions does not give exact results.26 The size chosen for the analysis regions was in powers of two, beginning with 2⁸ and ending in a smaller or equal size to the total size of the series being analyzed, that is to say: 2⁸, 2¹⁶, 2³², 2⁶⁴, etc. It is important to highlight that all these determinations were chosen with the purpose of calibrating the algorithm, to improve precision of the results.

The subset of the feature vector that characterizes the chaos-based features is calculated for each individual beat in the PCG signal, so each beat is described by a three-dimensional vector that contains:

• Correlation Dimension (D ₂)

• Largest Lyapunov Exponent (λ ₁)

• Hurst Exponent (H)

Classification and Validation

As explained before, the feature set matrix X, was composed by the time–frequency spectral, perceptual, and fractal characteristics of each beat segment. The dimension of the matrix X was q × s, q being the overall number of beats (q = 360), and s the number of features extracted (s = 149).

The outliers in the feature space were removed because they are considered with a random behavior leading to masking effects. The rule used for detecting the univariate outliers is:

$$ \frac{{\left| {x_i - {\bar{\mathbf x}}} \right|}} {{\left| {x_i - med({\mathbf{x}})} \right|}} > 4.5,\quad x_i \in {\mathbf{x}} $$

(24)

med(x) being the median value of an input random vector x with mean value ${\bar{\mathbf x}}.$

Once the feature matrix was estimated, each column of the matrix X is centralized and normalized (i.e., zero mean and ||·||₂ = 1). For time varying, time–frequency and perceptual features, following this translation and scaling procedure, they are shifted in such a way that none of these values is below 0. In this way, we compute the logarithm of each entry before proceeding with the classification stage, with the aim of minimizing the intraclass variability and increasing the separability of the classes. The aforementioned procedure is performed because these features are based on the signal’s energy, and the logarithm operator enhances its interpretation.

The automatic identification is carried out in a two class-problem: K1 (normal), and K2 (murmur). For this purpose, a k-nn classifier3 with k = 9 was used.

The contribution of the extracted features for the automatic auscultation has been evaluated by means of the detection accuracy. It was calculated experimenting with different combinations of the proposed families of parameters, namely, TV&TF, perceptual, and fractal features. The comparison of the different feature vectors was accomplished in the following ways:

• Feature vectors belonging to one family of parameters

• Feature sets composed by those characteristics that revealed to be the most discriminating from each family. With the aim of finding a feature subset that minimizes the classification error, a heuristic search was carried out. More specifically, a Sequential Forward Floating Selection Algorithm (SFFS) with a cost function based on k-nn3 was used to select the most significant features.

Validation of classification procedures is achieved according to the methodology suggested in Saenz-Lechon et al.,29 using a cross-validation strategy based on several partitions (10 folds) of the whole training dataset. The 70% of the samples in each fold were used for training whereas the remaining 30% were used for testing the algorithms. Since the decision is taken for each beat segment, and the database has been segmented in a beat basis, depending on the strategy followed for segmentation, the training and testing subsets can have feature vectors belonging to the same patients. To compare the robustness of the proposed methods to the intrasubject and intersubject beat variability, the validation was carried out following two different approaches: (a) the training and validation test sets were chosen without taking into account the relationship patient-recording, so the training and testing subsets are different but contain beats of all the patients stored in the database and (b) the validation was performed using recordings of different patients to those used for the training stage.

Experimental Results

The best filtering algorithm was selected using the cardiologist’s expertise after an exhaustive hearing session of PCG-filtered registers. The filtering with the Coiflet WT at level 8 of decomposition according to the method described showed the best performance. Nevertheless, in case of fractal-based feature extraction, it was found experimentally a degradation of the classification performance (it diminishes up to 59.2%) after either denoising or preprocessing filtering, confirming the results presented in Kantz and Schreiber.19

As mentioned above, the beat segmentation was interlocked with the detection of the R peak from DII of the ECG records. In case of the intrabeat segmentation, the performance of the proposed threshold energy algorithm was evaluated by means of a confusion matrix, obtaining the results presented in Table 2 for both, false negatives and false positives. The overall positive prediction was 92%, whereas the sensitivity was 100%.

Table 2 Intrabeat segmentation results

The accuracy has been evaluated for different feature sets by means of the Receiver Operating Characteristic (ROC),3 which plots the sensitivity vs. specificity for different decision thresholds (Fig. 8). Moreover, the area under the ROC curve (AUC) and its standard error (SE) were computed.

Figure 8

ROC curves for TV&TF, fractal, and perceptual analysis using the method of validation (a): (a) With filtering and (b) Without filtering

Table 3 shows a comparison of the accuracy obtained with different feature sets, with and without filtering and using the method of validation (a). It must be noticed that the filtering procedure lightly improved the accuracy for spectral and perceptual features, which is observed in the ROC curves (Fig. 8). Specifically, the number of false negatives decreased for filtered signal, meaning that false murmur detection is reduced. But in case of fractal features, filtering collapses down the accuracy up to 59.2% (Fig. 8b). Although the accuracy, obtained with the spectral feature set (95.28%), is comparable to the highest found in the literature,22 an objective comparison is not possible since the databases used are different. By further comparison, a 95% average score of Wang et al. 38 for murmur detection can be confronted. In general, the perceptual features did not give good classification performance. Though fractal features have the worst performance in case of filtered signals, if the preprocessing is omitted, this set becomes the best for classification, with an accuracy of 97.17%.

Table 3 Accuracy of the detector for different feature sets without feature extraction using the method of validation (a)

The AUC is also a measure of the classification accuracy, even though, in this case it is not so precise, because we have a k-nn classifier that gives discrete scores for each sample, and then, using 9 neighbors, the ROC curve is not smooth enough, since it has only 9 steps according to the scores that form it, independently from the number of samples used in its calculation. As can be seen in Table 3, the AUC value is greater than the accuracy value, but the proportions persist. The SE corresponds to the error of the AUC with a confidence interval of 5%, using a cross-validation process with 10 folds. The fractal features without filtering were also the ones that gave the least SE, which indicates its robustness for the samples used in the test.

The results using the second method of validation, (b), are shown in Table 4 and Fig. 9.

Table 4 Accuracy of the detector for different feature sets without feature extraction using the method of validation (b)

Figure 9

ROC curves for TV&TF, fractal, and perceptual analysis using the method of validation (b)

After a feature selection procedure, the best feature set is made up of the six most relevant features: the maximum of total spectral volume confined under the STFT surface between systole and diastole (Sp 1), the maximum of the overall area of energy under beat event strip of time between systole and diastole (Sp 2), the first principal component for GT spectrogram (Sp 3), the relative MFCC (Ac 1), the correlation dimension (Fr 1), and the LLE (Fr 2). The reduced feature set yielded better accuracy (96.39%) than the complete feature set (96.11%); this fact shows that the feature space reduction is necessary to minimize the computational cost and the data amount indispensable to carry out the diagnosis; besides, it lightly improves the accuracy of the classifier. The ROC curves, corresponding to the tests with the complete and reduced feature set, are shown in Fig. 10, and the AUC with their SE are shown in Table 5.

Figure 10

ROC curve for the reduced feature space

Table 5 Accuracy of the detector for different feature sets using the feature extraction algorithm

Table 5 also shows the classification results with different feature sets, obtained by means of the method explained in section “Classification and Validation” used to find relevant features. It can be observed that fractal features have a high discriminative capability, because using only two of this features the classification accuracy was 93.8%; on the other hand, using two spectral features we reached only an accuracy of 86.48%, and grew just to 87.5% when the three most relevant spectral features were used.

On the other hand, the influence of the different approaches for interval estimation of relevant characteristics is examined by calculating their discriminative capability. First, feature estimate within one beat interval is considered (Fig. 11a). Second, the estimate within three-beat-interval is also evaluated (Fig. 11b). Figure 11 shows the mean of each one of the aforementioned features (relevant fractal and spectral), with their corresponding standard deviation; a better discriminative capability is reflected in a larger distance between classes mean and a smaller deviation in each class. A detailed examination showed that the extended interval increases the discriminative capability for the spectral features. However, the three-beat-interval remarkably decreases the quality of estimation with fractal features because of the perturbations and artifacts that could appear when it is taken more than one beat for the analysis. In other words, the computation of fractal features is sensitive to beat-to-beat variations, reducing the quality of the estimation.

Figure 11

Discriminative capability on dependence of interval feature estimation: (a) One beat interval and (b) Three beats interval

Conclusions

To take into account the variability of the PCG induced by the murmurs, it is better to characterize directly the dynamic behavior of the heart sound recordings. According with the experimental results, the fractal features hold the inner structural dynamic of heart sounds. This fact can be explained by the presence of long-range (fractal) correlations, along with distinct classes of nonlinear interactions. As a result, the fractal features applied to the detection of murmurs emerged as the most robust characteristics in the sense of accuracy vs. computational load.

The characterization of the inherent variability of a process must reflect separately each of the possible sources of dynamic behavior (avoiding overlapping). Hence, the variability of the chaos features is linked with the analysis of a complete heartbeat, which defines the periodicity of the cardiac cycle. Concerning the perceptual and spectral features, their estimation may be focused on each biological event, so the four segments per heartbeat ought to be analyzed: S1 sound, systole, S2 sound, and diastole. The resulting performance improves significantly through adjusting the segmentation stage, which is necessary for the successful estimation of perceptual and spectral features. This task becomes more difficult for pathological records. It is important to note that the results obtained using perceptual and spectral features depend strongly of intrabeat segmentation, in fact, if components segmentation is not being well performed, then, the corresponding features barely can be considered as relevant. In this way, employing another reliable technique for intrabeat segmentation, the performance of these features could be improved. Nevertheless, the main problem is the adjustment and tuning of this algorithm, which in the case of fractal features is not necessary at all.

Regarding the feature selection, it is shown that for a reduced feature set (80% of reduction), the performance kept similar to the best one reported in the literature. Nevertheless, almost the same accuracy can be reached by using just two fractal features. Taking into consideration the difficulties above mentioned regarding the beat segmentation to compute the spectral and perceptual features, this extra effort does not seem to be worthy for working out neither with spectral nor with perceptual features.