Explaining Clustered Ventilation Defects Via a Minimal Number of Airway Closure Locations

Abstract

Computational models of the human lung have been developed to study lung physiology and have been used to identify the airways responsible for mechanical dysfunction in asthmatics. Tgavalekos et al. used models anatomically consistent with the human lung to link ventilation defects to the heterogeneous closure of small airways. Their approach implicitly assumed a high degree of independence between airway closures as indicated by the low compactness of the airway structures mapped to individual ventilation defects. Venegas et al. however, have found that significant mutual dependence of airways may play a role in patchy ventilation of asthmatics. This led us to explore the question to what extent anatomically consistent models can be built which do not implicitly assume high independence of airways but instead allow for the mutual dependence of airways responsible for ventilation defects. We propose an algorithm for generating subject-specific airway-tree models that minimize the number of airways that must be closed or severely constricted to cause observed ventilation defects. We also propose novel approaches for measuring the compactness of airway structures. Our approach shows that anatomically consistent models which link compact airway structures to ventilation defects can be built. Our model also shows that some ventilation defects may be caused by closures of larger airways than previously reported.

Introduction

The human lungs are a complex system of bifurcating airways that have been studied using a variety of models. Such models have been used to investigate gas mixing,2,18,21,31 aerosol deposition,3,19 flow distribution,6 airway thermodynamics,22 and airways responsible for dysfunction in asthmatics.25,26 Weibel33 proposed a conducting airway model which is symmetric and computationally inexpensive to use. However, asymmetry in real lungs makes this model undesirable for modeling many aspects of lung physiology. Horsfield et al. 12,13 constructed an airway model with regular asymmetry based on the difference in Horsfield order between child branches. Kitaoka et al. 15 proposed an algorithm for generating airway trees based upon fluid flow and showed results on an idealized lung volume. They reported the model generated from this idealized lung to be noticeably more asymmetric than the human airway tree. Garrity et al. 5 developed the Kitaoka model to incorporate motion from respiratory dynamics.

Tawhai et al. 24 proposed an algorithm for generating a three-dimensional model of the airway tree following an approach by Wang et al. 32 for creating bifurcating systems in two-dimensional volumes. Tawhai et al.’s algorithm represents individual airways as a hierarchy of bifurcating cylindrical tubes; the trachea bifurcates into two airways, which then bifurcate systematically to fill the volume of the lung space. The approach can be used to create a subject-specific airway-tree model given a representation of the lobes of any particular subject’s lungs. The lung lobes are necessary to constrain airway generation as it is known that airways peripheral to the lobar bronchi do not cross lung lobe boundaries. Lung lobes were obtained by mapping lung fissures segmented from the visual man project29 to lung surfaces segmented from magnetic resonance imaging (MRI). Tawhai et al. 24 reported anatomic measurements for a single generated airway-tree model. Tawhai et al. 23 later modified their approach by obtaining lung surfaces, lobes, and initial generations of the bronchial tree from high-resolution CT, assigning airway diameters based on morphometric properties of a branch with respect to its length and position in the tree, and allowing for smooth transitions between the diameters of connected cylindrical tubes.

Tgavalekos et al. 26 used positron emission tomography ventilation images and a single three-dimensional lung model provided by Tawhai et al. 24 to predict which airways in the model contribute to the degradation of lung function. Tgavalekos et al. examined lung function by mapping ventilation defects to the corresponding areas of the three-dimensional lung model. This mapping was achieved by scaling Tawhai et al.’s model to fit into the subject’s lung cavity. By matching oscillatory mechanics of the model to measurements taken from each of their subjects, they then determined patterns of airway constriction which could have caused such dropouts in ventilation. Tgavalekos et al. predicted that the observed ventilation defects could only be due to the closure of a large number of very small airways. Furthermore, Tgavalekos et al. 25 later used this model to observe spatial patterns of airway obstruction that best matched changes in oscillatory mechanics observed in several mild to moderate asthmatics.

To date, the approach by Tgavalekos et al. 25,26 has been implemented with only a single lung model produced by Tawhai et al. 24 This approach predicted that ventilation defects were only possible due to the closure of a large number of very small airways. The shape of the lungs and lung lobes used to generate the model by Tawhai et al. were taken from a subject who was not imaged in Tgavalekos et al.’s study. The mismatch in shape between a subject’s lungs and the airway tree model can introduce error into the analysis of which airways are responsible for ventilation defects. In principle, these errors can be minimized by generating airway models which conform to measurements of the lung observed from imaging data specific to each subject.

Venegas et al. 30 have recently asserted that the mutual dependence of serial and parallel pathways in the airway tree plays a significant role in airway closures. They observed such mutual dependence in a symmetric airway tree into which they embedded Anafi and Wilson’s single terminal airway model.1 It is unclear if Anafi and Wilson’s mechanism could be used to reproduce observed ventilation defects using an anatomically consistent model. A significant step in investigating how this mechanism may impact lung function is to construct an anatomically consistent model that allows for greater mutual dependence of airways within ventilation defects than can be produced by existing methods.

The goal of this paper is to predict what range of airways sizes can subtend ventilation defects if a maximal amount of mutual dependence between airways within a defect is allowed. This prediction cannot be made by directly applying Tawhai et al.’s algorithm as it was not designed to account for ventilation defects. In models generated using Tawhai et al.’s algorithm, airway branches arbitrarily cross ventilation defect boundaries (Fig. 1). Using models generated from Tawhai et al.’s algorithm to identify airways responsible for the defects forces the number of airway closures responsible for the defects to be significantly larger than the number of contiguous regions of ventilation defect. Despite their spatial proximity, these airways do not represent topologically compact structures in the airway tree. This implicitly enforces an assumption that the closure of any particular airway is largely independent of the closure of any other airway.

Figure 1

Airway tree generation with ventilation defects. Airway branches whose constriction would affect only the ventilation defect are drawn with solid lines. Other airway branches are drawn with dashed lines. The nearest common ancestor of the airways responsible for ventilating the defect is identified. Left: Tawhai et al.’s algorithm24 pays no attention to regions of airway defects. Airways are generated into and out of defect regions. In this example, four separate airway branches contribute to the ventilation defect region. Measured as a single structure, these four airways have a subtree depth d of 6.38 and a terminal-branch ratio c of 18/25. Right: Our algorithm constrains airway generation so that only a single airway branch crosses the boundary of an ventilation defect region. This airway structure has a subtree depth of 5.11 and a 1/1 terminal-branch ratio, indicating that our algorithm would link a more compact structure to this defect than the structure that would be linked to the defect by a defect agnostic algorithm

If significant mutual dependence between airways is enforced, a prediction on the range of sizes of airways that subtend ventilation defects can be made using our modified version of Tawhai et al.’s algorithm for generating airway tree models. Our method creates models that map ventilation defects to more compact airway structures than the approach by Tgavalekos et al.’s allows. To maximize the mutual dependence of airways responsible for ventilation defects, we propose a method for generating airway tree models that allow for a minimal number of airway constrictions to cause observed ventilation defects. We advance the methodology of Tawhai et al. 23 by incorporating information on ventilation defects. Our approach builds on our earlier work16 on generating personalized airway-tree models from hyperpolarized helium (HP ³He) MRI. Our approach incorporates an atlas for estimating lung fissure locations and requires the registration of both the atlas and HP ³He MRI scans for estimating the location of the lung lobes and ventilation defects. We describe two novel methods for measuring the compactness of airway structures and use the measures to examine the structural differences between our approach and a defect-agnostic approach based upon the technique of Tawhai et al. 24

We show that it is possible to generate a model consistent with measurements of lung morphometry which can also attribute ventilation defects to compact airway structures. Our models support Tgavalekos et al.’s conclusion that ventilation defects in asthmatics are caused by heterogeneous branch closures. However, while we still find that small defects are caused by the closure of small branches, our models suggest that larger defects can be caused either by the explicit closure of larger airways or by the constriction of a collection of airways which are more topologically compact within the airway tree than the collection of airways that the approach by Tgavalekos et al. identifies.

Methods

In this section we describe our laboratory protocol for image acquisition, our approach for generating an airway tree model, and the measurements we used to analyze the resulting models.

Laboratory Protocol

HP ³He MRI images were taken of eight human subjects by the Hyperpolarized Noble Gas MRI Laboratory at Brigham and Women’s Hospital (Table 1). Six of the subjects had a clinical history of asthma and five of these subjects took daily asthma medication. The other two subjects had healthy lungs. Two scans of each individual were taken. Each image was taken after the subject breathed in 1 L of gas. The first scan was a normal breath. The second scan was taken after patients had been given a methacholine challenge. Methacholine was given in increasing amounts until a subject exhibited a 20% drop in baseline forced expiratory volume in 1 second (FEV₁) or until a maximum allowed dose of 25 mg was reached. Methacholine constricts the airways of subjects resulting in regions of ventilation defect. Images were acquired with a slice thickness of 13 mm and voxel dimensions of 1.8 mm ×  1.8 mm in the coronal plane. The number of slices per subject varied between 8 and 12. Figure 2 shows examples of HP ³He MRI scans before and after the methacholine challenge.

Table 1 Subject data

Figure 2

HP ³He MRI of the lung before (left) and after (right) airway defects were induced using methacholine to constrict airways. Brightness relates to degree of ventilation. In the unconstricted lung, all regions of the lung are ventilating normally. In the constricted lung, large regions of the lung are receiving little or no ventilation while other regions are receiving comparatively higher ventilation than in the unconstricted lung

Overview of Approach for Generating Airway Tree Model

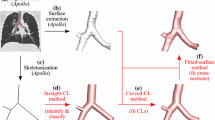
Our approach builds on our earlier work16 on generating personalized airway-tree models from HP ³He MRI. Both our current and previous approaches incorporate the major components of Tawhai et al.’s algorithm23 for generating airway-tree models. An overview of the entire algorithm is shown in Fig. 3. Given the baseline (Fig. 3b) and post-methacholine (Fig. 3a) scans of a subject, the algorithm generates a subject-specific airway tree model (Fig. 3i) in several steps. First, it extracts lung volumes from baseline HP ³He MRI scans (Fig. 3e). While useful for visualizing lung defects and lung volumes as a whole, HP ³He MRI is not of sufficient resolution to identify the fissures within the lung which separate the lobes from each other.

Figure 3

Overview of algorithm for generating personalized airway trees from hyperpolarized helium MRI and accounting for ventilation defects

To estimate the lung lobes, surfaces of the lung lobes (Fig. 3f) are extracted from the Visible Human Data Set (Fig. 3c). The Visible Human Data Set28 is a publicly available data set of cryosection images of the entire human body, including the lungs (see Fig. 4). By registering the extracted lung lobe surfaces to the HP ³He MRI scan, the algorithm determines an estimate of lung lobe locations (Fig. 3h). This registration is achieved by rigidly aligning the surface of the lungs in both data sets and then extrapolating the lung fissure locations from the visible human data set into the lungs imaged with HP ³He MRI.

Figure 4

Cryosection image from the Visual Human Data Set.28 Lung fissures are circled in white. Lung lobes and lung boundaries were hand marked to build a lung atlas

Regions of ventilation defect are then isolated using both the baseline and post-methacholine scans. To do this, the algorithm first registers the post-methacholine scan to the baseline scan (Figure 3d) and then compares the regions in the two images. We consider a voxel in the lung to represent a ventilation defect if the local average value of the baseline image is more than four times the local average value of the post-methacholine image. The local average value of a voxel is the average value of the image within a small region centered at that voxel. Connected component analysis8 is used to group neighboring voxels and yields a volumetric representation of the ventilation defects of the subject (Fig. 3g). The algorithm then divides defect volumes that cross lung lobe boundaries to maintain the lobe boundaries. In experiments, the region over which voxels were averaged to localize ventilation defects were typically of size 9 × 9 × 65 mm³. Defects smaller than 0.042 mL (roughly one voxel in the MRI scans) were not further considered.

Given an estimate of lung lobe locations and ventilation defects, the topology of our airway tree model can now be generated. We propose a two-phase algorithm which is described in detail in the appendix. The algorithm recursively subdivides the lung lobe volumes (Fig. 5) and grows an airway branch into each successive subdivision. Once a branch is grown into a ventilation defect, descendants of that branch are constrained to stay within the defect and no other branches are permitted to enter the defect.

Figure 5

Sample input data and two phases of the airway-tree generation algorithm. (a) The input data consists of the initial airway branches, lung lobe volume, and defect volumes. (b) In the first phase, the airway tree is grown until a branch has been generated into each ventilation defect. The lung lobe volume is subdivided without splitting any of the defect volumes. (c) In the second phase, the airway tree is completed. Branches are prevented from crossing defect boundaries. Since the defect region at the top was small enough to qualify as a terminating volume, no additional branches were added to it in the second phase of the algorithm

Each branch can be thought of as a tube through which air passes. Our algorithm creates a centerline model for the airway tree where each branch or tube has a beginning and end point but no diameter to indicate how much air can pass through that branch. Actual airway branches have some fluctuation of diameter across their length, but to simplify the model, an average diameter across the length of a branch can be assigned to each branch of the model. As in Tawhai et al.,24 we assigned diameters using data from Horsfield9 as mean values and a coefficient of variation of 0.1. An example of an airway tree generated by our algorithm is shown in Fig. 6.

Figure 6

Airway tree generated using our algorithm. Branches in red contribute to ventilated regions of the lung. Branches in blue have terminal branches which are exclusively within ventilation defects

Topological Measurements

An important part of verifying the accuracy of the airway-tree model our algorithm produces is being able to systematically describe the model and relate it to known measurements of the lung. There are several approaches to describing the position of an airway in the airway tree. The Weibel generation describes the relative position of an airway with respect to the stem of the tree.33 Each branch is assigned to a “generation” one higher than the parent branch it is connected to that is closer to the stem. Typically the stem is assigned to generation zero. The average generation of terminal branches, i.e., branches of the airway tree whose children are not conducting airways, was estimated to be between 16 and 18 though they can be found at significantly higher generations.24 An alternative to describing airway trees by generation is to use the Horsfield order,11 where terminal branches are assigned order one and parent branches are assigned one order higher than their child branches of highest order. Another alternative is the Strahler ordering.11 This assigns terminal branches to order one and parent branches are assigned one order higher if their children are of equal order or they are assigned to the order of the child with the highest order if the children have different orders from each other. Any connected set of branches with the same Strahler order are considered to be a single branch under this ordering system.

Several statistical measurements have been developed to describe the topology of the human airway-tree. The rates of decrease in branch length and increase in the number of branches as the tree is traversed from trachea to terminal branches can be characterized by the length and the branching ratios, respectively.13 The branching ratio R _b (i.e., the average number of children of each non-terminal branch) is the antilog of △log₁₀(number of branches)/△branch order. The length ratio R _l is the antilog of the absolute value of △log₁₀(mean length)/△branch order. R _b and R _l can be calculated using either Horsfield or Strahler ordering. In the current study, the Horsfield-based ratios are indexed by H (R _b,H, R _l,H) and the Strahler-based ratios are indexed by S (R _b,S, R _l,S). The symmetry of airway trees can be described using the branching and length ratios. When R _b,S = R _b,H = 2, a bifurcating tree has a symmetric branching pattern. Asymmetry in the branching pattern decreases R _b,H and increases R _b,S. Horsfield et al. 13 suggested that the relationship between the branching and length ratios is ideally $R_{\rm b,S}^\frac{1}{3} =R_{\rm l,S}$ based upon the concept of minimum flow resistance.

For a given set of airways, we are interested in having some measure of structural compactness, i.e., how much structure those airways share with each other in comparison to the amount of structure they share with airways outside of that set. We propose two approaches for measuring the structural compactness of a set of airways. An essential component of both measures is to identify the nearest common ancestor of the airways (Fig. 1). Among the set of paths from the trachea to any given set of the airways, the nearest common ancestor is the airway contained in all of the paths that is also furthest from the trachea. The trachea itself, for example, is the only common ancestor of all airways in the lung. One way to measure the compactness of a set of airways is to find the ratio of the number of their descendants that are terminal over the number of descendants of their nearest common ancestor that are terminal. We will refer to this compactness measure as the terminal-branch ratio c. It is 1/1 for the most compact structures and decreases as structures become less compact. A low value for the terminal branch ratio shows that relatively few terminal branches which are descendant from the nearest common ancestor come from the set of branches of interest. Another measure of compactness is the average number of branches along the paths from terminal branches descendant from a set of airways to the nearest common ancestor of these airways. We will refer to this measure as the subtree depth d, since it computes the average depth of the subtrees whose root is the nearest common ancestor. The subtree depth is a measure of the functional proximity of a structure’s terminal branches to each other within the topology of the airway tree and gives an approximation of how much structure is needed to connect the airways within a set. More compact structures will have smaller subtree depth than less compact structures as their terminal branches will be functionally closer to each other within the topology of the airway tree than less compact structures. We use these measures to report the compactness of the set of airways whose terminal branches end only in defect regions (Fig. 1).

Results

We generated an airway tree model for each of eight subjects for which HP ³He MRI scans were available. We report a total of 751 defect regions and a range of 72 to 125 defect regions in each subject. We differentiate between small defects which could be caused by the closure of a single terminal airway and clustered defects which we define to be caused by the closure of at least two terminal airways. According to this definition, 390 of the 751 measured defects were small and 361 clustered. The defect regions varied in size from 2.39 to 1688.16 mL with an average size of 157.71 mL. Ventilation levels were generally much lower inside defect regions than outside, although we measured a small overlap of levels (Fig. 7). At 1 L above functional residual capacity (FRC), the subjects had measured lung volumes ranging from 3.38 to 5.29 L with an average size of 4.21 L.

Figure 7

Distributions of ventilation levels inside and outside of ventilation defects averaged over eight subjects. The distributions overlay slightly. The ventilation level of each volume unit is computed from the intensity value of a voxel in the post-methacholine HP ³He MRI scaled into the range 0 to 40

We compared our airway tree models to models that we generated using the approach by Tawhai et al. 24 (we did not use Tawhai et al.’s later approach23 as it incorporated information from CT imaging unavailable in our study). Since Tawhai et al. did not specifically address the issue of ventilation defects, we refer to the method of mapping ventilation defects to a model generated using Tawhai et al.’s approach as a defect-agnostic approach. Our approach, on the other hand, is a defect-aware approach to generating subject-specific airway trees.

Both sets of airway tree models are generated into lung lobe volumes obtained from HP ³He MRI scans as described in our previous work.16 Both sets of airway tree models have topological measurements similar to those reported in the literature. Using our approach, we generated trees with an average of 28,373 terminal branches (26,007–29,866). Using Tawhai et al.’s approach, we generated models with an average of 29,087 terminal branches (26,810–31,635). The expected number of terminating branches in the human lung has been reported in several works. Weibel33 reported 65,536 terminating branches. Horsfield and Cumming11 reported 27,992 branches and Haefeli-Bleuer and Weibel7 reported an expected 26,000 to 32,000 terminal branches. Tawhai et al.’s original model24 contained 29,445 terminal branches. While generating models that are generally slightly lower than the 30,000 terminating airways set as the goal, both our approach and Tawhai et al.’s approach are well within the published range. Furthermore, both methods produce trees that are consistent to each other with respect to the number of terminating branches as, on average, they differ by only 751 branches.

Expected values for the average generation of terminating airways have also been reported.24 Estimates vary between 15 and 17.6. Using our approach, the average generation of terminal airways was 16.7 with individual models having average terminal generations between 16.35 and 17.34. Using Tawhai et al.’s approach, the average generation of terminal airways was 16.57 over all models with individual models having average terminal generations between 16.31 and 16.91. The average branching angle is 37.02°, only slightly below the ideal angle of 37.28° proposed by Horsfield and Cummings.10

For our approach, we report that R _b,S averaged 2.37, R _l,S averaged 1.39, R _b,H averaged 1.50, and R _l,H averaged 1.16. A comparison of branching and length ratios reported in the literature and for models generated using Tawhai et al.’s approach is provided in Table 2. The branching and length ratios were obtained from plots of the logarithm of the number of branches and the logarithm of the mean branch length against the Strahler or Horsfield order. Both approaches produced somewhat more symmetric trees than have been reported in the literature.

Table 2 Branching and length ratios reported in the literature and measured from models generated from 8 subjects following both Tawhai et al.’s and our approach

We show distributions of the generation number of airways responsible for ventilation defects for the defect-agnostic and defect-aware approaches in Figs. 8 and 9. For airway trees created with our defect-aware approach, the generation of airway branches that crossed defect boundaries generally increased as the size of the defect decreased. For airway trees generated by the defect-agnostic approach, there was no relation between the generation of an airway branch that crossed defect boundaries and the size of the defect for which that airway was partially responsible (Fig. 8). In our models, airway defects were mapped to constrictions of branches from the 4th through the 20th generation. As required by the constraints in our algorithm, the 751 defect regions could have been caused by the closure of as few as 751 airways. The defect-agnostic approach produced airway tree models in which defects were mapped to constrictions of branches from the 8th through the 25th generation. At least 15,024 airways would need to be closed to cause the 751 defect regions. We found no significant differences in the airway tree models of the asthmatic and non-asthmatic subjects in either approach (Fig. 9).

Figure 8

The distribution of the generation number in the generated airway tree models of the airways responsible for ventilation defects. The distribution shows the count of all airways whose terminal branches end only in defect regions. The size of the points indicates the logarithm of the average size of the defects in which each airway terminates. For airway tree models generated using our approach, only one airway is responsible for each defect and the generation of the airway branch responsible for that defect increases as the size of the defect decreases. For airway trees generated using a defect-agnostic approach, many more airways are responsible for the defects and there is no relation between the generation of the airway branch and the size of the defect for which that airway is partially responsible

Figure 9

The distribution of ventilation defect sizes against branch generation for all airways whose terminal branches end only in defect regions. We show the airways that must be closed to cause the observed defects following both a defect-agnostic approach (a) and our approach (b). In general, defects are attributed to the closure of larger branches in airway tree models generated using our approach than they are in airway tree models generated following the defect-agnostic approach. We report no significant differences in the airways responsible for observed defects in asthmatics as opposed to non-asthmatics

Tgavalekos et al. 26 reported that the size of airway closures in their data ranged from 0.22 mm to 2.39 mm in diameter. Similarly, using the defect-agnostic approach, the size of airway closures in our data ranged from 0.22 to 1.9 mm in diameter (average 0.43 mm). Only 21 of the 15,024 branch closures occurred between generation 0 and 10 (see Fig. 9a). Using our defect-aware approach, however, the size of airway closures ranged from 0.22 up to 6.32 mm in diameter (average 0.51 mm). In our model, 51 of 751 branch closures occurred between generation 0 and 10. Moreover, we note that, 33 of 55 branch closures for defects larger than 10 mL occurred between the zeroth and 10th generation (see Fig. 9b). Due to the physical relationship between airflow through an airway and the volume that the airway ventilates, small airways could not have created defects of these sizes. Since airways in generations 5 through 10 can be as small as 0.2 mm and as large as 6 mm,26 we project that the larger airways of these generations were responsible for many of the observed defects.

We report that the airway structures linked to clustered defects by our defect-aware approach are significantly more compact than the airway structures linked to defects by the defect-agnostic approach (Table 3). The average terminal-branch ratio is 1/1 for the defect-aware approach and only 9/50 for the defect-agnostic approach. The average subtree depth is only 5.1 branches for the defect-aware approach, but 8.8 for the defect-agnostic approach. The defect-agnostic approach links the least compact structures to some of the small defects (Fig. 10).

Table 3 Comparison of the structures linked to ventilation defects in airway trees created by the defect-agnostic and defect-aware approaches

Figure 10

Compactness of airway structures responsible for clustered ventilation defects vs. defect size. The terminal-branch ratio was computed for the airway trees generated by the defect-aware and defect-agnostic approaches. Our defect-aware approach links highly compact structures to clustered defects regardless of the defect size. The defect-agnostic approach only links structures as compact as those found in the defect-aware approach to the smallest defects. It also links some of the least compact structures to small ventilation defects

Discussion

The airway trees our approach generated have geometric properties consistent with measurements reported in the literature. They can explain observed lung defects with a minimal number of airway closures. Although our approach links each contiguous region of a ventilation defect to a single airway branch, we do not suggest that this single airway was in fact severely constricted or closed. Instead, more complex constriction patterns throughout the subtree of this airway may have resulted in the observed airway defect. This is consistent with evidence from mechanical simulations that suggests that ventilation defects are caused by the heterogeneous constriction over a larger range of airways.6

The compact airway structures of our models may allow for significant mutual dependence between the airways that caused the defects, a property Venegas et al. advocated.30 In contrast, the structures that the defect-agnostic approach maps to ventilation defects are so expansive that mutual dependence between airways is unlikely to be a significant contributing mechanism in defect formation. In general, physiological mechanisms in the lungs will be impacted by the geometry of the airway trees. We have shown how dramatically airway geometry can change while still falling within the bounds of what is currently understood to be normal human morphometry. Efforts to understand physiological mechanisms in the lungs need to carefully consider the possible impacts of airway geometry on the mechanisms.

We note that our algorithm does not take regions of hyperinflation into account and that additional work may be needed to correctly link airway structures to both regions of hyperinflation as well as regions of ventilation defect. Many modifications can be made to our algorithm to relax the degree of compactness desired in these structures and perhaps allow them to correctly link to regions of hyperinflaction. One possibility, for example, would be to allow any of the descendants of the first branch that is grown into a defect volume to freely cross the boundary of that defect volume. If no branches other than these descendants could cross the defect boundary, the resulting structures linked to airway defects would be less compact than those we currently achieve. They would also be significantly more compact than those which can be linked to the defects using a defect-agnostic approach.

We note also that our approach may incorrectly associate spatial continuity with topological compactness of airway structures. By specifically providing separate, unconnected defect volumes as an input to our airway tree generation algorithm, we prevent the creation of compact structures which could explain multiple defects. In our study, about half of the defect volumes were so small that only a single terminal branch was necessary to fully explain ventilation in those regions. These small defects represent about 1% of the total number of terminal volumes in the lung but they are indicative of the possibility that there are mechanisms in the lung which cause entirely independent closures of terminal airways.

A limitation of computational models based on small sets of images is that they are limited by the number and resolution of the images used to build the models. While our approach can create a model to describe a single set of data with an anatomically consistent airway tree that minimizes the number of necessary airway closures, it is beyond the scope of this paper to present a model that generalizes across multiple imaging sessions. While it may be possible to create such a model in a further study, it is not clear that any airway tree other than a subject’s actual airway tree could explain all observed ventilation patterns over multiple imaging sessions. We note, however, that de Lange et al. 4 observed that the location of roughly half of ventilation defects persist through multiple imaging sessions and about half of those defects also persist in size. So, while our approach is unlikely to produce the same model given separate imaging sessions, significant structural similarities may exist between such models. Furthermore, while the images used to create these models are not of sufficient resolution to visualize most of the airway branches themselves, the change in ventilation caused by a single terminal branch closure is well within the resolution of ventilation imaging. It is therefore unlikely that our algorithm will be highly sensitive to improvements in the resolution of HP ³He MRI.

We also report higher branching angles in the highest Strahler orders than previously reported.23 In CT, the airways corresponding to these orders as well as the lung lobes into which they project can be explicitly segmented and reliably measured. As a consequence of not having similarly detailed measurements available from our HP ³He MRI scans, we have less confidence in the correctness of measurements on high-order bronchial branches. Furthermore, we have only a few samples to measure statistics of the properties of the higher-order branches, whereas for more peripheral branches we have on the order of thousands or tens of thousands of samples. The branching angles of the peripheral airways are lower than those observed in the human lung. One of the improvements Tawhai et al. 23 made in the second version of their algorithm was a regrouping rule used during airway generation which resulted in a model with branching angles more closely mirroring those found in the human lung than were produced without the regrouping rule. This rule, however, is incompatible with the two-phase approach we propose. In particular, this affected the branching angles of peripheral airways, which are overly narrow in our models. Modifying our algorithm to achieve similar adherence to physiological measurements in modeling of branching angles is a non-trivial task. This may be a concern if models generated using our algorithm are used for other simulations, but has little impact on the conclusions we draw in this paper. The generation of an airway subtending any particular defect may well change, but it would be as likely to increase in generation as it would be to decrease.

We note that the images we acquired were taken at 1 L above FRC, which is approximately 70% of the volume of the lung at total lung capacity (TLC) as opposed to FRC which is approximately 45% of the volume of TLC. The measurements of lung morphometry in the literature that we compare our model to were obtained from lungs at TLC. Our imaging protocol was necessary to observe ventilation defects as they may not have been visible at TLC. This may be a source of error in our analysis. Lungs at TLC have uniformly distributed terminal branches while lungs at FRC have non-uniformly distributed terminal branches with a greater concentration of airways in the dependent region of the lung and a lower density in the non-dependent regions. This means that our models have fewer terminal airways in the dependent ventilated and defect regions of the lung and more terminal airways in non-dependent ventilated and defect regions of the lung than likely exist at FRC. We cannot quantify exactly what impact this error has on our conclusions because of the lack of measured data for lung anatomy at FRC. However, while the distribution of smaller airways may be affected by the differences between FRC and TLC, there should be little impact on the size of airways which subtend the larger defects. Models that correctly estimate distributions of peripheral airways would likely show defects in the dependent regions of the lung subtended by somewhat larger airways than our model predicts and defects in the non-dependent airways subtended by somewhat smaller airways than our model predicts.

In our study, roughly a third of the ventilation defects were smaller than the terminal volume limit. To ensure that an airway branch terminated in such small defect regions, if a branch was considered terminal and contained a single defect region at any point during processing, the algorithm ensured the branch ended within the defect region. Without this constraint, it may have been possible for some small defects not to be associated with any terminal airways. The constraint may have caused a bias for small airways to be attached to slightly higher generation branches than they otherwise would have been. However, as these small ventilation defects comprise less than 1% of the total measured volume of ventilation defects, their impact on overall lung mechanics is small. Furthermore, due to the partial volume effect, it is possible that ventilation defects as large as 0.34 mL were missed and that defects, particularly the smallest ones, may be significantly underestimated in size.

In addition to procedural nuances, the algorithm we presented is sensitive to a number of parameters that guide the airway tree generation. Changing these parameters will affect the airway tree. The values we used have been shown to be reliable in previous work. We used two parameters for determining if a branch should be terminal: the length of the branch and the volume into which the branch was generated. We used a length limit of 1.2 mm and a volume limit set to 1/20,000th of the lung volume. Setting higher limits than the values we chose would decrease the number of terminal branches and the average generation of the terminal branches. Estimates of the length of terminal branches have ranged from 1.5 to 1.72 mm.7,20,33 Tawhai et al. 24 justified a limit of 1.2 mm based on reported average lengths of the transitional bronchioles (1–1.5 mm7,20). Tawhai et al. 23 changed this limit to 2 mm citing a different range for the reported average length of the transitional bronchioles (1.5 mm7–1.78 mm33). Haefeli-Bleuer and Weibel7 reported average segment lengths for alveolar ducts at 0.73 and 1 mm for alveolar sacs 1 mm. The measurements by Haefeli-Bleuer et al. were taken with a degree of acinar distension at close to TLC. As the subjects in our study were not imaged with lungs held at TLC, the lengths of terminal bronchioles may be somewhat shorter and thus we opted for the shorter length limit of 1.2 mm. As in Tawhai et al.,24 we set a branching angle limit of 60° as has been reported as the usual limit of branching angle.9,27 We also adopted our branching fraction of 40% from Tawhai et al. 24

Our study relied on a single example of lung anatomy as an atlas and guide for fissure location. This may be a significant source of error in our algorithm as the resulting lung lobes may be significantly different than an individual’s actual lobes. In particular, our algorithm forces each defect to fall entirely within a single lung lobe. Accurate measurements of a subjects lung lobes may reveal that contiguous regions of ventilation defect may cross lobe boundaries. Such an observation would prove that defects can be caused by less compact structures than the structures our algorithm creates.

Ideally, the lung lobes and first seven or eight generations of the airway could be obtained from a CT scan of each subject. Lacking this resource, a future study may benefit from using a statistical atlas which could be obtained by registering images of several subjects into a single coordinate system. Such an atlas would describe potential fissure locations more accurately and would allow for the creation of a range of personalized airway trees that all fall within the range of normal human physiology.

Furthermore, registering lung volumes using an affine registration of lung surfaces does not produce a fully accurate alignment of lung anatomy. It has been demonstrated that deformations of the lung are not uniform.17 It may be possible to identify other features of anatomical importance for use in the registration process, for example, the initial branches of the bronchial tree, points of maximal curvature along the top and base of the lungs, or the axis of elongation. The lung lobes would also be useful for registration, but as they cannot be identified in HP ³He MRI, they will not be useful for our task.

The structural differences between the airway tree models generated by the defect-aware and defect-agnostic approaches may have an impact on other measurements and predictions of lung function. For example, Tgavalekos et al. 26 used measurements of lung mechanics to gain a deeper insight into the extent of airway constriction throughout the airway tree. Venegas et al. 30 observed significant mutual dependence of airways in simulation studies using a symmetric model. Performing a similar analysis using our personalized airway models may reveal additional information about the nature of ventilation defects but such an analysis is beyond the scope of this paper.

The comparison of our approach to generating airway trees to the defect-agnostic approach broadly applies to the two versions of the algorithm by Tawhai et al. 23,24 as well as to the approach by Tgavalekos et al. 26 to identifying airways linked to ventilation defects. For the purpose of identifying the airways linked to ventilation defects, the differences between the early and later versions of the algorithm by Tawhai et al. are minor in comparison to the topological changes induced by our algorithm. The algorithm by Tawhai et al. is agnostic to the defect boundaries and both versions would produce airway trees that link non-compact structures to defects. Tgavalekos et al.’s approach to identifying airways linked to ventilation defects inherits this characteristic. Tgavalekos et al.’s approach is additionally limited because it maps a model of an airway tree from one subject to the lungs and ventilation defects of another subject.

In summary, we have presented an algorithm for creating personalized models of the airway tree from HP ³He MRI scans of the lung. Our algorithm produces airway trees in which compact airway structures can explain ventilation defects. The resulting models are consistent with published anatomical measurements of the human airway and allow for the possibility that far fewer airway branches are responsible for ventilation defects than previously reported. Our work provides models that have significantly different airway topology from previous models and may be used to improve understanding of the significance of mutual dependence of airways, a property Venegas and Winkler explored in their symmetric lung model. We have proposed new approaches for measuring the compactness of airway structures and have used these measures to show that disregarding defect boundaries in the generation of an airway model results in a model which can only explain ventilation defects by a large number of disperse airway closures. As a further consequence of the airway topology we model, we find that ventilation defects in asthmatics may be caused not only by the closure of small peripheral airways in the range of 0.2 to 2.5 mm in diameter, but may also be caused by the closure of higher generation airways with diameters as large as 3 to 6 mm.

Appendix A: Airway Tree Generation Algorithm

Our algorithm for generating airway tree models extends Tawhai et al.’s defect-agnostic algorithm24 by incorporating information about ventilation defects. Tawhai et al.’s algorithm generates airway trees by dividing a lung volume and growing an airway branch into each of the subvolumes (Fig. 11). Recursive subdivisions of these “host volumes” allows for the creation of the complex branching structure of the airway tree. After determining separate volumes for each lung lobe, Tawhai et al.’s algorithm uses planar surfaces to further subdivide the volumes (Fig. 11b) and reconfigures volumes at each iteration so that individual voxels are assigned to the closest terminal or newly grown airways.

Figure 11

The approach by Tawhai et al. 24 for generating airway trees. (a) An airway branch with associated host volume shown in cross section as a rectangle. (b) The host volume is divided using a plane (dashed line). (c) Centroids for the two subvolumes are calculated (circles). (d) Child branches are generated toward the centroids of the subvolumes

The main idea of our method is modifying the volume splitting strategy of Tawhai et al. to avoid splitting defect volumes. Our method is a two-phase tree generation algorithm (Fig. 5). The first phase of our algorithm begins with a host volume, an airway branch ending within the host volume from which the next generation of branches will grow, and a set of defect regions within the host volume (Fig. 12a). A “base tree” is created such that a single branch of the tree is generated into each of the defect volumes. In phase 1, any time a defect volume is split (Fig. 12b), all voxels in the defect volume are assigned to the subvolume that holds the majority of the defect volume (Fig. 12c). Phase 1 of our algorithm is an iterative routine designed to only generate branches into volumes that contain airway defects. Unlike Tawhai et al.’s algorithm,23 which creates all the branches of one generation before creating branches of any following generations, our algorithm creates branches asynchronously across branch generations.

Figure 12

Our approach for incorporating ventilation defects into the generation of airway trees. (a) An airway branch with associated host volume containing two defect regions. (b) The host volume is divided using a plane (dashed line). (c) Defect regions crossing the divide are assigned to the subvolume in which they have the most overlap. (d) Centroids for the two subvolumes are calculated (circles). (e) Child branches are generated toward the centroids of the subvolumes

Once the base tree has been created, the airway tree is completed in a second phase by generating subtrees into all the defect volumes and filling out the tree in the remaining host volumes (Fig. 5c). We ensure that only descendants of the branch originally generated into a defect volume will be generated into that defect. This means no descendants of that branch will be generated outside of the defect volume. Maintaining volume boundaries is accomplished with “coherency labels.” A separate coherency label is created for each defect and associated with the first branch grown into a defect.

Our algorithm begins with the five volumes of the lung lobes with the associated collections of defect volumes within each lobe. Nine of the fifteen airways between generation 0 and 3 are determined manually so that a single airway branch enters each of the lung lobes. The airways from the trachea to the lung lobes are determined manually. Each lung lobe serves as a separate host volume and the branches into the lobes are given separate coherency labels. For computational efficiency, measurements and volume memberships are made with respect to individual voxels within the volumes. All volumes are resampled so voxels are 1 mm³. The two phases of our algorithm are detailed below.

Phase 1: Build Base Airway Tree. Given a branch with a coherency label, an associated host volume, and a set of defect volumes within the host volume (Fig. 5a), phase 1 produces an airway tree in which a single branch is generated into each defect volume (Fig. 5b). Few, if any, of the leaves of the tree will be terminal branches.

• Step A1. A plane is used to split each host volume into two subvolumes. The vectors formed by a branch and the parent of that branch define the splitting plane (Fig. 12b). Defect volumes are assigned to the subvolumes which contain them (Fig. 12c). Any defect volume that falls across the splitting plane boundary is assigned to the subvolume into which more of the defect falls.

• Step A2. A child branch is grown into each of the two subvolumes of each host volume, following steps C1–C4 below (Figs. 12d and 12e).

• Step A3. If a newly generated child branch ends in a defect volume V, the following occurs. The child branch is given a new coherency label. Each defect volume, except V, within the subvolume associated with the child branch is reassigned to its closest non-terminal leaf of the tree with the coherency label of the parent branch. Each voxels remaining in the subvolume that is not in V is reassigned to its closest non-terminal leaf of the tree with the coherency label of the parent branch.

• Step A4. Each newly grown child branch is checked to see if it is terminal (see Terminating Conditions below) and if its end point needs to be moved into a small defect. If a terminal child branch is associated with one or more defect volume then the end of the branch is moved to be within the closest defect volume C. Each defect volume except C is reassigned to its closest non-terminal leaf of the tree with the coherency label of the parent branch. Each voxel remaining in the subvolume that is not C is reassigned to its closest leaf of the tree with the coherency label of the parent branch.

• Step A5. The subvolumes become new host volumes and steps A1–A5 are repeated on all non-terminal branches whose host volumes contain defect volumes.

Phase 2: Completing the Airway Tree. Given an airway tree containing leaves which are not terminal and have associated host volumes and coherency labels (five branches in Fig. 5b), this phase produces an airway tree in which all leaves of the tree are terminal airways (Fig. 5c).

• Step B1. A plane is used to split each host volume into two subvolumes. The vectors formed by a branch and the parent of that branch define the splitting plane (Fig. 11b).

• Step B2. Two child branches are grown into the two subvolumes of each host volume (follow steps C1–C4 below as shown in Fig. 11c and 11d).

• Step B3. Each child branch is checked to see if it is terminal (see Terminating Conditions below). If a child branch is terminal, any voxels in the associated subvolume are reassigned to the host volume of their respective closest non-terminal branches with the coherency label of the parent branch.

• Step B4. The subvolumes become new host volumes and steps B1–B4 are repeated on all non-terminal branches.

Generating a Child Branch into a Volume

These steps are part of Tawhai et al.’s original algorithm. As they are used in both phase 1 and phase 2 of our algorithm, we report the steps separately here. Given a contiguous volume and a parent branch, these steps produce a new child branch which terminates within the given volume.

• Step C1. The center of mass of the volume is calculated (Figs. 11c and 5d).

• Step C2. The child branch is grown from the end of its parent branch in the direction of the center of mass of volume (Figs. 11d and 5e). The branching fraction, or length of the branch to be grown, is a percentage of the distance between the two points, typically 40%.

• Step C3. The angle between the child branch and its parent branch is checked to see if it falls within a reasonable bound, typically 60°. If the angle is larger than this bound, the branch is rotated so it satisfies this constraint.

• Step C4. If the branch does not end within the volume, its length is decreased until it falls within the volume.

Terminating Conditions

There are three conditions for determining if an airway branch is a terminal branch: the host volume associated with a branch is too small, the length of the branch is too small, or the branch generation is equal to the maximal generation. We wanted to generate airway trees that have between 26,000 and 32,000 branches.7 To achieve this, we set the volume limit as a function of the measured volume of the lung. As the majority of terminal branches will have volumes significantly smaller than this limit, we determined the limit as the volume of the lung divided by 20,000 units. We set the limit on branch length to 1.2 mm, consistent with the limit originally used by Tawhai et al. 24 The reported average length of the transitional bronchioles is on the order of 1 mm7 to 1.7 mm.20 We set the maximal generation for an airway branch to be 25.