Introduction

Oncologists are very careful to distinguish between cancer cure and cancer remission. They prefer to utilize the less reassuring terminology of cancer remission partly because the detection threshold of current screening techniques can be as high as 1010 cancerous cells.16 Using these technologies, it is impossible to distinguish between a cancer in remission and one that has been cured. Hence, it is not uncommon, to maximize the probability of patient survival, for chemotherapy treatments to last for months or even years beyond the onset of remission with no detectable cancerous cells.

The design of cancer treatments must balance the eradication of the cancer with the patient’s general well-being. The cancer is likely to return if the treatment intensity is insufficient; however, harsher treatments which increase the likelihood of cure may cause intolerable collateral damage and side-effects for the patient. The optimal treatment intensity and duration maximizes the survival likelihood while minimizing collateral damage and patient discomfort. As an example, an extended period (up to 2 years) of maintenance chemotherapy has been shown to be necessary for prolonged remission of childhood acute lymphoblastic leukemia.13 High drug metabolite levels are associated with a decreased risk of relapse22 and increased cytotoxicity in vitro.3

To assist with the design of the optimal treatment strategies, mathematical models have been used to estimate cancer cell populations and the response to chemotherapy. To name a few, analytical approaches have been used to examine the effect on specific cellular responses such as drug resistance,11 quiescent populations,2,7 spatial and diffusion effects,1,4 and cell cycle-specific drugs5,9 for use in optimal treatment designs.10,12,17,24 To date, most mathematical models employed to evaluate treatments are first-order approximations of the state of the cancerous cell population; cell behavior is averaged rather than considering all possible behaviors of individual cells. Because each cell is governed by events whose timing is uncertain, the state of the population becomes uncertain. This uncertainty underlies the refusal of an oncologist to guarantee cancer cure.

Unless continuous and comprehensive measurements of the state are taken, the actual state can only be spoken of in terms of probabilities and likelihoods. This is not to say that population-averaged models are inept, quite the contrary. When there are a large number of cells, the random fluctuations are insignificant once they are averaged over the entire population. However, as the cancer population approaches extinction, the behavior of individual cancerous cells becomes an important factor in determining the patient’s likelihood of cure.

Fredrickson,8 in his studies of sterilization, showed that complete eradication of a cell population can never be guaranteed, but the likelihood of elimination could be computed as a function of the sterilization parameters. He derived analytical solutions for the cell number probability distribution, which includes the likelihood of complete sterility or having zero residual cells, for a homogenous population undergoing pure, independent death processes. That is, an inoculation of N 0 cells is exposed to sterilization conditions where cell division is inhibited and death is induced. A time t later, the probability of having N cells is given by P N (t) where the probability of complete sterility during the process is P 0(t). Complete sterility can never be guaranteed, but its likelihood can be computed as a function of the time spent in a sterilizing environment and the sterilizing intensity. Analyzing chemotherapy treatments are extensions of this principle. Even though cancer cure cannot be guaranteed, estimating the likelihood of curing cancer provides a quantitative basis on which potential treatment protocols can be evaluated.

The modeling of random processes is accomplished either directly by random equations (e.g., the Langevin equation, Itô equation, etc.) or by deterministic differential equations in the probabilities for various realizations of the random process. A purely computational approach based on Monte Carlo simulations (which consist of artificial realizations of the process) is also popularly used in modeling random processes.

In what follows, we illustrate how stochastic equations of population balance models19–21 can be utilized to estimate the likelihood of complete eradication of cancerous cells. The probabilistic interpretation of population balance equations yields the cell number probability distribution (which describes the likelihood of having a given discrete number of cells) in which the probability of having zero cancer cells is the likelihood of cancer eradication. While, this distribution is difficult to calculate directly, the continuous properties of the expected population mean and standard deviation obtained from the stochastic formulation give insights on the behavior of the pure probabilistic model. Thus analysis of an age-structured binary cell division model reveals that an expected population that is six standard deviations less than one cancer cell provides a good estimate for a treatment duration that will result in a nearly 100% chance of having zero cancerous cells for a given patient.

Model Development and Methods

Cure of a clinical cancer is assured only when no cancerous cells remain. Since the timing of cell division and death are stochastic events, the number of cells at a given time is described by a cell number probability distribution. Thus, the likelihood of complete eradication of cancerous cells, or the probability of cure, at a given time is the probability of having zero cells at that time. The number of cancerous cells can be estimated by the expected population size (which is the mean number of the cell number probability distribution and thus a continuous rather than discrete quantity) predicted by a population balance model. While the estimated population size describes whether the number of cancerous cells is near zero, the certainty with which one is in this estimate is related to the standard deviation of the population size. We hypothesize, and demonstrate in the results, that the first and second moments describing the mean and standard deviation of the cancer cell population together provide an estimate of the likelihood of cancer eradication.

Introduction to Number and Product Densities

Variations in the population arise due to uncertainty in the timing of cellular events. For example, in an unstructured model, each cell undergoes a number of transitions at pre-specified rates. Multiplying the transition rate by an infinitesimal time interval dt gives the probability that an individual cell makes that transition during that time interval. This randomness implies that the actual number of cells in a population at time t, N(t), can only be known in a probabilistic sense.

In an age-structured model, the same uncertainty in the timing of transitions exists, but the probability of transition also depends on the time passed since a cell’s last transition, τ. Neither the number of cells nor the ages of those cells are known exactly. Hence, it is impossible to know the actual number density, \({n(\tau, t)},\) or the actual number of cells exactly. This uncertainty is contained in a master probability density function J v , where the probability that there are v cells having a given actual number density is

$${\Pr \left\{ {n(\tau ,t)=\sum_{i=1}^v {\delta (\tau -\tau_i )} }\right\}=J_v (\tau_1 ,\tau_2 ,\ldots ,\tau_v ;t)d\tau _1 d\tau_2\ldots d\tau_{v}.}$$

For a detailed description of the theory, see Ramkrishna.18, 19 It is possible to derive a differential equation for this master probability density but in general because of its combinatorial complexity its solution is not often desired. However, this function is the basis for other probabilistic functions which can be used to describe the system in somewhat lesser detail.

The expected number density, \({n_1 (\tau , t)},\) or first-order product density, is a commonly used property which is derived from the master probability density function. The first-order product density is the averaging over all age combinations of the probability density function:

$${E[n(\tau ,t)]=n_1 (\tau ,t)=\sum_{v=1}^\infty {\frac{1}{\left( {v-1}\right)!}\prod_{r=1}^{v-1} {\int\limits_0^\infty {J_v (\tau _1 ,\tau _2,\ldots ,\tau _{v-1} ,\tau ;t)d\tau _r } } }}$$

It is of interest to note that multiplying the expected number density by dτ represents all circumstances in which a cell can exist in the infinitesimal age range τ and τ + dτ. So, \({n_1 (\tau ,t)d\tau},\) besides being the average number of cells in the range \({{(\tau ,\tau +d\tau)}},\) is also the probability that one cell exists in that age range.

When the total number density is large, the cell behavior can be adequately described by the deterministic expected number density since fluctuations in cell behavior average out. Most population balance models are of sufficiently large systems and use formulations of the expected number density dynamics. However, if the number of cells is small, such as when the eradication of all cancerous cells is of concern, the variation in individual cell behavior becomes important, and a more intimate knowledge of the probability density function is required. Additional information is contained in each of the subsequent moments of the total population density. For example, while the expected number density also provides the first moment, or mean, of the total population density

$${E[N(t)]=N_1 (t)=\int\limits_0^\infty {n_1 (\tau ,t)d\tau },}$$

deviations in the total number density are captured through the variance, V[N(t)], where

$${V[N(t)]=E[N(t)^{2}]-E^{2}[N(t)].}$$

Just as calculation of E[N(t)] required knowledge of the first-order product density, \({n_1 (\tau ,t)},\) calculation of E[N(t)2] depends upon the second-order product density, \({n_2 (\tau ,\tau ^{\prime},t)}.\) The kth-order product density is given by:

$${n_k (\tau ^{(1)},\tau ^{(2)},\ldots ,\tau^{(k)};t)=\sum_{v=k}^\infty {\frac{1}{\left( {v-k}\right)!}\prod_{r=1}^{v-k} {\int\limits_0^\infty {J_v (\tau _1 ,\tau _2,\ldots ,\tau _{v-k} ,\tau ^{(1)},\tau ^{(2)}\ldots ,\tau ^{(k)};t)d\tau _r}}}.\,^{19}}$$

While additional information regarding the cell number probability distribution is contained in subsequent moments, these calculations for age-structured models can become computationally expensive. To estimate the likelihood of cancer eradication, the need for the full probability distribution can be circumvented. As shown in this article, the first and second moments, which yield the mean and standard deviation of the cancer cell population, are sufficient.

Age-Structured Stochastic Equations of Binary Cell Division

The mathematical models developed and utilized to study the cancerous cell population response to chemotherapeutic agents are based on a number of assumptions. Foremost, the population is homogeneous. That is, extrinsic cellular variations due to mutation or other sources are neglected. Intrinsic rather than extrinsic stochastic behavior is studied herein. Also, no external effects are considered other than death induced by a hypothetical chemotherapy treatment. The target of this model at present is for cell cycle non-specific drugs where there is no loss or change in drug efficacy during treatment. The effect of the immune system on removing cancerous cells is neglected along with cell signaling, nutritional requirement, potentially evolving drug resistance, or other environmental and spatial effects.

The cellular replication of mammalian cells is binary division: the division of one mother cell produces two daughter cells. In a population balance model of binary division, the mother cell is removed from the number density while two daughter cells are simultaneously created. Using an age-structured model where the age of a cell, τ, is the time since its last transition, cell division produces two cells of age zero. Each cell divides at a rate \({\Gamma (\tau)},\) which is assumed to be independent of external conditions, and dies at an age-independent rate, k, which is assumed to be a fixed constant whose magnitude is determined by intransient drug concentrations.

The model parameter values utilized herein are based either from in vitro cultures of established leukemia cell lines24 or from those observed clinically.26 For example, clinical proliferation fractions range between 10 and 100%,26 hence, quiescent rates evaluated yield proliferation fractions of 12, 54, 72, and 93%. Since external effects on cells are neglected, the in vitro doubling times of roughly 24 h24 are used as a basis for division rates rather than those of clinical cancers (e.g. 26.42 days for lymphomas26). The remaining text in this section determines the first two product densities which will be used to compute the mean and standard deviation of the cell population. Previously, Ramkrishna and Borwanker21 have shown that the mean and variance are functions of the first two product densities of the population balance equations.

First-Order Product Density

The population balance equations for the first-order product density, \({n_1(\tau, t)},\) under binary division have assumed that a dividing mother cell forms two newborn daughter cells of age zero. But the formation of two cells at the boundary contradicts the definition of a number density where a single entity only can exist at a given age at one time. The expected number density, \({n_1 (\tau , t)},\) is actually a combination of the number density for doublets formed via binary division, \({n_1^{2} (\tau , t)}\) (where the superscript is not to be misconstrued as an exponent), and the number density of singlet cells that remains after one of the doublets has transitioned, via division or death, \({n_1^1 (\tau ,t)},\) where \({n_1 (\tau ,t)=2n_1^2 (\tau ,t)+n_1^1 (\tau ,t)}\) (See Fig. 1).

Figure 1
figure 1

When a mother cell undergoes binary division, it is replaced by two identical daughter cells: Such doublets have total population density \({n_1^2 (\tau ,t)}\). Loss of one of the doublet cells through division or death leaves a residual single cell which is part of the single cell total population density, \({n_1^1 (\tau ,t)}.\) All cells, regardless of affiliation, are assumed to divide at a rate \({\Gamma (\tau )}\) and die at a rate k with the arrows denoting possible transitions and associated rates

Full size image

The dynamics of the first-order product density vector composed of the double and single number densities:

$${\mathbf{n}_{\mathbf 1} (\tau ,t)=\left[ {{\begin{array}{l} {n_1^2 (\tau ,t)} \\ {n_1^1 (\tau ,t)} \\\end{array} }} \right],}$$

is described by the population balance equation:

$${\frac{\partial \mathbf{n}_{\mathbf 1} (\tau ,t)}{\partial t}+\frac{\partial \mathbf{n}_{\mathbf 1} (\tau ,t)}{\partial\tau }=\mathbf{D}_{\mathbf 1}^{\mathbf{out}} (\tau )\mathbf{n}_{\mathbf 1} (\tau ,t)}$$
(1)

subject to the boundary and initial conditions:

$${\begin{array}{l}\mathbf{n}_{\mathbf 1} (0,t)=\int\limits_0^\infty {\mathbf{D}_{\mathbf 1}^{\mathbf{in}} (\tau )\mathbf{n}_{\mathbf 1} (\tau ,t)d\tau } \\\mathbf{n}_{\mathbf 1} (\tau ,0)=\left[ {{\begin{array}{l}{n_1^2 (\tau ,0)} \\{n_1^1 (\tau ,0)} \\\end{array} }} \right]=\left[ {{\begin{array}{l}{N_1^2 (0)g_1^2 (\tau ,0)} \\{N_1^1 (0)g_1^1 (\tau ,0)} \\\end{array} }} \right] \\\end{array}}$$

where

$${\mathbf{D}_{\mathbf 1}^{\mathbf{out}} (\tau )=\left[\begin{array}{cc}{-2\left( {\Gamma (\tau )+2k} \right)}& 0 \\{2\left( {\Gamma (\tau )+2k} \right)}& {-\left( {\Gamma (\tau )+k} \right)}\end{array} \right]\quad\hbox{ and }\quad\mathbf{D}_{\mathbf 1}^{\mathbf{in}}(\tau )=\left[ {{\begin{array}{cc}{2\Gamma (\tau )}& {\Gamma (\tau )} \\0& 0 \\\end{array} }} \right].}$$

While the literal initiation of a cancer will be a series of cellular events that will lead to the development of a cancer, herein it is assumed that no information is available about the cancer until its initial clinical observation. So, the initial condition for the model is based upon these macroscopic measurements. The total number of cancerous cells can be determined from direct observation of the cancer and the initial age distributions and singlet fraction can be found using methods developed by Sherer et al.25 This method relies on BrdU pulse-labeling of cells in the S cell cycle phase to create two subpopulations in unbalanced growth, from which transition rates can be determined, amidst the balanced growth of the total population. The initial age distributions can be calculated from these transition rates.

Note that the initial number density for the i-tuple is the product of the total number of i-tuple cells, \({N_1^i (t)},\) and the age distribution, \({g_1^i (\tau ,t)},\) at time t = 0 where:

$${N_1^i (t)=\int\limits_0^\infty {n_1^i (\tau ,t)d\tau } .}$$

These total number densities define the total first-order product density as demonstrated by Ramkrishna and Borwanker,21

$${E[N(t)]=N_1 (t)=2N_1^2 (t)+N_1^1 (t).}$$

Second-Order Product Density

The second-order product density correlates likely age combinations of cells where \({n_2 (\tau ,\tau ^{\prime},t)d\tau d\tau ^{\prime}}\) is the probability that one cell exists in both infinitesimal age intervals \({({\tau ,\tau +d\tau })}\) and \({({\tau ^{\prime},\tau ^{\prime}+d\tau })}.\) Since a double or single cell is possible in each interval, all combinations of cell multiples need be considered in the second-order product density. So, the second-order product density vector is given by

$${\mathbf{n}_{\mathbf{2}} (\tau ,\tau ^{\prime},t)=\left[{{\begin{array}{l}{n_2^{2,2} (\tau ,\tau ^{\prime},t)} \\{n_2^{2,1} (\tau ,\tau ^{\prime},t)} \\{n_2^{1,2} (\tau ,\tau ^{\prime},t)} \\{n_2^{1,1} (\tau ,\tau ^{\prime},t)} \\\end{array} }} \right],\quad {\mathbf{N}}_{\mathbf{2}} (t) \\=\left[ {{\begin{array}{l}{N_2^{2,2} (t)} \\{N_2^{2,1} (t)} \\{N_2^{1,2} (t)} \\{N_2^{1,1} (t)} \\\end{array} }} \right]=\int\limits_0^\infty{\int\limits_0^\infty \mathbf{n}_{\mathbf{2}} (\tau ,\tau ^{\prime},t)d\tau d\tau ^{\prime}}},$$

where \({n_2^{i,j} (\tau ,\tau ^{\prime},t)}\) denotes an i-tuple of age τ and a j-tuple of age τ′ at time t. Similar to the first-order product density, when one of the doublet cells divides or dies, it either forms a doublet or is removed while the residual cell remains that continues its pairing. The second-order population balance equation and boundary conditions are

$${\begin{aligned} &\frac{\partial \mathbf{n}_`{\mathbf 2} (\tau ,\tau ^{\prime},t)}{\partial t}+\frac{\partial \mathbf{n}_{\mathbf 2} (\tau ,\tau ^{\prime},t)}{\partial \tau }+\frac{\partial \mathbf{n}_{\mathbf 2} (\tau ,\tau ^{\prime},t)}{\partial \tau ^{\prime}}=\mathbf{D}_{\mathbf 2}^{\mathbf{out}} (\tau ,\tau ^{\prime})\mathbf{n}_{\mathbf 2} (\tau ,\tau ^{\prime},t) \\ &\mathbf{n}_{\mathbf 2} (\tau ,0,t)=\int\limits_0^\infty {\mathbf{D}_{\mathbf 2}^{\mathbf{in}} (\tau ^{\prime})\mathbf{n}_{2} (\tau ,\tau ^{\prime},t)d\tau ^{\prime}} +\mathbf{D}_{\mathbf 1} (\tau ,t) \\ \end{aligned}}$$
(2)

respectively, where for binary division

$${\mathbf{D}_{\mathbf 2}^{\mathbf{out}} (\tau ,\tau ^{\prime})=\left[{{\begin{array}{cccc}{-2\left( {\Gamma (\tau )-\Gamma (\tau ^{\prime})-2k} \right)}& 0& 0& 0 \\{2\left( {\Gamma (\tau ^{\prime})+k} \right)}& {-2\Gamma (\tau )-\Gamma (\tau ^{\prime})-3k}& 0& 0 \\{2\left( {\Gamma (\tau )+k} \right)}& 0& {-\Gamma (\tau )-2\Gamma (\tau ^{\prime})-3k}& 0 \\0& {2\left( {\Gamma (\tau )+k} \right)}& {2\left( {\Gamma (\tau ^{\prime})+k} \right)}& {-\Gamma (\tau )-\Gamma (\tau ^{\prime})-2k} \\\end{array} }} \right],}$$
$${\mathbf{D}_{2}^{\mathbf{in}} (\tau ^{\prime})=\left[{{\begin{array}{cccc}{2\Gamma (\tau ^{\prime})}& {\Gamma (\tau ^{\prime})}& 0& 0 \\0& 0& 0& 0 \\0& 0& {2\Gamma (\tau ^{\prime})}& {\Gamma (\tau ^{\prime})} \\0& 0& 0& 0 \\\end{array} }} \right],\hbox{ and}}$$
$${\mathbf{D}_{\mathbf 1} (\tau ,t)=\left[ {{\begin{array}{c}0 \\0 \\{2\Gamma (\tau )n_1^2 (\tau ,t)} \\0 \\\end{array} }} \right].}$$

The inhomogeneous vector in the boundary condition is due to the formation of a double and single pair whenever a double divides. The dividing cell creates a double at the boundary that is paired with the residual cell. So, while each product density equation is closed with respect to higher order product densities, the ith-order product density is a function of the ith and (i − 1)st product densities.

If cellular independence is assumed initially, the initial second-order product densities can be written in terms of its first-order counterparts. In making a pair, one item is selected from the first-order product density and the second item can be any of the remainder.

$${\mathbf{n}_{\mathbf 2} (\tau ,\tau ^{\prime},0)=\left[{\begin{array}{l} N_1^2 (0)g_1^2 (\tau )({N_1^2 (0)-1})g_1^2 (\tau ) \\ N_1^2 (0)g_1^2 (\tau )N_1^1 (0)g_1^1 (\tau ) \\ N_1^1 (0)g_1^1 (\tau )N_1^2 (0)g_1^2 (\tau ) \\ N_1^1 (0)g_1^1 (\tau )({N_1^1 (0)-1})g_1^1 (\tau ) \\ \end{array}} \right]}$$

In addition, cellular independence leads to initial variance of zero. Solution of the above system yields the second-order product density vector.

The general principles of product densities derived by Ramkrishna and Borwanker21 can be applied to the above system to yield a total second-order product density:

$${N_2 (t)=4N_2^{2,2} (t)+2N_2^{2,1} (t)+2N_2^{1,2} (t)+N_2^{1,1} (t)},$$

where the expected population size and its standard deviation are given by:

$${\begin{aligned}E\left[{N(t)} \right]&=N_1 (t) \\ \left({\hbox{Var}\left[ {N(t)} \right]} \right)^{1/2}&=\sqrt{N_1^1 (t)+4N_1^2 (t)+N_2 (t)-\left( {N_1 (t)} \right)^{2}} \\ \end{aligned}}.$$
(3)

Simulation Techniques

To correlate the likelihoods of cure with the expected population and the standard deviation both Monte Carlo simulation techniques and analytical solutions to the first- and second-order product density equations (Eqs. 1 and 2) are employed. The first- and second-order product densities yield the expected population and standard deviation but not the transient likelihood of cure. The aggregate of multiple Monte Carlo simulations can be used to estimate the likelihood of cure through time as well as the expected population and standard deviation.

The population balance equations were solved using the method of characteristics in order of increasing product density number. This method produces a series of ordinary differential equations describing each characteristic curve whose origins can be traced back to either the initial or boundary condition. The first-order product density utilized the method of successive generations; the first generation is known and each subsequent generation can be found directly from its parent generation.14 The second-order product density required the use of integrating factors to describe the inhomogeneous differential equations of the characteristic curves. The resulting differential equations are solved iteratively until the reciprocal dependence of the final solution and boundary condition converges.

To estimate the likelihood of cure during a treatment, 100 Monte Carlo simulations were performed using the constant number simulation method of Mantzaris,15 with a maximum sample size of 106 cells, which is an expansion of the work of Shah et al.23 Briefly, the initial sample size is known, but the ages of the initial sample are selected randomly with weights based on the known initial age distributions. The sample then undergoes a series of quiescent periods preceding a single cellular event. The duration of each quiescent interval is a random period based on unaltered state paths of the cells in the system. Once the period is identified, the state of each cell in the system is updated and a single cellular event is performed; randomly selected based on the state of the each cell before a new quiescent interval is selected.

A number of approximations were made to reduce the computations time. First, the age-dependent transition rates \({\Gamma (\tau )}\) correspond to normalized Gaussian distribution division age distributions with a mean μ and standard deviation σ6:

$${\Gamma (\tau )=\frac{2}{\sqrt{2\pi }}\frac{e^{-\left( {\frac{\tau-\mu }{\sqrt{2}\sigma }} \right)^{2}}}{\hbox{erfc}\left( {\frac{\tau-\mu }{\sqrt{2}\sigma }} \right)}.}$$

These transition rates are approximated by 15th-order polynomials with unnoticeable differences between the analytical and polynomial curves. In particular, this greatly reduces the computational burden of the numerous integrations over various intervals. Lastly, the age range is terminated at least four standard deviations from the mean. Since normalized Gaussian transition age distribution are used, this age interval encompasses >99.8% of cell divisions while limiting the age range under consideration to a reasonable maximum.

Results

Herein, the model of binary cell division and two variants are analyzed for patterns of cure by employing Monte Carlo methods and solutions of the first- and second-order product density models. The models are used to demonstrate that the expected population size and its standard deviation, which are given by first and second product densities according to Eq. (3), can provide an estimate of the likelihood of cure. The first variant of this process considers a variable patient response to chemotherapy where the death rate is a random variable. If patient responses to a treatment are non-uniform; the time at which individual patients are cured will vary significantly. Non-responding outliers will reach cure at a much slower rate. As the non-responders have significant cancerous cell populations for extended durations, this dramatically influences the likelihood of cure estimates. The second variant considers the possibility of cells entering and leaving a prolonged dormant state in which they are insusceptible to treatment yet cannot divide. This can take a variety of forms such as physical location, resistance development, or physiological state and will lead to greater population size variation.

Binary Division

The objective of this study is to identify the conditions on the first and second product densities when nearly all patients are cured as predicted by the Monte Carlo simulations. For a given patient, smaller expected cancer cell populations imply that cure is more likely, but how small is small enough? In addition, the standard deviation provides a sense of confidence in the expected population, but how certain is certain enough and does this give additional insights on cures? In the forthcoming section we examine the trends of the expected population size and its standard deviation for qualities that can be used to approximate cure scenarios.

Expected Population

Can one simply claim cancer is cured when the predicted cancer cell numbers are less than one (or some pre-defined value less than one?). Although this seems reasonable, this study demonstrates that the expected population alone is not a reliable indicator of cure. To illustrate the difficulties in relying upon the expected number, the expected cell population was found when 99% of Monte Carlo simulated patients were likely cured for a small parameter space of division and death rates (see Table 1). The expected cancerous cell populations vary by nearly an order of magnitude (0.0210–0.1542 cells).

Table 1 Comparison of treatment durations, t 99, and expected populations to reach at least 99% cure, E[N(t 99)], for 10,000 simulated patients
Full size table

If a sufficient cure is assumed to occur at an arbitrary fixed value of 0.1 cells, then some of the patients will be under-treated with detrimental consequences and others over-treated which is sub-optimal (see Table 2). Using this cure threshold, the range of cure percentages begins at 95.6% for the slow division and low death while the treatment for the fast division and slow death case is 99.7%. If a sufficient cure is assumed to occur at a lower fixed value of 0.01 cells for the expected value, then all patients with high division and high death rates will be over-treated spending an extraneous 44.2% of time on medication beyond what is considered necessary for likely cure. These discrepancies would likely be even greater if a broader parameter space is sampled. Thus, an expected population appropriate for gauging likely cure for a given situation is inestimable a priori.

Table 2 Using an expected number of cells to determine treatment duration leads to potential over and under exposures
Full size table

Standard Deviation

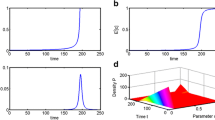
If providing a mean cell population threshold alone is insufficient to claiming cancer cure, what about claiming a cancer cure when the expected cell population number is less than one and the standard deviation of that cell population is also less than one? This seems like a more precise indicator of likely cure as this scenario requires both a low cancerous cell population and a certainty in this estimate. However, while a standard deviation less than one indicates that patients are entering remission; the variation in population is still significant enough where not all patients will be cured. As seen in Fig. 2, when the standard deviation and expected population are both below one, the cure percentage is roughly 80%. To find treatments necessary to nearly ensure cure \({(P_0 (t)\approx 1)},\) the range of population sizes must be restricted further. The mean and standard deviation of the population size should be reduced to an appropriate level.

Figure 2
figure 2

For binary division, an expected population that is at least six standard deviation below one cell, \({({\hbox{Var}[N]})^{1/2}\approx 0.1667},\) provides a good estimate for the minimum treatment sufficient to induce cure in nearly all patients: As the expected population and standard deviation decrease (shown in Fig. 2a), Fig. 2(b) shows how the corresponding likelihood of cure continually increases. The cure time, \({\hbox{t}_{6\sigma}},\) as estimated by the six-sigma approximation are indicated on the figures. For division rates with the same expected transition age, solution of the first-order product density equations (PBE) produces identical expected population dynamics (E[N], obtained by averaging the population sizes of 100 Monte Carlo simulations). The uncertainty in cell transitions is dominated by the death term so the standard deviation in the population sizes \({\left(({\hbox{Var}[N]})^{1/2}\right)}\) is nearly identical for the different division rates. This results in similar near identical cell number probability distributions shown in Fig. 2c

Full size image

To identify this appropriate level, an approximation is made of the total cell number probability distribution using the mean and standard deviations. It is desired to have a cancerous population with less than one cell. If a normalized Gaussian distribution is assumed with a mean that is one standard deviation less than one, then less than 67% of the distribution will be less than one. (The actual rates of cure are roughly 90% in Fig. 2.) While the actual distribution will most likely be of a different shape, this estimate provides a first approximation for the expected level of cure. Requiring that the mean is multiple standard deviations less than one only enhances the likelihood of cure.

Three transition rates, whose transition age distributions have identical means (24 h) but different standard deviations (2, 6 h, or Γ = 0.0289 h), were evaluated to test the impact of transition variability on the rate of cure. The identical expected population dynamics and minimal differences in the population standard deviations in Fig. 2a, lead to marginal differences in the likelihood of cure as a function of treatment duration as seen in Fig. 2b. Though, as anticipated, the most diverse transition rate, Γ = 0.6931 day, does asymptotically approach 100% cure most reluctantly. The similarity of total cell number standard deviations between division rates is due to magnitude of the death rate, which is the same for the division rates, relative to the division rate. The uncertainty in the total number of cells is due mostly to the uncertainty in the timing of the death process. This leads to similar cell number probability distributions (Fig. 2c) and their corresponding standard deviations.

For the cases tested in Fig. 2b, we found that cure was induced in all 100 Monte Carlo simulations if the mean is six standard deviations less than one. Interestingly, although not surprisingly, this matches the industrial convention of six-sigma: with high standards of quality control, the number of defects will be minimal. In this case, a stricter standard could be imposed, but since near cure is reached within the six-sigma convention; the benefits of extra treatment will be minimal. The six-sigma criterion is then tested for a larger initial cell population, 1010 cells, which is observed in acute myeloid leukemia16 remission, using the most diverse transition rate of Γ = 0.6931 day. As seen in Fig. 3, when the six-sigma criterion is reached after 81 days, the cure is likely near 100%. In fact, cure only becomes very likely after roughly 75 days, so the six-sigma convention seems to provide an estimate for the treatment required to achieve near cure within a reasonable time frame.

Figure 3
figure 3

The six-sigma estimate of cure time, t 6σ, is evaluated for a model of acute myeloid leukemia (based on 100 Monte Carlo simulations). The binary division model is applied to an initial population of 1010 cells with Γ = 0.6391/day and k = 1.0397/day

Full size image

Patient Variability

In the binary division model, it was assumed that the cancer in all patients behaves similarly; the growth and death rates are the same in all patients. However, one of the major issues in chemotherapy is non-uniformity of patients cancer response to a drug. While some patients respond well, others may have less favorable pharmacokinetics or tumor susceptibility. Even for those patients whose cancer responds favorably there will likely be variations in patient response.

This phenomenon is applied to the binary division model by using a random variable death rate. The form of the random variables is assumed to take a normalized Gaussian distribution with a standard deviation that is one-third of the mean death. Clinically, these distributions could be derived from statistics of patient responses or genetic polymorphisms. Regardless of the whether the rates are random variables or not, the structure of the binary division model remains unchanged.

When randomness is introduced into the death rate, cure is again very likely when the six-sigma threshold is reached as shown in Figs. 4a and 4b. In fact, 88% of the patients are cured after 250 days while the total expected population has decreased by only two orders of magnitude. This difference is due to a handful of non-responders to the medication with large cell populations while the majority of patients are at or near cure. The expected cancer population for the quarter of the population with the lowest death rates (least responsive) only decreases by an order of magnitude after 100 days. When a distinction is made between responders and non-responders, where the quarter of the population with the least drug activity (lowest death rates) is considered non-responders, there is a significant difference in the cure levels associated with treatments durations to reach near cure as estimated by the six-sigma threshold (see Fig. 4b). So, while almost all patients will likely enter clinical remission within 250 days, the amount of treatment required for likely cure is vastly different between the patients based on their drug responsiveness: 45 days for most responsive quarter of the population (highest death rates), 80 days for the second most responsive quarter, and 140 days for the third most responsive quarter (see Fig. 4a).

Figure 4
figure 4

Non-homogenous patient response to chemotherapy leads to a cure of 88% of the patient population within 250 days even though the expected cancerous cell population remains large. The death kinetics are described by a normal random variable with mean of 1.0397/day and standard deviation of 0.3119/day while the birth kinetics adhere to an age-independent rate of 0.6931/day. Results are based on 1000 Monte Carlo simulations. The patient population can be divided into quarters based on their death kinetics or level or responsiveness: 0–25% (least responsive), k < 0.8147/day; 25–50%, 0.8147/day < k < 1.0397/day; 50–75%, 1.0391/day < k < 1.2647/day; and 75–100% (most responsive), k > 1.2647/day. (a) The expected cell population from all patients slowly approaches one cell. Separating the patient population into quarters, it can be seen that this slow rate of decline is due to averaging the poor response behavior of the least responsive quarter (0–25%, k < 0.8147). (b) Even though the expected cancerous cell population is not near zero, significant levels of cure are obtained. Separating the total population into responders (the 75% of the population with the highest death rates) and non-responders (the 25% of the population with the lowest death rates), there the progressively shorter cure times for progressively more responsive quarters of the population: \({{t_{6\sigma} \left({0\hbox{-}25\%}\right) < t_{6\sigma } \left({25\hbox{-}50\%}\right) < t_{6\sigma } \left( {50\hbox{-}75\% } \right) < t_{6\sigma } \left({75\hbox{-}100\% } \right).}}\) (c) If non-responders are identified and their treatment adjusted to the minimum responder level (k = 0.8147/day) at 50 days or 100 days, the treatment duration for all patients to likely become cured is reduced

Full size image

If the non-responders could be identified (either through measuring genetic polymorphism, relevant enzyme levels, drug concentration, or a surrogate marker) their treatments could be adjusted accordingly. If this patient adjustment occurs after 100 days, 230 days of treatment are needed to reach the six-sigma criterion while if the treatment modification can be made after 50 days, only 195 days are needed for a patient to reach near cure based on six-sigma (see Fig. 4c). However, if the non-responders cannot be differentiated from the responders, then it is impossible to tell which patients are most likely in remission and all patients must be treated identically. Treatment outcomes for this “average” patient are inefficient for both responders and non-responders. The responders are exposed to treatments even after they are likely cured while many non-responders are never cured due to the finite duration of treatments. Thus, identification of the non-responders is critical as it not only increases their survival, but the financial burden and potential collateral damage of responders can be dramatically reduced relative to treatment suggested by the aggregate model.

Quiescence

For many cancers, there is a possibility that cells could “escape” and be impervious to the drug due to spatial location, quiescent periods, or somatic mutations. Ideally, chemotherapy should be applied until all of the cells in hiding are removed, so though the expected number of cells may be low, if some are in a quiescent state then the cure percentage may not be high. In modeling these effects, we make the assumption that cells impervious to chemotherapy are completely dormant in that they neither die nor divide. Also, all proliferation cells, single and paired cells, enter the dormant state as a single cell of age zero at a fixed rate q and re-enter proliferation as a single cell of age zero at a fixed rate p. These fixed transition rates imply that dormant transitions are completely random: the likelihood of entering dormancy does not depend on the age of a cell and the likelihood of leaving dormancy does not depend on the time duration spent in dormancy. These rates give the dynamics of the first-order product density of dormant cells, \({n_1^Q (\tau ,t)},\) subject to the initial condition \({n_1^Q (\tau ,0)=N_1^Q (0)g_1^Q (\tau ,0)}\) (see Fig. 5).

Figure 5
figure 5

Binary division model modified with the addition of a quiescent state. If cells can become temporarily dormant, cell behavior will depend on the whether a cell is dormant, \({n_1^Q (\tau ,t)},\) or actively proliferating, \({n_1^2 (\tau ,t)}\) or \({n_1^1 (\tau ,t)}.\) Arrows denote possible transitions and associated rates: entry rate to the dormant state, q, re-entry rate to proliferation, p, death rate, k, proliferation rate, \({\Gamma (\tau )}\)

Full size image

The effect of the dormant cancerous cell population is revealed in the changing slope of the expected population dynamics as shown by the lines labeled with continuous treatment, which represent averaged Monte Carlo simulation results, in Fig. 6a. When the entry and exit rates of the quiescent state are equal (p = q = 0.01/day), the majority of cells are initially in a proliferating state, so there is a large, nearly constant rate of death. After the majority of the proliferating cells have been exterminated, the dormant cell population dwarfs the number of proliferating cells, and the rate at which the expected total population approaches zero cells depends on the rate at which the dormant cells become active. This shift in death rate corresponding with the emergence of the quiescent population implies a potential relative advantage for cyclic over continuous chemotherapy may arise. In addition to the likely decrease in toxic side effects due to the recovery intervals, the rest periods in cyclic chemotherapy allow quiescent cells to enter and accumulate in the proliferation state, so each treatment cycle will have a higher specific death rate compared to the corresponding continuous treatment. However, a disadvantage is that the rest periods allow for division of the cancerous cells with no death. This leads to an increase in the total amount of treatment required to reach the same expected cancer population size.

Figure 6
figure 6

The six-sigma criterion holds for a binary division model with a quiescent cell population: based on the aggregate of 1000 Monte Carlo simulations. The figures in the left column (a, c, and e) contain simulations with a low rate of transition in both directions between quiescence and proliferation (p = q = 0.01/day). The figures in the right column (b, d, and f) contain simulation results for a higher rate of transition to quiescence (p = 0.01/day, q = 0.1/day). (a, b) The division rate is a fixed constant, Γ = 0.0289/h, while the death rate is k = 0.1/h when the drug is applied. For a continuous application of chemotherapy, the initially steep decline in the expected population becomes tempered as the fraction of dormant cells becomes prominent. This occurs more rapidly in figure (b) due to the shorter residence time in the proliferation state. Eventually, the lifetime in dormancy limits the rate of cure. In cyclic chemotherapy, 50 h boluses are separated by a 25 h rest period. (c, d) The division rate corresponds to a normalized Gaussian division age-distribution of mean of 24 h and standard deviation of 4 h while the death rate is k = 0.1/h. (e and f) There is a difference in the likelihood of cure as defined by the six-sigma threshold between age-structured and unstructured models. A cyclic chemotherapy schedule where 50-h treatments are separated by a 25-h rest period may have marginal benefits in certain cases (e) but not in others (f)

Full size image

To explore the effectiveness of cyclic chemotherapy, cycles of 50-h drug treatments followed by a 25-h rest period were simulated. When the entry and exit rates of the quiescent state are equal (p = q = 0.01/day), the total treatment time is nearly identical (∼900 h) with the cyclic schedule incorporating ∼500 h of rest time during the treatment. If the rate at which cells enter quiescence is increased (q = 0.1/h), the majority of cells are initially quiescent so the rate of death is limited by the rate at which quiescent cells enter proliferation (see Fig. 6b). Since the expected rate of cancer cell removal does not change significantly during the treatment, the relative advantages of cyclic chemotherapy are minimal. For this scenario, cyclic chemotherapy increases the amount of time of chemotherapy exposure required to achieve the six-sigma cure relative to continuous therapy by ∼800 h (∼2200 vs. ∼3000 h).

With the presence of multiple stages, such as quiescent and proliferating cells, the age distributions become transient even when an age-independent death rate is applied. While the specific division rate is independent of changes in the age distribution for the age-independent division rate studied above, for age-dependent division rates, the transient age distributions do become significant. This leads to fluctuations in the specific growth rate which produces periodic oscillations in the expected number density (see Figs. 6c and 6d). However, the validity of the six-sigma approximation for minimal sufficient treatment is not affected by the increase in population variation (see Figs. 6e and 6f). Regardless of the age dependence or treatment type, when comparing the times to cure, as estimated using the six-sigma threshold, the presence of a dormant population increases the treatment duration (Figs. 6e and 6f) necessary to reach a desired level of cure relative to non-dormant models (Figs. 2–4).

Discussion

The idealistic objective of chemotherapy is to cure all patients, but this would require chemotherapy treatments that are unreasonable in duration or dosage. A practical alternative is to maximize survival rates subject to patient limits. These limits could include factors that affect patient discomfort such as: drug dosage and duration, monetary costs, and physical well-being where the marginal benefit of over-treatment must be weighed against all costs involved. To this end both over-treatment and under-treatment are non-optimal situations and the question becomes one of identification of the appropriate treatment strategy that maximizes the cancer survival rates; or rather, one that minimizes treatment burden while still nearly ensuring cure. However, calculation of the cell number probability distribution required for such an analysis is difficult. To this end, we investigated whether an approximation of the system state, as described by the expected population size and its standard deviation, is sufficient to identify treatments that satisfy a more qualitative objective: almost ensure a given patient is cured without undue burden assuming that whether or not the necessary treatments are feasible is another matter altogether.

Using a binary cell division model system, and operating under the assumptions that all cells in a patient are governed by the same set of kinetics and external influences other than death due to chemotherapy can be neglected, we found that the expected population size and its standard deviation can identify treatments that cure nearly all patients. A small cancerous cell population is desired, but the expected population alone is a poor prognosticator; confidence that the population is small is required. Based on our model predictions, we found that a mean that is one standard deviation below one cancerous cell indicates that some patients have been cured, and a mean that is six standard deviations below one cell correlates well with extremely high cure percentages. Notably, this six-sigma criterion does not necessitate prolonged chemotherapy treatments.

When the binary division model was applied to a scenario where patient response was non-uniform, we found that identification of non-responders is extremely beneficial to both the responders and non-responders. If patients are treated equivalently, all patients are subjected to lengthy treatments which likely may not end in cure. If a patient’s response to a treatment can be quantified, treatment adjustments can be made for non-responders so they will be more likely to enter remission and for responders so they will not have to endure unnecessary periods of treatment. Lastly, the presence of a temporarily dormant and non-responsive tumor population lengthens the necessary period of chemotherapy as treatment must be given until no cells are dormant and all proliferating cells are removed. In such a case, cyclic chemotherapy may have potential relative advantage (i.e., similar results for less cumulative drug administration or else similar cumulative drug administration with the benefit of recovery periods) over continuous infusions. The period of time spent in dormancy is a very uncertain event and leads to greater population variation. This is especially prevalent for low expected population sizes. However, the six-sigma criterion still identifies treatments that are very likely to result in cure.

While this present work is limited to cell cycle non-specific treatment with intransient rate functions to ensure the clarity of the illustrative examples, the model framework can be adjusted for time-dependent functions. (Furthermore, the solution methodology would not require any modifications.) There are many factors that would lead to transient birth or death rates including drug schedules and evolving drug resistance. For example, drug schedules could produce transient drug levels that dynamically alter the birth and death rates. Sherer et al.24 use constitutive pharmacokinetic model to predict a changing exposure to toxic agents while a pharmacodynamic model translates these drug levels into a dynamic, and cell cycle-specific, cell death for an age-structured model. A similar constitutive pharmacodynamic model could be written describing the changes in the birth rate due to drug exposures. Alternatively, cells may develop drug resistance or up/down regulate pathways in response to a drug which would affect the efficacy of subsequent treatments. The development of drug resistance could be accounted for in the model by including discrete resistance levels10 or by introducing a second continuous variable which accounts for the observed or anticipated changes in pharmacodynamics.

The model situations presented above are gross simplifications of the real problem but they enable the exploration of utilizing stochastic mathematical models to estimate cure. The question remains, though: how will this approach be applied to a real system? What is the appropriate model framework and what are the model parameters? In addition, potential clinical treatments will be constrained by a patient’s health, so the treatments required to achieve likely cure are not feasible. These are non-trivial problems as the model framework will likely vary between diseases, patient response are difficult to predict, and key rate parameters are difficult to measure.

The application of this approach would come in the form of an inverse model. That is, the model itself would need to be matched to accumulated patient data. In this case, the most basic data required would include treatment protocols and the distribution of durations in which patients remained in remission. Potential model frameworks and rate parameters could be identified that matched the patient data. However, any patient discrimination data such as drug concentration or tumor proliferation indices or genetic predispositions could also be utilized (and may be necessary) in model and parameter refinement. Once the model is identified for a cancer, predictions could be made (as exemplified in this paper) on an individual basis for incoming patients. As mentioned early, the clinically related studies by Lillyman and Lennard13 and Schmiegelow et al.22 and the in vitro work of Bökkerink et al.3 hint at the positive relationship between metabolite levels, the corresponding death rates, and the resulting probability of cure. By modeling this system, the appropriate durations of treatment or treatment adjustments can be made quantitatively for individual patients. While the methodology presented in this work is not immediately ready for clinical application, it does provide a starting point for which more quantitative analyses of cancer treatments can be based.