Stability, Controllability, and Observability of the “Four State” Model for the Sarcomeric Control of Contraction

Abstract

A model of the sarcomeric control of contraction at various loading conditions has to maintain three cardinal features: stability, controllability (where the output can be controlled by the input), and observability (where the output reflects the effects of all the state variables). The suggested model of the sarcomere couples calcium kinetics with cross-bridge (XB) cycling and comprises two feedback mechanisms: (i) the cooperativity, whereby the number of force-generating (strong) XBs determines calcium affinity, regulates XB recruitment, and (ii) the mechanical feedback, whereby shortening velocity determines XBs cycling rate, controls the XBs contractile efficiency. The sarcomere is described by a set of four first-order nonlinear differential equations, utilizing the Matlab's Simulink software. Small oscillatory input was imposed when the state variables trajectories reached a steady state. The linearized state-space representations of the model were calculated for various initial sarcomere lengths. The analysis of the state-space representation validates the controllability and observability of the model. The model has four poles: three at the left side of the complex plane and one integrating pole at the origin. Therefore, the system is marginally stable. The Laplace transform confirms that the state representation is minimal and is therefore observable and controllable. The extension of the model to a multi-sarcomere lattice was explored, and the effects of inhomogeneity and nonuniform activation were described.

APPENDIX

The physiological model assumptions were derived from our previous studies.14 ^– 18 The assumptions relevant to present analysis of the effects of length oscillations on force development are introduced in here for clarity and convenience.

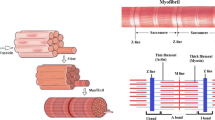
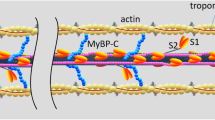
• 1. The regulatory unit includes a single troponin–tropomyosin complex, with seven neighboring actin monomers, and the adjacent myosin heads.

• 2. The XBs cycle between the weak and the strong conformations. A single ATP molecule is hydrolyzed when the XB turns from the weak to the strong conformation.7 Force is produced only by XBs at the strong conformation.

• 3. The active force is proportional to the number of XBs in the strong conformation, in the single overlap region between the actin and myosin filaments.

• 4. The XB behaves as a Newtonian viscous element.5 ^, 10 The average force per XB (F _XB) during steady shortening is a linear function of the shortening velocity (V)

  $$F_{{\rm XB}} = \bar F(1 - V/V_{\rm u} )$$

  (A.1)

  where$\bar F$is the force per XB at isometric regime (unitary force) and V _u is the maximal (unloaded) velocity.

• 5. The troponin-C regulatory protein has one low-affinity site for calcium binding that regulates XB cycling. Calcium binding to this low-affinity site regulates the rate of the actomyosin ATPase and XB transition from the weak to the strong conformation.3

• 6. Calcium may dissociate from troponin after the XB turns to the strong conformation. The strong XB can generate force without having bound calcium to the adjacent troponin.16 ^, 23

The system variables R, A, T, and U denote the density of the four regulatory units. The sum of regulatory units is constant:

$$R + A + T + U = {\rm TRo}$$

(A.2)

where the constant TRo denotes the total density of the troponin regulatory complexes.

The system (Fig. 1) is described by four first-order nonlinear differential equations:

$$\frac{{dA}}{{dt}} = k_\ell [{\rm Ca}]({\rm Tro} - A - T - U) - (f + k_{ - \ell } )A \nonumber\\ + (g_0 + g_1 V)T$$

(A.3)

$$\frac{{dT}}{{dt}} = fA - (g_0 + g_1 V + k_{ - \ell } )T + k_\ell [{\rm Ca}]U$$

(A.4)

$$\frac{{dU}}{{dt}} = k_{ - \ell } T - (g_0 + g_1 V + k_\ell [{\rm Ca}])U$$

(A.5)

$$\frac{{dSL}}{{dt}} = - V$$

(A.6)

where [Ca] is the free-calcium concentration.$k_\ell$ and$k_{ - \ell }$ represent the kinetic rates of calcium binding and dissociation from troponin, respectively.$k_\ell$ is assumed to be constant26 and diffusion limited, whereas the dissociation rate,$k_{ - \ell }$, is determined by the cooperativity mechanism [Eq. (3)] i.e.:

$$k_{ - \ell } = \frac{{k_\ell }}{{K_{[{\rm Ca}]} }}$$

(A.7)

An increase in the number of strong XBs raises calcium affinity through the cooperativity mechanism [Eq. (3)] and decreases the rate of calcium dissociation [Eq. (A.7 )].

The generated force is determined by the number of strong XBs (N _XB) at states T and U, in the single overlap region (L _s) between the thin and thick filaments. The number of the strong XBs, N _XB, [Eq. (1)] is a product of the density of strong regulatory units (states T and U) and the muscle volume of interest, that is defined by the muscle cross-section area (a) and the single overlap length (L _s).

The force (F) is a product of the number of strong XBs (N _XB) and the average force per XB, according to assumptions 3 and 4:

$$F = \bar FaL_{\rm s} (T + U)(1 - V/V_{\rm u} )$$

(A.8)

In general, the velocity is determined by coupling the equation for force development by the sarcomere [Eq. (A.8)] with the equation that represents the load that the sarcomere encounters.14 ^, 17 Coupling the force development by the sarcomere and the loading conditions yield an equation for the shortening velocity, and this equation is used for solving the state equation [Eqs. (A.3)–(A.6)], including the sarcomere length.