Neuronal Electrical Rhythms Described by Composite Mapped Clock Oscillators

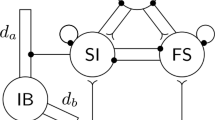
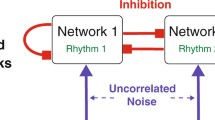
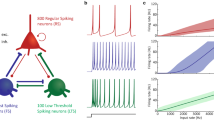
The Mapped Clock Oscillator (MCO) model is a representation of omnipresent transmembrane voltage oscillations in excitable cells. We present a generalized version of the MCO that can model neuronal electrical oscillations, both labile and omnipresent, entirely within the framework of a system of ordinary differential equations. The previously described MCO was a second-order system, whereas the model presented here, which we call the composite MCO (cMCO) is a fourth-order system. Furthermore, we show how this cMCO can also be adapted to describe a pair of cells that forms a functional unit, as illustrated here by a model of the CA3 pyramidal cell and its basket cell interneuron feedback loop. The model was able to reproduce the high frequencies (super gamma) and possibly chaotic dynamics observed in the biological system.

APPENDIX

This appendix describes the second-order MCO. The variables described here have the same meaning in the fourth-order cMCOs presented in this paper. Refer to Zariffa et al. 36 for more detailed explanations.

The MCO model was developed with the understanding that excitable cells can undergo rhythmic transmembrane depolarizations. These nonlinear oscillators have an “intrinsic frequency” but are influenced by their environment, including other nearby oscillators. Each oscillator is driven by a “clock,” consisting of two differential equations:

$$\dot{\alpha} = \omega \alpha (1-\alpha^{2})$$

(A.1)

$$\dot{\phi} = \omega$$

(A.2)

where ${\alpha}$ is the amplitude, ${\phi}$ is the phase and ${\omega}$ is the intrinsic frequency of the clock. Adding the effective stimuli (${S_{\alpha}}$, ${S_{\phi}}$, ${S_{\gamma1}}$, and ${S_{\gamma2}}$) applied to the clock's three input portals (called ${P_{\alpha}}$, ${P_{\phi}}$, and ${P_{\gamma}}$) and including refractoriness (${R(.)}$), we obtain:

$$\dot{\alpha} = \omega \alpha (1 + S_{\alpha} -\alpha^{2}) + S_{\gamma 1} \sin(\phi) + S_{\gamma 2} \cos(\phi)$$

(A.3)

$$\dot{\phi} = \omega (1 + R(\phi) S_{\phi}) + \frac{1}{\alpha} (S_{\gamma 1} \cos(\phi) - S_{\gamma 2} \sin(\phi))$$

(A.4)

where ${\dot\phi}$ and ${\alpha}$ are forced to be nonnegative (i.e. negative values are set to zero). This clock is then mapped by a static nonlinearity (e.g. representing transmembrane ionic transport mechanisms) onto an observable output, $y$, which is also affected by the effective stimulus (${S_{\rho}}$) applied to the mapper through its synaptic portal (${P_{\rho}}$):

$$y = a_{0} (1+S_{\rho}) + \alpha \sum_{k=1}^{N}[a_{k} T_{k}(\cos(\phi)) + b_{k} \sin(\phi) U_{k-1}\\ (\cos(\phi))]$$

(A.5)

where $y$ represents the transmembrane voltage, ${a_{0}}$ is the intrinsic average level, ${a_{k}}$, ${b_{k}}$ are the Fourier coefficients of the waveform of the intrinsic oscillation, ${T_{k}}$ and ${U_{k}}$ are the $k$th Tchebychev polynomials of the first and second type, respectively, $k$ is the harmonic index, ${S_{\alpha}}$, ${S_{\phi}}$, ${S_{\gamma1}}$, ${S_{\gamma2}}$, and ${S_{\rho}}$ represent the inputs to the four different portals of the oscillator (if the oscillator is uncoupled, then these are all zero), $R({\phi})$ is the refractoriness function, which ensures that the neuron stops being sensitive to frequency inputs while it is bursting. It is implemented as a highpass Butterworth function shown in Eq. (A.6).

$$R(\phi) = \frac{1}{\sqrt{1 + (\frac{2 \pi r}{\phi})^{2 N}}}$$

(A.6)

The Tchebychev polynomials are used in the static nonlinearity of the mapper because in the absence of any stimuli (${S_{\alpha}} = {S_{\phi}} = {S_{\gamma1}} = {S_{\gamma2}} = {S_{\rho}} = 0$) the static nonlinearity reduces to a standard Fourier series.2 The parameters of the static nonlinearity are the Fourier coefficients. Hence, the measured transmembrane voltage waveform of an uncoupled biological oscillator can be analyzed in a Fourier series to determine the model parameters of the mapper.

In Eqs. (A.3)–(A.5), four stimulus portals take their effect in different places. Refer to the main text and to Zariffa et al. 36 for a description of their meaning. In general, for the $n$th oscillator, having the set ${I_{nm}}$ of neighboring oscillators, the four portals are shown in Eqs. (A.7)–(A.11).

• Portal ${P_{\phi}}$:

  $$S_{\phi} = \frac{\sum_{m \epsilon I_{nm}}^{}(c_{\phi n m} y_{m}) - \beta_{\phi} y_{n} + a_{0} S_{\rho}}{\sigma_{n}}$$

  (A.7)

• Portal ${P_{\alpha}}$:

  $$S_{\alpha} = \frac{\sum_{m \epsilon I_{nm}}^{}(c_{\alpha n m} y_{m}) - \beta_{\alpha} y_{n}}{\sigma_{n}}$$

  (A.8)

• Portal ${P_{\gamma}}$:

  $$S_{\gamma 1} = \frac{\sum_{m \epsilon I_{nm}}^{}(c_{\gamma n m} \alpha_{m} \sin(\phi_{m}))}{\delta}$$

  (A.9)
  $$S_{\gamma 2} = \frac{\sum_{m \epsilon I_{nm}}^{}(c_{\gamma n m} \alpha_{m} \cos(\phi_{m}))}{\delta}$$

  (A.10)

• Portal ${P_{\rho}}$:

  $$S_{\rho} = g\left(\frac{\sum_{m \epsilon I_{nm}}^{}c_{\rho n m} \dot\phi_{m} - \beta_{\rho} \dot\phi_{n}}{{\rm sgn}(a_{0})\omega_{n}}\right)$$

  (A.11)

The function ${g()}$ has the general shape shown in Fig. 17.

FIGURE 17.

Synaptic transfer function. This function is used to ensure that the synaptic stimulation of the oscillator saturates, rather than become arbitrarily large as inputs increase.

The variables have the following meanings:

• ${\sigma_{n}}$ = ${(\sum_{k=1}^{N}(a_{k}^{2}+b_{k}^{2}))^{1/2}}$ is a normalization factor for the mapper, representing the amplitude of the intrinsic waveform.

• ${\delta}$ is a static clock normalization factor. Unless otherwise specified it is set to 0.1.

• ${\omega_{n}}$ is the $n$th oscillator's intrinsic frequency.

• ${\beta_{\phi}}$, ${\beta_{\alpha}}$, and ${\beta_{\rho}}$ are feedback factors.

• ${c_{\alpha}}$, ${c_{\phi}}$, ${c_{\gamma}}$, and ${c_{\rho}}$ represent the coupling factors between the oscillators. They are real numbers between 0 and 1, where 1 signifies that the corresponding portal is fully open, and 0 signifies that it is closed. The sign of ${c_{\rho}}$ is used to distinguish between excitatory and inhibitory synapses.

• ${y_{m}}$ is the transmembrane voltage of the driving oscillator.

• ${\eta}$ is a scaling factor for how much the resting level is allowed to vary.