Co-jumps and recursive preferences in portfolio choices

Abstract

This paper investigates a multivariate, dynamic, continuous-time optimal consumption and portfolio allocation problem when the investor faces recursive utilities. The economy we are considering is described through both diffusion and discontinuities in the dynamics. We derive an approximated closed-form solution to optimal rules by exploiting standard dynamic programming techniques. Our findings are manifold. First, we obtain dynamic optimal weights, inversely proportional to volatility. Second, we show that both co-jumps frequency and intensity play a crucial role, as they considerably limit potential losses in the investors’ wealth. Third, we prove that jumps in precision reinforce the effect of jumps in price, further reducing optimal allocation. Finally, we highlight how co-jumps may influence investors’ choices regarding intertemporal consumption.

1 Introduction

One of the critical dimensions in Finance is to tackle the long-standing issue of uncertainty in decision-making, namely to comprise the investors’ behaviour among variables describing the economy. From a mathematical perspective, defining the agent’s preference for information is equivalent to providing a suitable form of the (expected) utility to maximize the latter. This paper studies a multivariate, dynamic, continuous-time optimal consumption and portfolio allocation problem, assuming that the economy is described in an incomplete market by diffusion and discontinuities in the dynamics and that investors are represented through recursive preferences.

The literature has produced a considerable number of contributions within the portfolio decisions’ framework, primarily when the investors’ preferences only rely upon their risk aversion, see e.g. Lazrak (2004). Motivated by tons of empirical findings, see e.g. Duffie et al. (2000) among others, several authors generalized the pioneering work of Merton (1971) in incomplete markets: to name but a few, Liu (2007) exploits affine models to face volatility risk, Buraschi et al. (2010) also consider stochastic correlation in a multivariate framework, while Liu et al. (2003) provide a closed-form formula for optimal portfolio allocation by assuming discontinuities in the state variable dynamics: surprisingly, the optimal weights result to be independent of both the instantaneous volatility and the long-run mean level, implying a static allocation mechanism. The latter shortcoming has been overcome in Oliva and Renò (2018), where a Markowitz-compliant approximate solution is furnished for a Wishart model. In Jin and Zhang (2012), the authors examine a multi-asset model with constant volatility when the price can jump, also in the presence of ambiguity. Very recently, Jin et al. (2021) investigate the impact of tail risk on portfolio selection, showing that the presence of jump ambiguity might imply wealth losses. In a complete market framework, the optimal portfolio allocation in bank account, stock and non-redundant derivatives within a stochastic volatility framework can be derived, both in the absence and in the presence of jumps, see e.g. Liu and Pan (2003) and Branger et al. (2008), respectively. In a similar context, Cheng and Escobar-Anel (2021) solve a commodity-based portfolio allocation problem with separable preferences, including ambiguity, but without considering jump effects. The most common choice in the economic literature is to consider the so-called separable preferences where CRRA is undoubtedly the most famous and widely used, due to its mathematical convenience. CRRA shares several interesting features, such as the scale invariance and the dynamic consistency, see e.g. Wakker (2008). On the other hand, when consumption is included among the economic variables, a time-separable utility such as CRRA suffers from the drawback of forcing the parameters characterising both investment and consumption (i.e., risk aversion and intertemporal elasticity of substitution of consumption, respectively) to undergo an inverse proportionality relationship, see e.g. Weil (1989).

In this perspective, the literature has long questioned what the ideal solution might be, capable of providing analytical support for the observable investors’ behaviour. Hence, decision-makers might consider suitable utility functions to disentangle the investors’ risk aversion from the growth rate of consumption reactivity to the interest rate trend. To this end, the non-separable preferences have been introduced in the literature. As stressed in Kreps and Porteus (1978), even relaxing the separability assumption, such preferences continue to be scale-invariant and allow to use dynamic programming techniques to solve any associated optimisation problem. For these reasons, in the present paper, we focus on a particular family of non-separable preferences, known as stochastic differential utilities (SDU), introduced in Epstein and Zin (1989) for discrete-time models, and generalised in Duffie and Epstein (1992) in a continuous-time framework.

With this in mind, Kraft et al. (2013); Xing (2017); Kraft et al. (2017); Pu and Zhang (2021) provide suitable verification theorems for the associated Bellman equations used to solve some consumption-portfolio decision problems in diffusive markets. In contrast, Chen et al. (2021) examine the role played by information in continuous-time optimal consumption-portfolio problems when stock returns are unobservable. Sometime earlier, Chacko and Viceira (2005) introduce the precision process, intended as the inverse of volatility, to obtain dynamic optimal rules. Within the same framework, Faria and da Silva (2016) exhibit a small impact of the elasticity of intertemporal substitution of consumption (EIS) on optimal allocation, also in the presence of ambiguity.

This paper is part of the research strand dealing with optimal consumption-allocation problems when recursive utilities describe investors’ preferences. Differently from the extant literature, we assume an economy allowing for discontinuities in both the stock price and the state variable in a multivariate framework. More precisely, we intend to model the avowed empirical property such that peaks in volatility levels correspond to drops in the asset prices, see e.g. Eraker (2004); Todorov and Tauchen (2011); Bandi and Renò (2016). Moreover, since the changes mentioned above in price and volatility occur simultaneously, we dub them co-jumps, and introduce a unique counting process, typically a non-compensated Poisson, driving the non-diffusive component in the dynamics.

The main goal of the present paper is to quantify the impact of jumps on optimal consumption, as well as on the proportion of wealth invested in the risky asset, within the non-separable preferences framework. Such aforementioned optimal fractions share some important theoretical properties: first, the portfolio weights depend on the volatility through an inverse proportionality relationship. This is due to the choice to consider a non-affine model by using the precision process instead of the volatility one, as in Chacko and Viceira (2005). Furthermore, the aforementioned dependence on volatility makes the optimal weights genuinely dynamic, and guarantees a portfolio rebalancing after a market crash. Our theoretical results are obtained by exploiting classical dynamic programming techniques. It is worth noting that co-jumps’ presence produces a strongly non-linear Hamilton-Jacobi-Bellman equation, the latter being unable to be solved in an analytical form. Hence, we impose a linearisation condition for the jump component, as in Ascheberg et al. (2016) and Oliva and Renò (2018), and a (log-)linear expansion for the normalised aggregator of current consumption and continuation utility, as in Chacko and Viceira (2005), ensuring an approximate solution. We further analyse the economic implications of our theoretical results on real data, taking into account the investors’ characteristics. We first show that co-jumps’ frequency and intensity play a crucial role, serving as a further hedging tool. In detail, we find out that: (i) infrequent jumps mainly influence the risky allocation, (ii) the impact of the precision-jump size is less relevant than the price ones, although it is not negligible, (iii) the most significant effect on optimal allocation is due to frequent and large jumps in price, instead of rare jumps of the same magnitude, and (iv) the presence of co-jumps increases the consumption-wealth ratio for investors who are extremely willing to substitute consumption over time, hence the more prominent the investor’s propensity to save, the stronger this growth is. Finally, we measure the performances of the optimal rules through a suitable economic metric, namely the Wealth Equivalent Loss (WEL). Our findings show that investors who do not believe in the need to incorporate co-jumps can suffer significant losses in their investments. Furthermore, as the results proposed in this paper provide analytical but approximate solutions, we also measure the effectiveness of such approximations on possible investment losses. We perform a numerical study on real data when we can solve the problem without approximation; our findings guarantee that the proposed strategy is comparable to the true one, making our proposal reliable even in the most general case.

The paper is organized as follows. In Sect. 2 we describe our model and the investment problem we are going to solve. The main theoretical results are provided in Sect. 3. In Sect. 4 we provide some numerical experiments on real data, both for a fund of hedge funds and for a single index, to show how the presence of co-jumps might affect the investment choices. In Sect. 5 we measure the reliability of approximate solutions of the optimal allocation and consumption problem. Section 6 concludes. Technical details and mathematical proofs are available in the Appendices.

2 The investment problem and the financial setup

Let $\left( \Omega , \mathcal {F}, \{\mathcal {F}_t\}_{t \,\in \, [0,T]}, \mathbb {P}\right)$ a filtered probability space. Throughout the paper, we denote by $GL_N(\mathbb {R})$ the set of invertible matrices in $\mathbb {R}^{N \times N}$ and by $S_{N} ( \mathbb {R} )$ (resp., $S_{N}^+ ( \mathbb {R} )$) the set of the symmetric matrices (resp., the set of the symmetric and positive definite matrices) in $\mathbb {R}^{N\times N}.$

We first consider the process $M = \{M_t\}_{t \,\in \, [0,T]}$ representing the riskless asset, such that

$$\begin{aligned} \frac{dM_t}{M_t}= r dt, \, t \,\in \, [0,T] \,, \end{aligned}$$

where $r \in \mathbb {R}$ is the instantaneous rate of return. We also consider N risky assets $S_t = (S_{t,1}, \dots , S_{t,N})^{\prime } \in \mathbb {R}^{N \times 1}$ and assume a multivariate stochastic volatility model, where we exploit the inverse of the instantaneous variance-covariance matrix through a Wishart process. Such a state variable is dubbed co-precision. The dynamics are given by

$$\begin{aligned} {\left\{ \begin{array}{ll} dS_t = diag(S_t) \left[ \alpha dt + \sqrt{Y_t^{-1}} dZ_t + J dN(\lambda )_t \right] \\ dY_t= \left( \Omega \Omega ^{\prime } + KY_t + Y_t K^{\prime } \right) dt+ \sqrt{Y_t} d\bar{Z}_t Q+ Q^{\prime } \left( d\bar{Z}_t\right) ^{\prime } \sqrt{Y_t}+ \xi (Y_t)dN(\lambda )_t \end{array}\right. } \,, \end{aligned}$$

(2.1)

for any $t \,\in \, [0,T].$ The dynamics of the risky assets include the square matrix $diag(S_t),$ with $S_t$ in the diagonal and 0 on the off-diagonal elements, the drift $\alpha \,\in \, \mathbb {R}^{N\times 1}$ and the jump amplitude $J \,\in \, \mathbb {R}^{N\times 1}.$ A vector of Wiener processes $Z_t \in \mathbb {R}^{N \times 1}$ drives the diffusive part and a non-compensated Poisson process $N(\lambda )_t$ with intensity $\lambda \in \mathbb {R}$ describes the discontinuous component.

The Wishart stochastic (co-)precision includes $K, Q \in \mathbb {R}^{N \times N},$ while $\Omega \in GL_N(\mathbb {R})$ is such that $\Omega \Omega ^{\prime }= a Q Q^{\prime },$ with $a \in \mathbb {R}$ and $a > N-1,$ ensuring that $Y_t$ is positive definite and mean-reverting at each time, see e.g. Bru (1991). The matrix K represents the speed of the mean-reversion of the co-precision to its mean-reversion level $\bar{Y},$ which satisfies

$$\begin{aligned} a QQ^{\prime }+K \bar{Y}+ \bar{Y}K^{\prime }=0 \,. \end{aligned}$$

As highlighted in Oliva and Renò (2018), we expect the matrix K to be negative semi-definite. The diffusive part of $Y_t$ is driven by a matrix of Wiener processes $\bar{Z}_t \,\in \, \mathbb {R}^{N\times N}.$ The Wiener processes are correlated according to

$$\begin{aligned} Z_t= \bar{Z}_t \rho + \sqrt{1-\rho ^{\prime } \rho } \tilde{Z}_t \,, \end{aligned}$$

(2.2)

where $\rho \in \mathbb {R}^{N \times 1},$ $\tilde{Z}_t$ is a Wiener process in $\mathbb {R}^{N \times 1}$ and the elements of $\tilde{Z}_t$ and $\bar{Z}_t$ are all independent among them. Finally, we introduce a jump component for Y,  driven by the same Poisson process appearing in the dynamics of the risky assets, with a precision-jump amplitude $\xi (Y_t) \in S_N( \mathbb {R}).$ Throughout the paper, we assume a constant precision jump size, with

$$\begin{aligned} Y+ \xi (Y) \in S_{N}^+ (\mathbb {R}) \,, \end{aligned}$$

for all $Y \in S_{N}^+ (\mathbb {R}).$

We assume that the investor’s wealth $W = \{W_t\}_{t \,\in \, [0,T]}$ is apportioned among the risk-free asset M and the stock S,  also considering the related consumption $C = \{C_t\}_{t \,\in \, [0,T]},$ so that we have

$$\begin{aligned}&\frac{dW_t}{W_t}= w_t^{\prime } \frac{dM_t}{M_t}+ \pi _t^{\prime }\frac{dS_t}{S_t} - \frac{C_t}{W_t} \,, \end{aligned}$$

(2.3)

where $\pi _t \,\in \, \mathbb {R}^{N \times 1}$ is the vector of wealth invested in the risky assets at time t. We define by $\textbf{1}$ the $N \times 1$ vector of ones, so that the proportion of wealth invested in the riskless asset is given by $w_t'= 1- \pi _t^{\prime } \textbf{1}.$ Replacing the dynamics (2.1) in (2.3), we get the following budget constraint

$$\begin{aligned}&\frac{dW_t}{W_t}= \left[ r + \pi _t^{\prime }(\alpha - r \textbf{1} ) W_t - C_t \right] dt + \pi _t^{\prime } \sqrt{Y_t^{-1}} d Z_t +\pi _t^{\prime } J dN(\lambda )_t \,. \end{aligned}$$

(2.4)

Following Chacko and Viceira (2005), we consider a Duffie-Epstein recursive utility function, see e.g. Duffie and Epstein (1992), to describe investors’ preferences, namely we introduce a normalized aggregator of current consumption and continuation utility of the form

$$\begin{aligned} f(C,V) = \frac{\beta }{1 - \frac{1}{\psi }}(1-\gamma )V \left[ \left( \frac{C}{((1-\gamma )V)^{\frac{1}{1-\gamma }}}\right) ^{1-\frac{1}{\psi }} - 1 \right] \;, \end{aligned}$$

(2.5)

such that the investment problem to be solved is

$$\begin{aligned} V(t,W,y) = \max _{\{\pi _t,C_t\}} \mathbb E\left[ \int _t^{+\infty } f(C_s,V_s) ds \,\bigg |\, \mathcal {F}_t \right] \;, \end{aligned}$$

(2.6)

with (2.3) as intertemporal budget constraint. Eq. (2.5) depends on three parameters, namely the rate of time preference $\beta ,$ the elasticity of intertemporal substitution of consumption (EIS) $\psi ,$ and the risk-aversion parameter $\gamma .$

3 A closed-form formula for optimal allocation and consumption

To find a solution to the intertemporal optimization problem (2.6) we use standard dynamic programming techniques, so that we consider the associated Hamilton-Jacobi-Bellman equation (HJB, from now on), given by

$$\begin{aligned} 0&= \max _{\pi _t, C_t} \Bigg \{ f(C,V) + \frac{\partial V}{\partial t}+ \frac{\partial V}{\partial W} \left( \pi _t^{\prime }(\alpha -r \textbf{1}) +r \right) W_t - C_t \frac{\partial V}{\partial W} \nonumber \\&\quad + Tr \left[ \left( \Omega \Omega ^{\prime }+KY_t+Y_t K^{\prime } \right) \nabla V \right] \nonumber \\&\quad + \frac{1}{2} W_t^2 \pi _t^{\prime } Y_t^{-1} \pi _t \frac{\partial ^2 V}{\partial W^2} + \left( 2 \pi _t \nabla Q^{\prime } \rho \frac{\partial V}{\partial W} \right) W_t + \frac{1}{2} Tr ( 4 Y_t \nabla Q^{\prime } Q \nabla ) V \nonumber \\&\quad + \lambda \mathbb {E} \left[ V(W_t+\pi _t^{\prime } J W_t, Y_t + \xi ) - V(W_t, Y_t)\right] \Bigg \} \,, \end{aligned}$$

(3.1)

where $\nabla := \left( \frac{\partial }{\partial Y_{i,j}}\right) _{1\le i,j\le N}$, and the expectation in the last term of (3.1) is over the jump sizes. It is worth noting that, since we are considering constant values for J and $\xi ,$ in what follows the expectation in (3.1) will be unnecessary. The HJB equation is non-linear due to the aggregator f and the jump component. Besides, the non-linearity mentioned earlier implies the absence of an analytical solution, apart from some particular cases, see Chacko and Viceira (2005) for further details. Therefore, since we would like to carry our analyses on while remaining as general as possible, we propose a methodology for determining an analytical but approximate solution. To achieve this, we impose two restraints. Concerning the aggregator f,  we proceed according to the approach proposed in Chacko and Viceira (2005), where the consumption-wealth ratio is approximated using an appropriate log-linear expansion around the unconditional mean $\overline{c-w} := \mathbb E\left[ \frac{C_t}{W_t}\right] ,$ see Judd (1998) for further details. Concerning the jump component, we exploit a first-order Taylor expansion around $J\pi _t = 0,$ so that

$$\begin{aligned} (1 + J\pi _t)^{1-\gamma } = 1 + (1-\gamma )J \pi _t + o\left( J^2\pi _t^2 \right) \;, \end{aligned}$$

(3.2)

and ignore the term $o\left( J^2\pi _t^2 \right) ,$ see Oliva and Renò (2018) for an in-depth analysis. We show the reliability of such approximations in Sect. 5. We set $H = \frac{1-\gamma }{1-\psi }$ and guess that the solution to (3.1) is of the form

$$\begin{aligned} V(t,W,y) = \exp \left\{ -H \left( Tr(F_t Y_t) + G_t\right) \right\} \frac{W_t^{1-\gamma }}{1-\gamma } \;, \end{aligned}$$

(3.3)

where the matrix function $F_t \in S_{N}$ and the function $G \in \mathbb {R}$ have to be identified.

Now, we are ready to prove the following

Proposition 3.1

Consider the investment problem (2.6) with $\psi \ne 1$ and the associated HJB equation (3.1). Then, for $t\,\in \,[0,T],$ the value function is given in (3.3), while the optimal consumption and portfolio rules are given by

$$\begin{aligned} \frac{C_t}{W_t}&= \beta ^{\psi } \exp \left\{ -\left( Tr(F_t Y_t)+G_t\right) \right\} \;, \end{aligned}$$

(3.4)

$$\begin{aligned} \pi _t&= Y_t\left( \frac{(\alpha - r \textbf{1})}{\gamma } + \frac{2H F_t Q^{\prime } (-\rho )}{\gamma } + \frac{\lambda J e^{-H Tr(F_t \xi )}}{\gamma } \right) =:Y_t B_t \;, \end{aligned}$$

(3.5)

where $B_t \in \mathbb {R}^{N \times 1}$ and $F \in S_{N} , \, G \in \mathbb {R}$ satisfying the following system of ODEs

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{F}_t &{} = h_1 F_t+ (1-\psi )(\alpha -r \textbf{1}) B_t^{\prime } - F_t K-F_t K^{\prime }- \frac{\gamma (1-\gamma )}{2 H}B_t B_t^{\prime }-2 (1-\gamma ) F_t Q^{\prime } \rho B_t^{\prime } \\ &{}\quad - 2 F_t Q^{\prime } Q F_t + \lambda \frac{(1-\gamma )}{H} e^{-H Tr(F_t \xi )} J B_t^{\prime }, \; \; F_T=0 \\ \dot{G_t} &{} = -h_0+\beta \psi - h_1 \left( \psi \log (\beta ) + G_t \right) + (1-\psi ) r+\frac{\lambda }{H} \left( e^{-H Tr(F_t \xi )}-1 \right) \\ &{}\quad + Tr (F_t \Omega \Omega ^{\prime }) , \; \; G_T=0 \end{array}\right. } \end{aligned}$$

(3.6)

with $h_1 := \exp \left\{ \overline{c-w}\right\}$ and $h_0 := h_1 - h_1\log (h_1).$

Proof

See Appendix A.1. $\square$

An inspection of Proposition 3.1 shows that the optimal portfolio allocation, given by (3.5), comprises three terms: more precisely, $\frac{(\alpha - r \textbf{1})}{\gamma }$ is the myopic component, $\frac{2H F_t Q^{\prime } (-\rho )}{\gamma }$ is the intertemporal hedging demand, and $\frac{\lambda Je^{-HTr(F_t\xi )}}{\gamma }$ is the jump hedging demand. The first one depends on both the excess return and the risk-aversion parameter and describes the agents who completely ignore the multi-period nature of the investment. The latter is incorporated in the second term, relying on the investment opportunities $\sigma ,$ and the correlation between returns and volatility. The last term quantifies the hedging against tail risk and is related to the jump frequency $\lambda$ and magnitudes J and $\xi .$ While the absence of idiosyncratic risk ensures a positive myopic component, we can discuss the sign of the remaining terms. For the intertemporal hedging demand, we expect a negative correlation structure for correlated shocks to price returns and their variance-covariance matrix, since variances and covariances typically increase while prices decline. Assuming $\gamma >1,$ we distinguish two cases according to the value of EIS. For $\psi < 1,$ we have $H < 0,$ then the impact of the intertemporal hedging demand over the optimal consumption will be positive (resp., negative) when the function F is greater (resp., smaller) than zero. Vice versa, for $\psi > 1,$ we have $H > 0,$ thus the impact of the intertemporal hedging demand over the optimal consumption will be positive (resp., negative) when the function F is smaller (resp., greater) than zero. However, an in-depth analysis of Eq. (3.6) for F shows that $F_t < 0,$ for all $t \,\in \, [0,T],$ if $\psi <1,$ so that the intertemporal hedging demand curtails the optimal allocation, see Appendix B for further details. Concerning the jump hedging demand, we observe that its sign only depends on the price-jump amplitude, being positive (resp., negative) for $J > 0$ (resp., $J < 0$). On the other hand, the precision-jump component and the jump intensity affect the magnitude of the reduction/increase of the optimal allocation. More importantly, each component in (3.5) is proportional to the instantaneous precision, meaning that the allocation will reduce during volatile periods, reconciling the Markowitz intuition.

We would like to point out that, although it is taken for granted that modelling precision is equivalent to modelling variance (by assuming a 3/2-dynamics), this would still not be sufficient to overcome the problem of the non-dynamic nature of the investment. In the affine case, the optimal allocation depends neither on the long-run level nor the instantaneous volatility because of the choice to set the variance-risk premium proportional to volatility in the drift term. Therefore, using precision to model the state variable is not a trivial mathematical gimmick; instead, it is a requirement to obviate the imperative to impose a constraint on the drift architecture.

In addition, our investment strategy implies that, after a precision jump of size $\xi ,$ investors will change their allocation in the risky asset from $Y_t S_t$ to $(Y_t + \xi ) S_t.$ Since we impose a negative precision-jump size (to comply with the empirical evidence of positive peaks in volatility behind market crashes), we witness a reduction of risky investments after a market collapse, consistently with the current market practice. Such a circumstance is extensively discussed in Moreira and Muir (2017), where the authors argue that the mean-variance trade-off weakens in high-volatility regimes.

Finally, we provide some comments regarding the optimal consumption (3.4). As in Chacko and Viceira (2005), the log consumption-wealth ratio is an affine function of instantaneous precision. Furthermore, the role of jumps on optimal consumption cannot be directly inferred from (3.4), even though they affect $C_t$ through functions $F_t$ and $G_t,$ the latter being evaluated numerically.

From Proposition 3.1 we can obtain an approximated solution to the investment problem (2.5) when $\psi = 1.$ In this case, the aggregator simplifies as

$$\begin{aligned} f(C,V) = \beta (1 - \gamma )V \left( \ln (C) - \frac{1}{1-\gamma } \ln ((1-\gamma )V) \right) \;. \end{aligned}$$

(3.7)

Hence, we have the following

Corollary 3.2

Under the hypotheses of Proposition 3.1 and assuming that (3.7) holds true, the value function solving the investment problem (2.6) is

$$\begin{aligned} V(t,W,y) = \exp \left\{ Tr(\tilde{F}_{t} Y_t) + \tilde{G}_{t} \right\} \frac{W_t^{1-\gamma }}{1-\gamma } \;, \end{aligned}$$

(3.8)

where $\tilde{F}_{t}, \, \tilde{G}_{t}$ are deterministic functions satisfying the following system of ODEs

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{ \tilde{F}}_t &{} = \beta \tilde{F}_t - (1-\gamma ) (\alpha -r \textbf{1}) \tilde{B_t^{\prime }} - K \tilde{F}_t -\tilde{F}_t K^{\prime } + \frac{1}{2}\gamma (1-\gamma ) \tilde{B_t^{\prime }} \tilde{B_t} \\ &{} - 2 (1-\gamma ) \tilde{B_t^{\prime }}\tilde{F}_t Q^{\prime } \rho - 2 Tr(\tilde{F}_t' Q^{\prime } Q \tilde{F}_t) - \lambda (1-\gamma ) e^{Tr(\tilde{F}_t \xi )} J \tilde{B_t}, \, \tilde{F}_T = 0 \,, \\ \dot{\tilde{G}}_t &{} = - \beta (1-\gamma ) \log (\beta ) +\beta \tilde{G}_t -(1-\gamma ) r+(1-\gamma ) \beta - Tr(\tilde{\Omega }_t \tilde{\Omega }_t') \\ &{} + \lambda (1- e^{Tr(\tilde{F}_t \xi ) } ), \, \tilde{G}_T = 0 \,. \end{array}\right. } \end{aligned}$$

(3.9)

Moreover, the optimal consumption and portfolio rules are, for $t \,\in \, [0,T],$

$$\begin{aligned} \frac{C_t}{W_t}&= \beta \;, \end{aligned}$$

(3.10)

$$\begin{aligned} \pi _t&= Y_t \left( \frac{(\alpha -r \textbf{1})}{\gamma } + \frac{2 \tilde{F}_{t} Q^{\prime } \rho }{\gamma } + \frac{\lambda J e^{Tr(\tilde{F}_{t}\xi )}}{\gamma } \right) =: Y_t \tilde{B}_{t} \;. \end{aligned}$$

(3.11)

Proof

See Appendix A.2. $\square$

4 The impact of jumps and recursive preferences on optimal policies

In this Section, we show how the theoretical results provided in Sect. 3 work on real data. In particular, we focus on the general case $\psi \ne 1,$ and spotlight the role played by preferences in optimal allocation.

4.1 Numerical example: the multivariate case

In the first numerical example, we consider a portfolio with $N=12$ hedge funds from the Credit Suisse Hedge Fund index, namely Convertible Arbitrage (CA), Emerging Markets (EM), Equity Market Neutral (EMN), Event Driven (ED), Event Driven Distressed (EDD), Event Driven Multi-Strategy (EDMS), Event Driven Risk Arbitrage (EDRA), Fixed Income (FI), Global Macro (GM), Long/Short (L/S), Managed Futures (MF), and Multi-Strategy (MS).

Table 1 Parameter estimates for the Co-Jumps model ($\psi = 146.9339$), the Jumps-in-Price model ($\psi = 48.3789$), and the No-Jumps model ($\psi = 62.0173$)

The choice of considering hedge funds instead of the equity market is motivated by considering that the former are more exposed to the tail risk, as explained e.g. in Kelly and Jiang (2012). The numerical example is based on the parametrization provided in Oliva and Renò (2018), under three kinds of models, depending on the presence of the jump component. For the sake of completeness, we report the parameter estimates of the three models in Table 1. Furthermore, to be compliant with the empirical evidence, see e.g. Liu and Pan (2003) and Branger et al. (2008), we constrain the price-jump amplitudes to be smaller than zero. The results for the optimal allocation are provided in Table 2. We observe that the overall optimal allocation reduces as more sources of risk are included in the model. We also observe that the reduction in the overall allocation is minimal when only price jumps are considered (the variation is 0.4%). The presence of co-jumps, on the other hand, causes a sizeable decrease in the optimal investment in risky securities, equal to 10%.

Table 2 Percentage of optimal portfolio allocation for the No-Jumps model (second column), the Jumps-in-Price model (third column), and the Co-Jumps model (fourth column)

Table 3 Percentage of Optimal Portfolio weights, for total funds, evaluated at $t=0$ for Co-Jumps Model, Jumps-in-Price Model and No-Jumps Model, for different risk-aversion coefficients and elasticities of intertemporal substitution of consumption

Thus, we extend this analysis to different types of investors. As discussed in Sect. 3, a crucial role is played by the log-linearization coefficient appearing in (3.6). In what follows, we apply the scheme proposed in Chacko and Viceira (2005) and implement a recursive numerical procedure so that we fix an initial value for $h_1,$ we use it to calculate (3.4) and update $h_1$ until the convergence is reached. Furthermore, we consider investors with coefficients of relative risk-aversion ranging in [2, 40],  and elasticity of intertemporal substitution spanning between 1/2 and 1/40.

Remark 4.1

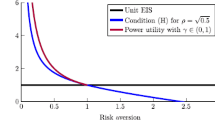
It is worth stressing that, while for the risk-aversion parameter, the empirical evidence suggests $\gamma > 1,$ the literature does not express a uniform agreement for the estimation of $\psi ,$ as highlighted in Kraft et al. (2013). Hall (1988), Campbell and Viceira (1999, 2001, 2002), and Vissin-Jorgensen (2002) provide a value for EIS smaller than one and justify this result on extensive analyses of aggregated and disaggregated data. On the other hand, Bansal and Yaron (2004); Bansal (2007) and Hansen and Singleton (2002) argue that such an estimate of the parameter $\psi$ is based on misspecification of the model, showing that ignoring the effects of time-varying consumption volatility and excluding fluctuating economic uncertainty leads to a severe downward bias in EIS estimates. However, while recognising the importance of an appropriate specification of the parameters characterising recursive preferences, it must be pointed out that this is beyond the scope of this paper. This is why in the following we will not address the estimation of the risk aversion and EIS parameters, but will provide a detailed sensitivity analysis of our numerical results w.r.t. changes in the parameters. We will also set specific values for $\gamma$ and $\psi$ when this will be strictly necessary for our study.

The optimal allocation is highest when there are no jumps in the dynamics, implying that the optimal allocation is mainly affected by co-jumps. When we consider both jumps in price and precision (top panel in Table 3), the optimal allocation reduces, compared to the no-jump case (bottom panel). For example, for $\gamma = 2$ and $\psi = 1/2,$ in the absence of jumps, the investment guarantees $7 \%$ more of the wealth allocated in the stock. Our findings confirm that price and volatility jumps can overshadow the skewness effect. Furthermore, the impact of EIS on the optimal portfolio weights is negligible. At the same time, the risk aversion parameter strongly affects the results. For example, if we quadruple $\gamma$ (moving from $\gamma = 5$ to $\gamma = 20$), the optimal allocation is reduced by more than $75\%$ of the previous value. The reduction proportion remains almost the same even when only price jumps are considered or if no jumps are assumed. We carry on a similar analysis for optimal consumption. More precisely, we evaluate

$$\begin{aligned} \frac{C_0}{W_0} = e^{\mathbb E\left[ c_0-x_0\right] }\times 100 \;, \end{aligned}$$

i.e., we consider the (exponentiated) optimal mean log consumption-wealth ratio for several values of EIS and risk-aversion parameter. The results are shown in Table 4, for a relative risk-aversion coefficient ranging in [0.75, 10],  and an elasticity of intertemporal substitution spanning between 1/0.75 and 1/3.

Table 4 Percentage of consumption-wealth ratio for each models (Co-Jumps Model, Only Jumps in Price and No-Jumps Model) for different risk aversion coefficient and elasticities of intertemporal substitution of consumption

When the elasticity of intertemporal substitution $\psi$ is small, investors are unwilling to substitute consumption in time. Instead, they prefer investing in portfolios with a higher consumption-wealth ratio. A bigger EIS corresponds to a lower value of the consumption-wealth ratio. We first focus on the last column of Table 4, namely, we comment on results for investors who are extremely reluctant to intertemporally substitute consumption. These investors wish to keep their expected consumption growth rate constant, regardless of the current investment opportunity set, by consuming the average return of their portfolios with a precautionary-savings adjustment for risk. Then, we study another borderline case, and we focus on extreme risk-averse parameters (last row in each panel of Table 4). In this case, investors are more likely to choose safer portfolios, thus achieving smaller returns. The polar opposite is represented by risk-tolerant investors, who are encouraged to allocate a more significant part of their wealth into risky assets so that an extreme risk-return profile will characterize the corresponding portfolios. This is why the consumption-wealth ratio is higher when investors are less risk-averse. Furthermore, we examine investors more willing to substitute consumption in time and assume $\psi >1.$ This implies that we concentrate on the first column in Table 4, so that, assuming $\beta > 0,$ market players would rather face higher savings but lower consumption, instead of those who are reluctant to substitute consumption. In such a situation, an investor with low-risk aversion $\gamma$ will result in a portfolio with higher expected returns: the higher EIS, the lower the consumption-wealth ratio. The reasoning above can be summarized by focusing on the percentage variation of the optimal consumption wealth ratio: if we halve EIS, e.g. going from 1/(1.25) to 1/(2.5),  the optimal consumption experiences an increase by $78\%$ if the investor is very risk-loving ($\gamma = 0.75$). Such an increment reduces to $76\%$ if the investor’s risk aversion is high enough ($\gamma = 10$). Finally, by comparing the Co-Jumps, Jumps in price, and No Jumps models, we detect that the presence of jumps affects the optimal consumption when $\psi <1.$ The effect is even more intense the smaller the EIS value. By comparing the mid and bottom panels in Table 4, we find that jumps in price reduce the optimal consumption, regardless of the risk aversion level, because of the greater risk investors are exposed to. However, the impact of jumps in volatility (or precision) is significant, as stressed by the comparison between the top and mid panel in Table 4. Therefore, we can state that jumps in volatility further reduce optimal consumption in a very significant way. When $\psi >1,$ we notice a different behaviour: investors exhibit more significant savings and negligible consumption. Moreover, if jumps in price are included, the average portfolio return reduces since investors consider a smaller portion of the risky asset. This implies that investors choose portfolios with low expected returns, so a higher $\psi$ corresponds to a higher consumption-wealth ratio.

To assess the effect of jumps in volatility, we resort to the Wealth Equivalent Loss (WEL), i.e. an economic metric that measures the possible loss suffered by an investor who assumes only jumps in price (or the absence of jumps) as a condition for determining the investment strategy. The WEL is defined as

$$\begin{aligned} WEL = 1 - \tilde{W}_t \;, \end{aligned}$$

where $\tilde{W}$ is obtained by equating the value function $V(t, y, \tilde{W}) = \exp \{-H(Tr(F_t Y_t)+ G_t)\}\frac{\tilde{W}_t^{1-\gamma }}{1-\gamma }$ associated with the strategy involving co-jumps and the value function $\hat{V}(t,y,1) = \exp \{-H(Tr(\hat{F}_t Y_t )+ \hat{G}_t)\}\frac{1}{1-\gamma }$ for the sub-optimal strategy, where $H = \frac{1-\gamma }{1-\psi }.$ More precisely,

$$\begin{aligned} \tilde{W}_t =&\left[ \frac{\exp \{-H( \hat{F}_t Y_t + \hat{G}_t) \}}{\exp \{-H( F_t Y_t + G_t )\}} \right] ^{\frac{1}{1 - \gamma }} = \left[ \exp \{(\hat{F}_t - F_t)Y_t + (\hat{G}_t- G_t) \}\right] ^{ -\frac{1}{1-\psi }} \;, \end{aligned}$$

(4.1)

where $F_t, G_t$ (resp., $\hat{F}_t, \hat{G}_t$) are the solutions to the ODEs provided in Proposition 3.1, suitably modified according to the presence (resp., the absence) of the jumps in volatility. Figure 1 shows the loss in wealth that an investor might suffer when she does not believe in jumps in volatility, as a function of the risk-aversion parameter $\gamma$ and the elasticity of intertemporal substitution of consumption $\psi .$ In particular, the figure shows that not including volatility jumps in the model would result in non-trivial losses in terms of wealth. For example, with a risk aversion parameter $\gamma =3$, the investor would suffer a monetary loss of about $5 \%$. This result reinforces the point that volatility jumps play a crucial role in determining the optimal behaviour of an investor in hedge funds portfolios.

4.2 Numerical example: the univariate case

To highlight the impact of jumps on the optimal allocation, in this section, we provide some analyses when a single fund (CA) is considered. The CA index displays a positive mean ($6.89\%$) and low standard deviation ($6.25\%$), making the fund attractive. However, it has negative skewness ($-2.73$) and high kurtosis (21.58), transforming the fund into a risky investment vehicle.

Fig. 1

Percentage of relative loss in wealth as a function of the risk aversion parameter with $\psi =0.8.$ The maturity investment is 1 year, the rate of time preferences is $\beta = 6\%,$ the risk-free rate is set to $r=0\%.$ The remaining parameters are given in Table 1.

Fig. 2

Optimal portfolio allocation (left chart) and consumption (right chart) as functions of time horizon, for several values of the risk-aversion parameter $\gamma .$ The EIS parameter is fix to $\psi =0.8.$ The rate of time preferences $\beta$ is set equal to $6 \%$ annually, the constant risk-free rate is equal to $r=0\%$. The remaining parameters are given in Table 1.

Our first analysis shows optimal portfolio allocation and consumption-wealth ratio, evaluated at $t=0,$ as functions of the investment time horizon, for different risk-aversion levels. The results are presented in Fig. 2. As expected, the optimal allocation decreases over time due to the negative intertemporal hedging demand, see e.g. Liu and Pan (2003) and Branger et al. (2008). Considering the parameters obtained through the calibration procedure and assuming $\gamma >1,$ the function F results to be negative, see Appendix B for further details. Furthermore, as the maturity becomes larger, both the intertemporal and jump hedging demands rise (in absolute value) to compensate for the additional risk by increasing the investment time horizon. Consequently, the value to be subtracted from the myopic component is more significant as the maturity is pushed back in time, leading to a reduction of the overall optimal allocation. Concerning the optimal consumption, we note a shrinkage of the latter when the maturity becomes larger, assuming a fixed elasticity of intertemporal substitution of consumption equal to $\psi = 0.8.$ This is not surprising, since an EIS smaller than one conveys that the agent is unwilling to base today.’s decision on events distant in time.

Fig. 3

Optimal portfolio allocation (left charts) and consumption (right charts) as functions of $\gamma$ (top) and $\psi$ (bottom), for different price-jump sizes. In top charts the EIS is fixed to $\psi =0.8,$ for the bottom ones the risk-aversion parameter is fixed to $\gamma = 3.$ The rate of time preferences $\beta$ is set equal to $6 \%$ annually, the constant risk-free rate is $r=0 \%$.The remaining parameters are given in Table 1.

To further clarify to what extent jumps may affect the optimal policies, we study the optimal portfolio weights and consumption-wealth ratio as functions of the risk aversion parameter $\gamma ,$ for various price-jump sizes J,  and keeping the precision-jump size fixed. The results are shown in Fig. 3 (top charts). We note that when the price-jump size reduces (in absolute value), the investor tends to take a more sizeable position in the risky asset, especially when the investor’s risk attitude goes to one, for a fixed value of EIS ($\psi =0.8$). From an economic point of view, this means that assuming a model with less exposure to the jump risk event leads to considering a considerable position in the risky asset.

The optimal consumption is affected by changes in the price-jump amplitude, albeit to a lesser degree. By choosing again $\psi =0.8$ and increasing (in absolute value) the price-jump size, the optimal consumption-wealth ratio reduces as a consequence of the lower expected portfolio returns. We further stress that the optimal consumption decreases as the investor’s risk aversion increases, as she will choose safer portfolios with a less expected portfolio return.

A similar study can be accomplished by analysing optimal allocation and consumption-wealth ratio as functions of EIS for different price-jump amplitudes, as shown in Fig. 3 (bottom charts). The numerical results confirm that the optimal allocation is not remarkably affected by EIS variations if we keep the risk-aversion parameter fixed. Moreover, in this case, the optimal allocation significantly increases if we consider a price-jump size equal to $J=-1 \%.$ Looking at the bottom-right chart of Fig. 3, we note that for an investor extremely reluctant to substitute consumption over time, a greater price-jump size (in absolute value) results in smaller consumption. As the investor becomes more willing to substitute consumption over time, the impact of jumps in price becomes negligible since these investors have more significant savings and lower consumption.

To investigate the effect of jumps in precision on optimal policies, we study the latter as functions of the precision-jump magnitudes, assuming different price-jump sizes. We refer to Fig. 4 for the corresponding results.

Fig. 4

Optimal portfolio allocation (left chart) and Optimal consumption-wealth ratio (right chart) as a function of precision-jump size, for different price-jump sizes. The risk-aversion parameter is $\gamma = 3,$ and the elasticity of intertemporal substitution is set equal to $\psi =0.8.$ The rate of time preferences $\beta$ is set equal to $6 \%$ annually, the constant risk-free rate is $r=0 \%$. The remaining parameters are given in Table 1.

We observe that introducing jumps in volatility produces a further effect for optimal weights: a more remarkable volatility jump translates into a smaller jump in precision, causing a reduction in the optimal portfolio allocation. However, such a curtailment has little impact and depends on the value of the price-jump size. Concerning the optimal consumption (right chart in Fig. 4), as expected, we witness a reduction for wider price-jump magnitudes (in absolute value): as the amplitude of the jump in precision rises (in absolute value), the consumption-wealth ratio decreases as well due to the reduction of the expected portfolio return.

Finally, we investigate the role played by the jump-frequency over the optimal portfolio weights, see Table 5.

Table 5 Percentage optimal portfolio allocation for different values of jump-intensity, price-jump size, risk-aversion parameter, and precision-jumps size

We assume that $freq = 1/(\lambda \times 12),$ i.e., we consider the jump frequency expressed in years and intended as the reciprocal of the jump intensity, adjusted by considering that the parameters are in the form of monthly estimates. More precisely, optimal portfolio weights are obtained by considering four jump intensities, namely $\lambda = \{0.007, \,0.0033, \, 0.0016, 0.0008\}.$ Such a set corresponds to a jump frequency of 11.94,  25,  50 and 100 years on average, respectively. Our findings move along three directions. First, we recover that the optimal portfolio allocation is significantly affected by jumps in price. We further note that infrequent jumps mainly influence the risky allocation. Moreover, we confirm that jumps in precision have little impact on optimal policy, regardless of the jump frequency. More precisely, the impact of the precision-jump size is less relevant but not negligible, especially when considering variations in the jump intensity. The investor tends to take a more prominent position in optimal allocation when the jump size is small: the smaller the jump intensity, the higher the portfolio allocation. Third, we observe that frequent and large jumps in price impact optimal allocation more than rare jumps of the same magnitude. Assuming that a jump occurs every 12 years, the allocation decreases by approximately $6.5\%$ if the price jump increases by 5 percentage points, namely, we move from $J = -20 \%$ to $J = -15\%.$ For rare jumps (e.g., one jump every 100 years), the variation of the optimal allocation is by $0.6\%.$ The proportions remain almost unchanged as the jump amplitudes in precision and/or the risk aversion parameter vary.

Fig. 5

Percentage of relative loss in wealth for the sub-optimal strategy without jumps as a function of the risk aversion parameter with different values for the elasticity of intertemporal substitution of consumption (EIS). The maturity investment is one year, the rate of time preferences is $\beta =6 \%$ and the risk-free rate is set to $r=0\%.$ The remaining parameters are given in Table 1.

We conclude our study with a sensitivity analysis for WEL w.r.t. the parameters characterising the preferences involved, namely the EIS and the risk-aversion parameters. We consider a span for the risk aversion coefficient $\gamma$ in [1.1, 10]. The results are illustrated in Fig. 5. First, we observe that excluding jumps from the model always results in a potential loss for investors, regardless of their risk attitudes and consumption tendencies, since WEL is always negative as a function of $\gamma ,$ for any value of $\psi .$ Our qualitative analysis also shows that as the elasticity of substitution of consumption increases and the investor’s risk aversion coefficient decreases, the loss suffered by the investor increases. Therefore, the aggressiveness of an investor who believes in the sub-optimal strategy (No-Jumps model) is rewarded through a maximum loss. As the investor becomes less aggressive, the potential loss she may incur decreases until a plateau is reached. When the investor’s propensity to consume increases ($\psi \ge 0.5$), we see a WEL trend similar to the previous one: the very aggressive investor reaches a maximum loss, which is more significant as the EIS grows.

5 The accuracy of the approximate solution

To understand whether the solutions proposed in Sect. 3 are accurate, we assess the reliability of the approximation assumptions. We recall that we are assuming two types of linearization procedures: one for the jump component and one for the logarithmic consumption wealth ratio.

5.1 Reliability of the jump-component linearization

To compare true and approximate solutions, we consider a simpler form of the model, where we consider only a single risky asset and by assuming that the precision $y_t$ is constant over time. More precisely, the dynamics (2.1) simplifies to the well-known Merton’s Jump-Diffusion model

$$\begin{aligned} {\left\{ \begin{array}{ll} &{}\frac{d S_t}{S_t} = \alpha dt + \sqrt{y_{0}^{-1}} d B_t+J d N_t \\ &{}dy_t=0 \end{array}\right. } \;. \end{aligned}$$

(5.1)

Assume first $\psi = 1.$ Under such assumptions, we write the investor’s indirect utility function as

$$\begin{aligned} V(t,W) = \frac{W_t^{1-\gamma }}{1-\gamma }\exp \{F_t\} \;, \end{aligned}$$

(5.2)

for any $t \,\in \, [0,T].$

If we do not linearize the jump component, the first order condition for the true optimal allocation weights is

$$\begin{aligned} 0=(\alpha -r)- \frac{\gamma \pi _t}{y_{0}} + \lambda (1+ \pi _t J)^{-\gamma } J \;, \end{aligned}$$

(5.3)

while the function F appearing in (5.2) is the solution to the following ODE

$$\begin{aligned} \dot{F}_t&= -\beta (1-\gamma ) \log (\beta )+\beta F_t -r(1-\gamma )-\pi _t(\alpha -r)(1-\gamma )+\beta (1-\gamma ) \nonumber \\&\quad +\frac{1}{2} \gamma (1-\gamma ) \frac{\pi _t^2}{y_{0}} - \lambda \left[ (1+J \pi _t)^{1-\gamma } -1 \right] . \end{aligned}$$

(5.4)

Both Eqs. (5.3) and (5.4) can be easily solved by using ad-hoc numerical procedures.

Analogously, when we linearize the jump component, the first order condition for the approximate optimal allocation weights is

$$\begin{aligned} 0=(\alpha -r)-\frac{\gamma \pi _t}{y_{0}}+ \lambda J \;, \end{aligned}$$

(5.5)

providing a closed-form expression for the optimal weights, while the function F appearing in (5.2) is the solution to the following ODE

$$\begin{aligned} \dot{F}_t&= - \beta (1-\gamma ) \log (\beta )+ \beta F_t - r(1-\gamma )- \frac{1}{2} \frac{(\alpha -r)^2 (1-\gamma )}{\gamma } y_{0}+ \beta (1-\gamma ) \nonumber \\&\quad -\frac{\lambda ^2 J^2 (1-\gamma )}{2 \gamma } y_{0}- \frac{J \lambda (1-\gamma )(\alpha -r)}{\gamma } y_{0} \;. \end{aligned}$$

(5.6)

By indicating with V and $\pi$ (resp., $\tilde{V}$ and $\tilde{\pi }$) the value function and the optimal weight for the true model (resp., the approximate model), we can evaluate the Relative WEL (RWEL), i.e. the percentage of initial wealth that can be sacrificed by an investor using the optimal strategy, in order to have the same indirect utility using the approximate one, see Ascheberg et al. (2016) for further details. The RWEL is obtained by equating $V(t,W(1-RWEL); \pi )=\tilde{V}(t,W; \tilde{\pi })$, hence, for $t \,\in \, [0,T],$ we get

$$\begin{aligned} RWEL = 1 - \frac{1}{1-\gamma } \exp \{\tilde{ F}_t - F_t\} \;. \end{aligned}$$

(5.7)

We execute a sanity check by comparing the true solution with the approximate one in terms of RWEL.

Table 6 Optimal approximate and true allocation weights and associated RWEL (expressed in percentage) for several risk aversions parameter $\gamma$ and price-jump sizes

The results are depicted in Table 6, for several risk aversion parameter values and price-jump amplitudes. We note that the approximate optimal strategy overestimates the true one, providing a potential loss. However, such a loss is minimal, varying between $0.0038\%$ (when $\gamma = 10$ and $J = -10\%$) to $0.0482\%$ (when $\gamma = 2$ and $J = -25\%$).

Now assume $\psi \ne 1.$ The investor’s indirect utility function is

$$\begin{aligned} V(t,W) = \frac{W_t^{1-\gamma }}{1-\gamma }\exp \{-H F_t\} \;, \end{aligned}$$

(5.8)

for any $t \,\in \, [0,T].$ As for the true strategy, the first order condition for the optimal allocation weights is given in (5.3), while the function F appearing in (5.8) is the solution to the following ODE

$$\begin{aligned} \dot{F}_t&= h_1 F_t-h_1\psi \log \beta + \beta \psi -h_0 +r(1-\psi )+\pi _t(\alpha -r)(1-\psi ) \nonumber \\&\quad - \frac{1}{2} \gamma (1-\psi ) \frac{\pi _t^2}{y_{0}} + \frac{\lambda }{H} \left[ (1+J \pi _t)^{1-\gamma } -1 \right] \,. \end{aligned}$$

(5.9)

As for the approximate strategy, the first order condition for the optimal allocation weights is given in (5.5) and the function F appearing in (5.8) is the solution to the following ODE

$$\begin{aligned} \dot{F}_t&= h_1 F_t-h_1\psi \log \beta + \beta \psi - h_0 +r(1-\psi )+\pi _t(\alpha -r)(1-\psi ) \\ \nonumber&- \frac{1}{2} \gamma (1-\psi ) \frac{\pi _t^2}{y_{0}} + \lambda (1-\psi )J \pi _t \,. \end{aligned}$$

The RWEL for $t \,\in \, [0,T]$ is

$$\begin{aligned} RWEL = 1 - \frac{1}{1-\gamma } \exp \{-H [\tilde{ F}_t - F_t ]\} \;. \end{aligned}$$

(5.10)

Table 7 RWEL (expressed in percentage) for several values of risk aversions parameter $\gamma ,$ elasticity of intertemporal substitution of consumption $\psi$ and price-jump sizes

We compare true and approximate solutions in terms of RWEL. The results are depicted in Table 7, for several values of risk aversion parameter $\gamma ,$ elasticity of intertemporal substitution of consumption $\psi ,$ and price-jump amplitudes. In this case, the potential loss is always lesser than $0.02 \%.$ As expected, the loss reduces for higher values of $\psi$ and $\gamma ,$ while heightens for larger price-jump magnitudes.

5.2 The accuracy of the consumption-wealth linearization

We recall that, in this paper, the consumption-wealth ratio is approximated using an appropriate log-linear expansion around the unconditional mean $\overline{c-w}:= \mathbb {E} \left[ \frac{C_t}{W_t} \right] .$ The reliability of such an approximation moves along the lines of Chacko and Viceira (2005) and can be measured by calculating the unconditional standard deviation of the optimal log consumption-wealth ratio, given by

$$\begin{aligned} \mid F_t \mid \sqrt{Var(y_t)}= \mid F_t \mid \sqrt{\frac{\sigma ^2 }{2k} \left( \theta + \frac{\xi \lambda }{k} \right) } \;. \end{aligned}$$

Figure 6 shows that the optimal consumption-wealth ratio exhibits high volatility only for investors with small values for $\gamma$ and $\psi .$ For example, when $\psi = 0.2,$ the standard deviation is about $1.5\%,$ while, for $\psi = 0.9,$ it is about $0.16 \%,$ when $\gamma = 2.$ Our results are corroborated by the discussion in Campbell and Koo (1997), where the authors explain that the approximation error can be considered bearable when the standard deviation of the log consumption-wealth ratio is smaller than $5\%.$

Fig. 6

Percentage values of the unconditional standard deviation of the optimal log consumption-wealth ratio.

6 Conclusions

In this paper, we propose an approximated solution to a dynamic allocation problem in multivariate incomplete markets, where the investor can access bonds and stock under the simultaneous jumps in price and volatility hypothesis. We further assume that investors have recursive preferences over intermediate consumption. Our theoretical results show that the optimal portfolio weights consist of three terms: a myopic component, an intertemporal hedging demand and a further illiquidity term depending on co-jumps. Such three components are inversely proportional to instantaneous volatility, generalizing the well-known Markowitz economic intuition. Moreover, investors will rebalance their portfolio after a market crash, decreasing their investment in risky assets. The presence of event risk significantly changes the optimal allocation. Our analysis suggests that jumps in prices and volatility have essential effects on optimal allocation strategy. Not including jumps leads to a hazardous attitude for the investor in considering a much larger risky stock allocation. The interplay between jumps in price and volatility reveals that they act as a hedging tool, significantly reducing the optimal allocation.

Appendices

A proof of theoretical results

1.1 A.1 Proof of Proposition 3.1

To determine the optimal policies we start from the HJB (3.1) equation associated to the investment problem, define $H:= \frac{1-\gamma }{1-\psi },$ and guess

$$\begin{aligned} V(t,W,y)= \exp \{ -H \left( Tr(F_t Y_t) + G_t \right) \} \frac{W_t^{1-\gamma }}{1-\gamma } \,. \end{aligned}$$

(A.1)

Furthermore, we set $\dot{F}_t =\frac{\partial F}{\partial t}$ and $\dot{G}_t =\frac{\partial G}{\partial t},$ and evaluate the partial derivatives of the value function appearing in the HJB equation, namely

$$\begin{aligned} \frac{\partial V}{\partial t}&= -H ( Tr(\dot{F}_t Y_t)+ \dot{G}_t) V \;, \end{aligned}$$

(A.2)

$$\begin{aligned} \frac{\partial V}{\partial W}&= (1-\gamma ) W_t^{-1} V \;, \end{aligned}$$

(A.3)

$$\begin{aligned} \nabla V&= -H F_t V \end{aligned}$$

(A.4)

$$\begin{aligned} \frac{\partial ^2 V}{\partial W^2}&= -\gamma (1-\gamma ) W_t^{-2} V \;, \end{aligned}$$

(A.5)

$$\begin{aligned} \nabla Q^{\prime } \rho \frac{\partial V}{\partial W}&= \nabla \frac{\partial V}{\partial W} Q^{\prime } \rho = -H F_t Q^{\prime } \rho V (1-\gamma ) W_t^{-1} \;. \end{aligned}$$

(A.6)

Moreover, we have

$$\begin{aligned} Tr(Y_t \nabla Q^{\prime } Q \nabla ) V = -H Tr(Y_t F_t Q^{\prime } Q F_t) V \;. \end{aligned}$$

(A.7)

Finally, we use the linearization (3.2), so that the jump component in the HJB equation becomes

$$\begin{aligned} V( W_t+ \pi _t^{\prime } J W_t, Y_t + \xi )- V(W_t, Y_t) = V \left( e^{-H Tr(F_t \xi )} (1+ \pi _t^{\prime } J)^{1-\gamma }-1 \right) \;. \end{aligned}$$

(A.8)

Hence, we replace all the partial derivatives (A.2) –(A.6), the condition (A.7) and (A.8) in (3.1), so that we obtain

$$\begin{aligned} 0&= \max _{ \{ \pi _t, C_t \}} \left\{ \frac{f(C_t, V_t)}{V_t} - H Tr (\hat{F}_t Y_t) - H \dot{G} + r (1-\gamma ) + \pi _t^{\prime } ( \alpha - r \textbf{1}) (1-\gamma )- \frac{C_t}{W_t }(1-\gamma ) \right. \nonumber \\&\quad \left. - H F_t Tr (\Omega \Omega ^{\prime }+KY_t+Y_t K^{\prime })- \frac{\gamma (1-\gamma )}{2} \pi _t^{\prime } Y_t^{-1} \pi _t -2 H \pi _t^{\prime } F_t Q^{\prime } \rho (1-\gamma )\right. \nonumber \\&\quad \left. -H Tr ( 2 Y_t F_t Q^{\prime } Q F_t) + \lambda \left[ e^{-H Tr(F_t \xi )} (1+ (1-\gamma )\pi _t^{\prime } J)-1 \right] \right\} =: \varphi (\pi _t, C_t) \;. \end{aligned}$$

(A.9)

The first term in (A.9) can be written as

$$\begin{aligned} \frac{f(C_t, V_t)}{V_t}&= H \beta \psi - \frac{H \beta \psi }{\left( (1-\gamma ) V \right) ^{\left( \frac{1}{1-\gamma } \right) \left( \frac{\psi -1}{\psi }\right) }} C_t ^{\frac{\psi -1}{\psi }} \;. \end{aligned}$$

(A.10)

Hence, we are able to determine the first order condition for optimal consumption

$$\begin{aligned} \frac{\partial \varphi }{\partial C_t}&= - \frac{H \beta \psi }{\left( (1-\gamma ) V \right) ^{\left( \frac{1}{1-\gamma } \right) \left( \frac{\psi -1}{\psi }\right) }} \frac{\psi -1}{\psi } C_t ^{\frac{1}{\psi } } - \frac{(1-\gamma )}{W_t} = 0 \;, \end{aligned}$$

(A.11)

and with some algebra we obtain (3.4). Similarly, we are able to determine the first order condition for optimal portfolio allocation

$$\begin{aligned} \frac{\partial \varphi }{\partial \pi _t^{\prime }}&= ( \alpha - r \textbf{1}) (1-\gamma ) - \gamma (1-\gamma ) \pi _t Y_t^{-1}\nonumber \\&\quad -2H F_t Q^{\prime } \rho (1-\gamma ) + \lambda (1-\gamma ) e^{-H Tr(F_t \xi )} = 0 \;, \end{aligned}$$

(A.12)

and (3.5) easily follows. Finally, we have to make explicit the expressions for F and G appearing in the value function. To do this, we replace the optimal consumption and portfolio allocation in (A.9) and we have

$$\begin{aligned} \frac{A_t }{H}&- Tr( \dot{F} Y_t) - \dot{G} + \frac{r (1-\gamma )}{H} + B_t^{\prime } Y_t \frac{( \alpha -r \textbf{1}) (1-\gamma )}{H} - F_t Tr(\Omega \Omega ^{\prime } + K Y_t + Y_t K^{\prime }) \nonumber \\&- \frac{\gamma (1- \gamma )}{2 H} B_t Y_t B_t^{\prime } - 2 F_t Q^{\prime } \rho Y_t B_t^{\prime } (1-\gamma ) -2 Tr(Y_t F_t Q^{\prime } Q F_t) \nonumber \\&+ \frac{\lambda }{H} \left[ e^{-H Tr(F_t \xi )} - 1\right] + \frac{\lambda (1-\gamma )}{H} e^{-H Tr(F_t \xi )} J B_t^{\prime } Y_t = 0 \;, \end{aligned}$$

(A.13)

where we set

$$\begin{aligned} B_t := \frac{(\alpha - r \textbf{1})}{\gamma } + \frac{2H F_t Q^{\prime } (-\rho )}{\gamma } + \frac{\lambda J e^{-H Tr(F_t \xi )}}{\gamma } \end{aligned}$$

(A.14)

and

$$\begin{aligned} A_t = \frac{f(C_t,V_t)}{V_t} - \frac{C_t}{W_t} (1-\gamma ) \;. \end{aligned}$$

(A.15)

With some algebra, we obtain $A_t = H \beta \psi - H \beta ^{\psi } \exp \{-(F_t + G_t)\} = H \beta \psi - H \beta ^{\psi } X^{-1}.$ The envelope condition ensures that

$$\begin{aligned} \beta ^{\psi } X^{-1}= \frac{C_t}{W_t}= \exp \{ \log {(C_t)} - \log {(W_t)}\}= \exp \{ c_t - w_t\}, \end{aligned}$$

(A.16)

so that

$$\begin{aligned} c_t-w_t= \log {(\beta ^{\psi } X^{-1})} = \psi \log {(\beta )}- Tr(F_t Y_t) -G_t. \end{aligned}$$

(A.17)

Moreover, using the first-order taylor expansion of $\exp \{c_t - w_t \}$ around its unconditional mean $\overline{c-w}$, we have

$$\begin{aligned} A_t \approx H \beta \psi - H \left[ h_0+ h_1(c_t-w_t) \right] , \end{aligned}$$

(A.18)

where $h_1 := \exp \{ \overline{c-w}\}$ and $h_0 := h1-h1 \log (h1).$ By replacing (A.18) and (A.17) in (A.13), we have

$$\begin{aligned}&\left( -\dot{F}_t + h_1 F_t + B_t^{\prime } \frac{(\alpha -r \textbf{1}) (1-\gamma )}{H} - F_t K - F_t K^{\prime } - \frac{\gamma (1-\gamma )}{2 H} B_t B_t^{\prime } - 2 F_t Q^{\prime } \rho B_t^{\prime } (1-\gamma ) \right. \nonumber \\&\left. -2 F_t Q^{\prime } Q F_t +\frac{\lambda }{H} (1-\gamma ) e^{-H Tr(F_t \xi )} J B_t^{\prime } \right) Tr(Y_t) \nonumber \\&+ \left( - \dot{G}_t +\beta \psi - h_0 -h_1 \left[ \psi \log (\beta ) - h_1 G_t \right] + \frac{r(1-\gamma )}{H} +\frac{\lambda }{H} \left[ e^{-H Tr( F_t \xi )} - 1\right] \right. \nonumber \\&\left. - Tr ( \Omega \Omega ^{\prime } F_t) \right) = 0 \;, \end{aligned}$$

(A.19)

implying that (3.6) holds.

1.2 A.2 Proof of corollary 3.2

To determine the optimal policies in the special case in which $\psi = 1$ we start from the HJB Eq. (3.1). We guess

$$\begin{aligned} V(t, W_t, Y_t)= \exp \{ Tr(\tilde{F}_t Y_t)+ \tilde{G}_t\} \frac{W_t^{1-\gamma }}{1-\gamma }. \end{aligned}$$

(A.20)

We evaluate the partial derivatives of the value function and obtain

$$\begin{aligned} \frac{\partial V}{\partial t}&= ( Tr(\dot{\tilde{F}}_t Y_t)+ \dot{\tilde{G}}_t) V \;, \end{aligned}$$

(A.21)

$$\begin{aligned} \frac{\partial V}{\partial W}&= V W_t^{-1} (1-\gamma )\;, \end{aligned}$$

(A.22)

$$\begin{aligned} \nabla V&= \tilde{F}_t V \end{aligned}$$

(A.23)

$$\begin{aligned} \frac{\partial ^2 V}{\partial W^2}&= -V \gamma (1-\gamma ) W_t^{-2} \;, \end{aligned}$$

(A.24)

$$\begin{aligned} \nabla Q^{\prime } \rho \frac{\partial V}{\partial W}&= \nabla \frac{\partial V}{\partial W} Q^{\prime } \rho = \tilde{F}_t Q^{\prime } \rho V (1-\gamma ) W_t^{-1}\; \end{aligned}$$

(A.25)

where $\dot{\tilde{F}}_t=\frac{\partial \tilde{F}}{\partial t},$ $\dot{\tilde{G}}_t=\frac{\partial \tilde{G}}{\partial t},$ and $Tr(Y_t \nabla Q^{\prime } Q \nabla ) V = Tr(Y_t \tilde{F}_t Q^{\prime } Q \tilde{F}_t) V.$ Thanks to the linearization (3.2), the jump component in the HJB equation can still be written as

$$\begin{aligned} V( W_t+ \pi _t^{\prime } J W_t, Y_t + \xi )- V(W_t, Y_t) = V \left( e^{ Tr(\tilde{F}_t \xi )} (1+ \pi _t^{\prime } J)^{1-\gamma }-1 \right) \;. \end{aligned}$$

(A.26)

When $\psi =1$ the normalized aggregator (2.5) takes the following form

$$\begin{aligned} f(C,V) = \beta (1 - \gamma )V \left( \ln (C) - \frac{1}{1-\gamma } \ln ((1-\gamma )V) \right) \;. \end{aligned}$$

(A.27)

If we replace the partial derivatives (A.21) – (A.25) in (3.1) and the normalized aggregator (A.27) in (3.1), we obtain,

$$\begin{aligned} 0&= \max _{ \{ \pi _t, C_t\}} \left\{ \frac{f(C_t, V_t)}{V} + Tr(\dot{\tilde{F}}_t Y_t) + \dot{\tilde{G}}_t + (1-\gamma ) \pi _t^{\prime } ( \alpha -r \textbf{1})+r (1-\gamma ) - \frac{C_t}{W_t} (1-\gamma ) \right. \nonumber \\ {}&\left. + Tr(\Omega \Omega ^{\prime }+K Y_t + Y_t K^{\prime }) \tilde{F}_t - \frac{1}{2} \pi _t^{\prime } Y_t^{-1} \pi _t \gamma (1-\gamma ) + 2 \pi _t^{\prime } \tilde{F}_t Q^{\prime } \rho (1-\gamma ) \right. \nonumber \\&\left. + 2 Tr( Y_t \tilde{F}_t' Q^{\prime } Q \tilde{F}_t)) + \lambda \left[ e^{Tr(\tilde{F}_t \xi )} (1+ (1-\gamma ) J \pi _t^{\prime })-1\right] \right\} =: \tilde{\varphi }(\pi _t, C_t) \;. \end{aligned}$$

(A.28)

We determine the first order condition for optimal consumption

$$\begin{aligned} \frac{\partial \tilde{\varphi }}{\partial C_t}&= \frac{\beta (1-\gamma )}{C} - \frac{(1-\gamma )}{W_t} = 0 \end{aligned}$$

(A.29)

and (3.10) easily follows. Similarly, we are able to determine the first order condition for optimal portfolio allocation

$$\begin{aligned} \frac{\partial \tilde{\varphi }}{\partial \pi _t}&= (1-\gamma ) (\alpha -r \textbf{1}) - Y_t^{-1} \pi _t \gamma (1-\gamma ) +2 \tilde{F}_t Q^{\prime } \rho (1-\gamma ) + \lambda e^{Tr( \tilde{F}_t \xi )} (1-\gamma ) J = 0 \;, \end{aligned}$$

(A.30)

so that we obtain the optimal portfolio rule (3.11). By using the optimal rules and with some algebra we obtain

$$\begin{aligned}&(-\beta Tr (\tilde{F_t} Y_t)+ Tr(\dot{\tilde{F}}_t Y_t) + (1-\gamma )(\alpha -r \textbf{1}) \tilde{B}_t' Y_t + K Tr( \tilde{F}_t Y_t)\nonumber \\&+ Tr(\tilde{F}_t Y_t) K^{\prime }- \frac{1}{2} \tilde{B}_t Y_t \tilde{B}_t' \gamma (1-\gamma ) \nonumber \\&+ 2 Q^{\prime } \rho \tilde{B}_t' Tr( \tilde{F}_t Y_t ) (1-\gamma ) + 2 Tr( Y_t \tilde{F}_t ' Q^{\prime }Q \tilde{F}_t) + \lambda e^{Tr ( \tilde{F_t \xi })} (1-\gamma ) J \tilde{B}_t' Y_t \nonumber \\&+ \beta (1-\gamma ) (\ln (\beta ) -1) \nonumber \\&- \beta \tilde{G}_t + \dot{\tilde{G}}_t + r (1-\gamma ) + Tr( \Omega \Omega ^{\prime }) + \lambda ( e^{Tr(\tilde{F}_t \xi } -1) = 0 \;. \end{aligned}$$

(A.31)

B Properties of $F_t$

The properties of the function $F_t$ are crucial to study the optimization problem. For this purpose, we make a change of variable by considering $\tau := T - t,$ so that the ODE (3.6) admits an initial condition. We have

$$\begin{aligned} \dot{F}_\tau&= -h_1 F_\tau - (1-\psi )(\alpha - r \textbf{1})\left( \frac{(\alpha - r \textbf{1})}{\gamma } + \frac{2H F_t Q^{\prime } (-\rho )}{\gamma } + \frac{\lambda J e^{-H Tr(F_t \xi )}}{\gamma } \right) \nonumber \\&+ F_\tau K+ K ' F_\tau + \frac{\gamma (1-\psi )}{2}\left( \frac{(\alpha - r \textbf{1})}{\gamma } + \frac{2H F_t Q^{\prime } (-\rho )}{\gamma } + \frac{\lambda J e^{-H Tr(F_t \xi )}}{\gamma } \right) \nonumber \\&\left( \frac{(\alpha - r \textbf{1})}{\gamma } + \frac{2H F_t Q^{\prime } (-\rho )}{\gamma } + \frac{\lambda J e^{-H Tr(F_t \xi )}}{\gamma } \right) ^{\prime } +2 (1-\gamma ) F_{\tau } Q^{\prime } \rho \nonumber \\&\left( \frac{(\alpha - r \textbf{1})}{\gamma } + \frac{2H F_t Q^{\prime } (-\rho )}{\gamma } + \frac{\lambda J e^{-H Tr(F_t \xi )}}{\gamma } \right) ^{\prime } + 2 F_{\tau } Q^{\prime } Q F_{\tau } - \lambda (1 - \psi )J \nonumber \\&e^{-H Tr(F_\tau \xi )}\left( \frac{(\alpha - r \textbf{1})}{\gamma } + \frac{2H F_t Q^{\prime } (-\rho )}{\gamma } + \frac{\lambda J e^{-H Tr(F_t \xi )}}{\gamma } \right) ^{\prime } \;, \end{aligned}$$

(B.1)

with $F_0=0,$ $\dot{F}_\tau = \frac{\partial F}{\partial \tau }$ and we set

$$\begin{aligned} B _\tau :=\frac{(\alpha - r \textbf{1})}{\gamma } + \frac{2H F_t Q^{\prime } (-\rho )}{\gamma } + \frac{\lambda J e^{-H Tr(F_t \xi )}}{\gamma } \;. \end{aligned}$$

Thanks to the updated boundary condition, the ODE (B.1) evaluated at $\tau = 0$ can be written as

$$\begin{aligned} \dot{F}_0&= -(1-\psi )(\alpha - r \textbf{1})B(0) + \frac{\gamma (1 - \psi )}{2}B(0) B(0)^{\prime } - \lambda (1-\psi )JB(0)^{\prime } \nonumber \\&= -\frac{\gamma (1 - \psi )}{2}B(0) B(0)^{\prime } \;. \end{aligned}$$

(B.2)

By assuming $\gamma >1$ and $\psi <1,$ from (B.2) it is straightforward to verify that $\dot{F}_0 < 0.$ Since F is continuous in $\gamma ,$ the previous discussion ensures that $F_\tau < 0.$ Analogously, we get $F_\tau > 0,$ for any $\tau ,$ when $\gamma >1$ and $\psi >1.$ Previous results are switched when $\gamma <1.$