Inconspicuousness and obfuscation: how large shareholders dynamically manipulate output and information for trading purposes

Abstract

I model a large shareholder who can affect firm fundamentals. I demonstrate that the large shareholder amplifies the component of his private information that is unforecastable by uninformed traders and thus alters the fundamental value of the firm to facilitate his trading profits: he obfuscates. I then construct a continuous time dynamic version of the model using Fourier transform methods. In the dynamic model, the large shareholder does not just simply amplify the unforecastable part of the fundamental: he also alters its stochastic structure. The model thus marries market microstructure with real resource allocation. There are two consequences: (i) the large shareholder induces the fundamental value of the firm to more closely mimic the noise traders, and (ii) market liquidity is reduced.

1 Introduction

Globalstar is a satellite communications company that has a fleet of 48 satellites in low earth orbit. The satellites are operationally similar to moving cell phone towers: they field signals from ground-based phones and other devices and redirect the signals to ground stations where they are forwarded to other phones or to the internet. The company’s niche is the absence of lags in the signals because the satellites are close to the ground, in contrast with companies that operate satellites in geostationary orbit.

The company’s enterprise value is approximately two billion dollars as of this writing, and it is publicly traded, but it is 57% owned by insiders. The dominant one by far is Jay Monroe; Monroe’s ownership flows mostly through a hedge fund, Thermo Capital, that he owns and controls. Monroe is both the CEO and the chairman of the board of Globalstar.

Monroe is privy to information about the firm that outside shareholders do not have, and is able to act on that information by altering decisions about products, production, personnel and myriad other matters—and can keep these decisions from the view of outside shareholders. Should Globalstar, which is in the main a satellite communications company, enter a new market, say to sell spectrum that it owns for satellite communication, that would compete against other companies that are in the private network business? Monroe would have inside knowledge, and could approve that entry or not—and also trade on that information.

Monroe does in fact trade shares in Globalstar. (Because he is officially an insider, he is required to disclose these trades after two business days, but they are carried out confidentially at the time of execution.¹$^{,}$²$^{,}$³) Monroe’s trades, and trading-related activity such as debt financing and acquisition negotiations that are initially carried on in secret, affect the market price of Globalstar. Knowing that he is a large shareholder, it is incumbent on Monroe to temper not only his trading but also his business decisions within Globalstar.

The perspective of the existing literature is that by being a large shareholder in Globalstar, Monroe faces risks that can be potentially deleterious to him,⁴ but his ability to monitor the firm and make production decisions can enable him to appropriately minimize those risks. Smaller shareholders might benefit from his incentives and receive lower returns in exchange for the monitoring incentive—that is, they might free ride: key papers include Admati et al. (1994), Shleifer and Vishny (1986), and DeMarzo and Uroševic (2006).

Monroe’s possession of private information about the underlying fundamentals of the firm suggests an alternative view: that he will attempt to use that information in trading. The thrust of this paper is that the combination of large shareholder status and Monroe’s interest in trading on his private information will lead him to actually alter the fundamentals of the firm, and in a way that rests fundamentally on a deep property of the Kyle model.

In pure trading models where informed large traders cannot affect firm value but do have private information as with the descendants of the standard Kyle (1985) model such as Back (1992), Back et al. (2000), Holden and Subrahmanyam (1992), and Foster and Viswanathan (1996), and also Kyle’s 1989 paper Kyle (1989), information is used by the market makers and by the informed rivals from current or past prices to impute the information of the informed traders. The informed traders know this, and attempt to trade on the part of their private signals that is unforecastable using public price information. As a result, total order flow looks like noise trade order flow; the informed traders hide behind the noise traders. The informed trades are thus inconspicuous. This inconspicuousness appears in other studies: Danilova (2010), who coined the term, and Back and Baruch (2007), each using very different technical frameworks, find this result.

As in other versions of the Kyle model, the expected profit of the informed trader is proportional to the product of the volatility of the fundamental value and the volatility of the noise trade. If the informed trader is also a large shareholder, he can affect the fundamental value of the stock by his actions, and so he can affect that profit by increasing the volatility of the value. That strategy emerges here.⁵

What is key is that the amplification is not merely the enlargement of the variance of the fundamental. In a static version of the model, the large shareholder increases the volatility of firm fundamentals in this way, but because he simultaneously adjusts his trading strategy, from the market maker’s perspective the increase in volatility is of the component of his private information that cannot be forecasted by market makers—the inconspicuous part of his trades. Thus, he obfuscates.

In reality, the shocks that impinge on firm value are dynamic. Inconspicuousness still emerges as a strategy: privately informed traders alter the dynamic (i.e. autoregressive) structure of their trades so that total order flow has the same dynamic structure as noise trade. But in addition, the large shareholder can affect the underlying fundamental value of the firm not only in the conventional static sense; he can affect the dynamic structure of the value, that is, its autoregressive structure. He can profit by altering this structure, because this improves his ability to hide his private information from other informed traders and from market makers. The large shareholder now not only increases volatility, he alters the serial correlation structure of the firm’s fundamental value process.

Altering the fundamentals distorts the allocation of resources in the real activities of firms. Thus, the view that stock markets operate to allocate capital to firms is far too simplistic: markets fundamentally alter firms.

1.1 Outline

That the large shareholder alters the time series structure of the fundamental is the central result of the paper. The result is highlighted in two ways: first, with a proof that pure amplification of the underlying fundamentals is suboptimal, and second, with a numerical characterization of how the time series structure is actually altered.

To lay the groundwork for these results I first briefly review the literature on the volatility impact of managerial and shareholder incentives on firm value volatility, and also the literature on the large shareholder problem. I then set out a static model with the ingredients of the basic Kyle 1985 model: stocks, informed traders, market makers and noise traders, but with the additional feature that the the informed trader is also a large shareholder who can affect the fundamental value of the first stock via a costly action.

By adding the additional feature that the informed traders base their trades not just on their private signal but also on the price, the model becomes equivalent to the Kyle (1989) setting. This is because with an assumed Gaussian distribution of the fundamental value of the firm and also Gaussian noise traders, the inherent quadratic objectives of the informed traders and the market makers leads to linear demand curves. Because they are linear one can completely solve for them in close form by finding their intercept and slope coefficients.

This equivalence carries over to the the dynamic model. Now the intercept and slope coefficients apply to histories of private signals and histories of prices, and so they effectively become functions that can be found using fixed point methods. Moreover, the fixed points of these functions can be interpreted in terms of time series properties such as persistence that in turn have economic meaning.

To find these functions I use linear operator and control theory, known to economists as frequency domain methods, which allow a succinct characterization of how endogenous dynamics are affected by incentives and by equilibrium considerations; I present a couple of basic results regarding the trading behavior of the informed traders, namely that in equilibrium they hide their trades so as to be inconspicuous—a result that is fairly trivial to show in the frequency domain setting—and I note how this relates to other modeling approaches. I then add the large shareholder to the dynamic model and demonstrate with these methods that his actions will alter the dynamic structure—that is, the time series or autoregressive structure—of the firm’s fundamentals. Some of the details about the methods are provided in a companion paper, Taub (2018) including a new algorithm for the key step of spectral factorization.

1.2 The frequency domain approach

A characteristic of the linear-quadratic, Gaussian, time-separable, stationary setting of the model is that the optimal policy rules can be expressed as linear weightings of the information histories. A key aspect of the equilibrium is that, because the model is stationary, there is no influence of finite-horizon boundaries and so these weights are unchanging, that is, they are independent of the history of realized shocks. To put it another way, the linear weightings on the history of observed signals that are optimal for each trader in each period are also optimal in future periods: the optimal strategies are dynamically consistent and stationary.

It was noticed in earlier literature that the first-order conditions associated with linear-quadratic models of this sort could be z-transformed and solved in the so-called frequency domain; a reference is Hansen and Sargent (1981). The idea is akin to Fourier transforming a function. The attraction of the method was that it formalized the idea of forecasting future actions of other agents in stochastic environments, a problem that systematically arises in rational expectations theorizing.

Whiteman (1985) noted that the optimization problem itself could be transformed to the frequency domain, and the optimization done there.⁶ Now the optimization problem looks for a function that embodies the weights that the optimal policy puts on the signal history: it is a variational problem.

The logical next step is to transform not just the optimization problem but the game itself to the frequency domain. Each trader solves an optimization problem in the frequency domain using the variational method, taking as fixed the trading functions of the other traders, with the optimization choosing a function to maximize this norm, rather than choosing trades directly.

The equilibrium of this game is a set of functions—linear filters—that when transformed to the time domain yields the optimal linear policy for the original game. In this sense the frequency domain game is timeless. Of course, the equivalence of the equilibria of the two games—the timeless frequency domain game and the time-domain game that is played in each period—must be established. This has been done in other papers, such as Bernhardt et al. (2010).

The usual equilibrium conditions hold: optimality of the functions for the individual traders and market clearing in the sense that price—the dynamic price process—correctly reflects conditioning information. The equilibrium is found by iterating the traders’ optimal policy functions. This iteration is thus a fixed point problem in the space of functions containing the linear policy rules. This facilitates using the topological structure of the function space, and is in general easier than the direct time domain approach.

In the frequency domain approach, the equilibrium output functions can be characterized in terms of their poles, that is, the inverses of the autoregressive parameters of the output processes. In fact the equilibrium will have infinitely many pole terms, and it is therefore necessary to use numerical methods to approximate the equilibrium. A central result, as I have already noted above, is that the equilibrium poles are in fact endogenous: the poles of the input shocks are altered by the strategic behavior of the large shareholder, changing the persistence of the fundamental value process of the firm.

I make use of the extensive literature on numerical methods that has built up for numerical analysis of frequency domain models. These methods, which are called state space methods, are further described in Taub (2018). A key part of these methods is that they include formal techniques for approximating functions in the frequency domain, and this is crucial for the model because the numerical iteration of the recursion that expresses the equilibrium in the frequency domain leads to a proliferation of pole terms that must be appropriately trimmed, and when simulating the model these methods must appropriately approximate the actual equilibrium functions. The state space method does exactly this.

2 Literature

The conclusion that the large shareholder will amplify the volatility of that part of the firm’s fundamentals that he observes privately seems intuitively reasonable: if you give a CEO options in the company stock, his incentive is to increase the volatility of the company stock price in order to increase the option price.^{7 8} This has already been noted by the literature: recent references include Camara and Henderson (2009), Goldman and Slezak (2006), Peng and Roell (2008), Goldstein and Guembel (2008) and Bolton et al. (2006).

Peng and Roell empirically document the increase in shareholder litigation when managers are given option contracts as incentives. Their conclusion is that such contracts encourage the managers to focus on short term share prices.

Bolton, Scheinkman and Xiong develop a model in which the short term focus of the managers when they are given such option contracts is potentially desirable, because it enables them to increase the short term speculative component of the share price, benefiting current shareholders. That finding is mirrored in a sense here because the model here includes noise traders who are the source of profit for the informed traders. Both Peng and Roell and Bolton, Scheinkman and Xiong focus on managerial behavior, rather than large shareholder behavior.

Goldman and Slezak develop a model in which managers can exert agency-style effort to manipulate earnings so as to increase the value of their incentive pay. They conclude however that the manager’s increased effort can actually increase shareholder welfare because the efforts are in the right direction, that is, they improve firm value.

Goldstein and Guembel develop a model of price manipulation that is more focused on the production side. Firm managers observe prices in the market and make investment decisions based on those prices because they contain information that the manager might not be able to directly observe. Informed speculators, distinct from the managers, know this and manipulate prices to profit from the manager’s response, rather than directly to their own private signals. This notion is reflected in the model here: the large shareholder observes market prices (including the prices of other stocks that might have correlated information) and acts on that information as well as his own.

Camara and Henderson analyze the effects of several types of incentive contracts, and the effects of penalties and risk aversion on manager behavior. Among other conclusions, they find that risk aversion limits the manager’s incentive to increase firm volatility.

There is also a literature that models the decision of the large shareholder to influence share value and simultaneously the effects of this influence on his profits from trading, which is the agenda here. Maug’s (1998) paper is a leading example. In his paper, which builds on a Glosten and Milgrom (1985) type of model, there are two states of the firm, and prices reflecting the market makers’ (possibly mistaken) assessment of this state. There is a large shareholder who decides whether to buy a controlling share of a traded firm, and once done, to improve the firm; Maug’s term for this is monitoring. The large shareholder’s decision is not observable to outsiders, particularly the market maker; this is the private information aspect of the model. The Maug model does not have private information in the sense of the Kyle model however; because the large shareholder monitors only with a mixed strategy probability, he does not make active use of his private information.

The paper of Kahn and Winton (1998) is similar: institutional investors such as hedge funds learn the state of the firm before trade, unlike Maug’s model, where they don’t have private information per se. They can then act to buy shares and improve the firm.

Both the Maug and Kahn and Winton articles have the free-rider problem of the large shareholder as the main focus: they can shed light on the issue because their models include households—essentially the noise traders of standard market microstructure models—as holding small shares in the firm and potentially benefiting from the large shareholder’s action. The model here is very different, in that the noise traders are exploited, not benefited, by the large shareholder’s actions. Additionally, Maug and Kahn and Winton have less focus on strategic information, which is the main focus here.

This literature has been recently extended, exemplified most recently by Edmans and Manso (2013) in which large shareholders, referred to as blockholders, trade in markets that are modeled in standard microstructure fashion, in order to impose discipline on managers. Specifically, managers hold stock in the firm, and firm value is positively affected by their efforts; blockholder trades reveal information about firm value and thus indirectly reward that effort. These models are static in nature however, and so the feedback from trades into actions that influence firm value are only indirect.

Finally, a recent paper by Collin-Dufresne and Fos (2013) has a model that is close in some respects to the model in this paper: an activist shareholder pays a cost $C(\omega )$ where $\omega$ is effort to affect the terminal value of the firm. (Mechanically, this effort increases the mean payoff directly rather than the variance.) In addition, the market only has a noisy signal of the activist’s initial holding of the stock, so there is a private information element. The insider trades on his information, but, unlike this paper, his effort to affect firm value comes only after he has accumulated his position at the terminal time. Their paper is thus set in a finite-horizon environment, as with the standard Kyle model, whereas in this paper the fundamental value of the firm is constantly and stochastically evolving. That in turn allows me to characterize how the large shareholder alters the stochastic process of the firm value; that is the main agenda of this paper.

3 The static model

To motivate the dynamic model I set out a simpler static model. The static model has a number of results that provide intuition and which generalize to the dynamic case.

The static model has basic setup like the static version of the standard Kyle (1985) model: there is a random fundamental value of the firm known to the informed trader but not to the market maker, and noise trade. Without action by the large shareholder firm value v is

$$\begin{aligned} v = e \end{aligned}$$

(1)

where e is Gaussian $N(0, \sigma _e^2)$. The large shareholder, who is also informed,⁹ receives a zero-mean Gaussian-distributed signal e of the value of the firm whose stock is traded.¹⁰ Unlike the basic Kyle model, the informed trader can affect the value of the firm via his actions.

As in the standard Kyle model, there is uninformed noise trade u that is also Gaussian: $u \sim N(0, \sigma _u^2)$. Additionally, there is a competitive market maker who sets price conditional on total order flow, which consists of the sum of the informed trader’s order and noise trade. The informed trader submits orders based not only on his private information but also based on this price.¹¹

The large shareholder The large shareholder can be viewed as dividing his efforts between trading activities that benefit only himself and public activities that he is required to carry out for the benefit of the firm. To enhance his trading profits, the large shareholder chooses $\theta$ to weight his private signal in order to alter fundamental value:

$$\begin{aligned} v = e - \theta e. \end{aligned}$$

(2)

Because the fundamental e is constructed to have a zero mean, it is immediately evident that the influence of $\theta$ will ultimately be on the variance of the fundamental e.

The large shareholder’s other activity is to act for the benefit of the firm, that is, as a fiduciary. These actions can be monitored and rewarded only on the publicly observable elements of firm fundamentals. The public fundamental does not enter in the valuation of the company for trading purposes precisely because it is public.¹² There is therefore a separability between the public and private parts of the firm.

To capture the fiduciary aspect of the large shareholder within the linear-quadratic structure of the Kyle model, the large shareholder’s actions on behalf of the company might then be expressed as exerting effort to hit a publicly observable target driven by a random variable $\eta$, independent of the privately observable fundamental e. The incentive for the large shareholder to hit the target can be represented by a penalty function

$$\begin{aligned} - C (\eta - \theta \eta ) ^2. \end{aligned}$$

with the same $\theta$ as the coefficient of the private fundamental in (2). The large shareholder thus faces a tradeoff: his actions to alter the private fundamental via his choice of the amplification factor $\theta$ will thus detract from his efforts to hit the public target.

The penalty is roughly in the spirit of the Maug and Kahn and Winton papers, in which the large shareholder is presumed able to influence the value of the firm in a positive way; here, the impact is via reducing a penalty by hitting a target via effort.

Because the penalty function does not directly interact with the pricing part of the model, and because only the variance of $\eta$ affects the optimization, it is more tractable to express it as a simple penalty function on $\theta$, with the influence of the fundamental e alone:

$$\begin{aligned} - C (\theta e) ^2. \end{aligned}$$

This simplification avoids complications that would otherwise camouflage the main result.

The large shareholder’s information The large shareholder’s informed trade x is a linear function of his private signal of value e, and of the net information in price. The latter assumption, that the informed trader observes price and submitting orders that are a function of that price, is equivalent to the assumption that the large shareholder submits a demand curve to the market.¹³

The large shareholder’s simultaneous observation of the firm value e and of the net information in price means that the large shareholder also effectively observes the noise trade.

Pricing Market makers receive the aggregate orders $x+u$ from the informed trader and from the noise traders, but are unable to distinguish individual trades. Market makers are competitive, so they construct price to be efficient, that is, to be an optimal forecast of the value v.

I focus only on linear equilibria in which the informed trader’s trade is linear; because the noise trade and fundamental value are Gaussian, the optimal forecast is a linear projection. Price is thus a linear function of order flow

$$\begin{aligned} p = \lambda \left( x + u \right) \end{aligned}$$

(3)

where $\lambda$ is a projection coefficient that expresses the signal extraction that is being carried out. The solution of linear projection is equivalent to finding the pricing coefficient $\lambda$ that minimizes the forecast error variance.¹⁴

The large shareholder’s problem The approach here assumes that that trading rule and pricing rule are linear in information, and the optimizing agent chooses the intensity or linear coefficient on each signal in his possession, rather than choosing his trade directly. In this model this choice applies to the large shareholder, who is informed, and to the market maker, who observes total order flow. Specifically, I assume that the large shareholder’s strategy consists of a triple $(b,\gamma ,\theta )$, with total order flow y defined by

$$\begin{aligned} y= x+u \end{aligned}$$

(4)

and with the large shareholder’s order defined by

$$\begin{aligned} x = be+\gamma (be+u) \end{aligned}$$

(5)

The coefficient $\gamma$ multiplies the net information in price, rather than price or total order flow.

Lemma 1

Let the informed trader’s order flow take the linear form

$$\begin{aligned} x = b e + \gamma (b e+u) \end{aligned}$$

(6)

Then the net information in price is

$$\begin{aligned} b e+u \end{aligned}$$

(7)

Proof

Applying the linear pricing rule to total order flow yields the price

$$\begin{aligned} \lambda (x+u)= \lambda (b e + \gamma (b e+u) +u) = \lambda (1+\gamma )(b e+u) \end{aligned}$$

(8)

Dividing by $\lambda (1+\gamma )$ yields the net information in price. $\square$

It should be emphasized that the large shareholder chooses $\theta$ and b separately, in the sense that the intensity b operates directly on e, the underlying fundamental, rather than on the compound object $(1-\theta )e$. As will be evident in the derivation, the optimal intensity b nevertheless is a linear function of $1-\theta$. When solving for the optimal $\theta$, the envelope condition for b causes the interaction terms $b(1-\theta )$ to drop out.

Also note that the amplification factor is allowed to operate only on e, but not on the noise trade u; this simply reflects the fact that the large shareholder can affect the firm’s fundamentals, but not the characteristics of the noise trade.

Equation (6) is then essentially a demand schedule in the spirit of Kyle’s 1989 model. I will refer to the coefficients of that demand schedule, b and $\gamma$, as trading intensities.

Expressing the trading strategies explicitly in terms of linear intensities b and $\gamma$ as in Eq. (6), the large shareholder’s objective can be stated as

$$\begin{aligned} \max _{b,\gamma \theta } E\left[ \left( e - \theta e - \lambda \left( x +u \right) \right) x - \frac{C}{2} (\theta e) ^2\Bigg | e, p\right] \end{aligned}$$

(9)

Substituting from the linear structure of the large shareholder’s order flow in (5), and from the linear pricing rule in (3), and carrying through the expectation and with the assumption that the private signal of e is uncorrelated with the noise trade u, the optimization problem becomes

$$\begin{aligned} \max _{\{b,\gamma ,\theta \}} \bigg \{ \left( \left( 1 -\theta \right) - b \left( 1+ \gamma \right) \lambda \right) (1+\gamma )b \sigma _e^2 - \left( 1+ \gamma \right) \lambda \gamma \sigma _u^2 - \frac{C}{2} \theta ^2 \sigma _e^2 \bigg \} \end{aligned}$$

(10)

3.1 Equilibrium

A definition of equilibrium can now be stated:

Definition 1

An indirect linear equilibrium is a tuple $(b, \gamma , \theta , \lambda ) \in R^4$ such that

• (i) Profit maximization: A trading and amplification strategy consisting of a triple $(b, \gamma , \theta ) \in R^3$ solves (10), conditional on the linear pricing rule $\lambda$, with information set (e, u), and

• (ii) Market efficiency: The linear pricing rule $\lambda$ minimizes the market maker’s forecast error variance of $E\left[ (1-\theta )e \big | b e + \gamma (b e+u)+u \right]$ conditional on the informed trader’s linear trading strategy $(b, \gamma , \theta )$ and the information from total order flow $b e + \gamma (b e+u)+u$.

To find the equilibrium one solves the large shareholder’s first order condition and then combines this with the market maker’s first order condition.

The large shareholder’s first order conditions The first-order conditions for b, $\gamma$, and $\theta$ can be found by differentiation and algebra as follows:

$$\begin{aligned} b = \frac{1}{2 \lambda (1+\gamma )} (1-\theta ) \qquad \gamma = - \frac{1}{2}\qquad \theta = - \frac{(1+\gamma ) b}{C} \end{aligned}$$

(11)

Thus, the large shareholder’s trading intensity on private information is modified by his alteration of the variance of the fundamental. Also, in taking the first order condition we have the option of viewing the intensity b as a function of $\theta$ from the solution, but by the envelope condition these terms drop out.

The market maker’s first-order condition I next show that the market maker’s pricing is linear conditional on the large shareholder’s linear order flow. In keeping with the indirect approach, rather than model this as finding the efficient pricing rule and establishing that it is linear, I begin with the market maker’s problem as choosing $\lambda$ directly as the control variable in an optimization problem that assumes linearity of the pricing rule, and takes as given the large shareholder’s linear trading rule. The optimization problem is to minimize the forecast error variance conditional on total order flow.

The market maker’s objective is

$$\begin{aligned} \min _\lambda E\left[ \left( (1-\theta )e - \lambda (b e + \gamma (b e+u) +u \right) )^2 \Big | b e + \gamma (b e+u) +u \right] \end{aligned}$$

(12)

The first order condition leads directly to the calculation of the projection:

$$\begin{aligned} \lambda = \frac{(1-\theta ) b(1 + \gamma )\sigma _e^2}{(1 + \gamma )^2( b^2 \sigma _e^2 + \sigma _u^2)} \end{aligned}$$

(13)

We can now establish that an equilibrium exists using these solutions and also characterize it.

Corollary 1

An indirect linear equilibrium exists, with solutions

$$\begin{aligned} b = \frac{\sigma _u}{\sigma _e} \quad \gamma = - \frac{1}{2}\quad \lambda = \frac{(1-\theta )\sigma _e}{\sigma _u} \quad \theta = - \frac{1}{2C} \frac{\sigma _u}{\sigma _e} . \end{aligned}$$

(14)

Proof

Using the solutions for b and $\gamma$ from (11), substitute into the solution for $\lambda$ from Eq. (13). Finally, substitute these solutions into the equation for $\theta$ in Eq. (11), choosing the negative root. The solution for $\theta$ then determines the effective variance of the fundamental, $\tilde{\sigma }_e$. Finally, the reduced form solutions found in Eq. (14) can be duplicated. $\square$

The approach used here, that the informed trader optimizes over the intensities on his signals, the fundamental firm value e, and total order flow y, is not a priori the same as optimizing over his order flow directly conditional on the signals; one could denote this the direct equilibrium, in contrast to the indirect equilibrium I have developed here, in which the informed trader optimizes over the intensities b, $\gamma$, and $\theta$. It is straightforward to demonstrate that the two approaches are equivalent; a similar demonstration is presented in Bernhardt et al. (2010).

3.2 Characteristics of the solution

The coefficient $\gamma$ has the following interpretation: it is the (negative of the) projection coefficient of the informed trader’s trade on public information onto publicly available information, namely price; in turn, price is informationally equivalent to total order flow.¹⁵ Because $\gamma$ is negative, the factor $1+\gamma$ is the coefficient of the forecast error of that projection. Thus, $\theta$ is proportional to the market maker’s forecast error coefficient $(1+\gamma )$ on the traded part of the large shareholder’s private signal, b; this is the same quantity on which the informed trader’s orders are based.

By (14), $\theta$ is negative, and so the modified fundamental $e-\theta e$ is in fact an amplification of the fundamental variance. But in addition, note that this term too is proportional to the forecast error coefficient $1+\gamma$. Thus, the amplification is only on the unforecastable part of the fundamental, limited only by the penalty C.

I summarize the main additional characteristics of the equilibrium as follows:

Proposition 1

• (i) The large shareholder amplifies the unforecastable part of his component of the fundamental.

• (ii) The large shareholder’s amplification of the unforecastable part of his component of the fundamental increases his profit.

• (iii) The large shareholder amplifies the market maker’s forecast error variance.

• (iv) The large shareholder reduces market liquidity.

• (v) The large shareholder increases price volatility.

Proof

(i) Using a projection algebra argument, Bernhardt and Taub (2006, p. 11) demonstrate that the order flow x is comprised of a linear function of the market maker’s forecast error of the informed trader i’s private signal e. For the large shareholder, this translates to

$$\begin{aligned} x = \frac{1+\gamma }{\lambda } E \left[ (1-\theta )e \Bigg | \left( (1-\theta )e - E\left[ (1-\theta )e \Bigg | x+u\right] \right) \right] \end{aligned}$$

where it should be noted that the inner expectation is conditioned on total order flow $x+u$. Factoring $1-\theta$ out of this expression, we have

$$\begin{aligned} x = (1-\theta )\frac{1+\gamma }{\lambda } E \left[ e \Bigg | \left( e - E\left[ e \Bigg | x+u\right] \right) \right] \end{aligned}$$

(15)

Because $\theta$ is negative, the key effect of the large shareholder is to not only amplify the private signal, but to amplify the unforecastable part of the signal.

(ii) Profit is

$$\begin{aligned} \pi = \lambda (1+\gamma ) \sigma _u^2 = \frac{(1-\theta )\sigma _e\sigma _u}{2}. \end{aligned}$$

(16)

Because the optimal $\theta$ is negative, $1-\theta$ exceeds unity and $\tilde{\sigma }_e > \sigma _e$.

(iii) The forecast error variance is

$$\begin{aligned} E \left[ ((1-\theta )e - \lambda (x + u))^2\right] = \frac{(1-\theta )^2 \sigma _e^2}{2} \end{aligned}$$

(17)

Because $\theta$ is negative, the forecast error variance exceeds the forecast error variance when there is no large shareholder.

(iv) Liquidity is the inverse of the price impact coefficient $\lambda$. From formula (14) and the fact that $\theta$ is negative in equilibrium, $\lambda$ is magnified in the large shareholder equilibrium.

(v) The volatility of price is:

$$\begin{aligned} E \left[ ( \lambda (1+\gamma ) (b (1-\theta )e + u))^2 \right] = \frac{{(1-\theta )^2\sigma _e}^2}{2} \end{aligned}$$

which is increased by the amplification factor $\theta$. $\square$

Thus, the large shareholder does in fact conform to intuition: he will effectively increase the volatility of the firm’s value, and he takes advantage of this excess volatility in the dimension in which he receives signals in his trading. Consequently the large shareholder has a larger profit than a correspondingly informed outsider; these profits come at the expense of the noise traders.

The increase in the effective fundamental variance increases the pricing coefficient $\lambda$, as would be expected: the signal to noise ratio has been increased. The increase of the forecast error variance is not obvious a priori, because the higher variance of the fundamental $\sigma _e^2$ raises the signal to noise ratio in order flow. This would be expected to increase $\lambda$—which it does—and thus reduce the overall forecast error variance. However, the way the signal is amplified is via the forecast error of the signal, and intuitively this should not improve the signal component, and this is the result.

The reduction in liquidity result (iv) stands in contrast to the liquidity findings in Maug’s paper Maug (1998): he finds that under certain conditions the large shareholder increases liquidity.

...if a larger fraction of the total shares is owned by the large shareholder, then fewer shares are held by households, making the market less liquid in these shares. We call this the liquidity effect. This loss of liquidity reduces the large shareholder’s expected gains from trading on private information. [Maug (1998) p. 67]

In the model here, the large shareholder’s impact is expressed as the variance of the private information about the firm to which he is privy; because he amplifies this variance, liquidity is reduced. Moreover, the direction of causality is reversed: in Maug’s model there is an initial amount of liquidity, to which the large shareholder responds. Here, liquidity is ultimately under the influence of the large shareholder. (However Maug’s extended model is a bit more subtle in that the large shareholder’s initial holdings of the firm can adjust before the main trades occur.)

The fact that the large shareholder amplifies the non-forecastable part of his order flow—obfuscation—suggests that in a dynamic setting the large shareholder might want to alter the time series structure of the fundamental. This conjecture is true and in the next section I set the groundwork for demonstrating this.

4 Adding dynamics

I will now set out a dynamic version of the model using a continuous time approach. I use the continuous-time analogue of Bernhardt et al. (2010) and Seiler and Taub (2008) in order to carry out the dynamic analysis. The main tools are the Laplace and Fourier transforms and the continuous-time analogue of the Wiener–Hopf equation. These tools are described in sections 6.A (pp. 216–220), 7.1–7.2 (pp. 221–228), and 7.A (262–264) of Kailath et al. (2000). An additional reference is Hansen and Sargent (1991).

The dynamic model differs significantly from the more standard approach exemplified by the paper of Back (1992), which uses a PDE approach to solving the dynamic Kyle model. In the original dynamic Kyle model the fundamental value of the firm is fixed, as is the time horizon. The only dynamic fundamental element of the model is the noise trade, which is Brownian motion. Because of the fixed horizon, the behavior of the equilibrium is strongly influenced by boundary conditions. In the model of this paper, the firm’s fundamental is itself a dynamic process, as is the signal observed by the informed trader. While increasing the complexity of the model in many dimensions, it also renders it stationary. The stationary model can be mapped to the frequency domain and then solved with essentially algebraic methods. More concretely, the transformed model reduces the solution process to finding functions that are the analogues of the coefficients b, $\gamma$, $\theta$ and $\lambda$ from the static model, namely $B(\cdot )$, $\varGamma (\cdot )$, $\varTheta (\cdot )$, and $\varLambda (\cdot )$, which are elements of a Hilbert space. The optimization problems of the informed traders and of the market makers can be expressed as variational problems in the frequency domain with optimization over these functions. Because the functions are in essence the generating functions of stochastic processes, they have clear economic interpretations, particularly with regard to the persistence of the processes.

In the standard market microstructure literature, the noise trade is assumed to be a Brownian process so that incremental noise trades are serially uncorrelated, while there is a single realization of the underlying asset value, as in the original Kyle 1985 model, or another Brownian process as in Danilova’s model Danilova (2010), so that information are highly persistent. By contrast, in this paper while I maintain the assumption of a persistent value process, I allow the degree of persistence to be a variable. This serves to highlight the starkly different dynamic structure of order flow and prices, differences that highlight the economic forces driving those processes.

In the next subsection I develop the technical elements of the dynamic model without the large shareholder, building on previous work. The conclusions regarding inconspicuousness are easily established in this framework. In subsequent sections I add the large shareholder and develop the main result: that the large shareholder obfuscates not only by amplifying the non-forecastable part of informed order flow, but by altering the fundamental of the firm itself.

4.1 Technical preliminaries

I begin with the assumption that the total cost of shares X(t) held by a trader at each time t is proportional to the discounted cost of acquiring them at each instant, $\int _0^t e^{-r s} p(s) x(s) ds$, where x(s)ds is the incremental shares acquired, r is the discount rate and p(t) is the price of a share at time t.

In the standard setup of the Kyle model, the underlying value is fixed, and is revealed at the terminal time T. There are two differences here: first, the horizon is infinite, and so the underlying value is effectively never revealed. Second, the value fluctuates stochastically, and meaning must be given to this fluctuation. The interpretation will be that at each moment there is a possibility that the firm will be bought, merged or terminate, with some probability that is independent of past or current states and associated hazard rate $\delta$; I will refer to this as conversion. Should the conversion occur, the discounted payoff for an informed trader is

$$\begin{aligned} e^{-rt} \overline{v}(t) \int _0^t x(s) ds \end{aligned}$$

where $\overline{v}(t)$ is the time-t realization of the stochastically evolving fundamental value, and this happens with probability $\delta e^{- \delta t}$. The probability-weighted expected payoff at time t is then

$$\begin{aligned} E\left[ e^{- r t} \delta e^{-\delta t} v(t) \int _0^t x(s) ds \bigg | \omega (0) \right] \end{aligned}$$

where $\omega (t)$ is the trader’s information at t. Thus, the expected profit over all dates of conversion is

$$\begin{aligned} E\left[ \int _0^\infty e^{-rt}\delta e^{-\delta t} \overline{v}(t) \int _0^t x(s) \, ds \, dt \bigg | \omega (0) \right] \end{aligned}$$

By changing the order of integration we can write the inner terms as

$$\begin{aligned} \int _0^\infty x(t) \int _t^\infty e^{- r s} \delta e^{- \delta s} \overline{v}(s) \, ds \, dt \end{aligned}$$

(18)

Defining the probability-discounted value of the asset at any moment as

$$\begin{aligned} v(t) \equiv e^{- \delta t} \int _t^\infty \delta e^{-(\delta +r) (s-t)} \overline{v}(s) \, ds \end{aligned}$$

we can write Eq. (18) as

$$\begin{aligned} E\left[ \int _0^\infty e^{-rt} x(t) v(t) dt \bigg | \omega (0) \right] . \end{aligned}$$

(19)

This then justifies writing discounted expected profit as

$$\begin{aligned} E\left[ \int _0^\infty e^{-rt} (v(t) - p(t)) x(t) dt \bigg | \omega (0)\right] . \end{aligned}$$

(20)

4.1.1 Value and noise trade process specifics

Let e(t) be the private information process for the informed trader, who is also the large shareholder. I assume that the process is a Gaussian, zero-mean white noise process, and it remains the case that the firm value is equal to this signal. Now however, the signal and consequently the firm value are stochastic processes. The raw or unmodified firm value process is a filtered version of this fundamental signal process:¹⁶

$$\begin{aligned} v(t) = \int _0^\infty \phi (\tau ) e(t-\tau ) d\tau \end{aligned}$$

(21)

It deserves emphasis that it is the probability-discounted payoff, v(t), that is defined using these primitives, rather than the raw payoff $\overline{v}(t)$.¹⁷

If the large shareholder modifies the fundamental, then he would choose an additional filter $\theta (\cdot )$ to convolve with the v process:

$$\begin{aligned} \int _0^\infty \theta (\tau ) dv(t-\tau ) \end{aligned}$$

(23)

so that the modified fundamental would be

$$\begin{aligned} \tilde{v}(t) = \int _0^\infty \phi (\tau ) dZ(t-\tau ) - \int _{\sigma =0}^\infty \int _0^\infty \theta (\sigma ) \phi (\tau ) dZ(t-\tau -\sigma ) \end{aligned}$$

(24)

Similarly, the noise trade process can be a filtered version of a fundamental white noise process n(t):

$$\begin{aligned} u(t) = \int _0^\infty \nu (\tau ) n(t-\tau ) d\tau . \end{aligned}$$

Both the value and noise processes are characterized by the filters $\phi$ and $\nu$. For the purposes of characterizing the model it will be assumed when necessary that the value and noise trade processes are Ornstein–Uhlenbeck processes, that is, analogues of autoregressive processes in discrete time settings. The filters are then in exponential form:

$$\begin{aligned} \phi (\tau ) = e^{-\rho \tau } \qquad \nu (\tau ) = e^{-\eta \tau }. \end{aligned}$$

In the limit, these processes become Brownian motions at $\rho =0$ and $\eta =0$, and white noise processes at the limit of the other extreme, $\rho = \infty$ and $\eta =\infty$. Economic intuition suggests that the value processes should be highly predictable; similarly intuition suggests that noise trade should not be persistent. To keep the model tractable I will assume that noise trade is white noise ($\eta =\infty$), but that the value process can have any degree of persistence, characterized by $0 \le \rho <\infty$.

Using the continuous time transform as described in Kailath et al. (2000, p. 217), the s-transforms of the filters for the value and noise trade processes are then $\varPhi = \frac{1}{s+\rho }$, which is the transform of an Ornstein–Uhlenbeck process and the identity matrix I respectively.¹⁸

4.2 Order flow and public information

Before carrying out the full transformation of the objective to the frequency domain, it will be helpful to convert the expression of the large shareholder’s trade from demand submission form as in Lemma 1, in which the large shareholder reacts directly to price, to an equivalent one in which the large shareholder bases his trade on the public information inherent in price. To keep the argument simple I will temporarily drop $\theta$, the large shareholder’s modification of the fundamental from the notation: the large shareholder will be treated as if he were a conventional informed trader, and I also temporarily drop the filter on the fundamental process, $\phi$.

Let $\varOmega (t)$ be the public information process, which is going to be equivalent to the information in price.¹⁹ In keeping with the assumption of linear strategies as in the static model, the informed trader’s trading strategy process is restricted to be a linear filtering of the histories of these processes:

$$\begin{aligned} x(t) = \int _{\tau =0}^\infty (b_{\omega }(\tau ) dZ(t-\tau ) + b_{\varOmega }(\tau ) \varOmega (t-\tau )d\tau ). \end{aligned}$$

Moreover, the linear filters $b_{\omega }(\cdot )$ and $b_{\varOmega }(\cdot )$ that constitute the trading strategy are assumed to be fixed, that is, they are independent of time. As with the static model, the filters, including that for the large shareholder, are assumed to operate directly on the fundamental processes; the impact of the large shareholder is felt via the value process and its impact on price.

The trading strategy filters chosen by the informed trader or large shareholder are elements of the space of square-integrable functions, taking account of discounting:

$$\begin{aligned} L_2(r) \equiv \left\{ f(\cdot ) \Big | \int _0^\infty e^{-rt} \left| f(t)\right| ^2 < \infty \right\} \end{aligned}$$

(25)

However, the focus will not be on the objective with this choice set, but rather elements of the transformed objective and control filters, which I will detail later.

In addition, noise traders exogenously submit an order flow process u(t). Adding up the informed and noise trade yields total order flow:

$$\begin{aligned} x(t) + u(t) = \left( \int _{\tau =0}^\infty (b_{\omega }(\tau ) dZ(t-\tau ) + b_{\varOmega }(\tau ) \varOmega (t-\tau )d\tau ) \right) + u(t). \end{aligned}$$

(26)

Defining the left hand side of (26) as $\varOmega (t)$, we have the recursion

$$\begin{aligned} \varOmega (t) = \int _{\tau =0}^\infty b_{\omega }(\tau ) dZ(t-\tau ) + \int _{\tau =0}^\infty b_{\varOmega }(\tau ) \varOmega (t-\tau ) d\tau + u(t). \end{aligned}$$

(27)

$\varOmega (t)$ is a stochastic process that also defines the market maker’s information process. It will be key for the further analysis to express this information process in modified form.

The right hand side of the $\varOmega (t)$ process in Eq. (27) is a convolution as described in Kailath et al. (2000, p. 217), but the integration is one-sided. However, if it is known in advance that the functions $b_{\omega }$ and $b_{\varOmega }$ are one-sided, the integral can be converted to two-sided form and obtain the Laplace transform of the equation.²⁰

Following Kailath, Sayed and Hassibi’s convention of using capital letters for the Laplace transform, the transform of Eq. (27) is:

$$\begin{aligned} O(s) = B(s) e(s) + B_{\varOmega }(s) O(s) + U(s). \end{aligned}$$

where B(s) is the transform of $b_{\omega }$ (see pp. 216–217 of Kailath et al. 2000). The convolutions have been converted into products as a result of the transform. With this transformation, it is now possible to solve for O(s) with straightforward algebra. This yields

$$\begin{aligned} O(s) = \left( 1 - B_{\varOmega }(s) \right) ^{-1} \left( B(s) e(s) + U(s)\right) \end{aligned}$$

(28)

The solution approach used in Bernhardt et al. (2010) can now be followed: define $\gamma$ as the filter characterized by the transform

$$\begin{aligned} \varGamma (s) = \left( 1 - B_{\varOmega }(s) \right) ^{-1} B_{\varOmega }(s) \end{aligned}$$

(29)

and then substituting from Eq. (27) into the order flow Eq. (26) and using (28) and (29), the order flow process becomes

$$\begin{aligned} x(t)= & {} \int _{\tau =0}^\infty b_{\omega }(\tau ) dZ(t-\tau )\nonumber \\&+ \int _{\tau =0}^\infty \gamma (\tau )\left( \int _{\sigma =0}^\infty b_{\omega }(\sigma ) dZ(t-\tau -\sigma ) + u(t-\tau ) \right) d\tau \end{aligned}$$

(30)

The bracketed term can then be viewed as the public information process inherent in the price process.

Maintaining the assumption of linear pricing, the price process is determined by a linear filter $\lambda$, with transform $\varLambda$, applied to total order flow:²¹

$$\begin{aligned} p(t)= & {} \int _0^\infty \lambda (\tau ) \Bigg [ \int _{\sigma =0}^\infty \int _{\nu =0}^\infty b_{\omega }(\sigma ) \left( 1 + \gamma (\nu )\right) dZ (t-\nu -\sigma -\tau ) d\sigma \nonumber \\&+ \int _{\nu =0}^{\infty } \gamma (\nu ) u(t-\nu -\tau )d\nu \Bigg ] d\tau \end{aligned}$$

(31)

These ingredients will now be combined to form the objective for the informed traders.

4.3 The informed trader’s objective

Resuming the explicit incorporation of $\theta (\cdot )$ and $\phi (\cdot )$, and expressing the informed trader’s actions in terms of the filters expressing the value process in Eq. (21), the price process in (31), and the order flow process from (30) which includes the public information process, we can write the time-domain objective (20) for the large-shareholder informed trader as

$$\begin{aligned}&\max _{\{b_{\omega }(\cdot ), \gamma (\cdot ), \theta (\cdot )\}} E \int _0^\infty e^{-rt} \Bigg ( \int _{\tau =0}^\infty \phi (\tau ) dZ(t-\tau )\! -\! \int _{\tau =0}^\infty \int _{\sigma =0}^\infty \phi (\tau ) \theta (\sigma ) dZ(t\!-\!\tau \!-\sigma )\\&\quad - \int _{\tau =0}^\infty \lambda (\tau ) \Bigg [\int _{\sigma =0}^\infty \int _{\nu =0}^\infty b_{\omega }(\sigma ) \left( 1 + \gamma (\nu )\right) dZ(t-\nu -\sigma -\tau ) d\sigma \nonumber \\&\quad + \int _{\nu =0}^{\infty } \gamma (\nu ) u(t-\nu -\tau )d\nu \Bigg ] d\tau \Bigg ) \nonumber \\&\quad \times \left( \int _{\tau =0}^\infty b_{\omega }(\tau ) dZ(t-\tau )+ \int _{\tau =0}^\infty \gamma (\tau )\left( \int _{\sigma =0}^\infty b_{\omega }(\sigma ) dZ(t-\tau -\sigma ) + u(t-\tau ) \right) d\tau \right) dt\nonumber \end{aligned}$$

(32)

where $b_{\omega }(\cdot )$ and $\gamma (\cdot )$ are elements of the space of exponentially bounded functions that are analytic and square integrable, that is, they are in $L^2_+(r)$ in Hansen and Sargent’s (1991) notation, with the integration adjusted for discounting, and with the optimization over the filters directly rather than over informed order flow x. With these elements in place, it is possible to state a preliminary definition of equilibrium:

Definition 2

An linear equilibrium is a quadruple $(b_\omega (\cdot ),\gamma (\cdot ),\theta (\cdot ),\lambda (\cdot ))$ elements of $L_2(r)$ such that

• (i) The functions $(b_\omega (\cdot ),\gamma (\cdot ),\theta (\cdot ))$ solve the informed trader/large shareholder’s optimization problem (32) taking as given $\lambda (\cdot )$ with information $\left( (e(t-s),\right. \left. u(t-s) \right) _{s=0}^\infty$ for all t, and

• (ii) The filter $\lambda (\cdot )$ in the market maker’s pricing rule in (31) is the conditional forecast of the value process at every time t, taking as given the informed trader’s trading rules $(b_\omega (\cdot ),\gamma (\cdot ),\theta (\cdot ))$.

The objective in (32) is nontrivial, because the choice of the optimal action each period is conditioned on information, which includes the history of endogenous actions, and similarly the pricing rule in (31) is a fairly complicated object. As in the static model in which the solution could be approached by first taking the expectation of the fundamentals and then seeking solutions of the optimal coefficients, the solution of the dynamic model is more straightforward if the objective is first converted to frequency domain form, with the choice variables converted from time-domain period-by-period actions to the choice of optimal Laplace transformed filters in the frequency domain.²² I next develop the recipe for converting the objective to frequency domain form.

At this point that the assumption that the choice objects $b_\omega$, $\gamma$ and so on, are restricted to be linear filters, means that the equilibrium, if it exists, will be a linear equilibrium. While the uniqueness of the equilibria in the Kyle model has long been a subject of exploration in the literature, I am imposing this linear structure as an assumption.

Once the conversion to the frequency domain occurs, the optimal filters are found by solving a static variational problem. It deserves emphasis that in the original time-domain statement of the informed trader’s objective and the market maker’s filtering problem, it is at least conceptually possible for the optimal filters $b_\omega$, $\gamma$ and so on to be nonstationary functions of time, that is at each time t the informed trader would choose filters $b_\omega (t,\cdot )\ne b_\omega (s,\cdot )$ for $s\ne t$. However, because the problem is time-separable with linear constraints and a quadratic objective, this will not be the case: the optimal filters will be stationary. This in turn means that the frequency domain version of the model in which the optimal filters are chosen directly also solves the time-domain version of the model.

5 The frequency-domain model

Whiteman (1985) constructed a discrete time model and then converted the objective itself into z-transform form. The optimization was then over linear operators or filters that were found via a variational derivative of the transformed objective.²³ This was achieved by imposing the constraint that the controls must be a linear filter of the information, and taking the expectation of the objective prior to optimizing over those filters; this is the extension of the similar operation that was carried out in going from Eqs. (9)–(10) in the static model. However, it is essential to reduce the covariance function of the fundamental processes—the white noise fundamentals—to a scalar covariance matrix. In continuous time, the equivalent operation is to make the fundamental covariance function $R_x(t)$ a Dirac $\delta$-function.²⁴

If the fundamental processes are serially uncorrelated, as is the case here by the assumption that the fundamental processes are white noise, then the expectation of an objective like (32) leaves an integral in which the integrand consists of products of functions. Fourier transforming these objects then yields a convolution in the frequency domain, and the variational derivative of these convolutions can then be calculated. Proceeding in this way with abstract functions f and g,

$$\begin{aligned} \int _0^\infty e^{-rt} f(t) g(t) dt = \int _{a-i \infty }^{a+i\infty } F(s) G^*(r-s^*) ds \end{aligned}$$

(33)

where the notation $G^*$ signifies the complex conjugate transpose of G, $G^*(r-s^*)$.²⁵ The $r-s^*$ term captures discounting, and where the integration is along a strip parallel to the imaginary axis in which $\hbox {Re}(s) = a$, where the functions F and G are analytic in the right half plane—that is, F and G have no poles or singularities in the region $\hbox {Re}(s) > - r$, and with a small enough to avoid poles and thus yield convergence, that is, $a<r$.²⁶ There are two parts to the integrand: the causal part F(s) and the anti-causal part $G^*(r-s^*)$, reflecting the inner product that is expressed in the objective.

The right hand side of (33) defines an inner product; formally, define

Definition 3

$H^2$ is the set of square integrable functions on the right half plane with inner product defined in (33) such that

$$\begin{aligned} H^2(r) = \left\{ F: \int _{a-i \infty }^{a+i\infty } F(s) F^*(r-s^*) ds < \infty \right\} . \end{aligned}$$

I will seek equilibria consisting of functions from this space.

5.1 Mapping the large shareholder’s problem to the frequency domain

In the static model, the market maker views the modified fundamental $(1-\theta )e$ as indistinguishable from a raw fundamental; similarly, the large shareholder solved for the optimal signal intensity coefficient b and the price information intensity coefficient $\gamma$ by treating the modified fundamental as a raw fundamental; the choice of the amplification coefficient could then be developed subsequently. This same strategy works in the dynamic model.

The large shareholder chooses the filter $\theta (\cdot )$ on his private signal in order to alter fundamental value:

$$\begin{aligned} v_t = \int _0^\infty \phi (\tau ) dZ (t-\tau ) - \int _0^\infty \int _0^\infty \theta (\sigma ) \phi (\tau ) dZ(t-\tau -\sigma ) d\sigma \end{aligned}$$

There are no intrinsic restrictions on the filter, other than that it must by analytic, i.e., it can be backward looking but not forward looking. Thus, the filter can be designed so that the stochastic structure in the underlying shocks is altered to be more or less persistent, and to have additional structure such as zeroes that make the price process noninvertible in some appropriate sense.

The penalty on the large shareholder’s action is

$$\begin{aligned} E \left[ \left( C^{1/2} \int _0^\infty \int _0^\infty \theta (\sigma ) \phi (\tau ) dZ (t-\tau -\sigma ) d\sigma \right) ^2 \right] , \end{aligned}$$

(34)

that is, the amplification is treated as a penalty process. The motivation for this penalty is the same is in the static model: one can think of the large shareholder as having a responsibility to hit stochastic targets that are public, as well as being interested in altering the privately observed fundamentals for the purpose of making trading profits. As in the static model, the essential features of the target-hitting formulation can be captured by a penalty formulation.²⁷

Applying the transform method to the informed trader’s problem, the transformed objective will be a function of the value process filter $\varPhi (s)$, the public information process filter O(s), the modification of the fundamental $\varTheta (s)$, the pricing filter $\varLambda (s)$, and the informed trader’s order flow X(s). The transform of the objective (32) is then

$$\begin{aligned}&\max _{X, \varTheta } \int _{a-i\infty }^{a+i\infty } \hbox {tr}\,\Big ({\varPhi }(s)-\varTheta (s) \varPhi (s)) - \varLambda (s)O(s)) X^*(r-s^*) R\nonumber \\&\quad - \frac{C}{2} \varTheta (s) \varPhi (s) \varPhi ^*(r-s^*) \varTheta ^*(r-s^*) \Big ) ds \end{aligned}$$

(35)

where O is the transform of the total order flow process from Eq. (28), and where $\varPhi (s)$ is the (vector) value process Laplace transform, the valuation process reflects the action of the large shareholder, with $\varTheta (\cdot )$ the transform of $\theta (\cdot )$. Because I solve the model using the indirect approach—that is, taking expectations on the assumption of linearity and then solving for the optimal filters—it is appropriate to simultaneously solve for X and $\varTheta$.

The internal pieces of X and $\varPhi$, $\varLambda$, and O can now be broken out. The causal and anti-causal pieces ($\varPhi -\varLambda O$ and $X^*$ respectively) are such that the Fourier transform of a sum is the sum of the Fourier transforms. The convolution of functions of the s operator translates into multiplication of functions in the s-domain: let $g(t) = \int _0^\infty h(\tau )m(t-\tau ) d\tau$, and consider the Fourier transform of $\int _0^\infty f(\sigma ) g(t-\sigma ) d\sigma$. Then it is immediate that

$$\begin{aligned} F(s) G(s)= F(s) (H(s) M(s)). \end{aligned}$$

(36)

Thus, the double integration in Eq. (34) is an iterated convolution, and thus the transform results in an iterated product $\varTheta (s) \varPhi (s)$.

With this result in hand one can write the Fourier transformed objective (35) with the explicit decomposition of the price process. Also, B(s) is the Fourier transform of the filter $b_{\omega }(t)$; $\varGamma (s)$ is the Fourier transform of $\gamma (t)$, and H is the Fourier transform of $1+ \gamma (t)$, so that

$$\begin{aligned} H(s) = 1+ \varGamma (s). \end{aligned}$$

(37)

With these ingredients the large shareholder-informed trader’s transformed order flow filters are a vector of transforms

$$\begin{aligned} \begin{pmatrix} B (1+\varGamma )&\varGamma \end{pmatrix} \end{aligned}$$

(38)

with each element corresponding to the filters operating on the fundamental process e(t) and on the noise trade fundamental u(t) via the public information process; the extra term in the first element adds the informed trader’s direct operation on his own signal. Similarly, the price process transform consists of the elements

$$\begin{aligned} \varLambda \begin{pmatrix} B H&H \end{pmatrix} \end{aligned}$$

operating on the individual fundamental process e(t) and the noise trade process u(t), and where the total order flow by all agents is captured by adding up the individual transforms in (38) and using the compact notation in (37). Finally, $\varPhi$ is the Fourier transform of the raw unmodified firm value process process that the informed trader/large shareholder sees in his signal, and which is the value process of the stock.

Combining these ingredients yields the s-transform of the objective (32). By assuming independence of the noise trade and fundamentals, we can write the objective in detail as

$$\begin{aligned}&\max _{\{B,\varGamma , \varTheta \}} - \int _{a-i\infty }^{a+i\infty } \hbox {tr}\,\Bigg \{ \begin{pmatrix} (\varPhi - \varTheta \varPhi ) - B H \varLambda \\ - H \varLambda \end{pmatrix} \begin{pmatrix} (1+\varGamma ^*) B^*&\varGamma ^* \end{pmatrix}R\nonumber \\&\qquad - \frac{C}{2} \varTheta \varPhi \varPhi ^* \varTheta ^* \Bigg \} ds \end{aligned}$$

(39)

where the causal and anti-causal parts reflect the inner product that is expressed in the objective, and where R is the covariance matrix function of the Dirac-$\delta$ fundamentals e(t) and u(t).²⁸ To keep the model tractable, I will assume as in Bernhardt et al. (2010)) and Seiler and Taub (2008) that the noise trade process is uncorrelated with the fundamental value and signal processes, so the covariance function R is block diagonal:

$$\begin{aligned} R = \begin{pmatrix} R_e &{} 0 \\ 0 &{} R_u \end{pmatrix}. \end{aligned}$$

(40)

which parallels equation (7) of Bernhardt et al. (2010).

It is key that the optimization in Eq. (39) is now over the functions B, $\varGamma$, and $\varTheta$. Before solving this problem, I state the similarly transformed problem of the market maker.

5.2 The market-maker’s objective

Similarly, the market-maker’s objective can be stated in the frequency domain. The market-maker strives to minimize the forecast error variance of price conditional on order flow:

$$\begin{aligned} \max _{\{\varLambda \}} -\!\! \int _{a-i\infty }^{a+i\infty } \hbox {tr}\,\left\{ \begin{pmatrix} (\varPhi \!-\varTheta \varPhi ) \!-\! B H \varLambda \\ \ - H \varLambda \end{pmatrix} \begin{pmatrix} (\varPhi ^*\!-\!\varPhi ^*\varTheta ^*)^* \!-\! \varLambda ^* H ^* B^*&\!-\! \varLambda ^* H ^* \end{pmatrix} R\right\} ds \end{aligned}$$

(41)

Again, it is key that the optimization in this problem is over the function $\varLambda$.

5.3 Equilibrium in the frequency domain

Having translated the model to the frequency domain, it is now possible to restate the equilibrium definition for the frequency domain version of the model. In the original time domain version of the problem, the equilibrium is a set of stochastic processes. Those processes can be characterized by the filters on the fundamental processes, and those filters when transformed are functions in $H^2$ that can be treated as algebraic objects that are the solutions of simultaneous equations. Solving for those functions implicitly solves for the equilibrium time-domain functions via inverse transforms.²⁹

Definition 4

A stationary dynamic linear Bayesian Nash equilibrium is a trading strategy triple $(B(\cdot ), \varGamma (\cdot ), \varTheta (\cdot ))$ of elements in $H^2$ and a linear pricing rule $\varLambda (\cdot ) \in H^2$ such that

• (i) The trading strategy solves the informed trader-large shareholder maximisation problem (39), conditional on the linear pricing rule and the information set characterized by R;

• (ii) The linear filter $\varLambda (\cdot )$ minimizes the market maker’s forecast error variance in Eq. (41) with the information in order flow, conditional on the informed trader’s trading strategy $(B(\cdot ), \varGamma (\cdot ), \varTheta (\cdot ))$

5.4 Solving the transformed model

As in the static model, the large shareholder can take as given the modified fundamental process, as expressed by the term $(1-\varTheta )\varPhi$, as the exogenous fundamental process when calculating the optimal trading strategy functions B and $\varGamma$, and then calculate the optimal $\varTheta$ separately. In keeping with the notation in the earlier analysis I will denote the value process after manipulation by the large shareholder by $\tilde{\varPhi }$. The large shareholder acts on his private signal which has filter $\varPhi$, so the modified value process filter might be

$$\begin{aligned} \tilde{\varPhi } = \begin{pmatrix}\varPhi (s)-\varTheta (s) \varPhi (s) \end{pmatrix}' \end{aligned}$$

The solution for the trading intensity filter B Following the steps in Bernhardt et al. (2010), the first-order conditions of the s-transformed objectives can be stated. First, the notation

$$\begin{aligned} {\mathscr {A}}^* \end{aligned}$$

denotes an arbitrary function is the s-domain that is anti-causal, that is, $A^*(s)=0$, for s in the right half-plane.

The variational first-order condition for B in the large shareholder’s objective (39) is

$$\begin{aligned} \Big [\left( \tilde{\varPhi }- B H \varLambda \right) (1+\varGamma ^*) - B (1+\varGamma )\varLambda ^* H ^*\Big ]\sigma _{e}^2 = {\mathscr {A}}^*, \end{aligned}$$

which is a Wiener–Hopf equation. In the uncorrelated case the elements are all scalars and will commute; the solution methods for continuous-time Wiener–Hopf equations outlined in Kailath, Sayed and Hassibi section 7.A can now be used. Gather terms to restate the equation as

$$\begin{aligned} B \Big [\varLambda H (1+\varGamma ^*) + (1+\varGamma ) H ^*\varLambda ^*\Big ] \sigma _{e}^2 = \tilde{\varPhi }(1+\varGamma ^*) \sigma _{e}^2 + {\mathscr {A}}^* \end{aligned}$$

(42)

As discussed further in Taub (2018), this equation can be solved via a three-step process: factorization, inversion, and projection. Thus, to solve (42), propose a factorization

$$\begin{aligned} GG^* \equiv \varLambda H (1+\varGamma ^*) + (1+\varGamma ) H ^* \varLambda ^* \end{aligned}$$

(43)

where by standard results G can be chosen to be analytic and invertible. Then the solution is

$$\begin{aligned} B = \left\{ \tilde{\varPhi }(1+\varGamma ^*) {G^*}^{-1}\right\} _+ G^{-1} \end{aligned}$$

(44)

where the projection or annihilator operator $\left\{ \cdot \right\} _+$ is defined by

$$\begin{aligned} \left\{ F(s)\right\} _+ = 0, \qquad \hbox {Re}(s) \le 0 \end{aligned}$$

Some interpretation of (44) is possible. The solution for B is the s-transform analogue of a projection coefficient. There are two elements in the numerator or covariance part of this projection coefficient: $\tilde{\varPhi }$, the filter characterizing the informed trader’s information, and $1+\varGamma$. As in the static setting, $\varGamma$ is itself (the negative of) a generalized projection coefficient of the informed trader’s order flow filter on his private signal against the total order flow.

The denominator of (44) is the analogue of the variance of that part of the price process that is driven by this forecast error. The solution for B in (44) is therefore transform of the forecast error of the projection of the informed trader’s information against the net information in total order flow process.

Before developing the first-order condition for $\varGamma$ the first-order condition for the market maker will be developed. That condition will be applied to simplify the large shareholder’s problem.

The solution for the pricing filter $\varLambda$ The market-maker strives to minimize the forecast error variance of price conditional on order flow:

$$\begin{aligned} \max _{\{\varLambda \}} - \int _{a-i\infty }^{a+i\infty } \hbox {tr}\,\left\{ \begin{pmatrix} \tilde{\varPhi }- B H \varLambda \\ \ - H \varLambda \end{pmatrix} \begin{pmatrix} \tilde{\varPhi }^* - \varLambda ^* H ^* B^*&- \varLambda ^* H ^* \end{pmatrix} R\right\} ds \end{aligned}$$

The market maker’s first order condition is

$$\begin{aligned} \begin{pmatrix} - H ^*B^*&- H ^* \end{pmatrix} R \begin{pmatrix} \tilde{\varPhi }- B H \varLambda \\ - H \varLambda \end{pmatrix} = {\mathscr {A}}^* \end{aligned}$$

(45)

where the matrices have been transposed under the trace operator. Also, the two separate terms of the first-order condition have been consolidated into a single one by taking the conjugate-transpose of the second term. Defining the function J via the factorization

$$\begin{aligned} J^*J \equiv \begin{pmatrix}B^*&1 \end{pmatrix} R \begin{pmatrix} B \\ 1 \end{pmatrix} = \begin{pmatrix}B^*&I \end{pmatrix} R \begin{pmatrix} B \\ I \end{pmatrix} = B^* R_e B + R_u. \end{aligned}$$

(46)

It is then possible to write the first-order condition as

$$\begin{aligned} H ^*J^*J H \varLambda = H ^*\begin{pmatrix}B^*&I\end{pmatrix} R \begin{pmatrix}\tilde{\varPhi }\\ 0 \end{pmatrix} + {\mathscr {A}}^* = B^* R_e \tilde{\varPhi }+ {\mathscr {A}}^*. \end{aligned}$$

where in the last step the block-diagonal structure of R has been used. Note also that the filter characterizing the total order flow process is JH.

Multiplying both sides by ${ H ^*}^{-1}$,

$$\begin{aligned} J^*J H \varLambda = {B^*}' R_e \tilde{\varPhi }+ {\mathscr {A}}^* \end{aligned}$$

(47)

with solution

$$\begin{aligned} \varLambda = H^{-1} J^{-1} \left\{ {J^*}^{-1}{B^*}' R \begin{pmatrix}\tilde{\varPhi }\\ 0 \end{pmatrix}\right\} _+ \end{aligned}$$

(48)

The interpretation of the solution in (48) is straightforward. The total order flow process process is implicitly defined by the filter J. The solution for $\varLambda$ is then the s-transform analogue of the projection coefficient of the true value process on total order flow.

I next return to the first-order condition for $\varGamma$, making use of the market-maker’s first-order condition (45).

The solution for $\varGamma$ The variational first-order condition for $\varGamma$ is

$$\begin{aligned} \begin{pmatrix} B^*&1\end{pmatrix} R \begin{pmatrix} \tilde{\varPhi }-B H \varLambda \\ - H \varLambda \end{pmatrix} + \begin{pmatrix}- \varLambda ^* B^*&- \varLambda ^* \end{pmatrix} R \begin{pmatrix} B (1+\varGamma ) \\ \varGamma \end{pmatrix} = {\mathscr {A}}^* \end{aligned}$$

(49)

Substituting from the market-maker’s first-order condition (45), the first term drops out, yielding

$$\begin{aligned} \begin{pmatrix} - \varLambda ^* B^*&- \varLambda ^* \end{pmatrix} R \begin{pmatrix} B (1+\varGamma ) \\ \varGamma \end{pmatrix} = {\mathscr {A}}^* \end{aligned}$$

Eliminating the $\varLambda ^*$ term yields

$$\begin{aligned} \begin{pmatrix} B^*&I \end{pmatrix} R \begin{pmatrix} B (1+\varGamma ) \\ \varGamma \end{pmatrix} = {\mathscr {A}}^*. \end{aligned}$$

Using the block-diagonal structure of R yields

$$\begin{aligned} J^* J \varGamma = - {B^*}R_e \begin{pmatrix} B \\ 0 \end{pmatrix} + {\mathscr {A}}^* \end{aligned}$$

(50)

with solution

$$\begin{aligned} \varGamma = - J^{-1} \left\{ {J^*}^{-1} {B^*}'R_e \begin{pmatrix} B\\ 0\end{pmatrix} \right\} _+ \end{aligned}$$

(51)

As was pointed out above, the solution (51) is the s-transform analogue of (the negative of) the projection coefficient of the informed trader’s filter on his private information against the information in total order flow.

This fact can be used to interpret the informed trader’s order flow strategy. Examining the informed trader’s frequency domain objective in (39), the informed trader’s order flow process is characterized by the vector of the filters

$$\begin{aligned} \begin{pmatrix} B (1+\varGamma )&\varGamma \end{pmatrix} \end{aligned}$$

acting on the vector of processes $\begin{pmatrix} e(t)&u(t) \end{pmatrix}'$; the $\varGamma$ terms express the projection on the information in price. Interpreting $\varGamma$ as negative—as was the case in the static example—this projection is subtracted from direct trade process on the private information itself, that is from the filter b acting directly on the process e(t). The interpretation is that the informed trader knows that any information the market makers can infer about his private information will be incorporated in price and thereby its profit potential neutralized. The informed trader thus trades only on the residual, unforecastable part of his private signal.

The transform method lends itself well to establishing this inconspicuousness result, and the associated result that the price process must be structurally equivalent to the value process itself, because the processes of the model can be characterized by their poles and zeroes:

Proposition 2

In an equilibrium,

• (i) The large shareholder executes his trades so that total order flow has the same autoregressive structure as the noise trade, that is, he hides and is inconspicuous;

• (ii) The autoregressive structure of the price process is identical to the autoregressive structure of the fundamental process.

Proof

This is a corollary of Propositions 4 and  5 in the Appendix. $\square$

The solution for $\varTheta$ I now turn to the first order condition for $\varTheta$, the large shareholder’s amplification factor. A key assumption now comes into play: that the large shareholder ignores the influence of the amplification factor $\varTheta$ on the pricing filter $\varLambda$, which appears in Eq. (48); in this sense the Bayesian Nash assumption is a binding constraint. The resulting variational first order condition is

$$\begin{aligned} - \varPhi ^* \begin{pmatrix} B (1+\varGamma ) \end{pmatrix} R_e - ( \varTheta \varPhi \varPhi ^* + \varPhi \varPhi ^* \varTheta ^*) \frac{1}{2}C = {\mathscr {A}}^* \end{aligned}$$

(52)

Consolidating via the conjugate transpose yields

$$\begin{aligned} - \varPhi ^* \begin{pmatrix} B (1+\varGamma ) \end{pmatrix} R_e - \varTheta \varPhi (s) \varPhi ^* C = {\mathscr {A}}^* \end{aligned}$$

(53)

Dividing out $\varPhi ^*$ then yields

$$\begin{aligned} - \begin{pmatrix} B (1+\varGamma ) \end{pmatrix} R_e - \varTheta \varPhi (s) C = {\mathscr {A}}^* \end{aligned}$$

The solution of the first-order condition for $\varTheta$ (53) is then straightforward:

$$\begin{aligned} \varTheta = - C^{-1} B (1+\varGamma ) R \varPhi ^{-1} \end{aligned}$$

(54)

Substituting this into the objective, the $\varPhi ^{-1}$ term cancels the $\varPhi$ term in the objective, leaving

$$\begin{aligned} \tilde{\varPhi } = \varPhi + B (1+\varGamma ) C^{-1}. \end{aligned}$$

(55)

Recall that $\varGamma$ is the transform of $\gamma (\cdot )$, which in turn is the dynamic analogue of the static projection coefficient $\gamma$. The expression $I+\varGamma$ is the transform of the forecast error filter. Thus, as with the static model, the term that is added on to the raw fundamental process $\varPhi$ by the large shareholder is simply the unforecastable part of the large shareholder’s trade!

6 Optimal obfuscation

In this section I carry out three tasks: First, I provide the main result of the paper: that the optimal $\varTheta$ necessarily alters the fundamental stochastic structure of the firm. Second, I outline how existence might be demonstrated. Third, I develop a numerical example to illustrate the main result about the structure of $\varTheta$.

6.1 Demonstrating the non-constancy of $\varTheta$

The large shareholder does not just amplify the unforecastable part of his trades, he also alters the time series structure of the fundamental process itself in order to improve trading profits. This is expressed as the non-constancy of $\varTheta$. To demonstrate this I make the following assumption:

Assumption 1

The unmodified fundamental process $\varPhi$ has only one pole.

The assumption allows the direct application of some useful theorems about the algebra of functions in the frequency domain, particularly the annihilator lemma, Lemma 1, in Taub (2018).

Proposition 3

Let Assumption 1 be met. Then the optimal $\varTheta$ is not a constant and therefore $(1-\varTheta )\varPhi$ is not proportional to $\varPhi$, that is, the large shareholder alters the autoregressive structure of the firm’s fundamentals.

Proof

The proof is by contradiction. Examining Eq. (54), $\varTheta = - C^{-1} B (1+\varGamma ) R \varPhi ^{-1}$, the result will follow if it can be demonstrated that $(1+\varGamma )B$ is not of order $\varPhi$. Recalling the solution for B from Eq. (44), $B = \left\{ \tilde{\varPhi }(1+\varGamma ^*) {G^*}^{-1}\right\} _+ G^{-1}$, we have

$$\begin{aligned} G^{-1} \left\{ {G^*}^{-1} \tilde{\varPhi }H^*\right\} _+ H \end{aligned}$$

Applying the annihilator lemma, Lemma 1 of Taub (2018), under the hypothesis that $\varTheta$ is a constant and therefore that $\tilde{\varPhi }$ is proportional to $\varPhi$, we have

$$\begin{aligned} \sim G^{-1} H \varPhi \end{aligned}$$

To establish that this expression not of order $\varPhi$, we can equivalently demonstrate that $\sim G^{-1} H$ is not a constant. Recalling the definition of G from Eq. (43),

$$\begin{aligned} \left| G\right| ^2 = GG^* \equiv [\varLambda H H^* + H H^*\varLambda ^*] = (\varLambda + \varLambda ^*)HH^* \end{aligned}$$

(56)

Defining

$$\begin{aligned} \varLambda + \varLambda ^* \equiv \left| L\right| ^2 \end{aligned}$$

By Lemma 1 in Taub (2018), $\varLambda$ is of order $\varPhi$; therefore L(s) is a function that has nontrivial zeroes as well as the same poles as $\varPhi$. Thus, L(s) is the product $N(s)\varPhi (s)$, and N(s) is a non-constant function. we can then write

$$\begin{aligned} G=LH \end{aligned}$$

and so $G^{-1} H = L^{-1}$ is a non-constant function, and so $G^{-1} H \varPhi$ is proportional to $N(s)^{-1}$, which is not proportional to $\varPhi$. $\square$

Thus, the large shareholder dynamically obfuscates: he not only amplifies the fundamental value process, he alters its time series structure by the market makers’ forecast error. In the numerical computation it is possible to say more: in attempting to amplify the non-forecastable parts of the fundamental, the large shareholder attempts to mimic the noise trade process.

6.2 Existence and characteristics of equilibrium

A proof of the of existence of equilibrium would use the iterative approach of Seiler and Taub (2008) and is beyond the scope of this paper. The complexity of the problem can be seen by considering how the equilibrium would work if Proposition 3 were not true, that is, if $\varTheta$ were in fact a constant. Conditional on a solution for the constant $\varTheta$, the modified fundamental process $(1-\varTheta )\varPhi$ is determined, and an equilibrium can be generated using the recursion approach of Seiler and Taub to determine B, $\varGamma$ and $\varLambda$. The optimal constant $\varTheta$ could then be determined from the solution for $\varTheta$ in Eq. (54). However, as developed in Proposition 3, the solution will have the property that $\varLambda$, the pricing filter, will be a function of $\varTheta$ even though this dependence is ignored by the large shareholder when optimizing due to the Nash assumption. Thus, to find the equilibrium $\varTheta$ it would be necessary to solve a fixed point problem for the system of equations for B, $\varGamma$, $\varLambda$ and also $\varTheta$,

$$\begin{aligned} \begin{aligned} B&= \left\{ \tilde{\varPhi }(1+\varGamma ^*) {G^*}^{-1}\right\} _+ G^{-1}\\ \varGamma&= - J^{-1} \left\{ {J^*}^{-1} {B^*}'R_e \begin{pmatrix} B \\ 0\end{pmatrix} \right\} _+\\ \varLambda&= H^{-1} J^{-1} \left\{ {J^*}^{-1}{B^*}' R \begin{pmatrix}\tilde{\varPhi }\\ 0 \end{pmatrix}\right\} _+\\ \varTheta&= - C^{-1} B (1+\varGamma ) R \varPhi ^{-1} \end{aligned} \end{aligned}$$

taking account of this dependency. Whilst a recursion leading to a fixed point for the system with a fixed $\varTheta$ can be developed along the lines of the similar problem in Seiler and Taub, the addition of the $\varTheta$ equation adds significant complexity.

6.3 Numerical characterization

As a step in the direction of at least characterizing the nature of the equilibrium, I next carry out a numerical calculation that would amount to a first step in an iterative approach: I posit that the dependence of $\varLambda$ on $\varTheta$ right hand side of the solution for $\varTheta$, Eq. (54), is ignored, and calculate the optimal iterated $\varTheta$ on the left hand side in order to roughly characterize the large shareholder’s strategy.

Stacking the first-order conditions for B and $\varTheta$ in Eqs. (42) and (53) yields the vector Wiener–Hopf equation,

$$\begin{aligned} \begin{pmatrix} H\varLambda H^* + H\varLambda ^* H^* &{} \varPhi H^* \\ H \varPhi ^* &{} C \varPhi \varPhi ^* \end{pmatrix} \begin{pmatrix} B \\ \varTheta \end{pmatrix} = \begin{pmatrix} \varPhi H^* \\ 0 \end{pmatrix} + {\mathscr {A}}^* \end{aligned}$$

(57)

The coefficient matrix on the left is Hermitian and so can be factored. The coefficient matrix can be written as

$$\begin{aligned} \begin{pmatrix} H^* &{} 0 \\ 0 &{} \varPhi ^* \end{pmatrix} \begin{pmatrix} \varLambda + \varLambda ^* &{} 1 \\ 1&{} C \end{pmatrix} \begin{pmatrix} H &{} 0 \\ 0 &{} \varPhi \end{pmatrix} \end{aligned}$$

(58)

The internal matrix is then easier to factor because only the upper left element is nonscalar.

Fig. 1

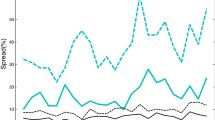
This figure plots the spectral densities of the $\varPhi$ process filter $(1-.93 z)^{-1}$ (dashed line), the insider’s amplification filter $(1-\varTheta )$ (dotted line) and the net process filter (solid line). The amplification filter amplifies high frequencies more than low frequencies, thus reducing the persistence of the fundamental

Carrying out the factorization and plotting the spectral density of the $\varPhi$ and $(1-\varTheta )\varPhi$ filters shows that $\varTheta$ amplifies high frequencies more than low frequencies—that is, it actually reduces the persistence of the fundamental (see Fig. 1). The intuition for the emphasis on high frequencies is that the large shareholder wants to masquerade as a noise trader (that is, to become even more inconspicuous), and the noise trade has zero persistence. Thus, the amplification factor moves the fundamental in the direction of white noise. Note also that the amplification factor increases the level of the spectral density at every frequency—that is, the overall volatility of the fundamental is increased, as the analytical model demonstrates.

In the description of the static model, I noted that it would be possible to frame the penalty term in a more realistic way, that is, as a cost imposed on the large shareholder for failing to hit a target that represents the public objectives of the firm, thus capturing the trade-off between the public and private incentives of the large shareholder. In the dynamic model, there is an added dimension to this trade-off: the target might be a process, $T(L) \eta _t$.

A $\varTheta$ that fails to match the autoregressive structure of the target process will entail a penalty beyond the penalty stemming from the difference in magnitude: the $\varTheta$ necessary to hit the target might have a very different structure from the $\varTheta$ that moves the fundamental in the direction of resembling the noise trade process. This will further alter $\varTheta$ and therefore move the private fundamental process away from the structure of the noise process.

One can look at it the other way: the visible target-hitting part of the large shareholder’s behavior is going to be influenced by the dark unobservable side, so that the $\varTheta$ process fails to directly offset the visible process $T(L)\eta (s)$. Thus, trading incentives that are hidden will distort the publicly observable allocation of resources of the firm.

7 Conclusion

The following phenomena were demonstrated:

• (i) The large shareholder amplifies the unforecastable part of the fundamental in order to increase his trading profits.

• (ii) In a dynamic setting, the informed trader behaves so as to be inconspicuous, so that total order flow has the autoregressive structure of the noise trade, and price has the autoregressive structure of the fundamental value process.

• (iii) In a dynamic setting, the large shareholder alters the autoregressive structure of the firm’s fundamental value process, that is, he dynamically obfuscates, and because this alteration is based on the market makers’ forecast error process, it does not increase the amount of information available to the market.

Given that the large shareholder’s trading profits can be enhanced by his alteration and amplification of the private signal, there is an incentive to acquire private information, along the lines set out in Bernhardt and Taub (2010). One usually unspoken element of private information models is the reason for the privacy or unobservability of the information. It is evident here that there are strong incentives to acquire private information and also to keep it private.

The amplification of this private information has a wider consequence. Recalling that Kyle’s $\lambda$ is a measure of price impact and is therefore inversely related to liquidity, and also that $\lambda$ is positively related to the volatility of the fundamental value of the stock, a property that extends appropriately in the dynamic model as well, then the large shareholder’s amplification of the volatility of the fundamental reduces market liquidity.

In a more elaborate model the large shareholder would be enjoined to hit publicly observable fundamental targets. This would cause the large shareholder’s activities to be divided between his fiduciary actions and the amplification of his privately observable shocks for trading purposes. The result is twofold. First, the autoregressive structure of the publicly observable shocks will cause the large shareholder’s amplification of the private shock to be influenced by the autoregressive structure of the private shock and of the noise trade structure.

Second, the publicly observable actions will be influenced by the amplification effect, and in a dynamic setting this will mean that the publicly observable shocks will be imperfectly offset not only in their magnitude but in their time series structure as well—this, despite the fact that the public shocks, private shocks and noise trade shocks can all be mutually independent. One can view the influence of the private and noise trade shocks as a kind of dark matter that distorts the allocation of resources in the firm.

Appendix: Some propositions about the order flow and price processes in equilibrium: Inconspicuousness

As also demonstrated in Bernhardt et al. (2010), Bernhardt and Taub (2008) and Seiler and Taub (2008), the forecast error characterization of the trading strategies has broader implications. First, because the informed traders do not want to be detected by the market makers or by their rivals, they hide behind the noise traders. This requires that the order flow process have no dynamic structure that would allow market makers to infer the informed trades. Therefore, the total order flow will have the same stochastic structure as the noise trade process.

Second, the price process must not have a dynamic structure that is fundamentally different from the dynamic structure of the fundamental asset value process, as this would allow the informed traders to arbitrage against it purely based on filtering the dynamic structure.

These results are general in that they hold for multiple informed traders. In this appendix the vector notation reflects this generality.

Proposition 4

The total order flow process filter

$$\begin{aligned} J H \end{aligned}$$

is a constant matrix. Therefore order flow has the same dynamic structure as the filter for the noise trade process u(t).

Proof

Add up the $\varGamma _i$ Eq. (50) across traders, yielding

$$\begin{aligned} J^* J \sum _i \varGamma _i = - {B^*}R_e \sum _i \begin{pmatrix}0 \\ \vdots \\ B_i \\ \vdots \\ 0\end{pmatrix} + {\mathscr {A}}^* \end{aligned}$$

Recalling the definition $H \equiv \sum _i \varGamma _i + I$ and using the vector expression B,

$$\begin{aligned} J^* J ( H -I) = - {B^*}R_e B + {\mathscr {A}}^*. \end{aligned}$$

From the definition of J in Eq. (46),

$$\begin{aligned} J^* J ( H -I) = - (J^*J - R_u) + {\mathscr {A}}^* \end{aligned}$$

where $R_u$ is the covariance function for the noise trade process. Also recall that it is assumed that the covariance functions for the fundamental processes are Dirac $\delta$ functions, so $R_u$ is a constant matrix. Because no further filter is applied to the noise trade process, noise trade is white noise.

Algebraic manipulation then yields

$$\begin{aligned} J^* J H = R_u + {\mathscr {A}}^*. \end{aligned}$$

Order flow is then

$$\begin{aligned} J H = \left\{ {J^*}^{-1} R_u\right\} _+ \end{aligned}$$

Because $R_u$ is a constant matrix, the projection operator eliminates all poles in the negative half plane. But J was constructed via factorization to have poles only in the positive half plane, and therefore the projection must be a constant. $\square$

Proposition 5

The price process filter

$$\begin{aligned} J H \varLambda \end{aligned}$$

has the same pole structure as the value process filter $\varPhi$, and therefore the price process has the same dynamic structure as the value process.

Proof

The filter for the price process is the order-flow filter JH multiplied by the pricing filter $\varLambda$.

Multiplying the first-order condition for $\varLambda$, (47) by ${J^*}^{-1}$ and applying the annihilator yields the equation for the price process,

$$\begin{aligned} J H \varLambda = \left\{ {J^*}^{-1} B^* R_e \varPhi \right\} _+. \end{aligned}$$

By the annihilator lemma, Lemma 1 in Taub (2018), the right hand side is the product of a constant matrix and $\varPhi$. Thus,

$$\begin{aligned} J H \varLambda = C R_e \varPhi . \end{aligned}$$

(59)

where C is a constant matrix $J(r+\rho )^{-1} B(r+\rho )$. $\square$

It should be noted that if the large shareholder chooses $\varTheta$, then the proposition holds for $\tilde{\varPhi }=(I-\varTheta )\varPhi$, where $\varPhi$ is the filter for the unmodified fundamental process. The application of the annihilator lemma, Lemma 1 from Taub (2018), then requires the matrix formulation in which the non-pole part of $\tilde{\varPhi }$ is represented by a pole at infinity.

1.1 Discussion and related literature

The results here are a little more general than some of the literature in the following sense. In Danilova (2010) for example, which has dynamic evolution of the fundamental value and a single informed trader, the hiding idea is termed inconspicuousness. But in that model, the asset fundamental value process and the noise trade are both Brownian processes with jumps, so the dynamic structure or order flow is no different than the price process. Here, by contrast, the noise trade is serially uncorrelated while the fundamental value process is serially correlated. Therefore in order to hide, the informed traders must adjust not just the magnitudes of their trades, but their dynamic pattern.