Energy flow characteristics of friction-induced nonlinear vibrations in a water-lubricated bearing-shaft coupled system

Abstract

Based on the energy flow theory of nonlinear dynamical system, the stabilities, bifurcations, possible periodical/chaotic motions of nonlinear water-lubricated bearing-shaft coupled systems are investigated in this paper. It is revealed that the energy flow characteristics around the equlibrium point of system behaving in the three types with different friction-paramters. (a) Energy flow matrix has two negative and one positive energy flow factors, constructing an attractive local zero-energy flow surface, in which free vibrations by initial disturbances show damped modulated oscillations with the system tending its equlibrium state, while forced vibrations by external forces show stable oscillations. (b) Energy flow matrix has one negative and two positive energy flow factors, spaning a divergence local zero-energy flow surface, so that the both free and forced vibrations are divergence oscillations with the system being unstable. (c) Energy flow matrix has a zero-energy flow factor and two opposite factors, which constructes a local zero-energy flow surface dividing the local phase space into stable, unstable and central subspace, and the simulation shows friction self-induced unstable vibrations for both free and forced cases. For a set of friction parameters, the system behaves a periodical oscillation, where the bearing motion tends zero and the shaft motion reaches a stable limit circle in phase space with the instant energy flow tending a constant and the time averaged one tending zero. Numerical simulations have not found any possible chaotic motions of the system. It is discovered that the damping matrices of cases (a), (b) and (c) respectively have positive, negative and zero diagonal elements, resulting in the different dynamic behavour of system, which gives a giderline to design the water-lubricated bearing unit with expected performance by adjusting the friction parameters for applications.

Graphic Abstract

1 Introduction

Water-lubricated bearings have been more and more used in the marine and pump industries to eliminate the pollution of metal bearings lubricated by oil and grease as well as to increase efficiency and reliability of marine propulsion systems. The first effective water-lubricated bearing made of lignum vitae was invented by John Penn in the 1840s while man-made plastic bearings and natural rubber bearings appeared in the 1920s, which had gradually predominated in pumps, naval and many commercial ships by the 1940s. The need for improved water-lubricated bearings was greatly recognised in 1942 when a number of U.S. ships suffered extensive combat damage at the Battle of Midway, after which, USA navy department began to carry out an extensive research on water-lubricated bearings and obtained a series of achievements and the only military specification of the water lubricated rubber bearings was created by MIL-DTL-17901C (SH) in 2005 [1]. Since the friction performance plays a key role in bearing vibration or noise, this specification especially describes the requirements for the test rig and scope of friction coefficients of bearing synthetic rubber facings.

Stern-tube bearing noise is associated with both the quantity of friction and the slope of friction–velocity curve [2], which involves bearing materials. To reduce bearing noises, many historical experimental and analytical investigations were reported [3,4,5]. For examples, Krauter [3, 4] focused on a three-degree-of-freedom (3-DOF) system to incorporate with the essential elements of the friction and vibration phenomena in their experimental model, in which a linear analysis was considered to determine the instability conditions of the system that may lead to frictional vibrations. Sinou et al. [6] proposed a numerical model incorporating realistic laws of local friction in base of experimental results to characterize the dynamics of a lubricated system and to study its complex global responses triggered by the local interfacial behaviour. Graf and Ostermeyer [7] have shown how the stability of an oscillator sliding on a belt will change, if a dynamic friction law with inner variable is considered instead of a velocity-dependent coefficient of friction, which demonstrates the unstable vibration can even be found in the case of a positive velocity-dependency of friction coefficient. Baramsky et al. [8] contributed the analytical and experimental results for the occurrence of friction-induced vibrations during tightening of bolted joints of the most used machine elements. Niknam and Farhang [9] employed a two-degree-of-freedom single mass-on-belt model to study friction-induced instability due to mode-coupling, in which numerical analyses are used to tackle the effect of three parameters related to belt velocity, friction coefficient, and normal load on the mass response. Ghorbel et al. [10] proposed a minimal 2-DOF disk brake model to investigate the effects of different parameters on mode-coupling instability, which considers self-excited vibration, gyroscopic effect, friction-induced damping, and brake pad geometry.

In designs of this type of berings, two research directions have been developing: one aims to obtain good friction characteristics using suitable geometric parameters with different facing layers and lubrications [11,12,13,14], and another is to create new bearing materials [15,16,17,18]. Recently, Smith [19] presented a paper on the design and lubrication of water-lubricated, rubber, cutlass bearings systems, which gave a methodology to predict the minimum film thickness between the journal and heavily loaded stave, including a 3D finite element (FE) model to predict generated pressures in cutlass bearings, and comparing with experimental data.

From the point view of sciences, the water-lubricated bearings system is a typical nonlinear system concerning friction-induced vibration noises, so that for good noise performance of this type of bearing systems, it is essential to investigate its integrated nonlinear characteristics. In the area on friction induced vibrations, Ibrahim [20, 21] contributed two important review papers, of which the first one concerns the mechanics of contact and friction and the second one discusses the dynamics and modeling of friction induced vibrations. Both of papers provide the comprehensive account of the main theorems and mechanisms developed in the historical literatures concerning friction-induced noise and vibrations with a quite wide references listed. Furthermore, Ding and Zhai [22] presented a review paper on the advances of friction dynamics in mechanics system, in which the common used friction models, friction related self-excited vibrations and their controls were presented. The interested readers may refer these three review papers for more information and references in this area.

More directly linking the topic of this paper, Simpson and Ibrahim [2] investigated the dynamic behaviour of nonlinear friction-induced vibration in water-lubricated bearings based on the traditional method dealing with nonlinear dynamical systems. Their paper developed an analytical nonlinear, two-degree-of-freedom model, which emulates the stern-tube bearing. Typical friction-speed curves were adopted based on the experimental results of Krauter [23]. The stability conditions of equilibrium were predicated. In the unstable cases, the nonlinear response behavior was examined by using numerical integration of the coupled equations of motion. The dependence of the relative sliding speed on time and its effect on the friction force was included in the numerical simulation. A control parameter that combines the influence of the normal load and the slope of the friction-speed curve was used to construct a bifurcation diagram which separated different response characteristics, including squeal, limit cycle, and stable regions.

To reveal nonlinear behavior of nonlinear dynamical systems, such as as discussed in the books by Guckenheimer and Holmes [24], Thompson and Stewart [25], Chen et al. [26] and Liu and Chen [27], Xing [28] developed a genralised energy flow theory to investigate nonlinear dynamical systems governed by ordinary differential equation in phase space. Important nonlinear phenomena such as, stabilities, periodical orbits, bifurcations and chaos can be revealed from the energy flow behavors of the systems [29]. The aim and motivation of this paper are to investigate the 2-DOF nonlinear model of the stern-tube bearing proposed in Ref. [2] to reveal its energy flow characteristics governing its nonlinear dynamical behavours, which is also as an example to further develop energy flow approach based on two scalar varaibles, genralised potentional and kinetic energies, to tackle complex nonlinear dynamical systems, especially in multi-dimensional phase spaces.

1.1 Dynamic modelling and equations of water-lubricated bearings

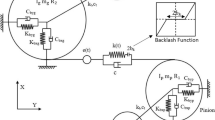
The marine propeller shafts are supported in stern tube bearings, which are lubricated by water and are almost all grooved, of which the scketched structure is shown in Fig. 1. The 2-DOF analytical model used in Ref. [2] is shown in Fig. 2, where the mass, stiffness, and damping coefficient of the bearing (subscript 1) and the flexible shaft (subscript 2) are denoted by m₁, m₂, k₁, k₂, c₁ and c₂, respectively. Here, the forces ${\hat{F}_{1}}$ and ${\hat{F}_{2}}$ denote possible prescribed external forces applied to the bearing and the shaft, respectively, while the force ${F_{f}}$ denotes the friction force acted to the bearing by the shaft, which is assumed in the viscous type propotional to the relative sliding speed of the friction pair with a viscous damping coefficient ${b}$, so that ${F_{f} = b(\dot{x}_{2} - \dot{x}_{1} )}$.

Fig. 1

Typical grooved stern tube bearing structure

Fig. 2

Analytical 2-DOF model of stern tube bearing

1.1.1 Viscous damping coefficient

Historically, the friction force was formulated by the friction model developed by Smith et al. [5] and used by Simpson and Ibrahim [2] in their 2-DOF analytical model, that is

$${ F_{f} = N[\mu_{{1}} + (\mu_{{0}} { - }\mu_{{1}} ){\text{e}}^{{{ - }aR\dot{\theta }}} ]},$$

(1)

where N denotes the normal bearing load; a is a constant with units of inverse velocity; ${{\mu }_{0}}$ and ${{\mu }_{1}}$ are the static and dynamic coefficients of friction, respectively; R represents the disk radius and ${\dot{\theta }}$ is the torsional velocity of the disk relative to the bearing. Considering only oscillatory motions of both the shaft and bearing, and representing the motion by the linear displacement, we can denote the relative sliding speed of the friction pair in the form

$${ \nu = R\dot{\theta } = \dot{x}_{2} { - }\dot{x}_{1} = z_{2} - z_{1} ,\;z_{1} = \dot{x}_{1} ,\;z_{2} = \dot{x}_{2} . }$$

(2)

Substituting Eq. (2) into Eq. (1) and then taking the derivative of the resultant equation with respect to the relative sliding speed, we obtain the visous damping coefficient as

$${ b = \frac{{{\text{d}}F_{f} }}{{{\text{d}}v}} = - Na\left( {\mu_{0} - \mu_{1} } \right){\text{e}}^{ - av} },$$

(3)

which, when the function ${{\text{e}}^{ - av}}$ is expanded into a Taylor series, becomes

$${ \begin{aligned} b = & \, - Na\left( {\mu_{0} - \mu_{1} } \right)\left[ {1 - av + \frac{1}{2}a^{2} v^{2} + o(v^{3} )} \right] \\ = & - Na\left( {\mu_{0} - \mu_{1} } \right)\left[ {1 - a\left( {z_{2} - z_{1} } \right) + \frac{1}{2}a^{2} \left( {z_{2} - z_{1} } \right)^{2} + o\left( {z_{2} - z_{1} } \right)^{3} } \right]. \\ \end{aligned} }$$

(4)

1.1.2 Dynamic equations of the friction pair system

Using the model shown in Fig. 2 and the second Newton’s law, we obtain the following two equations of motion of the system

$${ \begin{gathered} m_{1} \ddot{x}_{1} + c_{1} \dot{x}_{1} + k_{1} x_{1} = b(\dot{x}_{2} - \dot{x}_{1} ) + \hat{F}_{1} , \hfill \\ m_{2} \ddot{x}_{2} + c_{2} \dot{x}_{2} + k_{2} x_{2} = - b(\dot{x}_{2} - \dot{x}_{1} ) + \hat{F}_{2} , \hfill \\ \end{gathered} }$$

(5)

which can be rewritten in a matrix form

$${ {\varvec{M\ddot{X}}} + {\varvec{C\dot{X}}} + {\varvec{KX}} = {\hat{\varvec{F}}}},$$

(6)

where the mass, damping and stiffness matrices as well as the displacement and force vectors are resepctively defined as follows

$${ {\varvec{M}} = \left[ {\begin{array}{*{20}c} {m_{1} } & 0 \\ 0 & {m_{2} } \\ \end{array} } \right],\;{\varvec{C}} = \left[ {\begin{array}{*{20}c} {c_{1} + b} & { - b} \\ { - b} & {c_{2} + b} \\ \end{array} } \right],\;{\varvec{K}} = \left[ {\begin{array}{*{20}c} {k_{1} } & 0 \\ 0 & {k_{2} } \\ \end{array} } \right],\;{\varvec{X}} = \left[ {\begin{array}{*{20}c} {x_{1} } \\ {x_{2} } \\ \end{array} } \right],\,\;{\hat{\varvec{F}}} = \left[ {\begin{array}{*{20}c} {\hat{F}_{1} } \\ {\hat{F}_{2} } \\ \end{array} } \right] }.$$

(7)

Introducing the nondimensional parameters

$${ \begin{aligned} \zeta_{i} = & \frac{{c_{i} }}{{2\sqrt {k_{i} m_{i} } }},\;\gamma_{21} = \frac{{\omega_{2} }}{{\omega_{1} }},\;\omega_{i} = \sqrt {\frac{{k_{i} }}{{m_{i} }}} ,\;\eta_{12} = \frac{{m_{1} }}{{m_{2} }},\;y_{i} = \frac{{x_{i} }}{R},\;\hat{f}_{i} = \frac{{\hat{F}_{i} }}{\beta N},\;\;i = j = 1,2, \\ \tau = & \omega_{1} t,\;\mu_{01} = \mu_{0} - \mu_{1} ,\;\alpha = \frac{Na}{{m_{1} \omega_{1} }},\;\beta = \frac{{m_{1} \omega_{1}^{2} R}}{N},\;\psi = \alpha \beta = aR\omega_{1} , \\ \end{aligned} }$$

(8)

where ${\zeta_{i}}$ denote dimensionless damping coefficients, ${\gamma_{21}}$ ratio of circular frequencies, ${\omega_{i}}$ natural frequencies of the bearing and the shaft subsystems, ${\eta_{12}}$ mass ratio, ${y_{i}}$ dimensionless displacements, ${\tau}$ dimensionless time, ${\alpha}$ dimensionless friction coefficient, ${\beta^{ - 1}}$ dimensionless normal bearing load and ${\psi}$ the dimensionless value of constant ${\alpha}$. Using these dimensionless parameters, the dynamic equation of system can be written as

$${ {\varvec{m\ddot{y}}} + {\varvec{c\dot{y}}} + {\varvec{ky}} = {\hat{\varvec{f}}}},$$

(9)

where

$${ \begin{aligned} {\varvec{m}} = & \left[ {\begin{array}{*{20}c} 1 & 0 \\ 0 & {1/\eta _{{12}} } \\ \end{array} } \right],{\varvec{k}} = \left[ {\begin{array}{*{20}c} 1 & 0 \\ 0 & {\frac{{\gamma _{{21}}^{2} }}{{\eta _{{12}} }}} \\ \end{array} } \right],{\varvec{c}} = {\varvec{\hat{c}}} + {\varvec{\tilde{c}}},\begin{array}{*{20}c} {{\varvec{\hat{c}}}} \\ \end{array} = \left[ {\begin{array}{*{20}c} {2\zeta _{1} } & 0 \\ 0 & {\frac{{2\gamma _{{21}} \zeta _{2} }}{{\eta _{{12}} }}} \\ \end{array} } \right], \\ {\varvec{\tilde{c}}} = & \tilde{b}{\varvec{\tilde{I}}},{\varvec{y}} = \left[ {\begin{array}{*{20}c} {y_{1} } \\ {y_{2} } \\ \end{array} } \right],{\varvec{\hat{f}}} = \left[ {\begin{array}{*{20}c} {\hat{f}_{1} } \\ {\hat{f}_{2} } \\ \end{array} } \right],{\varvec{z}} = {\varvec{\dot{y}}},\begin{array}{*{20}c} {\tilde{b} = - \alpha \mu _{{01}} {\text{e}}^{{ - \psi {\varvec{\hat{I}z}}}} } \\ \end{array} , \\ {\varvec{\hat{I}}} = & \left[ {\begin{array}{*{20}c} { - 1} & 1 \\ \end{array} } \right],{\varvec{\tilde{I}}} = \left[ {\begin{array}{*{20}c} 1 & { - 1} \\ { - 1} & 1 \\ \end{array} } \right],\partial \tilde{b}/\partial z_{1} = \alpha \mu _{{01}} \psi {\text{e}}^{{ - \psi {\varvec{\hat{I}z}}}} \\ = & - \psi \tilde{b} = - \partial \tilde{b}/\partial z_{2} ,\dot{\tilde{b}} = \alpha \mu _{{01}} \psi {\text{e}}^{{ - \psi {\varvec{\hat{I}z}}}} {\varvec{\hat{I}\dot{z}}}. \\ \end{aligned} }$$

(10a)

For the approximation as shown in Eq. (4) adopted by Simpson and Ibrahim [2], the parameter ${\tilde{b}}$ and its derivatives are given by the following approximated formulations

$${ \begin{aligned} \tilde{b} \approx & - \alpha \mu _{{01}} (1 - \psi {\varvec{\hat{I}z}} + \frac{1}{2}\psi ^{2} {\varvec{z}}^{\text{T}} {\varvec{\tilde{I}z}}),\dot{\tilde{b}} \approx \alpha \mu _{{01}} \psi ({\varvec{\hat{I}\dot{z}}} - \psi {\varvec{\dot{z}}}^{\text{T}} {\varvec{\tilde{I}z}}),\partial \tilde{b}/\partial z_{1} = - \alpha \mu _{{01}} \psi (1 - \psi {\varvec{\hat{I}z}}) \\ = & - \partial \tilde{b}/\partial z_{2} ,\partial ^{2} \tilde{b}/\partial z_{1}^{2} = - \alpha \mu _{{01}} \psi ^{2} = - \partial ^{2} \tilde{b}/\partial z_{2}^{2} ,\partial ^{2} \tilde{b}/\partial z_{1} \partial z_{2} = \alpha \mu _{{01}} \psi ^{2} , \\ \end{aligned} }$$

(10b)

implying that the parameter ${\tilde{b}}$ is approximated by a quadratic function of the relative velocity ${(z_{2} - z_{1} )}$, its first derivatives are linear, and the second derivatives are constants.

1.2 Dynamic equations and equilibrium points

1.2.1 Equations in phase space

Using the state variables ${{\varvec{y}}}$ and ${{\varvec{z}}}$, we can rewrite Eq. (9) in the form of the phase space, i.e.

$${ \begin{array}{*{20}l} {{\varvec{\dot{y}}} = {\varvec{F}}_{y} = {\varvec{z}},} \hfill \\ {{\varvec{\dot{z}}} = {\varvec{F}}_{z} = {\varvec{m}}^{{ - 1}} [ - ({\varvec{\hat{c}}} + \tilde{b}{\varvec{\tilde{I}}}){\varvec{z}} - {\varvec{ky}} + {\varvec{\hat{f}}}],} \hfill \\ \end{array} }$$

(11)

of which, the vector

$${ {\varvec{F}} = \left[ {\begin{array}{*{20}c} {{\varvec{F}}_{y}^{{}} } \\ {{\varvec{F}}_{z}^{{}} } \\ \end{array} } \right] = {\tilde{\varvec{J}}}\left[ {\begin{array}{*{20}c} {\varvec{y}} \\ {\varvec{z}} \\ \end{array} } \right] + {\tilde{\varvec{f}}},\begin{array}{*{20}c} {} & {} \\ \end{array} {\tilde{\varvec{J}}} = \left[ {\begin{array}{*{20}c} {\varvec{0}} & {\varvec{I}} \\ { - {\varvec{m}}^{ - 1} {\varvec{k}}} & { - {\varvec{m}}^{ - 1} ({\hat{\varvec{c}}} + \tilde{b}{\tilde{\varvec{I}}})} \\ \end{array} } \right],\begin{array}{*{20}c} {} & {} \\ \end{array} {\tilde{\varvec{f}}} = \left[ {\begin{array}{*{20}c} {\varvec{0}} \\ {{\varvec{m}}^{ - 1} {\hat{\varvec{f}}}} \\ \end{array} } \right]},$$

(12)

is called the generalised force of system. Here, ${{\tilde{\varvec{J}}}}$ denotes the coefficient matrix of the state variable vector ${[{\varvec{y}}^{{\text{T}}} \begin{array}{*{20}c} {} \\ \end{array} {\varvec{z}}^{{\text{T}}} ]^{{\text{T}}}},$ which involves the nonlinear damping parameter ${\tilde{b}}$. The solution of Eq. (11) with a prescribed initial condition

$${ {\varvec{y}}(0) = {\hat{\varvec{y}}},\begin{array}{*{20}c} {} & {} \\ \end{array} {\varvec{z}}(0) = {\hat{\varvec{z}}},\begin{array}{*{20}c} {} & {} \\ \end{array} {\varvec{r}}_{0} = \left[ {\begin{array}{*{20}c} {{\hat{\varvec{y}}}^{{\text{T}}} } & {{\hat{\varvec{z}}}^{{\text{T}}} } \\ \end{array} } \right]^{{\text{T}}} },$$

(13)

gives an orbit starting from the position ${{\varvec{r}}_{0}}$ in the phase space as shown in Fig. 3.

Fig. 3

Orbit, position and tangent vectors at a point on the orbit of a dynamical system in phase space

The parameters of system, such as ${{k}_{1}}$, ${{c}_{1}}$ and ${{c}_{2}}$, can be functions of normal load and temperature. Krauter [4] developed empirical relationships for these parameters

$${ k_{1} = 116.52N + 10535.4\, {\rm {at}}\, 35{^\circ {\text{C}}},\;c_{1} = - 0.618T + 8.474,c_{2} = \frac{{m_{1} \omega_{2} \ln 2}}{{{\uppi }N}} }.$$

(14)

Typical values of these parameters were selected for constant values of normal load and temperature, i.e. N = 120 N (27 lb) and ${T =}$${35}$ ℃, by Simpson and Ibrahim [2] to investigate the nonlinear dynamical behaviour of system. We also use these chosen parameters to reveal the energy flow characteristics of system, and to rewrite Eqs. (11) and (12) in the form

$${ \begin{aligned} \left[ {\begin{array}{*{20}c} {{\dot{\varvec{y}}}} \\ {{\dot{\varvec{z}}}} \\ \end{array} } \right] = & {\tilde{\varvec{J}}}\left[ {\begin{array}{*{20}c} {\varvec{y}} \\ {\varvec{z}} \\ \end{array} } \right] + {\tilde{\varvec{f}}} = {\varvec{F}},\begin{array}{*{20}c} {} & {} \\ \end{array} {\tilde{\varvec{J}}} = {\tilde{\varvec{J}}}_{0} + {\tilde{\varvec{J}}}_{b} ,\begin{array}{*{20}c} {} & {} \\ \end{array} {\tilde{\varvec{J}}}_{0} = \left[ {\begin{array}{*{20}c} {\varvec{0}} & {\varvec{I}} \\ {{\varvec{\upgamma}}} & {{\varvec{\upzeta}}} \\ \end{array} } \right],\begin{array}{*{20}c} {} & {} \\ \end{array} {\tilde{\varvec{J}}}_{b} = \left[ {\begin{array}{*{20}c} {\varvec{0}} & {\varvec{0}} \\ {\varvec{0}} & {{\tilde{\varvec{b}}}} \\ \end{array} } \right], \\ {{\varvec{\upgamma}}} = & \left[ {\begin{array}{*{20}c} { - 1} & 0 \\ 0 & { - \gamma_{21}^{2} } \\ \end{array} } \right],\begin{array}{*{20}c} {} \\ \end{array} {{\varvec{\upzeta}}} = \left[ {\begin{array}{*{20}c} { - 2\zeta_{1} } & 0 \\ 0 & { - 2\gamma_{21} \zeta_{2} } \\ \end{array} } \right],\begin{array}{*{20}c} {} \\ \end{array} {\tilde{\varvec{b}}} = \tilde{b}{{\varvec{\upeta}}},\begin{array}{*{20}c} {} \\ \end{array} {{\varvec{\upeta}}} = \left[ {\begin{array}{*{20}c} { - 1} & 1 \\ {\eta_{12} } & { - \eta_{12} } \\ \end{array} } \right], \\ \end{aligned} }$$

(15)

from which in association with Eq. (10) we obtain

$${ \left[ {\begin{array}{*{20}c} {{\varvec{\ddot{y}}}} \\ {{\varvec{\ddot{z}}}} \\ \end{array} } \right] = {\tilde{\varvec{J}}}\left[ {\begin{array}{*{20}c} {{\dot{\varvec{y}}}} \\ {{\dot{\varvec{z}}}} \\ \end{array} } \right] + {\varvec{\dot{\tilde{J}}}}\left[ {\begin{array}{*{20}c} {\varvec{y}} \\ {\varvec{z}} \\ \end{array} } \right] + {\varvec{\dot{\tilde{f}}}}},$$

(16a)

$${\varvec{\dot{\tilde{J}}}}= {\varvec{\dot{\tilde{J}}}}_{b} = \left[ {\begin{array}{*{20}c} {\varvec{0}} & {\varvec{0}} \\ {\varvec{0}} & {{\varvec{\dot{\tilde{b}}}}} \\ \end{array} } \right],$$

(16b)

$${\varvec{\dot{\tilde{b}}}} = \dot{\tilde{b}}{{\varvec{\upeta}}}.$$

(16c)

1.2.2 Equilibrium point and Jacobian matrix

The point at which ${{\varvec{F}} = {\varvec{0}}}$ is called the equilibrium point of system. Obviously, if there is no external force (${{\hat{\varvec{f}}} = {\varvec{0}}}$), the origin (y = 0 = z) of phase space is an equilibrium point of system.

By using Eqs. (15) and (16), the Jacobian matrix of the system can be derived as

$${ \begin{aligned} & {\varvec{J}} = {\varvec{F}}\nabla ^{\text{T}} = \left( {\widetilde{{\varvec{J}}}{\varvec{r}} + \widetilde{{\varvec{f}}}} \right)\left[ {\begin{array}{*{20}c} {\frac{\partial }{{\partial {\varvec{y}}^{\text{T}} }}} \hfill & {\frac{\partial }{{\partial {\varvec{z}}^{\text{T}} }}} \hfill \\ \end{array} } \right] = \widetilde{{\varvec{J}}} + \overline{{\varvec{J}}} , \\& \overline{{\varvec{J}}} = \left[ {\begin{array}{*{20}c} {\frac{{\partial \widetilde{{\varvec{J}}}_{b} }}{{\partial {\varvec{y}}^{\text{T}} }}{\varvec{r}}} & {\frac{{\partial \widetilde{{\varvec{J}}}_{b} }}{{\partial {\varvec{z}}^{\text{T}} }}{\varvec{r}}} \\ \end{array} } \right] = \psi (\widehat{{\varvec{I}}}{\varvec{z}})\left[ {\begin{array}{*{20}c} {\varvec{0}} & {\varvec{0}} \\ {\varvec{0}} & {\widetilde{{\varvec{b}}}} \\ \end{array} } \right]. \\ \end{aligned} }$$

(17)

Here the gradient operator ${\nabla}$ is defined by

$${ \nabla = \frac{\partial }{{\partial {\varvec{r}}}} = \left[ {\begin{array}{*{20}c} {\partial /\partial {\varvec{y}}} \\ {\partial /\partial {\varvec{z}}} \\ \end{array} } \right],\begin{array}{*{20}c} {} & {} \\ \end{array} \nabla^{{\text{T}}} = \frac{\partial }{{\partial {\varvec{r}}^{{\text{T}}} }} = \left[ {\begin{array}{*{20}c} {\frac{\partial }{{\partial {\varvec{y}}^{{\text{T}}} }}} & {\frac{\partial }{{\partial {\varvec{z}}^{{\text{T}}} }}} \\ \end{array} } \right],\begin{array}{*{20}c} {} & {} \\ \end{array} {\varvec{r}} = \left[ {\begin{array}{*{20}c} {{\varvec{y}}^{{\text{T}}} } & {{\varvec{z}}^{{\text{T}}} } \\ \end{array} } \right]^{{\text{T}}} . }$$

(18)

Substituting Eq. (15) into Eq. (17), we finally obtain the Jacobian matrix

$${ {\varvec{J}} = {\tilde{\varvec{J}}}_{0} + [1 + \psi ({\hat{\varvec{I}}\varvec{z}})]{\tilde{\varvec{J}}}_{b} . }$$

(19)

Here the matrices ${{\tilde{\varvec{J}}}_{0}}$ and ${{\tilde{\varvec{J}}}_{b}}$ are defined by Eq. (15).

2 Energy flow formulations of system

2.1 Generalised potential energy and kinetic energy

We define two scalar variables: the generalised potential energy and generalised kinetical energy of system in the following forms.

Generalised potential energy and its time average

$${ E = \frac{1}{2}{\varvec{r}}^{{\text{T}}} {\varvec{r}} = \frac{1}{2}({\varvec{y}}^{{\text{T}}} {\varvec{y}} + {\varvec{z}}^{{\text{T}}} {\varvec{z}}),\begin{array}{*{20}c} {} & {} \\ \end{array} \left\langle E \right\rangle = \frac{1}{T}\int_{0}^{{\text{T}}} {E{\text{d}}t} = \frac{1}{2T}\int_{0}^{{\text{T}}} {{\varvec{r}}^{{\text{T}}} {\varvec{r}}{\text{d}}t.} }$$

(20)

Generalised kinetical energy and its time average

$${ K = \frac{1}{2}{\dot{\varvec{r}}}^{{\text{T}}} {\dot{\varvec{r}}} = \frac{1}{2}({\dot{\varvec{y}}}^{{\text{T}}} {\dot{\varvec{y}}} + {\dot{\varvec{z}}}^{{\text{T}}} {\dot{\varvec{z}}}),\begin{array}{*{20}c} {} & {} \\ \end{array} \left\langle K \right\rangle = \frac{1}{T}\int_{0}^{{\text{T}}} {K{\text{d}}t} = \frac{1}{2T}\int_{0}^{{\text{T}}} {{\dot{\varvec{r}}}^{{\text{T}}} {\dot{\varvec{r}}}{\text{d}}t} . }$$

(21)

Physically, these two scalars may not practical potential and kinetical energies, therefore we use the word generalised to distinguish them with practical physical quantities. Geometrically, as shown in Fig. 3, the generalised potential energy equals the half square of the distance of a point to the origin of phase space, i.e.

$${ E = \left| {\varvec{r}} \right|^{2} /2,\begin{array}{*{20}c} {} & {} \\ \end{array} \left| {\varvec{r}} \right|^{2} = {\varvec{y}}^{{\text{T}}} {\varvec{y}} + {\varvec{z}}^{{\text{T}}} {\varvec{z}}},$$

(22)

while the generalised kinetical energy equals the half square of the tangent vector, the velocity, at a point, i.e.

$${ K = \left| {{\dot{\varvec{r}}}} \right|^{2} /2,\begin{array}{*{20}c} {} & {} \\ \end{array} \left| {{\dot{\varvec{r}}}} \right|^{2} = {\dot{\varvec{y}}}^{{\text{T}}} {\dot{\varvec{y}}} + {\dot{\varvec{z}}}^{{\text{T}}} {\dot{\varvec{z}}}. }$$

(23)

Therefore, these two non-negative real scalars can be used to describe the postion and velocity at a point on the solution orbit of system in phase space, and to reveal related nonlinear dynamical behavours of system.

2.2 Energy flow equation and its time average

Pre-multiplicating Eqs. (13) and (15) by a row vector ${{\varvec{r}}^{{\text{T}}} = \left[ {\begin{array}{*{20}c} {{\varvec{y}}^{{\text{T}}} } & {{\varvec{z}}^{{\text{T}}} } \\ \end{array} } \right]}$ and its initial value ${{\hat{\varvec{r}}}^{{\text{T}}} (0)}$, respectively, we obtain the energy flow equation

$$\begin{aligned}& \dot{E} = P,P = {\varvec{r}}^{T} {\varvec{F}} = {\varvec{r}}^{T} \widetilde{{\varvec{J}}}{\varvec{r}} + \hat{p},\hat{p} = {\varvec{r}}^{T} \widetilde{{\varvec{f}}} = {\varvec{z}}^{T} \widehat{{\varvec{f}}}, \\ & \ddot{E} = {\varvec{\dot{r}}}^{T} {\varvec{F}} + {\varvec{r}}^{T} {\varvec{\dot{F}}} = 2K + {\varvec{r}}^{T} {\varvec{\ddot{r}}},E(0) = \hat{E} = {\varvec{\hat{r}}}^{T} {\varvec{\hat{r}}}/2 = ({\varvec{\hat{y}}}^{T} {\varvec{\hat{y}}} + {\varvec{\hat{z}}}^{T} \widehat{{\varvec{z}}})/2,\\ & \left\langle {\dot{E}} \right\rangle = \left( {\int_{0}^{T} {\dot{E}{\text{d}}t} } \right)/T = \left[ {\int_{0}^{T} {({\varvec{r}}^{T} \widetilde{{\varvec{J}}}{\varvec{r}} + \hat{p}){\text{dt}}} } \right]/T, \\ \end{aligned}$$

(24a)

of which, P denotes the power done by the generalised force of system, ${\hat{p}}$ is the power of the external forces and ${\dot{E}}$ represents the time change rate of generalised potential energy, called as the energy flow of system. Physically, the energy flow equation in Eq. (24a) implies that the energy flow of system equals the power done by the generalised force.

The energy flow equation in Eq. (24a) can be rewritten in the form

$${ \begin{gathered} \dot{E} = {\varvec{r}}^{{\text{T}}} ({\tilde{\varvec{E}}} + {\tilde{\varvec{U}}}){\varvec{r}} + \hat{p} = {\varvec{r}}^{{\text{T}}} {\tilde{\varvec{E}}\varvec{r}} + \hat{p},\begin{array}{*{20}c} {} & {} \\ \end{array} {\varvec{r}}^{{\text{T}}} {\tilde{\varvec{U}}\varvec{r}} = 0, \hfill \\ {\tilde{\varvec{E}}} = ({\tilde{\varvec{J}}} + {\tilde{\varvec{J}}}^{{\text{T}}} )/2,\begin{array}{*{20}c} {} & {} \\ \end{array} {\tilde{\varvec{U}}} = ({\tilde{\varvec{J}}} - {\tilde{\varvec{J}}}^{{\text{T}}} )/2, \hfill \\ \left\langle {\dot{E}} \right\rangle = \left[ {\int_{0}^{T} {({\varvec{r}}^{{\text{T}}} {\tilde{\varvec{E}}\varvec{r}} + \hat{p}){\text{d}}t} } \right]/T. \hfill \\ \end{gathered} }$$

(24b)

Here ${{\tilde{\varvec{E}}}}$ is a real symmetrical matrix, while ${{\tilde{\varvec{U}}}}$ is a real anti-symmetrical matrix.

2.3 Kinetic energy flow equation and its time average

Pre-multiplying Eq. (16a) by ${{\dot{\varvec{r}}}^{{\text{T}}}}$ and using Eqs. (14) and (16c), we obtain the kinetic energy flow and its time average

$${ \begin{gathered} \dot{K} = {\dot{\varvec{r}}}^{{\text{T}}} {\varvec{\ddot{r}}} = {\dot{\varvec{r}}}^{{\text{T}}} {\varvec{\tilde{J}\dot{r}}} + {\dot{\varvec{r}}}^{{\text{T}}} {\varvec{\dot{\tilde{J}}r}} + {\dot{\varvec{r}}}^{{\text{T}}} {\varvec{\dot{\tilde{f}}}} = {\dot{\varvec{r}}}^{{\text{T}}} {\varvec{\tilde{E}\dot{r}}} + {\dot{\varvec{z}}}^{{\text{T}}} {\varvec{\dot{\tilde{b}}z}} + {\dot{\varvec{r}}}^{{\text{T}}} {\varvec{\dot{\tilde{f}}}}, \hfill \\ \left\langle {\dot{K}} \right\rangle = \left( {\int_{0}^{T} {{\dot{\varvec{r}}}^{{\text{T}}} {\varvec{\ddot{r}}}} {\text{d}}t} \right)/T = \left[ {\int_{0}^{T} {({\dot{\varvec{r}}}^{{\text{T}}} {\varvec{\tilde{E}\dot{r}}} + {\dot{\varvec{z}}}^{{\text{T}}} {\varvec{\dot{\tilde{b}}z}} + {\dot{\varvec{r}}}^{{\text{T}}} {\varvec{\dot{\tilde{f}}}}){\text{d}}t} } \right]/T. \hfill \\ \end{gathered} }$$

(25)

2.4 Zero-energy flow surfaces and equilibrium points

Generally, the energy flow of system is a function of time and the position of a point in phase space, which generates a scalar field called as the energy flow field of the nonlinear dynamical system. Equation

$${ \dot{E} = 0},$$

(26)

defines a generalised surface or subspace in phase space, which is called as a zero-energy flow surface on which the energy flow vanishes. If an orbit of the nonlinear dynamical system is on a zero-energy flow surface, the distance of a point on the orbit is not changed with time.

Based on the theory of extreme values of a function and the geometrical meaning of generalised potential energy${E}$, we can conclude that the characteristics of orbit at a point on the zero-energy flow surface as follows.

• ${\ddot{E} > {0}}$, the generalised potential energy takes a local minimum-extreme value at this point compared with the points in the local domain around it. Therefore, with time going, the value of ${E}$ increases and the orbit backwards the origin of phase space.

• ${\ddot{E} = {0}}$, it cannot determine that generalised potential energy takes a local minimum- or maximum-extreme value at this point, and higher time derivatives are needed to give a solution.

• ${\ddot{E} < {0}}$, the generalised potential energy takes a local maximum-extreme value at this point compared with the points in the local domain around it. Therefore, with time going, the value of ${E}$ decreases and the orbit towards the origin of phase space.

If no external force ${\hat{p} = 0},$ there are the following three cases satisfying ${\dot{E} = 0}$ in Eq. (26).

• Case 1:${{\varvec{r}} = {\varvec{0}}}$, that represents the origin of phase space, at which the generalised potential energy is defined as zero;

• Case 2:${{\varvec{F}} = {\varvec{0}}}$, implying an equilibrium point of system, so that equilibrium points are on the zero-energy flow surface;

• Case 3: ${P = 0,\begin{array}{*{20}c} {} \\ \end{array} {\varvec{r}} \ne {\varvec{0}} \ne {\varvec{F}}},$ correseponding a generalised zero-energy flow surface.

Assume that ${{\varvec{r}}}$ denotes a point on an orbit on a zero-energy flow surface, ${P(t,{\varvec{r}}) = {\varvec{r}}^{{\text{T}}} {\varvec{F}} = r_{i} F_{i} = 0}$, and ${{{\varvec{\varepsilon}}}}$ is an small orbit variation around ${{\varvec{r}}}$, generally, the variation of energy flow caused by the orbit variation can be approximated to the quantities of ${\left| {{\varvec{\varepsilon}}} \right|^{2}}$ in the form

$${\begin{aligned} \Delta \dot{E} = & \dot{E}({\varvec{r}} + {\varvec{\varepsilon}} ) = ({\varvec{r}} + {\varvec{\varepsilon}} )^{\text{T}} {\varvec{F}}({\varvec{r}} + {\varvec{\varepsilon}} ) = (r_{i} + \varepsilon _{i} )F_{i} (r_{j} + \varepsilon _{j} ), \\ =\, & (r_{i} + \varepsilon _{i} )\left[ {F_{i} + F_{{i,j}} \varepsilon _{j} + 0.5F_{{i,jk}} \varepsilon _{j} \varepsilon _{k} + O(\varepsilon ^{3} )} \right] \\ =\,v & \varepsilon _{i} F_{i} + r_{i} F_{{i,j}} \varepsilon _{j} + \varepsilon _{i} F_{{i,j}} \varepsilon _{j} + 0.5r_{i} F_{{i,jk}} \varepsilon _{j} \varepsilon _{k} \\ =\, & {\varvec{\varepsilon }}^{\text{T}} {\varvec{p}} + {\varvec{\varepsilon }}^{\text{T}} ({\varvec{E}} + {\varvec{U}}){\varvec{\varepsilon }} + {\varvec{\varepsilon }}^{\text{T}} {\varvec{E}}_{1} {\varvec{\varepsilon }} = {\varvec{\varepsilon }}^{\text{T}} {\varvec{p}} + {\varvec{\varepsilon }}^{\text{T}} ({\varvec{E}} + {\varvec{E}}_{1} ){\varvec{\varepsilon }}, \\ \end{aligned} }$$

(27a)

where the energy flow gradient vector ${{\varvec{p}}}$, the energy flow matrices ${{\varvec{E}}}$ and ${{\varvec{E}}_{1}}$, and spin matric ${{\varvec{U}}}$ are given by

$${ \begin{array}{*{20}c} {{\varvec{p}} = {\varvec{F}} + {\varvec{J}}^{\text{T}} {\varvec{r}},{\varvec{E}} = ({\varvec{J}} + {\varvec{J}}^{\text{T}} )/2,{\varvec{U}} = ({\varvec{J}} - {\varvec{J}}^{\text{T}} )/2,} \\ {{\varvec{E}}_{1} = \frac{1}{2}r_{i} \nabla \nabla ^{\text{T}} F_{i} = {\mathbf{0}}_{{4 \times 4}} + {\mathbf{0}}_{{4 \times 4}} + {\varvec{B,B}} = \left[ {\begin{array}{*{20}c} {\mathbf{0}} & {\mathbf{0}} \\ {\mathbf{0}} & {\bar{\varvec{b}}} \\ \end{array} } \right],} \\ {\overline{\varvec{b}} = (z_{1} - \eta _{{12}} z_{2} )\left[ {\begin{array}{*{20}c} {\frac{{\partial ^{2} }}{{\partial z_{1} \partial z_{1} }}} & {\frac{{\partial ^{2} }}{{\partial z_{1} \partial z_{2} }}} \\ {\frac{{\partial ^{2} }}{{\partial z_{2} \partial z_{1} }}} & {\frac{{\partial ^{2} }}{{\partial z_{2} \partial z_{2} }}} \\ \end{array} } \right](\tilde{\varvec{b}}\hat{I}z) = (z_{1} - \eta _{{12}} z_{2} )\left[ {\begin{array}{*{20}c} {\frac{{\partial ^{2} \tilde{b}}}{{\partial z_{1} \partial z_{1} }}} & {\frac{{\partial ^{2} \tilde{b}}}{{\partial z_{1} \partial z_{2} }}} \\ {\frac{{\partial ^{2} \tilde{b}}}{{\partial z_{2} \partial z_{1} }}} & {\frac{{\partial ^{2} \tilde{b}}}{{\partial z_{2} \partial z_{2} }}} \\ \end{array} } \right](\hat{\varvec{I}}z)} \\ { = (z_{1} - \eta _{{12}} z_{2} )\psi ^{2} \tilde{b}\left[ {\begin{array}{*{20}c} 1 & { - 1} \\ { - 1} & 1 \\ \end{array} } \right](\hat{\varvec{I}}z) = \psi ^{2} \tilde{b}{\varvec{z}}^{\text{T}} \eta {\varvec{z}}\left[ {\begin{array}{*{20}c} 1 & { - 1} \\ { - 1} & 1 \\ \end{array} } \right].} \\ \end{array} }$$

(27b)

Here, we have used Eqs. (10a) and (15) and noticed that the components ${F_{1}}$ and ${F_{2}}$ of the vector ${{\varvec{F}}}$ are linear functions of ${{\varvec{y}}}$ and ${{\varvec{z}}}$, so that their second derivatives vanish.

For an equilibrium point satisfying ${{\varvec{F}}({\varvec{r}}) = {\varvec{0}}}$, Eq. (27a) becomes

$${ \Delta \dot{E} = \dot{E}({\varvec{r}},{{\varvec{\varepsilon}}}) = {\varvec{J}}^{{\text{T}}} {\varvec{r}} + {{\varvec{\varepsilon}}}^{{\text{T}}} ({\varvec{E}} + {\varvec{E}}_{1} ){{\varvec{\varepsilon}}}},$$

(28a)

which is further reduced to

$${ \Delta \dot{E} = \dot{E}({{\varvec{\varepsilon}}}) = {{\varvec{\varepsilon}}}^{{\text{T}}} {\varvec{E\varepsilon }}},$$

(28b)

for an equilibrium point ${{\varvec{r}}}$ = 0, and so that ${{\varvec{E}}_{1}}$ = 0. At the equilibrium point ${{\varvec{r}}}$ = 0 the second time derivative of the generalised energy in Eq. (24a) vanishes, so that we need to consider the variation of ${\dot{E}}$ around the point ${{\varvec{r}}}$ = 0 to investigate the orbit behaviour. From Eq. (28a) and the geometrical meaning in Eq. (22), we consider the variation of energy flow ${\dot{E}}$ to determine the characteristics of orbit as follows.

• If ${\left| {{\varvec{r}} + {{\varvec{\varepsilon}}}} \right| < \left| {\varvec{r}} \right|},$ then ${E({\varvec{r}} + {{\varvec{\varepsilon}}}) < E({\varvec{r}})},$ so that ${\Delta \dot{E} > 0}$ implies the flow towards the zero-energy flow surface, while ${\Delta \dot{E} < 0}$ indicates the flow backwards the zero-energy flow surface;

• If ${\left| {{\varvec{r}} + {{\varvec{\varepsilon}}}} \right| > \left| {\varvec{r}} \right|},$ then ${E({\varvec{r}} + {{\varvec{\varepsilon}}}) > E({\varvec{r}})},$ so that ${\Delta \dot{E} < 0}$ implies the flow towards the sero-energy flow surface, while ${\Delta \dot{E} > 0}$ indicates the flow backwards the zero-energy flow surface;

• If the flows from both sides of the zero-energy flow surface tend to it, this surface is an attracting surface.

• The local ability of equilibrium point ${{\varvec{r}}}$ = 0 can be determined by the behaviour of energy flow matrix ${{\varvec{E}}}$ as follows:

  $${ {\varvec{E}}:\left\{ {\begin{array}{*{20}l} {\text{definitely - negative, asymptotic stable,}} \hfill \\ {\text{semi - definitely - negative, stable,}} \hfill \\ {{\text{definitly or semi - definitly - positive, unstable}}{.}} \hfill \\ \end{array} } \right. }$$

  (29)

Figure 4 shows a case where the orbit intersects at a point ${{\varvec{r}}}$ on the energy flow surface. Since ${\Delta \dot{E} > 0}$ above the surface and ${\Delta \dot{E} < 0}$ under the surface, so that the flow along the orbit backwards this point and this point is an unstable point.

Fig. 4

Zero-energy flow surface and an unstable point ${\varvec{r}}$ determined by ${ \Delta \dot{E} }$

2.5 Energy flow matrix and energy flow characteristic factor

Both of matrices ${{\tilde{\varvec{E}}}}$ and ${{\varvec{E}}}$ are real symmetrical matrices, called as the energy flow matrices, the former is for the total energy flow in Eq. (24b), while the later for the incremental energy flow relative to the zero-energy flow surface in Eq. (27b). The real symmetrical matrix has its real eigenvalues ${\lambda_{I}}$ and corresponding eigenvector ${{{\varvec{\upxi}}}_{I}}$ satisfying the orthogonal relationships, such as for matrix ${{\tilde{\varvec{E}}}}$ in Eq. (24b), we have

$${ {\tilde{\varvec{\Phi }}}^{{\text{T}}} {\tilde{\varvec{\Phi }}} = {\varvec{I}},\begin{array}{*{20}c} {} & {} \\ \end{array} {\tilde{\varvec{\Phi }}}^{{\text{T}}} {\varvec{\tilde{E}\tilde{\Phi }}} = {\text{diag}}(\tilde{\lambda }_{I} ),\begin{array}{*{20}c} {} & {} \\ \end{array} {\tilde{\varvec{\Phi }}} = \left[ {\begin{array}{*{20}c} {{\tilde{\varvec{\xi }}}_{1} } & {{\tilde{\varvec{\xi }}}_{2} } & {{\tilde{\varvec{\xi }}}_{3} } & {{\tilde{\varvec{\xi }}}_{4} } \\ \end{array} } \right]. }$$

(30)

These eigenvectors span an energy flow space in which the vector ${{\varvec{r}}}$ can be represented by

$${ {\varvec{r}} = {\varvec{\tilde{\Phi }\tilde{\varphi }}}},$$

(31)

which, when substituted into Eq. (24b), gives

$${ \dot{E} = {\tilde{\varvec{\varphi }}}^{{\text{T}}} {\text{diag}}(\tilde{\lambda }_{I} ){\tilde{\varvec{\varphi }}} = \sum\limits_{I = 1}^{4} {\tilde{\lambda }_{I} } \tilde{\varphi }_{I}^{2} ,\begin{array}{*{20}c} {} & {} \\ \end{array} {\tilde{\varvec{\varphi }}}^{{\text{T}}} = \left[ {\begin{array}{*{20}c} {\tilde{\varphi }_{1} } & {\tilde{\varphi }_{2} } & {\tilde{\varphi }_{3} } & {\tilde{\varphi }_{4} } \\ \end{array} } \right]. }$$

(32)

Therefore, ${\tilde{\lambda }_{I}}$ represents the energy flow variation caused by a unit disturbance ${\tilde{\varphi }_{I}^{2} = 1}$ in the I-th principal direction ${\tilde{\varphi }_{I}}$ of the energy flow matrix. Therefore, we call ${\tilde{\lambda }_{I}}$ as the energy flow characteristic factors and we can conclude for a point of the orbit of nonlinear system.

• The positive, zero and negative value of the factors ${\tilde{\lambda }_{I}}$ respectively implies the energy flow increase, unchanged and decrease caused by the disturbance ${\tilde{\varphi }_{I}^{2}}$ in the I-th principal direction, from which the behaviour of energy flow increments at this point can be identified to judge the local dynamical behaviour, such as for local stability of orbits around an equilibrium point ${{\varvec{r}}}$ = 0, we have

  $${ \lambda_{I} :\left\{ {\begin{array}{*{20}l} {\text{negative , stable subspace,}} \hfill \\ {\text{zero, central flow subspace,}} \hfill \\ {{\text{positive, unstable subspace}}{.}} \hfill \\ \end{array} } \right. }$$

  (33)

• If its energy flow characteristic factors are not all semi-negative or not all semi-positive, there will exist a small subdomain around this point in the phase space determined by ${\dot{E} = 0}$, from which a zero-energy flow surface can be obtained.

2.6 Spin matrices and periodical orbit

The matrices ${{\tilde{\varvec{U}}}}$ in Eq. (24b) and ${{\varvec{U}}}$ in Eq. (27b) are two real skew-symmetrical matrices, called as spin matrices. For periodical orbits, it is neccesary that there exsist a time period ${T}$ and its corrsponding closed orbit ${\Gamma}$ such that the following integrations along the closed orbit hold, i.e.

$${ \begin{gathered} \left\langle {\dot{E}} \right\rangle = \frac{1}{T}\oint_{\Gamma } {_{{\hat{t}}}^{{T + \hat{t}}} \dot{E}{\text{d}}t = 0} ,\begin{array}{*{20}c} {} & {} \\ \end{array} \left\langle E \right\rangle = \frac{1}{T}\oint_{\Gamma } {_{{\hat{t}}}^{{T + \hat{t}}} E{\text{d}}t = \hat{E}} , \hfill \\ \hfill \\ \left\langle {\dot{K}} \right\rangle = \frac{1}{T}\oint_{\Gamma } {_{{\hat{t}}}^{{T + \hat{t}}} \dot{K}{\text{d}}t = 0} ,\begin{array}{*{20}c} {} & {} \\ \end{array} \left\langle K \right\rangle = \frac{1}{T}\oint_{\Gamma } {_{{\hat{t}}}^{{T + \hat{t}}} K{\text{d}}t = \hat{K}} , \hfill \\ \end{gathered} }$$

(34a)

where ${\hat{E}}$ and ${\hat{K}}$ are two positive constants. The stability of this periodical orbit can be determined by the values of the energy flow ${\Delta \dot{E}}$ around each point of the orbit as discussed for the zero-energy flow surface.

The time averaged kinetic energy can be re-written as

$${ \left\langle K \right\rangle = \frac{1}{{2T}}\oint_{\Gamma } {_{{\hat{t}}}^{{T + \hat{t}}} {\varvec{\dot{r}}}^{\text{T}} {\varvec{\dot{r}}}{\text{d}}t = \frac{1}{{2T}}} \oint_{\Gamma } {_{{\hat{t}}}^{{{\text{T}} + \hat{t}}} {\varvec{\dot{r}}}^{\text{T}} {\text{d}}{\varvec{r}} = \frac{1}{{2T}}} . }$$

(34b)

Physically, this integration denotes the circulation integral of velocity field ${{\dot{\varvec{r}}}}$ along the closed orbit and involves the skew-symmetrical spin matrix. To clarify this, we consider a 3-D vector field ${{\dot{\varvec{y}}} = {\varvec{f}}}$, the ${{\text{curl}}{\varvec{f}}}$, or ${\nabla \times {\varvec{f}}}$ at a point O is explained in Fig. 5. Here ${{{\varvec{\upnu}}}}$ is a unit vector, the projection of the ${{\text{curl}}{\varvec{f}}}$ onto ${{{\varvec{\upnu}}}}$ is defined as the limit of a closed line integral along the curve C in a plane orthogonal to ${{{\varvec{\upnu}}}}$, that is

$${ \left( {\nabla \times {\varvec{f}}} \right)_{\nu } = \left( {{\text{curl}}{\varvec{f}}} \right)_{\nu } = \mathop {\lim }\limits_{A \to 0} \left\{ {\frac{1}{A}\oint_{C} {{\varvec{f}} \cdot {\text{d}}{\varvec{y}}} } \right\} = \mathop {\lim }\limits_{A \to 0} \left\{ {\frac{1}{A}\oint_{C} {{\dot{\varvec{y}}} \cdot {\dot{\varvec{y}}}{\text{d}}t} } \right\} = \mathop {\lim }\limits_{A \to 0} \left\{ {\frac{2}{A}\oint_{C} {K{\text{d}}t} } \right\}},$$

(34c)

Fig. 5

Circulation integration along a path C, of which the positive direction obeys the right-hand rule, to define the cur1f

where A is the area enclosed by curve C. The ${{\text{curl}}{\varvec{f}}}$ can be denoted in a tensor form [30, 31]

$${ \left( {\nabla \times {\varvec{f}}} \right)_{i} = e_{ijk} f_{k,j} },$$

(34d)

where ${e_{ijk}}$ is the permutation tensor. The vector ${{\text{curl}}{\varvec{f}}}$ is a dual vector of a skew-symmetrical matrix ${{\varvec{U}}}$, spin matrix, satisfying the following relationship

$${ \begin{gathered} \left( {\varvec{U}} \right)_{ij} = U_{ij} = \frac{ - 1}{2}e_{ijk} \left( {\nabla \times {\varvec{f}}} \right)_{k} = \frac{ - 1}{2}e_{ijk} e_{krs} f_{s,r} \hfill \\ \hfill \\ \begin{array}{*{20}c} {} & {} \\ \end{array} = \frac{ - 1}{2}(\delta_{ir} \delta_{js} - \delta_{is} \delta_{jr} )f_{s,r} = \frac{{f_{i,j} - f_{j,i} }}{2} = \left( {\frac{{{\varvec{J}} - {\varvec{J}}^{{\text{T}}} }}{2}} \right)_{ij} . \hfill \\ \end{gathered} }$$

(34e)

Therefore, a positive time-averaged kinetic energy implies there must be a non-zero spin matrix for periodical orbits.

2.7 Bifurcation and chaos

The energy flow of a nonlinear dynamical system is affected by the bifurcation parameters to reveal the birfurcation characteristics of orbits. For example, different parameters result in different equilibrium points, zero-energy flow surfaces and energy flow characteristic factors etc.

Xing [28, 29] has discovered that a chaotic motion of nonlinear dynamical system can be considered as a periodical motion with an infinte long time period and the following integrations hold

$${ \begin{gathered} \left\langle {\dot{E}} \right\rangle = \mathop {\lim }\limits_{T \to \infty } \left\{ {\frac{1}{T}\oint_{\Gamma } {_{{\hat{t}}}^{{T + \hat{t}}} \dot{E}{\text{d}}t} } \right\} = 0,\begin{array}{*{20}c} {} & {} \\ \end{array} \left\langle E \right\rangle = \mathop {\lim }\limits_{T \to \infty } \left\{ {\frac{1}{T}\oint_{\Gamma } {_{{\hat{t}}}^{{T + \hat{t}}} E{\text{d}}t} } \right\} = \hat{E}, \hfill \\ \hfill \\ \left\langle {\dot{K}} \right\rangle = \mathop {\lim }\limits_{T \to \infty } \left\{ {\frac{1}{T}\oint_{\Gamma } {_{{\hat{t}}}^{{T + \hat{t}}} \dot{K}{\text{d}}t} } \right\} = 0,\begin{array}{*{20}c} {} & {} \\ \end{array} \left\langle K \right\rangle = \mathop {\lim }\limits_{T \to \infty } \left\{ {\frac{1}{T}\oint_{\Gamma } {_{{\hat{t}}}^{{T + \hat{t}}} K{\text{d}}t} } \right\} = \hat{K}. \hfill \\ \end{gathered} }$$

(35)

This implies that the time averaged mechanical energy ${\left\langle {E + K} \right\rangle}$ tends a constant when the average time tends to infinite. Also, for a chaotic motion, flows are restricted in a finite volume, so that the space averaged rate of volume strain of phase space must not be positive, i.e.

$${ \dot{\upsilon }_{V} = \frac{1}{V}\int_{V} {\dot{\upsilon } dV = } \frac{1}{V}\int_{V} {\sum\limits_{I = 1}^{n} {\lambda_{I} } dV \le 0.} }$$

(36)

3 Investigations of nonlinear water-lubricated bearing system

3.1 Zero-energy flow surface ${(\hat{f}_{1} = 0 = \hat{f}_{2} )}$

Using Eq. (24b), we obtain the energy flow surface ${\dot{E} = {\varvec{r}}^{{\text{T}}} {\tilde{\varvec{E}}\varvec{r}} = 0}$ of the system, i.e.

$${ \begin{array}{*{20}c} {{\varvec{r}}^{\text{T}} \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & {(1 - \gamma _{{21}}^{2} )/2} \\ 0 & 0 & { - 2\zeta _{1} - \tilde{b}} & {(1 + \eta _{{12}} )\tilde{b}/2} \\ 0 & {(1 - \gamma _{{21}}^{2} )/2} & {(1 + \eta _{{12}} )\tilde{b}/2} & { - 2\gamma _{{21}} \zeta _{2} - \eta _{{12}} \tilde{b}} \\ \end{array} } \right]{\varvec{r}}} \\ { = - (2\zeta _{1} + \tilde{b})z_{1}^{2} - (2\gamma _{{21}} \zeta _{2} + \eta _{{12}} \tilde{b})z_{2}^{2} + (1 + \eta _{{12}} )\tilde{b}z_{1} z_{2} + (1 - \gamma _{{21}}^{2} )z_{2} y_{2} = 0,} \\ \end{array} }$$

(37a)

where the nonlinear friction parameter

$${ \tilde{b} = - \alpha \mu_{01} {\text{e}}^{{ - \psi (z_{2} - z_{1} )}} },$$

(37b)

or its approximation to a second order of sliding speed

$${ \tilde{b}\begin{array}{*{20}c} { \approx - \alpha \mu_{01} (1 - \psi {\hat{\varvec{I}}\varvec{z}} + \frac{1}{2}} \\ \end{array} \psi^{2} {\varvec{z}}^{{\text{T}}} {\tilde{\varvec{I}}\varvec{z}}). }$$

(37c)

The zero-energy flow surface in Eq. (37a) is independent on the variable ${y_{1}}$, therefore, the axis ${o - y_{1}}$ is a zero-energy line of the system. On this line defined by the position vector ${{\varvec{r}} = \left[ {\begin{array}{*{20}c} {y_{1} } & 0 & 0 & 0 \\ \end{array} } \right]^{{\text{T}}}}$, the energy flow ${\dot{E} = 0}.$ For the prescribed parameters in Eq. (41), Eq. (37) governs the forms of zero-energy surfaces of system with the different values of ${\alpha}$ and ${\zeta_{1}}$ listed in Tables 1, 2 and 3, which will be given in Sect. 3.2.

Table 1 Energy flow characteristic factors at the equilibrium point of the system (${ \zeta _{2} = 0.008325 }$)

Table 2 Energy flow characteristic factors at the equilibrium point of the system (${ \zeta _{2} = 0.00 }$)

Table 3 Energy flow characteristic factors at the equilibrium point of the system (${ \zeta _{2} = 0.009 }$)

3.1.1 Linearazation at the fixed point ${(\hat{f}_{1} = 0 = \hat{f}_{2} )}$

Vanishing the generalised kinetical energy in Eq. (21) and using Eq. (15), we have

$${ \left[ {\begin{array}{*{20}c} 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ { - 1} & 0 & { - 2\zeta_{1} - \tilde{b}} & {\tilde{b}} \\ 0 & { - \gamma_{21}^{2} } & {\eta_{12} \tilde{b}} & { - 2\gamma_{21} \zeta_{2} - \eta_{12} \tilde{b}} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {y_{1} } \\ {y_{2} } \\ {z_{1} } \\ {z_{2} } \\ \end{array} } \right] = 0},$$

(38)

which gives an equilibrium point ${{\varvec{r}} = {\varvec{0}}}$. From Eqs. (10), (19), and (27b), at this point ${\tilde{b} = - \alpha \mu_{01}},$ ${{\varvec{J}} = {\tilde{\varvec{J}}}_{0} + {\tilde{\varvec{J}}}_{b}},$ ${{\varvec{E}}_{1} = 0}$, so that the energy flow matrix and the spin matrix in Eq. (27b) become

$${{\varvec{E}} = \left[ {\begin{array}{*{20}c} {\varvec{0}} & {\varvec{0}} \\ {\varvec{0}} & {{\overline{\varvec{E}}}} \\ \end{array} } \right],\;{\overline{\varvec{E}}} = \left[ {\begin{array}{*{20}c} 0 & 0 & {(1 - \gamma_{21}^{2} )/2} \\ 0 & {\alpha \mu_{01} - 2\zeta_{1} } & { - \alpha \mu_{01} (1 + \eta_{12} )/2} \\ {(1 - \gamma_{21}^{2} )/2} & { - \alpha \mu_{01} (1 + \eta_{12} )/2} & {\eta_{12} \alpha \mu_{01} - 2\gamma_{21} \zeta_{2} } \\ \end{array} } \right]},$$

(39a)

$${ {\varvec{U}} = \left[ {\begin{array}{*{20}c} 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & {\left( {1 + \gamma_{21}^{2} } \right)/2} \\ { - 1} & 0 & 0 & { - \alpha \mu_{01} \left( {1 - \eta_{12} } \right)/2} \\ 0 & { - \left( {1 + \gamma_{21}^{2} } \right)/2} & {\alpha \mu_{01} \left( {1 - \eta_{12} } \right)/2} & 0 \\ \end{array} } \right]. }$$

(39b)

3.1.2 Energy flow characteristic factors and vectors

For the approximated energy flow matrix ${{\varvec{E}}}$, using Eqs. (30)-(32), we can solve its energy flow characteristic factors and vectors. Obviously, we have a zero characteristic factor and its vector in the form

$${ \lambda_{1} = 0,\begin{array}{*{20}c} {} & {} \\ \end{array} {{\varvec{\upxi}}}_{1} = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 & 0 \\ \end{array} } \right]^{{\text{T}}} . }$$

(40a)

The rest three energy flow characteristic factors and vectors are obtained by solving the eigenvalue problem

$${ ({\vec{\varvec{E}}} - \lambda {\varvec{I}}){\vec{\varvec{r}}} = 0,\begin{array}{*{20}c} {} & {} \\ \end{array} {\vec{\varvec{r}}} = \left[ {\begin{array}{*{20}c} {y_{2} } & {z_{1} } & {z_{2} } \\ \end{array} } \right]},$$

(40b)

of which the characteristic equation is

$${ \left| {{\vec{\varvec{E}}} - \lambda {\varvec{I}}} \right| = 0. }$$

(40c)

The solutions of Eqs. (40b) and (40c) are three eigenvalues and eigenvectors ${\lambda_{I} ,\begin{array}{*{20}c} {} \\ \end{array} {\vec{\varvec{\xi }}}_{I} \begin{array}{*{20}c} {} \\ \end{array} (I = 2,\begin{array}{*{20}c} {} \\ \end{array} 3,\begin{array}{*{20}c} {} \\ \end{array} 4)}$,

$${ \lambda_{I} ,\begin{array}{*{20}c} {} & {} \\ \end{array} {{\varvec{\upxi}}}_{I} = \left[ {\begin{array}{*{20}c} 0 & {{\vec{\varvec{\xi }}}_{I}^{{\text{T}}} } \\ \end{array} } \right]^{{\text{T}}} ,\begin{array}{*{20}c} {} & {} \\ \end{array} I = 2,\begin{array}{*{20}c} {} \\ \end{array} 3,\begin{array}{*{20}c} {} \\ \end{array} 4. }$$

(40d)

3.2 Bifurcation of zero-energy flow surfaces around the fixed point

The dimensionless parameters studied in Ref. [2] are listed as follows

$${ \begin{aligned} \mu_{01} = & 0.111;\begin{array}{*{20}c} {} \\ \end{array} \zeta_{1} = 0.1116,\begin{array}{*{20}c} {} \\ \end{array} 0.111245,\begin{array}{*{20}c} {} \\ \end{array} 0.1111;\begin{array}{*{20}c} {} \\ \end{array} \zeta_{2} = 0.008325;\begin{array}{*{20}c} {} \\ \end{array} \gamma_{21} = 0.01; \\ \\ \eta_{12} = & 7.5 \times 10^{ - 4} ;\begin{array}{*{20}c} {} \\ \end{array} \beta = 3040.2;\begin{array}{*{20}c} {} \\ \end{array} \alpha = 2.0,\begin{array}{*{20}c} {} \\ \end{array} 2.5,\begin{array}{*{20}c} {} \\ \end{array} 3.0,\begin{array}{*{20}c} {} \\ \end{array} 3.5,\begin{array}{*{20}c} {} \\ \end{array} 4.0; \\ \end{aligned} }$$

(41)

based on which the obtained energy flow characteristic factors around the fixed point are given in Tables 1, 2 and 3, which shows the bifurcation of zero-energy flow surface affected by the bifurcation parameters: the dimensionless friction coefficient ${\alpha}$ and the dimensionless damping coefficients ${\zeta_{1}}$ and ${\zeta_{2}}$.

It is found that the all energy flow characteristic factors ${\lambda_{I} \begin{array}{*{20}c} {} \\ \end{array} (I = 2,\begin{array}{*{20}c} {} \\ \end{array} 3,\begin{array}{*{20}c} {} \\ \end{array} 4)}$, for the investigated parameters, include negative, positive and zero real numbers, so that the small local domain around the equilibrium point can be divided into a stable (${\lambda_{I} < 0}$), an unstable (${\lambda_{I} > 0}$) and a central flow subspace (${\lambda_{I} = 0}$), to reveal the local dynamic behaviour around the equilibrium point.

In the subspace span by the corresponding energy flow characteristic vectors ${\vec{\xi}_{I}}$ around the equilibrium point, the energy flow at point ${{\varvec{\varphi }} = \left[ {\begin{array}{*{20}c} {\phi_{2} } & {\phi_{3} } & {\phi_{4} } \\ \end{array} } \right]}$ can be formulated by Eq. (28), i.e.

$${ \dot{E} = \lambda_{2} \phi_{2}^{2} + \lambda_{3} \phi_{3}^{2} + \lambda_{4} \phi_{4}^{2}},$$

(42a)

and the zero-energy flow surface is governed by

$${ \dot{E} = \lambda_{2} \phi_{2}^{2} + \lambda_{3} \phi_{3}^{2} + \lambda_{4} \phi_{4}^{2} = 0. }$$

(42b)

Based on the results listed in Tables 1, 2 and 3, in a linearised approximation of system around the equilibrium point, there are following three local structures of zero-energy flow surfaces with its local dynamic behaviour.

3.2.1 Case (a): two negative and one positive characteristic factor (${\alpha = 2.0}$, ${\zeta_{1} = 0.1116},$ ${\zeta_{2} = 0.009}$)

In this case, such as for parameters ${\alpha = 2.0}$, ${\zeta_{1} = 0.1116}$ and ${\zeta_{2} = 0.009}$, the equation of zero-energy flow surface in Eq. (42b) becomes

$${ 0.512177\tilde{\varphi }_{2}^{2} + 0.001144\tilde{\varphi }_{3}^{2} = 0.512107\tilde{\varphi }_{4}^{2} },$$

(43a)

which is rewritten in the form

$${ \begin{gathered} \frac{{\tilde{\varphi }_{2}^{2} }}{{a_{2}^{2} }} + \frac{{\tilde{\varphi }_{3}^{2} }}{{a_{3}^{2} }} = \frac{{\tilde{\varphi }_{4}^{2} }}{{a_{4}^{2} }},\begin{array}{*{20}c} {} & {} \\ \end{array} \frac{{\tilde{\varphi }_{2}^{2} }}{{R_{2}^{2} }} + \frac{{\tilde{\varphi }_{3}^{2} }}{{R_{3}^{2} }} = \tilde{\varphi }_{4}^{2} , \hfill \\ \hfill \\ a_{2} = \frac{1}{{\sqrt {\left| {\lambda_{2} } \right|} }} = \frac{1}{{\sqrt {0.512177} }},\begin{array}{*{20}c} {} & {} \\ \end{array} a_{3} = \frac{1}{{\sqrt {\left| {\lambda_{3} } \right|} }} = \frac{1}{{\sqrt {0.001144} }},\begin{array}{*{20}c} {} & {} \\ \end{array} a_{4} \frac{1}{{\sqrt {\lambda_{4} } }} = \frac{1}{{\sqrt {0.512107} }}, \hfill \\ \hfill \\ R_{2} = \frac{{a_{2} }}{{a_{4} }} = \frac{{\sqrt {\lambda_{4} } }}{{\sqrt {\left| {\lambda_{2} } \right|} }},\begin{array}{*{20}c} {} & {} \\ \end{array} R_{3} = \frac{{a_{3} }}{{a_{4} }} = \frac{{\sqrt {\lambda_{4} } }}{{\sqrt {\left| {\lambda_{3} } \right|} }}, \hfill \\ \end{gathered} }$$

(43b)

of which the zero-energy flow surface and energy flow variations in the small domain around the equilibrium point is sketched in Fig. 6a, and the computer simulating surface is drawn in Fig. 6b, while the zero-energy surface based on Eq. (37) for nonlinear case is given in Fig. 6c.

Fig. 6

Zero-energy flow surface around equilibrium point for case (a) ${ (\alpha = 2.0,\zeta _{1} = 0.1116,\zeta _{2} = 0.009) }$ based on linearized Eq. (43a): a sketched one, b calculated one based on Eq. (43a), and c one based on nonlinear Eq. (37)

In Fig. 6a, the three characteristic vectors ${\vec{\xi}_{2}}$, ${\vec{\xi}_{3}}$ and ${\vec{\xi}_{4}}$ respectively with the three factors span a subspace in phase space ${o - y_{2} z_{1} z_{2}}$. This local linearized zero-energy flow surface is symmetrical to the coordinate plane ${o - {\vec{\xi}}_{2}{\vec{\xi}}_{3}}$ and axis-symmetrical to the axis $o - {\vec{\xi}}_{4}$, so that a plane perpendicular to axis $o - {\vec{\xi}}_{4}$ intersects the zero-energy flow surface in an elliptical curve of semi-axis ${\left| {\tilde{\varphi }_{4} } \right|R_{3} > \left| {\tilde{\varphi }_{4} } \right|R_{2}}$, as shown in Fig. 6 for the ones at ${\left| {\tilde{\varphi }_{4} } \right| = 1}$. The plane ${o - {\vec{\xi}}_{3} {\vec{\xi}}_{4}}$ intersects the zero-energy flow surface in the straight lines of ${\tilde{\varphi }_{3} = \pm \tilde{\varphi }_{4}^{{}} R_{3}}$. Based on Eq. (42a), at a disturbed point outside the zero-energy flow surface on the plane ${\tilde{\varphi }_{4}}$=const., the energy flow ${\dot{E} < 0}$, so that it intends to reduce the distance to the origin of space, implying the flow towards the zero-energy surface. For a disturbed point inside the zero-energy flow surface on the plane ${\tilde{\varphi }_{4}}$=const., the energy flow ${\dot{E} > 0}$ and it intends to increase the distance to the origin of space implying the flow also towards the zero-energy surface. Therefore, the zero-energy surface is an attracting surface. In this case, from Eq. (10a), the damping matrix of system at the fixed point takes

$${ {\varvec{c}} = \left[ {\begin{array}{*{20}c} {0.0012} & {0.2220} \\ {0.2220} & {0.0180} \\ \end{array} } \right]},$$

(43c)

with the positive diagonal damping coefficients in the system, so that the motions caused by initial conditions will be damped.

By using the MATLAB program in Ref. [28] and the nonlinear friction parameter in Eq. (37b), the results of numerical simulations with the initial conditions ${{\varvec{y}} = 10^{ - 6} \left[ {\begin{array}{*{20}c} 1 & 1 & 1 & 1 \\ \end{array} } \right]^{{\text{T}}}}$ for this case are given in Figs. 7, 8, 9. Figure 7 gives the time histories of displacement and velocity of the bearing and the shaft, which shows the damped oscillations. Figure 8 presents the phase diagram y(1)–y(3) of bearing unit and the one y(2)–y(4) of shaft unit, as well as the time histories of generalized potential energy and the distance of phase point to the origin, which indicates the orbit points in both phase diagrams move from outside to the origin, and the generalized potential energy and the distance of orbit point to the origin tend to zero with time increasing. Figure 9 shows the instant energy flow behaving a damped oscillation and the time history of phase space volume strain decreasing with time.

Fig. 7

Time histories of displacement and velocity of bearing and shaft ${ (\alpha = 2.0,\zeta _{1} = 0.1116,\zeta _{2} = 0.009) }$

Fig. 8

Phase diagram y(1)–y(3) of bearing and the one y(2)–y(4) of shaft, and time histories of generalized potential energy and distance of phase point to origin ${ (\alpha = 2.0,\zeta _{1} = 0.1116,\zeta _{2} = 0.009) }$

Fig. 9

Time history of instant energy flow, and phase space volume strain ${ (\alpha = 2.0,\zeta _{1} = 0.1116,\zeta _{2} = 0.009) }$

3.2.2 Case (b): one negative and two positive characteristic factors (${\alpha = 2.2}$, ${\zeta_{1} = 0.111245}$, ${\zeta_{2} = 0.008325}$)

Case 2 corresponds a zero-energy flow surface in Eq. (42b) governed by equation

$${ 0.514069\tilde{\varphi }_{2}^{2} = 0.0204843\tilde{\varphi }_{3}^{2} + 0.515312\tilde{\varphi }_{4}^{2} },$$

(44a)

which is rewritten in the form

$${ \begin{gathered} \frac{{\tilde{\varphi }_{2}^{2} }}{{a_{2}^{2} }} = \frac{{\tilde{\varphi }_{3}^{2} }}{{a_{3}^{2} }} + \frac{{\tilde{\varphi }_{4}^{2} }}{{a_{4}^{2} }},\begin{array}{*{20}c} {} & {} \\ \end{array} \tilde{\varphi }_{2}^{2} = \frac{{\tilde{\varphi }_{3}^{2} }}{{a_{3}^{2} /a_{2}^{2} }} + \frac{{\tilde{\varphi }_{4}^{2} }}{{a_{4}^{2} /a_{2}^{2} }}, \hfill \\ \hfill \\ a_{2} = \frac{1}{{\sqrt {\left| {\lambda_{2} } \right|} }} = \frac{1}{{\sqrt {0.514069} }},\begin{array}{*{20}c} {} & {} \\ \end{array} a_{3} = \frac{1}{{\sqrt {\lambda_{3} } }} = \frac{1}{{\sqrt {0.020483} }},\begin{array}{*{20}c} {} & {} \\ \end{array} a_{4} = \frac{1}{{\sqrt {\lambda_{4} } }} = \frac{1}{{\sqrt {0.515312} }}, \hfill \\ \hfill \\ R_{4} = \frac{{a_{4} }}{{a_{2} }} = \frac{{\sqrt {\left| {\lambda_{2} } \right|} }}{{\sqrt {\lambda_{4} } }},\begin{array}{*{20}c} {} & {} \\ \end{array} R_{3} = \frac{{a_{3} }}{{a_{2} }} = \frac{{\sqrt {\left| {\lambda_{2} } \right|} }}{{\sqrt {\lambda_{3} } }}. \hfill \\ \end{gathered} }$$

(44b)

The sketched zero-energy flow surface and energy flow variations around the equilibrium point is shown in Fig. 10a, while the computer drawn surface based on Eq. (44a) is given in Fig. 10b. The one for the nonlinear equation is like to the one shown in Fig. 6c, so neglected. The local linearised surface is symmetrical about the coordinate plane ${o - {\vec{\xi}}_{3} {\vec{\xi}}_{4}}$ and axis-symmetrical to the axis ${o - {\vec{\xi}}_{2}}$, so that a plane perpendicular to axis ${o - {\vec{\xi}}_{2}}$ intersects the surface in an elliptical curve of semi-axis${\left| {\tilde{\varphi }_{2} } \right|R_{3} > \left| {\tilde{\varphi }_{2} } \right|R_{4}}$, as shown in Fig. 10a for the ones at ${\left| {\tilde{\varphi }_{2} } \right| = 1}$. The plane ${o - {\vec{\xi}}_{2} {\vec{\xi}}_{3}}$ intersects the surface in the two straight lines of ${\tilde{\varphi }_{3} = \pm \tilde{\varphi }_{2} R_{3}}$. At a disturbed point outside the zero-energy flow surface on the plane perpendicular to the axis ${o - {\vec{\xi}}_{2}}$, the energy flow ${\dot{E} > 0}$ by Eq. (42a), so that this disturbance intends to increase the distance to the origin of space, implying the flow backwards the zero-energy surface. For a disturbed point inside the zero-energy flow surface, the energy flow ${\dot{E} < 0}$ and the disturbance intends to reduce the distance to the origin of space implying the flow also backwards the zero-energy surface. Therefore, this zero-energy surface is a divergence surface. In fact, for this case, the damping matrix of the system in Eq. (10a) becomes

$${ {\varvec{c}} = \left[ {\begin{array}{*{20}c} { - 0.0217} & {0.2442} \\ {0.2442} & { - 0.0222} \\ \end{array} } \right]},$$

(44c)

Fig. 10

Zero-energy flow surface around equilibrium point for case (b) ${ (\alpha = 2.2\;\zeta _{1} = 0.111245,\;\zeta _{2} = 0.008325) }$ based on Eq. (44a): a sketched one and b calculated one

that shows the negative diagonal damping coefficients for both bearing and shaft, so that the motions caused by initial conditions will be divergence.

The results of numerical simulations with the initial conditions ${{\varvec{y}} = 10^{ - 6} \left[ {\begin{array}{*{20}c} 1 & 1 & 1 & 1 \\ \end{array} } \right]^{{\text{T}}}}$ for this case are given in Figs. 11–13. Figure 11 gives the time histories of displacement and velocity of the bearing and shaft, which shows the divergence oscillations. Figure 12 presents the phase diagram y(1)–y(3) of bearing and the one y(2)–y(4) of shaft, as well as the time histories of generalized potential energy and the distance of phase point to the origin, which indicates the orbit points in both phase diagrams move far away to the origin, and the generalized potential energy as well as the distance of orbit point to the origin increase. Figure 13 shows the instant energy flow and the time history of phase space volume strain, of which both positively increase very fast at about non-dimension time 350.

Fig. 11

Time histories of displacement and velocity of bearing and shaft ${ (\alpha = 2.2\;\zeta _{1} = 0.111245,\;\zeta _{2} = 0.008325) }$

Fig. 12

Phase diagram y(1)–y(3) of bearing and the one y(2)–y(4) of shaft, and time histories of generalized potential energy and distance of phase point to origin ${ (\alpha = 2.2\;\zeta _{1} = 0.111245,\;\zeta _{2} = 0.008325) }$

Fig. 13

Time histories of a instant energy flow and b phase space volume strain ${ (\alpha = 2.2\;\zeta _{1} = 0.111245,\;\zeta _{2} = 0.008325) }$

3.2.3 Case (c): one zero and two opposite factors ${ (\alpha = 2.0, \, \zeta _{1} = 0.111,\;\zeta _{2} = 0.008325) }$

In this case, since there exsists a zero-energy flow characteristic factor, the dynamic behavour of the system may not be determined only based on linearised approximation as discussed below. In this case, the central energy flow investigation by considering higher-order terms is needed [28].

The zero energy flow serface around the origin becomes

$${ {0}{\text{.512142}}\tilde{\varphi }_{2}^{2} = 0.512142\tilde{\varphi }_{4}^{2} ,\;\tilde{\varphi }_{2}^{{}} = \pm \tilde{\varphi }_{4}^{{}} },$$

(45a)

corresponding two orthogonal planes perpendicular to the coordinate place ${o - {\vec{\xi}}_{2} {\vec{\xi}}_{4}}$ with the intersect lines and ${ \tilde{\varphi }_{2} = - \tilde{\varphi }_{4}},$ respectively, as shown in Fig. 14. In the domain containing axis ${ o - {\vec{\xi}}_{2}}$, the energy flow ${ \dot{E} < 0 }$, so that the orbit disturbance along ${ o - {\vec{\xi}}_{2}}$ axis will be towards the zero-energy flow surface, while in the domain containing ${ o - {\vec{\xi}}_{4}}$ axis, ${ \dot{E} > 0 }$, the disturbance along ${ o - {\vec{\xi}}_{4}}$ axis will be backwards the zero-energy surface. Therefore, the dynamic behaviour of the system cannot be predicted only based on linear approximation. The theoretical analysis relies on central energy flow theorem, which is more complex, so that here we will reveal the solution by numerically simulating the case with above parameters. Also, from linearised approximation, the summation of diagonal elements of the energy flow matrix ${ \varvec{E} }$ vanish, so that its time change rate of phase volume strain approximately vanishes, i.e.

$${ \dot{\upsilon } \approx \sum\limits_{{I = 1}}^{4} {\lambda _{I} } = 0},$$

(45b)

Fig. 14

Zero energy flow surface Eq. (45a) around equilibrium point for case 3: a sketched one, b calculated one ${ (\alpha = 2.0\;\zeta _{1} = 0.111,\;\zeta _{2} = 0.008325) }$

implying the volume of phase diagram should not change, which might not be true for the nonlinear equation with no linearazation.

Now, we show the numerical simulation results to explain above discussion. The damping matrix at fixed point takes value

$${ {\varvec{c}} = \left[ {\begin{array}{*{20}c} 0 & {0.2220} \\ {0.2220} & 0 \\ \end{array} } \right]},$$

(45c)

of which the diagonal damping coefficients of system vanish.

Figure 15 shows the time histories of displacement and velocity for both bearing and shaft units, from which it has been found that before the time 9.4 × 10⁴ s, the displacement and velocity of bearing increase, while the ones of shaft show oscillations, and both are in modulated style as indicated by enlarged picture in Fig. 18. The generalised potential energy and the orbit point distance to the origin of phase space are modulated oscillations with no obviously-change, and the phase diagram of shaft tends a periodical orbit as shown in Fig. 16. The energy flow shown in Fig. 17a has small values with no obviously change. When the simulation time reaches about 9.4 × 10⁴ s, the displacement and velocity of bearing are extreme large so that the simulation is stopped. Figure 17b shows the time history of phase space volume strain, indicating it increases with time and takes extreme large value at after the stop time. To explain this phenomenon, we check the friction damping matrix in Eq. (10a), which is propotional the factor ${ \tilde{b} = - \alpha \mu _{{01}} {\text{e}}^{{ - \psi {\varvec{\hat{I}z}}}} }$. Referring to the Fig. 15, since the amplitude of bearing velocity ${ z_{1} = y(3) }$ increases while the amplitude of shaft velocity ${ z_{2} = y(4) }$ is nearly unchanged, so that the power of friction function ${ {\text{e}}^{{ - \psi {\varvec{\hat{I}z}}}} = {\text{e}}^{{ - \psi (z_{2} - z_{1} )}} }$ will takes increased positive value, because of this, nonlinear friction force extremely increased, which causes a self-excited oscillation of the nonlinear bearing-shaft friction system.

Fig. 15

Time histories of displacement and velocity of bearing and shaft ${ (\alpha = 2.0\;\zeta _{1} = 0.111,\;\zeta _{2} = 0.008325) }$

Fig. 16

Phase diagram y(1)–y(3) of bearing and the one y(2)–y(4) of shaft, and time histories of generalized potential energy and distance of phase point to origin ${ (\alpha = 2.0\;\zeta _{1} = 0.111,\;\zeta _{2} = 0.008325) }$

Fig. 17

Time histories of a instant energy flow and b phase space volume strain ${ (\alpha = 2.0\;\zeta _{1} = 0.111,\;\zeta _{2} = 0.008325) }$

From the discussion on the zero-energy flow surfaces of three cases and the corresponding numerical simulations based on the nonlinear friction function in Eq. (37b), but not the approximated one in Eq. (37c) used in Ref. [2], we may conclude the stablity of system about the equlilibrium point y = 0 as follows:

• Case (a) when the energy flow matrix at the equilibrium point has two negative and one positive characteristic factor, the local zero-energy flow surface in the small domain around the equilibrium point behaves an attractive surface, and the system is stable to initial disturbance. We also simulated some cases reported in Ref. [2], which further confirm this conclusion is correct. For example, the three cases with ${ \alpha = 2.0,\zeta _{1} = 0.1116,~~0.1111,~~0.111245},$ studied based on the friction force approximation in Eq. (37c) in Ref. [2] were reported the stable case for ${ \zeta _{1} = 0.1116 }$ but unstable cases for the last two values of ${ \zeta _{1} = 0.1111,~~0.111245~ }$. We re-check these three cases by using the friction force Eq. (37b), and the simulation results confirm that for each case, the energy flow matrix has two negative and one positive characteristic factor given in Tables 1, 2 and 3, respectively, and the equilibrium point is stable.

• Case (b) when the energy flow matrix at the equilibrium point has one negative and two positive characteristic factors, the local zero-energy flow surface in the small domain around the equilibrium point behaves a divergence surface, and the system is unstable.

• Case (c) when the energy flow matrix at the equilibrium point has one zero factor and two same absolute value factors, one negative and another positive, the local zero-energy flow surface in the small domain around the equilibrium point behaves divergence in a sub-domain and attractive in another sub-domain as shown in Fig. 14. The dynamical behaviour about this case requires to undergo a higher order approximation analysis. The numerical simulation result shows a divergence self-excited oscillation, which might be miss-judged as a stable oscillation if the simulation time is not enough large. For example, Fig. 18, cut out from Fig. 15 (${ \alpha = 2.0,\zeta _{1} = 0.111 }$), shows the enlarged time histories of displacement and velocity of both bearing and shaft in the initial time before the simulation breaking, which seems a stable picture but unstable indicated by Fig. 15.

Fig. 18

Enlarged time histories of displacement and velocity in modulated styles for bearing and shaft in initial time-period before breaking time shown in Fig. 15${ (\alpha = 2.0\;\zeta _{1} = 0.111,\;\zeta _{2} = 0.008325) }$

3.3 Periodical oscillation ${(\tilde{f} = 0)}$

From Sect. 2.6, we know that for a possible periodical orbit, a necessary condition is that the spin matrix ${\varvec{U}}$ of the system must not vanish. From Eqs. (15), (19) and (27b), we obtain the spin matrix at the equilibrium point

$${{\mathbf{U}} = \left[ {\begin{array}{*{20}l} {\mathbf{0}} & {{\mathbf{I-}} {\varvec{\gamma}}} \\ {{\varvec{\gamma-}} {\mathbf{I}}} & {\mathbf{0}} \\ \end{array} } \right] \ne {\mathbf{0}}},$$

(46)

implying possible periodical orbits of the system. We simulate a case with parameters ${ (\alpha = 2.0\;\zeta _{1} = 0.111,\;\zeta _{2} = 0.008325) }$, of which there are two negative and one positive energy flow characteristic factors and a damping matrix at equilibrium point

$${ {\varvec{c}} = \left[ {\begin{array}{*{20}l} {0.0012} & {0.2220} \\ {0.2220} & 0 \\ \end{array} } \right] }.$$

(47)

Figure 19 shows that the displacement and velocity of bearing decrease with time, while the shaft ones are in a periodical motion. The phase diagram of bearing tends to the origin while the one of shaft shows a closed orbit, and the generalised potential energy as well as the distance of phase point to the origin behave modulated oscillation without obviously amplitude variations, as shown in Fig. 20. The instant energy flow curve behaviours a stable oscillation in Fig. 21a, and its time averaged one tends to zero with average time increasing as shown in Fig. 22. The phase space volume train descreases with time shown in Fig. 21b. According to the energy flow theory discussed in Sect. 2.6, this is a stable periodical motion of the system excited by initial conditions.

Fig. 19

Time histories of displacement and velocity of bearing and shaft ${ (\alpha = 2.0\;\zeta _{1} = 0.111,\;\zeta _{2} = 0.008325) }$

Fig. 20

Phase diagrams y(1)–y(3) of bearing and y(2)–y(4) of shaft, and time histories of generalized potential energy and distance of phase point to origin ${ (\alpha = 2.0\;\zeta _{1} = 0.111,\;\zeta _{2} = 0.008325) }$

Fig. 21

Time histories of a instant energy flow and b phase space volume strain ${ (\alpha = 2.0\;\zeta _{1} = 0.111,\;\zeta _{2} = 0.008325) }$

Fig. 22

Time histories of time-averaged energy flow ${ (\alpha = 2.0\;\zeta _{1} = 0.111,\;\zeta _{2} = 0.008325) }$

We have simulated the cases with parameters ${ (\alpha = 2.0\;\zeta _{1} = 0.1111,\;\zeta _{2} = 0.008325) }$ and ${ (\alpha = 2.12\;\zeta _{1} = 0.119725,\;\zeta _{2} = 0.0009) }$ [2], of which the energy flow matrix has two negative and one positive energy flow characteristic factors and both systems also behave the similar stable periodical oscillations as the one presented herein.

3.4 Forced oscillations ${ ({\tilde{f}} \ne {{0}}) }$

We respectively add an excitation force of amplitude 10⁻⁶, frequency 0.5 and phase angle 0, i.e. ${ \hat{f} = 10^{{ - 6}} \cos (0.5\tau )},$ on the bearing mass and the shaft mass to investigate the forced dynamic response of the system. The simulated results are given as follows.

3.4.1 Case (a): parameters ${ \alpha = 2.0\;\zeta _{1} = 0.1116,\;\zeta _{2} = 0.009 }$

Figures 23–26 give the simulation results, in which, with time increasing, the time histories of displacements and velocities shown in Fig. 23 tend stable forced modulated oscillations, the generalised potential energies and the distances of phase points to the origin tend stable pictures and the phase diagrams tend periodical orbits in Fig. 24, as well as the instant energy flows and the phase space volume strains in Fig. 25 also tend stable curves. Figure 26 confirms that the time-averaged energy flows tend zero with average time increasing. These typical results demonstrate that the forced vibrations are periodical motions of the system although the different curve styles due to different force added potions. Since the positive damping of the system, the free vibration components due to initial conditions are gradually damped, and a stable forced vibration is obtained. However, since the system is nonlinear, the frequency of the forced vibration does not equal the force frequency, so that the response curves behave modulated pictures compositing of two frequencies response.

Fig. 23

Dynamic response time histories of displacements and velocities of bearing and shaft of the system subject an external force: I) on bearing ${\hat{\mathrm{f}}} = \left[ {\begin{array}{*{20}l} 0 \hfill & 0 \hfill & {\varvec{\hat{f}}} \hfill & 0 \hfill \\ \end{array} } \right]^{{\text{T}}}$ and II) on shaft${ \hat{\mathrm{f}}} = \left[ {\begin{array}{*{20}l} 0 \hfill & 0 \hfill & 0 \hfill & {\hat{f}} \hfill \\ \end{array} } \right]^{{\text{T}}}$

Fig. 24

Phase diagrams y(1)–y(3) of bearing and y(2)–y(4) of shaft, and time histories of generalized potential energy and distance of phase point to origin: I) force on bearing ${ {\varvec{\hat{f}}} = \left[ {\begin{array}{*{20}l} 0 & 0 & {\hat{f}} & 0 \\ \end{array} } \right]^{{\text{T}}} }$ and II) force on shaft ${ {\varvec{\hat{f}}} = \left[ {\begin{array}{*{20}l} 0 & 0 & 0 & {\hat{f}} \\ \end{array} } \right]^{{\text{T}}} }$

Fig. 25

Time histories of a instant energy flow and b phase space volume strain in forced vibration: I) force on bearing ${ {\varvec{\hat{f}}} = \left[ {\begin{array}{*{20}l} 0 & 0 & {\hat{f}} & 0 \\ \end{array} } \right]^{{\text{T}}} }$ and II) force on shaft ${ {\varvec{\hat{f}}} = \left[ {\begin{array}{*{20}l} 0 & 0 & 0 & {\hat{f}} \\ \end{array} } \right]^{{\text{T}}} }$

Fig. 26

Curves of time-averaged energy flow vs average time for forced vibration: I) force on bearing ${ {\varvec{\hat{f}}} = \left[ {\begin{array}{*{20}l} 0 & 0 & {\hat{f}} & 0 \\ \end{array} } \right]^{{\text{T}}} }$ and II) force on shaft ${ {\varvec{\hat{f}}} = \left[ {\begin{array}{*{20}l} 0 & 0 & 0 & {\hat{f}} \\ \end{array} } \right]^{{\text{T}}} }$

3.4.2 Case (b): parameters ${ \alpha = 2.2,\;\zeta _{1} = 0.111245,\;\zeta _{2} = 0.008325 }$

In this case with main negative damping coefficients, the system behaves divergence oscillations, of which the dynamic response time histories of displacements and velocities in Fig. 27, the generalised potential energies and the distances of phase point to origin as well as the phase space volume strains in Fig. 28 increase very fast with time going.

Fig. 27

Dynamic response time histories of displacements and velocities of bearing and shaft in the system subject an external force: I) on bearing ${ {\varvec{\hat{f}}} = \left[ {\begin{array}{*{20}l} 0 & 0 & 0 & {\hat{f}} \\ \end{array} } \right]^{{\text{T}}} }$ and II) on shaft ${ {\varvec{\hat{f}}} = \left[ {\begin{array}{*{20}l} 0 & 0 & 0 & {\hat{f}} \\ \end{array} } \right]^{{\text{T}}} }$

Fig. 28

Time histories of generalized potential energy, distance of phase point to origin and phase space volume strain in forced vibration: I) force on bearing ${ {\varvec{\hat{f}}} = \left[ {\begin{array}{*{20}l} 0 & 0 & 0 & {\hat{f}} \\ \end{array} } \right]^{{\text{T}}} }$ and II) force on shaft ${ {\varvec{\hat{f}}} = \left[ {\begin{array}{*{20}l} 0 & 0 & 0 & {\hat{f}} \\ \end{array} } \right]^{{\text{T}}} }$

3.4.3 Case (c): parameters ${ \alpha = 2.0,\;\zeta _{1} = 0.111,\;\zeta _{2} = 0.008325}$

The forced vibration in this case is like the free vibration discussed for case 3 in Sect. 3.3, as shown in Fig. 29, the dynamic responses of displacements and velocities of both bearing and shaft increase until about time 3.3 × 10⁴ when the responses sharply increased and simulations stopped. To show the response curve details, Fig. 30 provides local enlarged curves before breaking time in Fig. 29, from which it is observed the dynamic responses behave the modulated vibrations before the simulation breaking. The curves of generalised potential energy, the phase diagram, etc. also show the characteristics, so they are neglected herein.

Fig. 29

Dynamic response time histories of displacements and velocities of bearing and shaft in the system subject an external force: I) on bearing ${ {\varvec{\hat{f}}} = \left[ {\begin{array}{*{20}l} 0 & 0 & 0 & {\hat{f}} \\ \end{array} } \right]^{{\text{T}}} }$ and II) on shaft ${ {\varvec{\hat{f}}} = \left[ {\begin{array}{*{20}l} 0 & 0 & 0 & {\hat{f}} \\ \end{array} } \right]^{{\text{T}}} }$

Fig. 30

Enlarged response time histories, before simulation breaking, of displacements and velocities of the system subject an external force: I) on bearing ${ {\varvec{\hat{f}}} = \left[ {\begin{array}{*{20}l} 0 & 0 & 0 & {\hat{f}} \\ \end{array} } \right]^{{\text{T}}} }$ and II) on shaft ${ {\varvec{\hat{f}}} = \left[ {\begin{array}{*{20}l} 0 & 0 & 0 & {\hat{f}} \\ \end{array} } \right]^{{\text{T}}} }$

3.5 Chaotic motions

With different friction parameters, we have tested several cases for free vibrations induced by given initial disturbances and for forced vibrations excited by external forces acted on the bearing and shaft masses in order to see if chaotic motions may be found. The simulations results have not shown any chaotic motions of this system.

4 Conclusion

Following the detailed describption of this investigation given above, we may conclude the main contributions as follows. The paper is a first one to study a nonlinear water-lubricated bearing-shaft coupled system using the energy flow approach, which practices and further confirmed an efective energy-flow means to tackle varous complex nonlinear systems and to investigate their nonlinear characteristics: stability, periodical motion, birfurcation and possible chaos.The results obtained for the investigated system have revealed that the dynamic behaviour about its equilibrium point is fully determined by the energy flow matrix and its characteristic factors. Three cases with different energy flow charactristic factors affected by the friction-parameters are discovered: (a) two negative and one positive factors, constructing an attractive local zero-energy flow surface, in which free vibrations show damped modulated oscillations allowing the system returning to its equlibrium state, while forced vibrations show stable oscillations; (b) one negative and two positive factors, spanning a divergence local zero-energy flow surface, so that the both free / forced vibrations are in divergence resulting an unstable system; (c) one zero and two opposite factors, constructing a local zero-energy flow surface dividing the phase space into stable, unstable and central subspace, and the simulation shows friction self-induced unstable vibrations in both free and forced cases. For a set of friction parameters, the system behaves a periodical oscillation, in which the bearing motion tends zero and the shaft motion tends a stable limit circle in phase space with the instant energy flow tends a constant and its time averaged one tends zero. Numerical simulations have not found any possible chaotic motions of the system. It is discovered that the damping matrices of cases (a), (b) and (c) respectively have positive, negative and zero diagonal elements, dominating the dynamic behavour in different cases of the system, which provides an approach to design the water-lubricated bearing unit with expecting performance in marine engineering applications by choosing suitable friction parameters to generate the expected damping matrix.