1 Introduction

Turbulence control offers significant advantages in various engineering applications. One of the most important techniques used to improve the efficiency of a working system is to reduce the surface drag caused by turbulent boundary layer (TBL) flow, and understanding TBL flow mechanisms is beneficial for the development of control methods. Quasi-streamwise vortices (QSVs) are typical coherent structure-inducing [1,2,3] bursting events that dominate the near-wall region, and are associated with most surface friction production [4,5,6]. The ejection process occurs on the updraft side of QSVs, wherein the low-speed fluids in the inner layer are lifted away from the wall to the outer layer with the transfer of the mass, energy, momentum, and vortices [7]. The sweep process occurs on the downdraft side of QSVs, wherein the high-speed fluids move downward to the wall, which is directly related to an increase in the skin friction [8, 9]. Thus, QSVs are the main factors that increase the surface friction, so altering the QSVs is a potential approach for achieving drag reduction [10, 11].

Numerous passive and active control methods have been developed based on this flow mechanism [12]. As a representative of the passive control methods, Wash and Choi et al. [13,14,15] achieved considerable drag reduction on riblet surfaces by conducting experiments and direct numerical simulations. In comparison with the passive control method, the active control method has wider adaptability to complex flows, and it enhances the control effectiveness [16,17,18,19], which has been confirmed by several experimental and simulation investigations [20,21,22,23,24,25,26,27,28,29]. Bai et al. [2] used a spanwise-aligned array of piezoceramic actuators to generate a transverse traveling wave along the wall surface. The actuator can induce a layer of highly regularized streamwise vortices to break the connection between the large-scale coherent structures and the wall, achieving a maximum drag reduction of 50%. Berger et al. [30] obtained a drag reduction of 40% via an open loop-controlled oscillating spanwise Lorentz force that disturbed the semi-equilibrium state between the near-wall streamwise vortices and the wall in channel flow. Zheng et al. [19] applied a single PZT actuator to break the near-wall streamwise vortices and achieved a drag reduction of 27%. Herein, we employed an active strategy based on the aforementioned achievements.

A basic property of turbulence is its multiscale characteristics. However, few studies have investigated the influence of active control on the TBL’s multiscale features. We provided a periodic perturbation to the TBL via a PZT actuator. To further observe the modification in the TBL’s multiscale characteristics because of the PZT actuator, we conducted hot-wire measurements. This study reports the drag reduction results with a PZT actuator over a wide range of frequencies and amplitudes, and the multiscale properties of the turbulence are analyzed. Finally, the control effect on the bursting process is observed.

2 Experimental setup and parameters

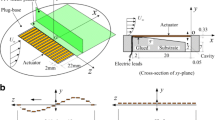
Figure 1 shows the experimental setup. The experiments were conducted in a closed loop wind tunnel. TBL flow developed along a flat plate, which was mounted vertically in the test section. Pitch angle was finely adjusted to ensure a zero-pressure gradient in the streamwise direction. A tripwire was fixed at \(x = 80\;{\text{mm}}\) downstream of the leading edge, and a sandpaper band was attached following the tripwire until \(x = 530\;{\text{mm}}\). The freestream velocity was \(U_{\infty } = 9\;{\text{m}}/{\text{s}}\). TBL was fully developed at the streamwise location of \(x = 1000\;{\text{mm}}\), wherein the end of the control mechanism and measurement was conducted at \(x = 1002\;{\text{mm}}\), as shown in Fig. 1. The thickness of the TBL was approximately \(\delta = 39.8\;{\text{mm}}\). Based on \(U_{\infty }\) and momentum thickness, \(\theta\), Reynolds number, \(Re_{\theta }\), was 2183.

Fig. 1
figure 1

Schematic of the experimental setup

Full size image

The PZT actuator was firmly pasted over the plate. The upper surface of the actuator was leveled with the plate’s surface. The effective length, thickness, and width of the actuator was \(30\), \(0.42\), and \(3.62\;{\text{mm}}\), respectively. The actuator comprised a 220-µm-thick PZT-5H material and 200-µm-thick phosphor-copper shim. The basic geometric information and material properties of the PZT actuator are listed in Table 1. The PZT oscillator was excited via a power source, which worked as a cantilever beam. The frequency and amplitude of the actuating voltage were adjustable over a wide range.

Table 1 Details of the PZT oscillator materials
Full size table

We tested three different experimental conditions, wherein the frequencies of actuation were set to 80, 160, and 240 Hz under the same voltage of 100 V. The corresponding amplitudes of the actuator were \(0.4\), \(0.6\), and \(0.2\;{\text{mm}}\), respectively, which were captured using a high-speed camera. The measuring equipment comprised an IFA-300 with a TSI-1621A-T1.5 miniature boundary layer probe [31, 32]. The sensing element of the probe was a tungsten wire with a diameter of 4 μm and length 1.25 mm. The calibration was conducted using an air velocity calibrator over the velocity range 0–15 m/s. Sampling rate and low pass cut-off frequency were 100 and 50 kHz, respectively. We obtained time sequences of the streamwise velocity signal at 74 different wall-normal locations. Each sequence comprised 222 velocity samples or approximately 42 s [33].

3 Results and discussion

3.1 Mean velocity profile

The outer scaled mean velocity profile, scaled using \(\delta\) and \(U_{\infty }\), is linear in the viscous sublayer [34], as shown in Fig. 2a. The profile slope is related to the skin-friction stress \(\tau_{w}\), according to

Fig. 2
figure 2

Distributions of the mean streamwise velocity in the a outer and b inner scaled units

Full size image
$$\tau_{w} = \rho v\partial U/\partial y ,$$
(1)

where the air flow density is 1.205 kg/m3 and kinematic viscosity coefficient \(v\) is 1.5 × 10−5 m2/s [35,36,37]. The friction velocity, \(u_{\tau }\), can be obtained as follows

$$u_{\tau } = \sqrt {\bar{\tau }_{w} /\rho } ,$$
(2)

where the overbar denotes time averaging. Figure 2b shows the mean velocity profiles normalized by \(u_{\tau }\), and \(U^{ + } = y^{ + }\) is evident for both uncontrolled and controlled cases over y+ = 3–5. The local skin-friction reduction is defined as follows

$$\Delta_{{\tau_{w} }} = \frac{{\left( {\bar{\tau }_{w} } \right)_{\text{on}} - \left( {\bar{\tau }_{w} } \right)_{\text{off}} }}{{\left( {\bar{\tau }_{w} } \right)_{\text{off}} }} \times 100\% ,$$
(3)

where the subscripts on and off denote measurements with and without control, respectively. Table 2 lists the drag reduction results for different cases. It can be seen that case 2 with the PZT frequency of 160 Hz and amplitude of 0.6 mm achieves the maximum drag reduction of 26.4%.

Table 2 Local skin drag reduction
Full size table

3.2 Wavelet energy distribution

The effects of the PZT actuator on multiscale characteristics of the turbulence were investigated by wavelet analysis, which is one of the most widely used multiscale signal processing methods. The definition of this method fits well with the physical characteristics of turbulence [38, 39]. Wavelet analysis includes a continuous wavelet transform (CWT) and discrete wavelet transform (DWT). To improve the computing efficiency and avoid redundant information, DWT was employed for data processing [40].

The wavelet transforms of a signal \(u\left( t \right)\) with scale \(r\) at position \(t\) are defined as follows [41]

$$w\left( {r,t} \right) = C_{\varPsi }^{ - 1/2} r^{ - 1/2} \mathop \smallint \limits_{\infty }^{\infty } \varPsi^{*} \left( {\frac{s - t}{r}} \right)u\left( s \right){\text{d}}s,$$
(4)

where \(\varPsi \left( t \right)\) is wavelet function, which satisfies the following admissibility condition

$$C_{\varPsi } = \mathop \smallint \limits_{\infty }^{\infty } \left| k \right|^{ - 1} \left| {\hat{\varPsi }\left( k \right)} \right|^{2} < \infty ,$$
(5)

where \(\hat{\varPsi }\left( k \right)\) denotes the Fourier transform of \(\varPsi \left( t \right)\). Equation (5) is the invertibility condition, which is a necessary condition for the signal \(u\left( t \right)\) to be reconstructed from its wavelet coefficients.

Instead of using CWT, the function \(u\left( t \right)\) can be decomposed into a series of self-similar orthonormal functions obtained via dilatations and translations of a mother function \(\varPsi_{00}\) [42]. By choosing separations \(r_{k} = 2^{ - k}\), a set of functions forming the orthonormal basis can be written as follows

$$\varPsi_{k,j} \left( t \right) = - 2^{ - k/2} \varPsi_{00} \left( {2^{k} t - j} \right).$$
(6)

If \(u\left( t \right)\) is sampled on a discrete mesh \(t_{j}\), the transformed function can be rewritten in a discrete form as follows

$$u\left( j \right) = \mathop \sum \limits_{r = 1}^{\infty } \mathop \sum \limits_{i = - \infty }^{\infty } w^{r} \left( i \right)\varPsi^{\left( r \right)} \left( {i - 2^{r} j} \right) ,$$
(7)

where r represents the discretized scale. The wavelet function \(\varPsi^{\left( r \right)} \left( {i - 2^{r} j} \right)\) should obey the following orthogonality condition:

$$\mathop \sum \limits_{k = - \infty }^{\infty } \varPsi^{\left( r \right)} \left( {k - 2^{r} i} \right)\varPsi^{\left( p \right)} \left( {k - 2^{p} j} \right) = \delta_{ij} \delta_{rp} .$$
(8)

Then the coefficients \(w^{\left( r \right)} \left( i \right)\) can be obtained as

$$w^{\left( r \right)} \left( i \right) = \mathop \sum \limits_{j = - \infty }^{\infty } \varPsi^{r} \left( {i - 2^{r} j} \right)u\left( j \right) .$$
(9)

The reconstructed signal at every scale can be computed as follows

$$u\left( j \right)^{r} = \mathop \sum \limits_{i = - \infty }^{\infty } w^{r} \left( i \right)\varPsi^{\left( r \right)} \left( {i - 2^{r} j} \right).$$
(10)

In this experiment, DWT in the fluctuating velocity signals was calculated using Daubechies 4 wavelet function. Figure 3 shows the linear relation between the logarithmic characteristic frequency \(f_{r}^{w}\) and scale level r.

Fig. 3
figure 3

Relation between the scale level \(r\) and characteristic frequency \(f_{r}^{w}\)

Full size image

Figure 4 shows the percentage of the reconstructed fluctuations’ energy with respect to the total energy, \({{\left\langle {u_{r}^{{{\prime }2}} } \right\rangle } \mathord{\left/ {\vphantom {{\left\langle {u_{r}^{{{\prime }2}} } \right\rangle } {\left\langle {u^{{{\prime }2}} } \right\rangle }}} \right. \kern-0pt} {\left\langle {u^{{{\prime }2}} } \right\rangle }}\), which is a function of the scale levels and wall-normal positions. In Fig. 4a, the uncontrolled case indicates that the inner peak appears at y+ = 10–14 at a scale level of 9, corresponding to the most energetic structures in the near-wall turbulence, i.e., the QSVs. Figure 4b–d show the results of the controlled cases. It can be seen that the PZT vibration concentrates the energy at scale levels of 10, 9, and 8, corresponding to the vibration frequencies of 80, 160, and 240 Hz, respectively, which means that the PZT actuator, as expected, has a periodic impact on the downstream flow fields where the hot-wire is measured. As shown, the wall-normal region perturbed by the PZT actuator primarily exists at \(y^{ + } < 40\).

Fig. 4
figure 4

Energy distribution with the scale and normal position under a the uncontrolled case, b 100 V and 80 Hz, c 100 V and 160 Hz, and d 100 V and 240 Hz

Full size image

According to Wallace et al. [26], typical bursting events, i.e., sweeps and ejections, are closely correlated with each other at a wall-normal position of 15 wall units. In our study, the vibrations affected this position range. The turbulent energy distribution, as shown in Fig. 4, indicates that the impact of the actuator was concentrated in the range y+ = 10–15. Therefore, the time series of the original and reconstructed fluctuating signals at \(y^{ + } = 14\) in the uncontrolled case and case 2 (100 V and 160 Hz) were compared to investigate the effects of PZT on the scale corresponding to the vibration frequency. In Fig. 5a, b, it can be seen that the original fluctuation \(u^{ + }\) overlaps better with the reconstructed fluctuation \(u_{r}^{ + }\) at a scale level of 9, i.e., corresponding to 160 Hz, in the controlled case than that in the uncontrolled case. This implies that the fluctuation components at this dominating scale are coupling to the PZT actuation.

Fig. 5
figure 5

Comparison between the streamwise fluctuating signal \(u^{ + }\) and reconstructed fluctuating signal \(u_{r}^{ + }\) at a scale level of 9 for a the uncontrolled case,\(u^{ + }\): black line; \(u_{r}^{ + }\): red line, and b case 2,\(u^{ + }\): black line; \(u_{r}^{ + }\): green line

Full size image

3.3 Turbulent intensities

First, some definitions need to be stated for clarity. The vibration scales indicate the scales approximately corresponding to the vibration frequencies 80, 160, and 240 Hz, which are 10, 9, and 8, respectively. Scales with higher characteristic frequencies than the vibration frequencies are defined as smaller scales, whereas those with lower characteristic frequencies are defined as larger scales. Table 3 lists the definitions of the analyzed scalesbelow.

Table 3 Definition of the analyzed scales
Full size table

The turbulent intensity distribution is observed at various scales, which is represented by \(u_{\text{rms}}^{ + }\). As shown in Fig. 6a–c, in the main region affected by the vibrations, i.e., y+ = 10–15, the turbulent intensities are enhanced by the vibrations on smaller scales. Moreover, in case 2, the vibrations obviously weaken the intensities at larger scales; however, they have only a slight effect at larger scales in cases 1 and 3. Generally, in the near-wall region, the vibrations redistributed the energy to different scales [29].

Fig. 6
figure 6

Comparison of the turbulence intensities at different scales between the uncontrolled case and cases a 1, b 2, and c 3

Full size image

3.4 Skewness

The skewness, \({{\left\langle {u_{r}^{{{\prime }3}} } \right\rangle } \mathord{\left/ {\vphantom {{\left\langle {u_{r}^{{{\prime }3}} } \right\rangle } {\left\langle {u_{r}^{{{\prime }2}} } \right\rangle^{3/2} }}} \right. \kern-0pt} {\left\langle {u_{r}^{{{\prime }2}} } \right\rangle^{3/2} }}\), describes the symmetry of the turbulence fluctuations’ probability distribution function (PDF). Positive skewness indicates that high-momentum sweep events with positive streamwise fluctuations are dominant, and negative skewness corresponds to low-speed eject events with negative streamwise fluctuations. Based on the wavelet decomposition, the wall-normal distributions of the skewness at different scales are shown in Fig. 7a–c. In case 2, the skewness value decreases dramatically, whereas it experiences almost no change in case 3. The skewness is positive in the near-wall region of y+ = 10–15 for all cases. For cases 1 and 2, the skewness in the near-wall region decreases (close to zero) significantly, implying a better symmetry of the PDF for streamwise fluctuations. Then likely reason is that the PZT actuator induces flow structures with a certain frequency and highly fluctuating amplitude, and that the generated structures result in an alteration of the sweep events in the near-wall region.

Fig. 7
figure 7

Comparison of the skewness of the vibration scales between the uncontrolled case and cases a 1, b 2, and c 3

Full size image

3.5 Flatness

Figure 8 shows the distribution of the flatness factor, \({{\left\langle {u_{r}^{{{\prime }4}} } \right\rangle } \mathord{\left/ {\vphantom {{\left\langle {u_{r}^{{{\prime }4}} } \right\rangle } {\left\langle {u_{r}^{{{\prime }2}} } \right\rangle^{2} }}} \right. \kern-0pt} {\left\langle {u_{r}^{{{\prime }2}} } \right\rangle^{2} }}\), at different scales, which is a classic indicator of the turbulence fluctuation’s intermittency. A flatness larger than 3 implies a strong intermittency introduced by sweep events with highly fluctuating momentum. As shown, the flatness of controlled cases decreases at smaller scales and vibration scales, and it has a very obvious drop over the vibration scales. The variation in the flatness is positively correlated with the drag reduction effect. Therefore, this result indicates that the PZT actuator effectively reduces the intermittency and modulates the velocity fluctuation to be more periodic, especially for the vibration scales.

Fig. 8
figure 8

Comparison of the flatness at different scales between the uncontrolled case and cases a 1, b 2, and c 3

Full size image

The PDFs of the streamwise fluctuation at \(y^{ + } = 14\), where the inner spectral peak is located, are plotted in Fig. 9a–c according to the skewness and flatness results. The results of case 2 are presented and are compared with those of the uncontrolled case. The change in PDF is apparent under perturbation, as shown in Fig. 9a–c. At larger scales, the PZT control shortens the PDF tails, which means that the vibration concentrates the kinematic energy to the mean flow by weakening the large-scale structures in the near-wall turbulence. These results agree with the previous conclusion. On the vibration and smaller scales, the vibration causes the PDF to have longer tails on both sides, implying an increase in the probability of high-amplitude fluctuations. It indicates that the fluctuations of the vibration and smaller scales have high intensity. Combined with the results of the flatness factor, it shows that the PZT disturbance caused fluctuations on the vibration and smaller scales with high intensity and low intermittency.

Fig. 9
figure 9

Comparison of the velocity fluctuation PDFs at \(y^{ + } = 14\) in the uncontrolled case (black circles) and case 2 (red squares) at a scale = 8; b scale = 9; and c scale = 10

Full size image

Based on the study reported by Jiang and Zhang [43], bursting process components are the fluctuations that cause the flatness factor (FF) to be larger than 3. The two principal indicators used for our analysis of the data intermittency were the FF and local intermittency measure. FF is defined as follows:

$${\text{FF}}\left( r \right) = \frac{{u_{r}^{{{\prime }4}} \left( t \right)_{t} }}{{u_{r}^{{{\prime }2}} \left( t \right)_{t}^{2} }}.$$
(11)

This function gives the level of intermittency at scale level r. Therefore, the difference with respect to the Gaussian statistics with an FF equal to 3 can be directly obtained.

The local intermittency measure (LIM) is defined as follows:

$${\text{LIM}}\left( {r,t} \right) = \frac{{u_{r}^{{{\prime }2}} \left( t \right)}}{{u_{r}^{{{\prime }2}} \left( t \right)_{t} }}.$$
(12)

According to Camussi and Guj [40], LIM is a good qualitative indicator of the intermittency and magnitude of the energy fluctuations. Overall, detecting the bursting process indicates extracting the components in the fluctuations that make FF larger than 3 using these two indicators. The extraction procedure can be summarized as follows. For a certain scale, LIM can be computed as a function of t and threshold level l, can be set for LIM. The initial value of l is set to \(l_{0} = u_{\hbox{max} }^{\prime 2} /u^{\prime 2} \left( t \right)_{t}\), where \(u_{\hbox{max} }^{\prime 2}\) is the maximum value of the fluctuations over the entire time domain at this scale. Then, FF of the fluctuation components \(u^{\prime}\left( {t_{i} } \right)\) (\({\text{LIM}}\left( {t_{i} } \right) < l = l_{0}\)) can be calculated. If FF is larger than 3, l is reduced from \(l_{0}\) by several times at a certain rate. At each time, the FF of the fluctuation components \(u^{\prime}\left( {t_{i} } \right)\) (\({\text{LIM}}\left( {t_{i} } \right) < l\)) is calculated. The detecting process stops when the FF of \(u^{\prime}\left( {t_{i} } \right)\left( {{\text{LIM}}\left( {t_{i} } \right) < l} \right)\) drops to 3 and \(l = l_{{\left( {{\text{FF}} = 3} \right)}}\). Finally, the fluctuation components \(u^{\prime}\left( {t_{j} } \right)\)\(\left( {{\text{LIM}}\left( {t_{j} } \right) > l_{{\left( {{\text{FF}} = 3} \right)}} } \right)\) are extracted as the bursting process. The completion status of the detection process is shown in Fig. 10. The black line denotes the fluctuation at a scale level of 9, whereas red line denotes the bursting processes detected at this scale.

Fig. 10
figure 10

Schematic diagram of the coherent structure extraction method

Full size image

According to this detection method, the statistical results of the bursting process can be studied at all scales. To obtain an overall understanding of the process, we superimposed the energy of the bursting process, \(E_{\text{b}}\), and total energy, \(E\), at all scales. Their ratios are obtained in Fig. 11a. \(E_{\text{b}} /E\), which represents the relative importance of the bursting process, reflecting the fact that the vibration weakens the bursting process and that the case of 100 V and 160 Hz has the best performance. The impact is concentrated at \(y^{ + } < 40\). These results are in agreement with those reported by Zheng et al. [18]. Combined with the drag reduction effect, it appears that the streamwise vortices in the buffer layer experience direct interference due to the PZT actuator, which leads to a breakdown in the burst mechanism in the inner region, thereby reducing the drag. The bursting process includes eject and sweep events with low- and high-speed fluids, respectively. To observe the impact of the vibration more carefully, the sweep and eject events were extracted according to the positive and negative fluctuation signals, respectively. Figure 11b, c show the proportion of eject and sweep event energy, i.e., \(E_{\text{e}}\) and \(E_{\text{s}}\), respectively, relative to \(E\). As can be seen, the relative intensities of the eject and sweep events were both weakened by the vibration in the near-wall region. Even though the energy proportions of the eject and sweep events were different in the original fluctuations, the weakening degrees due to the vibrations were nearly same for the positive (sweep) and negative (eject) fluctuations. According to Fig. 7, the vibrations produced strong fluctuations in the positive and negative symmetries in the near-wall region; therefore, the impacts on the positive and negative signals were similar.

Fig. 11
figure 11

Distribution of the energy ratio of a the bursting process \(E_{\text{b}}\) with respect to the original fluctuations \(E\), b eject process \(E_{\text{e}}\) with respect to \(E\), and c sweep process \(E_{\text{s}}\) with respect to \(E\)

Full size image

4 Conclusions

This experiment was conducted considering the Reynolds number of \(Re_{\theta } = 2183\) under three different conditions. The impact of a single PZT actuator on the statistical characteristics in the TBL was investigated using various methods. Statistics were gathered from the streamwise fluctuating velocity signals, measured using a single hot wire in the near-wall region. The major conclusions of the study are as follows.

  1. 1.

    From a multiscale point of view, in the near-wall region, the actuator redistributes the energy into different scales.

  2. 2.

    The changes in the skewness and flatness revealed that the PZT actuator, actuated at a certain frequency by a voltage with a sinusoidal waveform, effectively interferes with the sweep events, reduces the intermittency at smaller scales and on the vibration scales, and enhances the symmetry of the velocity signals at the vibration scales. Furthermore, the structure composition appears ordered. The PDF results indicate that the perturbation caused the fluctuations at the vibration scales and the smaller scales to have high intensity and low intermittency.

  3. 3.

    Based on the change in the flatness, the characteristics of the bursting events were analyzed. The results indicate that the vibrations restrain the bursting process for \(y^{ + } < 40\), which indicates that the streamwise vortices in the buffer layer experience direct interference due to the PZT control, leading to a reduction in the drag.