Pressure drop and bubble velocity in Taylor flow through square microchannel

Abstract

Interface tracking simulations of gas–liquid Taylor flow in horizontal square microchannels were carried out to understand the relation between the pressure drop in the bubble part and the curvatures at the nose and tail of a bubble. Numerical conditions ranged for 0.00159 ≤ Ca_T ≤ 0.0989, 0.0817 ≤ We_T ≤ 25.4, and 8.33 ≤ Re_T ≤ 791, where Ca_T, We_T, and Re_T are the capillary, Weber, and Reynolds numbers based on the total volumetric flux. The dimensionless pressure drop in the bubble part increased with increasing the capillary number and the Weber number. The curvature at the nose of a bubble increased and that at the tail of a bubble decreased as the capillary number increased. The variation of the curvature at the tail of a bubble was more remarkable than that at the nose of a bubble due to the increase in the Weber number, which was the main cause of large pressure drop in the bubble part at the same capillary number. The relation between the bubble velocity and the total volumetric flux was also discussed. The distribution parameter of the drift-flux model without inertial effects showed a simple relation with the capillary number. A correlation of the distribution parameter, which is expressed in terms of the capillary number and the Weber number, was developed and was confirmed to give good predictions of the bubble velocity.

1 Introduction

Taylor flow consisting of elongated bubbles separated by liquid slugs is one of the typical flow patterns in microchannels and is known to have good performances in heat and mass transfer. Understanding the flow characteristics of Taylor flow, e.g., the pressure drop and the bubble velocity, is indispensable for the design and development of efficient microdevices such as microreactors and micro heat exchangers.

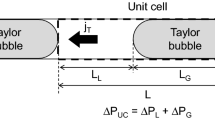
The pressure drop in Taylor flow has often been modeled as the sum of the pressure drops in the bubble part ΔP_B and the liquid slug part ΔP_L (Chung and Kawaji 2004; Warnier, et al. 2010; Minagawa et al. 2013; Eain et al. 2015; Kurimoto et al. 2017, 2019, 2020; Kawahara et al. 2020), i.e.,

$$-\frac{dP}{dz}=\frac{{\Delta P}_{B}+{\Delta P}_{L}}{L}$$

(1)

where dP/dz is the pressure gradient of one unit cell consisting of a Taylor bubble followed by a liquid slug, and L the length of the unit cell. Kurimoto et al. (2020) measured dP/dz in square microchannels. They calculated ΔP_B as

$${\Delta P}_{B}=-\frac{dP}{dz}L-\frac{{c}_{s}}{{Re}_{T}}\frac{{L}_{L}}{{D}_{h}}\frac{{\rho }_{L}{j}_{T}^{2}}{2}$$

(2)

where c_s = 56.9 (Shah 1978), L_L is the length of a liquid slug, ρ_L the liquid density, j_T the total volumetric flux, D_h the hydraulic equivalent diameter of a channel, and Re_T the Reynolds number defined by

$${Re}_{T}=\frac{{\rho }_{L}{j}_{T}{D}_{h}}{{\mu }_{L}}$$

(3)

where µ_L is the liquid viscosity. The dimensionless pressure drop, ΔP_B^* (= ΔP_BD_h/σ), in the bubble part increased with increasing the capillary number Ca defined by

$$Ca=\frac{{\mu }_{L}{u}_{B}}{\sigma }$$

(4)

where u_B is the bubble velocity, and σ the surface tension. The dimensionless pressure drop also increased with increasing the bubble Weber number We or the bubble Reynolds number Re, i.e., inertial effects contribute to the increase in ΔP_B^*. The Weber and Reynolds numbers are defined by

$$We=\frac{{\rho }_{L}{u}_{B}^{2}{D}_{h}}{\sigma }$$

(5)

$$Re=\frac{{\rho }_{L}{u}_{B}{D}_{h}}{{\mu }_{L}}$$

(6)

Wong et al. (1995b) derived an analytical solution describing the relation between ΔP_B^* and the bubble shape in the limiting case of Ca → 0. The dependence of ΔP_B^* on Ca and We at a finite Ca would be also related with the deformation of the bubble shape. Three-dimensional interface tracking simulations have been carried out to obtain the shapes of Taylor bubbles, in particular the liquid film thickness, in square microchannels (Zhang et al. 2016; Ferrari et al. 2018; Magnini and Matar 2020; Magnini et al. 2022). However, the relation between ΔP_B^* and the bubble shape at a finite Ca has not been discussed yet.

Some numerical studies discussed the velocities of bubbles in square microchannels. Ferrari et al. (2018) showed that the bubble velocities increase with increasing Ca and are larger than those in a circular microchannel. Magnini and Matar (2020) pointed out that the bubble velocities with negligible inertial effects agree well with those of the propagation velocities of air fingers in a square channel (De Lózar et al. 2008). They also investigated inertial effects on the bubble velocities in a square channel. The bubble velocity of small Ca increased with increasing Re at high Re, whereas it was constant at low Re. At a large Ca, the bubble velocity decreased and then increased with increasing Re. No correlations of the bubble velocity have been developed in spite of its importance in modeling Taylor flow.

Numerical simulations of Taylor flows in square microchannels were therefore carried out to investigate the relation between the bubble shape and ΔP_B^* and to discuss the bubble velocity. An interface tracking method based on the volume of fluid method was used for the numerical simulations, which dealt with a single unit cell consisting of a bubble and a liquid slug (Langewisch and Buongiorno 2015; Kurimoto et al. 2018).

2 Numerical method and conditions

2.1 Interface tracking method

The continuity and momentum equations for two incompressible Newtonian fluids based on the one-fluid formulation are given by

$$\nabla \bullet {\varvec{V}}=0$$

(7)

$$\rho \left[\frac{\partial {\varvec{V}}}{\partial t}+{\varvec{V}}\bullet \nabla {\varvec{V}}\right]=-\nabla P+\nabla \bullet \mu \left[\nabla {\varvec{V}}+{\left(\nabla {\varvec{V}}\right)}^{T}\right]+\sigma \kappa {\varvec{n}}\delta$$

(8)

where V is the velocity, t the time, ρ the density, P the pressure, µ the viscosity, κ the mean curvature of the interface, n the unit normal to the interface, δ the delta function which is non-zero only at the interface, and the superscript T denotes the transpose. The density is given by

$$\rho =\left(1-C\right){\rho }_{G}+C{\rho }_{L}$$

(9)

where C is the cell-averaged volume fraction of the liquid phase, and the subscripts G and L denote the gas and liquid phases, respectively. Computational cells are filled with the liquid phase when C = 1, and with the gas phase when C = 0. A cell with 0 < C < 1 contains an interface. The viscosity is given by the harmonic mean (Tryggvason et al. 2011):

$$\frac{1}{\mu }=\frac{1-C}{{\mu }_{G}}+\frac{C}{{\mu }_{L}}$$

(10)

The height function technique (Francois et al. 2006) is adopted to evaluate κ. The advection and diffusion terms are discretized by using the CIP (cubic interpolated propagation) scheme (Takewaki and Yabe 1987) and the second-order centered-difference scheme, respectively. The surface tension force is accounted for in the discretized pressure gradient by adopting the ghost fluid method (Kang et al. 2000).

The following advection equation of C is solved to capture the interface motion by means of a combination of the NSS (non-uniform subcell scheme) (Hayashi and Tomiyama 2018) and the operator splitting method (Rider and Kothe 1998):

$$\frac{\partial C}{\partial t}+\nabla \bullet C{\varvec{V}}=C\nabla \bullet {\varvec{V}}$$

(11)

The divergence correction term C∇·V is introduced to conserve the fluid volume.

2.2 Computational domain and numerical condition

The computational domain is shown in Fig. 1, where x, y, and z are the Cartesian coordinates. The dimensions of the domain in the x, y, and z directions were 0.5D_h, 0.5D_h, and L, respectively. The boundaries at x = y = 0 were symmetric and those at x = y = 0.5D_h were no-slip walls. An instantaneous bubble velocity with the opposite sign (–u_B(t)) was imposed on the walls and the instantaneous acceleration of the bubble with the opposite sign was added to Eq. (8) to fix the bubble position (Wang et al. 2008). The boundaries at z = 0 and L were periodic and a constant pressure gradient was imposed between z = 0 and L for driving a flow. The initial bubble shape consisted of a cylindrical section and two hemispheres at the front and rear of the cylindrical section with the radius of 0.45D_h. The initial bubble length was set based on L and the void fraction α of the unit cell. Thus, dp/dz, L, and α were input values for simulations. The computational domain was initially divided into uniform cells with the size h, which were the coarsest cells, i.e., the base cells. Finer cells were embedded into the base cells in the vicinity of the interface by a quadtree manner. The size of the computational cells, h^l, at the lth refinement level was h/2^l, where l = 0 for the base cell. The finest refinement level l_max was three. l = l_max when the magnitude of the local level set function at a vertex of the coarsest cell was smaller than h. l = 2 for base cells neighboring to the cells of l = 3. The minimum and maximum cell sizes were h³ = 0.5D_h/128 and h⁰ = 0.5D_h/16, respectively.

Fig. 1

Computational domain and initial bubble shape

The numerical simulation in two cases (D_h = 298 µm, ν_L/ν_W = 1.0, α = 0.395, dp/dz = 0.360 MPa/m; D_h = 298 µm, ν_L/ν_W = 5.6, α = 0.404, dp/dz = 0.753 MPa/m, where ν_L and ν_W are the kinematic viscosities of liquid and water, respectively) were carried out with 1.5 times finer meshes to check the mesh size dependence. The changes in the bubble velocities due to the increase in the spatial resolution were less than 1.4%.

Water and glycerol-water solutions of five different concentrations (12, 21, 30, 41, and 52 wt%) were used as the liquid phase. Their liquid properties are shown in Table 1 (Ishikawa 1968). The gas density and gas viscosity were 1.19 kg/m³ and 1.8 × 10^–2 mPa·s, respectively.

Table 1 Liquid properties

3 Results and discussion

3.1 Pressure drop in bubble part

Figure 2 shows a comparison of ΔP_B^* between the experimental data (Kurimoto et al. 2020) and the numerical predictions. The numerical data agree well with the experimental data. The present numerical method can therefore reproduce well the characteristics of bubbles in Taylor flow through the square microchannels. At low Ca, the bubble interface forms very thin liquid films near the center planes of the channel, i.e., x–z plane at y = 0 mm or y–z plane at x = 0 mm, the thicknesses of which are less than the minimum cell size for Ca ≤ 0.00289. However, large liquid films, in which cells are adequately assigned, are formed at the corner of the channel in all cases. This result would indicate that adequate spatial resolution for the films at the corner is important to reproduce the flow characteristics of Taylor bubbles in a square microchannel. At Ca ≈ 0.02, We = 10.9 at ν_L/ν_W = 1.0 in D_h = 298 µm and We = 0.318 at ν_L/ν_W = 5.6 in D_h = 298 µm. The increase in ΔP_B^* is therefore due to the inertial effect. The numerical results are also tabulated in Table A1 in Appendix. It should be noted that the two data points for u_B > 2 m/s at ν_L/ν_W = 1.0 in D_h = 298 µm are not used in Fig. 2 since the rear of the bubble was oscillating in time due to a large inertial effect, which made it difficult to clearly define the length of the bubble part. The solid and broken lines are drawn using the following correlation:

Fig. 2

Comparison of ΔP_B^* between experimental and numerical data

$${\Delta P}_{B}^{*}={c}_{1}{Ca}^{{c}_{2}}$$

(12)

The coefficients, c₁ and c₂, are 7.106 and 2/3, respectively, in the analytical solution for the limiting case of Ca → 0 (Wong et al. 1995b), and 3.17 × 10⁴ and 1.15 in an empirical correlation for an N₂-water system in a 490 µm channel (Choi et al. 2010). The experimental and numerical data of ν_L/ν_W = 1.0 are close to the correlation of Choi et al. The increase in ν_L/ν_W decreases ΔP_B^*, and the data deviate from their correlation and lie within the range between the two correlations. The comparison suggests that the inertial effect should be introduced to improve Eq. (12).

Figure 3a shows the bubble shape and the profile of the pressure P^* normalized by the maximum pressure on the z-axis at Ca = 2.09 × 10^–2 and We = 0.318, where z^* = z/L. The front shape of the bubble is slightly slender than the rear shape and the flat interface region parallel to the channel walls is formed in the middle of the bubble. The red solid line and the black dashed lines in the P^*-z^* graph represent the predicted pressure profile and the Darcy-Weisbach equation based on j_T, respectively. The pressure in the liquid phase decreases with increasing z^* and agrees well with the Darcy-Weisbach equation, while it in the bubble is almost constant. The pressure jump at the interface is caused by the surface tension and its magnitude corresponds to σκ.

Fig. 3

Bubble shapes and normalized pressure profiles on z-axis

The bubble shape and P^* at Ca = 2.01 × 10^–2 and We = 10.9 are shown in Fig. 3b. Compared with the bubble shape in Fig. 3a, the front shape of the bubble is more slender and the liquid film is thicker due to the increase in We. The pressure in the liquid phase deviates from the Darcy-Weisbach equation as reported in literature (He and Kasagi 2008). The pressure drop ΔP_B^J between P^* at the tail and the nose of the bubble is larger than that in Fig. 3a. The bubble shape and P^* at Ca = 6.56 × 10^–2 and We = 3.15 are shown in Fig. 3c. By comparing with the result in Fig. 3a, it can be understood that the increase in Ca makes the liquid film thicker and ΔP_B^J larger.

It has thus been confirmed that bubble shape changes with the variation of Ca and We, which also affect ΔP_B^J. The dependence of the curvatures at the nose and tail of a bubble on Ca and We is discussed below.

Figure 4 shows the relation between the curvatures of a bubble and Ca. Figures 4a–c show the curvatures, K_n and K_t, at the nose and tail of a bubble normalized by D_h and the difference between them, respectively. The black and red symbols represent the curvatures in the center and diagonal planes for the cross section of the channel, i.e., x–z plane at y = 0 mm and the plane tilted with the angle of 45° with respect to the x-coordinate, respectively, as shown in Fig. 4b. The curvatures were evaluated by the height function method based on the volume fraction (Cummins et al. 2005). The difference in the curvatures between the planes is negligibly small. The broken line in the figure is the theoretical value for Ca → 0 (Wong et al. 1995a), in this limiting case a bubble has the fore-aft symmetry so that K_n = K_t. The nose curvature is close to the theoretical value for Ca < 2.9 × 10^–3 and becomes larger with increasing Ca. The curvature at ν_L/ν_W = 1.0 becomes slightly larger than that at ν_L/ν_W = 5.6 for Ca > 1.4 × 10^–2, i.e., the increase in We makes the nose curvature slightly larger. The tail curvature is also close to the theoretical value for Ca < 2.9 × 10^–3, while it decreases with increasing Ca. The curvature at ν_L/ν_W = 1.0 becomes lower than that at ν_L/ν_W = 5.6 for Ca > 8.3 × 10^–3, i.e., the increase in We makes K_tD_h smaller. The difference in K_t between ν_L/ν_W = 1.0 and 5.6 is more remarkable than K_n, i.e., the deformation of the tail shape is strongly affected by the inertial effects. The tendencies of (K_n – K_t)D_h on Ca and We correspond to those of ΔP_B^* shown in Fig. 2. Therefore, the deviation of ΔP_B^* from that in the small Ca limit mainly relates with K_t.

Fig. 4

Curvatures at nose and tail of bubble

3.2 Bubble velocity

The relation between u_B and j_T is shown in Fig. 5. The bubble velocity increases with increasing j_T and is higher than those of the homogeneous model, i.e., u_B = j_T. The bubble velocity in a channel has often been correlated by the following drift-flux model (Zuber and Findlay 1965; Kawahara et al. 2009; Howard and Walsh 2013; Minagawa et al. 2013; Kurimoto et al. 2017):

$${u}_{B}={c}_{0}{j}_{T}+{v}_{Gj}$$

(13)

where c₀ is the distribution parameter, and v_Gj the drift velocity, which is known to be small in horizontal microchannels. The solid line in the figure means Eq. (13) with c₀ = 1.37 and v_Gj = 0, where c₀ was determined by the least-squared method. Although the drift-flux model with constant c₀ represents the overall trend of the data, the data are scattered implying that c₀ is not constant and depends on j_T, D_h, and ν_L/ν_W.

Fig. 5

Relation between u_B and j_T

The relation between c₀ and Ca_T is shown in Fig. 6, where Ca_T is the capillary number based on j_T:

Fig. 6

Relation between c₀ and Ca_T

$${Ca}_{T}=\frac{{\mu }_{L}{j}_{T}}{\sigma }$$

(14)

Numerical predictions without and with inertial effects (Magnini and Matar 2020) are also plotted, where the ranges of Re_T are Re_T ≤ 10 and 1 ≤ Re_T ≤ 2000, respectively. The distribution parameter obtained in the present numerical simulation increases with increasing Ca_T. The distribution parameters at ν_L/ν_W = 3.4 and 5.6 agree well with the data without inertial effects by Magnini and Matar and they can be expressed by the following fitting equation:

$${c}_{0}=2.34{Ca}_{T}^{2/3}+1.05$$

(15)

The power of 2/3 has been found to appear in an analytical solution of the liquid film thickness and the pressure drop for the limiting case of Ca → 0 (Bretherton 1961; Wong et al. 1995b). Even though the largest value of Ca_T is about 0.1, the power of 2/3 works well for correlating c₀. The distribution parameter at ν_L/ν_W = 1.0 shows a steep increase for Ca_T > 0.012 and deviates from Eq. (15) with increasing Ca_T. The data for 1.3 ≤ ν_L/ν_W ≤ 2.2 lie between those at ν_L/ν_W = 1.0 and Eq. (15). Most of the numerical data with inertial effects by Magnini and Matar also show c₀ larger than Eq. (15).

The numerical data are plotted on the Re_T-Ca_T and We_T-Ca_T planes in Figs. 7a, b, respectively, to make clear the region in which the inertial effect is present, where the open symbols are for c₀ agreeing with Eq. (15) within 1.5% deviation and the closed symbols are for the other c₀ data. The Weber number, We_T, is defined by

Fig. 7

Classification of c₀ data

$${We}_{T}=\frac{{\rho }_{L}{j}_{T}^{2}{D}_{h}}{\sigma }$$

(16)

The Reynolds number Re_T at the boundary of the classification decreases with increasing Ca_T. On the other hand, the boundary of the classification is roughly We_T ≈ 10, although it tends to increase with increasing Ca_T.

Han and Shikazono (2009) proposed a correlation of liquid film thickness, the functional form of which was derived from a scaling analysis. Kurimoto et al. (2020) reported that the functional form can be used to calculate ΔP_B^*. Let us utilize the functional form for correlating c₀, that is,

$${c}_{0}=\frac{a{Ca}_{T}^{2/3}}{b+c{Ca}_{T}^{2/3}-d{We}_{T}^{e}}+f$$

(17)

where a, b, c, d, e, and f are positive constants. This equation can be regarded as an extension of Eq. (15) by implementing the inertial effect in the denominator of the first term on the right-hand side. Employing a = 2.34 and f = 1.05 as in Eq. (15) yields

$${c}_{0}=\frac{2.34{Ca}_{T}^{2/3}}{F}+1.05$$

(18)

where $F=b+c{Ca}_{T}^{2/3}-d{We}_{T}^{e}$ and solving the above equation for F gives

$$F=\frac{2.34{Ca}_{T}^{2/3}}{{c}_{0}-1.05}$$

(19)

The values of F calculated using the data of Ca_T and c₀ are plotted against We_T in Fig. 8, which shows that F tends to decrease with increasing We_T and decreasing Ca_T. Therefore, the form of F, Eq. (19), is reasonable. The constants were obtained as b = 0.85, c = 1.24, d = 0.0115, and e = 1.07. Thus,

Fig. 8

Relation between F and We_T

$${c}_{0}=\frac{2.73{Ca}_{T}^{2/3}}{1+1.46{Ca}_{T}^{2/3}-0.0135{We}_{T}^{1.07}}+1.05$$

(20)

Equation (20) is compared with the present data and the data with inertial effects by Magnini and Matar (2020) in Fig. 9. The correlation agrees well with 92% of the data with errors smaller than ± 5%, whereas it remarkably overestimates two data with inertial effects in the ranges of Ca_T ≥ 0.05 and We_T ≈ 50. It should however be noted that We_T = 50 corresponds to a very large j_T, e.g., j_T ~ 6 m/s for air–water Taylor flow in a 100 µm microchannel, and this is much larger than a typical volumetric flux used in microdevices.

Fig. 9

Comparison of c₀ between predicted data and Eq. (20)

The bubble velocity u_B calculated from Eqs. (13) and (20) is compared with the present data in Fig. 10.The correlations agree well with 98% of the data to within ± 3% errors in the ranges of 0.00159 ≤ Ca_T ≤ 0.0989 and 0.0817 ≤ We_T ≤ 25.4.

Fig. 10

Comparison of u_B between predicted data and correlations

4 Conclusion

Interface tracking simulations of single slug units in Taylor flow through a square microchannel was carried out to understand the relation between the pressure drop in the bubble part and the nose and tail shapes of a bubble. A correlation of the bubble velocity was also developed. The following conclusions were obtained:

• (1) The pressure drops in the bubble part of Taylor flows through square microchannels can be well predicted by using the interface tracking method.

• (2) With increasing in the capillary number Ca, the nose curvature increases while the tail curvature decreases, so that the pressure drop in the bubble part increases.

• (3) The decrease in the tail curvature due to the increase in the Weber number, in other words the inertial effect, is more remarkable than the increase in the nose curvature for Ca > 8.3 × 10^–3, which causes the deviation of the pressure drop in the bubble part from that in the small Ca limit.

• (4) The distribution parameter c₀ is increased by the inertial effects, and the criterion for whether the inertial effect is negligible or not can be roughly expressed by the Weber number.

• (5) The developed c₀ correlation gives good predictions of the bubble velocity in the following applicable ranges: 0.00159 ≤ Ca_T ≤ 0.0989 and 0.0817 ≤ We_T ≤ 25.4.

Appendices

Appendix A Numerical data

Table A1 shows the numerical data obtained in this study. The void fraction, the pressure gradient and the unit length at ν_L/ν_W = 1.0 and 5.6 are the same as in the experiment by Kurimoto et al. (2020)

Table A1 Numerical data

Appendix B. Comparison between measured ΔP _B ^* and predicted ΔP _B ^J

Figure B1 shows a comparison between measured ΔP_B^* and predicted ΔP_B^J. The predicted ΔP_B^J becomes higher than the measured ΔP_B^* as Ca increases. The ΔP_B^* is calculated from Eq. (2) assuming that the Darcy-Weisbach equation is valid everywhere in the liquid slug. The difference between P^* in the liquid phase and the Darcy-Weisbach equation, however, becomes larger with increasing Ca as shown in Fig. 3. Therefore, the assumption becomes inappropriate with increasing Ca and it should be noted that ΔP_B obtained with Eq. (2) include some pressure drop in the liquid part

Fig. B1

Comparison between measured ΔP_B^* and predicted ΔP_B^J

Appendix C. Relation between c ₀ and K _n D _h

The relation between c₀ and K_nD_h is shown in Fig. C1. The c₀ increases with increasing K_nD_h and lies onto a single curve though a slight variation due to the liquid properties and the hydraulic diameter is present.

Fig. C1

Relation between c₀ and K_nD_h

Appendix D. Bubble radii R _c and R _d at midpoint of bubble length

The liquid film thickness of a Taylor bubble is generally defined at a constant film thickness region. Some of Taylor bubbles in the present study do not have such a region since they do not have enough lengths, e.g., the bubble shown in Fig. 2(b). In this Appendix, the liquid film thickness at the midpoint L_B/2 of the bubble length L_B is considered. Figure D1 shows the dimensionless bubble radii, R_c and R_d, in the center and diagonal planes, respectively. The R_c and R_d are defined by

$${R}_{c}=1-\frac{2{\delta }_{c}}{{D}_{h}}$$

(D1)

$${R}_{d}=\sqrt{2}-\frac{2{\delta }_{d}}{{D}_{h}}$$

(D2)

where δ_c and δ_d are the liquid film thicknesses at L_B/2 in the center and diagonal planes, respectively. The R_c data for Ca ≤ 0.00289 are not included in the figure due to very thin film thicknesses. The R_c and R_d at low We are close to the numerical data without inertial effects by Magnini and Matar (2020) and the inertial effects make R_c and R_d small drastically, i.e., the liquid film becomes thicker.

Fig. D1

R_c and R_d at L_B/2