1 Introduction

Magnetic beads have contributed greatly to the development of fast and reliable diagnostics. In the scenario where magnetic beads are functionalized with specific reagents, they enable target detection by capturing the analyte in the fluid sample (Wu and Voldman 2020). In addition, magnetic beads can be controlled with an external array of electromagnets in such a manner that they can also transport analytes within various chambers inside a microfluidic chip for further analyte processing (Khizar et al. 2020). In this way, they offer a double functionality. Magnetic beads have also been used for microfluidic mixing, which has been proven to enhance binding reactions for more reliable and faster diagnostics (Reenen et al. 2014). However, mixing in microfluidic devices still remains challenging.

This is due to the small chip dimensions and consequently low Reynolds numbers. Mixing in such dimensions is solely caused by diffusion which is slow at typical microfluidic chip dimensions, while many applications require fast analysis and well-mixed conditions (Lin et al. 2020). These applications would exclude microfluidic technologies if not for passive and active methods to enhance mixing. The former methods involve the incorporation of geometrical structures that cause local fluid perturbations in the microfluidic channels while the latter provoke disturbances within the fluid via the application of an external force (Shanko et al. 2019).

Passive mixing structures are relatively easy to implement inside a channel during the fabrication process. These structures can be zig zag channel configurations (Razavi Bazaz et al., 2020), staggered herringbone designs (Stroock and McGraw 2004), obstacles in the fluid path (Agarwal et al., 2020) or even double layer microfluidics (Zhao et al. 2020). However, these structures are not tunable after incorporation, they generally require long channel lengths, and they only work in the case of generated fluid flow, such as in common microchannels in which flow is generated by external means, e.g., by a micropump.

Active approaches require the introduction of an external force to induce mixing. Forces can be ultrasonic, acoustic, pressure or magnetic stimuli that either perturb the fluid directly (e.g., acoustic) or indirectly (e.g., magnetic). These approaches have been studied to achieve fast mixing and are adaptable, making them great candidates for applications where fast mixing is an essential requirement (Bayareh et al. 2020), especially in the absence of generated fluid flow such as in stagnant microreaction chambers in which, during a biochemical assay, no flow is induced by external means. As a downside, they are considered complicated and expensive in terms of fabrication needs.

Magnetic bead mixing offsets for the high chip fabrication costs, as usually an external (electro)magnet is used for actuation, and the magnetic beads are low cost and can be relatively easily added. Mixing efficiency depends on the complex dynamics of structures formed by the magnetic beads that may cause chaotic fluid behavior within the microfluidic chip. Dynamic complex structures, such as magnetic bead chains and/or magnetic bead clusters have been proven to enhance mixing (Gao et al. 2012).

Recently, we have shown that applying an out-of-plane rotating magnetic field can induce global swarming of magnetic microbeads in a circular microfluidic chamber, leading to chaotic fluid flow and effective mixing (Shanko et al. 2021).We found that under certain conditions, increased fluid kinetics due to the motion of the magnetic beads contribute to faster and more efficient immunoassay sensing. However, an out-of-plane configuration will hinder optical visualization. An in-plane magnetic field would improve (visual) detection of any process occurring in the chamber, which is a requirement for point-of-care devices. Therefore, in this study we use an in-plane rotating magnetic field and quantify the induced mixing efficiency.

To potentially enhance the mixing in a circular microreaction chamber we add static and magnetically embossed mushroom-shaped structures which we integrate in a circular array outside and surrounding the chamber (van Pelt et al. 2017). These mushrooms generate time-dependent localized gradients which result in controlled magnetic bead transportation inside the chamber, and we assess their additional mixing potential. Finally, we carry out numerical simulations to examine how to combine the best of two worlds of passive and active mixing, by combining magnetic bead actuation, magnetic mushrooms, and passive geometrical mixing structures on the chamber wall.

2 Materials and methods

2.1 Design and fabrication of microfluidic devices

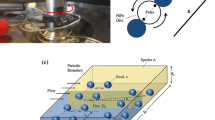
We performed mixing experiments in circular microfluidic chambers with a diameter of 3 mm and a height of 500 µm, as schematically shown in Fig. 1a. In one variant of the device, mushroom-shaped magnetic structures surround the circular chamber. Figure 1b is a schematic of the mushroom configuration, which also indicates the local magnetic field created by the presence of the mushrooms when exposed to an external magnetic field. To determine the most dominating mushroom design parameters that generate the strongest local magnetic field gradients, we initially performed COMSOL simulations building on our earlier work (van Pelt et al. 2017). The number of mushrooms in the array and the wall thickness (Wth) between a mushroom and the chamber play the most significant role in gradient generation. The stem length (Lst) follows as the second most important parameter while the mushroom width (Wst) and the head diameter (Mh) have limited to no influence on magnetic field. Accommodating for physical limitations on the available space in the electromagnetic setup and the fabrication limitations, the following choices were made. A circular array of 10 mushrooms is placed 300 µm away from the chamber edge (defining the wall thickness Wth). Each mushroom stem is 3.3 mm long (stem length Lst), and 400 µm wide (stem width Wst), and has a head diameter of 630 µm (Mh).

Fig. 1
figure 1

Schematic of the exploded view of (a) the simple no-mushroom chip (left) and the mushroom chip (right), along with fabrication materials and PMMA sheet thicknesses (th). The circular chamber diameter is 3 mm. (b) Schematic representation of the magnetic mushroom configuration. Mh corresponds to the mushroom head diameter which is chosen as 630 µm, Wth corresponds to the wall thickness between the chamber with the magnetic beads and the mushroom which is 300 µm in this work, Lst corresponds to the stem length equal to 3.3 mm, Wst is the width of the mushroom stem at 400 µm and Nd corresponds to distance of one mushroom to its neighbour and here it equals 250 µm. The dotted lines represent the local magnetic flux lines due to the external magnetic field. Magnetic beads and mushrooms are not to scale (color figure online)

Full size image

In this paper, we employ out-of-cleanroom facilities utilizing laser cutting techniques and molding. More specifically, a 250 µm thick Poly(methyl methacrylate) (PMMA) sheet with a chamber diameter of 3 mm and additional mushroom-like structures around the circumference are cut using a CO2 laser (Laser 2000, BOFA international, Germany) followed by filling the empty mushroom structures with a paste consisting of carbonyl iron powder (CIP, 99.5%, Sigma Aldrich) mixed in a photo-active glue (Norland optical adhesive 81, USA) which is solidified under UV (UVL-56 Handheld, Upland, USA) overnight for the curing of the mixture. Hence, the mushrooms have a uniform thickness of 250 µm. Last, a 250 µm thick PMMA sheet with a cut chamber is added on top; the resulting chamber height is 500 µm, of which the bottom half has the mushrooms around the circumference. In parallel, another 500 µm thick PMMA sheet is also cut with a circle of diameter 3 mm which is taped to the 3 mm thick bottom plain holder, forming the simple non-mushroom chamber. After the solutions are injected in the microfluidic chamber (see below), the fluid cell is covered with a glass slide of diameter 8 mm and thickness 170 µm. The last step assures a closed system.

2.2 Magnetic actuation

For the external manipulation of the magnetic beads, a custom octopolar electromagnetic setup has been constructed (Gao et al. 2013). The setup consists of two sets of four electromagnets in two orthogonal planes; the electromagnets are configured at a 90˚ angle difference to their neighbor. These planes correspond to a horizontal or in-plane and vertical or out-of-plane orientation (Fig. 2a). To facilitate magnetic mixing with a more straightforward and easy access design setup, in this work, we demonstrate the use of only in-plane electromagnets (P5-8 in Fig. 2a).

Fig. 2
figure 2

The setup and the chips featuring mushrooms. (a) A schematic of the octopolar electromagnetic setup; only the poles in the horizontal in-plane configuration (yellow, P5–P8) are activated in this work. (b) The fabricated microfluidic chamber placed in the octopole with additional mushrooms in a circular array around the circumference (color figure online)

Full size image

The setup is next placed under a microscope (Leica DM4000M, Germany) featuring an sCMOS camera (DFC9000 GT, Leica, Germany). The fabricated chips are positioned at the center of the octopolar setup (Fig. 2b). In the experiments, an in-plane rotational magnetic field of 30 Hz and 35 mT is applied for 2 min using the horizontal set of electromagnets.

2.3 Visualization of magnetic bead dynamics

The induced magnetic bead dynamics, generated fluid velocities and mixing performances, are studied in both the simple circular chamber as well as the mushroom chamber for comparison. For the visualization of the dynamics of magnetic beads, a solution of magnetic beads (Ø = 10 µm, Micromer-M COOH, Micromod, Germany) diluted in DI water (concentration of 6000 beads/µL) is manually injected into the chamber which is subsequently covered by the glass slide. We next employ bright field microscopy and apply the in-plane rotating magnetic field at 35 mT, 30 Hz for 2 min.

2.4 Visualization of fluid velocities

The visualization of the induced fluid velocities and fluid profiles due to the magnetic bead movement is achieved with Particle Imaging Velocimetry (PIV) (DaVis 8.4, LaVision, Germany). For this, a mixture of magnetic beads (concentration of 6000 beads/µL) and a high seed of passive fluorescent fluid tracers (Ø = 2 µm, green fluorescent polymer microspheres, Fluoro-Max, USA) is injected into the chamber. The PIV measurement lasts for approximately 5 s after the 2 min protocol. To better visualize the fluid motion across the whole height of the chamber, two focal planes are used, namely a focal plane of depth of field of 90 µm focusing near the bottom of the chamber (at chamber height 45 µm from the bottom) and the same plane shifted approximately 300 µm higher to visualize a higher plane of the chamber (at chamber height 345 µm from the bottom).

2.5 Mixing experiments

For the quantification of the mixing, a Mixing Index (MI) based on the method of intensity of segregation is used. This method is commonly used for mixing performance assessments and is also herein used as a measure of mixing. The MI is defined as (Gao et al. 2014):

$$\mathrm{MI}=\frac{1}{N}\frac{{\sum }_{N}{\left({I}_{k}-\frac{{\sum }_{N}{I}_{k}}{N}\right)}^{2}}{{(\frac{{\sum }_{N}{I}_{k}}{N})}^{2}}=\frac{var (I)}{{\overline{I} }^{2}},$$

In this equation, \({I}_{k}\) is the fluorescent intensity [0–255] at pixel k and \(\overline{I }\) is the intensity averaged over N pixels. This indicates that in a perfectly mixed scenario \(\mathrm{MI}=0,\) whilst in a fully unmixed system \(\mathrm{MI}=1\). To obtain comparable results to the different mixing at different actuation conditions, the mean of a series of three experimental sets with similar initial MI states are collected. The Relative Mixing Index (RMI) is a normalized version of the MI and is instead used as a mixing quantification method; the RMI defined as the MI divided by the MI of first attained image (initial state of experiment).

Experimentally, this method requires the use of two solutions with two colors (e.g., black and white). In microscopy fluorescent mode, the magnetic bead solution is not visible, while another solution seeded with fluorescent tracers is seen. This solution is 75% glycerol (99% purity, Sigma Life Sciences, USA) and 25% highly concentrated fluorescent tracers. For these experiments, a custom solution injection method is applied. Initially, the chamber is filled with the magnetic bead solution. The chamber is next covered with the glass slide. The glass slide is then shifted to reveal a minor part of the chamber where 500 nL of the viscous fluorescent solution is injected. The slide is next brought back to its initial position to fully cover the chamber. Last, after a 13 min waiting time the magnetic field is applied, and images are obtained every second. This waiting time ensures the elimination of disturbances caused due to the initial solution injection. All mixing experiments are triplicated, and their mean is plotted.

2.6 Numerical simulations

To optimize the design of the magnetic mushroom structures, we carried out simulations using COMSOL (reported in the SI). To validate our experimental results of velocity fields and mixing performance, we performed numerical simulations using StarCCM + (Buul 2020), (Matsunaga and Nishino 2014). In these simulations, the magnetic beads, their resulting motion and the hydrodynamic interactions at play are not explicitly simulated since this would lead to unfeasible computation times and capacity, because this would require to explicitly solve for the motion of thousands of magnetic particles interacting with the external field, with each other, and with the fluid. Hence, we simplified the problem to make the simulations feasible and we accounted for the effect of the magnetic particles’ motion on the fluid flow by introducing boundary conditions at the chamber side wall, and internally within the chamber to represent the effect of magnetic bead clusters in the central region. For both the mushroom and no-mushroom situations, the outside wall boundary conditions are a tangential velocity that decreases linearly from bottom to top of the chamber, with values obtained from our experimental outcome. This boundary condition accounts for the effect of magnetic particles transported along the sidewall. For both situations, different velocities are used, as also observed from the experiments (see the results section). The top and bottom walls are assigned no-slip conditions. Clusters of magnetic particles rotating in the central region of the chamber (which happens in the no-mushroom situation), are modeled as rotating disks. MatLab generates 20 random positions of Ø = 150 µm and 20 µm thick disks that are next used in a SiemensNX CAD-system to position the islands accordingly. The positions are random only in-plane, but at a chamber height of 50 µm, as observed from the experiments. Each disk face is assigned a unique name necessary for StarCCM + to assign a local rotation rate of 31.4 rad/s together with the axis of the position coordinates. The chosen rotation rate corresponds to the actual experimental rotational frequency—it is noted that while the experimentally applied magnetic frequency is 30 Hz, the measured magnetic bead cluster frequency is 6 × slower at 5 Hz. The information on the rotation and the fixed position of the clusters used as an input in this numerical analysis are values retrieved from the experiments. The time step used is 0.04 s, and the mesh size is 20 μm. Diffusion occurs through numerical diffusion, because the passive scalar is defined as convection only. The effective numerical diffusion constant is calculated to be 1.2 10–9 m2/s.

3 Theory of magnetic bead dynamics

Superparamagnetic microbeads of 10 µm diameter are manipulated within the chip using an external magnet. These beads consist of ferromagnetic nano-domains incorporated inside a polymer matrix. In the absence of a magnetic field, the nano-domains have random magnetic orientations, and the beads, therefore, have zero net magnetization and they do not interact magnetically (as depicted in Fig. 3a, i1). When such superparamagnetic beads are subject to a magnetic field \({\varvec{H}}\) with flux density \({\varvec{B}}={\mu }_{0}{\varvec{H}}\), the nanomagnetic dipoles align to the magnetic field lines and the magnetic particles obtain a net magnetic dipole moment \({{\varvec{m}}}_{{\varvec{p}}}=\frac{{V}_{p}{\chi }_{p}{\varvec{B}}}{{\mu }_{0}},\) where \({V}_{p}\) is the particle volume, \({\chi }_{p}\) is effective magnetic particle susceptibility, and \({\mu }_{0}\) is the magnetic permeability of free space (4π × 10–7 NA−2). Dipolar interactions between beads align them into structures such as chains or clusters (Fig. 3, i2).

Fig. 3
figure 3

Key elements for magnetic bead mixing in the presence of magnetic mushrooms. (i) The basic modes of magnetic bead motion in the absence and presence of a magnetic field and magnetic gradients and the relevant forces. Image adapted from (Shanko et al. 2021) (ii) Schematic of the working principle of mushrooms in a circular array around the chamber circumference of a microfluidic chip, and when applying an in-plane counterclockwise rotating external magnetic field. Only half of the chamber is shown here (color figure online)

Full size image

Due to the shape anisotropy of magnetic bead chains or clusters, their collective magnetic moment \({{\varvec{m}}}_{{\varvec{c}}}\) is higher in the direction of their long axis. Should the magnetic field become rotational, these structures start rotating as well, as the magnetic moments are continuously trying to align to the magnetic field lines due to a magnetic torque \({{\varvec{\tau}}}_{\mathbf{m}\mathbf{a}\mathbf{g}}={{\varvec{m}}}_{{\varvec{c}}}\times {\varvec{B}}\) which scales with the square of the flux density (magnitude \({{\varvec{B}}}^{2}\)). This is the mechanism behind chain and cluster rotation and this possibly results in local mixing (Fig. 3, i3).

Since the chain structures are in a liquid, their rotation is counteracted by a viscous drag torque \({{\varvec{\tau}}}_{{\varvec{d}}\mathbf{r}\mathbf{a}\mathbf{g}}\). The ratio of viscous drag to the acting magnetic torque is represented by the Mason number, defined for a two-particle chain as (Petousis et al. 2007):

$$ {\text{Ma}} = 12^{2} \eta \omega /\mu_{0} \chi H^{2} , $$
(1)

ω being the angular velocity of the applied magnetic field with magnitude \(H\), and \(\eta\) being the fluid viscosity. If Ma is small, magnetic effects are dominant and the chains or the clusters are stable. For large Ma, viscous drag is dominant, and chains and clusters break up more easily. In high-volume fractions, the clusters coagulate to form disk like structures (Nagaoka et al. 2005). In addition to responding to the magnetic torque resulting in rotation, magnetic beads are drawn towards higher magnetic fields resulting in translation (Fig. 3, i3) due to the magnetic force which depends on the gradient of the magnetic field as \({{\varvec{F}}}_{\mathbf{m}\mathbf{a}\mathbf{g}}=\left({{\varvec{m}}}_{{\varvec{p}}}\bullet \nabla \right)\mathbf{B}=\left({V}_{p}{\chi }_{p}/{\mu }_{0}\right)({\varvec{B}}\bullet \nabla ){\varvec{B}}\).

Therefore, the magnetic force always transports a particle in a gradient. In turn, this causes a counteracting hydrodynamic drag force \({{\varvec{F}}}_{\mathbf{d}\mathbf{r}\mathbf{a}\mathbf{g}}=6{\varvec{\pi}}{\varvec{\eta}}{\varvec{r}}{\varvec{U}}\) where \({\varvec{r}}\) is the particle radius and \({\varvec{U}}\) is the particle velocity relative to the fluid. The combination of all forces and torques leads to a combinational rotational and translational motion of the structures. Note that these considerations assume a spherical shape of the microbeads, which we use here since these are most commonly used and they are commercially available. Beads with an elongated shape, for example, have inherent shape anisotropy and will therefore experience stronger magnetic torques.

The situation in our experiments is shown in Fig. 3ii, schematically depicting half of our circular microfluidic chamber in top view. If an external in-plane rotating field is applied, the magnetic beads form chains and clusters which start rotating. Since the applied field has a small magnetic gradient directed radially outward, the beads experience a small gradient force that drives them to the chamber periphery in the end. When adding the static magnetic mushrooms around the circumference of the chamber, a local magnetic field is induced by these structures, since they locally modify the external applied field, as indicated in Fig. 1b. This local magnetic field contributes to a fast translational bead motion. There are at least two major effects: first, the mushrooms cause a general gradient, directed radially outward, that leads to attraction towards the outer chamber side wall; and second, the conveyor belt effect described by van Pelt et al. (2017) occurs: for particles close to the wall, the local time-dependent field results in forces and torques that lead to rotation, which effectively transports the particles along the wall. Detailed theory on the mushrooms has been provided elsewhere (van Pelt et al. 2017), but the mechanism is also depicted in the schematic of Fig. 3ii. Note that the beads move around the chamber circumference opposite to the rotation direction of the magnetic field, i.e., clockwise versus counterclockwise.

4 Results and discussion

4.1 Magnetic bead dynamics

The magnetic bead dynamics in both the simple and the mushroom chamber are shown in Fig. 4, as well as movies 2.1. and 2.2 in the supplementary information. Initially, the magnetic beads are homogeneously distributed over the chamber floor. In the presence of a magnetic field, the magnetic beads start forming various structures (as seen in Fig. 4 and Movies 2.1. and 2.2).

Fig. 4
figure 4

Magnetic bead dynamics in the absence of mushrooms (No mushrooms) and in the presence thereof (Mushrooms). A sequence of images at various times is obtained in a 2 min magnetic actuation protocol at 35 mT and 30 Hz. Scale bars are 250 µm (color figure online)

Full size image

4.1.1 Local magnetic bead dynamics

The Mason number (Eq. 1) will predict the local behavior of the bead clusters/chains within the fluid. The dimensionless magnetic susceptibility of our magnetic beads is measured to be 0.043 (see S.I. text 1). The Mason number is calculated at 0.72 for the no-mushroom case at 35 mT and at an angular velocity of 188.5 rad/s (30 Hz). On the other hand, the Mason number for the mushroom case is found at 1.19 at the center of the chamber, a value significantly higher. Viscous drag is therefore more prominent in the mushroom case, as the mushrooms generate higher magnetic field strengths (COMSOL simulations performed on our mushrooms resulted in a simulated generated magnetic field strength of 45 mT at the center of the chamber, see S.I. text 1). The higher Mason number (i.e., more prominent viscous drag) in the mushroom case results in more loose and less spherical structures than for the no-mushroom case, as expected.

4.1.2 Global magnetic bead dynamics

As shown in Fig. 4, the no-mushrooms case generates large, initially mostly non isotropic but later isotropic, rotating structures that are slowly moving towards the circumference of the chamber following the gradients induced by the applied magnetic field (t = 12 s). At some point in time, this leads to a collective motion of magnetic beads moving along the chamber circumference combined with rotating cluster structures in the center of the area (t = 25 s). Over time, the latter merge to form larger rotational structures moving outward. At approximately 2 min, an agglomerate of magnetic beads is rotating along the whole circumference (t = 120 s). On the other hand, the magnetic structures (chains/clusters) in the presence of the mushrooms are not only smaller but also are dispersed throughout the lateral plane, and the particles are attracted more quickly to the chamber circumference due to the additional gradient generated by the mushrooms. Quickly, therefore, a global collective rotational motion of magnetic beads is noticed to rotate along the whole chamber circumference.

4.1.3 Direction of the rotating structures

From Movies 2.1. and 2.2, it can be seen that magnetic bead chains and clusters are not only rotating as a whole but there are also beads rotating along the exterior of the whole cluster in both cases. The rotational motion of the clusters follows the direction of the applied magnetic field (counterclockwise), being caused by the magnetic torque \({{\varvec{\tau}}}_{\mathbf{m}\mathbf{a}\mathbf{g}}\). In addition, the cluster structures are moving towards the circumference of the chamber exhibiting a translational motion due to the gradient magnetic force \({{\varvec{F}}}_{\mathbf{m}\mathbf{a}\mathbf{g}}\). Upon hitting the outer wall, the structures break down and form a band of beads “pacing” along the periphery but this time in the opposite direction (clockwise). This phenomenon, though observed in both cases, occurs at different timescales.

The process of magnetic bead dynamics is accelerated in the presence of mushrooms and smaller clusters are being formed with weaker dipolar interactions. Nonetheless, the main differences are noticed within the first 2 min of magnetic field actuation. Exceeding the 2 min, all the magnetic bead structures have broken down on the side walls. After the initial 2 min protocol, a big cluster of beads rotating along the circumference in the no- mushrooms is noted.

4.2 Fluid dynamics

The fluid flow dynamics is observed in two separate focal planes within the chamber both with a depth of field of 90 µm. This separation aids to the better visualization of the volumetric motion of the fluid and subsequently the understanding of the effect of the presence of the mushrooms. The differences between the two states are shown in Fig. 5 that shows results from particle image velocimetry (PIV), as well as in S.I. Movies 3.1–3.4 for the no-mushroom case and in S.I. Movies 3.5 to 3.8 for the mushroom case.

Fig. 5
figure 5

PIV results of the fluid profile and velocities in the simple circular chamber (No-mushrooms) and in the mushroom chamber (Mushrooms). The results are obtained for two separate focal planes with a 90 µm field of view; one plane is focused near the floor of the chamber at chamber height = 45 µm (images on the left) and the other plane in the top part of the chamber height = 335 µm (images on the right). Scale bar is 250 µm (color figure online)

Full size image

4.2.1 Fluid profile

The rotating structures in the no-mushroom state generate, first, fluid perturbations mainly in the central area of the chamber and close to the floor and, second, a circulatory flow across the whole circumference. At the top plane, a rotating collective motion of an agglomeration of magnetic beads is shown to induce a flow almost along the whole chamber. On the other hand, the fluid profile generated by the magnetic bead motion due to the local gradients from the mushrooms induces a stable profile of global circulatory flow. This fluid profile of global circulatory flow is shared between the two planes with almost no difference noticed, in a qualitative sense.

4.2.2 Fluid velocities

Significant differences between the two cases are noted. In the absence of mushrooms, the global flow around the chamber circumference has a maximum fluid velocity of \({v}_{\mathrm{bottom}}=350\mathrm{ \mu m}/\mathrm{s}\) in the bottom plane and \(\boldsymbol{ }{v}_{\mathrm{top}}=175\mathrm{ \mu m}/\mathrm{s}\), in the top plane. The mushrooms induce significantly higher fluid velocities: \({v}_{\mathrm{bottom}}=800\mathrm{ \mu m}/\mathrm{s}\) in the bottom plane and \( {v}_{\mathrm{top}}=550\upmu m/s\) in the top plane with a velocity gradient across the lateral dimension in a band approximately 700 µm far from the wall, leaving the central area possibly unmixed.

To validate our experimental results, we performed numerical simulations of the 3D fluid flow in the two cases: the no-mushroom and the mushroom chambers, see Fig. 6. The clockwise global rotational circulatory flow in both situations was simulated by imposing a linear velocity profile on the outer chamber with a maximum at the bottom and a minimum at the top (no mushroom:\({v}_{\mathrm{bottom}}=350\mathrm{ \mu m}/\mathrm{s}\) and \( {v}_{\mathrm{top}}=175\mathrm{ \mu m}/\mathrm{s}\), mushroom: \({v}_{\mathrm{bottom}}=800\mathrm{ \mu m}/\mathrm{s}\) and \( {v}_{\mathrm{top}}=550\upmu m/s\) in accordance with the measured velocities (Fig. 6 inserts).

Fig. 6
figure 6

Simulated fluid profiles in two different states in a plane at 40 µm height in the chamber. (a) Fluid streamlines generated in the absence of mushrooms where magnetic bead clusters are rotating in place. Their angular velocity is 31.4 rad/s and their size is 150 µm diameter and 20 um thickness. 20 clusters are placed randomly in the chamber and a counterdirectional global flow along the circumference is simulated with a gradient velocity ranging from 350 µm/s at the bottom plane to 175 µm/s at the top. (b) Streamlines generated in the presence of mushrooms. The global flow is simulated with a gradient ranging from 800 µm/s at the bottom plane to 550 µm/s at the top plane (color figure online)

Full size image

The no-mushroom simulation showcases 20 randomly allocated clusters modeled by islands with a diameter 150 \({\varvec{\upmu}}\mathrm{m}\) and a height of 20 \({\varvec{\upmu}}\mathrm{m}.\) These dimensions correspond to fifteen magnetic beads forming an isotropic structure across and two magnetic beads over the height, rotating in a counterclockwise manner at an angular velocity of 31.4 rad/s (Fig. 6) and elevated 40 \(\mathrm{\mu m}\) from the floor of the simulated microfluidic chamber (Ø = 3 mm). The resulting fluid profiles are similar to those obtained with the PIV analysis (Fig. 5- left column).

4.3 Mixing

The mixing index is assessed in the two measurement planes to obtain insight into the volumetric mixing effect of the different experimental sets. The results are shown in Fig. 7 for the experiments and in Fig. 8 for the numerical simulations. Both actuation cases (mushrooms and no mushrooms) are compared to a state where no magnetic actuation is induced (i.e., mixing happens only through diffusion). S.I. Movies E4.1–E4.4 (experiments) and S.I. Movies N4. 1 and N4.2 (simulations) show how the mixing evolves over time. Clearly, both magnetic actuation cases improve mixing, but efficient mixing is best achieved in the no-mushroom case since a lower mixing index is achieved, in shorter time, for both experiments and simulations. The difference between the top and bottom focal planes is small. Note, that the experimentally determined relative Mixing Index does not go below approximately 0.5 within the time frame of the measurements. We believe that this is caused at least partly by the difficulty of analyzing the experiments, which is complicated by the presence of the magnetic microbeads in the images. Another effect that complicates the quantitative experimental assessment of mixing is the poor reproducibility of the initial situation, i.e. the initial spatial distribution of fluorescent tracers within the chamber may vary between measurements. Nevertheless, we can still compare the levels of the mixing with each other and draw conclusions about relative mixing efficiency. To determine the relative Mixing Index more reliably, we suggest the following future improvements: (1) apply a more advanced image analysis of the obtained images to remove the influence of the presence of magnetic microbeads on the result of the mixing analysis; (2) re-design the mixing chamber by adding channels as inlets and outlets, so that the working fluid and the fluorescent solution can be flown in and out of the chamber in a controlled fashion, rather than injecting them by hand; this will improve the reproducibility of the initial distribution of the fluorescent solution.

Fig. 7
figure 7

Experimental results of the mixing performance as a function of time in a 2 min rotational magnetic actuation protocol (35 mT and 30 Hz). The relative mixing index results are shown for both the focal planes (near the bottom floor and near the top of the chamber). It is evident that the rotating particle clusters present especially in the no-mushroom chamber, enhance the mixing performance of the system, whereas the presence of mushrooms decreases the mixing (color figure online)

Full size image
Fig. 8
figure 8

Simulated mixing performance as a function of time in a 2 min simulation. The Mixing Index is calculated based on the intensity of segregation method. The evolution of mixing over time is also visualized at different time points (t = 0 s, t = 10 s, t = 20 s, t = 50 s, t = 90 s and t = 120 s) (color figure online)

Full size image

The mixing performance in the no-mushroom case is most likely due to the introduction of local fluid perturbations by the local magnetic cluster rotation in the center of the chamber (leading to local mixing). Furthermore, the translational motion of the clusters towards the outer wall adds to the mixing potential with the resulting counter directional global circulatory magnetic bead motion contributing to mixing even more (global mixing).

The presence of the mushrooms seems to have a negative effect on the mixing. The original hypothesis in adding the mushrooms was that they would enhance the magnetic microbead dynamics through the influence of the local time-dependent magnetic fields induced by the mushrooms (illustrated in Fig. 1), and therefore may enhance mixing. But, although we found that the mushrooms do enhance the fluid velocity in the microchamber as shown in the previous section, they do not lead to enhanced mixing—i.e., a larger fluid velocity is not necessarily related to better mixing. The reason is that, due to the additional magnetic field gradients generated by the mushrooms, the magnetic beads translate much more quickly to the chamber wall so that the rotating particle clusters are quickly eliminated, as shown in Fig. 4. And precisely these rotating clusters induce fluid perturbations within the central area of the microchamber that cause the mixing in the no-mushroom situation.

The numerically obtained mixing index shown in Fig. 8 is qualitatively similar to the experimental results of Fig. 7, with the no-mushroom case generating better mixing in comparison to the mushrooms. The quantitative difference between the simulated and the experimentally obtained mixing index may be caused by two effects. First, the values for the mixing index as found for the experiments may be overestimated by the inherent difficulty to quantitatively analyze the obtained images, which is complicated by the presence of the magnetic microbeads as we have argued above—hence, the experimental relative mixing index does not go below approximately 0,5 within the time frame of the experiments. Second, it may be explained by consideration of the (artificial) numerical diffusion present occurs in the simulations. The numerical diffusion is determined with a 3D version of the 2D method of Bailey (Bailey 2017) as 1.2 10–9 m2/s for the used time-step and mesh-size. This is approximately 5000 larger than the diffusion calculated using the Stoke–Einstein equation (Han et al. 2011) for the passive fluorescent fluid tracers used in the mixing experiments. In principle, the numerical diffusion can be tuned by varying the time-step and mesh-size, however, attempts to do this led to numerical instabilities and convergence problems. Hence, the numerical and the experimental results presented here may not be compared in a quantitative sense but only qualitatively.

The simulation results confirm that the mushrooms, although inducing high fluid velocities, suffer from the absence of flow perturbations in the central area of the chamber thus leaving the system partially unmixed. In the absence of the mushrooms, on the other hand, the presence of the rotating micro islands perturbs the fluid in the central area in addition to the peripheral counter directional global fluid motion, which makes this approach an ideal candidate for mixing in microfluidic chambers under no-external-flow conditions.

4.4 Combining mushrooms and geometrical features

The mushrooms have proven to be efficient in inducing high velocity fields in the chamber in comparison to the simple no-mushroom chamber, but they do not necessarily generate high mixing efficiencies due to the homogeneous fluid profile. Adding geometrical features inside the chamber to introduce flow perturbations, i.e., adding passive mixing features, may help to enhance mixing by combining the best of two worlds: active and passive mixing. We have carried out preliminary numerical simulations to explore this potentially synergetic effect.

Four rectangular-shaped passive structures of length 440 µm, height 421 µm and width 80 µm are added on the “ceiling” of the microfluidic chamber at a distance of 80 µm from the side walls (Fig. 9a).

Fig. 9
figure 9

The synergetic effect of the active mixing induced by magnetic beads in the presence of mushrooms combined with the passive mixing by added obstacles in the fluid path. (a) Fluid streamlines generated in the case of the mushrooms with additional passive rectangular structures at a distance of 80 µm from the wall and the indicated dimensions. These structures are added to perturb the flow and possibly mix the central area of the chamber for higher mixing efficiency. (b) Simulated mixing performance of the system during a 2 min simulation. The mixing evolution over time is also visualized at different time points (t = 0 s, t = 10 s, t = 20 s, t = 50 s, t = 90 s and t = 120 s). The mushroom only case is added here from Fig. 8, for comparison (color figure online)

Full size image

As can be seen in Fig. 8a, these simple structures perturb the global fluid flow around the circumference of the microchamber and the streamlines depict the additional flow structures towards the central area of the chamber. However, it is noticed that the center is not mixed. The added geometry does play a role in achieving better mixing efficiencies (Fig. 9b and S.I. Movie N5.1). These simple structures will do the trick and improve the mixing performance by 18% (Simulated MIgeometry = 0.25 and MImushrooms = 0.43 accordingly after 2 min simulation time).

We anticipate that optimized passive geometries can significantly increase the mixing efficiency of the system further, while also taking advantage of the high fluid velocities induced by the movement of magnetic beads in the presence of mushrooms in a microfluidic chamber with a stagnant fluid. This optimization of structures can be done by applying an iterative optimization procedure using the numerical model.

5 Conclusion

In this paper, we applied an in-plane rotating magnetic field to a simple cylindrical microchamber and we studied the induced dynamics of magnetic beads present in the chamber, as well as the generated fluid flow and the mixing performance of the system. Building on previous work (van Pelt et al. 2017), we next explored the effect on these phenomena of the addition of a circular array of soft magnetic mushroom-like microstructures integrated in the device around the chamber. The induced fluid profiles and mixing efficiencies were assessed both experimentally and numerically.

In the simple chamber, the rotating field was found to cause the combination of, first, a global rotating flow counter to the external field rotation induced by magnetic particles moving along the chamber side wall, with second, local flow perturbations induced by rotating magnetic bead clusters in the central area of the chamber, rotating in the same direction as the external field. This combination led to efficient mixing performance. Adding the mushrooms resulted in local gradients that were found to accelerate the magnetic bead and fluid motion compared to the simple chamber. However, the mixing performance was found poorer than for the simple chamber, since the magnetic beads rotated only along the periphery of the chamber leaving the central area of the chamber unmixed. These findings were confirmed by our numerical study.

To enhance the mixing induced by the mushrooms while still take advantage of the induced high fluid velocities we added passive mixing structures on the chamber floor (as simple obstacles in the fluid path) in a numerical study. The structures were found to create supplementary vortices that caused fluid perturbations throughout the chamber, resulting in significantly better mixing. We anticipate that optimization of the passive mixing geometries will further increase the mixing efficiency of the system.

Taken together, an in-plane rotating magnetic field can generate high magnetic bead mixing efficiencies in a cylindrical microchamber with an initially stagnant fluid. This micromixing method is, therefore, a good candidate for application in diagnostic microfluidic devices in which the biochemical assay, involving for example target capture and other (bio)chemical reactions, happens in a microfluidic chamber under no-flow conditions. Especially when the assay involves magnetic beads, our method can be naturally applied to induce mixing and enhance the assay, which is particularly critical for point-of-care testing. The addition of both static magnetic mushrooms and passive mixing geometries can lead to both high fluid velocities and enhanced mixing.