An integrated microfluidic chip for generation and transfer of reactive species using gas plasma

Abstract

Reactive species produced by atmospheric-pressure plasma (APP) are useful in many applications including disinfection, pretreatment, catalysis, detection and chemical synthesis. Most highly reactive species produced by plasma, such as ^·OH, ¹O₂ and ${\text{O}}_{2}^{ \cdot - }$, are short-lived; therefore, in situ generation is essential to transfer plasma products to the liquid phase efficiently. A novel microfluidic device that generates a dielectric barrier discharge (DBD) plasma at the gas–liquid interface and disperses the reactive species generated using microbubbles of ca. 200 µm in diameter has been developed and tested. As the bubble size affects the mass transfer performance of the device, the effect of operating parameters and plasma discharge on generated bubbles size has been studied. The mass transfer performance of the device was evaluated by transferring the reactive species generated to an aqueous solution containing dye and measuring percentage degradation of the dye. Monodisperse microbubbles (polydispersity index between 2 and 7%) were generated under all examined conditions, but for gas flow rate exceeding a critical value, a secondary break-up event occurred after bubble formation leading to multiple monodisperse bubble populations. The generated microbubble size increased by up to ~ 8% when the device was operated with the gas plasma in the dispersed phase compared to the case without the plasma due to thermal expansion of the feed gas. At the optimal operating conditions, initial dye concentration was reduced by ~ 60% in a single pass with a residence time of 5–10 s. This microfluidic chip has the potential to play a significant role in lab-on-a-chip devices where highly reactive species are essential for the process.

Introduction

The generation and applications of gas plasmas in microfluidic devices have received increased attention recently. Plasmas have a great potential to play a key role in many microfluidic applications such as disinfection (Maw et al. 2015), catalysis (Belder et al. 2006), detection (Hoshino et al. 2011; Kelly et al. 2005) and chemical synthesis (Mitchell et al. 2001; Kikutani et al. 2002). Among the different types of plasma, atmospheric-pressure plasma (APP) is one of the most versatile types of plasma that can be used in microfluidics due to the ease of implementation and integration into a microfluidic chip. In addition, it eliminates the need of a vacuum system that is required to maintain a low-pressure plasma discharge, which could significantly increase the cost and complexity of the microfluidic system. Furthermore, applications of APPs are increasing rapidly due to its ability to generate various reactive species that are useful in industrial treatment processes and in organic chemistry (Gorbanev et al. 2017; Benedikt et al. 2018; Xu et al. 2019). The reactive species generated from a plasma depends on the feed gas supplied between the electrodes and the subsequent reactions between the direct plasma products. For instance, an air feed produces reactive oxygen species (ROS) such as ozone, hydroxyl radicals, superoxide and singlet oxygen and reactive nitrogen species (RNS) such as peroxynitrites, nitric oxide and nitrogen dioxide (Eliasson et al. 1987; Sakiyama et al. 2012). These highly reactive species are beneficial for many lab-on-a-chip processes, but the transfer of these species to a liquid target in microfluidic devices has rarely been reported.

Dielectric barrier discharge (DBD) is one of the least complex APP architectures that can be integrated into a microfluidic device. Miclea et al. (2001) fabricated a plasma microchip using two glass plates coated with thin aluminium electrodes to form a DBD to dissociate halogenated hydrocarbons. The resulting metastable halogen atoms were fed into diode laser atomic absorption spectrometry for detection (Miclea et al. 2001). Lozano-Parada and Zimmerman demonstrated that despite frequent recombination of plasma species at microchannel walls, ozone production at microscale can be highly efficient due to low power consumption and fast reaction time for ozone generation compared to ambipolar diffusion (Lozano-Parada and Zimmerman 2010). Kim et al. reported a commercial ozone generation system that uses a large number of microchips operated in parallel to scale-up ozone production efficiently (Kim et al. 2013, 2017). This parallel microfluidic system was found to be reliable, efficient and low in weight and volume over conventional ozone generators. Recently, Masters et al. used CNC milling to simplify the manufacturing process of a plasma microchip with integrated electrodes and to improve the scale-up of production (Masters et al. 2015). Furthermore, ROS generated by an array of microchannel plasma jets have been used to treat simulated drinking water biofilms (Sun et al. 2018) and microcapillary DBDs have been adopted to synthesise nanomaterials such as diamondoids (Oshima et al. 2012).

Efficient transfer of reactive species generated by plasma to liquid targets depends on the interfacial area available for mass transfer. A high gas–liquid interfacial area is desired in many industrial mass transfer applications such as distillation, absorption, hydrogenation and bioreactors (Arjunwadkar et al. 1998). High gas–liquid interfacial area generated using microbubbles has been used in macroscale plasma reactors for pretreatment of biomass (Wright et al. 2018a), increasing the solubility of microcrystalline cellulose (Bandulasena et al. 2018) and E. coli disinfection in synthetic wastewaters (Wright et al. 2019). Similarly, gas–liquid interfacial area inside microfluidic devices can be increased by in situ production of microbubbles. Various device geometries, such as flow-focusing junctions, T-junctions, co-flow arrangements and cavitation nozzles have been developed to produce monodispersed microbubbles in microchannels (Garstecki et al. 2005; Raven et al. 2006; Peyman et al. 2012). The formation mechanisms of microbubbles in these devices have been extensively investigated, and the effects of key parameters, such as geometric features, fluid properties and operating gas and liquid flow rates, on the mechanics and the dynamics of bubble formation (e.g., bubble growth rate, detach time, bubble size and distribution) have been studied both theoretically and experimentally (Wang et al. 2017; Dollet et al. 2008).

In this study, a novel microfluidic device that combines the formation of monodisperse microbubbles and plasma generation into a single microchip has been developed, thereby enhancing transfer rates of ROS across the gas–liquid interface of the bubbles. More specifically, an on-chip DBD plasma system was built near the flow-focusing junction to generate a He/O₂ plasma at the monodisperse microbubble generation site. ROS such as O₃, O, ^·OH and ¹O₂ generated by the plasma were transferred to the liquid via microbubbles (Park et al. 2010). The plasma is discharged at the immediate vicinity of the gas–liquid interface of the microbubbles to enhance mass transfer efficiency of both the short-lived and long-lived plasma species into the liquid phase. Microbubbles produced at high number densities provide high surface area-to-volume ratios, disperse the reactive species efficiently under laminar flow conditions and achieve required transfer within a shorter reaction channel length. In the first stage of this study, bubble generation process was characterised by varying the gas and the liquid flow rates in the absence of plasma. Then, bubble generation under plasma discharge was studied to elucidate the effect of plasma on bubbles generation and to identify effective strategies to control the bubble formation process. The second stage of the study involved a chemical reaction between the transferred ROS and an organic dye in order to analyse the device performance. This microbubble chip integrated with plasma has a potential in various controlled microscale applications including plasma–liquid electrochemistry, nanoparticle synthesis and organic synthesis.

Methodology

Microfluidic chip design and fabrication

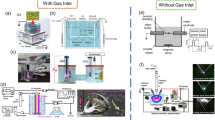
The design of the microfluidic device for in situ plasma discharge and microbubble generation is shown in Fig. 1. The device contains a gas inlet, a liquid inlet and an outlet for the bubbly flow. The gas flow that enters the chip is first passed through two aluminium strips covered by polydimethylsiloxane (PDMS) dielectric barriers for the DBD plasma formation. Immediately after the plasma generation zone, gas flows through a nozzle to reach the flow-focusing site where bubbles are generated. The liquid stream entering the microchip is split into two equal steams at the entrance and directed to the bubble generation nozzle from either side of the gas jet. Bubbles formed at the orifice are then elongated and broken-up at the entrance to the collection chamber.

Fig. 1

Design of the microchip a plan view of the microchip, b end elevation of the microchip, c channel dimensions, d dimensions near the bubble generating site and e microscopic image of the bubble formation site

The design shown in Fig. 1 was fabricated using standard photolithography and PDMS replica moulding techniques (Lin et al. 2002). The channels for the fluid flow were created by bonding cured PDMS layer (500 µm) with moulded channels to a thin glass cover slide (150 µm). Bonding of the glass and PDMS layers was carried out by exposing the clean PDMS and glass surfaces for a sufficient time to seal completely. All the microchannels in the device are 150 µm deep and have a rectangular cross section. Following the formation of the channels for the fluid flow, aluminium electrodes (50-µm-thick tape) were positioned outside the chip near the bubble generating nozzle and fixed into position by introducing two further PDMS layers as shown in Fig. 1b. This configuration provides a vertical separation distance of 800 µm between the aluminium electrodes. Figure 1c, d provides dimensions of the microchannel network.

Experimental set-up

The experimental set-up is shown in Fig. 2. The system consists of the microfluidic device described in Sect. 2.1, a syringe pump (KD scientific 100 legacy), a mass flow controller (Alicat MC 100 sccm), a white light LED source (Kern Dual Fiber Unit LED), a high-speed camera (Photon Fastcam, M2.1) with microscope lens (INFINITY KC IF-3), an in-house built full-bridge resonant high voltage–power supply, a computer, an oscilloscope (Tektronix DPO 4104B), a high voltage probe (Tektronix P6015), a 220-nF capacitor (WIMA MKS 4-R) and a low voltage probe (Pico, TA150). For all the experiments, a syringe pump was used to pump (flow rate range from 120 to 180 ml/h) liquid solutions into the microchip, while the mass flow controller was used to supply (volumetric gas flow rate range from 0.2 to 2 sccm) gas into the microchip. The microbubble formation and pinch-off were then captured and recorded with the high-speed camera. For the experiments with plasma, an AC sinusoidal voltage of 5 kV_rms at 24 kHz was applied across the gas channel continuously using the high voltage–power supply. This set-up was used for both parts of the experimental study, i.e. for microbubble characterisation and mass transfer.

Fig. 2

Experimental set-up for operating the microfluidic device. Gas and the liquid flow rates supplied to the microchip were controlled using a mass flow controller and a syringe pump, respectively. A high voltage supply is connected to the electrode to generate plasma inside the gas channel

Microbubble characterisation

A series of experiments were performed to study the effect of the gas and the liquid flow rates and the plasma discharge on bubble generation. Deionised water containing 1 wt % poly (vinyl alcohol) (PVA) was pumped into the microchip at a flow rate ranging from 120 to 180 ml/h. Simultaneously, helium gas was supplied to the microchip at a flow rate ranging from 0.2 to 2 sccm. The flows were allowed to equilibrate for at least 2 min before images were taken. Microbubbles generated at the orifice and near the collection channel were recorded with the high-speed camera at a frame rate of 3000 fps. Experiments with these flow parameters were then repeated with the plasma discharge present, and images were recorded at the same frame rate. To better understand the microbubble formation mechanism, additional experiments were performed in which images were recorded at a higher frame rate of 10,000 fps. All experiments were repeated at least three times, and the error bars represent the standard deviation of these repeats.

Microbubble size distributions were determined from the images recorded near the collection chamber. For each experiment, a minimum of 200 microbubbles were captured. To automate the bubble sizing procedure, a MATLAB™ code was developed to detect the outer edge of the microbubbles. At least 80% of the bubbles were recognised by the code automatically. The code calculated the circumference of the microbubble projections on the images which was then used to estimate the bubble diameters. The size distribution was then obtained, including the average diameter and the polydispersity index ($\sigma$). Bubble images recorded at high frame rate and high magnification were then analysed to understand the bubble formation mechanism and production of daughter bubbles.

To study the effect of surfactant concentration on microbubble size produced, PVA concentration in the solution was varied from 1 critical micelle concentration (CMC) to 5 CMC, and experiments were carried out at a gas flow rate of 0.8 sccm and a liquid flow rate of 150 ml/h with and without the plasma. Surface tension and viscosity of the solutions were measured using a drop shape analyser (KRUSS, DSA100) and a rheometer (TA instruments, Discovery HR-3), respectively.

Mass transfer experiments

Mass transfer performance of the microfluidic device was determined by degrading indigo dye solutions with the reactive oxygen species (ROS) produced by the plasma at different operating conditions. An indigo stock solution was made from 0.6 g potassium indigo trisulphonate (C₁₆H₇K₃N₂O₁₁S_3, molar mass: 616.72 g/mole) dissolved in 1 litre of deionised water. A 50 ml of the stock solution was then mixed with 200 ml of deionised water (making a solution of 120 ppm indigo concentration), and then, 1% PVA was dissolved into the solution. The solution was pumped into the microfluidic reactor at a flow rate ranging from 120 to 180 ml/h, while He and O₂ gas mixture (20% He) was supplied into the reactor at a flow rate ranging from 0.2 to 2 sccm. The plasma was ignited, and 5 ml of the treated indigo solution was collected at the outlet of the reactor into a vial for analysis (Scheme 1).

Scheme 1

Chemical transformation of indigo trisulphonate in the presence of ozone (Bader and Hoigné 1981)

In the presence of reactive oxygen species (ROS), potassium indigo trisulphonate undergoes chemical reaction by breaking the C=C bond in the dye molecules and forming potassium isatin-5-sulphonate and potassium isatin disulphonate as shown in Eq. 1. This reaction decolourises the indigo dye; hence, by measuring the colour change, the extent of the mass transfer/reaction can be quantified. This colour change can be quantified by the change in absorption at 605 nm (Bader and Hoigné 1981). This indigo reaction has been widely used to characterise other plasma–liquid systems (Gao et al. 2013; Wright et al. 2018b; Ruma et al. 2018). Firstly, a calibration curve was obtained by measuring the transmitted light intensity for known dilutions of the initial indigo dye solution. The intensity of transmitted light detected at 605 nm wavelength was recorded for each diluted fraction. Then, for the mass transfer experiments, treated indigo solutions collected from the reactor were subjected to the above procedure to measure transmitted light intensity. The concentration of the indigo compound can then be analysed using Beer–Lambert law as shown in Eq. 2 (Bader and Hoigné 1981).

$$ A = \log_{10} \frac{{I_{0} }}{I} = \varepsilon cl , $$

(2)

where A is the absorbance, $I_{0}$ is the light intensity at 605 nm wavelength (for indigo), I is the transmitted light intensity measured,$\varepsilon$ is the molar absorption coefficient, $c$ is the concentration and $l$ is the optical path length through the solution. The absorbance is therefore proportional to the indigo concentration, and the proportionality constant ($\varepsilon l$) was determined from the known concentration of a non-treated indigo solution prior to the experiments. This technique was used to quantify the indigo concentration in the solution after a single pass through the device for all operating conditions mentioned above. The reaction time was assumed to be equal to the residence time of the fluid mixture (i.e. liquid and bubbles) in between the orifice and the collection point. The residence time was calculated as the ratio between the total channel volume from the orifice to the tube outlet and the combined fluid flow rate (volumetric gas flow rate + liquid flow rate).

Power calculation

All plasma experiments were performed with the same input voltage (5 kV_rms). The power delivered to the plasma under this condition was measured using the Lissajous method (Taglioli et al. 2016; Yehia 2016), with a high voltage probe recording the voltage applied to the device and a low voltage probe recording the voltage across the series sensing capacitor on the low voltage side. Differences in the probe delays were compensated for in the power calculation and for all gas flow conditions considered in this study, and the power was found to be 120 mW ± 12%.

Results and discussion

Effect of operating parameters on the microbubble size

It was observed that most of the microbubbles generated in the device were compressed between the top and the bottom surfaces of the microchannel, because the bubbles generated were larger than the depth of the microchannel. Bubbles smaller than the height of the channel (only a very small fraction of the total bubble population) adhered to the top surface of the channel and deformed due to the buoyant force. Therefore, all bubbles observed in the experiments were not spherical. It was assumed that the contact angles of the squashed bubbles on the channel walls (both on the PDMS and the glass surface) were very low (≈ 2 deg) (Abeywickrema et al. 2018). Therefore, the shape of the squashed microbubbles was considered to be a symmetrical ellipsoid (oblate spheroid). The diameters measured and reported in this study are equivalent to two equal semi-axis length of the spheroid, which is known as the equatorial diameter, $d_{\text{e}}$. The depth of the microchannel (150 µm) was taken as the height (h) of the spheroid. The validity of this assumption was verified prior to bubble size analysis.

Considering a case where monodisperse microbubbles (polydispersity index $\sigma$ < 4%, defined later) are produced within the device. The volume of an oblate spheroid ($V_{\text{s}}$) is given by

$$ V_{\text{s}} = \frac{1}{6}\pi d_{\text{e}}^{2} h, $$

(3)

Then, the total volume of gas ($V_{b}$) within $n$ bubbles generated in time $t^{\prime}$ can be calculated as

$$ V_{\text{b}} = \frac{1}{6}n\pi h\overline{{d_{e}^{2} }} , $$

(4)

where $\overline{{d_{e}^{2} }}$ is the average of $d_{\text{e}}^{2}$ for the bubbles generated during time $t^{\prime}$.

If the shape of the bubbles within the microchannel can be represented by oblate spheroid, total volume of bubbles calculated using Eq. 4 should be equal to the gas discharged by the mass flow controller during the bubble generation process ($V_{\text{inlet}}$). Since the device is operated at low pressure (~ 1 bar), any volume change of the gas can be neglected. Volume change of gas due to humidity change was also neglected due to low-temperature (20 °C) operation. The total amount of gas discharged during bubble generation process is calculated as

$$ V_{\text{inlet}} = t^{\prime}Q_{\text{ig}} , $$

(5)

where $Q_{\text{ig}}$ is the volumetric gas flow at the mass flow controller at standard conditions. The operating time $\left( {t^{\prime}} \right)$ for this analysis was obtained by measuring the number of frames to produce 20 microbubbles and multiplying that by the time between two frames (0.1 ms when images recorded at 10,000 fps). This analysis was carried out at a liquid flow rate of 150 ml/h with the gas flow rate ranging from 0.2 sccm to 1 sccm, as these operating conditions produce a single bubble population with a low polydispersity index. Gas volumes calculated by Eqs. 4 and 5 are compared in Table 1.

Table 1 Comparison of gas volumes $V_{\text{b}}$ and $V_{\text{inlet}}$ calculated at $Q_{\text{l }}$= 150 ml/h

The difference between the volumes of gas discharged at the mass flow controller and the gas volumes is calculated using image analysis, and Eq. 4 agrees well within 5% for all operating conditions tested. This confirms our assumption that microbubbles recorded in the device are of oblate spheroid shape is valid; hence, average equatorial diameter ($d_{\text{e,av}}$) will be used in reporting bubble sizes produced in the device. Bubble size distributions acquired from image analysis were then used to determine the effects of volumetric gas flow rate, $Q_{\text{ig }}$(flow rate measured by the mass flow controller), and the liquid flow rate, $Q_{\text{l }}$, on the microbubble size generated. Plasma was turned off for the first stage of the study.

Typical bubble generation process at the orifice is shown in Fig. 3. As both the gas and liquid flow into the flow-focusing area, gas–liquid interface forms a narrowing gas jet due to the liquid streams arriving from either side of the nozzle. As the gas–liquid interface passes the orifice (narrowing section) into the collection nozzle, gas expands and starts forming a bubble. Due to liquid drag from either side, the bubble starts to elongate in the flow direction until necking occurs. At this stage, the connection between the bubble and the gas flow is dynamically unstable and leads to bubble break-up. This newly generated bubble is entrained with the liquid flow but moves slower than the surrounding liquid due to viscous dissipation at the bubble–wall contact. The tip of the gas–liquid interface retracts back to the flow-focusing area following a break-up event. Bubbles moving in the collection chamber form highly ordered flowing bubble lattices. This sequence of events completes the cycle for bubble generation at low gas and liquid flow rates. A microscopic image of the bubbles produced in this regime and their respective bubble size distribution is shown in Fig. 4a.

Fig. 3

Microscopic images showing elongation and break-up of bubbles formed at Q_l = 120 ml/h and Q_ig = 1.5 sccm. Four consecutive bubbles generated are denoted as B0, B1, B2 and B3. a B1 is formed, and B0 is elongated. b B1 elongating and B0 stabilising. c B2 detaching and B1 breaking up. d B2 starts to elongate and B1 breaking complete. e B2 elongating. f B3 formed and B2 elongated further. g B3 elongating and B2 stabilising

Fig. 4

Microscopic images of the microbubbles generated and the corresponding bubble size distribution at different operating conditions without plasma (a) $Q_{\text{l}} =$ 120 ml/h and $Q_{\text{ig}} =$ 0.6 sccm, (b) $Q_{\text{l}}$ = 120 ml/h and ${\text{Q}}_{\text{ig}}$ = 1.5 sccm, (c) $Q_{\text{l}}$ = 120 ml/h, $Q_{\text{ig}}$ = 2 sccm and (d) $Q_{\text{l}} =$ 150 ml/h and $Q_{\text{ig}} =$ 2 sccm

However, when the gas flow rate exceeds a critical value at a given liquid flow rate, newly generated bubbles (B1) get squashed between the preceding bubble (B0) and the newly forming bubble (B2)—see Fig. 3c. This leads to elongation of the bubble (B1) in the transverse direction to the flow and could break-up into two or multiple bubbles. This observation agrees with the previous work where the bubble generation mechanism in a flow-focusing system changed into a different regime, when the gas flow rate exceeded a critical value (Garstecki et al. 2004). We believe that this transition occurs due to an increase in bubble density inside the observation chamber, when the gas volumetric flow rate exceeds the critical value for the device while the liquid flow rate is kept constant. There are several forces acting on a bubble that has just been formed (B1)—(i) drag force from the liquid flowing around the bubble, (ii) surface tension force at the top and bottom surfaces of the channel where bubble makes contact with channel walls, (iii) viscous dissipation where a thin film exists between the bubble and the channels, (iv) elastic shape restoring forces and (v) contact pressure force acting within the forming bubble (B2) that exerts a force on the formed bubble (B1). These forces elongate and destabilise bubble B1 and, if high enough (above the critical flow rate), will result in a break-up. The following bubble (B2) will only get elongated (no break-up); hence, this bubble splitting process is alternative. Break-up events that occur at the entrance to the collection chamber can be different depending on the flow parameters used. This could result in several bubble populations for a single experiment as shown in Fig. 4b–d. Let us denote the initial bubble populations produced at the orifice as $P_{0}$. If a single bubble break-up event occurs repeatedly, two daughter bubble populations are produced—$P_{1}^{i}$ (smaller daughter bubbles) and $P_{1}^{j}$ (larger daughter bubbles). High gas and liquid flow rates could lead to two break-up events which lead to four daughter bubble populations—$P_{1}^{i}$ and $P_{1}^{j}$ from the first break-up event and $P_{2}^{i}$ and $P_{2}^{j}$ from the second break-up event.

At $Q_{\text{l }}$ = 120 ml/h and $Q_{\text{ig}}$ = 0.6 sccm, a single bubble population ($P_{0}$) is produced with no break-up events as shown in Fig. 4a. This is the typical outcome at low gas and liquid flow rates. When the gas flow rate is increased to 1.5 sccm (keeping $Q_{\text{l }}$ at 120 ml/h, unchanged), a single repeated bubble break-up occurs. In this special case, daughter bubbles produced are approximately equal in size; therefore, only two bubble populations are produced ($P_{0}$ and $P_{1}$) as shown in Fig. 4b. Images taken at this operating condition show that the daughter bubbles have moved away from the axis of the chamber and form a highly ordered lattice. Further increase in the gas flow rate to 2 sccm leads to unequal daughter bubbles from the single repeated break-up event (Fig. 4c). We believe that this is due to symmetry breaking nature of the bubble splitting process. At high gas and liquid flow rates tested, i.e. $Q_{\text{l }}$ = 150 ml/h, $Q_{\text{ig}}$ = 2 sccm, two repeated bubble break-up events occur with unequal bubble sizes leading to five bubble populations ($P_{1}$, $P_{1}^{i}$, $P_{1}^{j}$, $P_{2}^{i}$ and $P_{2}^{j}$) as shown in Fig. 4d.

The average equatorial diameter ($d_{\text{e,av}}$) and polydispersity index ($\sigma$) for bubble size distributions are shown in Fig. 5. Variations in bubble sizes in a bubble population were calculated using polydispersity index ($\sigma$) defined as

$$ \sigma = \frac{\delta }{{d_{\text{e,av}} }} \times 100\% , $$

(6)

where $\delta$ is the standard deviation of measured equatorial diameters. In cases where daughter bubbles are produced and more than one peak was observed in the bubble size distributions shown in Fig. 4, $\sigma$ was calculated separately for each bubble population and shown in the same figure using arrows leading from the initial bubble populations. For the lower liquid flow rates tested (i.e. 120 and 150 ml/h), $d_{\text{e,av}}$ of the main population increases with $Q_{\text{ig }}$ and a linear relationship is observed. For a given gas flow rate, a higher liquid flow rate always produced the smallest bubbles due to high liquid momentum and drag acting on the forming bubble. Therefore, the microbubble size is dependent on the flow ratio between $Q_{\text{ig }}$ and $Q_{l }$, whereby as $Q_{\text{ig }}$ /$Q_{\text{l }}$ increases, $d_{e,av}$ increases (except for $Q_{\text{l }}$ = 180 ml/h whereby the trend changes after $Q_{\text{ig }}$ exceeds 0.8 sccm). This was expected due to the reduction in the shear stress and elongation when $Q_{\text{l }}$ decreases (Dietrich et al. 2008). Daughter bubbles were produced at $Q_{\text{ig }}$ > 1.5 sccm, $Q_{\text{l }}$ = 120 ml/h and at $Q_{\text{ig }}$ > 2 sccm, 150 ml/h. Transition of the bubble generating regime for daughter bubble production started at a lower $Q_{\text{ig }}$ for $Q_{\text{l }}$ = 120 ml/h compared to that of $Q_{\text{l }}$ = 150 ml/h, and this could be due to the higher density of bubbles at the entrance to the collection chamber compressing the newly formed or forming bubbles as described earlier. In contrast, for the higher liquid flow rates tested (i.e. 180 ml/h), $d_{\text{e,av}}$, increased with $Q_{\text{l }}$ up to $Q_{\text{ig }}$ = 0.8 sccm in a linear manner followed by a gradual drop $d_{\text{e,av}}$ beyond $Q_{\text{ig }}$ = 0.8 sccm. No daughter bubble population was observed at this liquid flow rate. This can be identified as another critical flow rate at which high liquid shear stress breaks up bubbles earlier in the growth phase and produces smaller bubbles that are stable and less susceptible to split in the collection chamber.

Fig. 5

a Effect of the gas and the liquid flow rate on the average equatorial bubble diameter, $d_{\text{e,av}}$. $P_{0}$ and $P_{1}$ are the main bubble population and the daughter bubble population generated due to bubble break-up, respectively. Arrows indicate the break-up of some initial bubbles (from $P_{0} )$ to daughter bubble populations ($P_{1}^{j}$ and $P_{1}^{i}$). b Effect of gas and liquid flow rate on the variation in bubble sizes quantified using polydispersity index, $\sigma$

The polydispersity index ($\sigma$) for bubble size distributions shown in Fig. 5b varied between 2 and 7% and did not have a clear correlation with the gas flow rate. However, device operated at low liquid flow rates (120 ml/h and 150 ml/h) produced the least variability, where $\sigma$ < 5% for all gas flow rates. $\sigma$ for daughter bubble populations was reported separately on the same graph, and all values are below 5%. This result clearly demonstrates the capability of the device to generate monodisperse microbubbles. For the higher liquid flow rate of $Q_{\text{l }} =$ 180 ml/h, operating condition at which no new bubble populations were observed, an increase in $\sigma$ was observed for $Q_{\text{ig }}$ > 0.8 sccm. Under these flow conditions, bubbles are significantly smaller than the bubbles observed at the lower liquid flow rates tested; hence, the bubble generation frequency increases dramatically. This limits the time for the gas–liquid interface to retract completely after bubble necking; therefore, variation in bubble growth time can be expected.

Effect of plasma on bubble generation

As the main purpose of the device is to transfer reactive species generated by the plasma to the liquid phase, it is essential to study the effect of plasma discharge on the microbubble generation. $d_{\text{e,av}}$ measured with the plasma at various gas and liquid flow rates are shown in Fig. 6a. The trends observed in this graph are almost identical to that of with no plasma discharge, whereby an increase in the ratio $Q_{\text{ig }}$/ $Q_{\text{l }}$ leads to an increase in $d_{\text{e,av}}$. However, the magnitude of $d_{\text{e,av}}$ values has changed for all inlet gas flow rates. Calculations confirmed that all $d_{\text{e,av}}$ values increased by 5–8% as a result of the plasma. A comparison of this effect is shown in Fig. 6b, where $d_{\text{e,av}}$ values are compared with and without the plasma effect at $Q_{\text{l }}$ = 150 ml/h. It is interesting to note that daughter bubbles were produced at $Q_{\text{ig }} \ge$ 1.5 sccm with plasma compared to that of operation at $Q_{\text{ig }} \ge$ 2 sccm without plasma. A further study was conducted to investigate the change in microbubble formation time and the volumetric gas flow rate at the bubble forming orifice ($Q_{\text{or}}$) when operated with the plasma discharge.

Fig. 6

a Effect of the gas and the liquid flow rate on the average equatorial bubble diameter, $d_{\text{e,av}}$ with Plasma. b) Comparison of bubble size produced with and without plasma at $Q_{\text{l }}$= 150 ml/h. $P_{0}$ and $P_{1}$ are the main bubble population and the daughter bubble population generated due to bubble break-up, respectively. Arrows indicate the break-up of some initial bubbles (from $P_{0} )$ to daughter bubble populations

Volumetric gas flow rate at the orifice ($Q_{\text{or}}$) was determined as before by calculating the volume of 20 bubbles produced in the device and time for their formation in the presence of plasma. Table 2 and Fig. 7 show that plasma discharge increases the volumetric gas flow rate by 17–25% due to thermal expansion. Gas is supplied to the device at ~ 1 bar and 20 °C in all experiments, but as the gas flows through the plasma generation zone gas temperature increases. This leads to an increase in the volumetric gas flow rate at the orifice ($Q_{\text{or}}$ at a temperature of $T_{\text{or}}$) compared to the inlet gas flow supplied by the mass flow controller ($Q_{\text{ig }}$ at 20 °C). The temperature of the gas plasma ($T_{\text{plasma }}$) depends on various factors such as geometric features of the device, electric field applied, material properties and gas flow rate, but most DBD plasmas operate in the temperature range of 40–150 °C (Förster et al. 2005; Joussot et al. 2010; Wei et al. 2011; Daeschlein et al. 2012). Due to the heat losses through the microchannel walls, $T_{{{\text{or}} \ne }} T_{\text{plasma}}$.

Table 2 Comparison between $Q_{\text{ig}}$ and $Q_{\text{or}}$ at $Q_{\text{l }}$ = 150 ml/h with plasma

Fig. 7

Percentage volumetric gas flow rate increase due to plasma and estimated gas temperature at the orifice for $Q_{\text{l }}$= 150 ml/h and various gas flow rates

In addition to the thermal expansion of the gas, several other factors associated with the plasma could affect bubble generation. Gas flow through a plasma is unstable due to micro-discharges and shear instabilities (Lietz et al. 2017), and this could lead to high variability in the bubbles generation process. However, $\sigma$ for microbubbles produced with plasma varied between 2 and 7% in this study. It is also reported that surface tension could be affected by the plasma species dissolved in the liquid (Yoon et al. 2018; Sommers et al. 2011) and as a consequence could alter bubble generation process. To ascertain whether these effects played a role in the bubble generation process in addition to thermal expansion, $d_{\text{e,av}}$ was plotted against the flow rate at the orifice ($Q_{\text{or}}$) for both with and without plasma at 150 ml/h. In contrast to Fig. 8a, where $d_{\text{e,av}}$ vs $Q_{\text{ig }}$ graphs for operation with plasma and without plasma are separate, $d_{\text{e,av}}$ vs $Q_{\text{or}}$ graphs shown in Fig. 8b overlapped. This suggests that the change in volumetric gas flow rate by the plasma discharge was the main factor that affected bubble size. The gas temperature at the orifice ($T_{\text{or}}$) can be estimated by using combined ideal gas law as shown in Eq. (7).

$$ \frac{{P_{1 }^{'} V_{1} }}{{T_{1} }} = \frac{{P_{2}^{'} Q_{\text{or}} }}{{T_{\text{or}} }}, $$

(7)

where $P_{1}^{'}$, $V_{1}$ and $T_{1}$ are pressure, volumetric flow rate and temperature of the gas at the inlet of the device and $P_{2}^{'}$, $Q_{\text{or}}$ and $T_{\text{or}}$ are that of at the orifice, respectively. The pressure change due to plasma discharge was assumed to be negligible for these calculations. Figure 7 shows that the percentage increase in the gas flow rate from $Q_{\text{ig}}$ to $Q_{\text{or}}$ is proportional to $T_{\text{or}}$ and combined with the results shown in Fig. 8b provides evidence to confirm that the bubble size increases under plasma operation was due to the thermal expansion of the gas.

Fig. 8

a Comparison of $d_{\text{e,av}}$ Vs $Q_{\text{ig }}$ measured with and without plasma at $Q_{\text{l }}$= 150 ml/h and b effect of the volumetric gas flow rate at the orifice ($Q_{\text{or}}$) on $d_{\text{e,av}}$ with and without plasma at $Q_{\text{l }}$= 150 ml/h

Effect of surfactant concentration

Surfactant (PVA) was dissolved in all test solutions to obtain stable microbubbles and reduce bubble coalescence. Surfactants reduce the free energy required to produce bubble surfaces by reducing the interfacial surface tension (Langevin 2017). Since test solutions used in the experiments contained PVA at a concentration of 1 CMC or above, measured surface tension was 45 mN/m for all solutions. However, viscosity increased gradually with CMC and the results are shown in Fig. 9. It was observed that the average diameter of the bubbles decreases as the viscosity increases for both cases (i.e. with and without plasma), when the fluid flow rates were kept constant. These results agree with droplet formation in a T-shaped microchannel (Xu et al. 2006). It is possible that both the viscosity increase and the change in dynamic surface tension associated with increasing surfactant concentration contributed to this effect. Furthermore, the difference in average microbubble size produced for the two cases was reduced at high CMC values. This result suggests that liquid viscosity is a control parameter that can be manipulated to optimise the bubble size for mass transfer when operated with the plasma.

Fig. 9

Average equatorial diameter ($d_{\text{e,av}}$) of the microbubbles produced at $Q_{\text{ig }}$= 0.8 sccm and $Q_{\text{l }}$= 150 ml/h with and without plasma and viscosity of the liquid at different surfactant concentrations

Mass transfer of reactive species

Mass transfer performance of the microfluidic device was evaluated by measuring the degradation of indigo solutions for single pass treatments. The results are shown in Fig. 10. For all three liquid flow rates tested, the highest indigo degradation occurred at $Q_{\text{ig}} \approx$ 0.8 sccm, while the lowest dye degradation occurred at $Q_{\text{ig }}$ = 0.2 sccm. As the gas flow rate through the plasma generation zone increases, concentration of reactive species in the plasma effluent is expected to increase proportionately. However, since the power input to the plasma is constant (120 mW ± 12%), concentration of reactive species in the gas effluent is expected to plateau at high gas flow rates. Furthermore, we found that microbubble size increases with $Q_{\text{ig }}$ (as shown in Fig. 6a); hence, the mass transfer rates could be affected. Due to these competing effects, decolourisation percentage at $Q_{\text{ig }} \ge 0.4$ observed in Fig. 10 is nearly constant for all liquid flow rates. The difference in decolourisation percentage observed at various liquid flow rates in Fig. 10 could be due to several reasons. Consider the case where gas flow rate is kept constant and the liquid flow rate is increased gradually. Firstly, the residence time of the liquid in contact with the bubbles will decrease providing less time for mass transfer. Secondly, high liquid throughput treats a higher liquid volume within a given time; therefore, concentration reduction of indigo will be less compared to that of at low $Q_{\text{ig }}$. Finally, bubble size decreases with the liquid flow rate as shown in Fig. 6a and will affect mass transfer rates.

Fig. 10

Effect of gas and liquid flow rates on concentration reduction in the indigo solutions

In Fig. 10, decolourisation percentages reported at each liquid flow rate treated different volumes of liquid in a given time. In order to compare the transfer rate of reactive species under different operating conditions, the amount of dye degraded per a unit time should be considered. Figure 11 is plotted by multiplying the percentage decolourisation with the respective liquid flow rate under which the experiment was carried out. Overlap of graphs for different liquid flow rates suggests that the influence of the liquid flow rate on the mass transfer rate is negligible. Slight drop in degradation rate at the higher liquid flow rate may be attributed to insufficient residence time of the liquid in the device for mass transfer. Figures 10 and 11 do not provide a clear correlation between the bubble size produced and mass transfer as mixing patterns at the orifice and bubble lattices formed at the collection chamber may also play a part in mass transfer.

Fig. 11

Average indigo decolourisation rate calculated by the percentage degradation multiplied by the liquid flow rate against the inlet gas flow rate

In designing a microfluidic device for generation and transfer of reactive species, it is useful to know the volumetric mass transfer coefficient ($K_{\text{L}} a$). Concentration measurements of species are generally used with Eq. 8 to estimate the $K_{\text{L}} a$, where $C_{i}^{*}$ is the physical solubility of species ${\text{i}}$ in the solution, $C_{\text{i, inlet}}$ and $C_{{i , {\text{outlet}}}}$ are liquid phase concentration of species $i$ at the inlet and outlet and $t$ is the residence time (Yue et al. 2007).

$$ K_{\text{L}} a = \ln \left( {\frac{{C_{\text{i}}^{*} - C_{\text{i, inlet}} }}{{C_{\text{i}}^{*} - C_{\text{i, outlet}} }}} \right) \cdot \frac{1}{t}. $$

(8)

In this study, several plasma species were produced and transferred to the solution, and most of them are known to decolourise the dye. In order to estimate the $K_{\text{L}} a$ values for each species, separate concentration measurements are required. These measurements are difficult as most reactive species require specific probes that selectively measure their concentration. Furthermore, short lifespan of highly reactive species makes it difficult to detect them in the bulk liquid as their effective diffusion lengths vary from ~ 10⁻⁸ to 10⁻⁴ m (Liu et al. 2015). Even though the indigo decolourisation percentages reported in Fig. 10 are useful in comparing mass transfer efficiency at different operating parameters, these results cannot be used to determine $K_{\text{L}} a$.

Decolourisation of indigo dye presented in this study is comparable to previous studies reported in the literature. For instance, Ruo-bing et al. (2005) and Gao et al. (2013) achieved a discoloration rate of 40% with a 20-min treatment and 99% with a 15-min treatment in a batch reactor, respectively. At the optimal conditions, this study achieved up to 60% decolouration within 5–10 s of treatment using the combined plasma microbubble chip developed. This result clearly demonstrates the potential of this microfluidic reactor for transferring reactive species continuously into a target liquid.

Conclusions

A microplasma reactor and a flow-focusing microbubble generator have been integrated into a single microfluidic chip for efficient transfer of reactive species generated by the plasma to the liquid phase. Proximity of plasma discharge to the gas–liquid interface was a key feature of the device to maximise transfer short-lived species. Monodisperse microbubbles were generated in the range of 135–350 µm depending on the flow parameters. For the low liquid flow rates tested (120, 150 ml/h), a linear positive relationship was found between the average bubble diameters and the inlet gas flow rate. At the higher liquid flow rate tested (180 ml/h), bubble size increased linearly with the inlet gas flow rate up to a critical value after which the bubble size decreased gradually. Depending on the liquid flow rate, there was a critical inlet gas flow rate at which daughter bubbles started to appear due to high bubble density at the entrance to the collection chamber. Plasma discharge led to an increase in the microbubble sizes produced mainly due to the thermal expansion of the gas. At surfactant concentrations above the critical micelle concentrations (CMC), microbubble size decreased with the surfactant concentration due to an increase in the liquid viscosity. Decolourisation of indigo dye depended on the operating conditions used in the experiment. At the optimal operating conditions, i.e. with a liquid flow rate of 120 ml/h and a gas flow rate of 0.8 sccm, 60% decolourisation of indigo dye was achieved in a single pass. Residence time at these operating conditions was ~ 10 s. Efficient transfer of highly reactive species such as reactive oxygen and nitrogen species and free radicals are beneficial in developing new lab-on-a-chip devices and processes. Therefore, the integrated microplasma microbubble reactor developed here has the potential to play a significant role in future microfluidic devices.